Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 1

Ćwiczenie 2 (63)

Procesy fizyczne w lampach elektronowych.

Cel ćwiczenia:

Wyznaczenie termoelektrycznej pracy wyjścia elektronów metodą prostych Richardso-
na dla wolframu.

Zagadnienia:

1. Zjawisko termoemisji.
2. Zależność prądu nasycenia od temperatury katody.
3. Wzór Richardsona - Dushmana.

4.

Prawo Stefana-Boltzmanna.

Pytania kontrolne:

5. Wyjaśnij powstawanie napięcia kontaktowego.
6. Objaśnij wpływ napięcia anodowego na wartość prądu anodowego w lampie elek-

tronowej.

7. W oparciu o pasmową teorię budowy ciał stałych, wyjaśnij zjawisko termoemisji i

różne wartości pracy wyjścia dla różnych metali.

8. Wyjaśnij zasadę obliczania kąta nachylenia prostej z wykresu.
9. Zmiana wartości oporu ciał stałych w funkcji temperatury.

Literatura:
H. Szydłowski, Pracownia fizyczna, PWN, W - wa, 1977, rozdz. 7, & 25.
D. Halliday, R. Resnick, Fizyka, t.II, PWN, W - wa, 1967, str. 162 - 174.
C. Kittel, Wstęp do fizyki ciała stałego, PWN, W - wa, 1970, str. 255 - 257
M. Skórko, Fizyka, PWN, W - wa, 1976, str. 255 - 257.

A. Wprowadzenie.

I. Celem ćwiczenia jest zbadanie zależności natężenia prądu emisji termoelektrycznej
od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu metodą prostych
Richardsona.

Zjawisko termoemisji elektronów.

Zjawisko emisji termoelektrycznej wygodnie jest zbadać przy pomocy lampy elektronowej,
np. AZ-1. Doświadczenie wykazuje, że gęstość prądu nasycenia j

n

( wielkość wyrażająca

prąd termoelektryczny z jednostki powierzchni emitującego układu ) wzrasta nadzwyczaj
szybko ze zwiększeniem temperatury katody.
Teoria kwantowa zjawiska termoelektrycznego pozwala na obliczenie wartości j

n

. Wyraża-

ją wzór Richardsona - Dushmana:

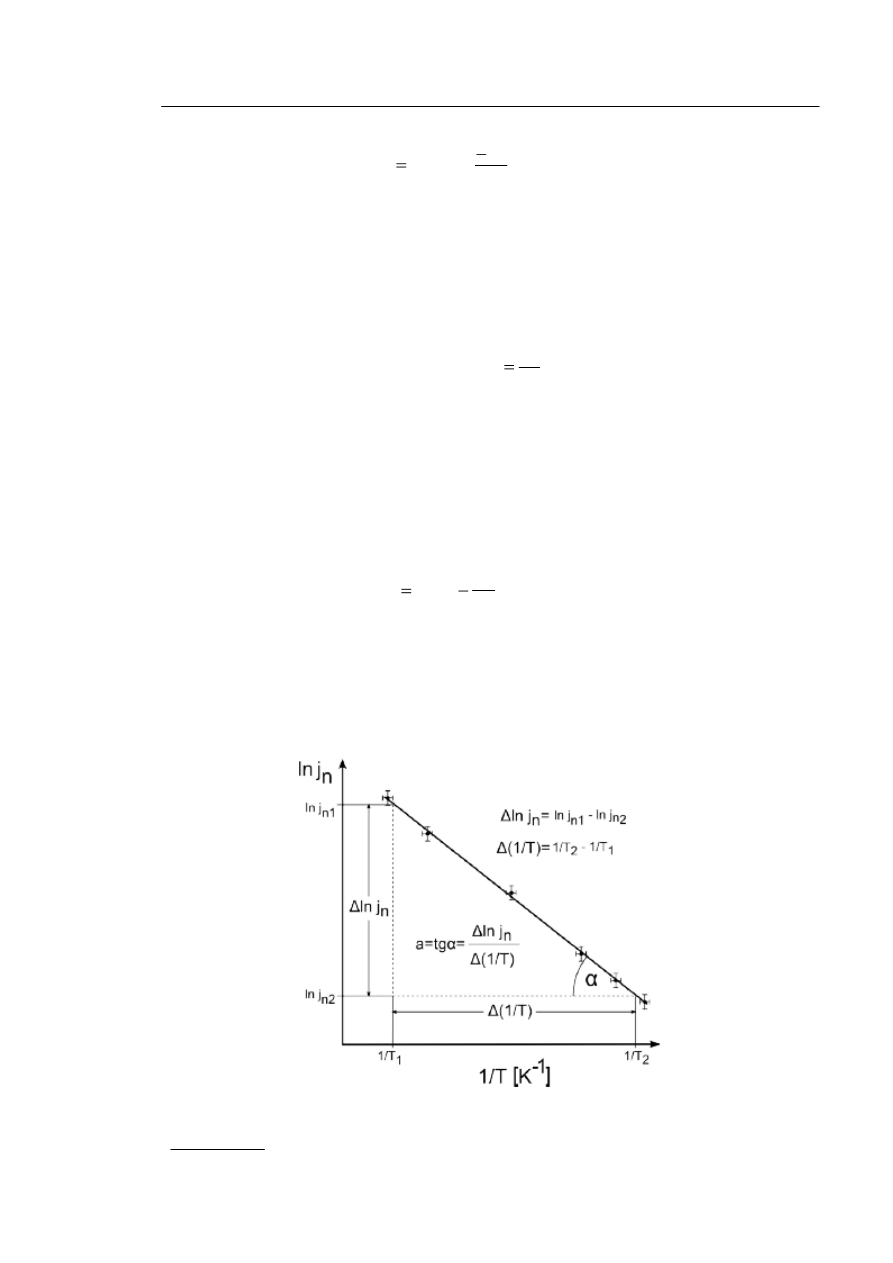
Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 2

kT

W

BT

j

n

exp

2

(1)

gdzie:

T - temperatura bezwzględna w K,
W - praca wyjścia,
k - stała Boltzmanna,

B - stała emisyjna zależna od stanu powierzchni metalu i stopnia jego czystości,

j

n

- gęstość prądu nasycenia,

k

n

n

S

I

j

I

n

- natężenie prądu nasycenia,

S

k

- powierzchnia katody.

II.

Praca wyjścia.

Pomiar prądu nasycenia I

n

oraz znajomość temperatury katody "T" pozwala znaleźć

pracę wyjścia W [ eV]. Logarytmując wzór (1) i dokonując pewnych uproszczeń, uzy-
skujemy:

kT

W

const

j

n

ln

(2)

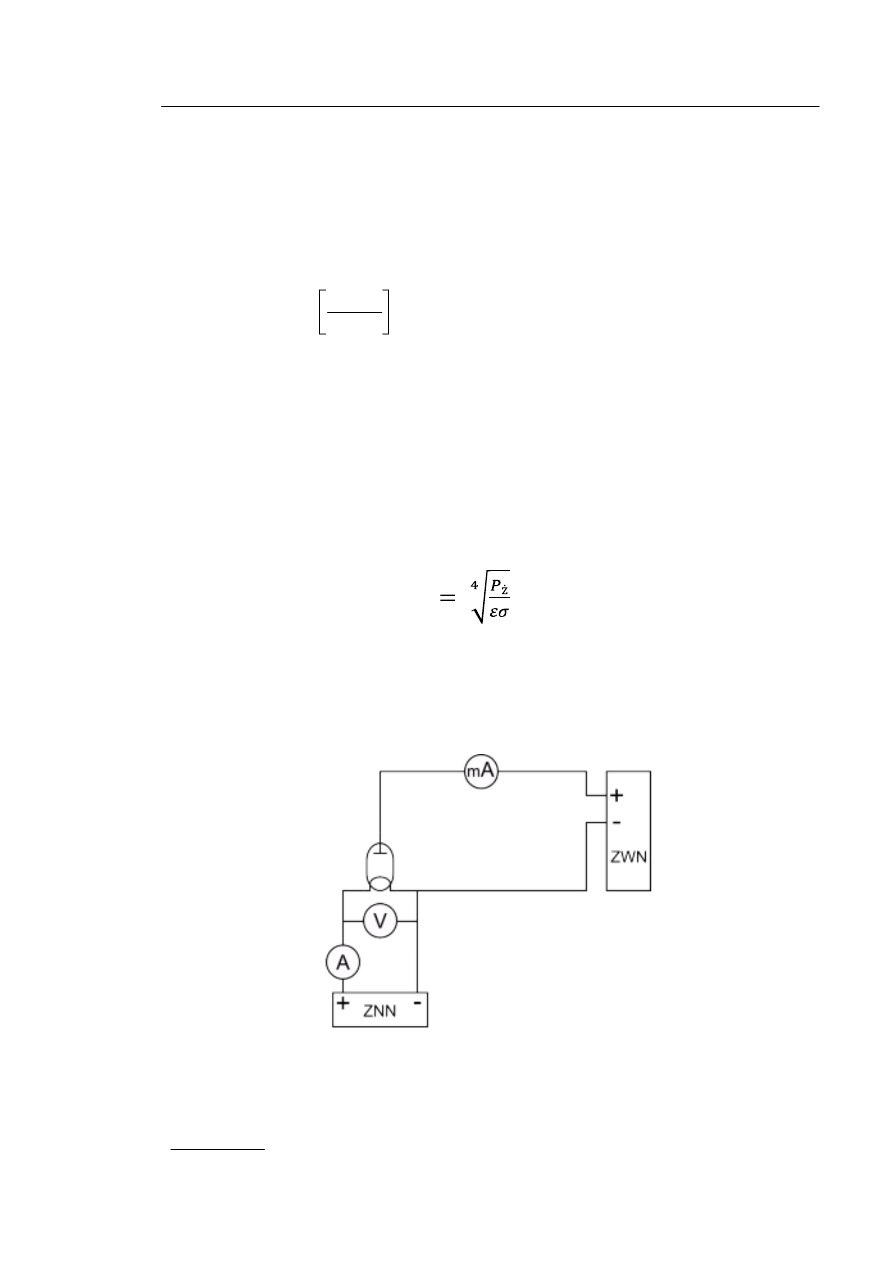
Wykresem zależności (2) w układzie współrzędnych ln j

n

i 1/T jest tzw. prosta Richard-

sona.
Z wykresu i w oparciu o wzór (2) wyznaczamy pracę wyjścia "W"

W = k · tgα (3)

Rys. 1. Prosta Richardsona.

Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 3

III. Wyznaczanie temperatury katody T.

Temperaturę katody wyznaczamy w oparciu o prawo Stefana - Boltzmanna. Moc wypro-
mieniowana przez jednostkę powierzchni katody o temperaturze T wynosi:

P

e =

ε σ T

4

(4)

gdzie:

σ - stała = 5,67 x 10

-12

4

2

K

cm

W

ε - emisyjność całkowita (równa 0,5 dla katody lampy AZ -1).

Przyjmując ( w przybliżeniu ), że cała pobierana przez katodę moc zużywa się na promie-
niowanie, otrzymujemy:

P

ż

=P

e

(5)

gdzie:

P

ż

- tzw. moc właściwa katody czyli moc żarzenia przypadająca na jed-

nostkę powierzchni katody.

Ze wzorów ( 4 ) i ( 5 ) otrzymujemy:

T

=

(6)

B. Przebieg ćwiczenia

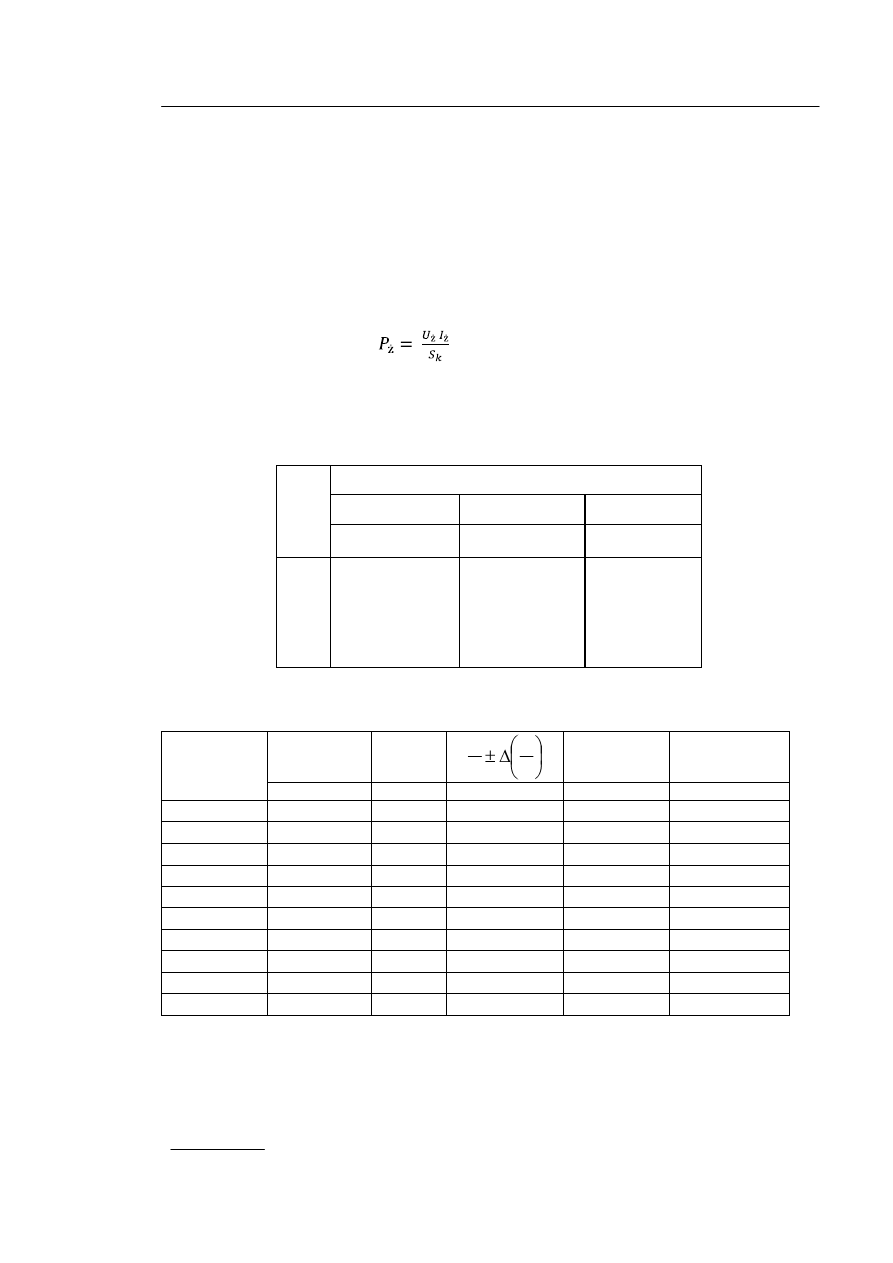
Pomiar prądu nasycenia i mocy właściwej katody należy przeprowadzić w układzie
pomiarowym wg schematu:

Rys. 1.

Schemat układu pomiarowego. ZNN – zasilacz niskiego napięcia w obwodzie żarzenia lampy, V, A

– woltomierz i amperomierz mierzą odpowiednio napięcie i natężenie prądu żarzenia, ZWN – zasilacz
wysokiego napięcia w obwodzie anodowym lampy, mA – miliamperomierz mierzy natężenie prądu ano-
dowego.

Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 4

1. Ustawić napięcie anodowe U

a

= 150 [V] (zasilacz ZS - 1) i dokonać pomiarów prądu

nasycenia I

n

, w zależności od prądu żarzenia I

ż

, poczynając od wartości 0,54 A i zwięk-

szając ją co 0,02 [A] aż do osiągnięcia wartości prądu nasycenia I

n

= 30 mA.

UWAGA! - Po każdej zmianie prądu żarzenia odczekać kilka minut do ustalenia się
temperatury katody.

2. Wszystkie dane pomiarowe zestawić w Tabeli nr 1, a wyniki obliczeń w Tabeli 2.
pamiętając, że

, czyli j

n

= f( P

ż

) .

Tabela 1.

Wyniki pomiarów.

Lp.

U

a

= 150[V]

I

ż

±ΔI

ż

U

ż

± ΔU

ż

I

n

±ΔI

n

[A]

[V]

[mA]

1
2

.
.

n

Tab. 2. Wyniki obliczeń.

Lp.

P

z

± ΔP

z

T

T

T

1

1

j

n

lnj

n

± Δlnj

n

[W]

[

0

K]

[(

0

K)

-1

]

[mA/cm

2]

1

2

3

4

5

6

7

8

9

10

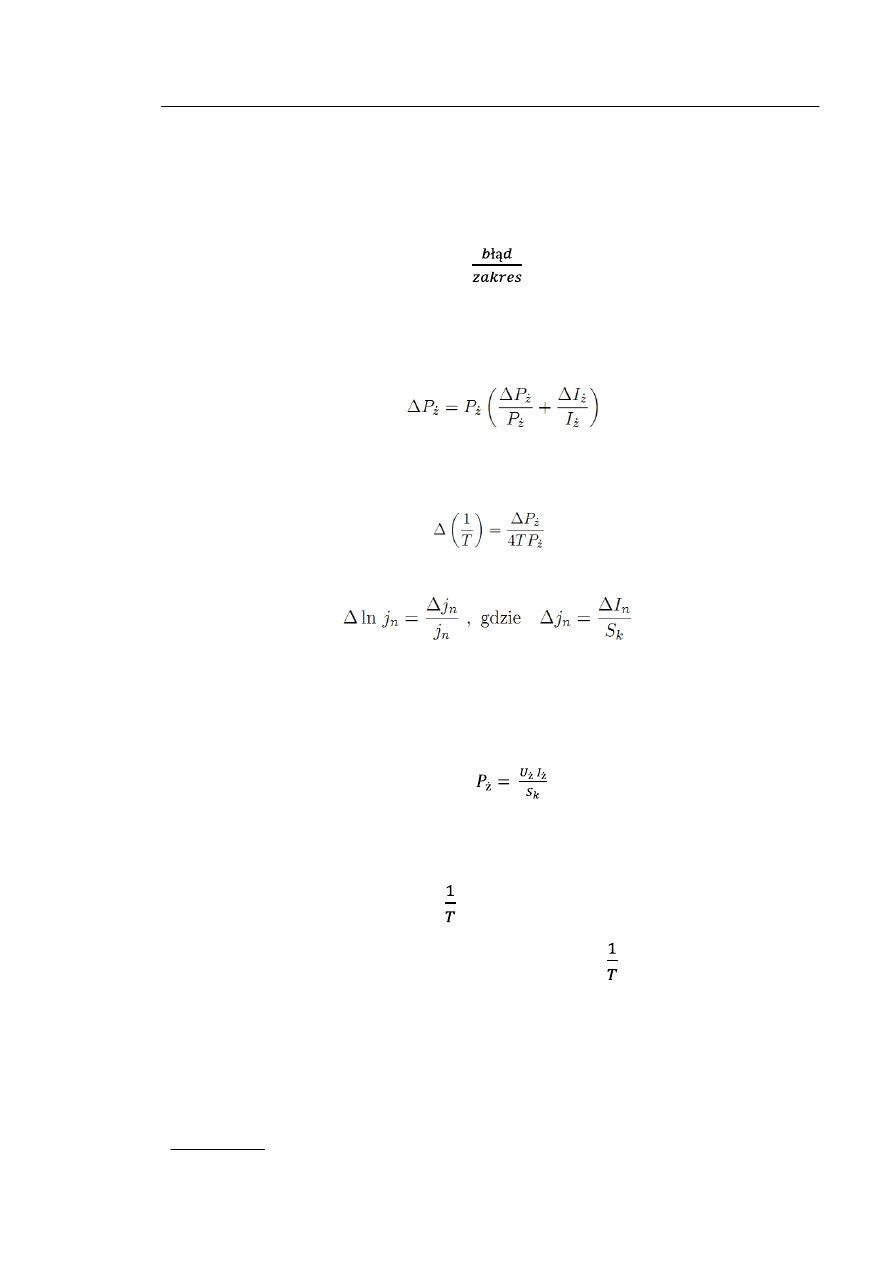
Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 5

C.

Opracowanie wyników:

1. Błędy pomiaru napięcia ∆U

ż

i natężenia ∆I

ż

prądu żarzenia oraz prądu nasycenia

∆I

n

obliczamy w oparciu o klasy mierników wskazówkowych i zakresy pomia-

rowe korzystając z definicji klasy miernika:

klasa =

· 100

i podanych w instrukcji stanowiska formuł dla mierników cyfrowych.

2. Błędy maksymalne ∆P

ż

obliczamy ze wzoru

.

3. Temperaturę katody i jej odwrotność obliczamy z czterema cyframi znaczącymi,

błąd maksymalny odwrotności temperatury obliczamy ze wzoru

.

4. Błąd logarytmu gęstości prądu nasycenia obliczamy ze wzoru

.

Zwróć uwagę, że na Rys.1 również występuje ∆ln j

n

, lecz w innym kontekście.

5. Wykonać wykres j

n

= f(I

ż

).

6. Wykonać wykres zależności j

n

od mocy właściwej

,

dla lampy AZ-1 przyjąć S

k

= 1cm

2

.

7. Ze wzoru (6) dokonać obliczenia temperatury katody T. Przyjąć ε = 0,5.

8. Wykreślić zależność ln

j

n

= f (

)

9. Wyznaczyć w oparciu o wykres zależności ln

j

n

= f (

) i wzór (3) na pracę wyj-

ścia elektronu z katody lampy AZ-1. Podać jej wartość w eV z dokładnością do
dwóch cyfr znaczących (w ćwiczeniu nie wyznaczamy błędu pracy wyjścia) i
porównać i a z danymi z literatury.

10. Na wszystkich wykresach zaznaczyć błędy maksymalne poszczególnych pomia-

rów.

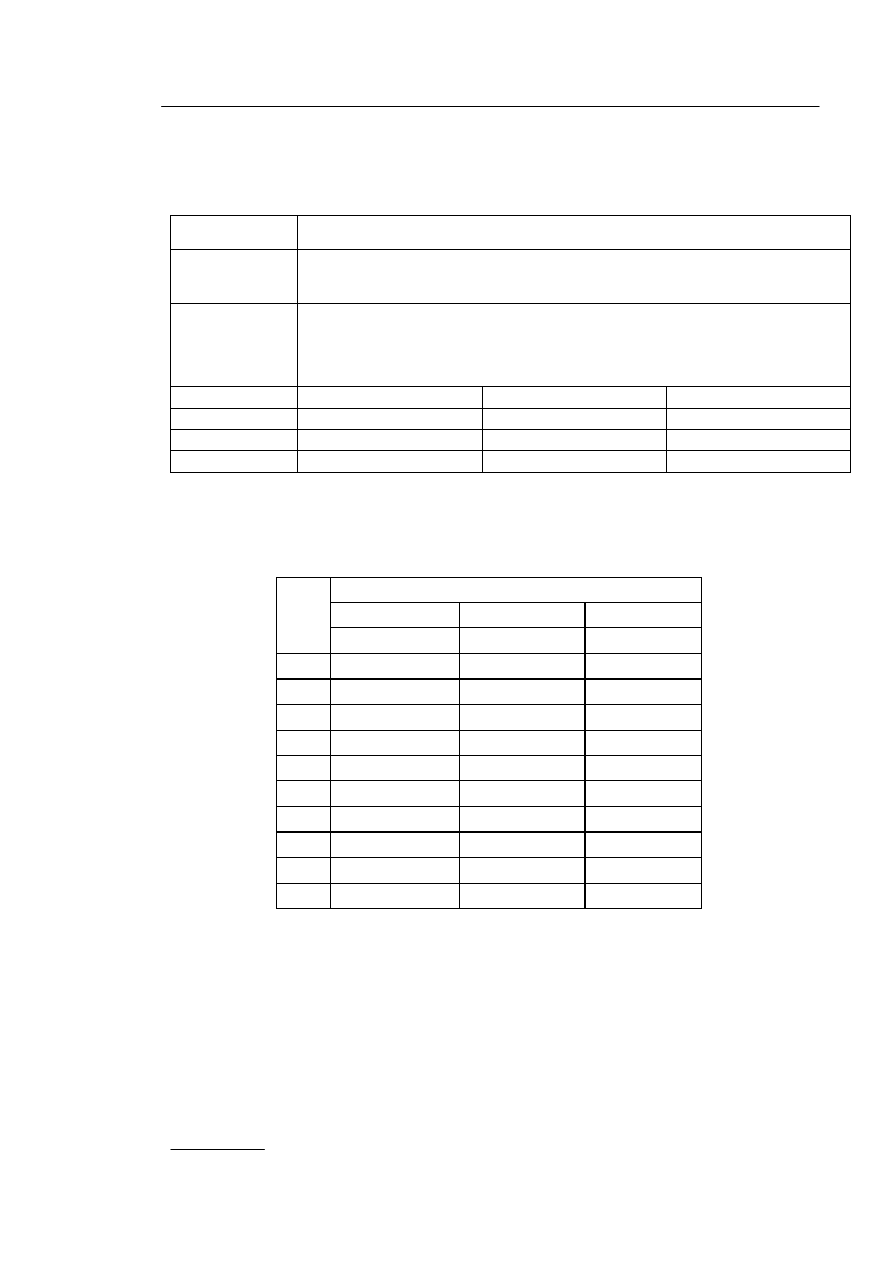
Ćwiczenie 02 (63). Procesy fizyczne w lampach elektronowych.

str. 6

Ćw.2. (63) Procesy fizyczne w lampach elektronowych

Protokół pomiarowy

Ćw.63.

Laboratorium z fizyki

Rok akadem.:

Temat:

Procesy fizyczne w lampach elektronowych

Kierunek:

Grupa:

Imię i Nazwisko:

Ocena

Data Zaliczenia

Podpis

L

S

K

Tab. 1. Wyniki pomiarów.

Lp.

U

a

= 150[V]

I

ż

±ΔI

ż

U

ż

± ΔU

ż

I

n

±ΔI

n

[A]

[V]

[mA]

1

2

3

4

5

6

7

8

9

10