1. Zasada pomiaru
Celem ćwiczenia jest zbadanie zależności natężenia prądu emisji termoelektrycznej od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu metodą prostych Richardsona.
Gęstość prądu nasycenia jn - wielkość wyrażająca prąd termoelektryczny z jednostki powierzchni katody - wzrasta ze wzrostem jej temperatury. Wartość jn wyraża wzór Richardsona - Duchmana:
![]()
(1)
jn - gęstość prądu nasycenia
T - temperatura
Ww - praca wyjścia
k - stała Boltzmana
W interesujących nas zakresach temperatur, decydujący wpływ na wartość prądu nasycenia ma wykładnik potęgowy.Logarytmujac wzór (1) otrzymujemy: ![]()
(2)
Wykresem tej zależności w układzie współrzędnych (lnjn, 1/T) jest prosta Richardsona:
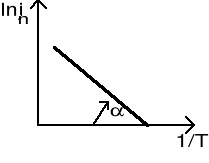
Wyrażenie ![]()
jest współczynnikiem kierunkowym prostej. Z wykresu i w oparciu o wzór (2) można więc wyznaczyć pracę wyjścia Ww:
Ww = k tg
Temperaturę katody można wyznaczyć w oparciu o prawo Stefana - Boltzmana. Moc wypromieniowywana przez jednostkę powierzchni katody o temperaturze T (i jednocześnie moc żarzenia na jednostkę powierzchni katody - zużywana przez katodę na promieniowanie) wynosi:
![]()
= 5,67*10-12 W/cm2K4
= 0,5 (emisyjność całkowita lampy)
Stąd temperatura wynosi:
![]()
2. Układ pomiarowy
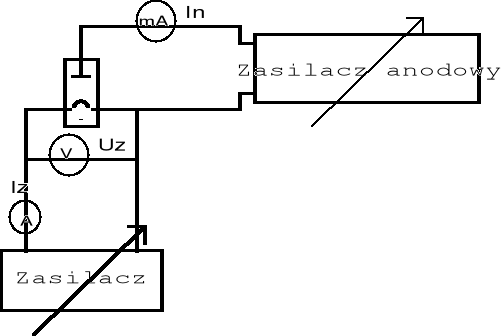
3. Ocena dokładności pojedynczych pomiarów
amperomierz (Iż) - miernik uniwersalny METEX
- zakres: 2 A
- sposób obliczania błędów pomiarowych:
1,2 % wartości wskazywanej + wartość ostatniej cyfry
miliamperomierz (In):
- ilość podziałek: 75 (zakresy: 7,5; 15)
60 (zakres 30)
- klasa dokładności: 0,5
- zakresy: 7,5 mA; 15 mA; 30 mA
woltomierz (Uż):
- ilość podziałek: 60
- klasa dokładności: 0,5
- zakres: 3
4. Tabela wyników
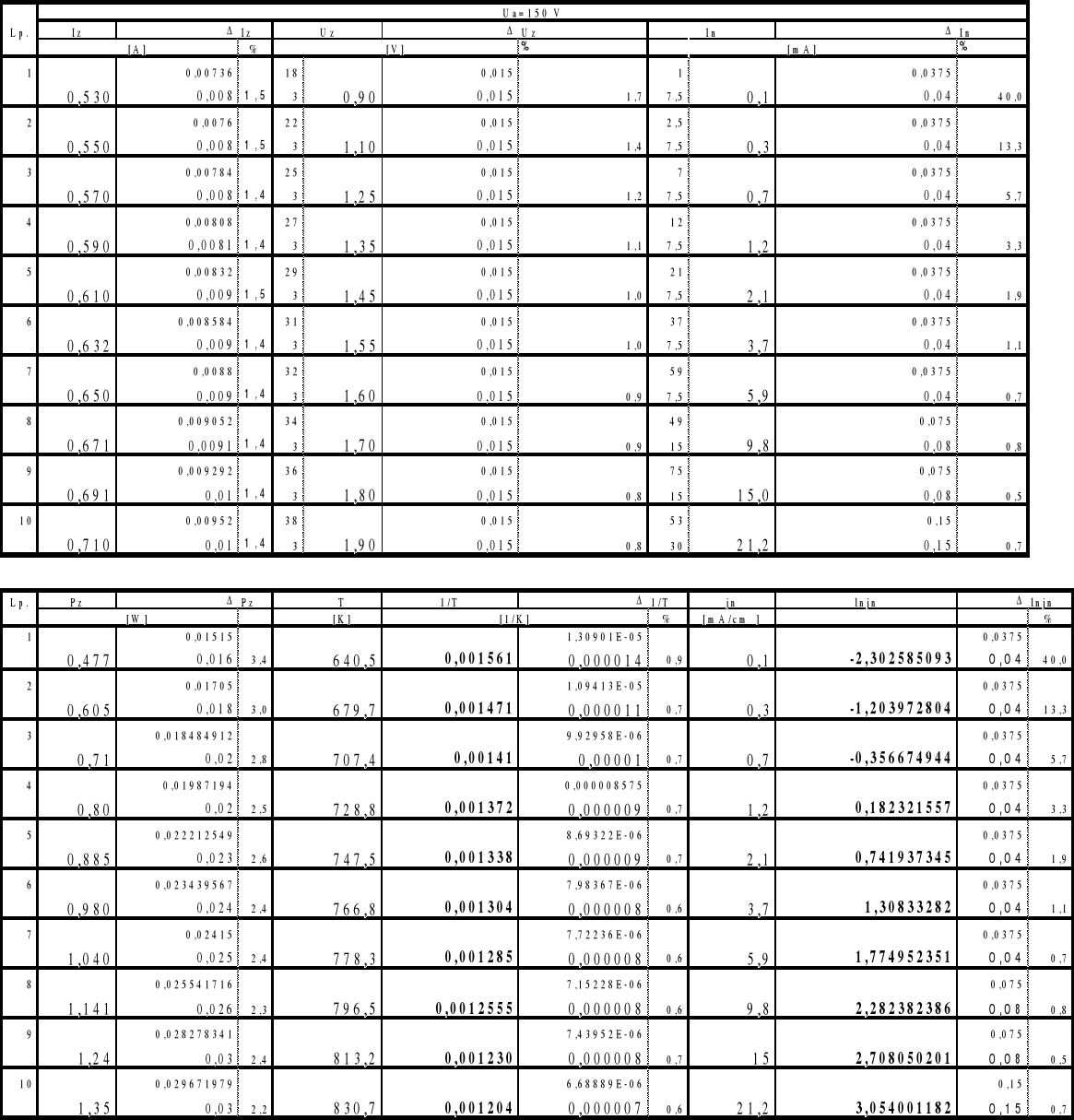
4b. Wykres
Na wykresie lnjn=f(1/T) narysowałem trzy proste:
środkową - przechodzącą przez 9 z 10. prostokątów błędów możliwie najbli- żej punktów pomiarowych ;
oraz dwie proste - pod największym i najmniejszym z możliwych kątów
Tangens kąta nachylenia tych trzech prostych obliczyłem na następującej zasadzie:
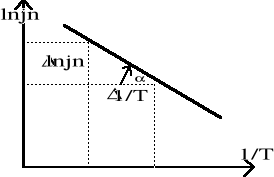
![]()
Tangensy nachylenia posczególnych prostych wynoszą:
![]()
![]()
![]()
5a. Przykładowe obliczenia
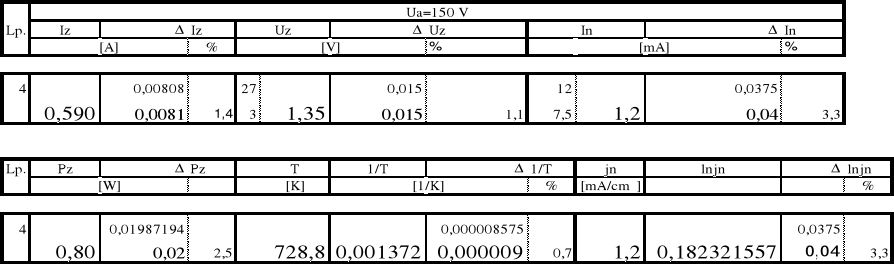
Iż = 0,590 A
Iż= [(1,2%*0,590)+0,001] A = 0,008008 A 0,0081 A
Iż = (0,5900 0,0081) A
Uż :
(zakres 3V; 60 podz.; wychylenie 27 podz.)
Uż = 1,35 V
Uż:
klasa przyrządu: 0,5
Uż= [(0,5*3)/100] V = 0,015 V 0,015 V
Uż = (1,350 0,015 ) V
In:
(zakres 7,5 mA; 75 podz.; wychylenie 12 podz.)
In = 1,2 mA
In:
klasa przyrządu: 0,5
In= [(0,5*7,5)/100] mA = 0,0375 mA 0,04 mA
In = (1,20 0,04 ) mA
![]()
Sk=1 cm2
Pz= 0,59*1,35/1 = 0,7965 W
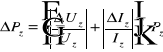
= (0,015/1,350+0,04/1,20)*0,7965 =
0,01987194 0,02
Pż= (0,78 0,02) W
![]()
728,8 K
1/T = 0,001372 /K
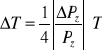
=[(0,25*0,02)*0,001372]/K = 0,000008575 /K
0,000009 /K
1/T = (0,001372 0,000009) /K
![]()
= (1,20/1) mA/cm2 = 1,20 mA/cm2
lnjn= 0,182331557
lnjn=(In/In)*lnjn= 0,04 mA/cm2
lnjn=0,18 0,04) mA/cm2
5b. Obliczenie pracy wyjścia
Korzystając z obliczonych na podstawie wykresu lnjn=f(1/T) tangensów kątów prostych, można korzystając ze wzoru
W = k tg
obliczyć pracę wyjścia elektronów:
k = 1,380662*10-23 J/K
1J = 6,242*1018eV
tg1=14309,675
W = 14309,675*1,380662*10-23 = 1,97567*10-19 J =
= 1,2332132 eV
tg2=15135,112
W =15135,112*1,380662*10-23 = 2,08964*10-19 J =
= 1,3043532 eV
tg3=16973,264
W = 16973,264*1,380662*10-23 = 2,34343*10-19 J =
= 1,462769 eV
6. Dyskusja błędów
Błędy zastosowanych przyrządów pomiarowych podane są w punktach 3. i 5a. W tabeli wyników podane są błędy przed i po zaokrągleniu oraz błąd procentowy. Błędy wielkości złożonych zostały obliczone metodą różniczki logarytmicznej, gdyż wszystkie one są wielkościami iloczynowymi.
![]()
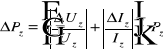
![]()
( i - stałe) 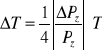
![]()
(Sk - stała) 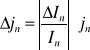
Należy zauważyć, że rozbieżność wartości tangensa kąta nachylenia prostej wynikająca z błędów pomiarowych naniesionych na wykres nie jest duża i nie wpływa znacząco na ostateczny błąd wartości pracy wyjścia. Wynosi ona :
1,46 - 1,23 = 0,23 eV
Końcowy błąd wynosi więc ok. 8,8%.
7. Zestawienie wyników
Wynik jest porównywalny z wartościami pracy wyjścia różnych metali, podawa-nymi w tabelach - od 1,8 eV dla litu do 4,7 eV dla srebra. W tabelach nie znalazłem pierwiastka o dokładnie takiej samej pracy wyjścia, pocieszam się jednak faktem, iż mój wynik jest tego samego rzędu wielkości, co dane tabelaryczne.
Praca wyjścia elektronu z katody badanej lampy wynosi:
Ww = 1,23 1,46 eV
2 Piotr Ciskowski. Opracowanie doświadczenia 63.
Wyszukiwarka
Podobne podstrony:
Cw 02 (63) Procesy fizyczne w lampach elektronowych
LAMPA63, Temat: Procesy fizyczne w lampach elektronowych.
Laboratorium urządzeń i procesów, Zasada modelowania elektrycznego, POLITECZNIKA LUBELSKA
Laboratorium urządzeń i procesów, Zasada modelowania elektrycznego v2, POLITECHNIKA LUBELSKA
Laboratorium z chemii fizycznej poczta elektroniczna
Dioda-wiad ogolne, Szkoła, Politechnika 1- 5 sem, SEM IV, Elektronika i Energoelektronika. Laborator
Ćw 4 - Badanie twardości i udarności wybranych materiałów elektroizolacyjnych, Politechnika Poznańsk
Tranzystor bipolarny-gac, Szkoła, Politechnika 1- 5 sem, SEM IV, Elektronika i Energoelektronika. La
elektronika-8, Laboratorium Podstaw Elektroniki Politechniki Lubelskiej
Elektronika 5 protokół, Laboratorium Podstaw Elektroniki Politechniki Lubelskiej
Wyznaczanie równoważnika elektrochemicznego miedzi, laboratorium fizyczne, Laboratorium semestr 2 RÓ
Badanie układów o promieniowym rozkładzie natężenia pola magnetycznego, GRONEK9, Laboratorium Podsta
Badanie układów o promieniowym rozkładzie natężenia pola magnetycznego, GRONEK9, Laboratorium Podsta
więcej podobnych podstron