
SPRAWOZDANIE
TEMAT: Parcie hydrostatyczne.
1. Cel ćwiczenia.
Celem wykonanego ćwiczenia było określenie wartości parcia hydrostatycznego metodą
doświadczalną dla następujących przypadków:
- zbiornik napełniony wodą, pływak pusty
- zbiornik pusty, pływak napełniony wodą,
- zbiornik i pływak napełniony wodą.
2. Wstęp teoretyczny.
Parcie hydrostatyczne jest siłą powierzchniowa, z jaką ciecz pozostająca w spoczynku oddziałuje na
ścianę zbiornika lub przeszkodę w nim umieszczoną. Wielkość parcia hydrostatycznego można
określić trzema sposobami:
a. metoda rachunkowa;
W tej metodzie korzysta się ze wzoru
P=γ h
s
A
gdzie: P – parcie hydrostatyczne [N]
γ – ciężar objętościowy cieczy [N/m
2
]
h
s
– zagłębienie środka ciężkości, na którą działa ciecz, pod jej swobodną powierzchnią [m]
A – pole powierzchni na którą działa ciecz [ m
2
].
b. metoda rachunkowo-wykreślna;
Metoda ta polega na sporządzeniu wykresu parcia hydrostatycznego, a następnie obliczeniu parcia
ze wzoru:
P=γ V
gdzie V – objętość bryły parcia hydrostatycznego.
c. metoda doświadczalna;
Metoda ta polega na wyznaczeniu wielkości siły parcia hydrostatycznego przez zrównoważenie
szalek wagi. Kładąc odważniki na odpowiednie szalki wagi doprowadzamy jej ramiona do
poziomu. W ten sposób wyrównujemy momenty powstałe od siły parcia oraz od siły ciężkości
działającej na ramieniu wagi. Szukany parametr wyznaczamy z równości momentów:
Ga(lub b)=Pc , P=
Ga(lub b)
c
gdzie długość ramienia c wyznaczamy ze wzoru:
c=h
s
+
I
x
o
h
s
A
+
d
gdzie
G- ciężar szalki;

a (lub b) – długość ramienia wagi;
c – ramię siły parcia
d - wzniesienia osi obrotu nad zwierciadło wody w zbiorniku lub pływaku.
I
xo
– moment bezwładności pola A względem osi głównej odśrodkowej.
3. Wyniki doświadczenia.
Przedstawiamy poniżej tabelę z wynikami doświadczenia laboratoryjnego:
4. Obliczenia.
Wartości zmierzone na pływaku:
R
0
= 0,38 m
R
1
= 0,2 m
R
2
= 0,3 m
a = 0,34 m
b = 0,44 m
d=0,035 m
bok pływaka j = 0,1 m
grubość ścianki dolnej k = 0,004 m
grubość ścianki górnej l = 0,006 m
Wartości stałe:
T = 295,15 K
ρ = 997,8 kg/m
3
g = 9,81 m/s
2
WARIANT I.
a. Metoda rachunkowa.
Dla H=15cm
P=γ h
s
A
γ =ρ
g =997,8∗9,81=9788,42[ N /m
2
]
Wariant
I
0,15
0,44
0,16575
0,20
0,44
0,44010
II
0,15
0,44
0,14050
0,20
0,44
0,46035
III
0,15
0,44
0,01510
0,20
0,44
0,08000
Wysokość zwierciadła H
[m]
Długość
ramienia
b
[m]
Waga
odważników
[kg]
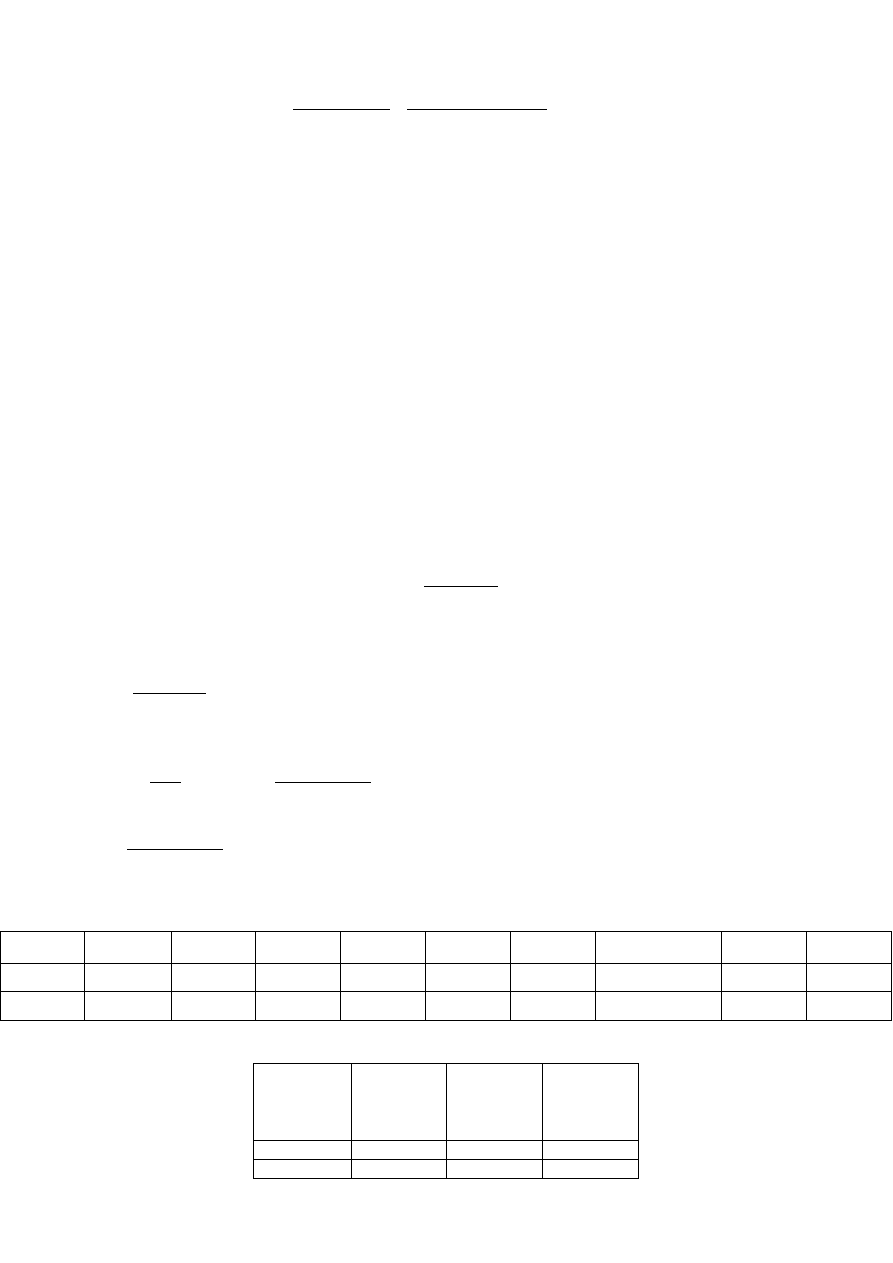
h
s
=
H −(R
0
−
R
2
)
2
=
0,15−(0,38−0,30)
2
=
0,035 [m]
A=0,1∗0,05=0,005[m
2
]
P=9788,42∗0,035∗0,005=1,713[ N ]
Pozostałe wyniki przedstawiono w tabeli.
b. Metoda rachunkowo-wykreślna
P=V ∗γ
Objętość bryły parcia:
V =[0,5∗(R
2
−
d )
2
]∗
o=[0,5∗(0,3−0,23)
2
]∗
0,1=0,000245 m
3
P=0,000245∗9788,42=2,398[ N ]
c. Metoda doświadczalna
P=
Ga(lub b)
c
G=m∗g =0,16575∗9,81=1,6260[ N ]
I
x
0
=
0,1∗0,05
3
12
=
0,000001042[m
4
]
c=h
s
+
I
x
o
h
s
A
+
d =0,035+
0,000001042
0,035∗0,005
+(
0,38−0,15)=0,271 m
P=
1,6260∗0,44
0,271
=
2,64 [ N ]
Reszta wyników przedstawiona w tabeli.
H [m]
m [kg]
hs [m]
A[m2]
d [m]
n [m]
o [m]
Ixo [m^4]
V [m^3]
c [m]
0,15
0,16575
0,035
0,005
0,23
0,05
0,1
0,000001042
0,000245
0,271
0,2
0,44010
0,060
0,01
0,18
0,1
0,1
0,000008333
0,000720
0,254
H[m]
0,15
1,713
2,398
2,64
0,2
5,873
7,048
7,48
Parcie
rachunkowe
[N]
Parcie
rachunkowo
wykreślne [N]
Parcie
doświadczaln
e [N]

WARIANT II
a. Metoda rachunkowa.
DLA H=15cm
P=γ h
s
A
γ =ρ
g =997,8∗9,81=9788,42[ N /m
2
]
h
s
=
H −(R
0
−
R
2
+
0,006)
2
=
0,15−(0,38−0,30+0,006)
2
=
0,032 [m]
A=0,092∗0,044=0,00405 [m
2
]
P=9788,42∗0,032∗0,00405=1,268 [N ]
Pozostałe wyniki przedstawiono w tabeli.
b. Metoda rachunkowo-wykreślna
V =[0,5∗(R
2
−
d −k )
2
]∗
n=[0,5∗(0,3−0,23−0,004)
2
]∗
0,044=0,000095832 m
3
P=V ∗γ =0,000095832∗9788,42=0,9380 [ N ]
c. Metoda doświadczalna
P=
Ga(lub b)
c
G=m∗g =0,14050∗9,81=1,3783 [N ]
I
x
0
=
0,092∗0,044
3
12
=
0,0000006531[m
4
]
c=h
s
+
I
x
o
h
s
A
+
d =0,032+
0,0000006531
0,032∗0,00405
+(
0,38−0,15)=0,267 m
P=
1,3783∗0,34
0,267
=
1,7549[ N ]
Pozostałe wyniki uwzględniono w tabeli.
H [m]
m [kg]
hs [m]
A[m2]
d [m]
n [m]
o [m]
Ixo [m^4]
V [m^3]
c [m]
0,15
0,14050
0,032
0,004048
0,23
0,044
0,092 0,000000653 0,000095832
0,2670
0,20
0,46035
0,057
0,008096
0,18
0,088
0,092 0,000005225 0,000592064
0,2483

WARIANT III
a. Metoda rachunkowa.
DLA H=15cm
P=P
z
−
P
p
gdzie Pz - parcie wywołane przez ciecz ze zbiornika
Pp - parcie wywołane przez ciecz z pływaka
zatem:
P=1,713−1,268=0,445[ N ]
Pozostałe wyniki uwzględniono w tabeli.
b. Metoda wykreślno-rachunkowa
V =
[
0,5∗k
2
+
k∗( R
2
−
d )
]
∗
o=[0,5∗(0,004
2
)+
0,004∗(0,3−0,23)]∗0,1=0,0000288 m
3
P=0,0000288∗9788,42=0,2819 N
Pozostałe wyniki uwzględniono w tabeli
c. Metoda doświadczalna:
P=
0,1481∗0,44
c
G=m∗g =0,0151∗9,81=0,1481[ N ]
Korzystając z wartości policzonych w wariantach I i II:
c=
A
Z
∙ c
Z
−
A
P
∙ c
P
A
Z
−
A
P
=
0,005∗0,271−0,00405∗0,267
0,005−0,00405
=
0,2867 [N ]
gdzie A
Z
– pole powierzchni, na jaką działa ciecz w zbiorniku
c
Z
- ramię siły parcia w przypadku wariantu dla napełnionego zbiornika
A
P
- pole powierzchni, na jaką działa ciecz w pływaku
c
P
- ramię siły parcia w przypadku wariantu dla napełnionego pływaka
zatem:
H[m]
Parcie rachunkowe [N]
0,15
1,268
0,9380
1,7549
0,2
4,517
5,795
6,1833
Parcie
rachunkowo
wykreślne [N]
Parcie
doświadczalne
[N]
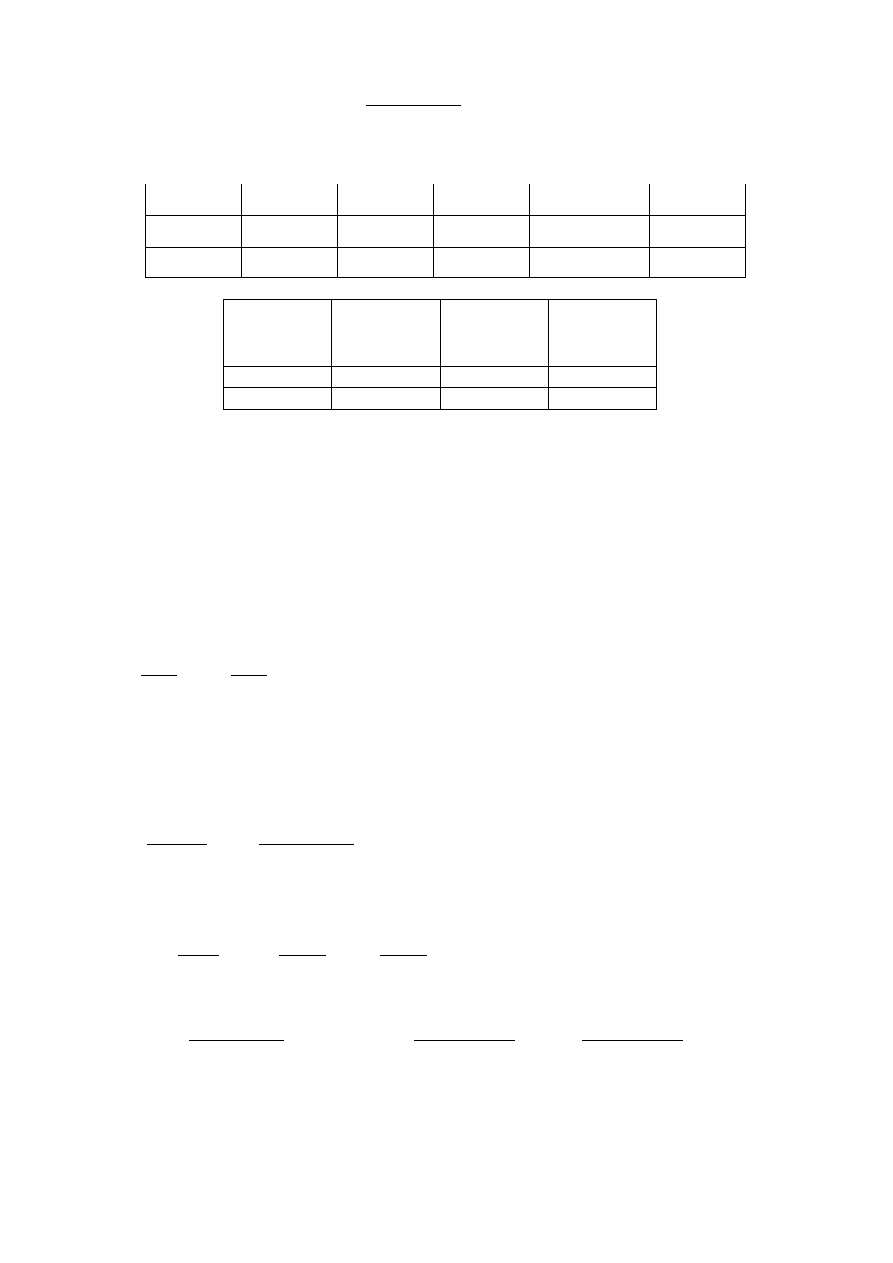
P=
0,1481∗0,44
0,2867
=
0,2266[ N ]
Pozostałe wyniki uwzględniono w tabeli.
5. Rachunek błędów.
W ramach doświadczenia przyjęliśmy następujące błędy rachunkowe:
Δa, Δb, Δd, Δn, Δo= 0,001[m]
Δm = 0,001 [kg]
Δh
s
= 0,001[m]
ΔA=0,000001 [m]
ΔV = 0,000001 [m
3
]
- niepewność obciążenia ΔG
Δ
G=
∣
∂
G∣
∣
∂
m∣
∗
Δ
m+
∣
∂
G∣
∣
∂
g∣
Δ
g =g∗Δ m=9,81∗0,001=0,00981 [N ]
Obliczenia poniższych niepewności obliczono dla H=15cm
WARIANT I
- Błąd momentu parcia
Δ
I
x
o
=
2∗o∗n
2
12
∗
Δ
n=
2∗0,1∗0,05
2
12
∗
0,001=0,0000000417[m
4
]
- Błąd ramienia parcia:
Δ
c=Δ h
s
+
1
h
s
∗
A
∗
Δ
I
x
O
+
I
x
O
h
s
2
∗
A
∗
Δ
h
s
+
I
x
O
h
s
∗
A
2
∗
Δ
A+Δ d
Δ
c=0,001+
1
0,035∗0,005
∗
0,0000000417+
0,000001042
0.035
2
∗
0,005
∗
0,001+
0,000001042
0.035∗0,005
2
∗
0,000001+0,001=0,0024 m
H [m]
m [kg]
Ap [m^2]
Az[m^2]
V [m^3]
c [m]
0,15
0,0151
0,00405
0,005
0,0000288
0,2876
0,20
0,0800
0,0081
0,01
0,0000488
0,2776
H
0,15
0,445
0,2819
0,2266
0,2
1,356
0,4777
1,2441
Parcie
rachunkowe
Parcie
rachunkowo
wykreślne
Parcie
doświadczaln
e
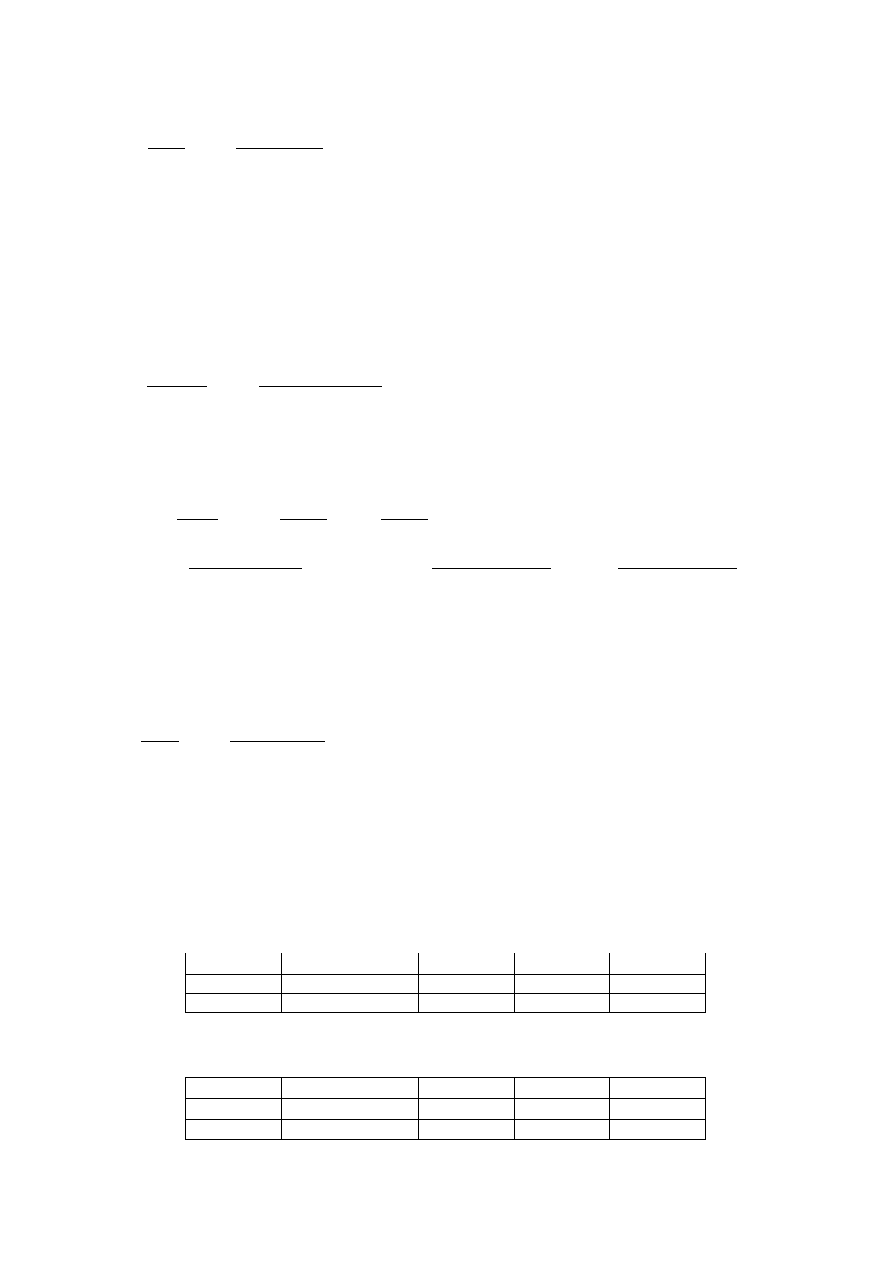
- Błąd parcia doświadczalnego
Δ
P
d
=
G∗b
c
2
∗
Δ
c=
1,626∗0,44
0,271
2
∗
0,0024=0,0235[ N ]
- Błąd parcia rachunkowego
Δ
P
r
=
γ ∗
h
s
∗
Δ
A+γ ∗A∗Δ h
s
=
9788,42∗0,035∗0,000001+9788,42∗0,005∗0,001=0,04898[ N ]
WARIANT II
- Błąd momentu parcia
Δ
I
x
o
=
2∗o∗n
2
12
∗
Δ
n=
2∗0,092∗0,044
2
12
∗
0,001=0,0000000297[m
4
]
- Błąd ramienia parcia:
Δ
c=Δ h
s
+
1
h
s
∗
A
∗
Δ
I
x
O
+
I
x
O
h
s
2
∗
A
∗
Δ
h
s
+
I
x
O
h
s
∗
A
2
∗
Δ
A+Δ d
Δ
c=0,001+
1
0,032∗0,00405
∗
0,0000000297+
0,0000006531
0,032
2
∗
0,00405
∗
0,001+
0,0000006531
0,032∗0,00405
2
∗
0,000001+0,001
Δ
c=0,00223 m
- Błąd parcia doświadczalnego
Δ
P=
G∗a
c
2
∗
Δ
c=
1,3783∗0,34
0,267
2
∗
0,00239=0,01466 [N ]
- Błąd parcia rachunkowego
Δ
P
r
=
γ
∗
h
s
∗
Δ
A+
γ
∗
A∗
Δ
h
s
=
9788,42∗0,032∗0,000001+9788,42∗0,00405∗0,001=0,03965[ N ]
Pozostałe wyniki zestawiono w poniższych tabelach:
WARIANT I
WARIANT II
H [m]
Δ Ixo [m^4]
Δc [m]
Δ Pd [N]
Δ Pr
0,15
0,0000000417
0,00241
0,0235
0,04898
0,20
0,0000001667
0,00251
0,0740
0,09794
H [m]
Δ Ixo [m^4]
Δc [m]
Δ Pd [N]
Δ Pr
0,15
0,0000000297
0,00223
0,01466
0,03965
0,20
0,0000001187
0,00226
0,05624
0,07930

6. Wnioski
W wyniku doświadczenia doszliśmy do wniosku, iż wraz ze wzrostem wysokości napełniania
zbiornika, wzrasta wartość parcia hydrostatycznego.
Możemy również zauważyć, iż parcie wyznaczone metodą doświadczalną różni się od pozostałych
wyników. Takie różnice wartości mogą być spowodowane dużą możliwością popełnienia błędów, np.
źle odczytanie wartości, niedokładne oszacowanie równowagi wagi, złe dobranie odważników,
napełnienie zbiornika z błędem odczytu. Wszystkie te błędy mogą wynikać z niedoskonałości oka
obserwatora.
Wyszukiwarka
Podobne podstrony:
Parcie na 6
Projekt ścianka szczelna, parcie odpor wykres Model
32 parcie
,pytania na obronę inż,ciśnienie hydrostatyczne i parcie hydrostatyczne
parcie1, Ochrona Środowiska, semestr III, MECHANIKA PŁYNÓW, Mech. płynów - przodek, laborki, laborki
PARCIE HYDROSTATYCZNE NA ŚCIANĘ PŁASKĄ
więcej podobnych podstron