Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

Notatki do ćwiczeń z przedmiotu „

Notatki do ćwiczeń z przedmiotu „

Podstawy wytrzymałości materiałów

Podstawy wytrzymałości materiałów

”

”

Arkusz 09

Arkusz 09

: Skręcanie – przekroje dowolne

: Skręcanie – przekroje dowolne

1. Skręcanie przekrojów kołowych – definicje, pojęcia, wzory

Teoria dotycząca skręcania – na podstawie wykładu i książek: [1], [2], ewentualnie także [3].

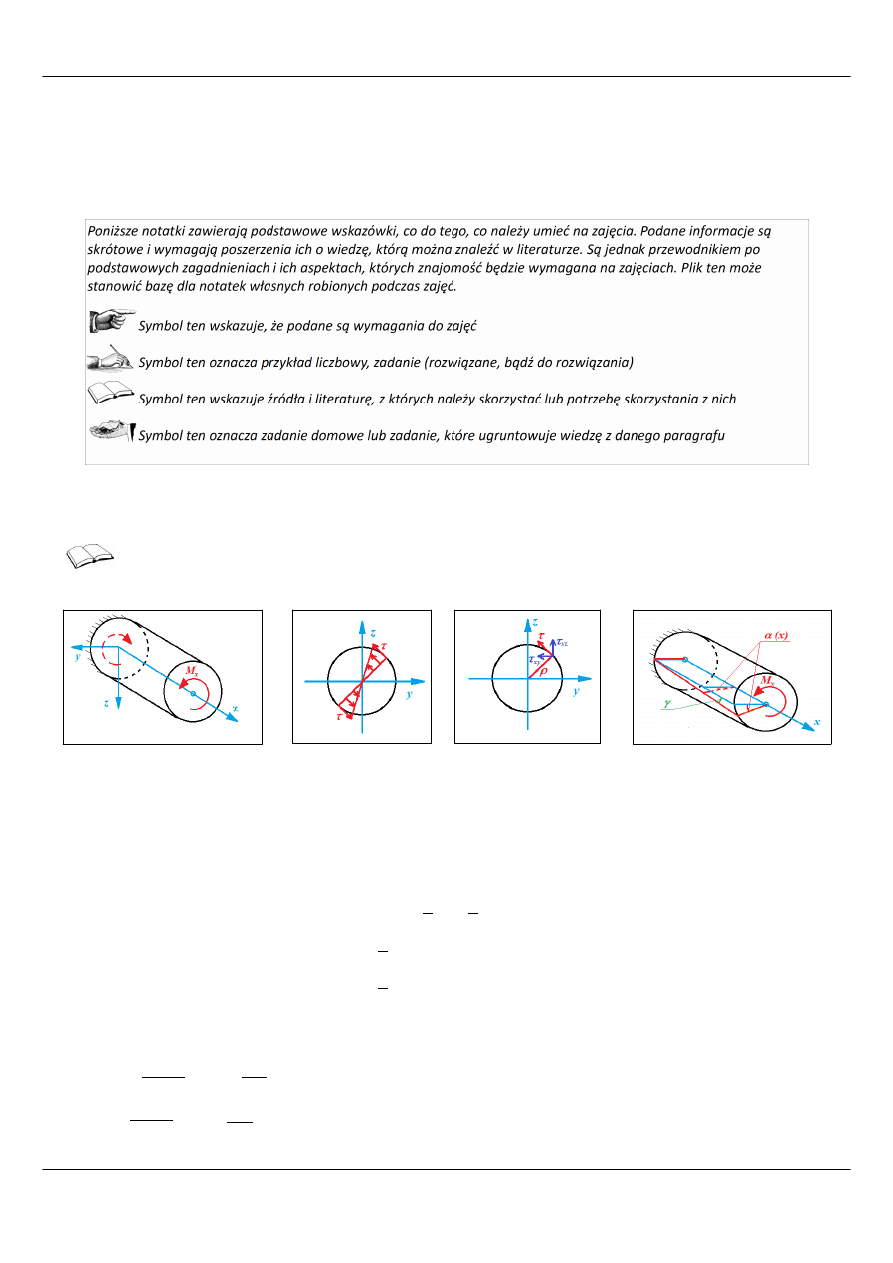
Kilka poniższych rysunków ilustruje pojęcia i wzory związane ze skręcaniem przekrojów kołowych.

1.a) NAPRĘŻENIA
Tensor naprężenia dla przypadku skręcania ma postać określoną poniżej; w tym stanie, zgodnie z równaniami Hooke'a,
generowany jest przestrzenny stan odkształcenia:

T

σ

=

[

0

τ

xy

τ

xz

τ

yx

0

0

τ

zx

0

0

]

⇔

związki konstytutywne

T

ε

=

[

0

1
2

γ

xy

1
2

γ

xz

1

2

γ

yx

0

0

1
2

γ

zx

0

0

]

Związek funkcji naprężenia z funkcją siły przekrojowej ma postać:

gdzie M

x

(x)

jest momentem skręcającym w przekroju o odciętej x,

natomiast I

x

(x)

jest momentem biegunowym bezwładności w tym

przekroju.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Rysunek 1: Proste skręcanie

Rysunek 3: Wektory

naprężenia

Rysunek 4: Deformacja i

odkształcenie



xy

( x , z) =

M

x

( x)

I

x

( x)

⋅ z

[

Nm

m

4

⋅m = Pa

]



xz

(x , y) =

M

x

( x)

I

x

( x)

⋅ y

Rysunek 2: Rozkład

naprężeń w przekroju

poprzecznym

[

Nm

m

4

⋅m = Pa

]

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

Gdy zamiast układu kartezjańskiego, skorzystamy z biegunowego, wzór na naprężenia ma postać:

( x , ρ) =

M

x

( x)

I

x

( x)

⋅ρ

.

Wzór na biegunowy moment przekroju kołowego:

I

x

= I

0

= I

p

= I

y

+ I

z

= π R

4

2

= π D

4

32

.

1.b) ODKSZTAŁCENIA I DEFORMACJA
Związek funkcji przekrojowej z funkcją odkształcenia ma postać:

gdzie M

x

(x)

jest momentem skręcającym w przekroju o odciętej x, natomiast I

x

(x)

jest

momentem biegunowym bezwładności w tym przekroju. G(x) jest modułem
Kirchhoffa (zależnym od materiału, w związku z czym może być zmienny na długości
elementu).

Następujące pojęcia mają związek z deformacją i odkształceniem w przypadku prostego skręcania:

•

jednostkowy kąt skręcenia:

θ(x) =

M

x

( x)

G

⋅I

x

( x)

[

rad
m

]

•

bieżący kąt skręcenia:

α ( x) =

∫

θ(x)dx =

∫

M

x

(x) dx

G

(x)⋅I

x

( x)

[

rad

]

•

całkowity kąt skręcenia (dla elementu o ciągłej charakterystyce):

α ( x) =

∫

0

l

M

x

(x) dx

G

(x)⋅I

x

( x)

[

rad

]

•

całkowity kąt skręcenia (dla elementu o skokowo zmiennej charakterystyce):

α ( x) =

∑

i

M

x

i

⋅l

i

G

i

⋅I

x

i

[

rad

]

2. Przykłady prętów kołowych – przypadki statycznie wyznaczalne

Przypomnienie: reakcje możemy wyznaczyć z równań równowagi wtedy, gdy liczba tych równań odpowiada liczbie
nieznanych reakcji. Mówimy wówczas o układach statycznie wyznaczalnych.

Dla układów statycznie wyznaczalnych pracujących w stanie prostego skręcania rozpatruje się najczęściej następujące
zagadnienia: znalezienie sił przekrojowych, znalezienie naprężeń, wyznaczenie wykresu jednostkowego i bieżącego kąta
skręcenia, wyznaczenie całkowitego kąta skręcenia.

Zgodnie z warunkiem wytrzymałościowym

τ

max

⩽ k

s

(k

s

- dopuszczalne naprężenia na ścinanie) lub warunkiem

użyteczności

θ

max

⩽ θ

dop

lub

α

max

⩽ α

dop

lub

α

total

⩽ α

dop

można także wyznaczać potrzebne parametry konstrukcji:

średnicę, materiał, wymiary.

Należy rozwiązać przykłady: 15.5.1, 15.5.2 z książki [2] oraz zadania nr: 5.1 / str. 63 i 5.3 / str. 65 z książki [4].

Uwaga! Może się zdarzyć, że (tak jak w zadaniu 5.1) należy przeliczyć obroty i moc silnika na moment skręcający, który
one powodują. Proszę samemu odnaleźć odpowiedni wzór – będzie on wymagany.

3. Przykłady prętów kołowych – przypadki statycznie niewyznaczalne

W tych przypadkach, kiedy nie mamy wystarczającej liczby równań do obliczenia reakcji, trzeba znaleźć warunki, które
dadzą równania na nadprogramowe niewiadome. Dla skręcania zagadnienie to dotyczy najczęściej obustronnie
utwierdzonej konstrukcji. W związku z tym dodatkowym warunkiem będzie geometryczny warunek: całkowity kąt
skręcenia równy zero.

Należy rozwiązać przykład 15.5.3 z książki [2] oraz zadania nr: 5.10 / str. 69 , 5.12 / str. 70 z książki [4].

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

γ

xz

( x , y) =

M

x

( x)

G

(x)⋅I

x

( x)

⋅ y

γ

xy

( x , z) =

M

x

(x)

G

( x)⋅I

x

(x)

⋅ z

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

4. Skręcanie przekrojów prostokątnych

Teoria dotycząca skręcania prętów prostokątnych – na podstawie wykładu i książek: [1], [2], ewentualnie
także [3].

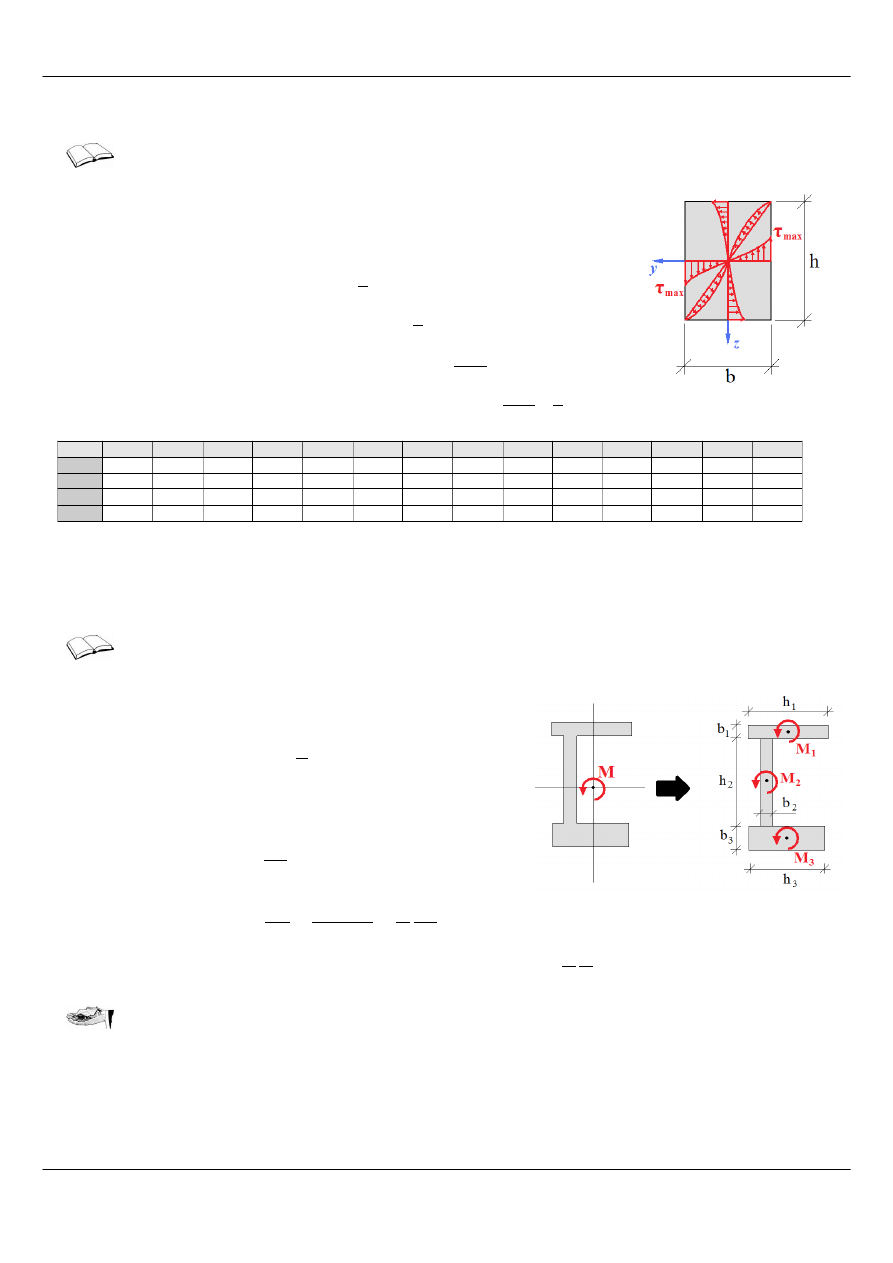
Dla przekrojów prostokątnych rozkład naprężeń jest nieliniowy, ilustruje go Rysunek 5.
Podstawowe wzory przedstawione są poniżej. Są to wzory przybliżone, a wartości
współczynników

α

i

β

należy odczytać z Tabela 1.

•

Moment biegunowy przekroju:

I

x

=β

(

h
b

)

b

3

h

.

•

Wskaźnik wytrzymałości na skręcanie:

W

x

=α

(

h
b

)

b

2

h

.

•

Maksymalne naprężenie styczne w przekroju:



max

=

M

x

max

W

x

•

Maksymalne naprężenie w połowie krótszego boku:

τ'

max

=

M

x

b

I

x

δ

(

h
b

)

5. Skręcanie przekrojów cienkościennych otwartych

Teoria dotycząca skręcania prętów cienkościennych otwartych – na podstawie wykładu i książek: [1], [2],
ewentualnie także [3].

•

Przekrój rozważamy jako złożony z poszczególnych małych

prostokątów. Wówczas dla każdego prostokąta osobno oblicza się

moment biegunowy:

I

xi

=β

i

(

h

i

b

i

)

b

i

3

h

i

, natomiast moment

biegunowy całego przekroju to

I

x

=

∑

i

=1

n

I

xi

.

•

Moment skręcający przekrój rozkłada się na poszczególne

prostokąty wg wzoru:

M

xi

=

M

x

I

x

I

xi

.

•

W każdym prostokącie składowym należy obliczyć maksymalne

naprężenie styczne



max ,i

=

M

xi

W

xi

=

M

x

β

i

b

i

3

h

i

I

x

α

i

b

i

2

h

i

=

β

i

α

i

M

x

I

x

b

i

.

•

Zastępczy wskaźnik wytrzymałości dla całego przekroju:

W

x

= min

i

(

α

i

β

i

I

x

b

i

)

.

Należy rozwiązać przykład 15.7.1.1, 15.7.1.2 z książki [2].

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

Rysunek 5: Rozkład naprężeń przy

skręcaniu prostym pręta prostokątnego ([5])

Tabela 1: Współczynniki do obliczania przekrojów prostokątnych skręcanych ([5])

1

1,25

1,5

1,75

2

2,5

3

3,5

4

5

6

8

10

∞

0,2082

0,2212

0,2310

0,2390

0,2459

0,2576

0,2672

0,2751

0,2817

0,2915

0,2984

0,3071

0,3123

0,3333

0,1406

0,1717

0,1958

0,2143

0,2287

0,2494

0,2633

0,2733

0,2808

0,2913

0,2983

0,3071

0,3123

0,3333

0,6753

0,7763

0,8476

0,8966

0,9301

0,9681

0,9854

0,9934

0,9970

0,9994

0,9999

1,0000

1,0000

1,0000

0,6753

0,7111

0,7280

0,7359

0,7394

0,7418

0,7423

0,7424

0,7425

0,7425

0,7425

0,7425

0,7425

0,7425

h/b
α(h/b)
β(h/b)
γ(h/b)
δ(h/b)

Rysunek 6: Podział przekrojów cienkościennych na figury

składowe przy skręcaniu ([5])

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

Przekrój aproksymowany jest układem trzech prostokątów:

b

1

=5 mm , h

1

= 20 mm ,

h

1

b

1

= 4, α

1

= 0,282 , β

1

= 0,281

b

2

=5 mm , h

2

= 30 mm ,

h

2

b

2

= 6, α

2

= 0,299 , β

2

= 0,299

b

3

=5 mm , h

3

= 10 mm ,

h

3

b

3

= 2, α

3

= 0,246 , β

3

= 0,229

Moment biegunowy:

I

x

=

∑

i

=1

3

b

i

3

h

i

β

i

= 2110 mm

4

Wskaźnik wytrzymałości:

W

x

= min

i

=1,2 ,3

(

α

i

β

i

I

x

b

i

)

= min

(

423,5 ; 422 ; 453,3

)

= 422 mm

3

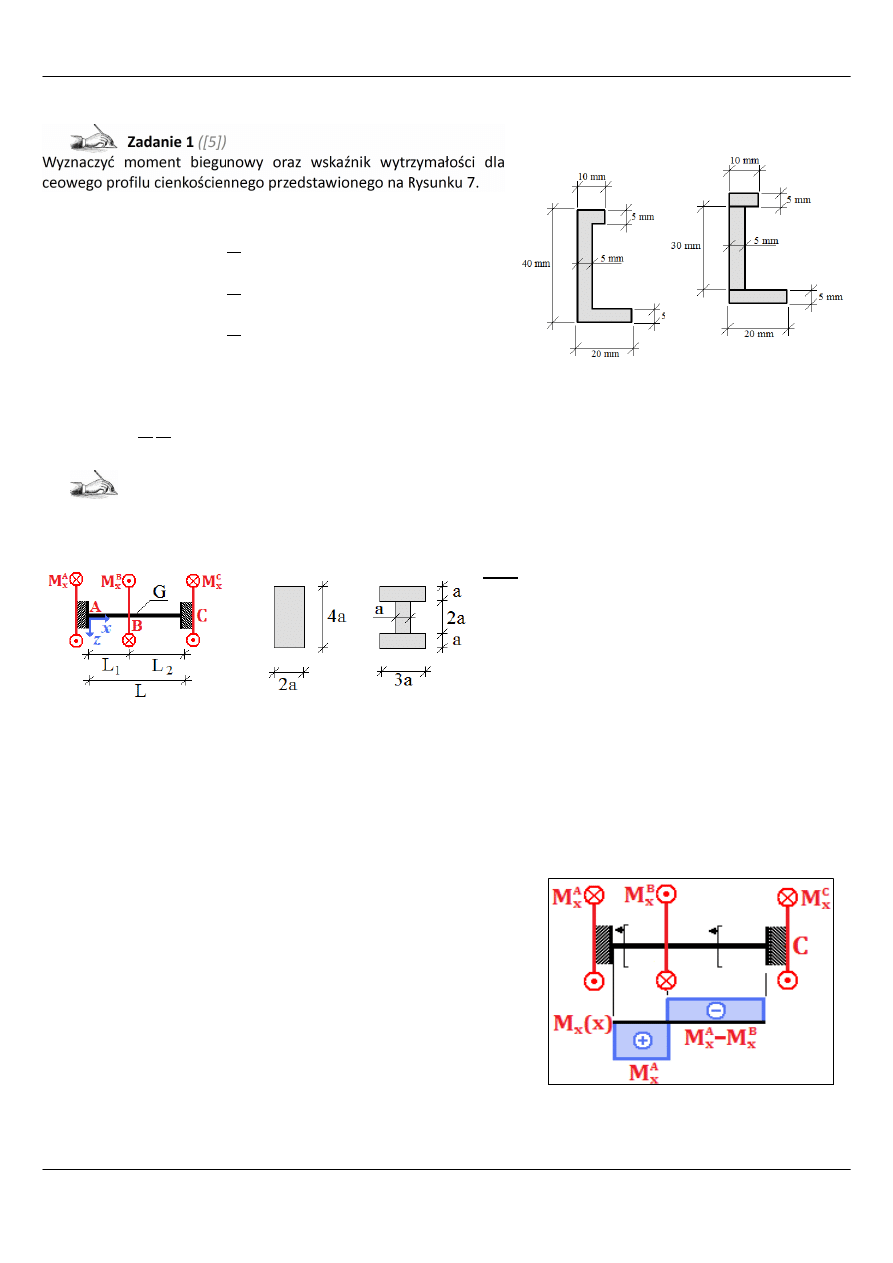
Zadanie 2

(Na podstawie [5])

Pręt obustronnie utwierdzony jest obciążony momentem skupionym M. Wyznaczyć reakcje podporowe i maksymalne
naprężenie styczne. Porównać wyniki dla obu rodzajów przekroju poprzecznego (A) i (B).

Dane:

•

M

x

B

= 50 kNm

•

L

1

= 20 cm

,

L

2

= 30 cm

•

L

= L

1

+ L

2

= 50 cm

•

moduł Kirchhoffa:

G

= 82 GPa

•

dopuszczalne naprężenie przy ścinaniu:

k

s

= 125 MPa

•

wymiar a=5cm

1) Zadanie jest statycznie niewyznaczalne.

2) Po przyjęciu układu współrzędnych oraz oznaczeniu punktów charakterystycznych A-C, przyjmujemy także symboliczne
oznaczenia reakcji na podporach.

3.a) Nieznane reakcje podporowe wyznaczymy z warunku równania równowagi rzutu sumy sił na oś x:

∑

X

= M

x

B

M

x

A

M

x

C

= 0 ⇒ M

x

C

=M

x

B

M

x

A

…

3.b) … oraz z warunku zerowania się przemieszczeń w punktach x=0 i x=L,
czyli

α

tot

= 0

.

Rozkład momentów skręcających na długości pręta znajduje się na
rysunku 9.

M

(x) =

{

x

∈(0, L

1

) ⇔

M

x

A

x

∈( L

1,

L

) ⇔

M

x

A

M

x

B

= M

x

C

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4

Rysunek 7: Przekrój ceowy do Zadania 1 ([5])

Rysunek 8: Ilustracja do zadania 2

([5])

Rysunek 9: Rozkład momentów skręcających

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

Całkowity kąt skręcenia na końcu pręta:

α

tot

=

M

x

A

⋅L

1

GI

x

+

( M

x

A

M

x

B

)⋅L

2

GI

x

=

M

x

A

(L

1

+ L

2

)

GI

x

M

x

B

L

2

GI

x

= 0

.

A zatem wyliczamy wartość nieznanej reakcji podporowej:

α

tot

=

1

G I

x

[

M

x

A

L

M

x

B

L

2

]

= 0

⇒

M

x

A

= M

x

B

L

2

L

= 30 kNm

.

Reakcja na drugiej podporze:

M

x

C

= M

x

B

M

x

A

= 20 kNm

.

Do dalszych obliczeń wybieramy maksymalny moment skręcający:

M

x

max

= M

x

A

= 30 kNm

.

4) Maksymalne naprężenia dla przekroju prostokątnego należy zacząć od parametrów geometrycznych:

b

= 2 a = 10 cm

,

h

= 4 a = 20 cm

, a zatem:

α( h/b) = α (2)= 0,246

.

Wskaźnik wytrzymałości przy skręcaniu wynosi:

W

x

=α( h/b)b

2

h

= 492 cm

3

.

Stąd maksymalne naprężenie ścinające:



max

=

M

x

max

W

x

= 30⋅10

3

Nm

0,492

⋅10

6

m

3

= 60,98MPa

.

Warunek nośności można sprawdzić porównując dopuszczalne i maksymalne naprężenia:



max

k

s

⋅100 % = 81,3 %

.

5) Maksymalne naprężenia dla przekroju dwuteowego również należy zacząć od parametrów geometrycznych:

b

1

= a = 5 cm

,

h

1

= 3a = 15 cm

β

1

=β(3) = 0,263

;

α

1

= α (3) = 0,267

b

2

= a = 5 cm

,

h

2

= 2 a = 10 cm

→

β

2

=β(2) = 0,229

;

α

2

= α (2) = 0,246

b

3

= a = 5 cm

,

h

3

= 3a = 15 cm

→

β

3

=β(3) = 0,263

;

α

3

= α (3) = 0,267

•

Dla powyższych wartości należy obliczyć momenty biegunowe przypadające na pojedyncze elementy, tj półki:

I

x1

= I

x3

= β

1

b

1

3

h

1

= β

3

b

3

3

h

3

= 493,13 cm

4

i środnik:

I

x2

= β

2

b

2

3

h

2

= 286,25 cm

4

oraz moment biegunowy dla

całego przekroju:

I

x

=

∑

i

=1

3

β

i

b

i

3

h

i

= 1270cm

4

.

•

Znając momenty biegunowe można podzielić momenty skręcające przypadające na poszczególne części

przekroju, i tak mamy momenty przypadające na półki:

M

x1

=M

x3

=

M

x

I

x

⋅I

x1

=

M

x

I

x

⋅I

x3

= 11,626 kNm

i moment

przypadający na środnik:

M

x2

=

M

x

I

x

⋅I

x2

= 6,749 kNm

.

Dla sprawdzenia:

M

x1

+ M

x2

+ M

x3

= 2⋅11,626 kNm+ 6,749 kNm = 30 kNm = M

x

.

•

Maksymalne naprężenia w półkach:



max1

= 

max3

=

M

x

I

x

β

1

α

1

b

1

=

M

x

I

x

β

3

α

3

b

3

= 116,11 MPa

Maksymalne naprężenia w środniku:



max2

=

M

x

I

x

β

2

α

2

b

2

= 109,73 MPa

Warunek nośności:



max

k

s

⋅100 % = 93 %

.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

6. Skręcanie przekrojów cienkościennych zamkniętych (metoda przybliżona)

Teoria dotycząca skręcania przekrojów cienkościennych zamkniętych – na podstawie wykładu i książek: [1],
[2], ewentualnie także [3].

Najważniejsze wzory dotyczące skręcania przekrojów cienkościennych zamkniętych:

•

moment biegunowy: I

x

= 4 A

s

2

⋅

[

∮

ds

δ( s)

]

1

dla

δ=const. : I

x

=

4

δ A

s

2

S

,

•

wskaźnik wytrzymałości na skręcanie:

W

x

= 2 A

s

δ

min

,

•

maksymalne naprężenie ścinające:



max

=

M

x

max

2 A

s

δ

min

,

gdzie

A

s

jest polem powierzchni ograniczonym linią środkową.

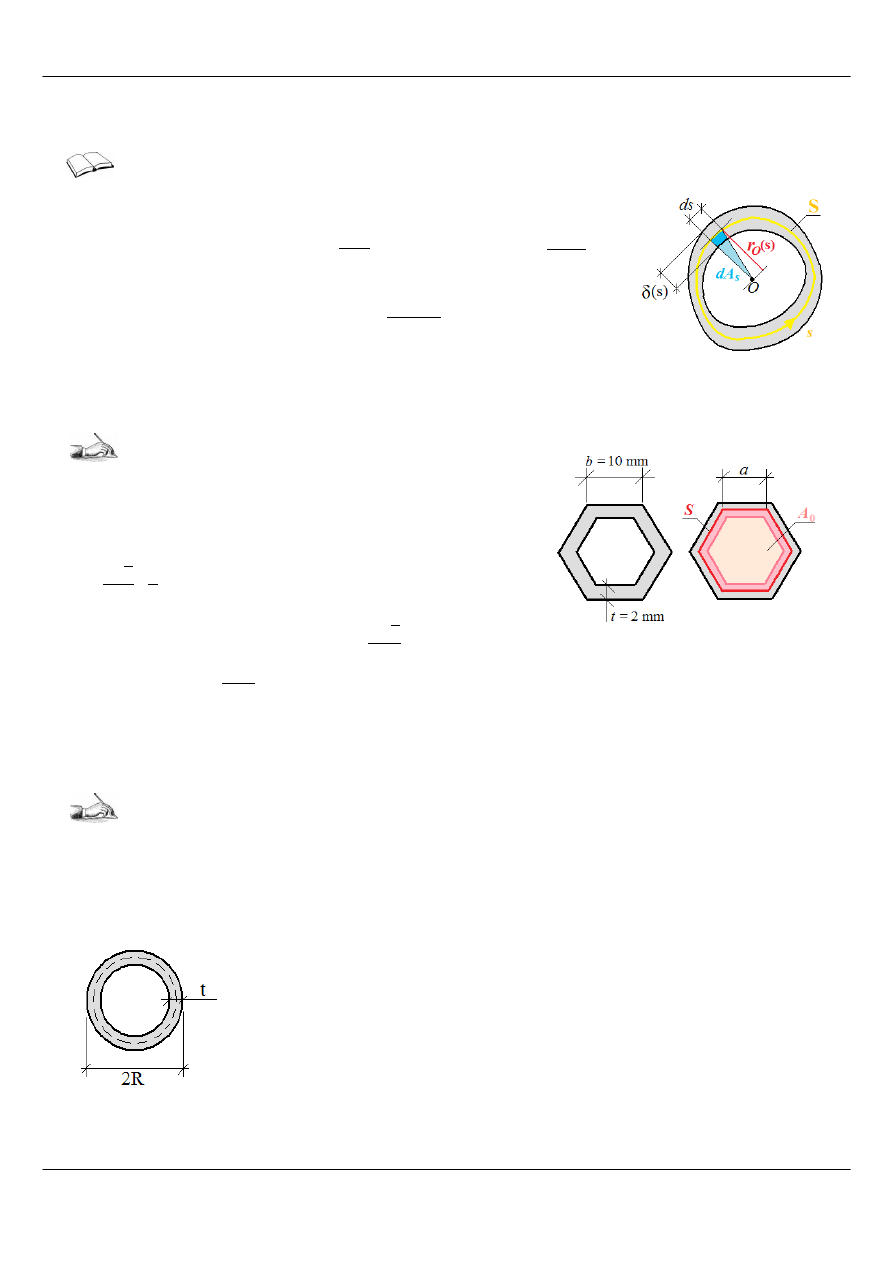
Zadanie 3

([5])

Wyznaczyć moment biegunowy oraz wskaźnik wytrzymałości dla
foremnego, sześciokątnego profilu cienkościennego (Rysunek 11).

Długość jednego boku sześciokąta środkowego:

a

= 2⋅

(

b

⋅

√

3

2

1

2

⋅t

)

⋅tg 30

∘

= 8,845 mm

Długość linii środkowej:

S

= 6 a = 53,072 mm

Pole zawarte wewnątrz linii środkowej:

A

s

= 6⋅a

2

√

3

4

= 203,258 mm

2

.

Moment biegunowy:

I

x

=

4 t A

s

2

S

= 6227,587 mm

4

.

Wskaźnik wytrzymałości na skręcanie:

W

x

= 2 A

s

t

= 813 mm

3

.

Zadanie 4

(Na podstawie [5])

Dany jest wspornik wykonany z pręta cienkościennego, rurowy, skręcany stałym momentem M=1kNm. Wyznaczyć
maksymalne naprężenie styczne oraz całkowity kąt skręcenia. Zadanie rozwiązać metodą ścisłą (jak dla przekrojów
kołowych/rurowych) i przybliżoną (dla przekrojów cienkościennych zamkniętych). Sprawdzić jak zmieni się wartość
maksymalnego naprężenia oraz całkowitego kąta skręcenia po rozcięciu rury wzdłuż tworzącej na całej długości pręta
(przekrój cienkościenny otwarty).

Dane:
Obciążenie:

M=1kNm

Długość pręta:

L

= 1 m

Promień zewn.:

R

= 2,5 cm

Grubość:

t

= 2 mm

Moduł Kirchhoffa:

G

= 85 GPa

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

Rysunek 11: Ilustracja do Zadania 3 ([5])

Rysunek 10: Skręcanie przekroju

cienkościennego ([5])

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

1) Metoda ścisła (przekrój kołowy/rurowy):

Moment biegunowy:

I

x

=

π R

4

2

π( R t)

4

2

= π

2

[

R

4

(R t)

4

]

= 17,402 cm

4

Maksymalne naprężenie ścinające:



max

= M

I

x

⋅R=

1

⋅10

3

17,402

⋅10

8

⋅2,5⋅10

2

= 143,66⋅10

6

Pa

Całkowity kąt skręcenia na przedziale

x

∈ 〈0 ; L〉

:

α( x) =

∫

M

(x)

GI

x

dx

=

M

⋅x

G

⋅I

x

+ C

Z warunku utwierdzenia w x = 0 wyznaczamy stałą całkowania C = 0.

Kąt skręcenia:

α( L) = M⋅L

G

⋅I

x

=

1

⋅10

3

⋅1

85

⋅10

9

⋅17,402⋅10

8

= 0,0676 [rad ]

2) Metoda przybliżona (profil cienkościenny zamknięty):

Pole obszaru ograniczonego linią środkową:

A

s

=π

(

R

1
2

t

)

2

= 18,096 cm

2

.

Długość linii środkowej:

S

= 2π

(

R

1
2

t

)

= 15,080 cm

.

Minimalna grubość przekroju:

δ

min

= t = 2 mm

.

Moment biegunowy:

I

x

=

4

δ A

s

2

S

= 17,372 cm

4

.

Wskaźnik wytrzymałości:

W

x

= 2 A

0

δ

min

= 7,238 cm

3

.

Maksymalne naprężenie ścinające:



max

=

M

W

x

=

M

2 A

s

δ

min

= 138,16 MPa

.

Całkowity kąt skręcenia:

α ( L) =

M

⋅L

GI

x

= 0,0678 [rad ]

.

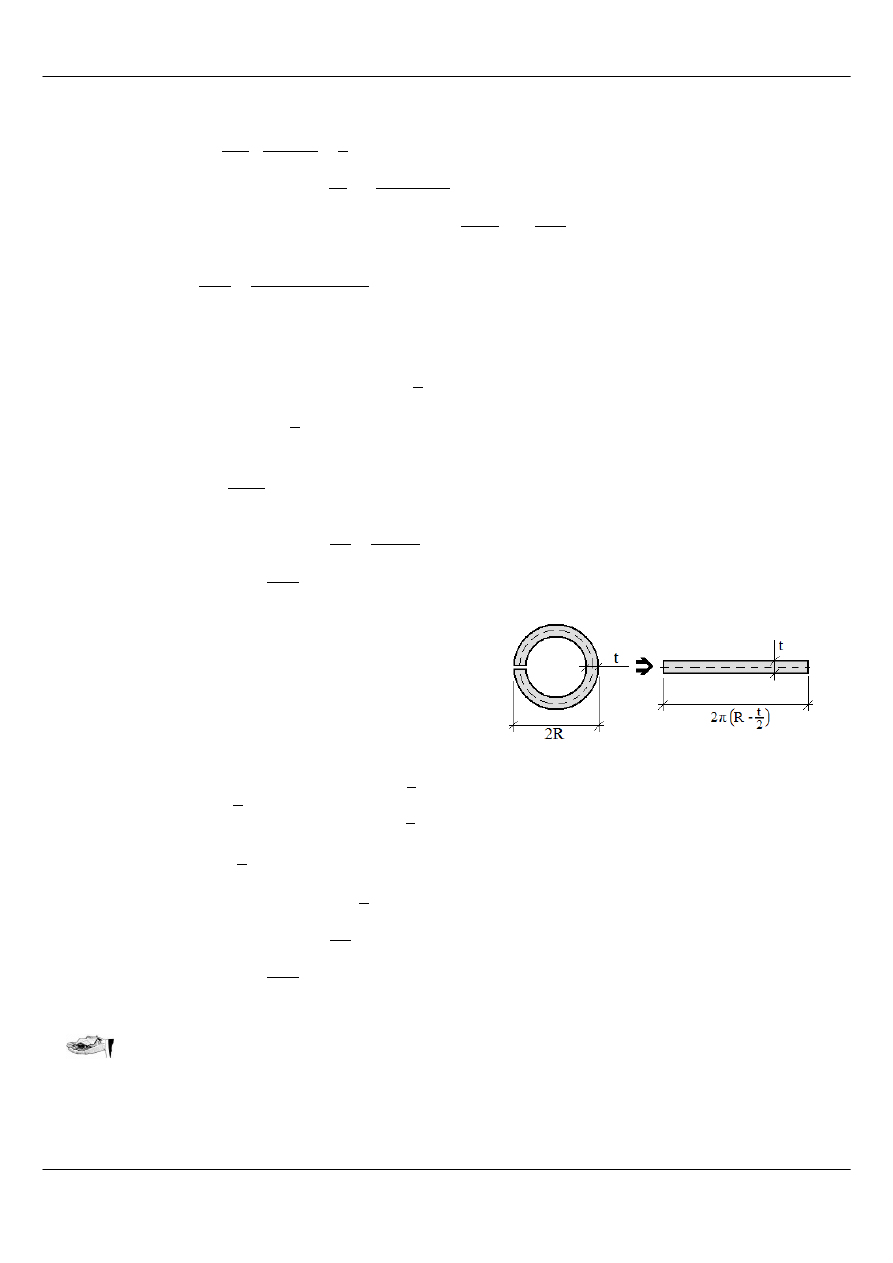
3) Pręt rozcięty (przekrój cienkościenny otwarty):
Po rozcięciu profilu w jednym miejscu wzdłuż tworzącej rury na
całej długości pręta, traktowany jest on jako profil cienkościenny
otwarty. Aproksymować go można pojedynczym prostokątem o
szerokości równej grubości ścianki i długości równej długości linii
środkowej (Rysunek 12):

{

b

= δ = 0,2 cm

h

= S=15,080 cm

⇒

h

b

= 75,4 ⇒

{

α(75) =

1
3

β(75) = 1

3

Moment biegunowy:

I

x

=β

(

h
b

)

b

3

h

= 0,0402 cm

4

.

Wskaźnik wytrzymałości na skręcanie:

W

x

=α

(

h
b

)

b

2

h

= 0,201 cm

3

.

Maksymalne naprężenie ścinające:



max

=

M

W

x

= 4975,124 MPa

.

Całkowity kąt skręcenia:

α( L) = M⋅L

GI

x

= 29,266 [rad]

.

Należy rozwiązać przykład 15.7.1.3, 15.7.1.4 z książki [2] oraz wybrane zadania z rozdziału 6 od str. 73
z książki [4].

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

Rysunek 12: Przekrój rozcięty ([5])

Arkusz 09: Skr

ę

canie – przekroje dowolne. Arkusz przeznaczony do

ć

wicze

ń

z przedmiotu „Podstawy wytrzymało

ś

ci materiałów” na

II roku dziennych studiów Wydziału In

ż

ynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 20142015.

• Umiejętność rozwiązywania zadań prętów statycznie wyznaczalnych i niewyznaczalnych (wykres kąta
skręcenia, jednostkowego kąta skręcenia, momentów skręcających; wykresy naprężeń w elemencie
i w przekroju poprzecznym; warunki projektowe, wyznaczanie średnic, wymiarów oraz dopuszczalnych
obciążeń) – wszystkie rodzaje przekrojów.
• Znajomość wzorów i umiejętność ich wykorzystania (naprężenia, odkształcenia, deformacje, moment
skręcający od pracującego silnika) – wszystkie rodzaje przekrojów.
• Postać macierzy naprężenia i odkształcenia dla skręcania prostego. Definicja skręcania.

7. Literatura

[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie

poszerzone i poprawione, Kraków 2004, rozdział 15

[3] Niezgodziński M., Niezgodziński T. "Wytrzymałość materiałów", Wydawnictwo Naukowe PWN, Warszawa 2009
[4] Niezgodziński M., Niezgodziński T. "Zadania z wytrzymałości materiałów", Wydawnictwo WNT, Warszawa 2012
[5] dr inż. Paweł Szeptyński, ilustracje i zadania

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4