ALGORYTM

02

–

SORTOWANIE

PRZEZ

WSTAWIANIE

POŁÓWKOWE

Opis algorytmu

Algorytm sortowania przez wstawianie połówkowe rozpoczynamy od podzielenia ciągu porównywa-

nych elementów:

n

a

a

a

,

...

,

,

2

1

na dwa ciągi:

a)

wynikowy

1

2

1

,

...

,

,

−

i

a

a

a

,

b)

źródłowy

n

i

i

a

a

a

,

...

,

,

1

+

.

W każdym kroku, począwszy od i = 2, 3, … , n, i – ty element ciągu źródłowego przenosimy do ciągu

wynikowego wstawiając w odpowiednie miejsce (czyli w takie miejsce, żeby wszystkie elementy ciągu wyni-
kowego pozostawały ułożone w odpowiedniej kolejności od wartości najmniejszej do największej). Zauważmy,
ż

e ciąg wynikowy, do którego należy wstawić nowy element, jest już uporządkowany. W związku z tym mo-

ż

emy zastosować szybszą (niż w przypadku algorytmu sortowania przez proste wstawianie) metodę ustalania

miejsca wstawienia nowego elementu. Możemy zastosować metodę przeszukiwania połówkowego, w której
próbkuje się ciąg wynikowy w środku i dzieli do dalej znowu na połowę, aż nie znajdziemy miejsca w którym
należy wstawić nowy obiekt.

for

(i=2; i<=n; i++)

{
Ustaw x = a[i];
Wstaw x w odpowiednim miejscu ciągu wynikowego (miejsce, w którym
należy wstawić x znajdujemy metodą przeszukiwania połówkowego).
}

Algorytm (w pseudokodzie)

Krok 1:

Dla i = 2,3,...,n powtarzaj Kroki 2 - 12

Krok 2:

Ustaw x = a[i]

Krok 3:

Ustaw k = 1

Krok 4:

Ustaw p = i - 1

Krok 5:

Powtarzaj Kroki 6 – 9 tak długo,

jak spełniony jest warunek: k <= p

Krok 6:

m = (k + p) div 2

Krok 7:

Jeżeli x < a[m] wówczas wykonaj Krok 8

Krok 8:

p = m - 1

w przeciwnym razie wykonaj Krok 9

Krok 9:

k = m + 1

Krok 10:

Dla j = i-1,i-2,...,k powtarzaj Krok 11

Krok 11:

Ustaw a[j+1] = a[j]

Krok 12:

a[k] = x

Algorytm (w języku C++)

for

(i=2; i<=n; i++)

{
x = a[i];
k = 1;
p = i - 1;

while

(k <= p) {

// dzielenie całkowitoliczbowe – całkowita część z dzielenia //
m = (k + p) / 2;

if

(x < a[m])

p = m - 1;

else

k = m + 1;

};

for

(j=i-1; j>=k; j--)

a[j+1] = a[j];

a[k] = x;
}

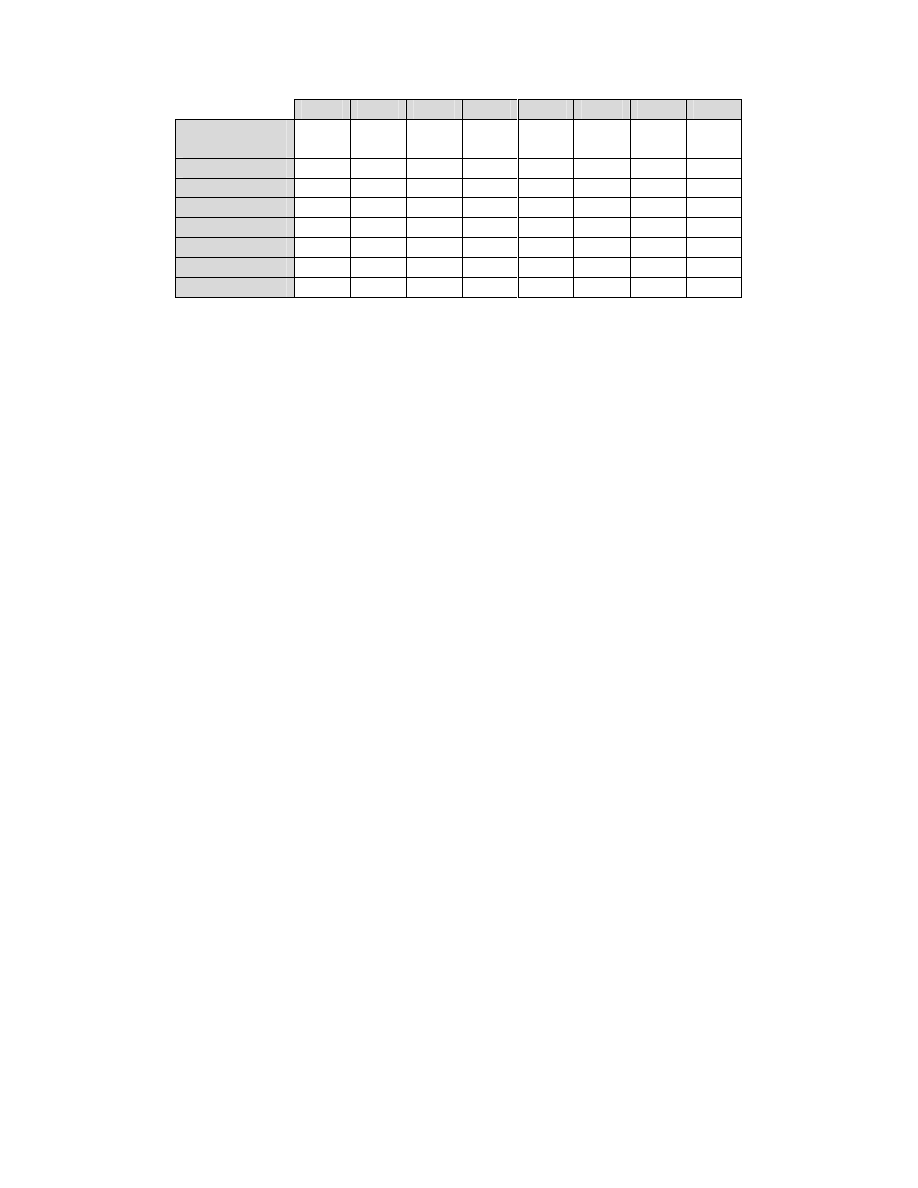
Przykład

Niech dany będzie następujący ciąg wartości:

a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8]

Wartości
początkowe

44

55

12

42

94

18

6

67

i = 2

44

55

12

42

94

18

6

67

i = 3

12

44

55

42

94

18

6

67

i = 4

12

42

44

55

i = 5

i = 6

i = 7

i = 8

i = 2
x = a[2] = 55
k = 1
p = 1

// Pętla while ---------------------- //
Czy k <= p ? (Czy 1 <= 1 ?)
Tak
m = (1 + 1) / 2 = 1
Czy (x < a[1]) ? (Czy 55 < 44)
Nie
k = 2;
// ---------------------------------- //

Nie jest spełniony warunek pętli for (pomijamy pętlę)

a[2] = 55

i = 3
x = a[3] = 12
k = 1
p = 2

// Pętla while ---------------------- //
Czy k <= p ? (Czy 1 <= 2 ?)
Tak
m = (1 + 2) / 2 = 1
Czy (x < a[1]) ? (Czy 12 < 44)
Tak
p = 0;

Czy k <= p ? (Czy 1 <= 0 ?)
Nie (wychodzimy z pętli)
// ---------------------------------- //

// Pętla for ------------------------ //
j = 2
a[3] = a[2] = 55

j = 1
a[2] = a[1] = 44
// ---------------------------------- //

a[1] = 12

i = 4
x = a[4] = 42
k = 1
p = 3

// Pętla while ---------------------- //
Czy k <= p ? (Czy 1 <= 3 ?)
Tak
m = (1 + 3) / 2 = 2
Czy (x < a[2]) ? (Czy 42 < 44)
Tak // Przechodzimy do lewej połowy ciągu //
p = 1;

Czy k <= p ? (Czy 1 <= 1 ?)
Tak
m = (1 + 1) / 2 = 1
Czy (x < a[1]) ? (Czy 42 < 12)
Nie // Przechodzimy do prawej połowy ciągu //
k = 2;

Czy k <= p ? (Czy 2 <= 1 ?)
Nie (wychodzimy z pętli)
// ---------------------------------- //

// Pętla for ------------------------ //
j = 3
a[4] = a[3] = 55

j = 2
a[3] = a[2] = 44
// ---------------------------------- //

a[2] = 42

...