Materiały pochodzą z Platformy 

Edukacyjnej Portalu 

www.szkolnictwo.pl

Wszelkie  treści  i  zasoby  edukacyjne  publikowane  na  łamach  Portalu  www.szkolnictwo.pl    mogą  być  wykorzystywane  przez  jego 
Użytkowników 

wyłącznie 

w  zakresie  własnego  użytku  osobistego  oraz  do  użytku  w  szkołach  podczas  zajęć  dydaktycznych.  Kopiowanie,  wprowadzanie  zmian, 
przesyłanie, 

publiczne 

odtwarzanie 

i  wszelkie  wykorzystywanie  tych  treści  do  celów  komercyjnych  jest  niedozwolone.  Plik  można  dowolnie  modernizować  na  potrzeby 
własne 

oraz 

do 

wykorzystania 

w szkołach podczas zajęć dydaktycznych.

„Potęga matematyki polega 

na pomijaniu wszystkich 

myśli zbędnych i cudownej 

oszczędności operacji 

myślowych”

Ernest Mach

POLE KOŁA.

Umiesz obliczyć pole kwadratu, prostokąta, 
trójkąta, trapezu itp. Koło jest figurą o 
regularnym kształcie posiadającą 
powierzchnie. W tej lekcji dowiesz się jak 
obliczyć pole powierzchni koła.

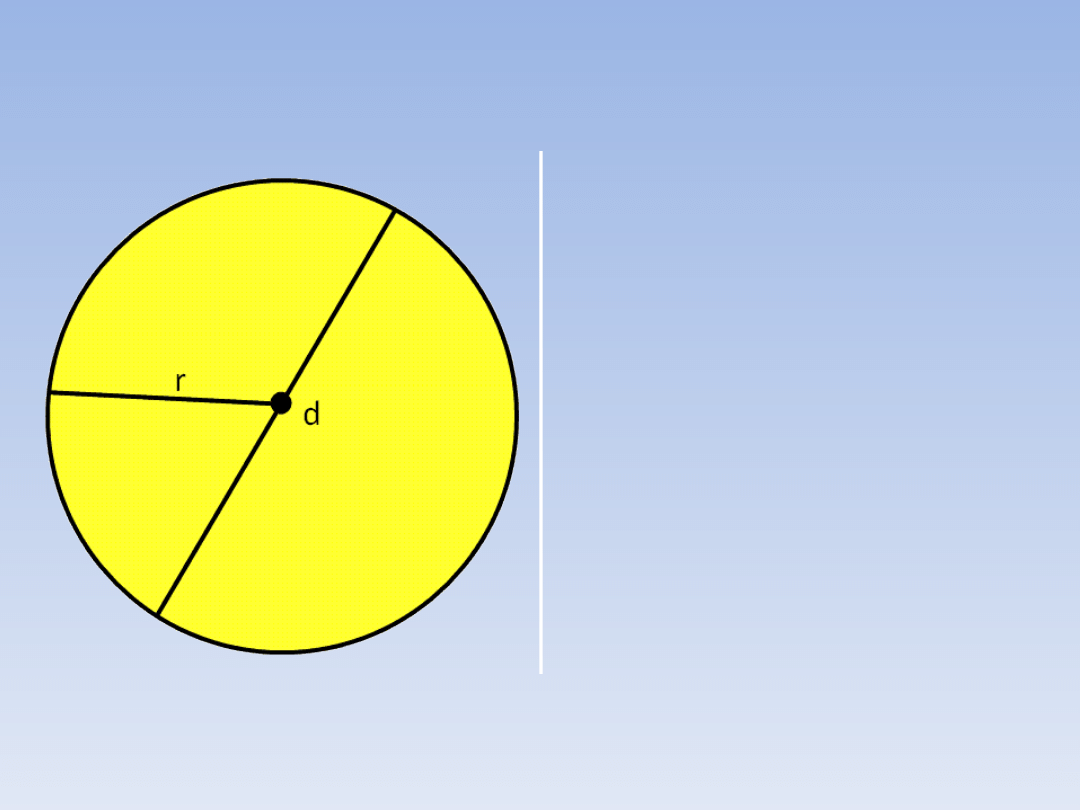
OZNACZENIA.

Przyjmujemy 
następujące 
oznaczenia:
r – długość 
promienia
d – długość 
średnicy
P – pole koła

Ważne:

d = 2r

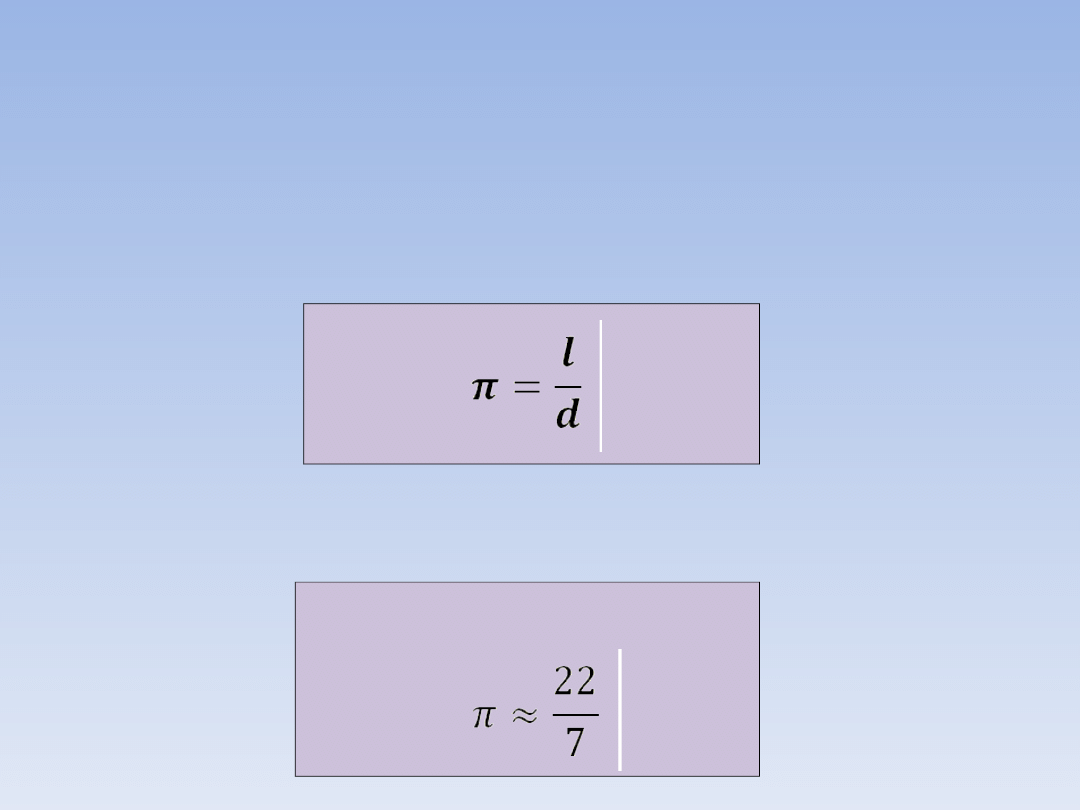
LICZBA π.

Przypomnijmy (dokładne informacje 
znajdziesz w lekcji „Koło. Okrąg. Liczba π”):

l – długość okręgu
Najczęściej stosowane przybliżenia:

   π ≈ 3,14

POLE KOŁA.

Pole koła o danej długości promienia – r, 
obliczamy korzystając ze wzoru:

P = πr

2

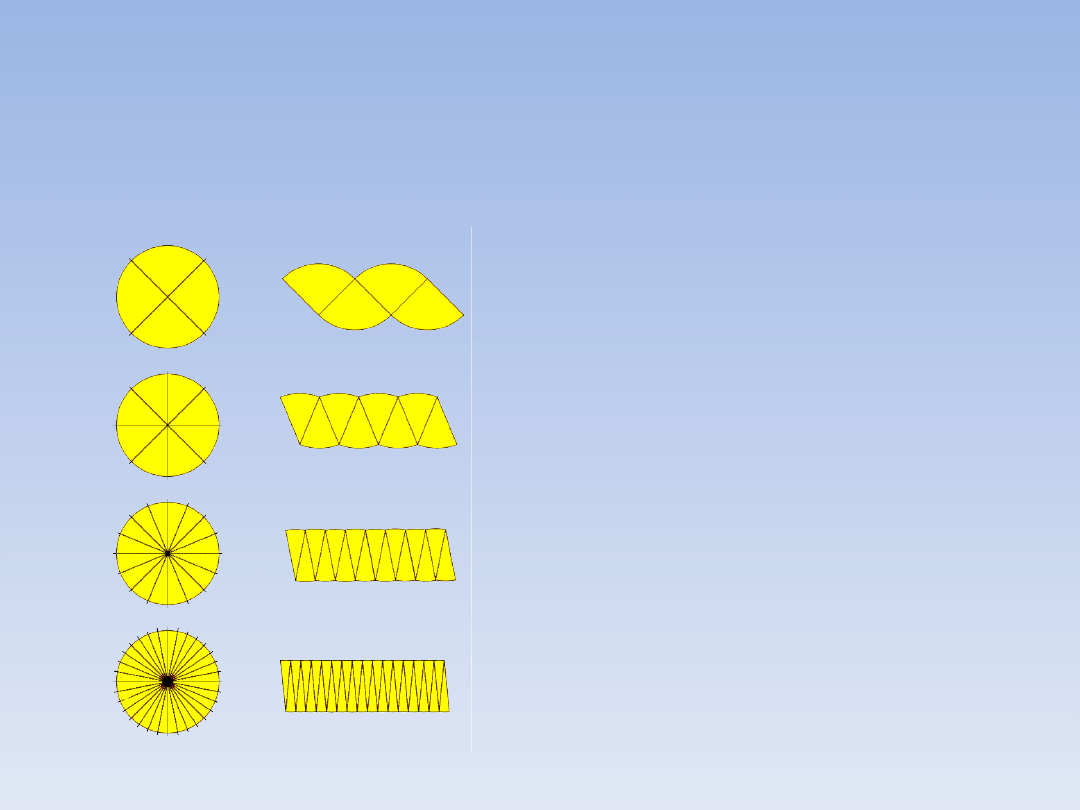
DLACZEGO P = πr

2

?

Koło można podzielić w taki sposób, że 
powstałe fragmenty po ułożeniu obok siebie 
utworzę prostokąt:

Krótszy bok tego 
prostokąta ma 
długość r, a dłuższy 
πr (połowy długości 
okręgu). Im więcej 
części tym powstała 
figura bardziej 
przypomina 
prostokąt. Po 
wymnożeniu 
otrzymujemy

P = πr

2

PRZYKŁADY.

PRZYKŁAD 1.
Oblicz pole koła o promieniu długości 6.
r = 6
P = πr

2 

P = π ∙ 6

2

 = 36π

PRZYKŁAD 2.
Oblicz pole koła o promieniu długości π.
r = π
P = πr

2 

P = π ∙ π

2

 = π

3

PRZYKŁADY.

PRZYKŁAD 3.
Oblicz pole koła o średnicy długości 10.
d = 10
d = 2r
r = 10 : 2 = 5
P = π ∙ 5

2

 = 25π

Przykład 4. 
Podaj przybliżoną wartość pola koła z 
przykładu 3.
π ≈ 3,14
P = 25π
P ≈ 25 ∙ 3,14 = 78,5

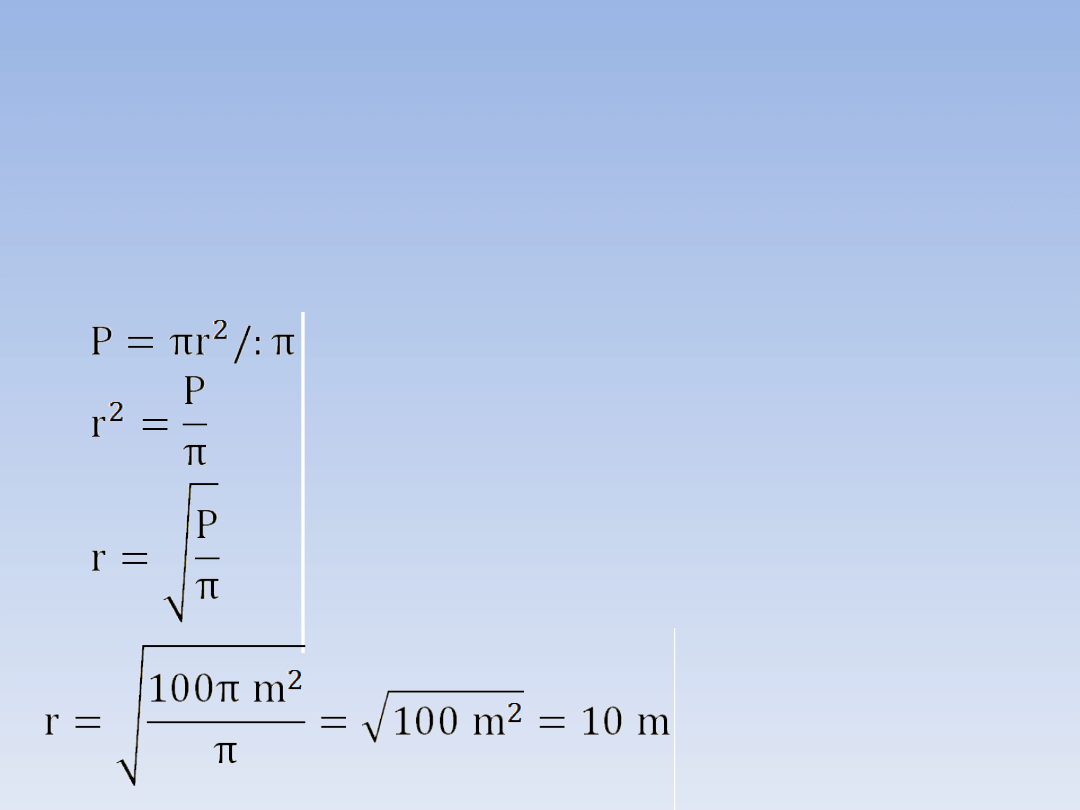
PRZYKŁADY.

PRZYKŁAD 5.
Jaki jest promień koła o polu 100π m

2

?

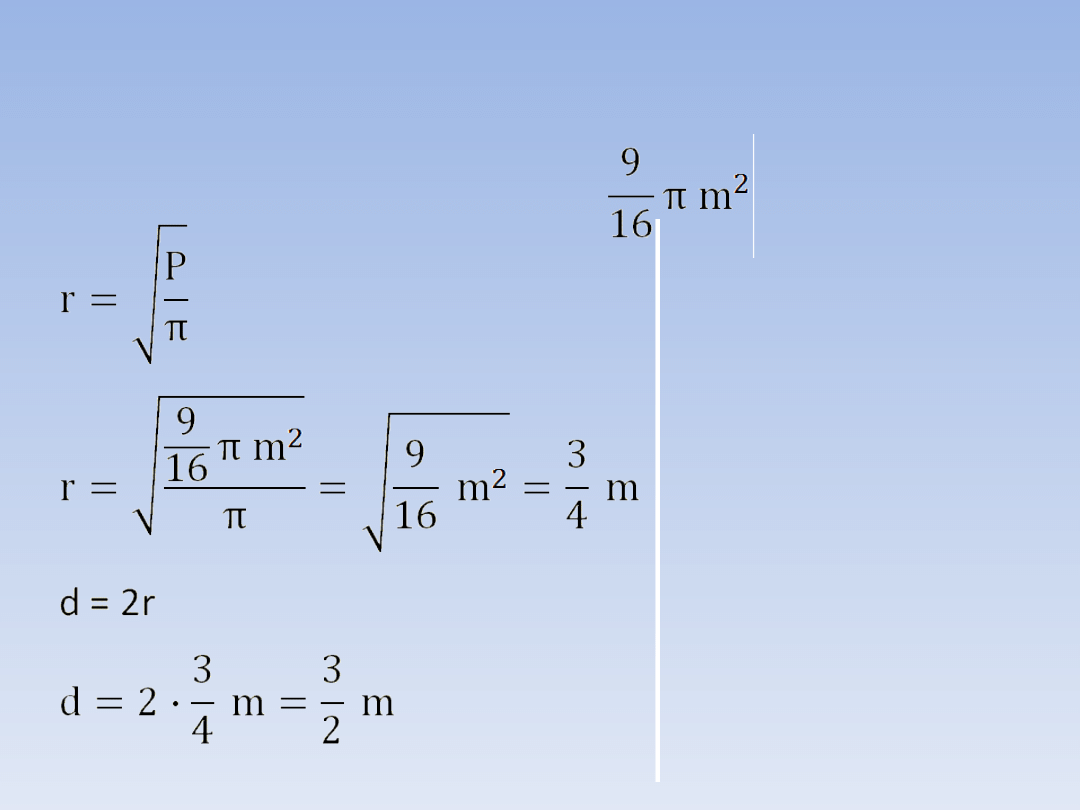
PRZYKŁADY.

PRZYKŁAD 6.
Jaka jest średnica koła o polu                  .

PRZYKŁADY.

PRZYKŁAD 7.
Oblicz pole koła o obwodzie 2π.
Wzór na długość okręgu (obwód koła):
l = 2πr
Z treści zadania wiadomo, że:
l = 2π – bez żadnych obliczeń możemy 
znaleźć r, widać       że r = 1
A więc:
P = πr

2 

P = π ∙ 1

2

 = π

PRZYKŁADOWE 

ZADANIA.

ZADANIE 1.
Majtkowie na statku zaczęli krzyczeć, że w 
mesie jest zbyt ciemno. Zdenerwowany 
bosman zapiął pas i krzyknął:
-Hej do czorta! Nie buntować mi się! Przez te 
cztery bulaje wpada tyle samo światła co 
przez dwa okna o wymiarach 0,5 m x 0,75 
m.
- Bosman jak zwykle nas buja – westchnął 
najstarszy z majtków.
Każdy bulaj ma średnicę 50 cm. Czy bosman 
bujał czy nie?

Bulaj – okno na statku – ma kształt koła dla zachowania  większej wytrzymałości.

PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
d = 50 cm = 0,5 m
r = 0,5 ∙ d – połowa śrenicy
r = 0,25 m
π ≈ 3,14
P

b

 = πr

2 

P

b

 = π ∙ (0,25 m)

2

 = 0,0625π m

2

P

b

 ≈ 0,0625 ∙ 3,14 m

2 

= 0,19625 m

2

Dla 4 bulajów mamy:
4 ∙ 0,19625 m

2

 = 0,785 m

2

PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
 Wymiary okna: 0,5 m x 0,75 m, więc jego 
pole to:
P

o

 = 0,5 m ∙ 0,75 m = 0,375 m

2

Dla dwóch okien mamy:
2 ∙ 0,375 m

2 

= 0,75 m

2

 

Wynika z tego, że bosman nie bujał.

PRZYKŁADOWE ZADANIA.

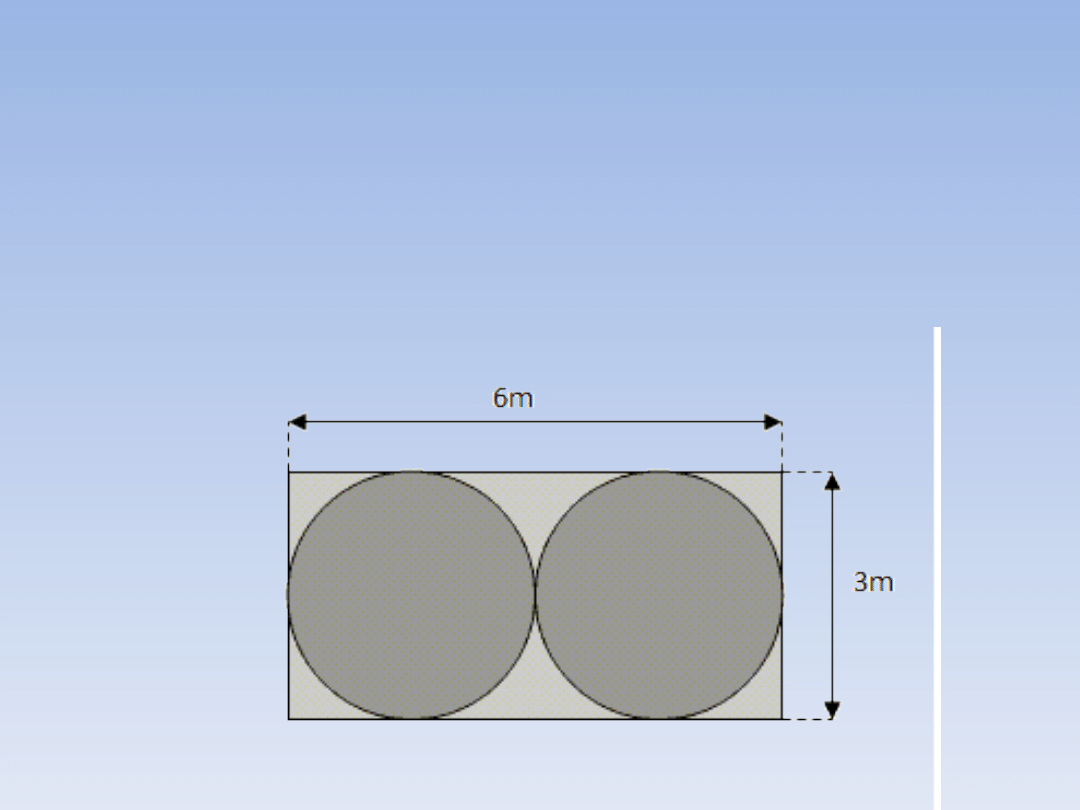
ZADANIE 2.
Prostokątny trawnik o wymiarach 6 m x 3 m 

podlewają dwa spryskiwacze (rysunek). Jaki 
obszar trawnika pozostaje niepodlany? W 
obliczeniach przyjmij π ≈ 3,14

PRZYKŁADOWE 

ZADANIA.

ZADANIE 2 – ciąg dalszy.
Obliczamy najpierw pole trawnika:
P

t

 = 6 m ∙ 3 m = 18 m

2

Następnie pole obszaru podlewanego – są to 

2 koła o średnicy 3 m czyli ich promień to 
1,5 m.

P = 2 ∙ π ∙ (1,5 m)

2 

= 4,5π

 

m

2

P ≈ 4,5 ∙ 3,14 m

2 

= 14,13 m

2

Obszar niepodlany to 
P

t

 – P

 

= 18 m

2 

- 14,13 m

2

 = 3,87 m

2

PRZYKŁADOWE 

ZADANIA.

ZADANIE 3.

Oblicz pole narysowanego pierścienia.

Aby obliczyć pole pierścienia wystarczy 

od pola dużego koła odjąć pole 

mniejszego (pole otworu). 

PRZYKŁADOWE 

ZADANIA.

ZADANIE 3 – ciąg dalszy.
Dla dużego koła mamy:
r

1

 = 6 + 4 = 10

P

1

 = π ∙ 10

2

 = 100π

Dla mniejszego koła mamy:
r

2

 = 6

P

2

 = π ∙ 6

2

 = 36π

Pole pierścienia:
P = P

1

 – P

2

 = 100π - 36π = 64π