Liczby kwantowe

Dr inż. Katarzyna Kozłowska

Główna liczba kwantowa

 Główną liczbę kwantową - n
 Wartości całkowitych liczb dodatnich: 1, 2, 3,…
 Określa powłokę elektronową do której należy elektron
 Główna liczba kwantowa n określa energię powłoki

elektronowej

Wartość n

Symbol literowy

1

K

2

L

3

M

4

N

5

O

6

P

Poboczna (dodatkowa, orbitalna,
azymutalna) liczba kwantowa

 Oznacza się literą – l

 Przyjmuje wartości: od 0, 1, 2, .......do ( n-1)

Jest to liczba kwantowa opisująca niewielkie różnice energii

elektronów danego poziomu energetycznego związane z

różnicami ich orbitalnego momentu pędu

 Dla atomów zawierających więcej niż jeden elektron - trzeba

znać równocześnie liczbę n oraz l -by określić poziom

energetyczny odpowiadający orbicie elektronowej

 Poboczna liczba kwantowa l - uściśla wartość energii elektronu

 Charakteryzuje kształt orbitali atomowych

Przykład obliczenia wartości
kwantowej liczby pobocznej - l

Dla pierwszej powłoki n = 1

Liczba poboczna l przyjmie wartość:

l = n - 1 = 1 -1 = 0

Dla drugiej powłoki gdzie n = 2

Liczba poboczna l ma wartości:

0 oraz n - 1 = 2 - 1 =1

czyli - dwie wartości liczby pobocznej:

l = 0,1

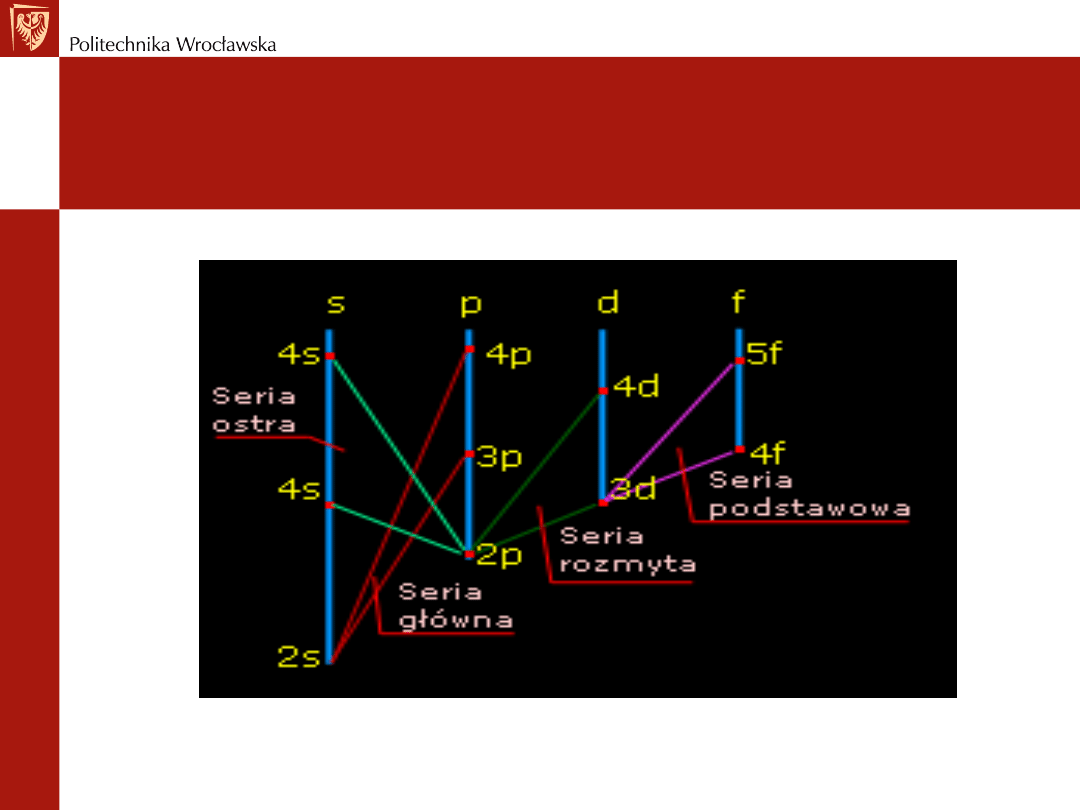
Schemat poziomów energetycznych
w atomie litu

Oznaczenia

 s dla serii ostrej /sharp/,

 p dla serii głównej /principle/,

 d dla serii rozmytej /difusel/

 f dla serii podstawowej /fundamental/

 dalej - porządek alfabetyczny

 Stan s, dla którego l = 0 – stan - któremu odpowiada

moment pędu równy zeru

 Gdy l przyjmuje wartości różne od zera - całkowita funkcja

falowa odbiega od symetrii sferycznej i w układzie pojawia

się moment pędu

Magnetyczna liczba kwantowa

W teorii Schrodingera - magnetyczna liczba kwantowa m -

reprezentuje składową momentu pędu w kierunku dowolnej osi

współrzędnych - na przykład w kierunku osi z

Co to oznacza?

Że wektor orbitalnego momentu pędu nie może ustawić się pod

dowolnym kątem do linii sił przyłożonego pola magnetycznego

Może ustawić się tylko w dozwolonych wybranych kierunkach

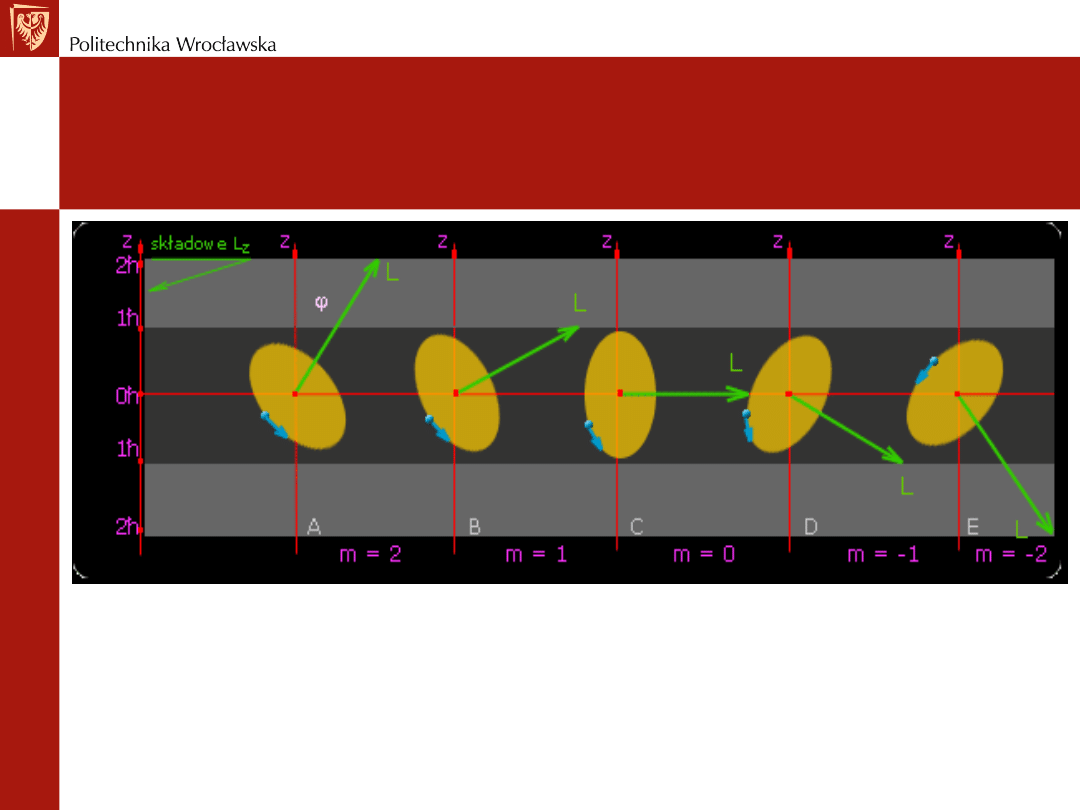
Wektor orbitalnego momentu L

 Wektor orbitalnego momentu L jest skwantowany w przestrzeni
 Względem danego kierunku z dozwolone są jedynie pewne

ustawienia wektora L

 Gdy l = 2 - kwantyzacja przestrzenna wektora orbitalnego

momentu pędu daje składowe Lz = 0h, +/-1h, +/-2h.

Magnetyczna liczba kwantowa

W znaczeniu fizycznym -magnetyczna liczba kwantowa m
- określa niewielkie różnice energetyczne pomiędzy
elektronami o tej samej liczbie kwantowej n i l oraz
wzajemne ustawienie się orbitali w przestrzeni pod
wpływem zewnętrznego pola magnetycznego

Magnetyczna liczba kwantowa

o Przy braku zewnętrznego pola magnetycznego orbitale nie

mają określonego kierunku w przestrzeni i nie różnią się

energią - są

zdegenerowane

o Degeneracja

- oznacza istnienie dwóch lub więcej różnych

stanów o tej samej energii

o Stany p są trzykrotne, stany d - pięciokrotne, a stany f -

siedmiokrotnie zdegenerowane

o Liczba m może przyjmować (2l + 1) wartości

o m = - l, -(l - 1), ......-1, 0, +1, .......,+(l -1) +l

Przykład:

dla l = 2 liczba magnetyczna m przyjmie wartości:
- 2, - (2 -1), 0, +(2 -1) , +2

m = -2, -1, 0, +1, +2

Zjawisko Zeemana

Magnetyczna liczba kwantowa m pozwoliła na wyjaśnienie
tzw.

Zjawiska Zeemana

- polegającego na dalszym

rozszczepieniu składników subtelnej budowy prążków
widmowych w polu magnetycznym

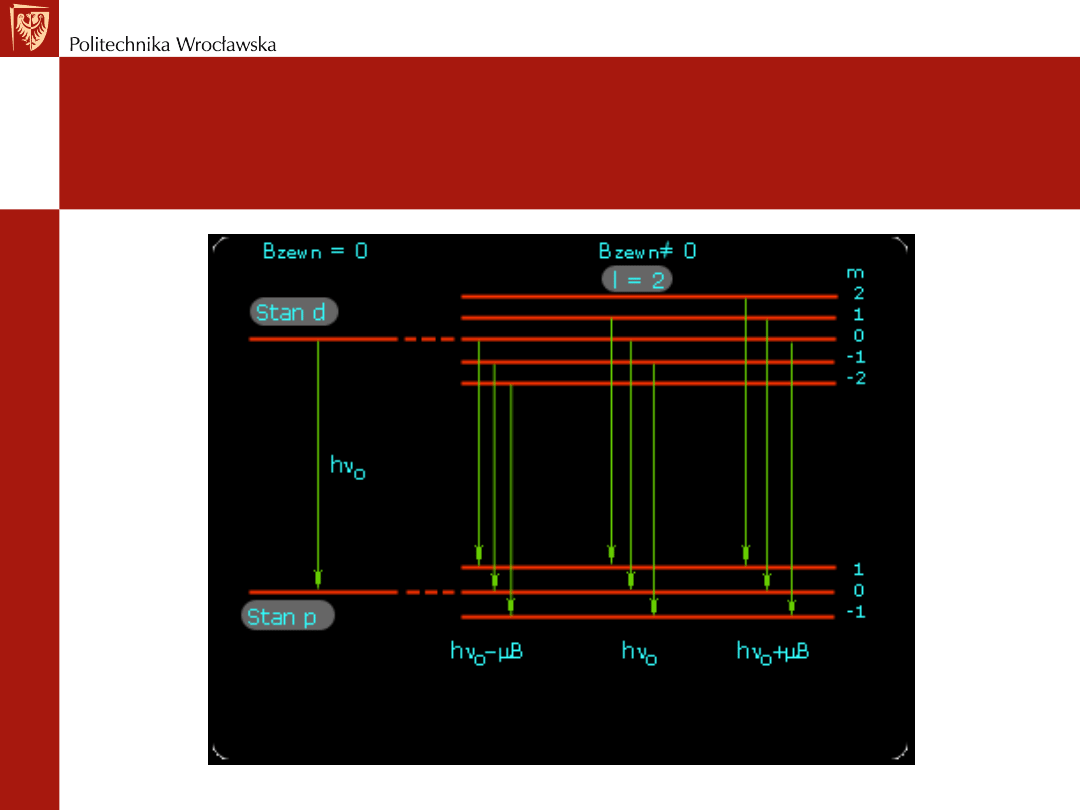
Zjawisko Zeemana

Zjawisko Zeemana

W nieobecności zewnętrznego pola magnetycznego w
wyniku przejścia ze stanu d do stanu p powstaje tylko jedna
linia widmowa. Gdy przyłożone zostanie zewnętrzne pole
magnetyczne, wtedy możliwych jest sześć przejść, chociaż
będą występować jedynie trzy rozróżnialne energie

Zjawisko Zeemana jest jednym z najbardziej bezpośrednich
potwierdzeń koncepcji kwantyzacji momentu pędu

Spinowa liczba kwantowa

o Linie widmowe rozszczepiają się w bardziej skomplikowany

sposób, niż wynika to z efektu Zeemana - zjawisko to
nazwano

anormalnym zjawiskiem Zeemana

o Niekiedy następuje rozdwojenie linii - co wskazuje na

rozdwojenie poziomów energetycznych

o Wskazywało to na istnienie liczby kwantowej która może

przybierać tylko dwie wartości

Spinowa liczba kwantowa

Rozdwojenie linii widmowych - wyjaśnił Goudsmit i

Uhlenbeck

Elektron oprócz takich właściwości jak ładunek i masa ma

jeszcze inną, immanentną własność, a mianowicie spinowy

moment pędu – spin, który jest wynikiem ruchu

obrotowego elektronu wokół własnej osi - ruch ten opisuje

spinowa liczba kwantowa s

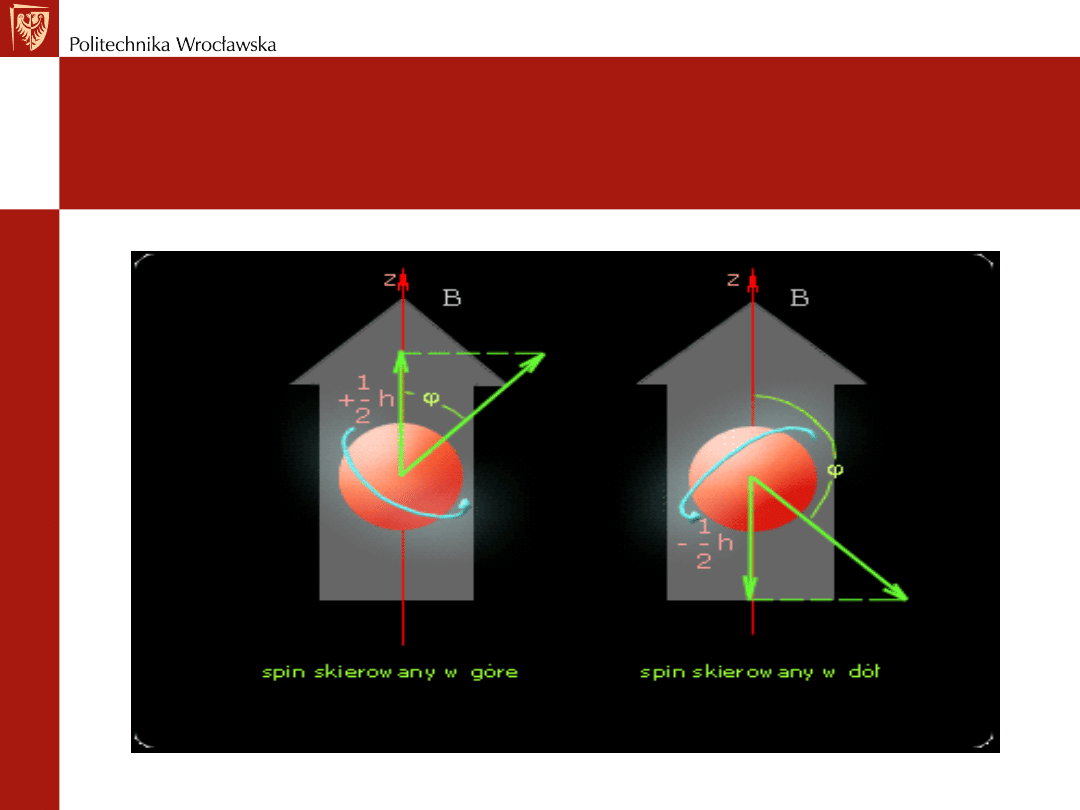
Spinowy moment pędu elektronu

Spinowa liczba kwantowa

 Spinowa liczba kwantowa – s

 Ma wyłącznie wartość 1/2 dlatego nie wprowadza

dodatkowego rozróżnienia stanów energetycznych

 Gdy przyłoży się zewnętrzne pole magnetyczne (B) -

składowa momentu pędu Ls w kierunku z jest skwantowana:

L

sz

= m

s

h / 2

gdzie; m

s

= +/-1/2 magnetyczna spinowa liczba kwantowa

Gdy ms = +1/2 - spin skierowany w górę
ms = -1/2 - spin skierowany w dół

Liczby kwantowe

Liczby kwantowe

Wartości

Liczba możliwych
wartości

Główna, n
Orbitalna, l

Magnetyczna, m
Spinowa, s
Magnetyczna spinowa,
ms

1, 2, 3, ....
0, 1, 2,...,(n - 1)

0, +/-1, +/-2,...,+/-l
1/2
+/-1/2

dowolna
n

2l + 1
1
2s + 1 = 2

Orbitale atomowe

Dla opisu stanu jednego elektronu w atomie ma
zastosowanie tylko jedna funkcja falowa nazywana

orbitalem.

Jest to najmniejszy obszar przestrzeni

wokółjądrowej, w którym prawdopodobieństwo
znalezienia elektronu o określonym zasobie
energii wynosi 90%. Każdemu orbitalowi można
przyporządkować maksymalnie dwa elektrony.

Orbital

jest określony za pomocą trzech liczb

kwantowych n, l, m

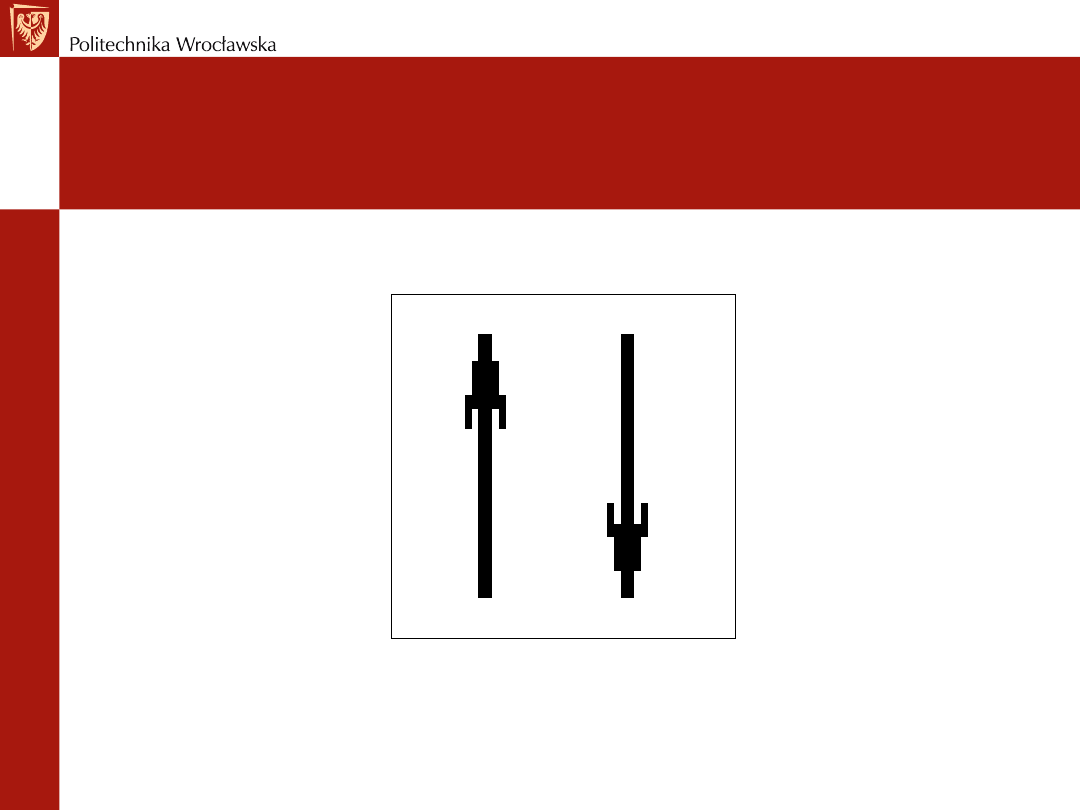
Symboliczne przedstawianie
orbitali atomowych

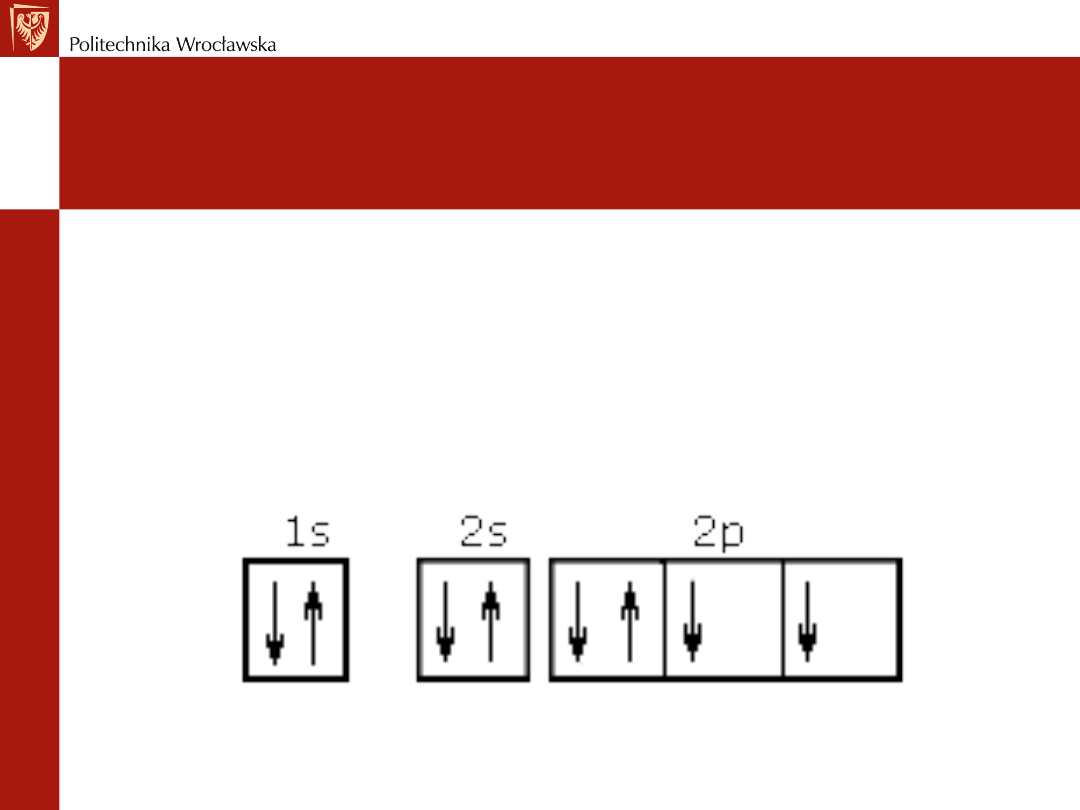
Sposób wypełniania orbitali

 Jeżeli l = 0, m = 0 i występuje tylko jeden orbital
 Jeżeli l = 1 to m przyjmuje wartości -1, 0, +1 – trzy wartości

m to trzy orbitale

 l jest niezależna od n - lecz musi spełniać warunek 0 < l < n

Trzy zasady

Przy przedstawianiu budowy powłok mają zastosowanie trzy

zasady:

o zasada rozbudowy

o zakaz Pauliego

o reguła Hunda

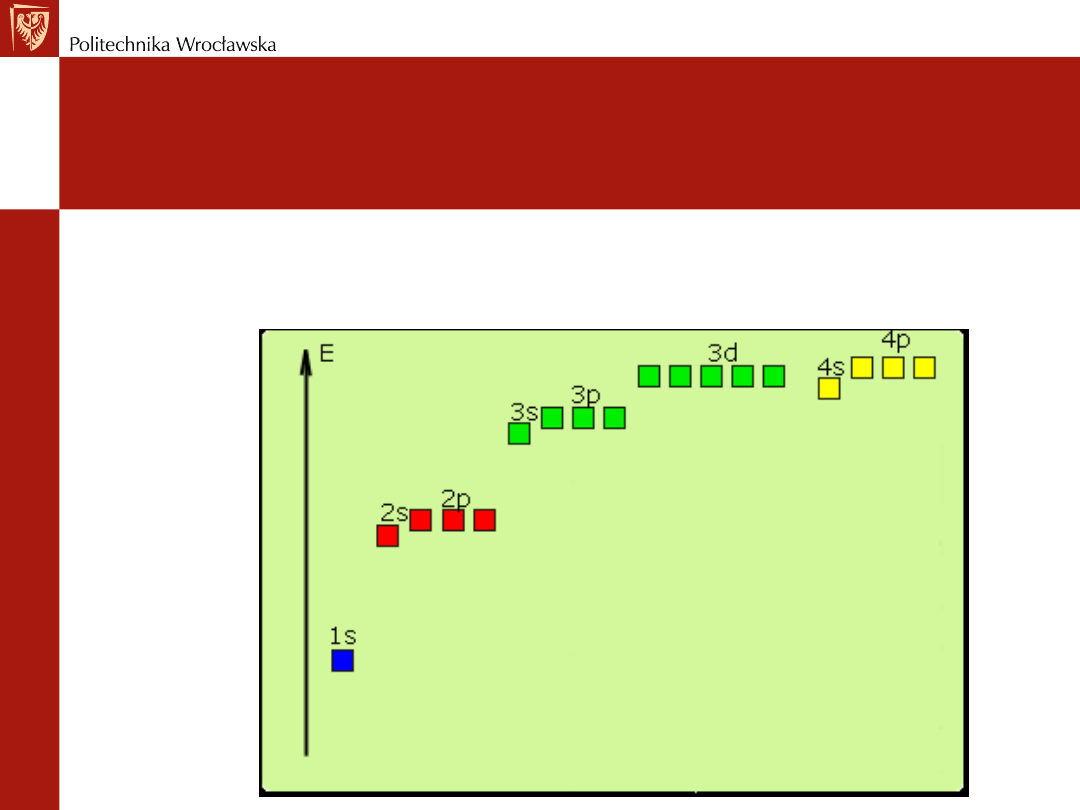
Zasada rozbudowy

Zasada ta mówi, że kolejne orbitale są zajmowane w
porządku wzrastającej energii

Zakaz Pauliego

Dwa elektrony mogą zajmować ten sam orbital tylko wówczas -

gdy ich spiny są przeciwne

tj. zorientowane w przeciwnych kierunkach

Nie mogą istnieć dwa elektrony w identycznym stanie

kwantowym -

tzn. mające identyczne wartości pięciu liczb kwantowych (n, l,

m, s, m

s

)

Zakaz Pauliego

 Wolfgang Pauli /1950 - 1959 / - zauważył, że obecność

jednego elektronu na orbitalu wyklucza możliwość

znalezienia się na nim innego elektronu o tej samej

orientacji spinu

 Jest on słuszny także dla wiązań chemicznych elektronów w

ciałach stałych i budowy jądra atomowego

 Na podstawie zakazu Pauliego - można wyliczyć

maksymalną liczbę elektronów jaka może pomieścić się na

poszczególnych powłokach i podpowłokach atomu

Maksymalna pojemność powłok
wynosi:

Numer

powłoki

Maksymalna

ilość

elektronów

1

2

2

8

3

18

4

32

5

50

Maksymalna liczba elektronów
dla podpowłok wynosi:
s – 2
p – 6
d – 10
f - 14

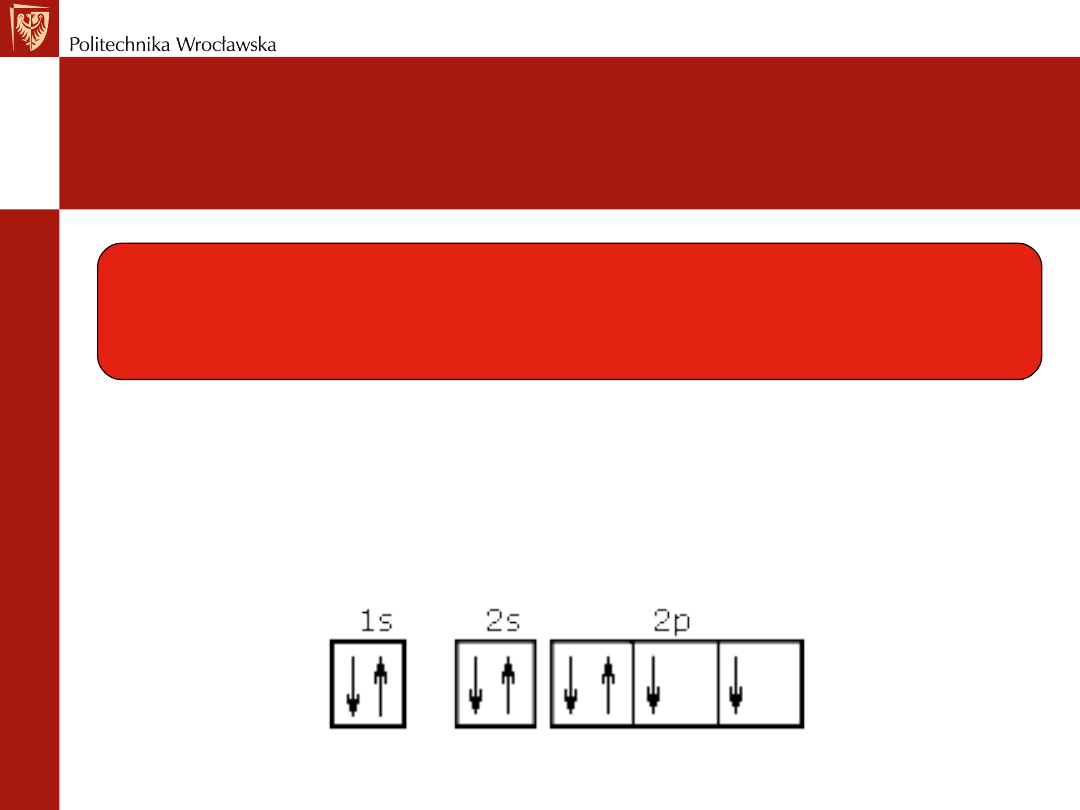
Reguła Hunda

Elektrony obsadzają orbitale w taki sposób,

aby liczba niesparowanych elektronów w danej podpowłoce

była możliwie największa

Oznacza to, że przy zapełnianiu kolejnych orbitali elektronami

wszystkie orbitale odpowiadające (orbitale o tych samych

liczbach kwantowych n i l) zostaną zapełnione najpierw po

jednym elektronie o spinie równoległym, a dopiero potem

drugim elektronem o spinie przeciwstawnym

Orbital typu s

 " Kształt orbitalu"

-powierzchnia graniczną
obejmującą większą część
gęstości
prawdopodobieństwa

 Ruch elektronu w obrębie

orbitali s prawdopodobnie
odbywa się wzdłuż
promienia w kierunku od i
dośrodkowym

Orbital typu p

 Elektrony w powłoce n = 2 mogą mieć wartość liczby pobocznej

l = 0 i 1 tzn. oprócz orbitalu s pojawiają się orbitale p

 Trzy zdegenerowane / tzn. o jednakowej energii/ orbitale p mają

w przybliżeniu kształt figur powstałych przez obrót ósemki

dookoła podłużnej osi i są ustawione względem siebie w

przestrzeni pod kątem prostym

 Prawdopodobieństwo znalezienia się elektronu w środkowej

części jest równe zeru

Orbital typu d i f

• Poziom n = 3 obejmuje podpoziomy s, p, d
• Orbitale typu f mają symetryczny rozkład w przestrzeni