Właściwości
energetyczne
sygnałów

„Teoria sygnałów” Zdzisław Papir

•Definicja energii i mocy sygnału

•Energia sygnału w dziedzinie
częstotliwości

•Moc sygnału w dziedzinie
częstotliwości

•Zmienna losowa, proces losowy

•Analiza widmowa procesów losowych

•Podsumowanie, przykłady

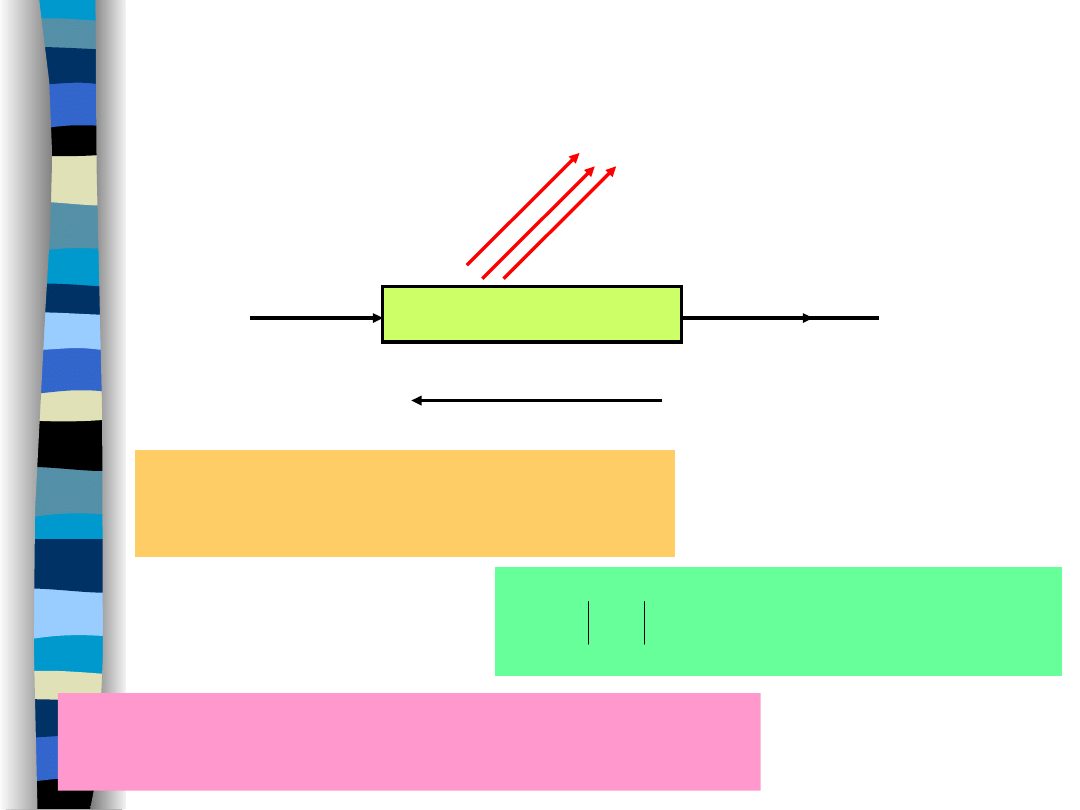
Definicja energii
sygnału

„Teoria sygnałów” Zdzisław Papir

   

 

 

R























t

x

dt

t

x

dt

t

i

t

u

E

,

2

i(t) = x(t)

u(t) = x(t)

E

R = 1 

 

   

 

C























t

x

dt

t

x

t

x

dt

t

x

E

,

*

2

Sygnał nazywamy energetycznym,
jeżeli E < .

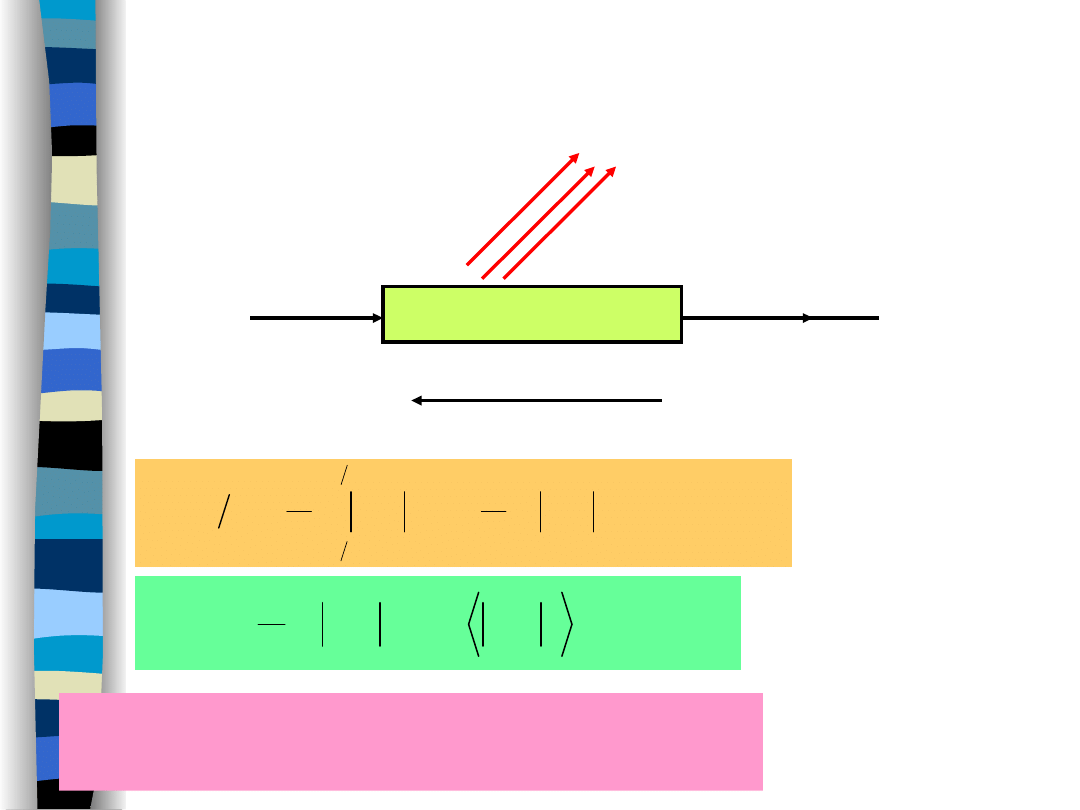
Definicja mocy sygnału

„Teoria sygnałów” Zdzisław Papir

i(t) = x(t)

u(t) = x(t)

P = E/T

R = 1 

 

 

 

C

















t

x

dt

t

x

T

dt

t

x

T

T

E

P

T

T

T

,

1

1

2

2

2

2

 

 

 

C













t

x

t

x

dt

t

x

T

P

T

T

,

1

lim

2

2

Sygnał nazywamy sygnałem mocy,
jeżeli P < .

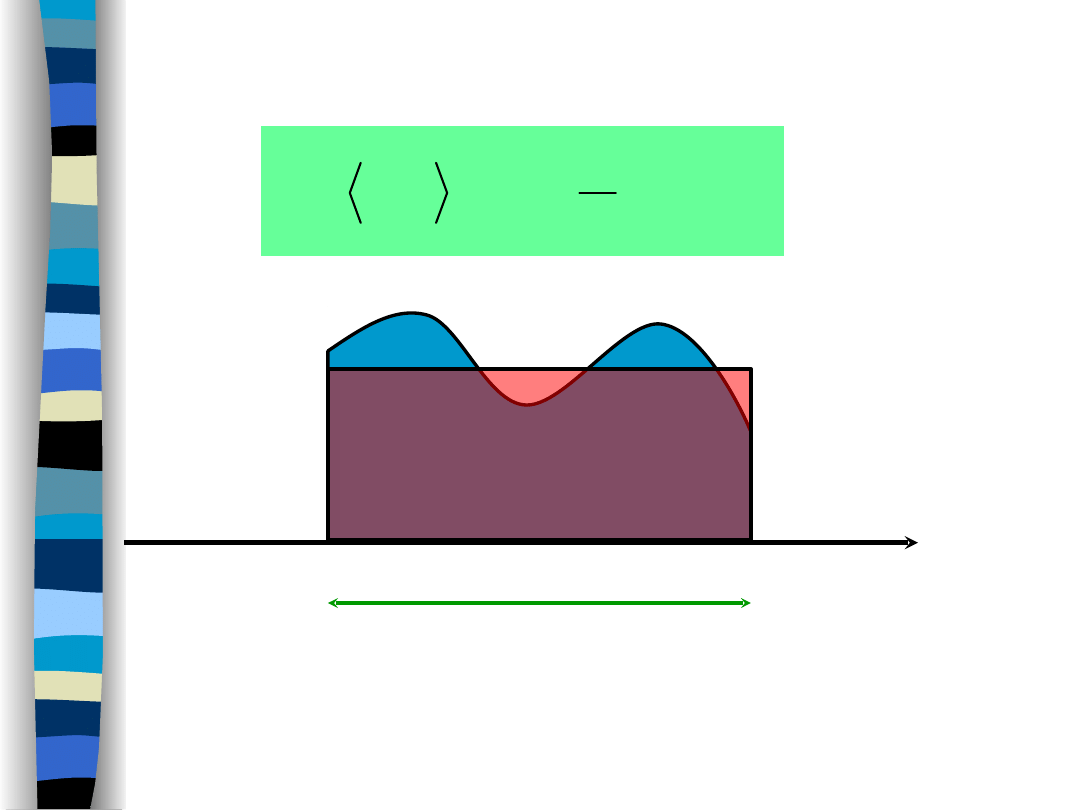
Uśrednianie po czasie

„Teoria sygnałów” Zdzisław Papir

 

 











T

T

dt

t

v

T

t

v

v

1

lim

~

Uśrednianie po czasie zastępuje wielkość fluktuującą
wielkością stałą równoważną w sensie całki oznaczonej.

v(t)

v~

T

t

0

t

0

+ T

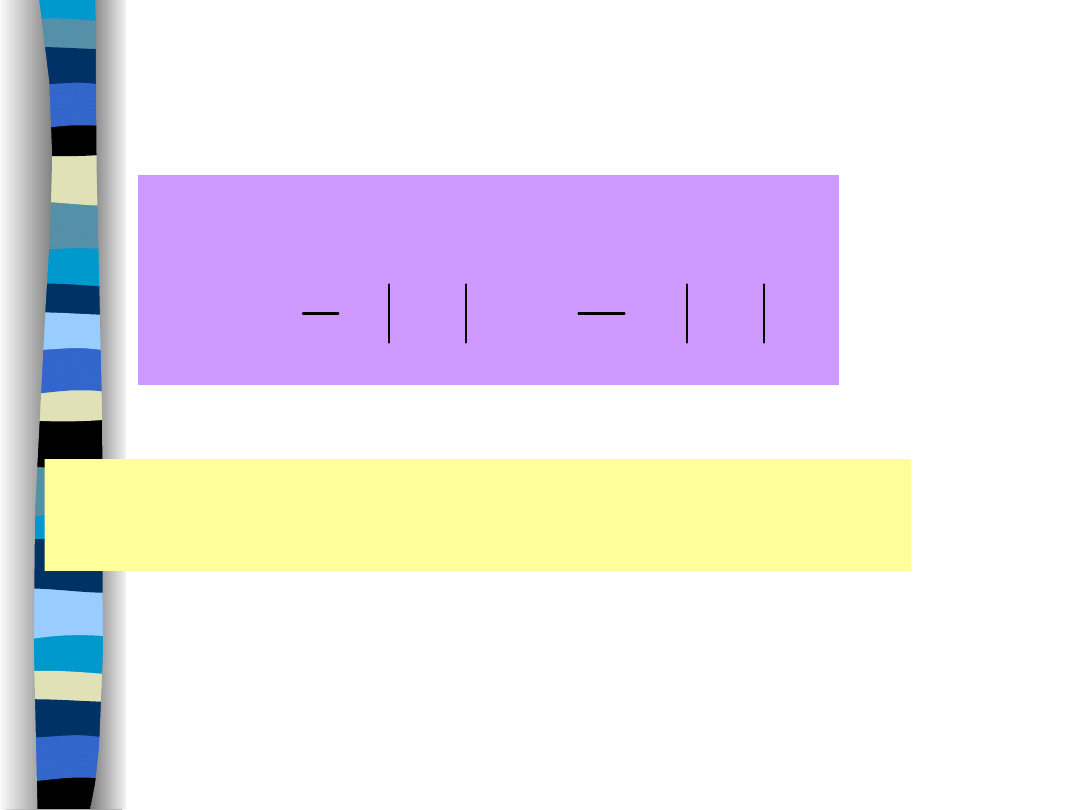
Moc sygnału okresowego

„Teoria sygnałów” Zdzisław
Papir

  



 

 

















0

2

0

2

0

1

1

lim

T

T

T

dt

t

x

T

dt

t

x

T

P

T

t

x

t

x

Moc sygnału okresowego jest równa
jego mocy za jeden okres.

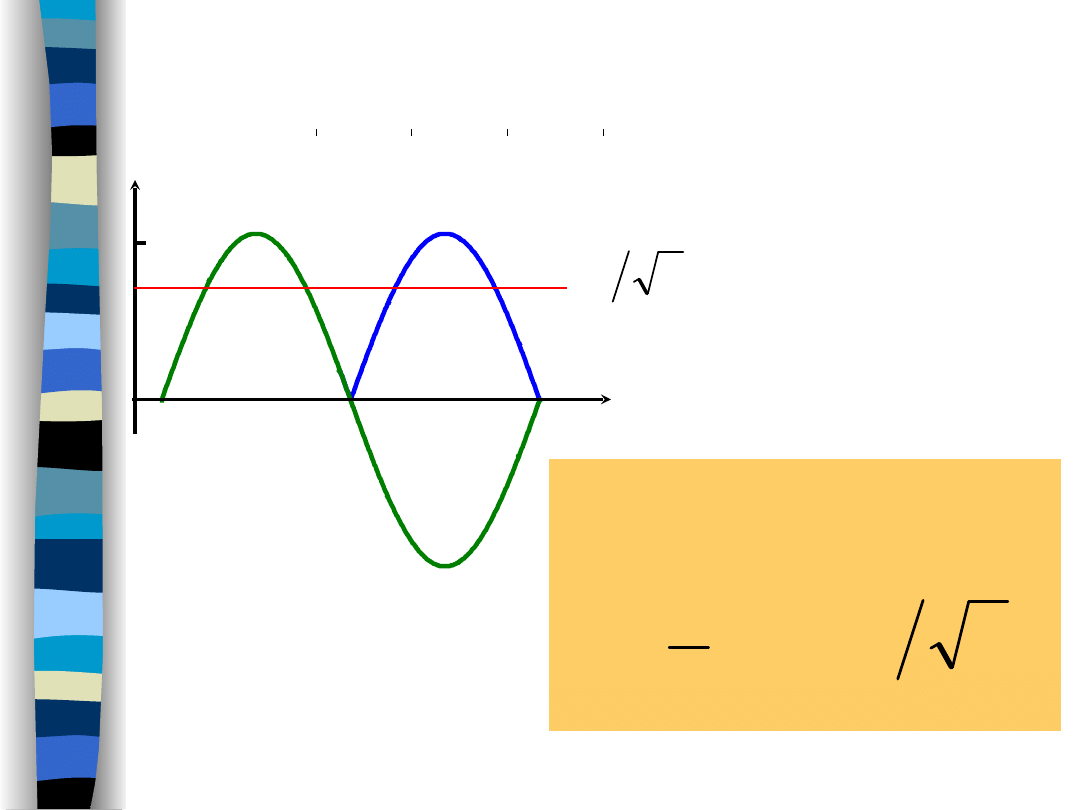
Moc sygnału okresowego -
sygnał harmoniczny

„Teoria sygnałów” Zdzisław Papir

 









2

2

2

2

1

sin

a

a

P

t

a

t

x













2

a

a

Energia sygnału
w dziedzinie
częstotliwości

„Teoria sygnałów” Zdzisław Papir

 

 

 

 



































0

2

2

2

1

2

1













d

X

d

X

dt

t

x

E

t

x

R

 

 

2





X

S



Twierdzenie Parsevala

Widmowa gęstość energii (widmo gęstości energii):

Funkcja korelacji dla sygnału
energetycznego

„Teoria sygnałów” Zdzisław Papir

 

 

2





X

S



 





 

   

 

 

 

 





  





























































































dt

t

x

t

x

dt

d

e

X

t

x

d

e

dt

e

t

x

X

d

e

X

X

d

e

X

X

t

j

j

t

j

j

j











































*

*

*

*

2

2

1

2

1

2

1

2

1

2

1

F

 

 

 

  



















dt

t

x

t

x

R

X

S









*

2

Funkcja korelacji dla sygnału
energetycznego

„Teoria sygnałów” Zdzisław Papir

 

 

 

 

  





















dt

t

x

t

x

R

X

S

t

x









2

R

Funkcja korelacji jest parzysta:

 

 







R

R

Funkcja korelacji jest ograniczona z maksimum R(0):

 

 

E

R

R



 0



Widmowa gęstość energii dla sygnałów rzeczywistych
jest funkcją parzystą:

 

 







S

S

Funkcja korelacji jako miara
podobieństwa sygnałów

„Teoria sygnałów” Zdzisław Papir

 

 





   

 































dt

t

dt

t

t

x

c

dt

t

c

t

x

e

c

2

opt

2

2

min







   

 

 

   

 























































dt

t

dt

t

t

x

dt

t

x

e

dt

t

dt

t

t

x

c

2

2

2

2

min

2

opt









Funkcja korelacji jako miara
podobieństwa sygnałów

„Teoria sygnałów” Zdzisław Papir

Nierówność

Schwarza

   

 

 





































dt

t

dt

t

x

dt

t

t

x

2

2

2

0





 













dt

t

x

e

2

2

min

0

 

   

 





































dt

t

dt

t

t

x

dt

t

x

e

2

2

2

2

min





   

 

 

t

t

x

dt

t

t

x

















0

   

   

t

t

x

t

t

x







Funkcja korelacji jako miara
podobieństwa sygnałów

„Teoria sygnałów” Zdzisław Papir

Z nierówności
Schwarza:

   

 

 



































dt

t

dt

t

x

dt

t

t

x

2

2

2





   

 

 



























dt

t

dt

t

x

dt

t

t

x

2

2







wynika:

1





Współczynnik



jest określany jako współczynnik korelacji

czyli podobieństwa sygnałów x(t) oraz



(t).

   

 



















dt

t

dt

t

t

x

c

2

opt





Funkcja korelacji jako miara
podobieństwa sygnałów

„Teoria sygnałów” Zdzisław Papir

 

  



 

 





























dt

t

dt

t

x

dt

t

t

x

2

2











Analiza korelacji (podobieństwa) może uwzględniać
przesunięcie sygnałów względem siebie.

 

  















dt

t

t

x

R







Funkcja

interkorelacji

sygnałów x(t) oraz



(t):

Funkcja

autokorelacji

sygnału x(t):

 

  















dt

t

x

t

x

R





Funkcja korelacji i widmowa
gęstość energii - filtracja

„Teoria sygnałów” Zdzisław Papir

)

(



H

)

(t

x

 

t

y

 

 





x

x

S

R



 

 





y

y

S

R



 

   

 

   

 

   



















x

y

S

H

S

X

H

Y

X

H

Y

2

2

2







Widmowa gęstość energii jest modyfikowana przez kwadrat
ch-aki a-cz.
Cha-ka f-cz nie zmienia widmowej gęstości energii.

Moc sygnału
w dziedzinie
częstotliwości

„Teoria sygnałów” Zdzisław Papir

 

 









 

 

 

 

 

 



















































































d

S

T

X

P

d

X

T

dt

t

x

T

P

t

x

T

dt

t

x

T

P

T

t

t

t

T

t

t

t

t

x

t

x

T

T

T

T

T

T

T

T



 



 



2

2

2

2

2

0

0

0

0

lim

2

1

2

1

lim

1

lim

1

lim

,

,

0

,

,

Twierdzenie Parsevala

widmo gęstości mocy

 

t

x

T

 

t

x

0

t

T

t 

0

Moc sygnału
w dziedzinie
częstotliwości

„Teoria sygnałów” Zdzisław Papir

 

 























d

S

T

X

P

T

T



 



 



2

lim

2

1

Widmowa gęstość mocy (widmo gęstości mocy):

 

 

T

X

S

T

T

2

lim











Funkcja autokorelacji sygnału mocy:

 

  



  























t

x

t

x

dt

t

x

t

x

T

R

T

T

*

*

1

lim

posiada identyczne właściwości jak funkcja autokorelacji
sygnału energetycznego, w szczególności:

 

 





S

R



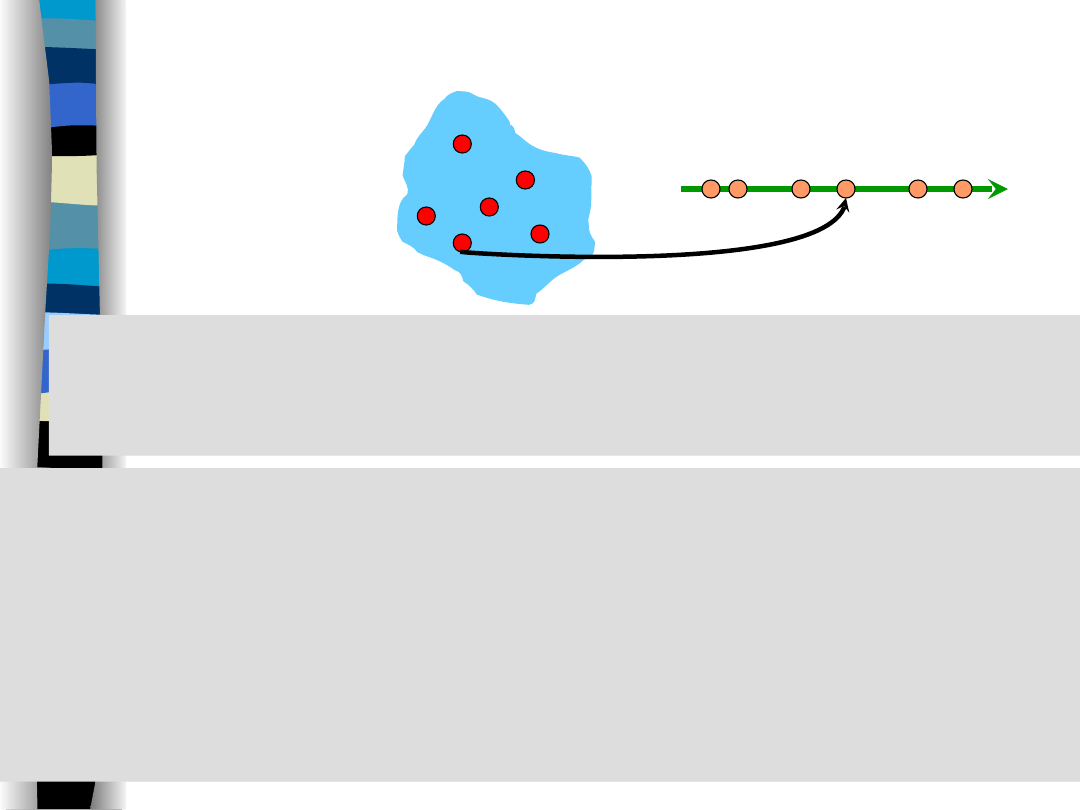
Zmienna losowa

„Teoria sygnałów” Zdzisław Papir

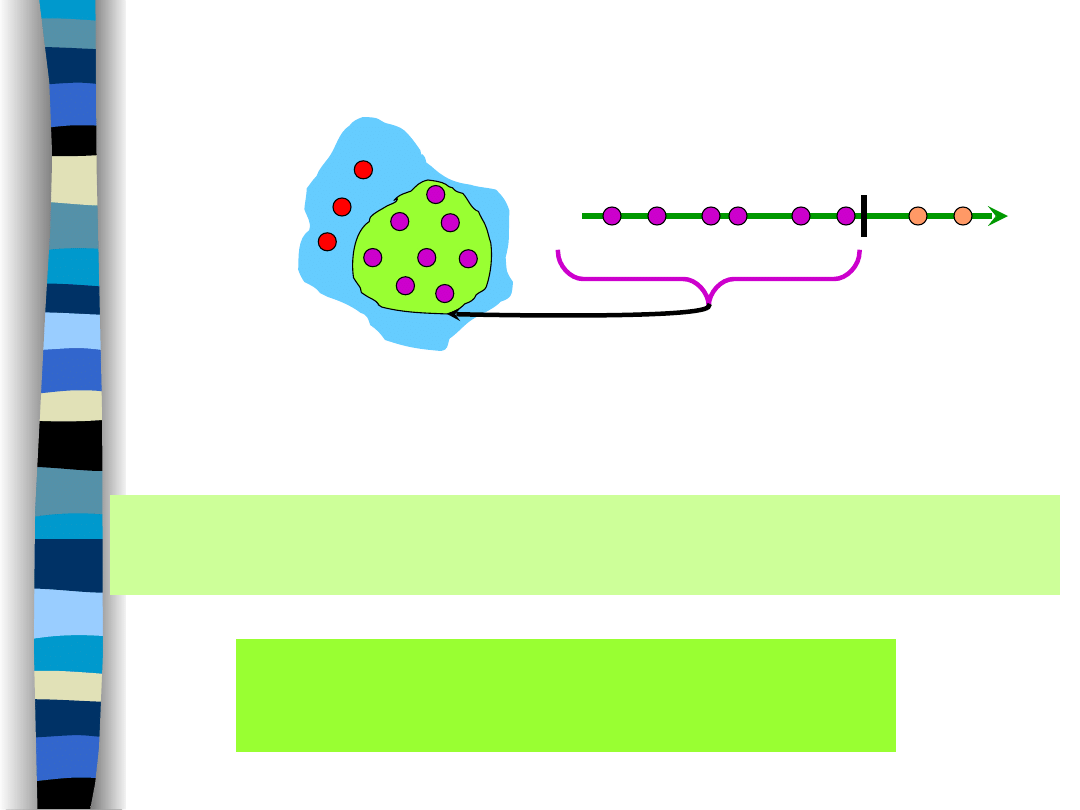
Zmienna losowa

x

jest w istocie rzeczy

funkcją (losową)

przyporządkowującą

zdarzeniom elementarnym

liczby (rzeczywiste).

W zastosowaniach telekomunikacyjnych mamy do czynienia
ze zmiennymi losowymi w takich sytuacjach jak: napięcie w
układzie elektronicznym (z uwzględnieniem szumów), liczba
rozmów telefonicznych w ustalonym przedziale czasu czy
liczba przekłamanych bitów w słowie kodowym.

Zmiena losowa jest wygodnym modelem, gdy nie jesteśmy
w stanie uchwycić w modelu wszystkich mechanizmów.

R





x(



)

Dystrybuanta zmiennej losowej

„Teoria sygnałów” Zdzisław Papir



 

 





 

 











i

i

x

x

F





Pr

Pr

Pr

A

x



i

R

Pr{x(



)  x}x

A

Dystrybuanta zmiennej losowej

 

 





x

x

F







x

Pr

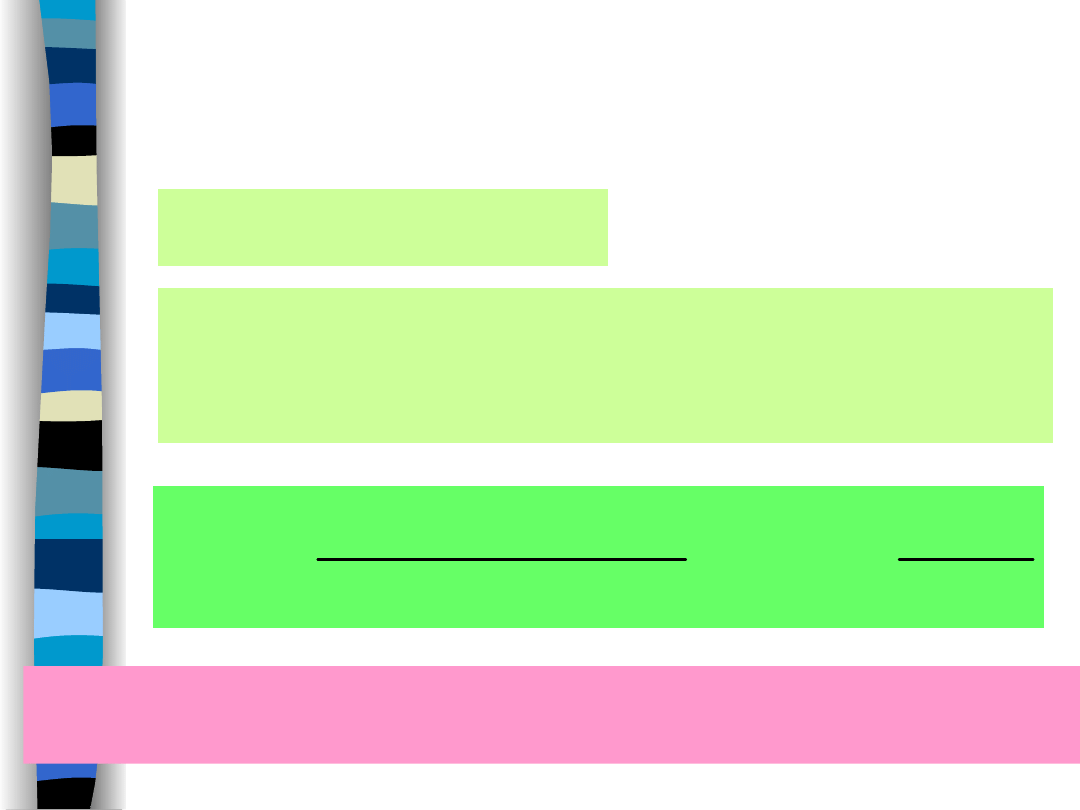
Gęstość prawdopodobieństwa
zmiennej losowej

„Teoria sygnałów” Zdzisław Papir

Dystrybuanta zmiennej losowej

 

 





x

x

F







x

Pr





 

 





 





 

x

x

f

x

x

x

x

x

x

x

F

x

x

F

































x

x

Pr

Pr

 





 

 

dx

x

dF

x

x

F

x

x

F

x

f

x



 

















0

Kształt funkcji gęstości prawdopodobieństwa wskazuje
na „preferowany” zakres wartości zmiennej losowej x.

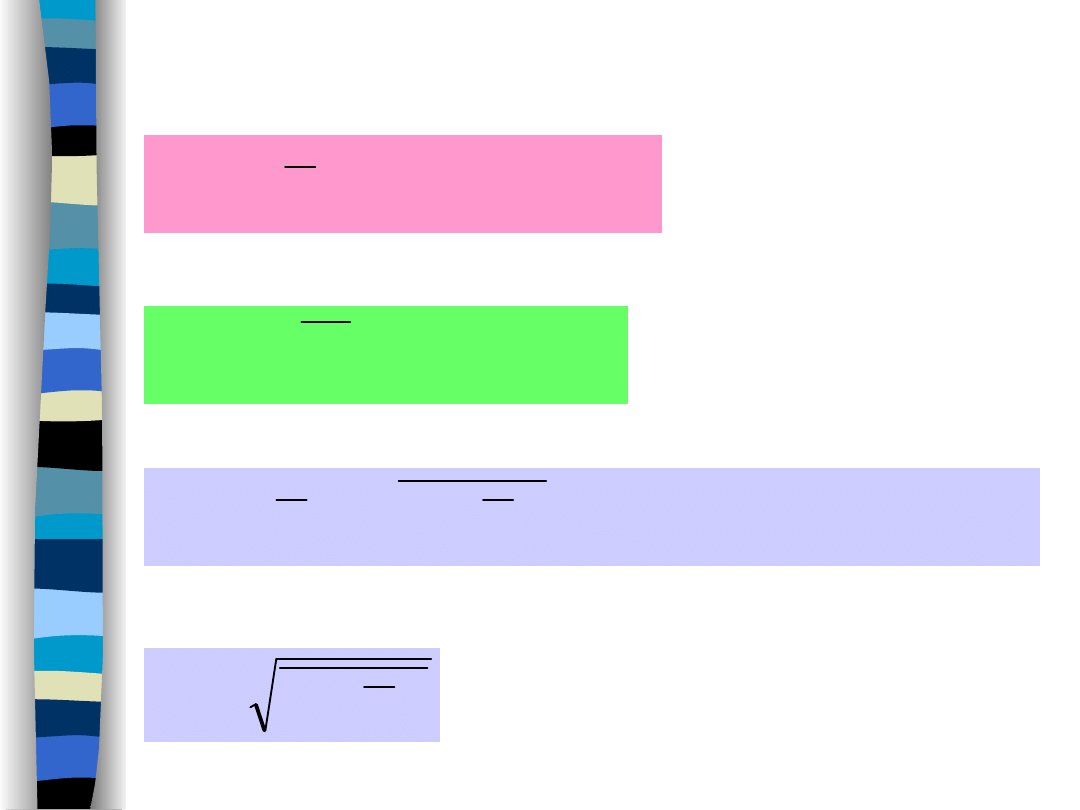
„Teoria sygnałów” Zdzisław Papir

Momenty zmiennej losowej

Wartość średnia zmiennej losowej

 

 















dx

x

xf

x

x

x



E

Wartość średniokwadratowa zmiennej losowej

 

 













dx

x

f

x

2

2

2

E

x

x

Wariancja zmiennej losowej















  





















dx

x

f

x

2

2

2

2

E

x

x

x

x

x

x





Odchylenie standardowe zmiennej losowej





2

x

x

x







„Teoria sygnałów” Zdzisław Papir

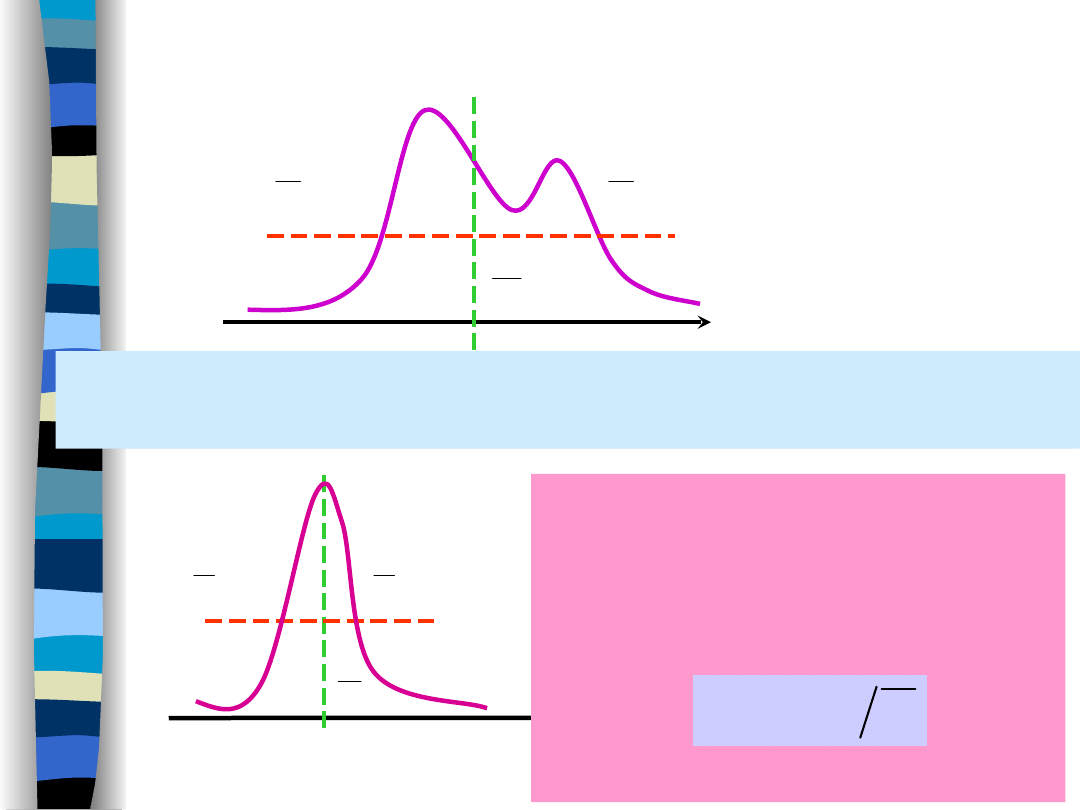
Momenty zmiennej losowej

Odchylenie standardowe jest miarą rozrzutu wartości
zmiennej losowej wokół jej wartości średniej.

x

x

x

x





x

x





x

x

x

x





x

x





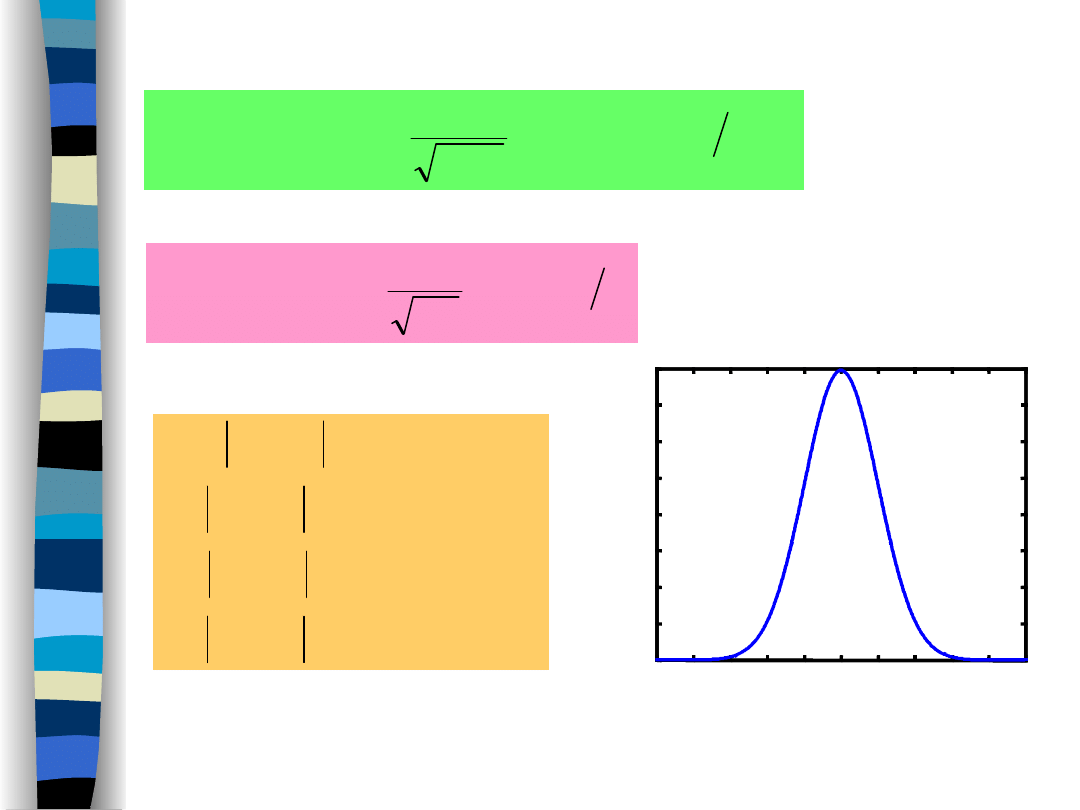
Im mniejsza jest wartość
współczynnika
rozproszenia zmiennej
losowej c

x

,

tym

bardziej zmienna losowa
„przypomina”
stałą deterministyczną (c

x

=

0).

x

x

x





c

„Teoria sygnałów” Zdzisław Papir

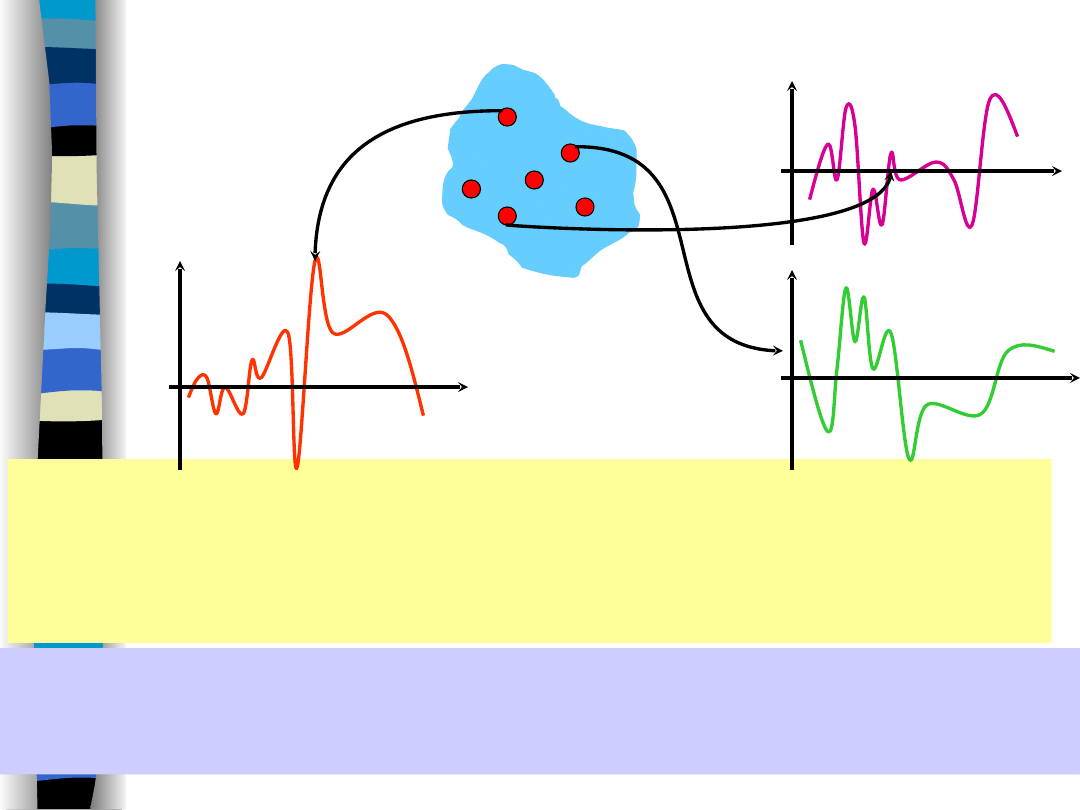
Zmienna losowa normalna





 









2

2

2

exp

2

1

:

,

















x

x

f

N

 

 





2

exp

2

1

:

1

,

0

2

x

x

f







N

0

+

+2

-

+3

-2

-3

 





 





 





 





9999

,

0

4

1

,

0

Pr

997

,

0

3

1

,

0

Pr

95

,

0

2

1

,

0

Pr

68

,

0

1

,

0

Pr

























N

N

N

N

„Teoria sygnałów” Zdzisław Papir

x(t,



)

x(t=const,



=var) – zmienna losowa

x(t=var,



=const) – realizacja procesu losowego

x(t=var,



=var)

– zbiór realizacji procesu losowego

x(t=const,



=const)

– liczba





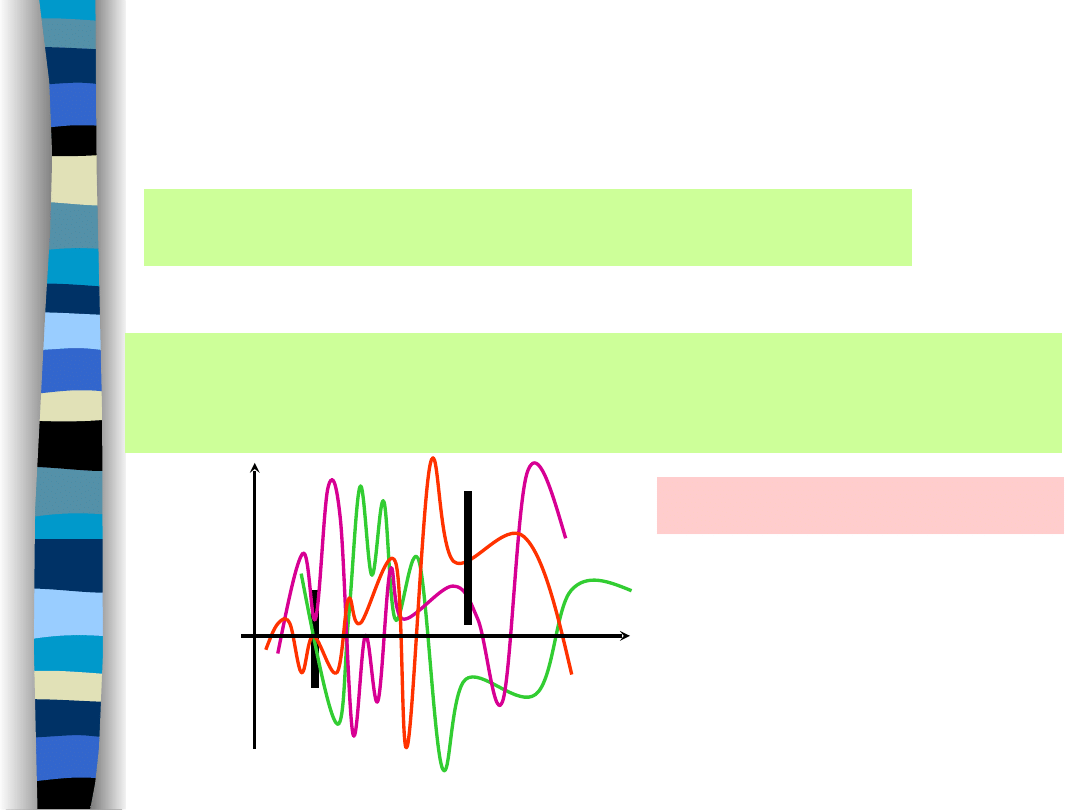
Realizacja procesu losowego

x(t,



)

jest zwykłym, deterministycznym

przebiegiem czasowym; losowość procesu nie jest nieodłączną właściwością
tej funkcji, a przejawia się wyłącznie w losowym jej wyborze.

Procesy
losowe

x(t,



)

x(t,



)

x(t,



)

Gęstości prawdopodobieństwa
procesu losowego

„Teoria sygnałów” Zdzisław Papir

 





 

x

t

x

f

x

x

t

x













;

,

Pr



x

Gęstość prawdopodobieństwa I rzędu

Gęstość prawdopodobieństwa II rzędu

 





















2

1

2

1

2

2

2

1

1

1

,

;

,

,

,

Pr

x

x

t

x

x

f

x

x

t

x

x

x

t

x





































x

x

2

x

2

2

x

x









t

1

1

x

x 



1

x

t





 

t

x

f

t

x

x

f

,

0

,

;

,

2

1







Wartości średnie procesu
losowego

„Teoria sygnałów” Zdzisław Papir

Wartość średnia procesu losowego

 

 

 













dx

t

x

xf

t

t

;

x

x



Wartość średniokwadratowa procesu losowego

 

 











dx

t

x

f

x

t

;

2

2

x

 









 

 

t

t

R

t

R

dx

dx

t

x

x

f

x

x

t

R

2

2

1

2

1

2

1

0

,

,

;

,

,

x

x

x

x









 



















Funkcja autokorelacji procesu losowego

 

 

















2

1

2

1

2

1

,

;

,

,

dx

dx

t

x

x

f

t

x

t

x

t

C



























x

x

x

Funkcja autokowariancji procesu losowego

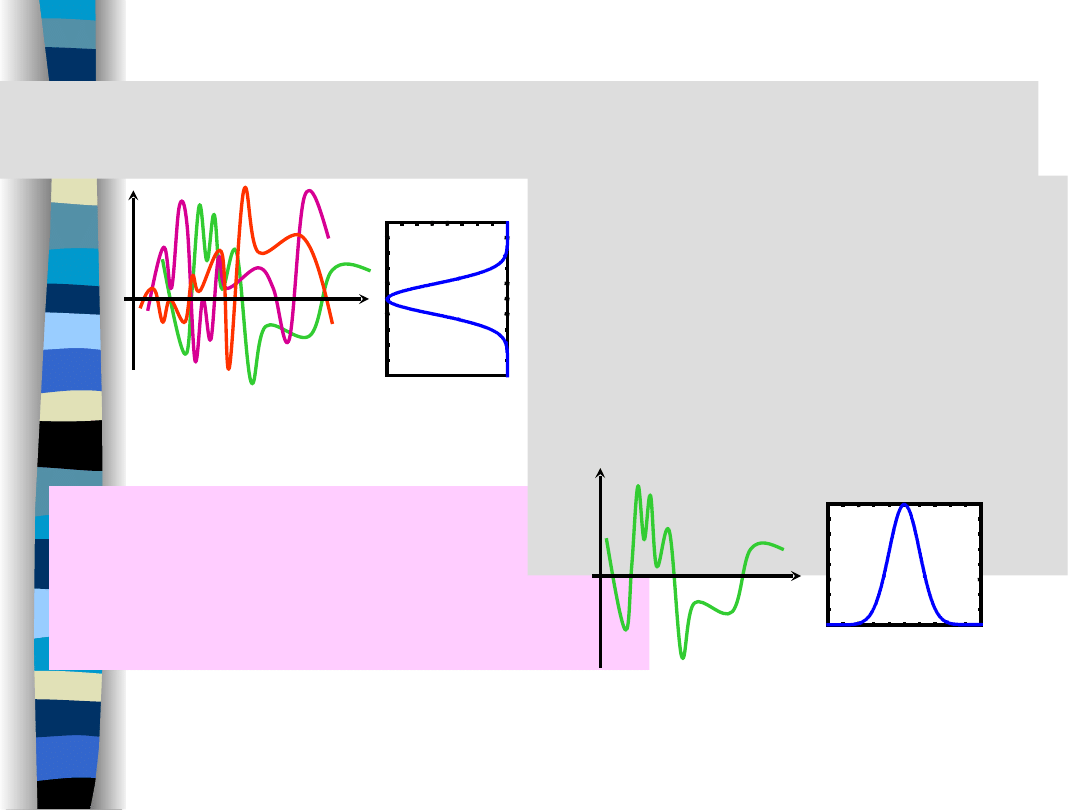
Wartości średnie procesu
losowego

„Teoria sygnałów” Zdzisław Papir

Wartości średnie procesu są

średnimi „po zbiorze”

(ensamble averages), gdyż są wyliczane

Wartości średnie „po czasie”

(time averages) są wyliczane
z

pojedynczych realizacji

procesu losowego

.

dla

ustalonych chwil

czasu ze zbioru
wszystkich realizacji
procesu losowego

na

podstawie

rozkładu

wartości procesu

reprezentowanych przez

gęstości
prawdopodobieństwa

.

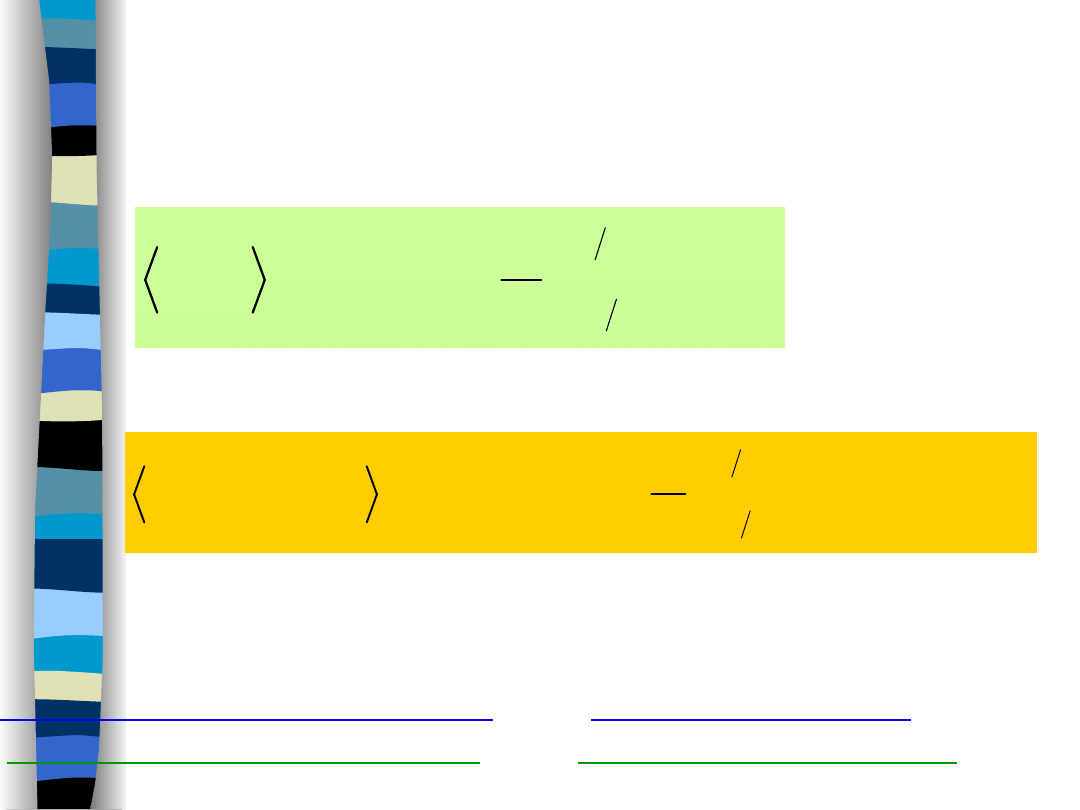
Wartości średnie „po czasie”
procesu losowego

„Teoria sygnałów” Zdzisław Papir

 

 













2

2

1

lim

~

T

T

T

dt

t

T

t

x

x

x

Wartość średnia „po czasie” procesu losowego

Autokorelacja „po czasie” procesu losowego

  



 

  



















2

2

1

lim

~

T

T

T

dt

t

t

T

R

t

t







x

x

x

x

x

Symbol

~

podkreśla, że operacja uśredniania po czasie

została wykonana dla pojedynczej realizacji procesu losowego.

Wartość średnia po czasie jest zmienną losową,
a

autokorelacja po czasie jest procesem losowym.

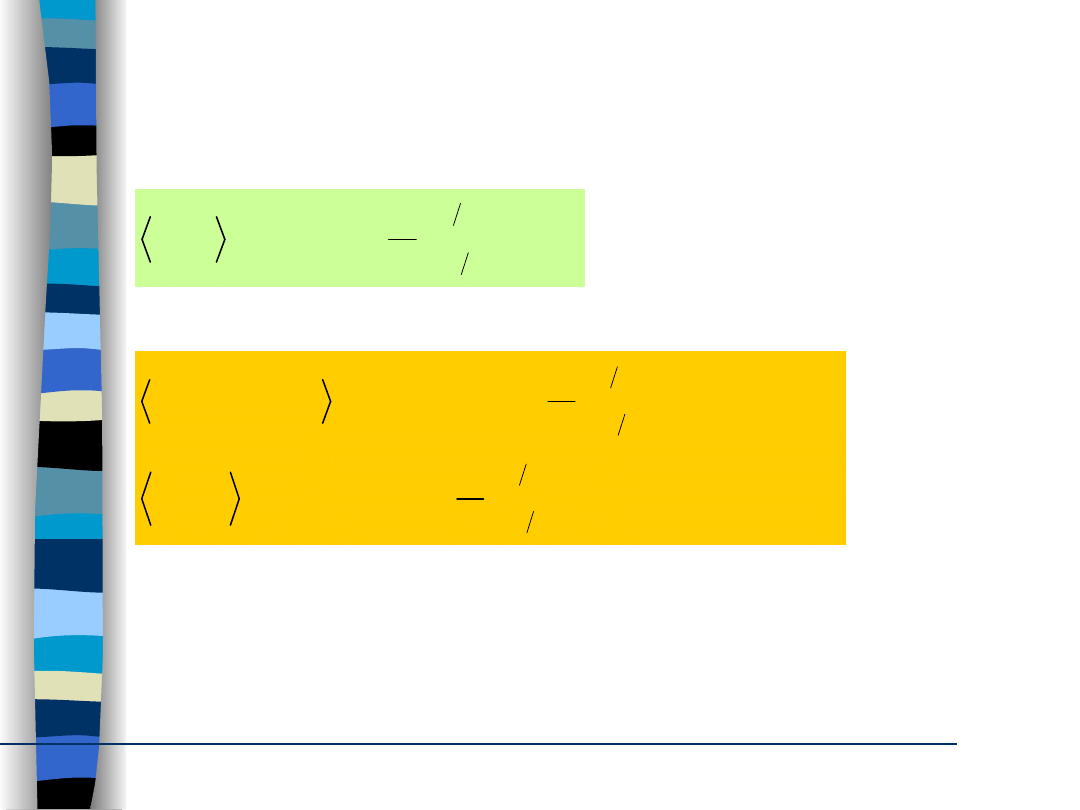
Wartości średnie „po czasie”
procesu losowego

„Teoria sygnałów” Zdzisław Papir

 

 













2

2

1

lim

~

T

T

T

dt

t

T

t

x

x

x

Wartość średnia „po czasie” procesu losowego

Autokorelacja „po czasie” procesu losowego

  



 

  



 

 

 

































2

2

2

2

2

2

1

lim

0

~

1

lim

~

T

T

T

T

T

T

dt

t

T

t

dt

t

t

T

t

t

x

x

x

x

x

x

x

x

R

R







Istnienie

granic wartości średniej po czasie

oraz

autokorelacji po czasie

gwarantują

twierdzenia ergodyczne.

Konsekwencja:
realizacje procesu losowego są sygnałami mocy.

Stacjonarny proces losowy

„Teoria sygnałów” Zdzisław Papir

 













dx

x

xf

x

x



Proces losowy jest stacjonarny (w szerszym sensie), jeżeli
jego

wartość średnia nie zależy od czasu:

a

funkcja korelacji zależy wyłącznie od długości

horyzontu obserwacji



, a nie od jego położenia na osi czasu

czasu (t, t +



):

 





 

 

dx

x

f

x

R

dx

dx

x

x

f

x

x

R























2

2

2

1

2

1

2

1

0

;

,

x

x

x





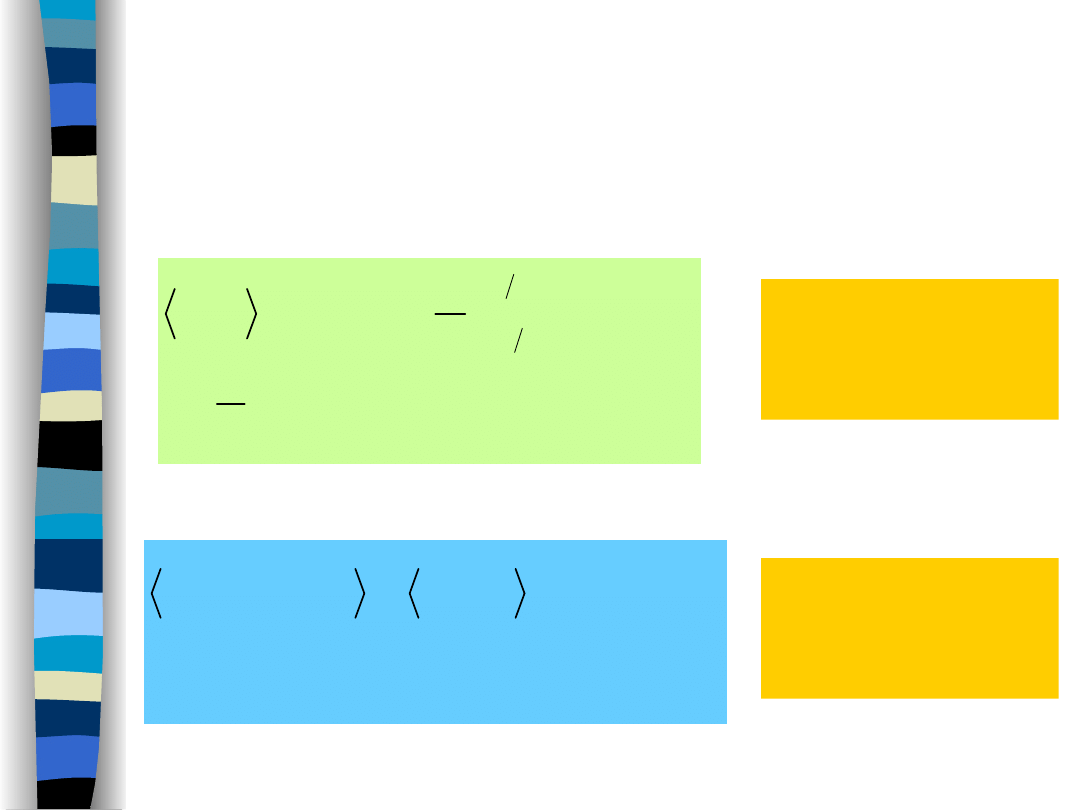
Ergodyczny proces losowy

„Teoria sygnałów” Zdzisław Papir

Losowy proces stacjonarny jest ergodyczny, jeżeli
jego

wartości średnie po zbiorze są równe

wartościom średnim po czasie.

 

 

 





























-

x

x

x

x

dx

x

xf

dt

t

T

t

T

T

T

1

Pr

1

Pr

2

2

1

lim

~

Ergodyczność
wartości
średniej

  



 

 





2

1

2

1

2

1

1

Pr

1

Pr

;

,

dx

dx

x

x

f

x

x

R

R

t

t































x

x

x

x

Ergodyczność
funkcji
korelacji

Analiza widmowa
procesów losowych

„Teoria sygnałów” Zdzisław Papir

Realizacje procesu losowego są sygnałami mocy, więc
każdej realizacji można przyporządkować
funkcję korelacji własnej,

 

  



 

  





















2

2

1

lim

~

T

T

T

dt

t

t

T

t

t

t







x

x

x

x

x

x

R

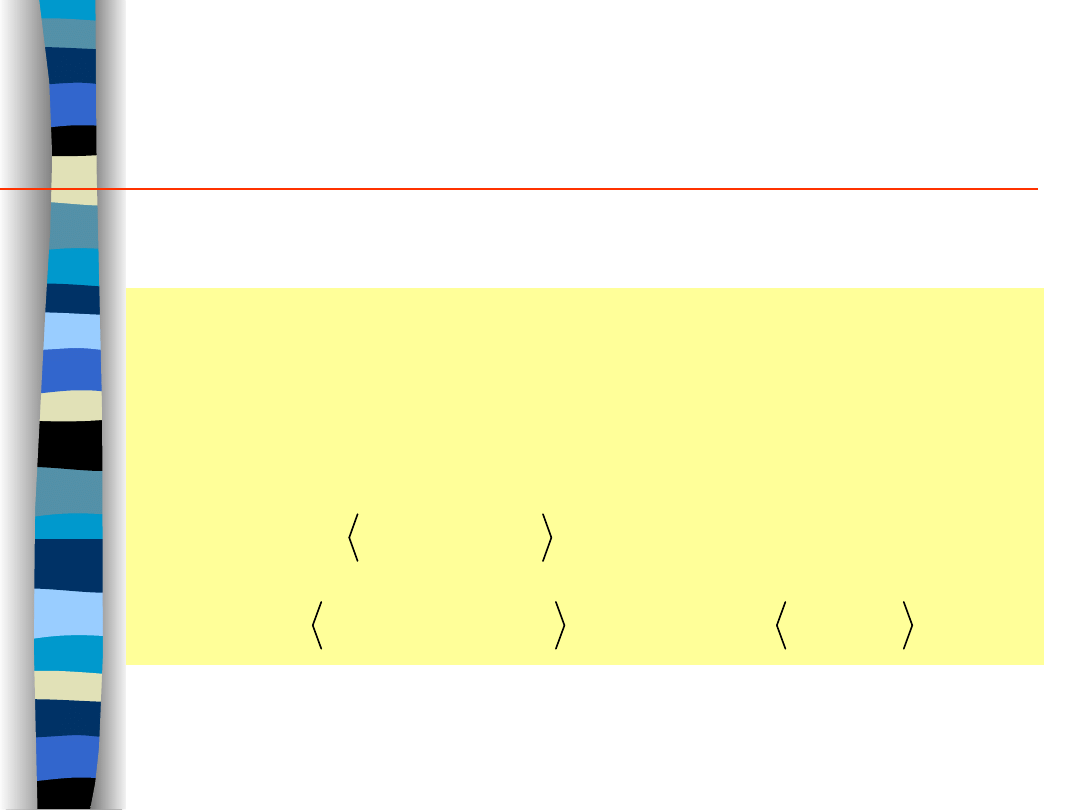
a przez przekształcenie Fouriera widmo gęstości mocy:

 

 

 

 













 















d

e

t

j

x

x

x

x

R

S

R

~

~

~

F

„Teoria sygnałów” Zdzisław Papir

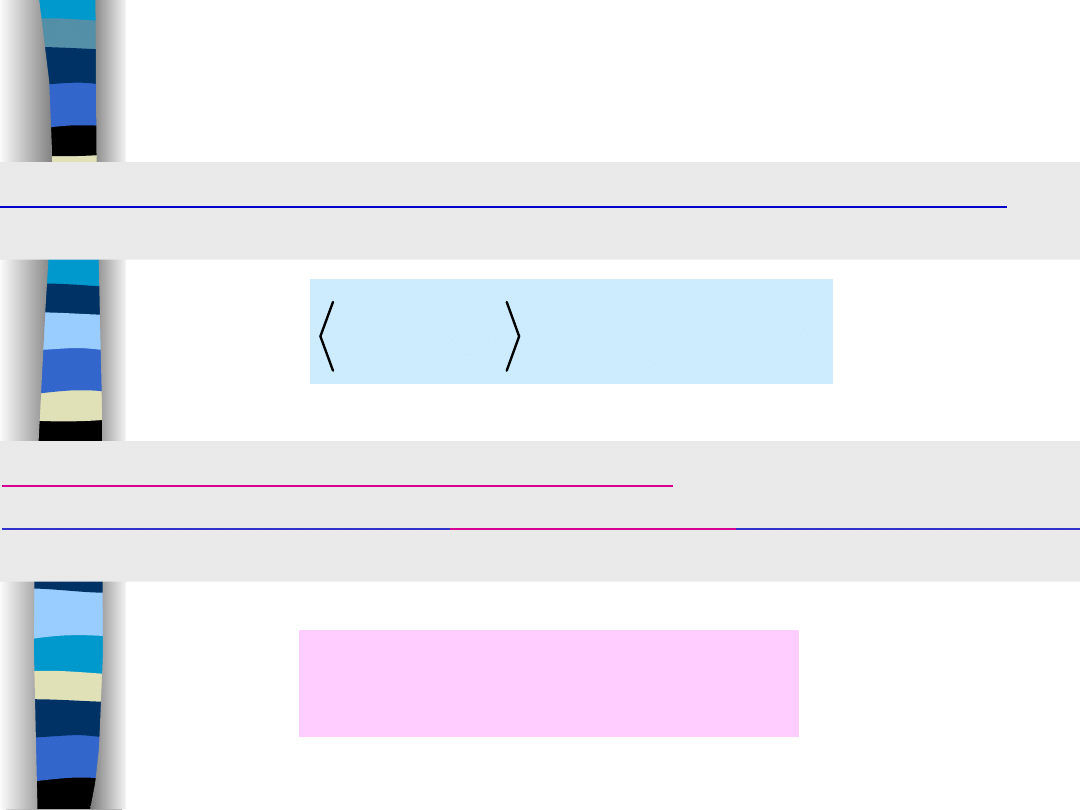
Uśrednione widmo gęstości mocy procesu losowego
otrzymujemy w wyniku uśredniania (w zbiorze realizacji)
widm gęstości mocy poszczególnych realizacji.

 

 

 

 

 

 





 





 

  







 

  







 











































d

e

t

R

d

e

t

t

S

d

e

t

t

S

d

e

S

d

e

t

j

j

j

j

j



































































 





,

E

E

~

~

~

~

~

E

E

x

x

x

x

x

x

x

x

x

x

x

x

x

x

R

S

R

S

R

F

Uśrednione widmo gęstości
mocy procesu losowego

„Teoria sygnałów” Zdzisław Papir

Uśrednione widmo gęstości
mocy procesu losowego

Twierdzenie Wienera – Chinczyna

Widmo gęstości mocy

stacjonarnego

procesu losowego

jest transformatą Fouriera funkcji korelacji.

 

 





x

x

S

t

R

 

F

,

 

 





x

x

S

R

 

F

Uśrednione widmo gęstości mocy procesu losowego jest trans-
formatą Fouriera funkcji korelacji uśrednionej po czasie.

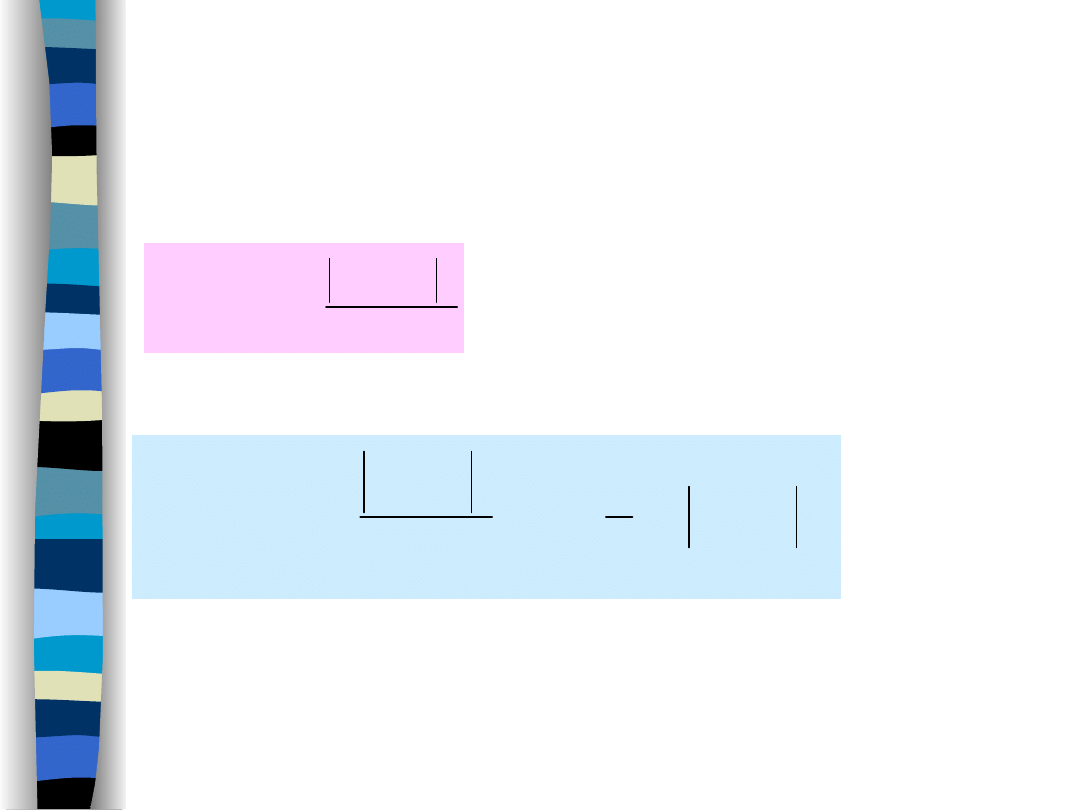
„Teoria sygnałów” Zdzisław Papir

Uśrednione widmo gęstości
mocy procesu losowego –
metoda alternatywna

 

 

T

X

S

T

T

x

2

lim











Widmo gęstości mocy deterministycznego sygnału mocy:

Widmo gęstości mocy procesu losowego:

 

 

 













































2

2

~

E

1

lim

~

lim

E







T

T

T

T

T

T

S

X

X

x

można otrzymać w wyniku uśredniania (po zbiorze)
widm gęstości mocy poszczególnych realizacji, a te są
deterministycznymi sygnałami mocy.

Podsumowanie

„Teoria sygnałów” Zdzisław Papir

•

Twierdzenie Parsevala pozwala wyznaczyć energię/moc

sygnału w dziedzinie częstotliwości.

•

Widmowa gęstość energii/mocy określa energię/moc sygnału

przypadającą na poszczególne częstotliwości sygnału.

• Widmowa gęstość energii/mocy jest transformatą Fouriera
funkcji autokorelacji.

•

Funkcja autokorelacji opisuje podobieństwo sygnału do

jego opóźnionej w czasie repliki.

• Funkcja autokorelacji sygnału mocy jest określona podobnie
do funkcji autokorelacji sygnału energii; definicja uwzględnia
dodatkowo uśrednianie po czasie.

• Filtracja sygnału powoduje przekształcenie widmowej
gęstości energii/mocy przez kwadrat cha-ki a-cz.

• Realizacje procesu losowego są deterministycznymi
sygnałami mocy.

• Uśrednione widmo gęstości mocy procesu losowego jest
transformatą Fouriera funkcji autokorelacji (uśrednionej – w
przypadku procesów losowych niestacjonarnych).

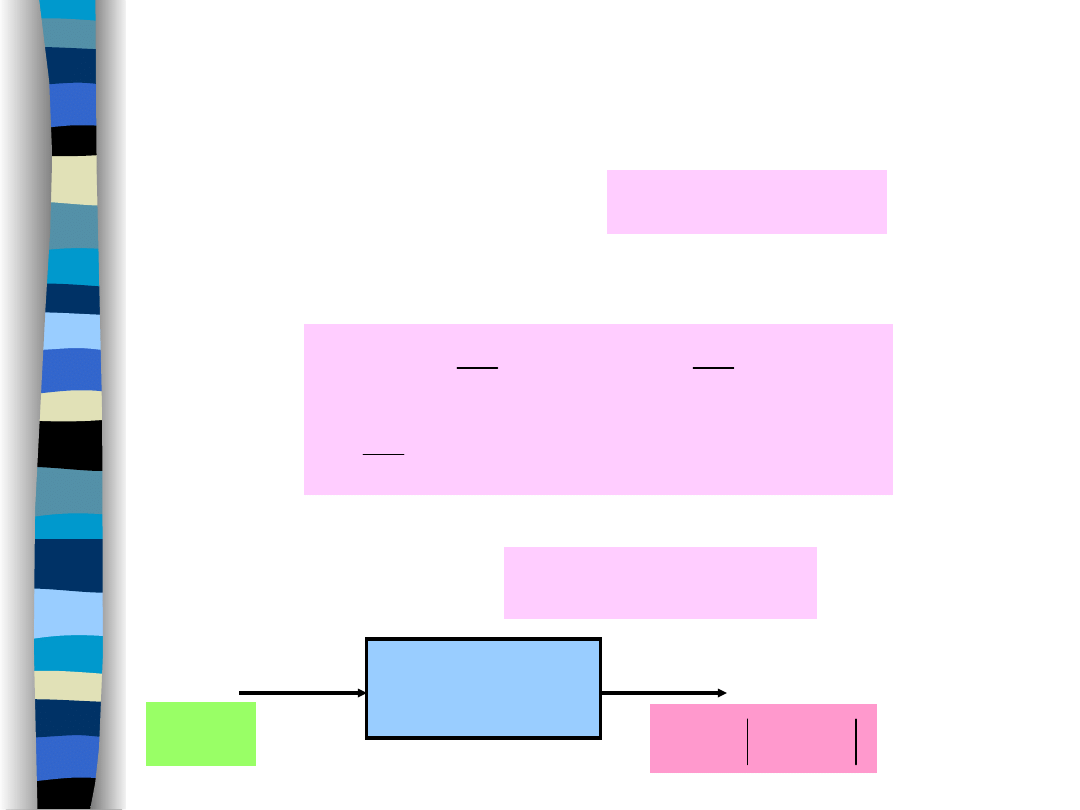
Właściwości widma gęstości
energii/mocy

„Teoria sygnałów” Zdzisław Papir

•Widmo gęstości energii/mocy jest zawsze transformatą
Fouriera funkcji autokorelacji:

 

 





x

x

S

R

 

F

•Widmo gęstości energii/mocy pozwala określić energię/moc
sygnału w wybranym pasmie częstotliwości oraz energię/moc
całkowitą:





 

 

 





















































d

S

P

d

S

d

S

P

x

x

x

2

1

2

1

2

1

,

d

g

d

g

g

d

•Widmo gęstości energii/mocy jest funkcją parzystą dla
sygnałów rzeczywistych:

 

 





x

x

S

S





)

(



j

H

 



x

S

   

2





j

H

S

x

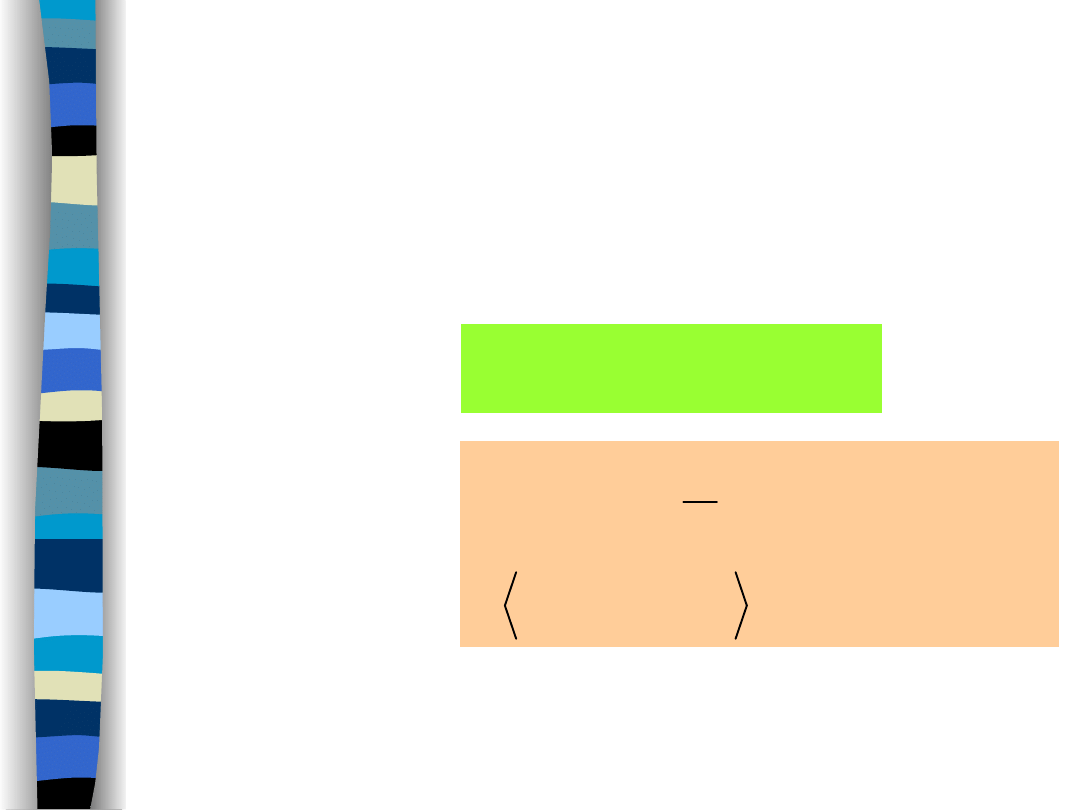
Podsumowanie –
właściwości
funkcji autokorelacji

„Teoria sygnałów” Zdzisław Papir

Niezależnie od rodzaju sygnału (deterministyczny, losowy)
funkcje autokorelacji, aczkolwiek definiowane w odmienny
sposób posiadają identyczne właściwości.

•Deterministyczny
sygnał energii:

 

  















dt

t

x

t

x

R

x





*

•Deterministyczny
sygnał mocy:

 

  



  

























t

x

t

x

dt

t

x

t

x

T

R

T

T

x

*

*

1

lim

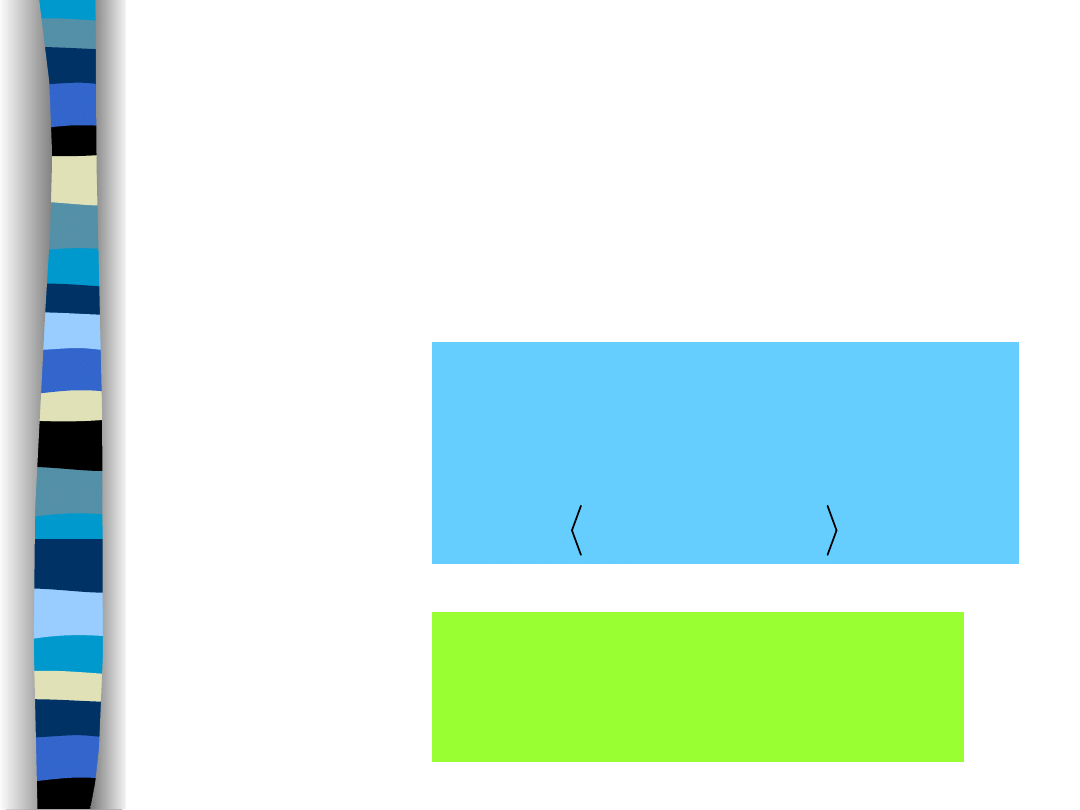
Podsumowanie –
właściwości
funkcji autokorelacji

„Teoria sygnałów” Zdzisław Papir

Niezależnie od rodzaju sygnału (deterministyczny, losowy)
funkcje autokorelacji, aczkolwiek definiowane w odmienny
sposób posiadają identyczne właściwości.

 





 



  





 



  





t

t

R

t

t

t

R

dx

dx

t

x

x

f

x

x

t

R

x

x

x

x

x

x

x































E

E

,

,

;

,

,

2

1

2

1

2

1

• Niestacjonarny
proces losowy:

 





 



  





t

t

E

R

dx

dx

x

x

f

x

x

R

x

x

x

x























2

1

2

1

2

1

;

,

• Stacjonarny
proces losowy:

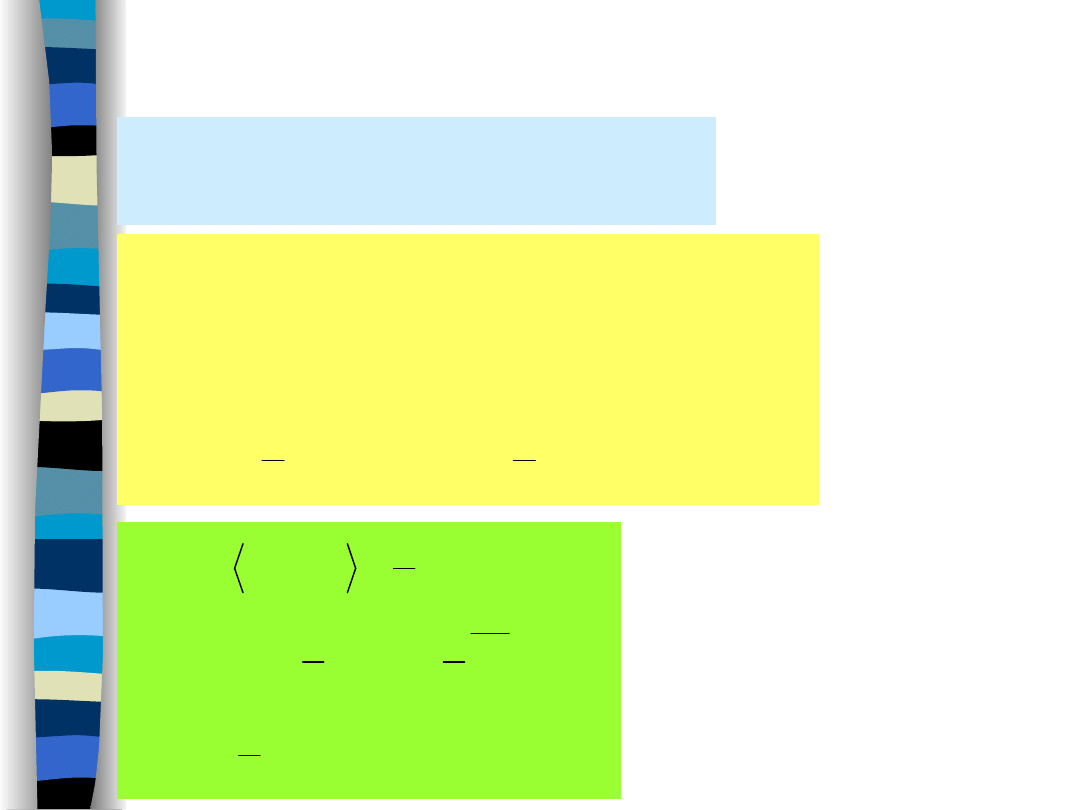
Przykład – modulacja
amplitudy

„Teoria sygnałów” Zdzisław Papir

 

 

 

amplitudy

modulacja

cos

0

~

losowy,

proces

y

stacjonarn

0









t

t

t

t





x

x

x

 







  





 



  









 

 





 

 

  













































































t

R

R

t

R

t

t

R

t

R

t

t

t

t

t

R

t

t

t

t

t

R

0

0

0

0

0

0

0

0

2

cos

2

1

cos

2

1

,

cos

cos

,

cos

cos

E

,

cos

cos

E

,

x

x

x

x

x

x

x

 

 

 

 

 

 













0

0

2

0

4

1

2

1

0

2

1

0

cos

2

1

,

















































x

x

x

x

x

S

S

S

R

R

P

R

t

R

R

Przykład – kod
transmisyjny
bipolarny NRZ

„Teoria sygnałów” Zdzisław Papir













 

    







































n

k

q

p

a

E

a

E

n

k

a

E

a

a

E

p

q

a

p

a

n

k

n

n

k

n

n

,

,

1

1

1

Pr

1

Pr

2

2

2



Symbole a

n

są

niezależne.

T

2
T

4
T

6
T

+1

-1

t

x(t)

nT

(n+1)T

a

n

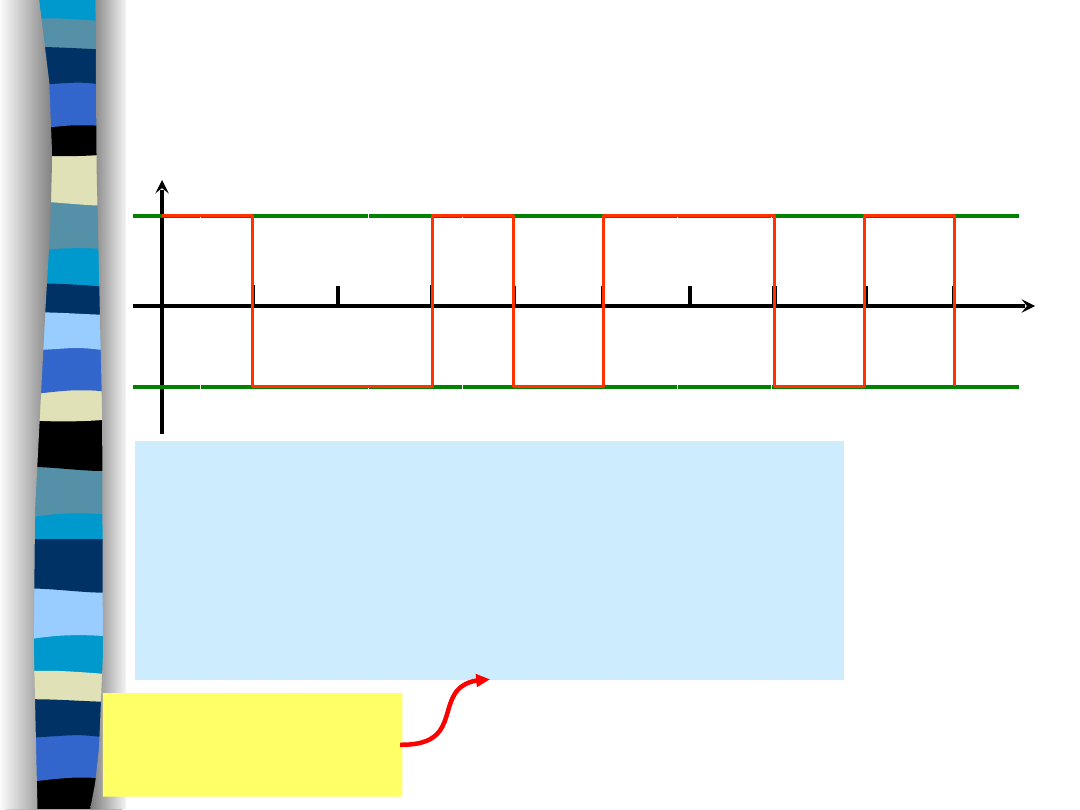
Kod transmisyjny bipolarny NRZ -
funkcja korelacji

„Teoria sygnałów” Zdzisław Papir

T

2
T

3
T

4
T

t

+1

(p –
q)

2

-T

 



,

t

R

x

T-



2T-



3T-









T







0

 

 



 







T

T

T

q

p

T

t

R

R





































2

2

1

1

1

,

x

x

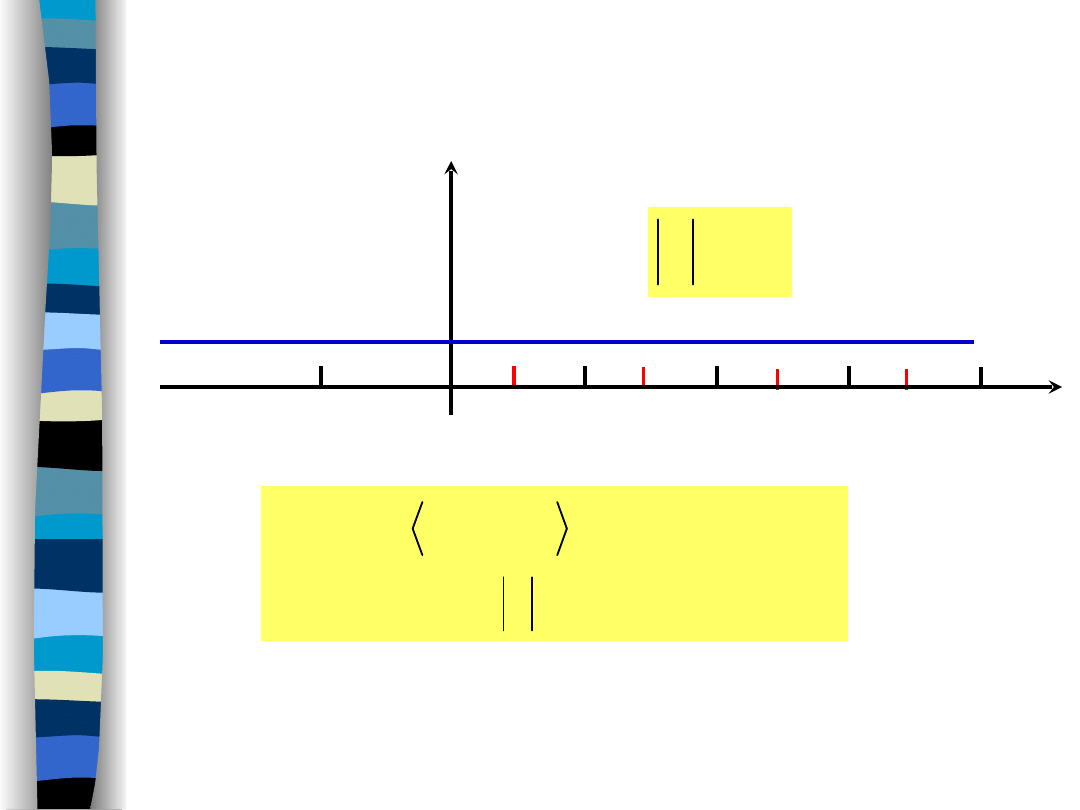
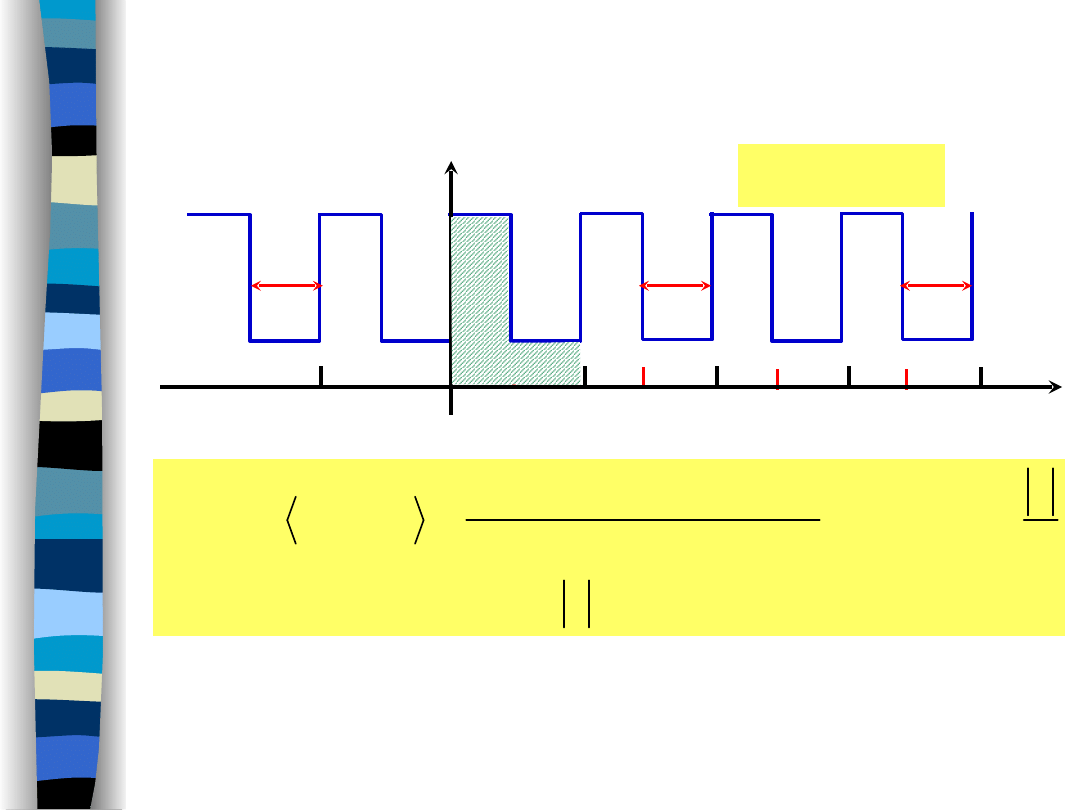
Kod transmisyjny bipolarny NRZ -
funkcja korelacji

„Teoria sygnałów” Zdzisław Papir

 

  



T

q

p

t

R

R



















2

2

,

x

x

T

2
T

3
T

4
T

t

+1

(p –
q)

2

-T

 



,

t

R

x

T-



2T-



3T-



T





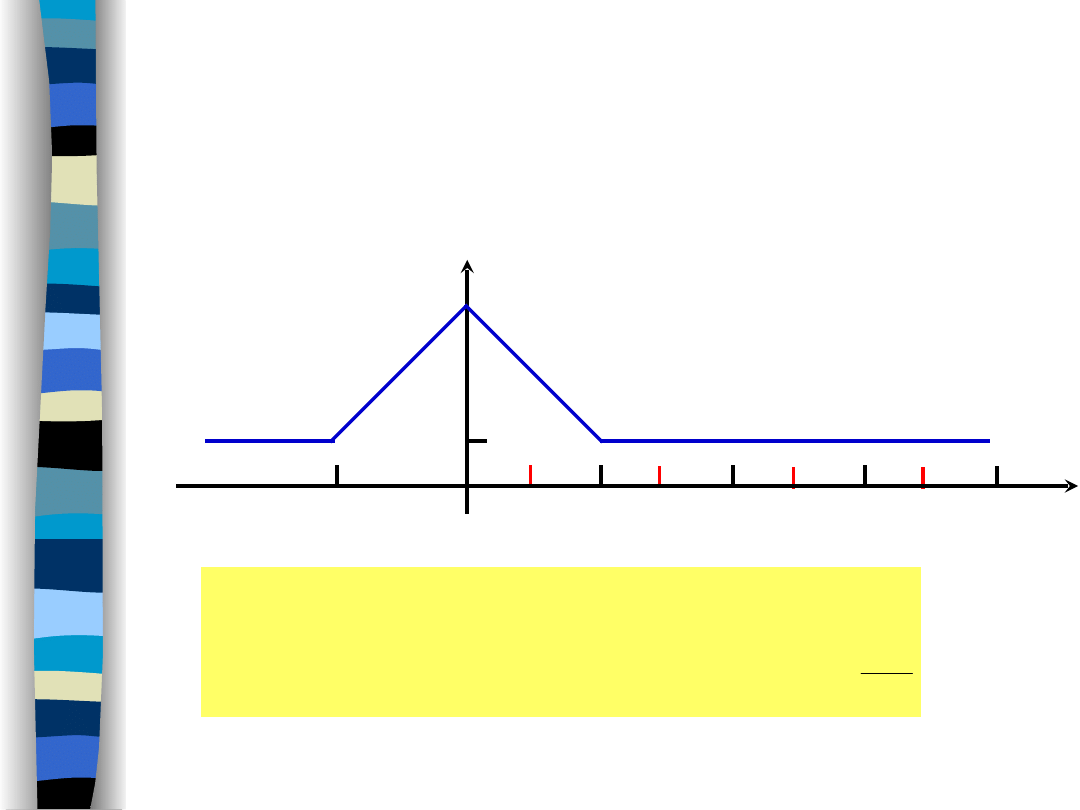
Kod transmisyjny bipolarny NRZ -
uśredniona funkcja korelacji
& widmowa gęstość mocy

„Teoria sygnałów” Zdzisław Papir

T

2
T

3
T

4
T

t

+1

-T

 



x

R

T-



2T-



3T-



 





 

 

 





 





2

Sa

1

2

1

2

2

2

2

2

2

T

T

R

S

R

T







































x

x

x

F

2



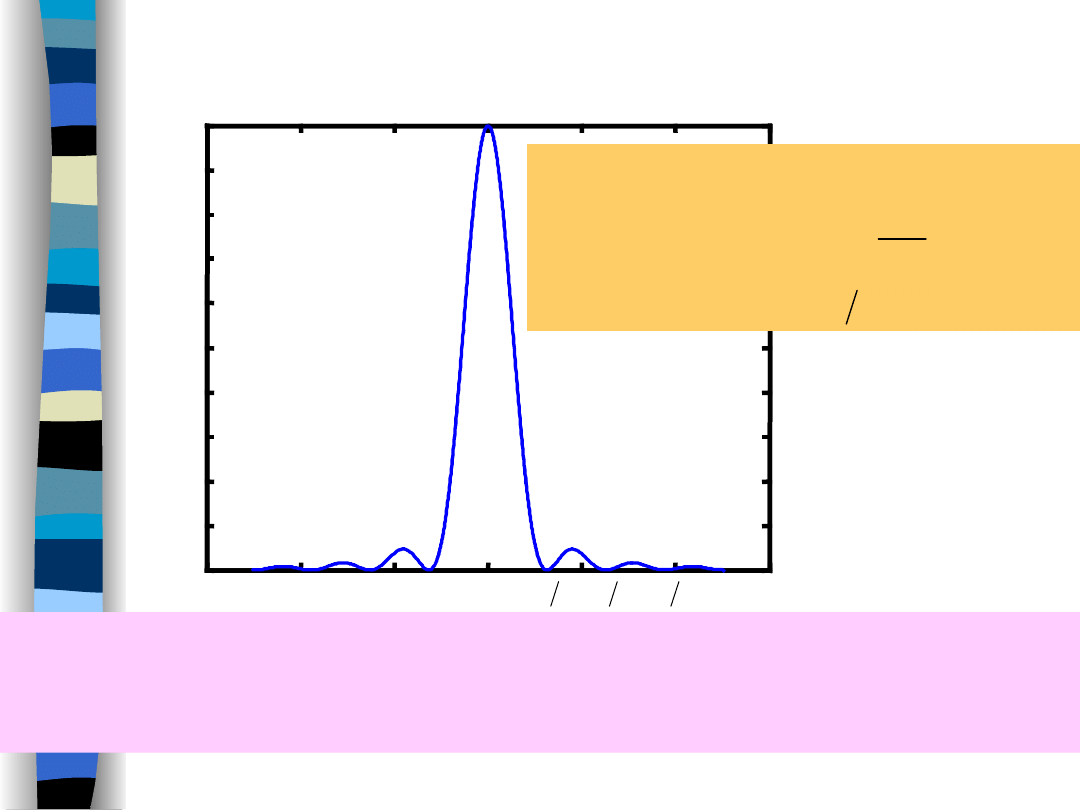
Kod transmisyjny bipolarny NRZ -
widmowa gęstość mocy

„Teoria sygnałów” Zdzisław Papir

f
[Hz]

T

2

T

1

T

3

Widmo gęstości mocy sygnału cyfrowego jest skupione w
pasmie 0 < f < 1/T; twierdzenie Nyquista orzeka, że pasmo
dwukrotnie węższe 0 < f < 1/2T jest wystarczające.

 

 

 

 





2

1

Sa

2

Sa

2

2

2















q

p

fT

T

T

T

R

S

R

T













x

x

x

F

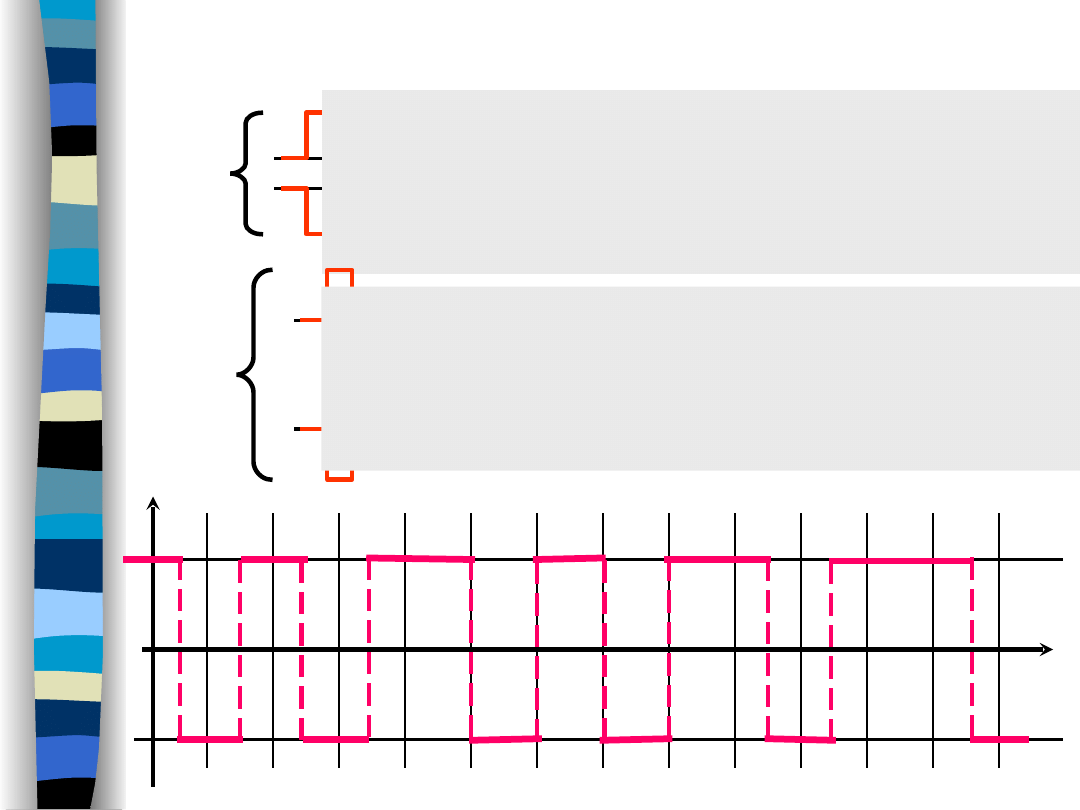
Kody transmisyjne - kod Millera

„Teoria sygnałów” Zdzisław Papir

„0”

• zachowanie polaryzacji przy przejściu
„1”  „0”

• zmiana polaryzacji przy przejściu
„0”  „0”

„1”

• zachowanie polaryzacji przy przejściu
„1”  „1”

• zachowanie polaryzacji przy przejściu
„0”  „1”

1 0

0

0

1 1

0

0

0

0 1 1

1

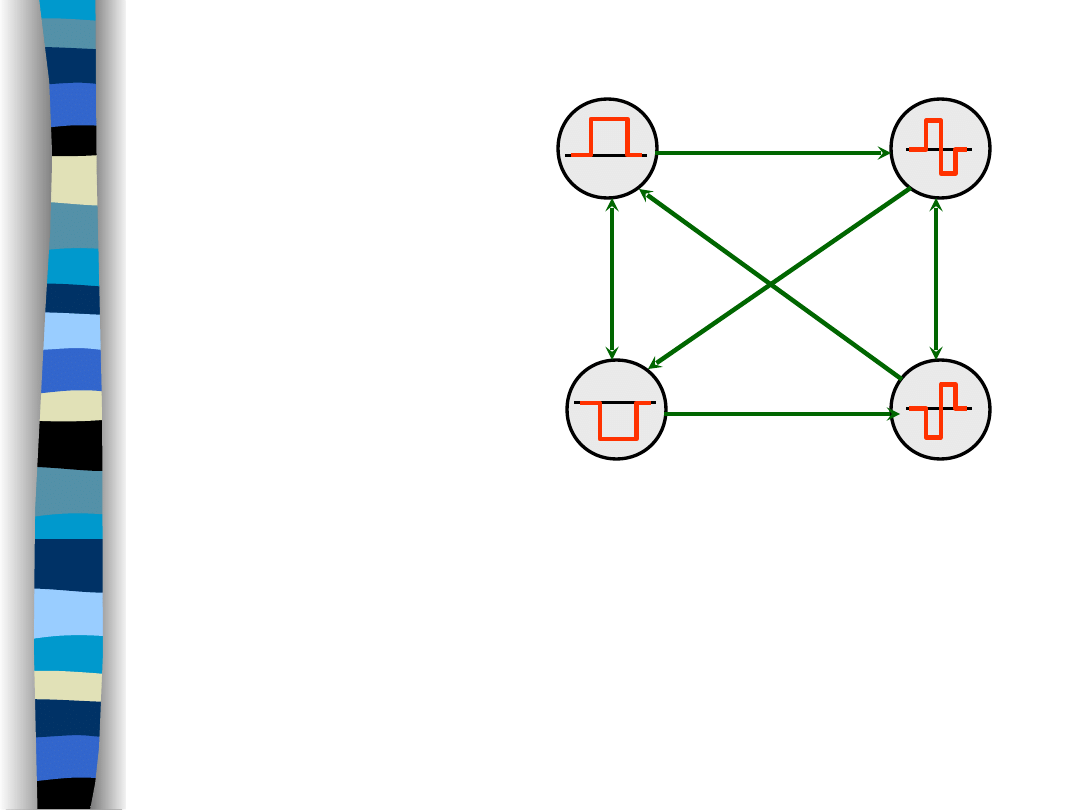
Kody transmisyjne - kod Millera

„Teoria sygnałów” Zdzisław Papir

„1”

„0”

„1”

„1”

„0”

„0”

Właściwości kodu Millera:

• eliminacja składowych n-cz widma

• istotny poziom timing content

• koncentracja widma w wąskim pasmie

• sekwencje „0...” lub „1...” – rozproszenie widma

• sekwencja „0 1 1...” – istotny poziom składowej dc

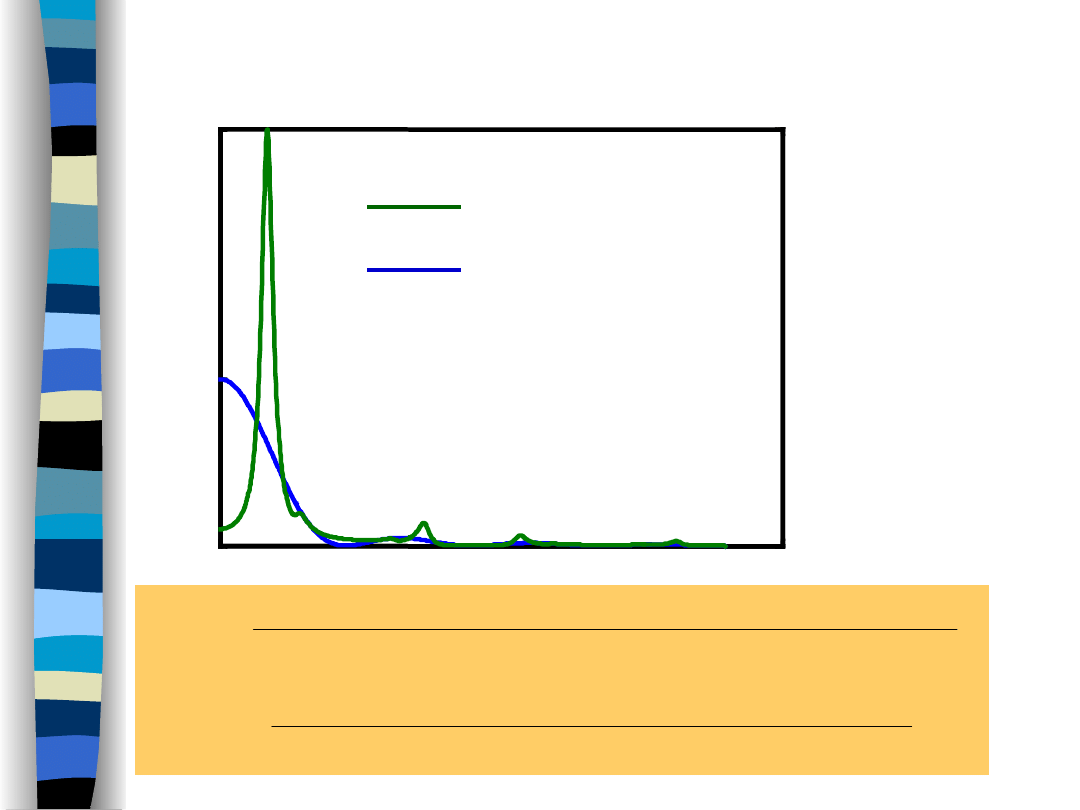
Kody transmisyjne - kod Millera

„Teoria sygnałów” Zdzisław Papir

 









fT

T

f

fT

fT

fT

fT

fT

T

f

fT

fT

fT

fT

S



























8

cos

8

17

2

8

cos

2

7

cos

8

6

cos

2

5

cos

12

8

cos

8

17

2

4

cos

5

3

cos

12

2

cos

22

cos

2

23

2

2

2

2

























x

kod bipolarny NRZ

kod Millera

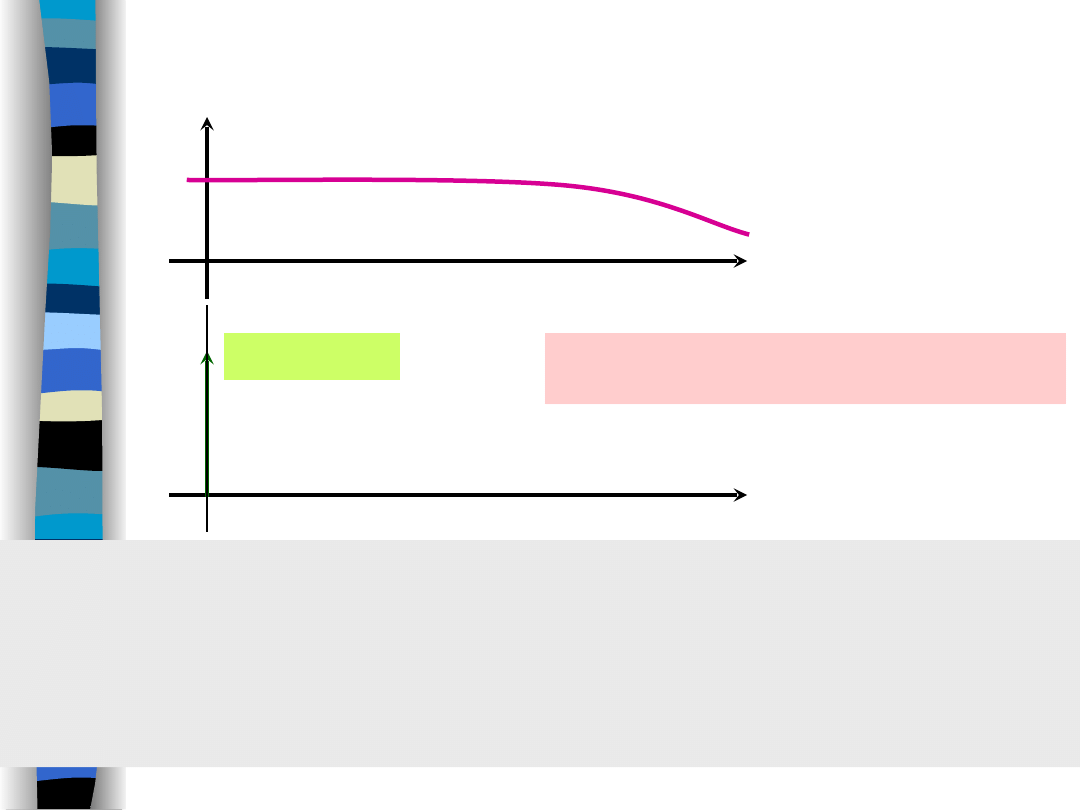
Przykład – szum
gaussowski

„Teoria sygnałów” Zdzisław Papir





~THz

 

 

 













 





S

R

F

 

 









R



Szum biały ma płaskie widmo gęstości mocy w bardzo
szerokim zakresie częstotliwości.
Funkcja korelacji szumu białego ma charakter impulsowy;
wartości szumu białego w dowolnie bliskich chwilach czasu
nie są skorelowane ze sobą.

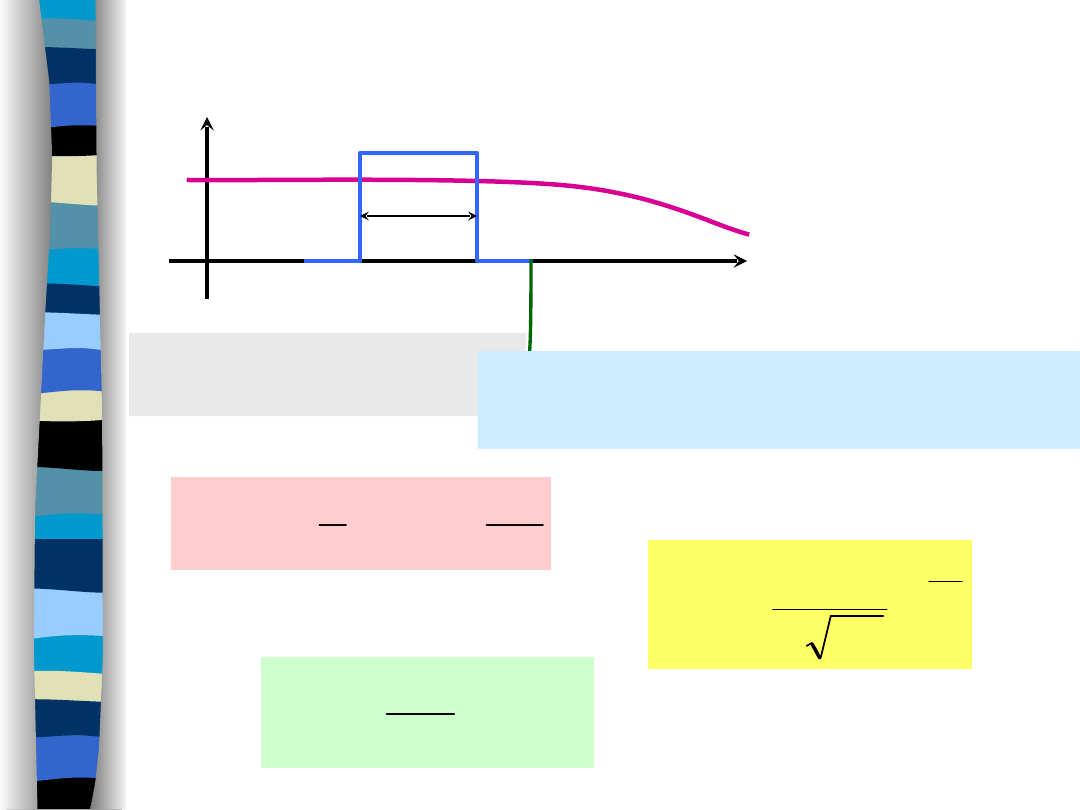
Przykład – szum
gaussowski

„Teoria sygnałów” Zdzisław Papir





~THz

W

Idealny filtr pasmowo-

przepustowy

Szum gaussowski po filtracji jest
nadal szumem gaussowskim.









W

W

d

N













1

2

 







2

2

2

1

x

e

x

f





 

 









W

W

R

Sa

