Wykład 3 

Wnioskowanie 

statystyczne c.d.

Testowanie hipotez na 

przykładzie testu t studenta

 

 

 

 

 

 

 

 

2

2

2

1

2

1

2

1

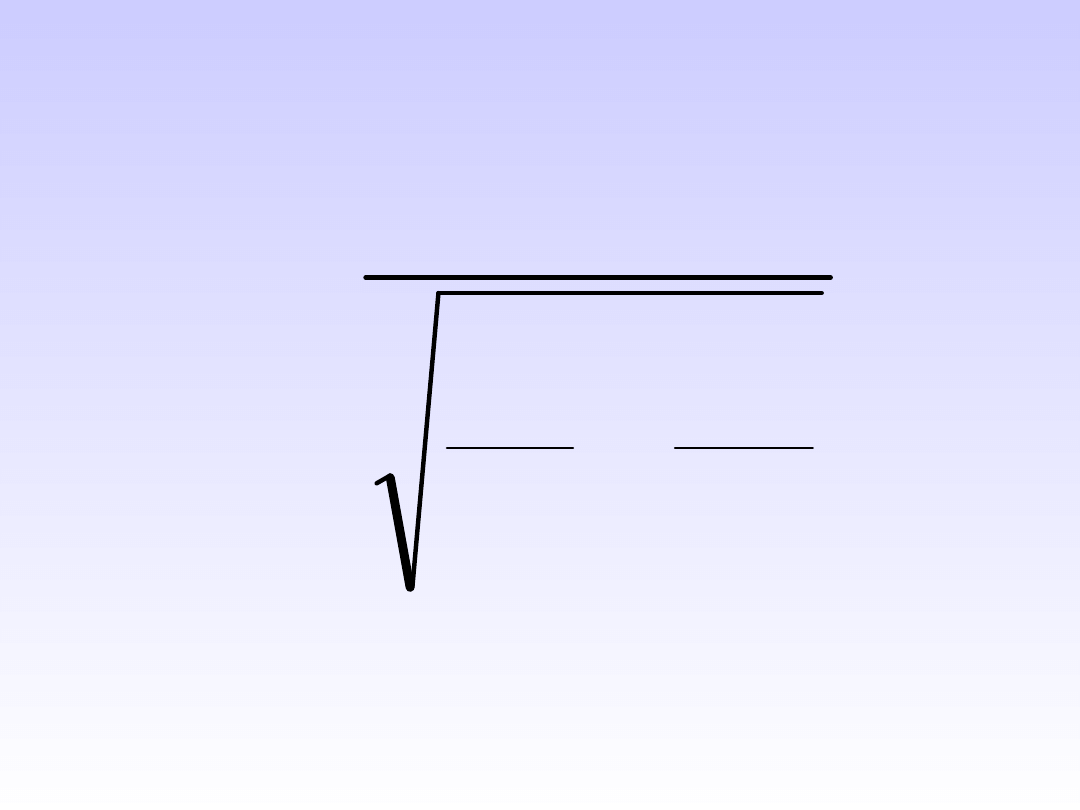
N

s

N

s

x

x

z







 

 

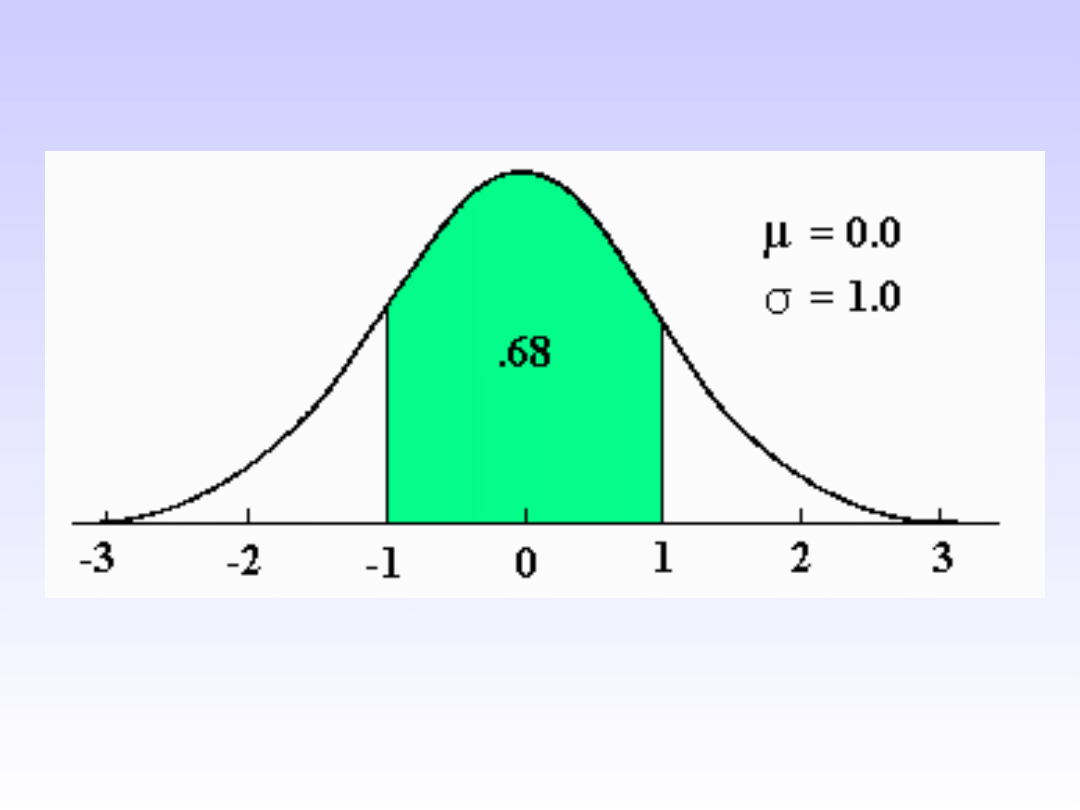
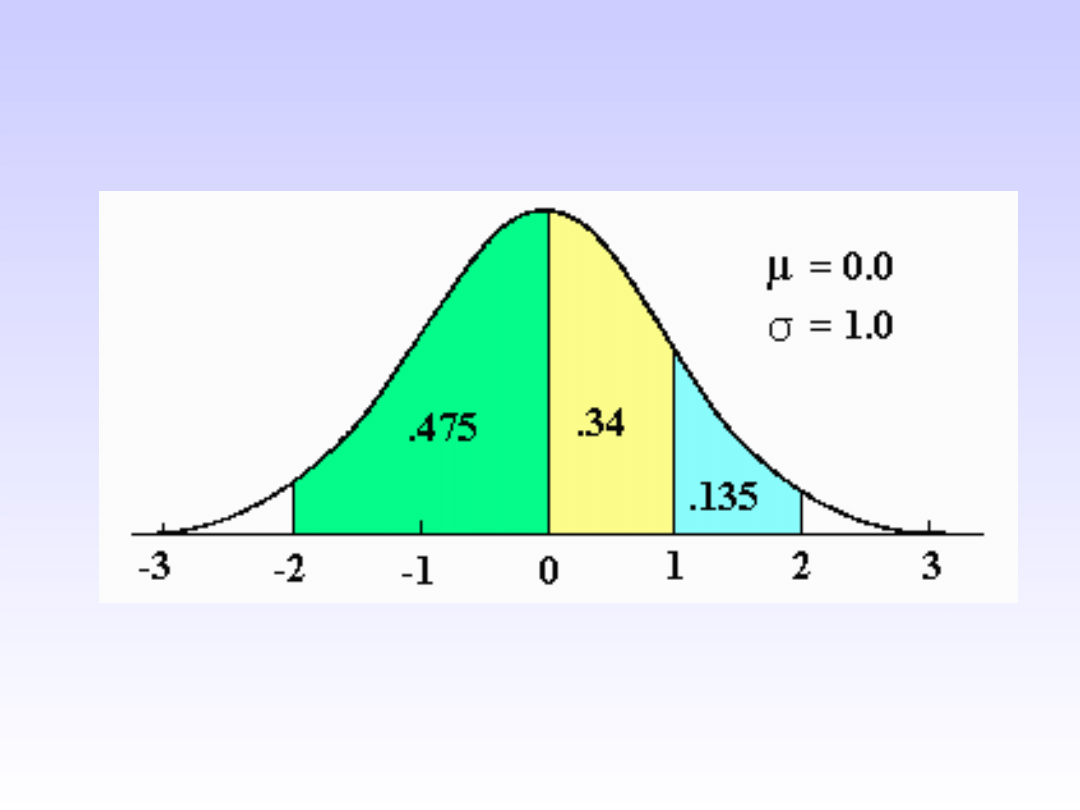
• W wypadku dużych prób przedziały 

ufności dla średnich można 
konstruować w oparciu o statystyki z 
próby (średnią w próbie, OS w próbie, 
N) oraz w oparciu o właściwości 
krzywej normalnej

• W wypadku małych prób (N < 30), 

konstruowanie statystyk w oparciu o 
krzywą normalną obciążone jest 
błędem.

 

 

• Dla małych prób, różnica między 

średnią z próby a średnią w 
populacji jest większa, a przedziały 
ufności węższe, niż wynikałoby to z 
właściwości rozkładu normalnego

• Dla małych prób, testy statystyczne 

oparte n krzywej normalnej 
odrzucają prawdziwą hipotezę 
zerową częściej niż powinny.

 

 

Rozkład t i test t Studenta

• Nazwa testu: autor William S. 

Gosset (1876-1937) - “A Student of 
Statistics”

• test t Studenta
• Nazwy testów statystycznych:

– symbol literowy
– nazwisko autora (autorów)

 

 

• Test z: Mnożnik dla granicy obszaru 

krytycznego jest niezależny od 
wielkości próby i wynosi 1,96 (dla 
obszaru dwustronnego) i 1,65 (dla 
obszaru jednostronnego

• Test t: Mnożnik dla granicy obszaru 

krytycznego zależy od wielkości 
próby

 

 

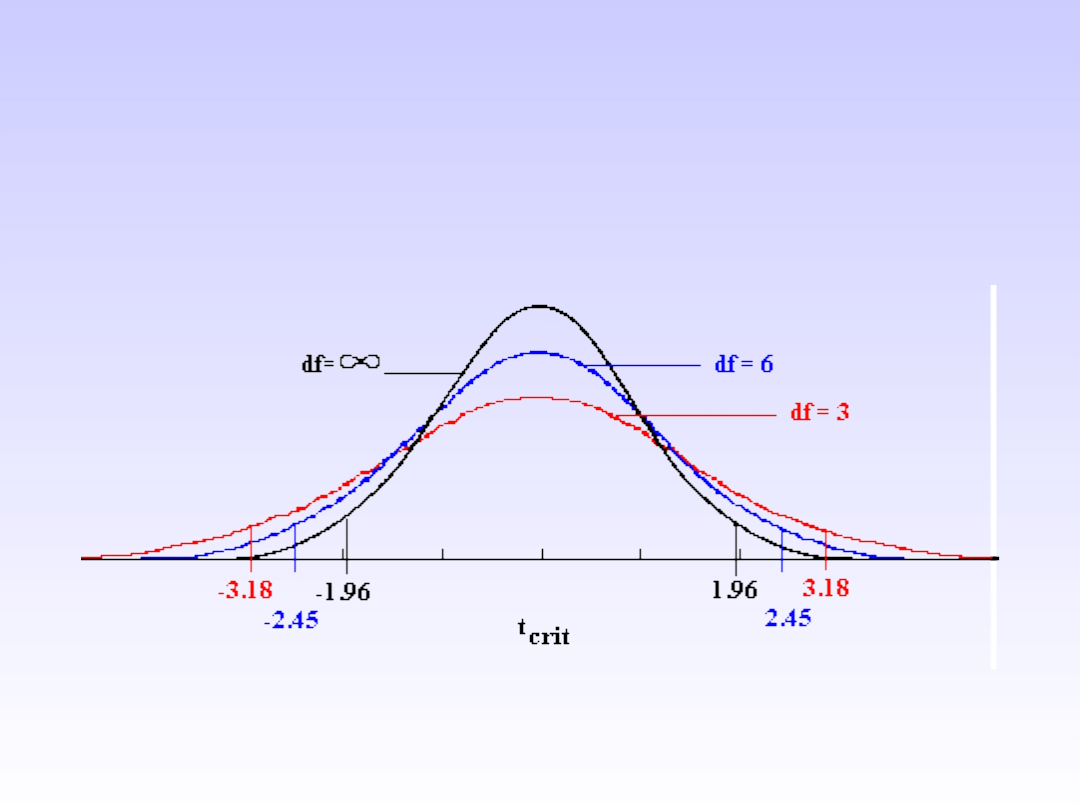
Rozkład t a rozkład 

normalny

 

 

 

Przeznaczenie 

międzygrupowego testu t 

studenta

• Badanie istotności różnic między 

dwiema średnimi

• = Badanie związku między 

zmienną nominalną z dwiema 
kategoriami ze zmienną 
interwałową (ilorazową)

 

 

• Zmienna niezależna:

– nominalna z dwiema kategoriami

• Zmienna zależna

– interwałowa lub ilorazowa

 

 

Typy zmiennych 

niezależnych

• Manipulowalne
• Niemanipulowalne (organizmiczne)

– "z natury" dychotomiczne
– "z natury" ciągłe, ale zdychotomizowane

• podział całej próby na dwie grupy

– wg średniej
– wg mediany (w wypadku np. skośnych rozkładów)

• wykorzystanie skrajnych części grupy

– np. skrajne kwartyle

 

 

Założenia testu t studenta

• skale pomiarowe
• normalność rozkładów zmiennych 

zależnych w badanych populacjach 

(test Lillierorsa, test Shapiro-Wilka)

• homogeniczność wariancji w 

badanych populacjach (test Levena)

• liczebność próby

– test t daje poprawne wyniki w małych 

próbach, ale mała wtedy jest jego moc

 

 

• Wariancje różne, a próby 

różnoliczne: najbardziej 
niebezpieczna sytuacja.

• Niejednakowość wariancji jest 

mało niebezpieczna, jeśli obie 
próby są duże i nie różnią się 
zbytnio liczebnością

 

 

Wersje testu t studenta

• Dla danych międzygrupowych

– wersja zakładająca homogeniczność 

wariancji

– wersja nie zakładająca 

homogeniczności wariancji

• Dla pomiarów zależnych
• Dla jednej średniej

 

 

Pomiary zależne

• Istota: oba pomiary są skorelowane
• Kiedy powstają pomiary zależne:

– Manipulacja "wewnątrz" osób 

badanych

– Dobór parami
– Badanie małżonków, rodzeństwa itp.
– ...

 

 

• Test dwustronny - hipoteza 

bezkierunkowa

H

0

: 

1

 = 

2

H

1

: 

1

  

2

• Test jednostronny: (hipoteza 

kierunkowa

H

0

: 

1

 > 

2

H

1

: 

1

  

2

H

0

: 

1

 < 

2

H

1

: 

1

  

2

 

 

Dla tego samego t, poziom p jest 

dwukrotnie niższy w wypadku hipotezy 
jednostronnej niż dwustronnej.

• Hipotezy kierunkowe są "korzystniejsze" w 

tym sensie, że przy tych samych wynikach z 
badań, jeśli hipoteza jest kierunkowa, szansa 
na istotność statystyczną rezultatu jest 
większa

• Nie znaczy to, że można po zakończeniu 

badań i obliczeń zmieniać hipotezę, 
która pierwotnie była bezkierunkowa, na 
kierunkową. Postępowanie takie ociera 
się o fałszowanie wyników.

 

 

• Szczególny typ hipotezy zerowej - dla 

hipotezy badawczej postulującej, że 
średnia uzyskana w badaniach różni się 
od pewnej z góry założonej wartości

• H

1

: 

1

  4,541           H

0

: 

1

 = 4,541

•

Np: czy nasza próba (np. pacjenci 
schizofreniczni w Krakowie) istotnie różnią 
się w danej zmiennej od pacjentów w USA, 
których nie badaliśmy, ale których wyniki 
znamy

 

 

Test t - streszczenie

• Służy do testowania różnic między dwiema 

średnimi (pochodzącymi z danych 
międzygrupowych albo z powtórzonego 
pomiaru); albo do testowania hipotezy 
dotyczącej jednej średniej

• Zmienna niezależna nominalna z dwiema 

kategoriami, zmienna zależna co najmniej 
przedziałowa

• Rozkłady zmiennej zależnej powinny być z 

grubsza normalne, a wariancje w 
porównywanych populacjach z grubsza 
podobne