Pole

Pole

 

 

magnetyczne

magnetyczne

 

 

 

 

•

Już 2500 lat p.n.e. Chińczycy stosowali „kompas”

Już 2500 lat p.n.e. Chińczycy stosowali „kompas”

•

W VI p.n.e. Tales z Miletu obserwował przyciąganie 

W VI p.n.e. Tales z Miletu obserwował przyciąganie 

i odpychanie traw przez rudę żelaza (magnetyt)

i odpychanie traw przez rudę żelaza (magnetyt)

•

W XVI n.e. Gilbert stwierdził, że Ziemia jest 

W XVI n.e. Gilbert stwierdził, że Ziemia jest 

magnesem, a największe przyciąganie występuje na 

magnesem, a największe przyciąganie występuje na 

biegunach

biegunach

•

Słowo „magnetyzm” wywodzi się od nazwy okręgu 

Słowo „magnetyzm” wywodzi się od nazwy okręgu 

Magnesia w Azji Mniejszej 

Magnesia w Azji Mniejszej 

 

 

 

 

•

Wstępnie pole magnetyczne definiujemy jako substancje 

materialną,  która oddziałuje z pewną silą na poruszający się 

ładunki elektryczne, przewodniki z prądem oraz dipole 

magnetyczne. 

•

Wówczas same pole to jest wytwarzane przez ładunki 

elektryczne, przewodniki z prądem oraz stałe magnesy. 

•

Współczesna teoria świadczę, że siły magnetyczne wynikają 

wprost z teorii względności, prawa Coulomba i zasady 

niezmienności ładunku elektrycznego.

•

Historycznie zostało przyjęto, że zwrot linii pola jest ustawiony 

od bieguna północnego N do bieguna południowego S.

N

S

 

 

 

 

•

Zwykle wykonane w postaci sztabki lub 

Zwykle wykonane w postaci sztabki lub 

podko-wy. 

podko-wy. 

•

Oddziaływają na siebie wzajemnie siłami 

Oddziaływają na siebie wzajemnie siłami 

mag-netycznymi, tak że ich końce 

mag-netycznymi, tak że ich końce 

przyciągają się lub odpychają w 

przyciągają się lub odpychają w 

zależności od tego, czy zbliża-my je do 

zależności od tego, czy zbliża-my je do 

siebie biegunami różnoimiennymi, czy 

siebie biegunami różnoimiennymi, czy 

jednoimiennymi.

jednoimiennymi.

•

W magnesach naturalnych efekty 

W magnesach naturalnych efekty 

magnetyczne są najsilniejsze na końcach 

magnetyczne są najsilniejsze na końcach 

magnesu, nazwa-nych biegunami.

magnesu, nazwa-nych biegunami.

•

Obserwacje można przeprowadzić przy 

Obserwacje można przeprowadzić przy 

pomo-cy 

pomo-cy 

opiłków żelaza

opiłków żelaza

 lub 

 lub 

igły 

igły 

magnetycznej. 

magnetycznej. 

Opiłki żelazne w pobliżu 

Opiłki żelazne w pobliżu 

magnesu namagne-sują w taki sposób, że 

magnesu namagne-sują w taki sposób, że 

same stają się dipolami magnetycznymi i 

same stają się dipolami magnetycznymi i 

ustawiają wzdłuż pola magnetycznego.

ustawiają wzdłuż pola magnetycznego.

 

 

 

 

•

Szczegółowe badania pokazali, że pole magnetyczne w 

Szczegółowe badania pokazali, że pole magnetyczne w 

odróżnieniu od elektrycznego, nie posiada odrębnych 

odróżnieniu od elektrycznego, nie posiada odrębnych 

ładunków swobodnych wytwarzają-cych te pole. 

ładunków swobodnych wytwarzają-cych te pole. 

•

Przykładowo, podział sztabki magnesu nie prowadzi do 

Przykładowo, podział sztabki magnesu nie prowadzi do 

rozdzielenia bie-gunów magnetycznych. Nie da się 

rozdzielenia bie-gunów magnetycznych. Nie da się 

wyodrębnić pojedynczych biegunów.

wyodrębnić pojedynczych biegunów.

N

S

N

S N

S

 

 

 

 

•

Ziemia posiada również własne pole magnetyczne. Bieguny 

magnetyczne nie pokrywają się z biegunami geograficznymi.

Geograficz
na 
Północ

Geograficzne 
Południe

Magnetycz
ne 
Południe

Magnetycz
na 
Północ

Ziemskie 
pole
magnetyc
zne

Ziemskie 
pole
magnetyc
zne

 

 

 

 

Pojęcie indukcji magnetycznej 

Pojęcie indukcji magnetycznej 

B

B

F





Na poruszający się w polu magnetycznym ładunek elektryczny działa 

Na poruszający się w polu magnetycznym ładunek elektryczny działa 

pewna siła, która jest wprost proporcjonalna do ładunku 

pewna siła, która jest wprost proporcjonalna do ładunku 

q

q

 i 

 i 

prędkości 

prędkości 

v

v

 .

 .



qvBsin 

 

 

F

gdzie 

gdzie 





 jest kątem pomiędzy wektorami prędkości 

 jest kątem pomiędzy wektorami prędkości 

v

v

 i indukcji 

 i indukcji 

B

B

B

q

F













+

q



B



+

q

Kierunek pola

max

F



lub postaci wektorowej



 

 

 

 

Wyznaczanie wartości indukcji 

Wyznaczanie wartości indukcji 

magnetycznej

magnetycznej

Gdy wektor siły jest pod kątem 

Gdy wektor siły jest pod kątem 

prostym do wektora prędkości.

prostym do wektora prędkości.

B

const

v

q

F





max

Wartością indukcji magnetycznej 

Wartością indukcji magnetycznej 

B

B

 nazywamy stosunek 

 nazywamy stosunek 

wartości maksy-malnej siły działającej na ładunek 

wartości maksy-malnej siły działającej na ładunek 

q

q

 

 

poruszający się prostopadle do kie-runku linii sił pola, do 

poruszający się prostopadle do kie-runku linii sił pola, do 

iloczynu tego ładunku i wartości prędkości, jaką się porusza.

iloczynu tego ładunku i wartości prędkości, jaką się porusza.

 

 

 

 

Indukcja magnetyczna

Indukcja magnetyczna

dla nieskończonego prostoliniowego przewodnika jest

dla nieskończonego prostoliniowego przewodnika jest

 

 

wprost 

wprost 

proporcjonalna do natężenia 

proporcjonalna do natężenia 

I 

I 

odwrotnie proporcjonalna do 

odwrotnie proporcjonalna do 

odległości 

odległości 

r

r

, tzn.

, tzn.

jest współczynnikiem proporcjonalności, 

jest współczynnikiem proporcjonalności, 

r

I

k

B

m



  

przenikalność magnetyczna bezwzględna w próżni

przenikalność magnetyczna bezwzględna w próżni

 

 

     

     







2

0

m

k

gdzie

Am

Vs

7

0

10

4









 

 

 

 

Strumień indukcji 

Strumień indukcji 

magnetycznej

magnetycznej







 

 

- strumień indukcji (strumień magnetyczny)

- strumień indukcji (strumień magnetyczny)

•

B – wartość indukcji magnetycznej

B – wartość indukcji magnetycznej

•

S – pole powierzchni 

S – pole powierzchni 

•

Jednostką jest WEBER

Jednostką jest WEBER

Strumień  indukcji  to  iloczyn  skalarny  wektora 
indukcji  magnetycznej  B  przez  wektor  pola 
powierzchni  S  i  cosinusa  kąta  zawartego 
między tymi wektorami



cos

BS

S

B













 

 

 

 

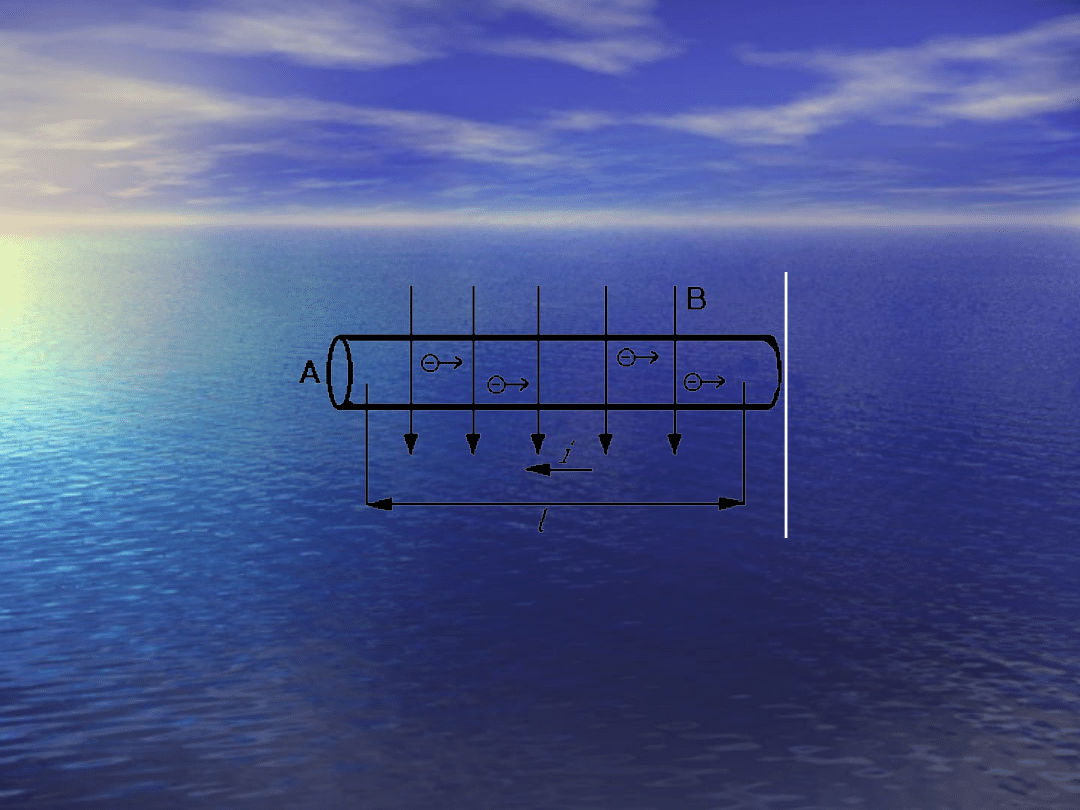
Rysunek przestawia przewodnik z 

Rysunek przestawia przewodnik z 

prądem w polu magnetycznym o 

prądem w polu magnetycznym o 

indukcji B skierowanej prostopadle do 

indukcji B skierowanej prostopadle do 

tego przewodnika

tego przewodnika

•

l – długość drutu

l – długość drutu

•

i

i

 – natężenie prądu płynącego przez drut

 – natężenie prądu płynącego przez drut

•

B

B

 

 

– wartość indukcji magnetycznej pola

– wartość indukcji magnetycznej pola

•

A – pole przekroju przewodnika

A – pole przekroju przewodnika

 

 

 

 

Średnia wartość siły 

Średnia wartość siły 

F

F

’ działającej na 

’ działającej na 

pojedynczy elektron w przewodniku wynosi:

pojedynczy elektron w przewodniku wynosi:

Siła działająca na ładunek punktowy 

Siła działająca na ładunek punktowy 

w polu magnetycznym

w polu magnetycznym

n

jB

B

ne

j

e

F





'

B

ev

vB

q

F

u







sin

'

0

(sinθ=1, gdyż przyjęliśmy, że przewodnik 

ustawiony jest prostopadle do pola)
v

U

 – prędkość unoszenia (v

U

 =j/ne)

n – liczba elektronów przypadających na 

jednostkę objętości

 

 

 

 

Siła działająca na cały 

Siła działająca na cały 

przewodnik

przewodnik

Całkowita siła działająca na przewodnik z prądem 

Całkowita siła działająca na przewodnik z prądem 

jest równa iloczynowi siły działającej na pojedynczy 

jest równa iloczynowi siły działającej na pojedynczy 

ładunek przez ilość ładunków w drucie:

ładunek przez ilość ładunków w drucie:

n

jB

nAl

F

nAl

F





'

)

(

Ponieważ iloczyn jA jest natężeniem prądu i 
płynącego w przewodniku, ostateczny wzór 
wygląda więc następująco:

ilB

F 

 

 

 

 

Ogólna postać 

Ogólna postać 

równania

równania

Powyższe równanie jest prawdziwe jedynie w 
przypadku, gdy drut tworzy z wektorem B kąt prosty. 
W ogólnym przypadku:

F=

F=

i 

i 

l 

l 





 B

 B

l – wektor o wartości równej długości drutu i o 
zwrocie określonym przez kierunek prądu

Możemy także obliczać siłę F działającą na dowolny 
przewodnik, nie tylko prostoliniowy. Korzystamy 
wówczas z równania:

dF=

dF=

i 

i 

d

d

l 

l 





 B

 B

Gdzie dl to długość przewodnika o dowolnym 
kształcie, a siłę F oblicza się poprzez 
odpowiednie całkowanie odcinka dl

 

 

 

 

 

 

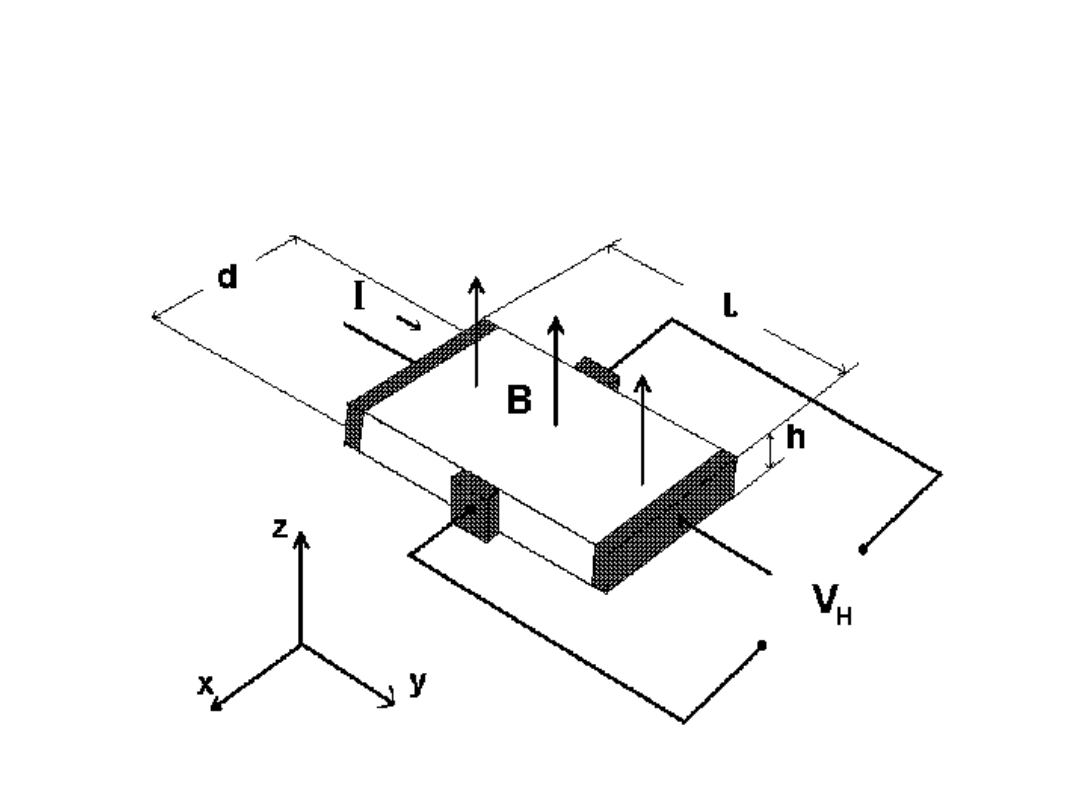
   Przez prostopadłościenną próbkę 

półprzewodnika płynie, w kierunku 

y

, prąd 

elektryczny o natężeniu 

I

.

 

 

 

 

 

 

Na ładunek 

Na ładunek 

q

q

 

 

poruszający się z prędkością 

poruszający się z prędkością 

v 

v 

w polu magnetycznym 

w polu magnetycznym 

B

B

 

 

działa siła 

działa siła 

Lorentza:

Lorentza:

 

 

F=q(v

F=q(v

 

 

x

x

 

 

B)

B)

Siła ta powoduje odchylanie się nośników 

Siła ta powoduje odchylanie się nośników 

ładunku tworzących prąd 

ładunku tworzących prąd 

I

I

 

 

w kierunku 

w kierunku 

poprzecznym do kierunku przepływu prądu 

poprzecznym do kierunku przepływu prądu 

I

I

 

 

i prostopadłym do pola magnetycznego 

i prostopadłym do pola magnetycznego 

B

B

. 

. 

Spowoduje to wystąpienie gradientu 

Spowoduje to wystąpienie gradientu 

koncentracji nośników ładunku w tymże 

koncentracji nośników ładunku w tymże 

kierunku i pojawienie się wywołanego tym 

kierunku i pojawienie się wywołanego tym 

gradientem 

gradientem 

pola elektrycznego

pola elektrycznego

.

.

 

 

 

 

Poprzeczne pole elektryczne 

Poprzeczne pole elektryczne 

E

E

H

H

 

 

 

 

powstałe 

powstałe 

wskutek rozdzielenia ładunków dodatnich i 

wskutek rozdzielenia ładunków dodatnich i 

ujemnych spowoduje wystąpienie dodatkowej 

ujemnych spowoduje wystąpienie dodatkowej 

siły działającej na nośniki prądu. W stanie 

siły działającej na nośniki prądu. W stanie 

stacjonarnym (równowagi dynamicznej) 

stacjonarnym (równowagi dynamicznej) 

całkowita poprzeczna siła działająca na 

całkowita poprzeczna siła działająca na 

nośniki ładunku będzie równa zeru, wobec 

nośniki ładunku będzie równa zeru, wobec 

tego mamy:

tego mamy:

-q·E

-q·E

H

H

=-q·(v 

=-q·(v 

x

x

 

 

B)

B)

 

 

 

 

Ponieważ napięcie pomiędzy dwoma punktami 

Ponieważ napięcie pomiędzy dwoma punktami 

w polu elektrycznym jest równe iloczynowi 

w polu elektrycznym jest równe iloczynowi 

natężenia tego pola i odległości pomiędzy 

natężenia tego pola i odległości pomiędzy 

punktami, a także z geometrii układu 

punktami, a także z geometrii układu 

(prostopadłość wektorów 

(prostopadłość wektorów 

v

v

, 

, 

B

B

, i 

, i 

E

E

H

H

)

)

V

V

H

H

=E

=E

H

H

·d=v·B·

·d=v·B·

d

d

V=

V=

j

j

_

_

n

n

e

e

stą

stą

d

d

V

V

H

H

=

=

j

j

_

_

n

n

e

e

Bd=R

Bd=R

H

H

jB

jB

d

d

gdzie R

gdzie R

H 

H 

to tzw. Stała 

to tzw. Stała 

Halla

Halla

Półprzewodnik typu 

Półprzewodnik typu 

n:

n:

Półprzewodnik typu 

Półprzewodnik typu 

p:

p:

R

R

H

H

=-

=-

R

R

H

H

=

=

1

1

_

_

_

_

1

1

n

n

e

e

p

p

e

e

 

 

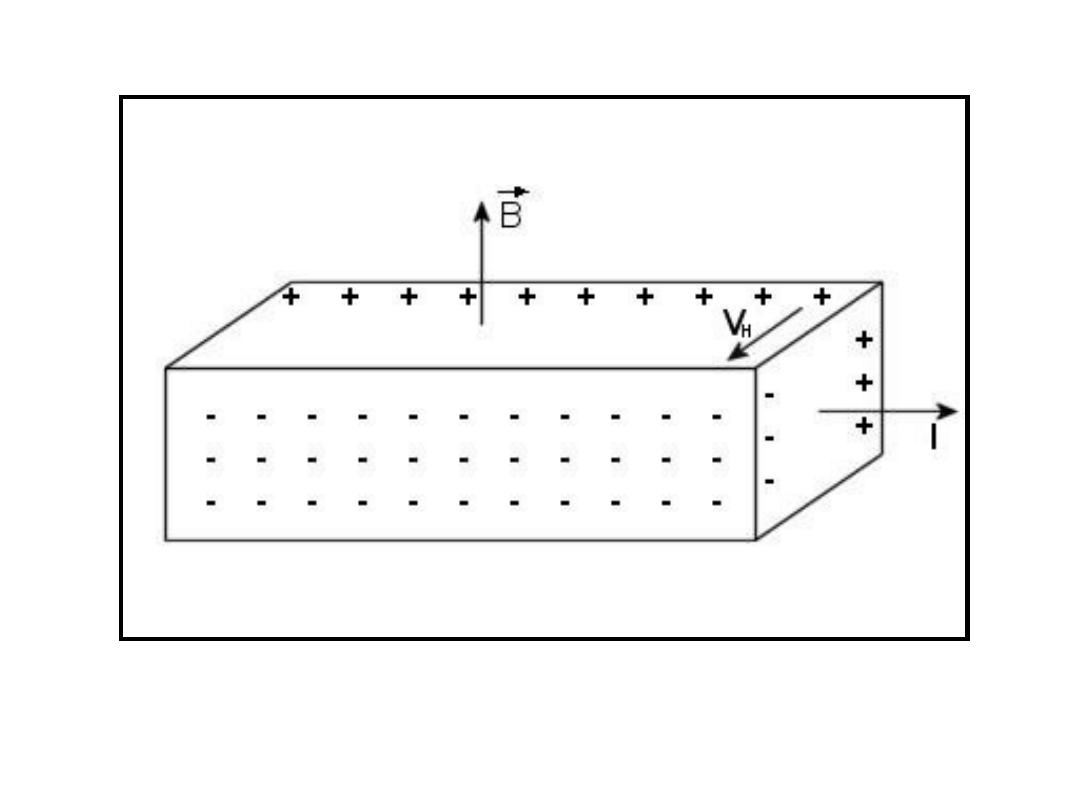
Wynik doświadczenia Halla

Wynik doświadczenia Halla

 

 

 

 

F

v

-q

r

B – indukcja pola 
       magnetycznego
F – siła odchylająca
q – ładunek
v – prędkość ładunku
r – promień toru

 

 

 

 

r

mv

qvB

2



Z drugiego prawa Newtona mamy:

Z drugiego prawa Newtona mamy:

czyli

czyli

qB

mv

r 

Prędkość kątowa ładunku wynosi:

Prędkość kątowa ładunku wynosi:

r

v





m

qB





czyli

czyli

 

 

 

 

Możemy teraz wyznaczyć wzór na częstość:

Możemy teraz wyznaczyć wzór na częstość:

m

qB









2

2





Częstość nie zależy od prędkości. Szybkie 

Częstość nie zależy od prędkości. Szybkie 

cząstki  poruszają  się  po  dużych  orbitach, 

cząstki  poruszają  się  po  dużych  orbitach, 

wolne  po  małych,  ale  każda  z  nich 

wolne  po  małych,  ale  każda  z  nich 

potrzebuje  tego  samego  czasu  do 

potrzebuje  tego  samego  czasu  do 

wykonania jednego obrotu.

wykonania jednego obrotu.

 

 

 

 

Przykład.

Przykład.

  

  

Elektron o energii 10 eV krąży po 

Elektron o energii 10 eV krąży po 

płaszczyźnie prostopadłej do jednorodnego 

płaszczyźnie prostopadłej do jednorodnego 

pola magnetycznego o indukcji

pola magnetycznego o indukcji

 

 

.

10

0

,

1

4

T





Prędkość elektronu o energii kinetycznej 

Prędkość elektronu o energii kinetycznej 

K można wyznaczyć za pomocą wzoru:

K można wyznaczyć za pomocą wzoru:

m

K

v

2



 

 

 

 

Po wyznaczeniu prędkości możemy obliczyć promień

Po wyznaczeniu prędkości możemy obliczyć promień

orbity:

orbity:

m

,

T

C

,

m/s

,

kg

,

qB

mv

r

11

0

10

10

6

1

10

9

1

10

1

9

4

19

6

31























a następnie wyznaczyć częstość cyklotronową:

a następnie wyznaczyć częstość cyklotronową:

Hz

kg

T

C

m

qB

6

31

4

19

10

8

,

2

10

1

,

9

2

10

10

6

,

1

2





























s

Hz

T

7

6

10

6

,

3

10

8

,

2

1

1















oraz okres obrotu: 

oraz okres obrotu: