
Teoria Grafów
G=(V,E);
V=V(G)- zbiór wierzchołków (niepusty), |V(G)|
=n(G);
E=E(G)- zbiór krawędzi (zbiór par
wierzchołków).
N
G
(v) = {u
V: uv
E }– otwarte sąsiedztwo
wierzchołka v;
Jeśli u,v
V, to uv
E
N
G
[v]= N
G
(v)
{v} - domknięte sąsiedztwo wierzchołka v;
Dla X
V, N
G
(X) = U
v
X
N
G
(v); N
G
[X]=N
G
(X)
X.
Stopień wierzchołka v w grafie G- liczba krawędzi, których
końcem jest ten wierzchołek;
d
G
(v) = | N
G
(v)|.
Graf nieskierowany (tzn. E jest zbiorem par
nieuporządkowanych), bez pętli i krawędzi
wielokrotnych
nazywamy grafem prostym.

Typy grafów
1. Graf pełny
G=(V,E) jest grafem pełnym, jeśli
u,v
V
uv
E
G=K
n
– graf pełny o n wierzchołkach
|V|=n, |E|=n(n-1)/2
2. Dopełnienie grafu G jest to graf Gd=(V,Ed), gdzie
Ed={uv: u,v
V,u
v, uv
E }.
3. Graf dwudzielny
Graf G=(V,E) jest dwudzielny, jeśli zbiór jego wierzchołków
może być podzielony na dwa zbiory V
1
, V
2
w ten sposób, że
każda krawędź grafu G łączy wierzchołek należący do V
1
z wierzchołkiem należącym doV
2.
W grafie dwudzielnym wszystkie cykle są parzyste.

Jeśli |V
1
|=r, |V
2
|=s, to graf pełny dwudzielny oznaczamy K
r,s
.
Graf K
1,n-1
nazywamy gwiazdą.
Szlak jest to ciąg wierzchołków (v
1,
v
2,...,
v
n-1,
v
n
) (w którym
dozwolone są powtórzenia) taki, że v
1
v
2,
v
2
v
3,...,
v
n-1
v
n
są
różnymi krawędziami grafu (dozwolone są powtórzenia
wierzchołków, ale nie krawędzi).
Ścieżka- szlak, w którym żadne dwa wierzchołki nie
powtarzają się. Szlak postaci (v
1,
v
2,...,
v
n,
v
1
), w którym
(v
1,
v
2,...,
v
n-1,
v
n
) jest ścieżką, nazywamy cyklem.
Graf G jest spójny, jeśli
u,v
V
istnieje ścieżka łącząca u z v.
Twierdzenie 1 (lemat o uściskach dłoni)
Dla każdego grafu G=(V,E),
v
V
d
G
(v) = 2|E|.
Twierdzenie 2 (wniosek)
W każdym grafie G=(V,E) liczba wierzchołków stopnia
nieparzystego jest parzysta.
Twierdzenie 3 Jeśli G jest grafem spójnym o n wierzchołkach, to
n-1
|E|
n(n-1)/2.
Drzewa
Drzewem nazywamy graf spójny bez cykli. Jeśli v
V(T) jest
wierzchołkiem stopnia jeden, to v nazywamy liściem albo
wierzchołkiem końcowym.

Twierdzenie 4 Jeśli T jest drzewem o n wierzchołkach, to
|E(T)|=n-1.
Twierdzenie 5 Jeśli T jest drzewem o n wierzchołkach, to
następujące warunki są równoważne:
a) T jest drzewem,
e) dowolne dwa wierzchołki grafu T są połączone dokładnie
jedną ścieżką,
f) T nie zawiera cykli, ale dla każdej pary u,v, gdzie u,v są
wierzchołkami i uv nie jest krawędzią, T+uv posiada
dokładnie jeden cykl.
b) T nie zawiera cykli i ma n-1 krawędzi,
c) T jest spójny i ma n-1 krawędzi,
d) T jest spójny i dla każdej jego krawędzi uv graf T-uv
jest niespójny,

Twierdzenie 6 (Cayley’a)
Algorytm wyznaczania kodu Prufera:
Aby wyznaczyć kod Prufera dla danego drzewa T na zbiorze
wierzchołków {1,...,n}, należy:
a) znaleźć najmniejszy wierzchołek stopnia jeden, powiedzmy v.
Niech w będzie wierzchołkiem połączonym z v;
b) zapisać w oraz usunąć wierzchołek v wraz z krawędzią vw;
c) Jeśli w drzewie pozostała więcej niż jedna krawędź, to przejść
do kroku a); w przeciwnym razie zakończyć algorytm.
Otrzymany ciąg liczb jest kodem Prufera dla drzewa T.

Algorytm otrzymywania drzewa z kodu:
Dla zadanego ciągu liczb (a
1
, a
2
,..., a
n-2
) wybranych w dowolny
sposób ze zbioru {1,...,n}, aby wyznaczyć drzewo T, dla którego
ciąg ten jest kodem Prufera, należy:
1. Zapisać dwie listy; pierwszą a
1
, a
2
,..., a
n-2
oraz drugą 1,2,...,n
i rozpocząć ze zbiorem wierzchołków {1,...,n} i pustym zbiorem
krawędzi.
2. Wyznaczyć z drugiej listy najmniejszą liczbę, powiedzmy i,
która nie występuje na pierwszej liście. Usunąć pierwszy
element z pierwszej listy, powiedzmy j, usunąć i z drugiej listy
oraz dodać do zbioru krawędzi ji.
3. Jeśli pierwsza lista zawiera co najmniej jedną liczbę, to
przejść do punktu 2. Jeśli pierwsza lista jest pusta, to druga
będzie się składać z dokładnie dwóch liczb. Dodać do zbioru
krawędzi ostatnią, której wierzchołkami są właśnie te liczby
i zakończyć algorytm.

Leonard Euler
1707-1783
Grafy Eulera

- w wieku lat 13-tu zaczął studiować teologię;
- w wieku lat 16-tu ukończył studia matematyczne;
- znalazł matematyczny dowód na istnienie Boga;
- wymyślił popularną teraz łamigłówkę SUDOKU;
- opublikował ponad 900 prac z różnych
dziedzin, był wielkim popularyzatorem
matematyki;
- 77 miejsce na 100 postaci, które miały
największy wpływ na dzieje ludzkości
(opracowanie Michaela Harta- na 2 miejscu
Newton, na 33 Szekspir);
- jest autorem hipotezy, że Ziemia jest
wewnątrz pusta, w centrum ma słońce, na
dodatek ta przestrzeń jest zamieszkana
(UFO- forum top secret);
- słynny „wzór Eulera” wymyślił mając zaledwie roczek.
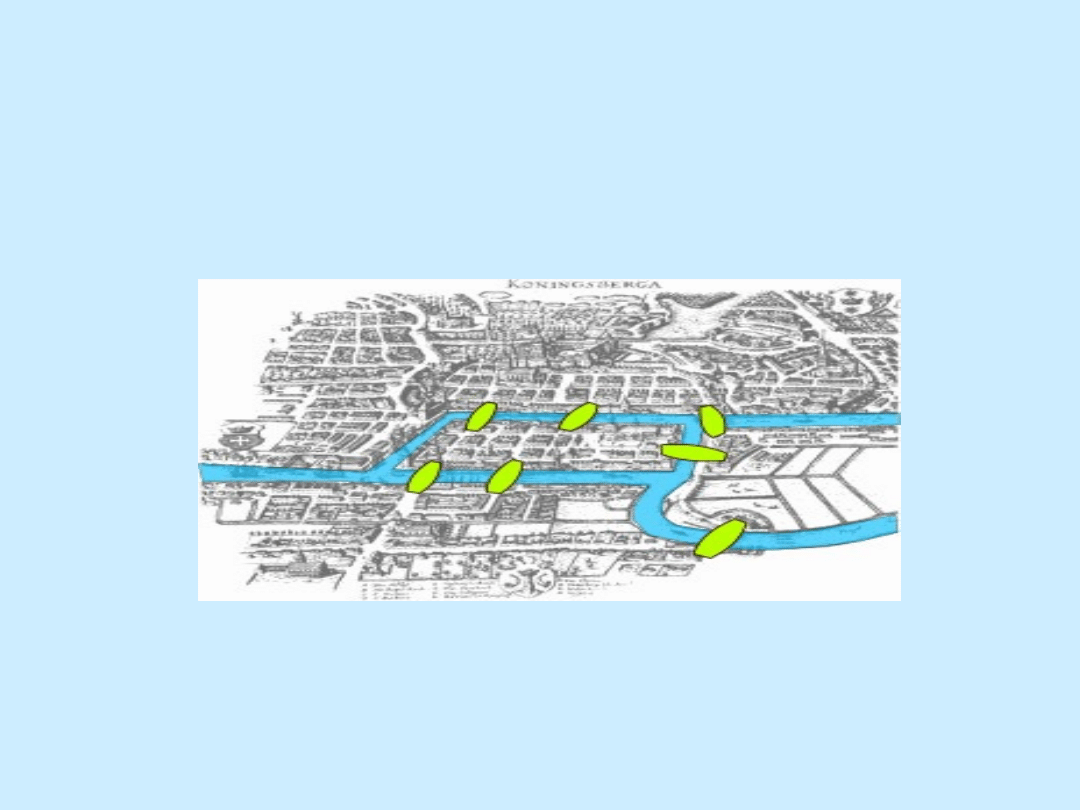
Mosty królewieckie - 7 mostów łączących brzegi
rzeki Pregoły (1736)
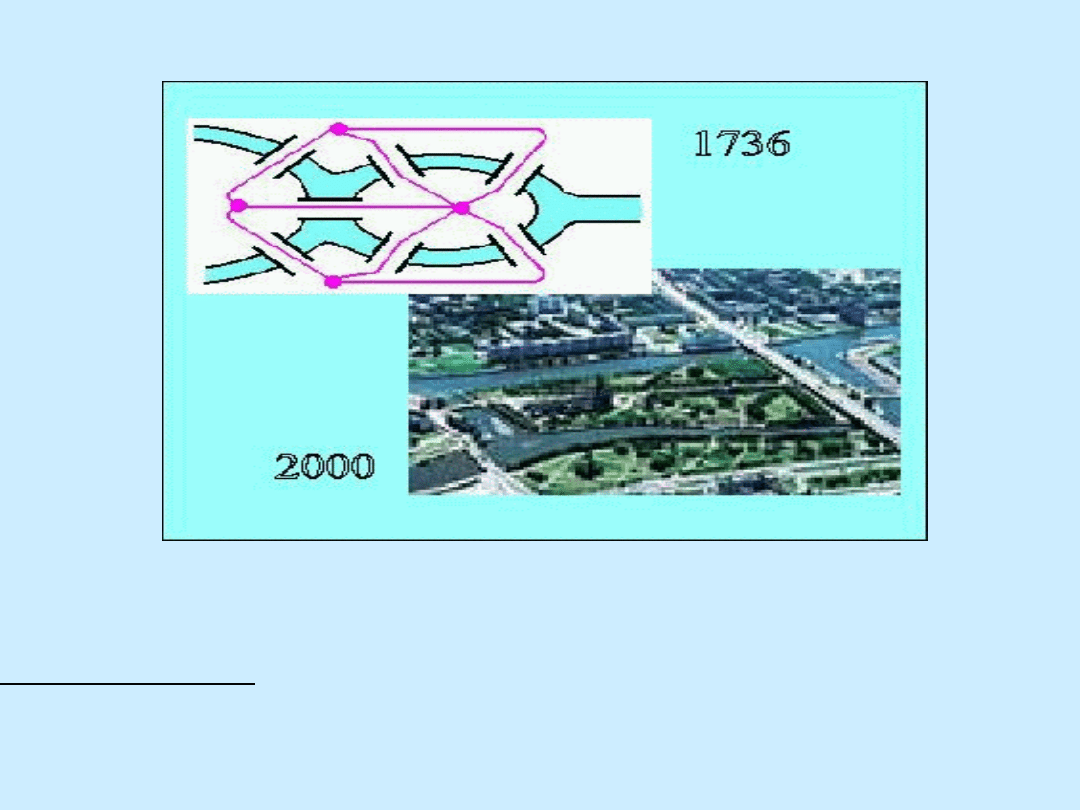
Pytanie Eulera: czy można przejść przez miasto przechodząc
przez każdy most dokładnie jeden raz ?
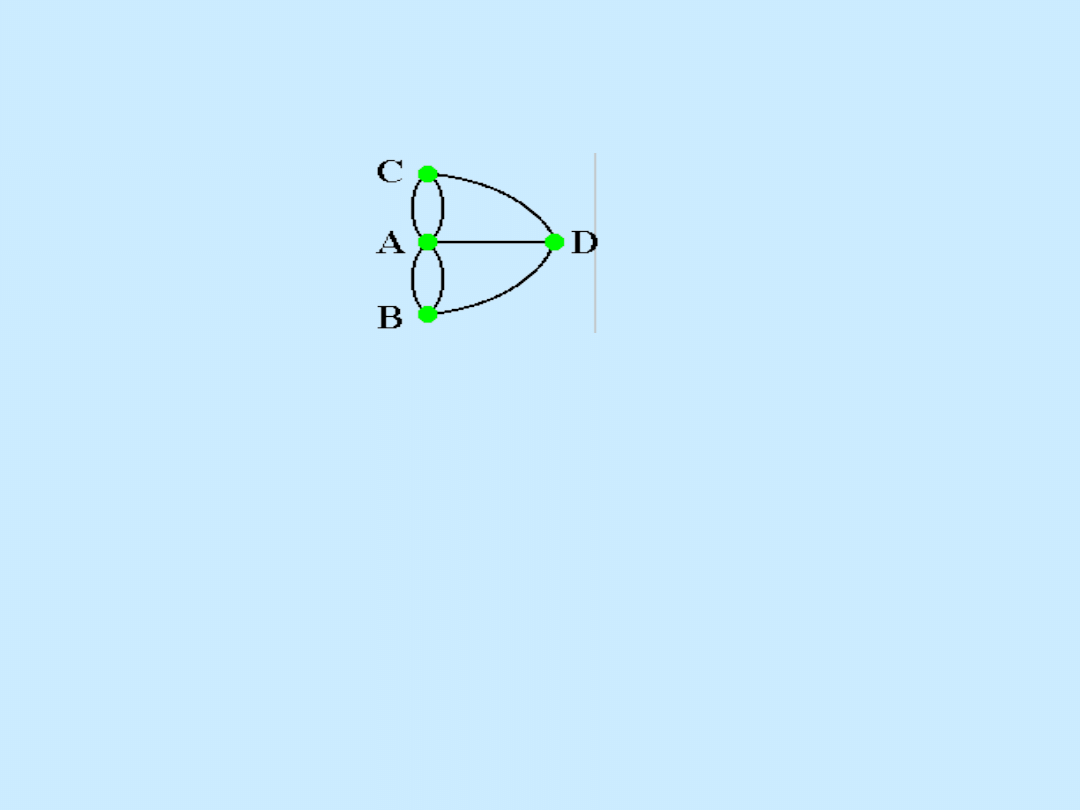
Zastępujemy obszary lądu wierzchołkami a
mosty krawędziami:
Czy można przejść przez cały graf, używając każdej krawędzi
dokładnie raz? (czy graf jest eulerowski?)
Graf jest eulerowski wtedy i tylko wtedy, gdy każdy
jego wierzchołek ma stopień parzysty.

The Graph Theory Hymn
Text by BOHDAN ZELINKA
Music by ZDENĔK RYJÁČEK
English text by DONALD A. PREECE
Seven bridges spanned the River
Pregel,
Many more than might have been
expected;
Königsberg's wise leaders were
delighted
To have built such very splendid
structures.
Refrain:
Eulerian graphs all have this
restriction:
THE DEGREE OF ANY POINT IS
EVEN.
That's the oldest graph result
That mankind has ever known.

Hymn Teorii Grafów
Nowej wiedzy Euler dał podstawy
przez co zyskał całe wieki sławy.
My śladami Mistrza podążamy
i naukę jego rozwijamy.
Więc Koledzy, na koniec powstańmy,
wznosząc toast głośno zaśpiewajmy:
Niechaj żyje nam Teoria Grafów,
obwieszczajmy ją całemu światu.
Ref. Eulera graf, to fakt oczywisty,
wszystkie wierzchołki ma stopni parzystych-
to doskonale znana jest
w Teorii Grafów pierwsza z tez.

Szlak domknięty- taki, który kończy się w swoim punkcie wyjścia.
Szlak Eulera (cykl Eulera)- szlak domknięty, przechodzący przez
wszystkie krawędzie grafu.
Graf eulerowski- graf zawierajacy szlak Eulera.
Twierdzenie 7 (Eulera-Hierholtza)- warunek konieczny
i dostateczny na to, aby graf był eulerowski
Niech G będzie grafem spójnym. Następujące trzy własności
są równoważne:
1. Każdy wierzchołek w G ma stopień parzysty;
2. Istnieje p cykli c
1
, c
2
,..., c
p
takich, że każda krawędź grafu G
należy do dokładnie jednego cyklu (G można przedstawić jako
sumę rozłącznych krawędziowo cykli);
3. G jest eulerowski.

Algorytm- jak przejść po grafie eulerowskim używając każdej
krawędzi dokładnie raz? (korzystając z dowodu twierdzenia E-H)
1. Wybieramy dowolny wierzchołek v
0
V(G) i cykl c zawiera v
0;
2. Wszystkie krawędzie c oznaczamy cechą 0;
3. Wybieramy cykl c’, „sąsiedni” z cyklem już wybranym i jego
krawędziom przypisujemy cechę c+1, gdzie c jest cechą
poprzednio wybraną- tak do wyczerpania grafu G;
4. Startujemy z v
0
i idziemy wzdłuż cyklu oznaczonego symbolem 0
aż do spotkania wierzchołka v
i
incydentnego z nie odwiedzaną
jeszcze krawędzią oznaczoną wyższym symbolem. Wybieramy
krawędź z najwyższą cechą aż do wyczerpania wszystkich krawędzi.

Algorytm Fleury’ego.
Niech G będzie grafem eulerowskim. Wtedy następująca
konstrukcja jest wykonalna i daje w wyniku cykl Eulera
w grafie G:
1. Usuwaj z grafu przechodzone krawędzie i wierzchołki
izolowane powstałe w wyniku usuwania tych krawędzi.
2. W każdym momencie przechodź przez „most” tylko wtedy,
gdy nie masz innej możliwości.
Zacznij cykl w dowolnym wierzchołku u i przechodź krawędzie
w dowolnej kolejności, dbając jedynie o zachowanie zasad:

Grafy Hamiltona.
Def. Spójny graf G jest grafem Hamiltona (hamiltonowskim),
jeśli zawiera cykl przechodzący przez wszystkie wierzchołki grafu G.
Twierdzenie 8 (Ore)
Jeżeli dla każdych dwóch nie sąsiednich wierzchołków grafu G
suma ich stopni jest nie mniejsza niż ilość wszystkich
wierzchołków w G, to G jest hamiltonowski.
Twierdzenie 9 (Diraca)
Jeżeli graf G ma co najmniej trzy wierzchołki i stopień każdego
z wierzchołków jest równy co najmniej połowie ilości wierzchołków
w G, to G jest hamiltonowski.

Twierdzenie o małżeństwach
Kasia zna Maćka, Adama i Kubę;
Monika – Adama i Kubę;
Jola zna Kubę, Łukasza i Tomka;
Marta – Adama i Maćka;
Renia zna Kubę, Adama i Maćka;
Magda – Michała, Łukasza i Bartka.
Czy jest możliwe znalezienie męża dla każdej z dziewcząt?
( tj. dla każdej innego chłopca spośród tych których zna)
Przykład
1

W grupie dziewcząt każda może wybrać męża
spośród chłopców, których zna,
wtedy i tylko wtedy, gdy w każdym podzbiorze dziewcząt
(powiedzmy r spośród z nich),
dziewczyny te znają co najmniej r chłopców.
Twierdzenie Halla o małżeństwach

Agata zna Janka i Zbyszka;
Asia – Pawła i Zbyszka;
Aga zna Janka, Zbyszka, Piotrka i Michała;
Amelia – Pawła, Piotrka, Wojtka i Jurka;
Ala zna Janka i Michała;
Ania – Pawła i Janka.
W tym przypadku każdy zbiór k dziewcząt zna przynajmniej k chłopców.
Przykład 2

Agata
Asia
Aga
Ameli
a
Ala
Ania
Janek
Paweł
Zbysze
k
Piotrek
Michał
Wojtek
Jurek
Co poradzimy Ani???
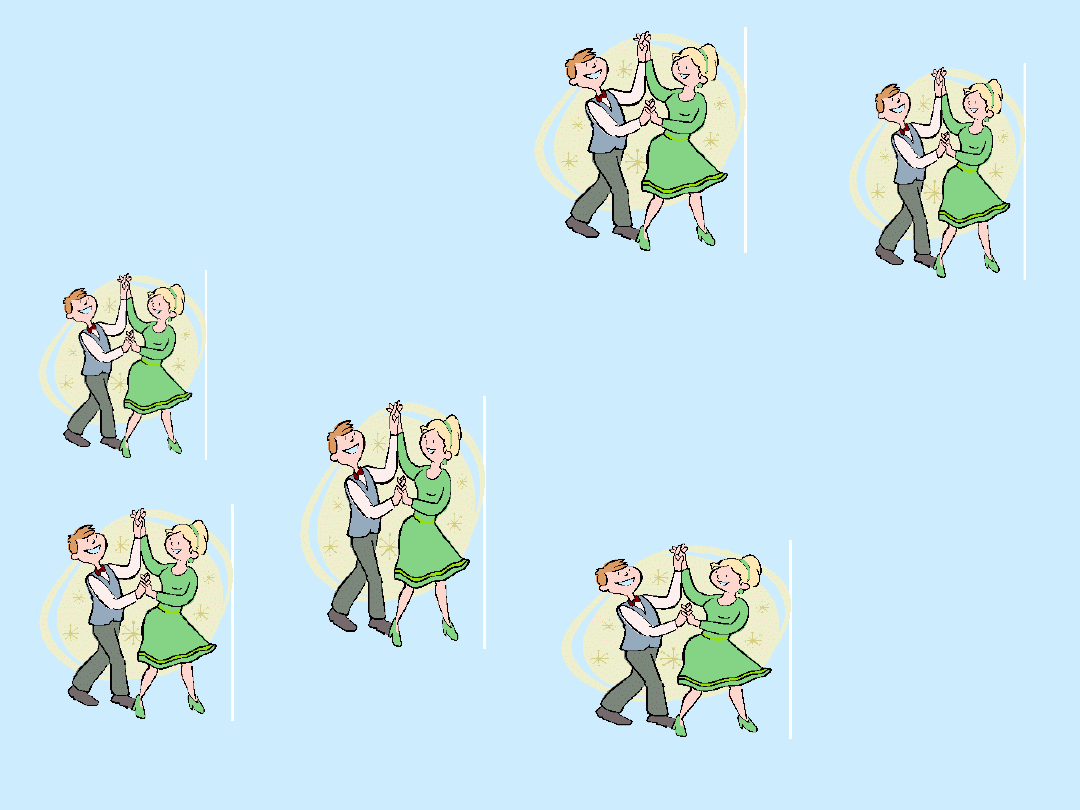
Ania
Paweł + Asia
Janek + Agata
Zbyszek + Aga
Michał + Ala
Piotrek + Amelia
Wojtek
Jurek
Janek + Ania
Zbyszek + Agata
Wojtek + Amelia
Piotrek +Aga
Paweł + Asia
Michał + Ala

Twierdzenie Halla- wersja transwersalowa.
Transwersala- system różnych reprezentantów.
Dana jest uporządkowana rodzina
= (A
1
,
A
2
,...,
A
n
).
Zbiór X
U
i=1,...,n
A
i
jest transwersalą rodziny
, gdy:
1. |X|=n, X={a
1
, a
2
,..., a
n
};
2. a
i
A
i
, i=1,...,n, to znaczy a
i
reprezentuje zbiór
A
i
dla każdego i.
Przykład
A
1
={1,3}
A
2
={2,3}
A
3
={1,3,4,5}
A
4
={2,4,6,7}
A
5
={1,5}
A
6
={1,2}
A
1
={1,
3
}
A
2
={
2
,3}
A
3
={1,3,
4
,5}
A
4
={2,4,
6
,7}
A
5
={1,
5
}
A
6
={
1
,2}

Twierdzenie (Halla- wersja transwersalowa)
Rodzina
= (A
1
,
A
2
,...,
A
n
)
ma transwersalę
wtedy i tylko
wtedy, gdy dla każdego podzbioru I
{1,...,n}, I={i
1
,...,i
r
}
|
A
i1
A
i2
...
A
ir
|
r = |I|.
A
i1
– zbiór chłopców znanych dziewczynie 1
A
ir
– zbiór chłopców znanych dziewczynie r
R = |I|- moc podzbioru dziewcząt

Twierdzenie Halla- wersja grafowa.
Skojarzenie (matching) w grafie dwudzielnym G=(V
1
, V
2
, E)
jest to zbiór krawędzi E’
E taki, że każdy wierzchołek z V
1
należy do krawędzi z E’ i krawędzie te są wierzchołkowo rozłączne.

Twierdzenie (Halla- wersja grafowa)
Jeżeli G=(V
1
, V
2
, E) jest dwudzielny, to istnieje skojarzenie
zbioru V
1
w zbiór V
2
wtedy i tylko wtedy, gdy
dla każdego X
V
1
, |N
G
(X)|
|X|.
Skojarzenia- zawarte związki małżeńskie;
Ilość sąsiadów- ilość znajomych chłopców;
Graf ma skojarzenie wtedy i tylko wtedy, gdy każda
dziewczyna znajdzie męża spośród chłopców, których zna

Kolorowanie krawędzi.
Mając dany graf, chcemy pokolorować jego krawędzie tak,
by żadne krawędzie tego samego koloru nie miały wspólnego
wierzchołka.
Najmniejszą liczbę kolorów potrzebną do pokolorowania
krawędzi grafu G nazywamy indeksem chromatycznym
grafu G i oznaczamy
e
(G).
Jeśli największy stopień wierzchołka w grafie wynosi
, to
e
(G)
.
Twierdzenie (Koniga)
Jeśli G jest grafem dwudzielnym, gdzie wierzchołek
o największym stopniu ma stopień
, to
e
(G) =
.
Twierdzenie (Vizinga)
Jeśli G jest grafem, to
(G)
e
(G)
(G)+1.
Kolorowanie wierzchołków.
Dany jest graf G=(V,E). Będziemy rozważać funkcję f:V
N.
Jest ona poprawnym kolorowaniem wierzchołków grafu G,
jeśli dla każdych dwóch wierzchołków u,v, takich, że uv
E(G),
f(u)
f(v).
(G)=min{|f(v)|} (minimum po wszystkich możliwych
kolorowaniach)- liczba chromatyczna grafu G.
Liczba chromatyczna grafu G- najmniejsza liczba kolorów
potrzebna do prawidłowego pokolorowania grafu G.
Wielomian chromatyczny.
Jeśli G=(V,E) jest grafem, a k
N, to oznaczmy przez P
G
(k)
liczbę różnych kolorowań (prawidłowych) grafu G w dokładnie
k kolorów.
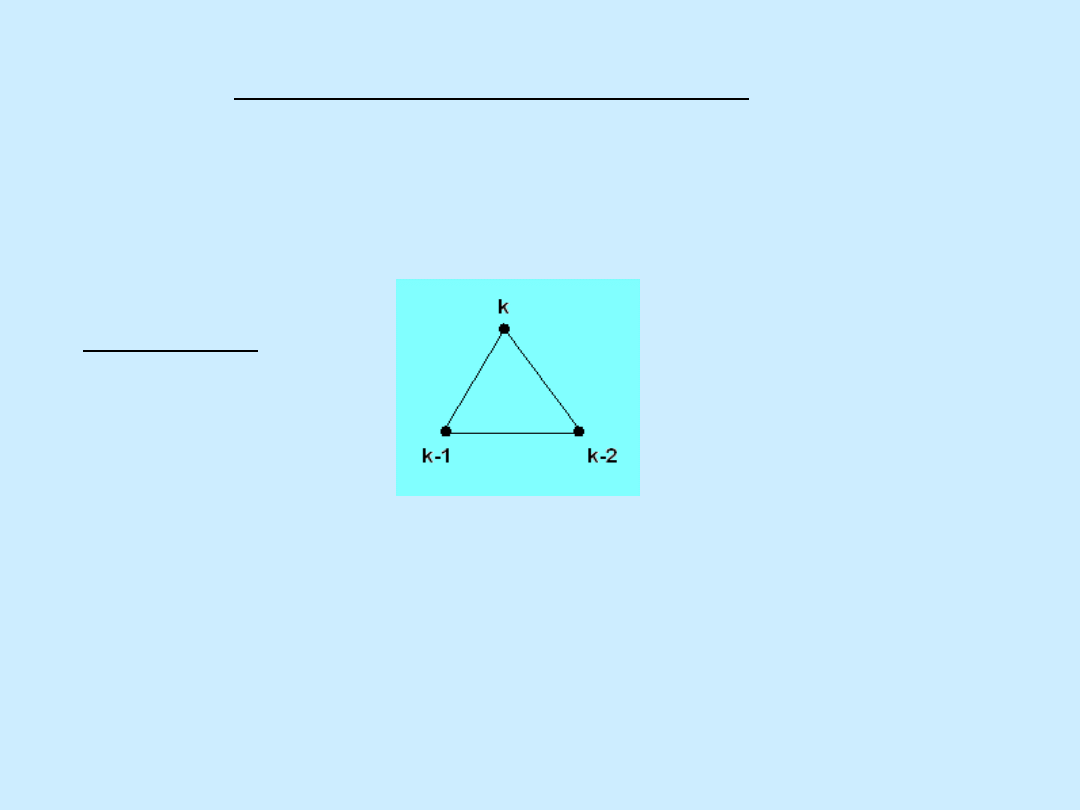
Przykład
P
K
3
(k)=k(k-1)
(k-2)
P
K
5
(6)=6 · 5 · 4 · 3 · 2 · 1
P
K
5
(4)=4 ·3 ·2 ·1 · 0 – nie da się pokolorować w cztery kolory
Grafu pełnego o pięciu wierzchołkach
P
K
n
(k)=k(k-1)(k-2)...(k-(n-1))

(G)- najmniejsze k
N takie, że P
G
(k) > 0.
Jeśli u,v są wierzchołkami grafu G i nie są połączone krawędzią,
to przez G+uv oznaczmy graf powstały z G przez dodanie
krawędzi uv.
Jeśli u,v są wierzchołkami grafu G, to przez G
(u=v)
oznaczmy
graf powstały z G przez ściągnięcie wierzchołka u do v.
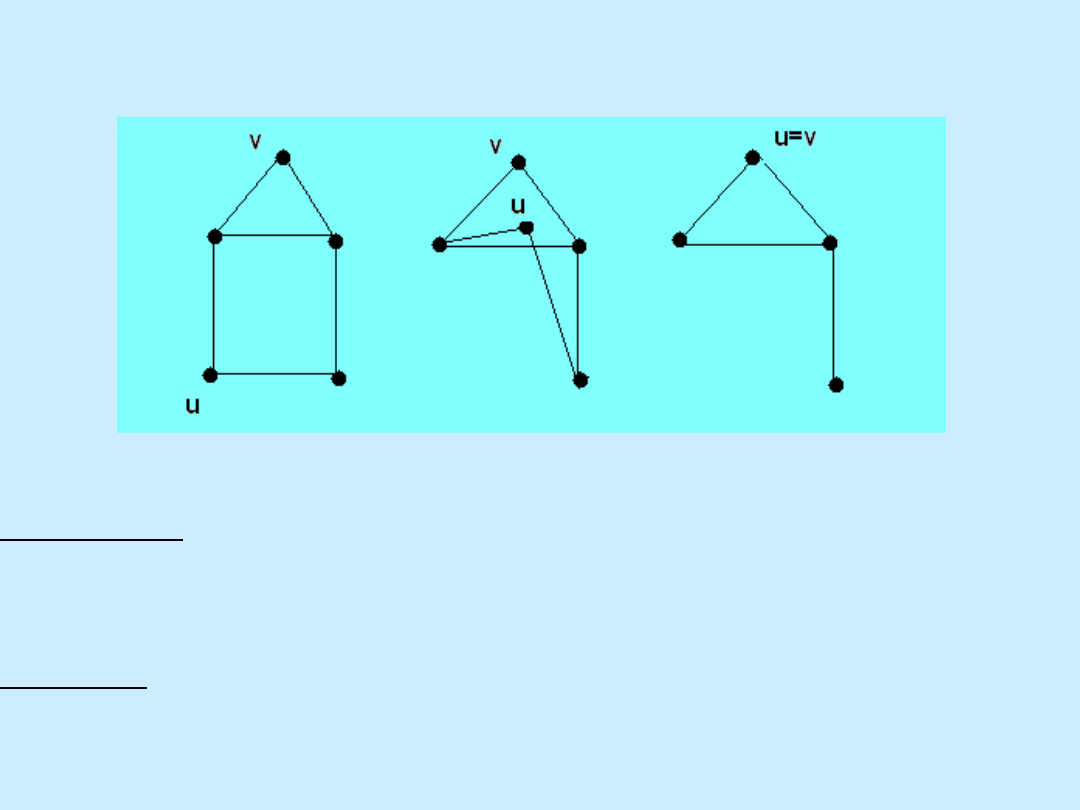
Twierdzenie Jeśli u,v są wierzchołkami grafu G i uv nie jest
krawędzią tego grafu, to P
G
(k) = P
G+uv
(k)+P
G(u=v)
(k).
Zadanie Znaleźć P
G
(k) oraz
(G), jeśli G jest cyklem
pięciowierzchołkowym z jedną cięciwą.
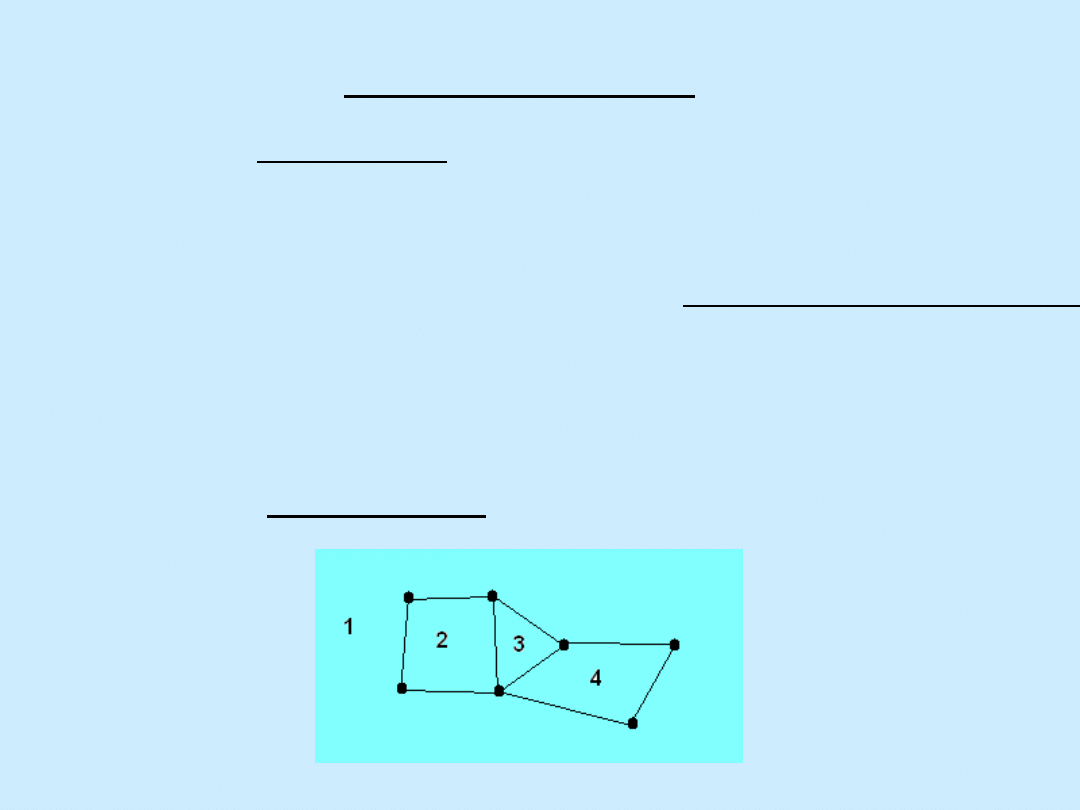
Grafy planarne
Graf G=(V,E) jest planarny, jeżeli może być narysowany na
płaszczyźnie tak, że dowolne jego krawędzie „spotykają się”
co najwyżej we wspólnym wierzchołku końcowym.
Każdy rysunek takiego grafu jest jego planarną reprezentacją.
Mając daną planarną reprezentację grafu, można rozpatrywać
zbiór punktów na płaszczyźnie, które nie należą do tej
reprezentacji: zbiór ten w naturalny sposób dzieli się na
„kawałki” zwane regionami.

Twierdzenie (wzór Eulera)
Jeśli G=(V,E) jest spójnym grafem planarnym, to w dowolnej
jego planarnej reprezentacji liczba regionów f jest równa
|E|-|V|+2.
Twierdzenie Dla każdego grafu planarnego G=(V,E),
i
k(O
i
)= 2|E|, gdzie k(O
i
) oznacza ilość krawędzi
ograniczających obszar O
i
.
Twierdzenie Jeśli G=(V,E) jest spójnym grafem planarnym o co
najmniej trzech wierzchołkach, to |E|
3|V|-6.
Twierdzenie Jeśli G=(V,E) jest spójnym grafem planarnym
dwudzielnym o co najmniej trzech wierzchołkach, to |E|
2|V|-4.
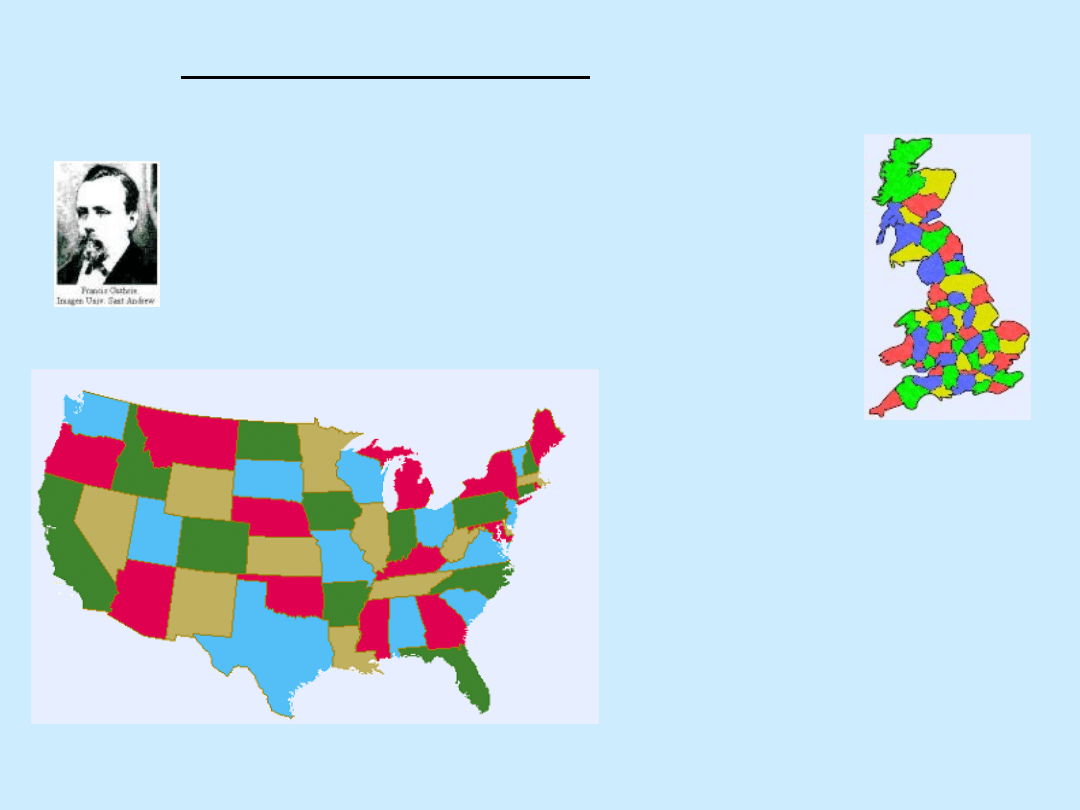
W 1852 roku Francis Guthrie kolorował
mapę Anglii, zauważył, że cztery kolory
wystarczą, by każde dwa sąsiadujące
hrabstwa różniły się barwą. Pomyślał:
czy cztery barwy
wystarczą do
pokolorowania dowolnej,
nawet najbardziej
skomplikowanej mapy?
Kolorowanie map
1976 : Kenneth Appel, Wolfgang Haken, wspomagani w sprawach
komputerowych przez studenta Johna Kocha.
Lata 90. XX wieku: Neil Robertson, Dan Sanders, Paul Seymour
i Robin Thomas- dowód bardziej strukturalny.
Pierwszy dowód pojawił się dopiero w roku 1879.
Przedstawił go Alfred Kempe, londyński prawnik. Był
to zapewne najsłynniejszy fałszywy dowód w całej
historii matematyki.
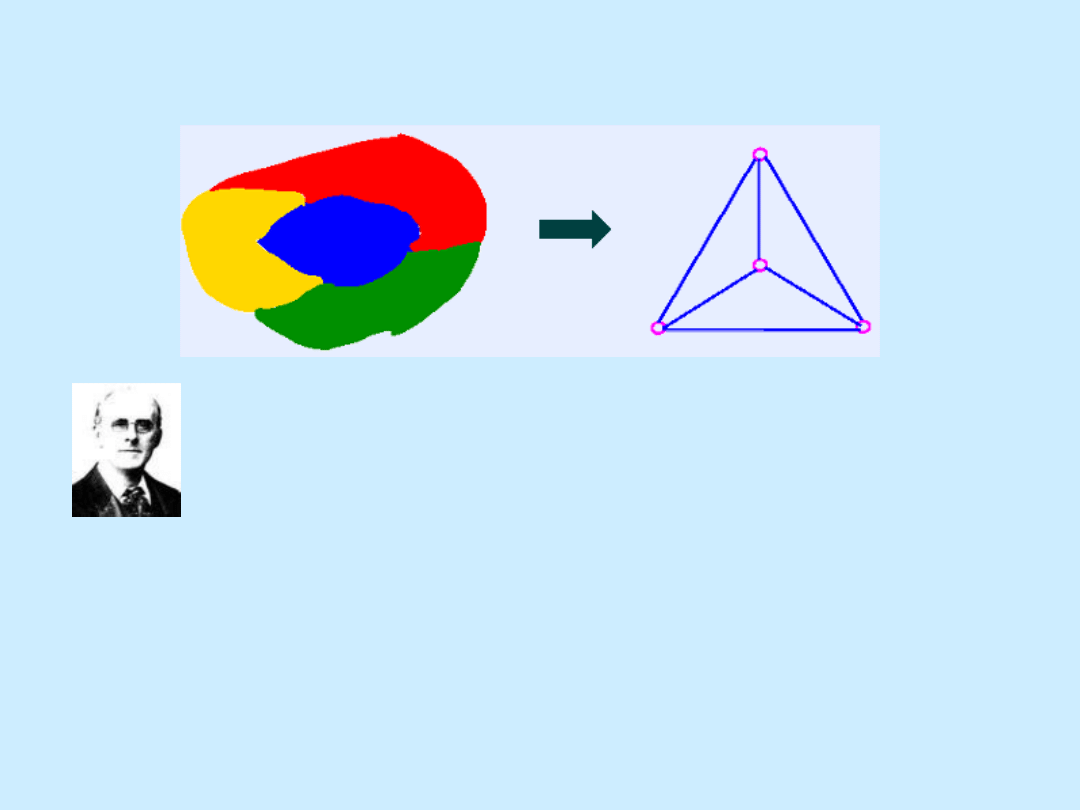
Wierzchołki to obszary (państw), krawędzie - gdy obszary mają jedną
lub więcej wspólnych granic.

Kolorowanie mapy jest równoważne z kolorowaniem
wierzchołków grafu planarnego.
Twierdzenie Każda mapa może być pokolorowana pięcioma
kolorami.

Fundamentalny zbiór cykli
Niech
oznacza zbiór wszystkich podgrafów spinających
grafu G=(V,E), tzn.
= {(V,E’): E’
E}.
W zbiorze
określamy dodawanie , przyjmując dla
dowolnych (V,E’), (V,E”)
,
(V,E’) (V,E”) = (V,E’ E”),
gdzie E’ E” jest różnicą symetryczną zbiorów E’ oraz E”.
W zbiorze
określamy mnożenie przez liczby z {0,1};
dla dowolnego G’= (V,E’)
mamy
1*G’=G’;
0*G’=(V,
).
Zbiór
z dodawaniem jest przestrzenią wektorową nad
ciałem {0,1}.

Wektorem zerowym jest graf (V,
), a wektorem przeciwnym
do G’ jest G’.
Niech
C
oznacza zbiór tych podgrafów spinających grafu G,
w których stopień każdego wierzchołka jest parzysty.
Zauważmy, że elementami zbioru
C
są cykle i sumy
krawędziowo rozłącznych cykli grafu G rozumiane jako jego
podgrafy spinające.
C
jest podprzestrzenią przestrzeni
.
Podprzestrzeń
C
nazywamy przestrzenią cykli grafu G.
Bazę C przestrzeni
C
złożoną jedynie z cykli nazywamy
bazą cykli grafu G.

Weźmy pod uwagę graf G=(V,E) i jego drzewo spinające T=(V,E’)
oraz wszystkie krawędzie {e
1
,...,e
m
}
E-E’, których liczba jest
równa |E|-|V|+1.
Dodanie krawędzi e
i
=uv do drzewa T tworzy dokładnie jeden
cykl c
i
złożony z krawędzi e
i
i jedynej drogi T(u,v).
Tak więc zbiór C={c
1
,...,c
m
} jest bazą cykli grafu G, nazywamy ją
fundamentalną bazą cykli wyznaczoną przez drzewo spinające T.
Dowolny cykl w G można wyrazić jako różnicę symetryczną
pewnych cykli bazowych w odniesieniu do drzewa T.
Zbiór cykli bazowych rozpina zatem przestrzeń
C.

Problem pięciu królowych (1850 r).
Jaka jest najmniejsza liczba królowych jaka może być
rozmieszczona na szachownicy 8 x 8 tak, by każde pole było
w zasięgu jakiejś królowej?
Problem pięciu królowych-problem znalezienia „zbioru
dominującego” o mocy 5.
Dominowanie w grafach.

Zbiór D
V(G) jest zbiorem dominującym w
grafie G, jeśli każdy wierzchołek ze zbioru
V(G)-D w grafie G jest dominowany przez
wierzchołek ze zbioru D.
Dla danych wierzchołków x,y grafu G mówimy, że x dominuje y,
jeśli x=y albo jeśli xy
E(G). W takim razie x dominuje siebie
i wszystkie wierzchołki sąsiednie z wierzchołkiem x.
Jeśli D jest dominujący w G, to każdy nadzbiór D’
D też jest
dominujący.
Z drugiej strony, nie każdy podzbiór D”
D jest dominujący w G.

Zbiór dominujący D jest minimalny dominujący, jeśli żaden
podzbiór właściwy D”
D nie jest dominujący.
Twierdzenie Zbiór dominujący D jest minimalnym zbiorem
dominującym wtedy i tylko wtedy, gdy dla każdego wierzchołka
u
D zachodzi jeden z dwóch warunków:
a) u jest izolowany w D;
b) istnieje v
V-D, dla którego N
G
(v)
D = {u}.
Moc najmniejszego zbioru dominującego w grafie G nazywamy
liczbą dominowania grafu G i oznaczamy
(G).
Moc największego zbioru minimalnego dominującego w grafie G
nazywamy górną liczbą dominowania grafu G i oznaczamy
(G).
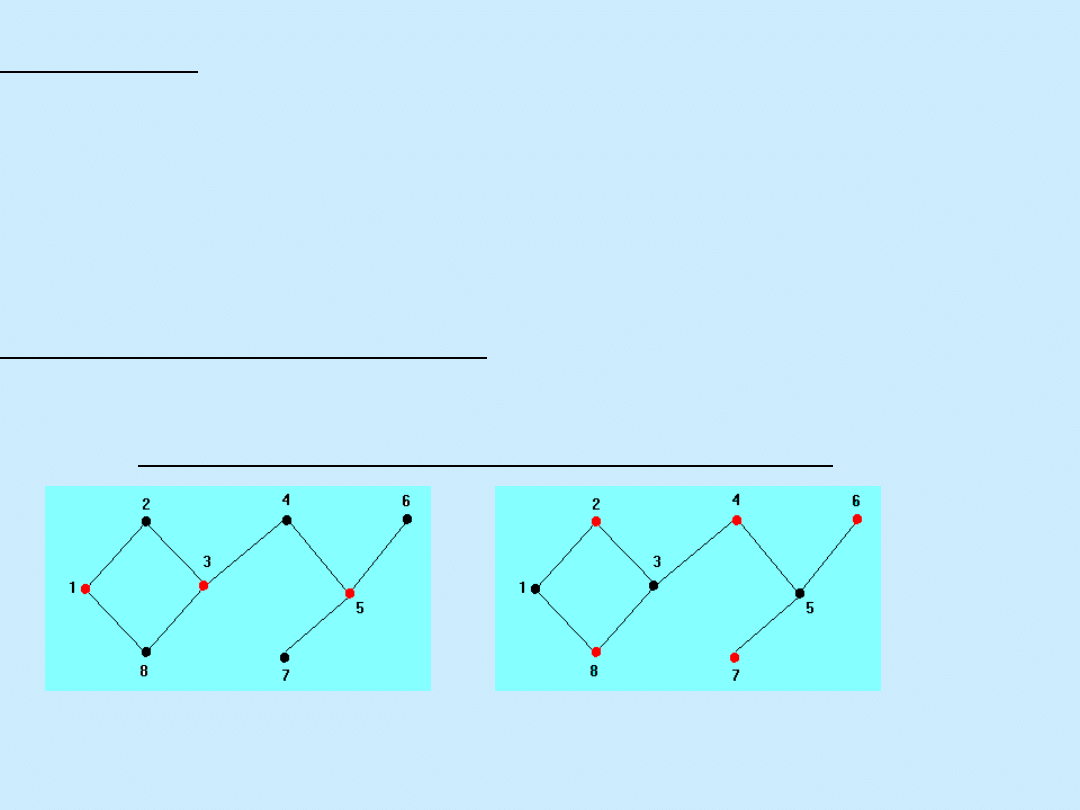
(G)=3
(G)=5

Niech D - zbiór dominujący i niech u
D. Mówimy, że
wierzchołek v jest prywatnym sąsiadem wierzchołka u
(w odniesieniu do D), jeśli N
G
[v]
D = {u}.
Zbiór prywatnych sąsiadów wierzchołka u:
PN[u,D]={v : N
G
[v]
D = {u} }.
u
PN[u,D], jeśli jest izolowany w podgrafie indukowanym
G[D], wtedy mówimy, że u jest swoim własnym prywatnym
sąsiadem.
Zbiór dominujący D jest minimalny dominujący wtedy i tylko
wtedy, gdy każdy wierzchołek z D ma przynajmniej jednego
prywatnego sąsiada.

Twierdzenie Dla każdego grafu G,
(G)
n -
(G).
Twierdzenie Jeśli graf G nie ma wierzchołków izolowanych
oraz diam(G)
3, to
(Gd) = 2, gdzie Gd jest dopełnieniem grafu G.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
Wyszukiwarka
Podobne podstrony:
Ruciński A Teoria Grafów 1, wyklad6
Ruciński A Teoria Grafów 1, wyklad1
Ruciński A Teoria Grafów 1, wyklad10
Ruciński A Teoria Grafów 1, wyklad12
Ruciński A Teoria Grafów 1, wyklad4
Ruciński A Teoria Grafów 1, wyklad11
Ruciński A Teoria Grafów 1, wyklad2
teoria grafow wyklad
Ruciński A Teoria Grafów 1, wyklad9
Ruciński A Teoria Grafów 1, wyklad8
Ruciński A Teoria Grafów 1, wyklad5
Ruciński A Teoria Grafów 1, wyklad7
Ruciński A Teoria Grafów 1, wyklad3
Ruciński A Teoria Grafów 1, wyklad6
Ruciński A Teoria Grafów 1, wyklad1
Ruciński A Teoria Grafów 1, wyklad10
Ruciński A Teoria Grafów 1, wyklad12
formalizm juesej, Teoria Literatury [ wykłady prof. M. Kuziak], Teoria literatury
więcej podobnych podstron