WYKŁAD 3.

Kliki i zbiory niezależne

• Ile

co najmniej

krawędzi gwarantuje

istnienie kliki wielkości k?

• Ile

co najwyżej

krawędzi gwarantuje

istnienie zbioru niezależnego
wielkości k?

• Ile

co najmniej

wierzchołków

gwarantuje klikę wielkości k

lub

zbiór niezależny wielkości l ?

Ile krawędzi gwarantuje

K_3 ?

• n^2/4

nie gwarantuje, bo K(n/2,n/2)

• Tw. (Mantel, 1907)

Jeśli graf o

n

wierzchołkach ma więcej niż

n^2/4

krawędzi, to zawiera trójkąt.

• Dowód:

G – graf bez trójkąta, v

--wierzchołek o stopniu Δ, N(v) –

zbiór sąsiadów v w G. Zbiór N(v)

jest niezależny, stąd

4

)

(

2

/

n

n

e(G)











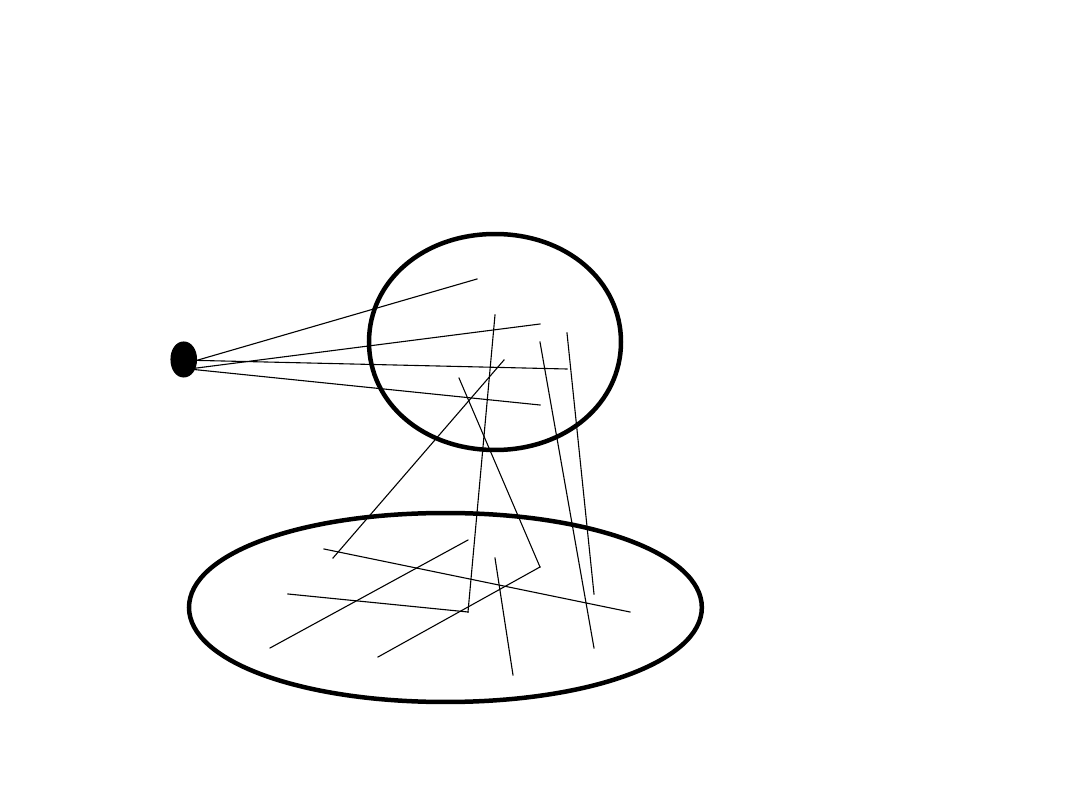
Ilustracja dowodu Tw.

Mantla

v

N(v)

n-Δ-1

Δ

V-{v}-N(v)

Wniosek z dowodu Tw.

Mantla

• Jeśli n jest parzyste, G ma n^2/4 krawędzi

i nie zawiera K_3, to G=K(n/2,n/2).

• Jeśli n jest nieparzyste, G ma (n^2-1)/4

krawędzi i nie zawiera K_3, to G=K((n-
1)/2,(n+1)/2).

• Dowód dla n parzystego

: w dowodzie Tw.

Mantla równość e(G)=n^2/4 zachodzi
tylko, gdy Δ=n/2 i nie ma krawędzi o obu
końcach w V-N(v).

Uogólnienie problemu

• Dane: graf H i liczba naturalna n;
• Graf G nie zawierający H, o n

wierzchołkach i

największej

możliwej

liczbie krawędzi nazywamy

ekstremalnym

dla H i n, a jego liczbę krawędzi oznaczamy
przez

ex(n,H).

• Na przykład, dla n parzystego i H=K_3,

K(n/2,n/2)

jest ekstremalny, a

ex(n,K_3)=n^2/4.

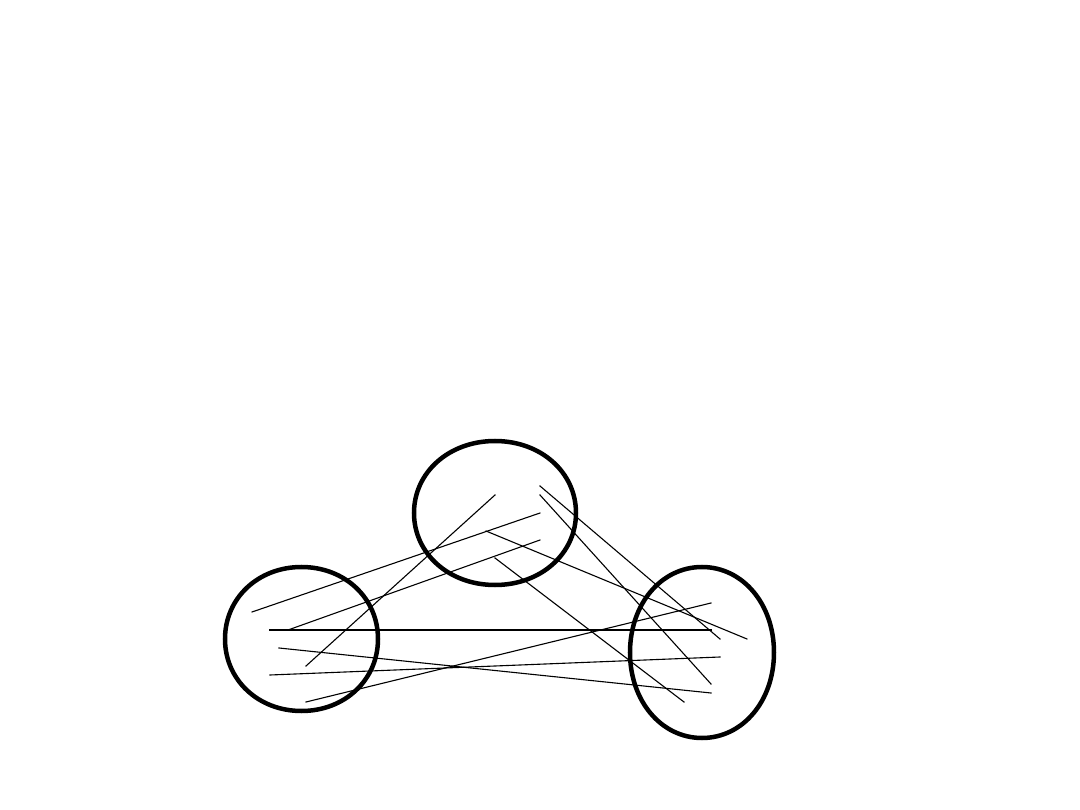
Tw. Turána -- intuicja

Żeby upchnąć jak najwięcej krawędzi

unikając K_{k+1}, trzeba budować

k-dzielny graf pełny.

n/k

n/k

n/k

Tw. Turána

Graf Turána

T_k(n)

to k-dzielny graf pełny, którego podział

wierzchołków składa się z k-r zbiorów mocy q i r zbiorów

mocy q+1. Dla n=1,...,k-1 przyjmujemy

T_k(n)

= K_n.

Oznaczmy

t_k(n)

=e(T_k(n)). Jasne, że

k

r

r,

qk

n, n

k











0

Tw.Turána 1941

Jedynym grafem

ekstremalnym dla K_{k+1} i n jest graf
Turána T_k(n). W szczególności

t_k(n)

})

ex(n,K_{k



1

t_k(n)

})

ex(n,K_{k



1

Dowód Tw. Turána

• Indukcja względem n: prawda dla

n=1,...,k.

• Załóżmy, że n>k a G jest grafem

ekstremalnym dla n i K_{k+1}.

• G musi zawierać klikę K={x_1,...,x_k}

mocy k.

• Z zał.ind. e(G-K) nie przekracza t_k(n-k).

• Każdy wierzchołek grafu G-K ma w K co

najwyżej k-1 sąsiadów.

 

 

n

t

k

k

k

n

k

n

t

G

e

k

k



























2

)

1

)(

(

)

(

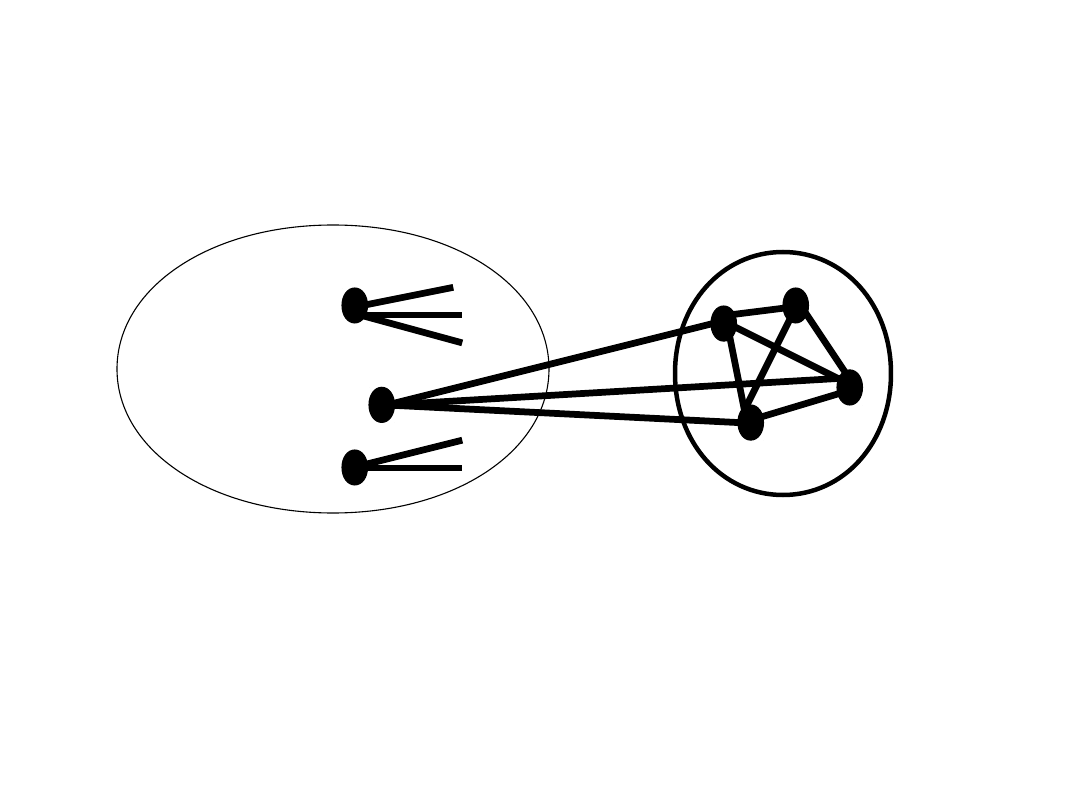
Ilustracja: k=4

K

G-K

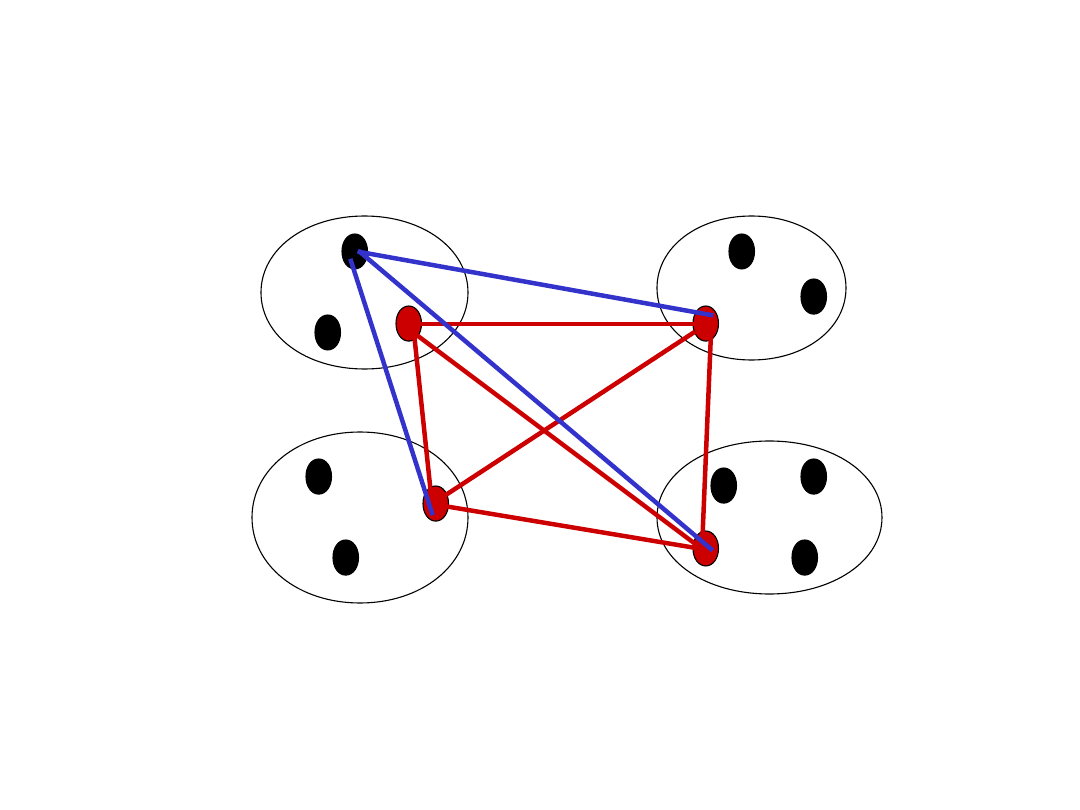
Ilustracja: grafy Turána

n=13, k=4, t_k(13)-t_k(9)=

6

+

9•3

Dowód Tw. Turána – c.d.

• G jest ekstremalny, więc e(G)=t_k(n).

• Zatem każdy wierzchołek w G-K ma

dokładnie

k-1 sąsiadów w K.

• Niech V_i={v: vx_i nie jest

krawędzią}.

• Zbiory V_i są niezależne i pokrywają V,

więc G jest k-dzielny.

• Ale jedynym ekstremalnym grafem k-

dzielnym jest graf Turána T_k(n). 

Oszacowania liczb Turána

• Łatwo pokazać, że (

ćwiczenia

)

 

2

2

1

n

k

k

n

t

k





 

k

k

n

n

t

k

n

1

2

lim

1























Ile krawędzi gwarantuje

α>2 ?

nie gwarantuje, bo

2K_{n/2}

(tutaj n

parzyste)

czyli dopełnienie grafu Turána.
Ale mniej już tak – na podstawie Tw. Turána.















2

2

/

2

n

Oszacowanie α z dołu

• Tw. Caro’79 i Wei’81

 









V

v

v

d

G

1

1



Dowód

: Dla każdej permutacji

wierzchołków π, niech l(π) będzie
liczbą wierzchołków mających
wszystkich sąsiadów „na prawo”.
Tworzą one zbiór niezależny, więc

   





l

G 

Dowód – c.d.

• Niech ł(v) będzie liczbą permutacji, w

których v ma wszystkich sąsiadów na prawo.
Wtedy

 

 







v

v

ł

l





• oraz

 

1

!

)!

1

(

!

1

























v

v

v

v

d

n

d

n

d

d

n

v

ł

• Zatem istnieje π takie, że

 









V

v

v

d

l

1

1



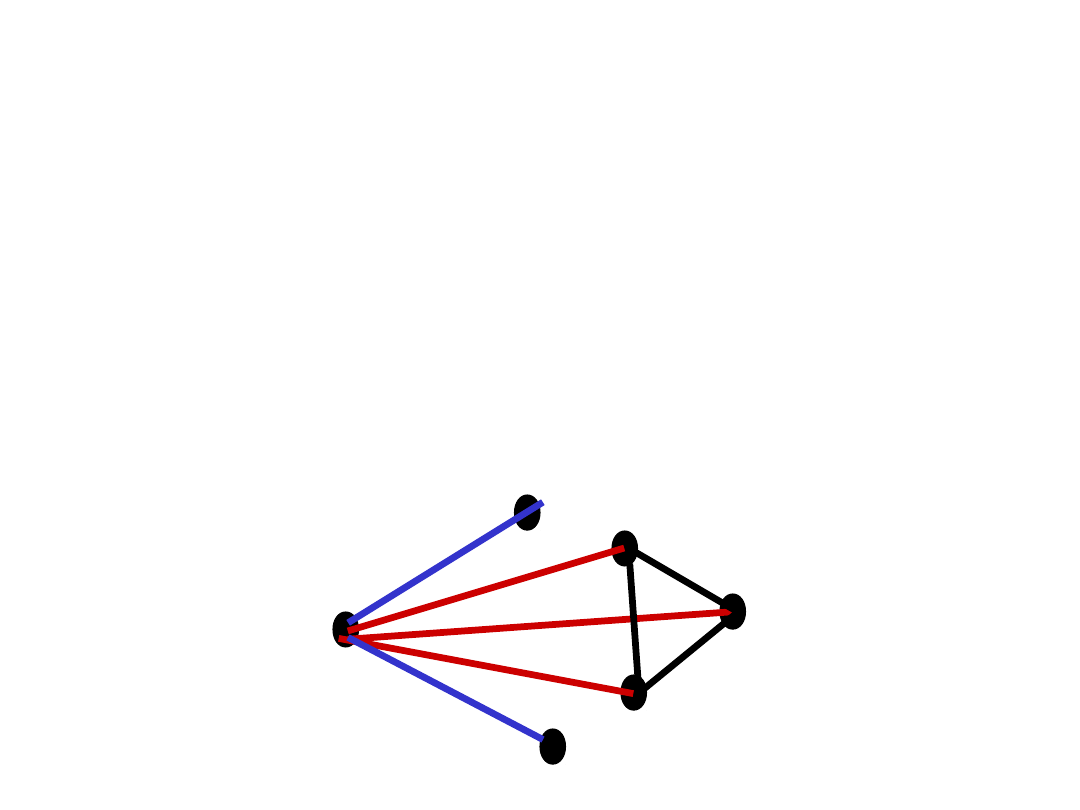
Ilustracja

v

N(v)

Przyjęcie na 6 osób

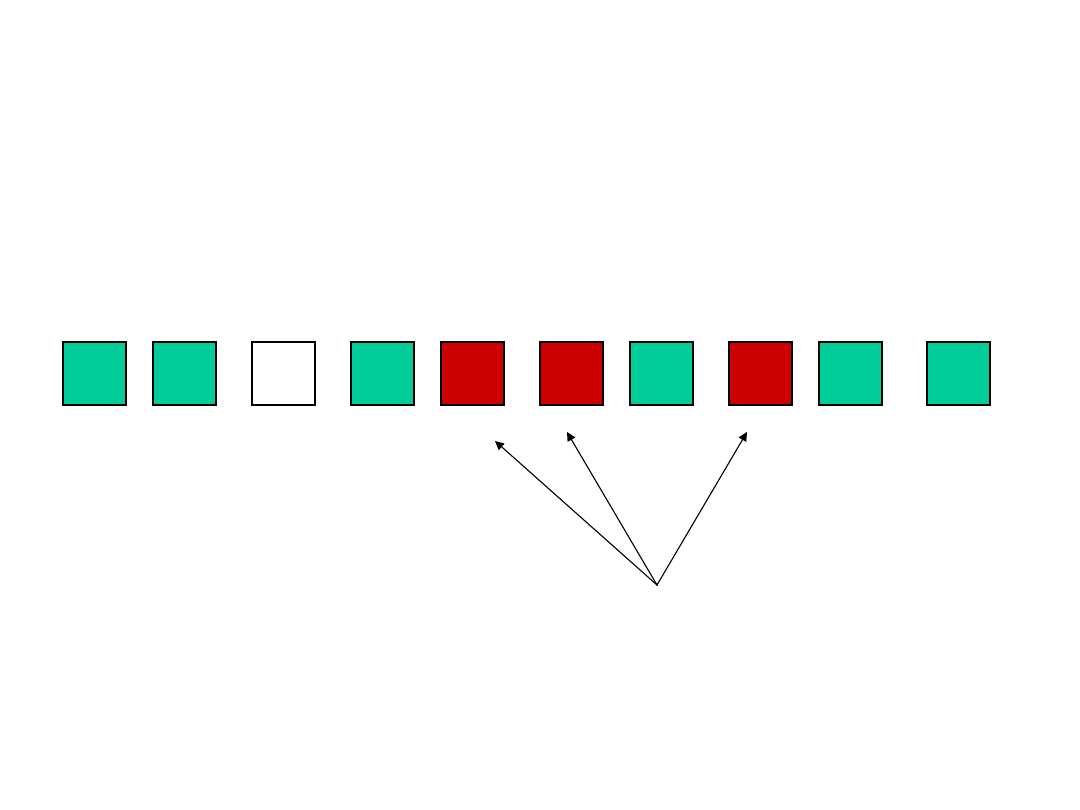
• Wśród dowolnych trzech osób

zawsze

są co najmniej dwie tej samej płci.

• Wśród dowolnych sześciu osób

zawsze

są co najmniej trzy, które się

znają

LUB

co najmniej trzy, które się

nie znają.

A

B

C

D

E

F

Liczba K_3 łącznie w

grafie i jego dopełnieniu

Goodman 1959

Łącznie trójkątów w grafie

na n wierzchołkach i jego dopełnieniu
jest co najmniej n(n-1)(n-5)/24.

Dowód

: Niech t_i będzie liczbą

indukowanych podgrafów grafu G o 3
wierzchołkach i i krawędziach, i=0,1,2,3.









2

1

2

1

t

t

d

n

d

v

V

v

v













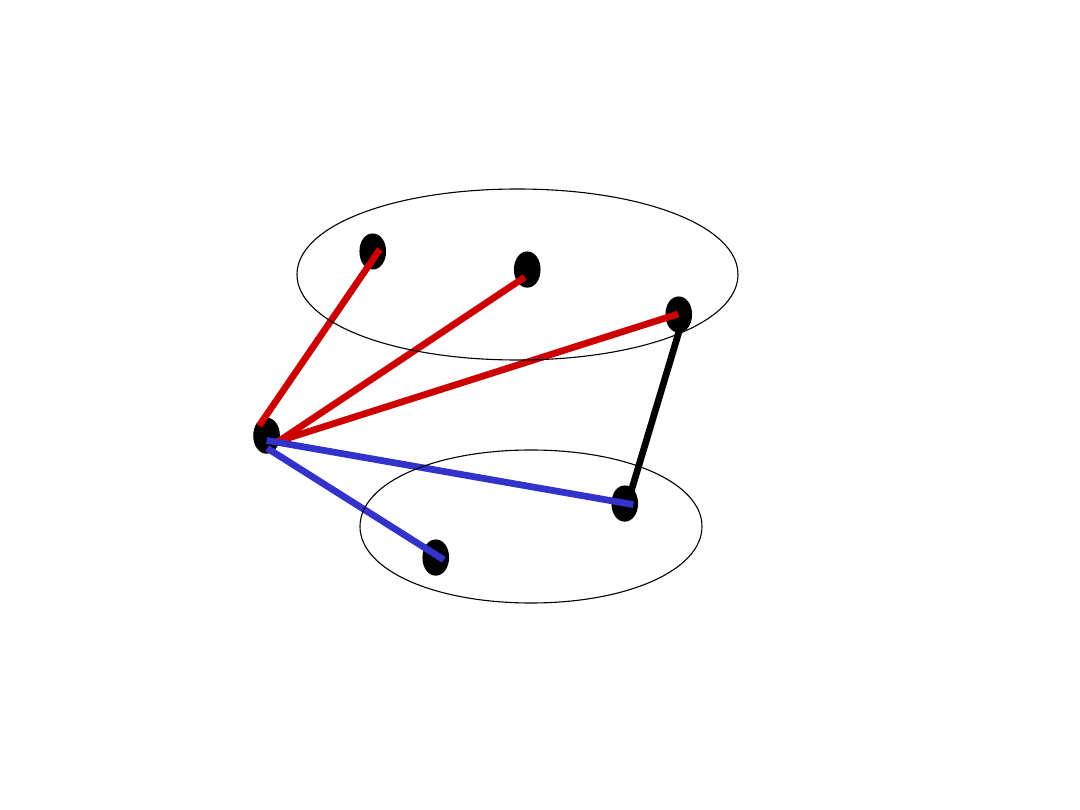
Ilustracja

v

d_v

n-1- d_v

Dowód tw. Goodmana --

dokończenie

2

2

1

3

0

2

1

2

3

)

(

3











 





































n

n

n

t

t

n

t

t

Tw. Ramseya

Notacja „strzałkowa” Erdősa-Rado

:

Piszemy n



(k,l), gdy każdy graf na n

wierzchołkach zawiera klikę mocy k

LUB

zbiór niezależny mocy l (równoważnie,
jego dopełnienie zawiera klikę mocy l).

Przykład: 6



(3,3)

Tw. (Ramsey 1930)

Dla wszystkich

naturalnych k i l, istnieje n takie, że
n



(k,l).

Dowód tw. Ramseya

• Indukcja względem k+l

• Jeśli k=2 to l



(k,l).

• Zawsze: n



(k,l) wgdy n



(l,k)

• Weźmy k>2 i l>2; niech n_1



(k-1,l),

n_2



(k,l-1) (

tutaj stosujemy zał.

ind

.)

• Pokażemy, że n_1+n_2



(k,l).

• W dowolnym grafie G na n_1+n_2

wierzchołkach, każdy wierzchołek v

ma albo co najmniej n_1 sąsiadów

albo co najmniej n_2 nie-sąsiadów.

Dowód tw. Ramseya – c.d.

• Bez straty ogólności (symetria!) przyjmijmy

przypadek pierwszy i do podgrafu
indukowanego G[N(v)], gdzie |N(v)|=n_1,
zastosujmy własność n_1



(k-1,l).

• Jeśli G[N(v)] zawiera zbiór niezależny mocy

l, to koniec dowodu.

• Jeśli G[N(v)] zawiera klikę mocy k-1, to ta

klika wraz z wierzchołkiem v tworzy klikę
mocy k. 

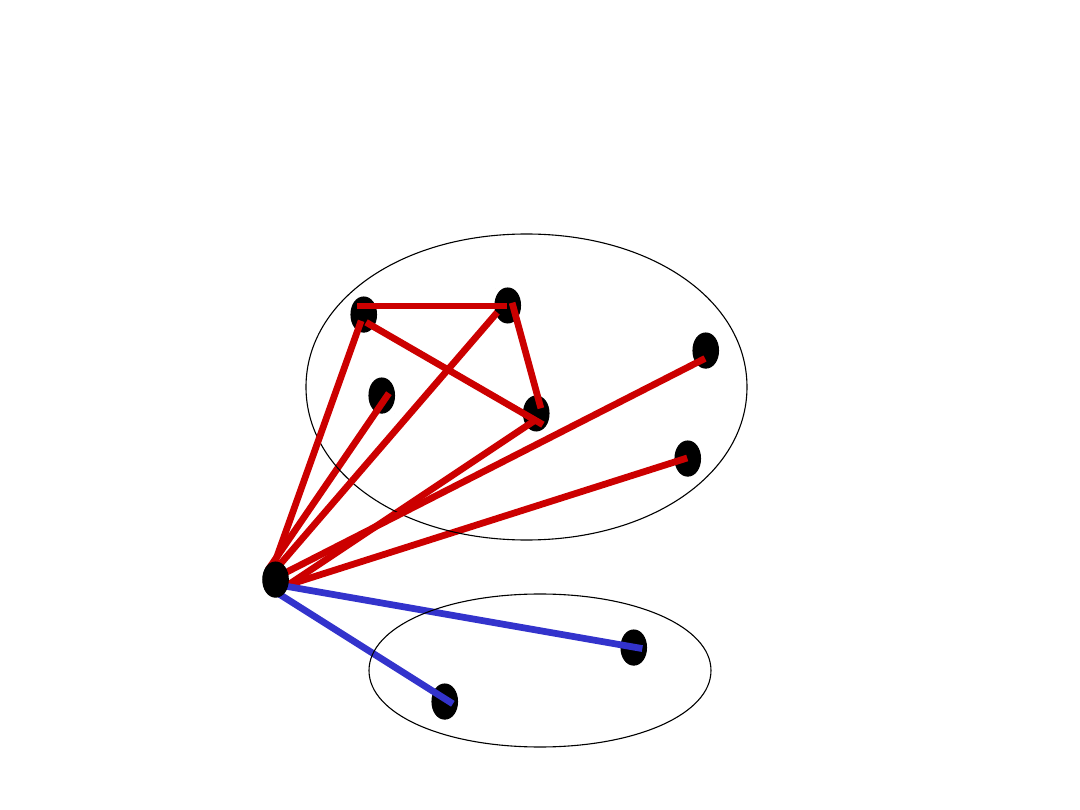
Ilustracja

v

n_1=R(k-1,l)

n_2=R(k,l-1)

Liczby Ramseya

• R(k,l) to najmniejsza liczba n taka, że n



(k,l).

• R(3,3)=6 bo 6



(3,3) oraz istnieje graf na 5

wierzchołkach (

jaki?

) taki, że ω=α=2.

• Z dowodu Tw. Ramseya wynika rekurencja

)

1

,

(

)

,

1

(

)

,

(









l

k

R

l

k

R

l

k

R

10

4

6

)

2

,

4

(

)

3

,

3

(

)

3

,

4

(











R

R

R

9

3

4



)

,

R(

18

)

4

,

3

(

2

)

4

,

4

(



 R

R

9

)

4

,

3

(



R

18

)

4

,

4

(



R

?

)

5

,

5

(



R

Oszacowania liczb

Ramseya

k

c

k

k

k

k

R

k

4

1

2

2

)

,

(





















2

/

2

)

,

(

k

k

k

R



(1)

(2)

Gra ramseyowska -- online

Opis gry

: Zaczynając od pustego grafu, w

każdej rundzie

Konstruktor

rysuje krawędź

a

Malarz

maluje ją jednym z dwóch kolorów.

Malarz

przegrywa, gdy pojawi się

monochromatyczny trójkąt.

Ile rund może przetrwać

Malarz

, zakładając,

że obaj gracze grają bezbłędnie?

Na pewno nie więcej niż 15 (

dlaczego

?), ale

czy

Konstruktor

może osiągnąć wygraną

wcześniej?

Przykład gry