Grafy inaczej, czyli

inne modele grafów

• Multigrafy
• Grafy z wagami
• Grafy skierowane
• Hipergrafy

• Grafy losowe (MPK 410, STL 510)

Multigrafy

• Multigrafy to grafy z wagami na krawędziach;

wagi to lczby naturalne – krotności krawędzi.

• Problem Chińskiego listonosza: znaleźć

rozpięty nadgraf eulerowski o najmniejszej

wadze.

• Inny problem: znaleźć rozpięty nadgraf o

najmniejszej maksymalnej wadze krawędzi, w

którym wszystkie stopnie są różne.

• Wariant: jak wyżej, ale chcemy tylko, by pary

sąsiednich

wierzchołków miały różne stopnie

(stopnie w roli kolorów wierzchołków).

• Dla K_n odpowiedź wynosi 3

(ćw.)

Grafy z wagami

• G=(V,E,w), w:E



R

• Wagę podgrafu określamy jako sumę wag

jego krawędzi.

Klasyczne problemy optymalizacji

:

• MST

– znaleźć rozpięte drzewo o minimalnej

wadze.

• Optimal Assignment Problem

– znaleźć

skojarzenie doskonałe w grafie dwudzielnym

K_{n,n} o minimalnej (maksymalnej) wadze.

• TSP

– znaleźć cykl Hamiltona o minimalnej

wadze (problem w klasie

NP– zupełnej

).

Parametry ułamkowe

• Skojarzenie ułamkowe

to funkcja

w:E



[0,1] taka, że dla każdego v







e

v

e

w

1

)

(

• α’*(G)

to największa waga

skojarzenia ułamkowego w grafie
G, czyli rozwiązanie problemu PL

1

)

(

:

gdy

,

)

(

MAX













e

v

E

e

e

w

v

e

w

Parametry dualne

• Wierzchołkowe pokrycie ułamkowe

to funkcja w:V



[0,1] taka, że dla

każdej krawędzi e=uv

1

)

(

)

(



 v

w

u

w

• β*(G)

to najmniejsza waga

wierzchołkowego pokrycia
ułamkowego w grafie G, czyli
rozwiązanie problemu PL

1

)

(

)

(

:

gdy

,

)

(

MIN













v

w

u

w

G

uv

v

w

V

v

Twierdzenie o dualności

PL

• Tw. o dualności

:

β*(G)=

α’*(G)

–

tzn.

ułamkowe tw. Königa

zachodzi

dla wszystkich grafów.

• Dla grafów dwudzielnych zachodzi

tw.

Königa:

β(G)=

α’(G)

.

• Zatem, dla grafów dwudzielnych

α’(G) ≤ α’*(G)

=

β*(G)

≤ β(G)=

α’(G)

,

a więc

α’(G) = α’*(G)

.

Grafy skierowane

Graf skierowany (digraf)

to para (V,A),

gdzie A jest zbiorem uporządkowanych
par różnych wierzchołków z V.

Elementy zbioru A nazywamy

łukami

, a na

rysunkach parę (u,v) przedstawiamy w
postaci

strzałki

z u do v.

u

v

Orientacje, turnieje i grafy

podskórne

• Z (nieskierowanego) grafu G można

utworzyć graf skierowny nadając

kierunek każdej krawędzi –

orientacja

grafu G.

• Turniej

to orientacja grafu pełnego K_n

• Odwrotnie, z digrafu D można utworzyć

zwykły (multi)graf G(D) ,,wymazując”

wszystkie strzałki – tzw.

podskórny graf

nieskierowany

digrafu D.

Odpowiednik Tw. Diraca

• Półstopnie wejścia i wyjścia

, d^-(v), d^+(v)

Twierdzenie Diraca dla digrafów

. Jeśli

wszystkie półstopnie wejścia i
wyjścia są większe bądź równe n/2,
to D zawiera skierowany cykl
Hamiltona. 

Spójność i odpowiednik

Tw. Eulera

• Digraf D jest

spójny

, gdy jego graf

podskórny G(D) jest spójny.

• Digraf D jest

silnie spójny

, gdy dla

każdej pary wierzchołków (u,v)

istnieje w D skierowana ścieżka z u

do v.

Tw. Eulera dla digrafow.

Spójny digraf

D ma skierowany obchód Eulera

wgdy dla każdego v: d^-(v)=d^+(v).

Silna spójność orientacji

• Czy dany, spójny system dróg G można

zmienić na

jednokierunkowy

, tak, by

każdy wszędzie mógł (legalnie) dojechać?

• Chodzi tu o silnie spójną orientację grafu

G.

• Jeśli G ma most, to nie.

Tw. o silnie spójnej orientacji (Robbins

1939).

Jeśli G jest 2-krawędziowo-spójny,

to posiada silnie spójną orientację.

Silna spójność turnieju

Tw. (Moon 1966)

Jeśli D jest silnie spójnym

turniejem, to dla każdego k=3,…,n każdy

wierzchołek leży na skierowanym cyklu

długości k.

Szkic dowodu (ind. wzgl. k):

• Ustal wierzchołek u i pokaż, że u leży na

skierowanym trójkącie.

• Pokaż, ze skoro u leży na cyklu C_k, to leży też

na cyklu C_{k+1}. 

Wniosek.

Turniej ma skierowny cykl Hamiltona

wgdy jest silnie spójny.

Liczba chromatyczna a

najdłuższa ścieżka

skierowana

• Niech l(D) będzie długością najdłuższej

ścieżki skierowanej w D.

Tw. (Roy 67, Gallai 68)

χ(G(D))

≤

l(D) +1.

Wniosek.

χ(G)=min {l(D)+1}, gdzie

minimum jest wzięte po wszystkich
orientacjach G.

Dowód wniosku

Dowod Wniosku:

Pokolorujmy G

optymalnie kolorami 1,2,…, χ i
skierujmy krawędzie od koloru
mniejszego do większego. Wtedy
najdłuższa skierowana ścieżka nie
będzie dłuższa niż χ-1. Nierówność
w drugą stronę wynika z

Tw. (Roy

67, Gallai 68).



Ilustracja

1

2

χ

Skierowane ścieżki

Hamiltona w turnieju

Wniosek (Redei, 1934)

Każdy turniej

ma ścieżkę Hamiltona.

Dowod:

Jeśli D jest turniejem, to

χ(G(D))=n

i na podstawie

Tw.

(Roy 67, Gallai 68)

ma ścieżkę skierowaną długości n-1.

Dowód indukcyjny (

ćw.

)

Królewskie zbiory

niezależne

Tw. (Chvatal i Lovasz, 1974)

Każdy digraf posiada

zbiór niezależny, z którego każdy inny wierzchołek

jest osiągalny ścieżką skierowaną długości 1 lub 2.

Szkic dowodu:

indukcja względem n; w kroku

indukcyjnym usunąć wierzchołek v wraz ze

zbiorem sąsiadów N^+(v) (strzałki wychodzące). 

Wniosek.

Każdy turniej ma króla, tzn. wierzchołek, z

którego każdy inny wierzchołek jest osiągalny

ścieżką skierowaną długości 1 lub 2.

Dowod:

α(G(D))= α(K_n)=1. 

Dowód indukcyjny (

ćw.

)

Hipergrafy

• Hipergraf

to para H=(V,E), gdzie E to

rodzina niepustych pozdbiorów zbioru V.

• V – zbiór wierzchołków, E – zbiór krawędzi
• Hipergraf jest

k-jednostajny

, gdy wszystkie

krawędzie mają tę samą moc k.

• Hipergraf 2-jednostajny to po prostu

graf

.

Skojarzenia i pokrycia

hipergrafów

• Skojarzenie

to zbiór rozłącznych krawędzi.

• α’(H)

– moc największego skojarzenia w H.

• Pokrycie

to zbiór wierzchołków, który

przecina każdą krawędź.

• β(H)

– moc najmniejszego pokrycia w H.

• Jasne: α’(H)

≤

β(H)

• Problem

: Kiedy α’(H) = β(H) ???

Problemy NP-zupełne

• W przeciwieństwie do grafów, wyznaczenie α’

(H) jest problemem z klasy

NP-zupełnej.

• Nawet, jeśli ograniczyć sie do hipergrafów 3-

jednostajnych.

• Pokażmy równoważność

(redukcję

wielomianową)

tego problemu z obliczaniem

α(G):





α’(H)= α(L(H)), gdzie L(H) –

graf

krawędziowy (albo: przecięć)

hipergrafu H.





α(G)= α’(St(G)), gdzie St(G) jest

hipergrafem gwiazd

, tzn. wierzchołkami są

krawędzie G, a krawędziami są maksymalne

gwiazdy w G. (

ćw

)

Hipergrafy 2-kolorowalne

•

H nazywamy

2-kolorowalnym

, gdy jego

wierzchołki można pomalować 2 kolorami tak,

by każda krawędź mocy co najmniej 2 zawierała

wierzchołki obu kolorów.

•

Podhipergraf indukowany przez U

to

H[U]=(U,E’), gdzie E’sklada sie ze wszystkich

niepustych części wspólnych zbioru U z

krawędziami H.

•

H jest

zrównoważony

, gdy każdy podhipergraf

indukowany jest 2-kolorowalny.

Tw. (Berge i Las Vergnas, 1970)

Każdy

zrównoważony hipergraf spełnia własność

Königa: α’(H) = β(H).

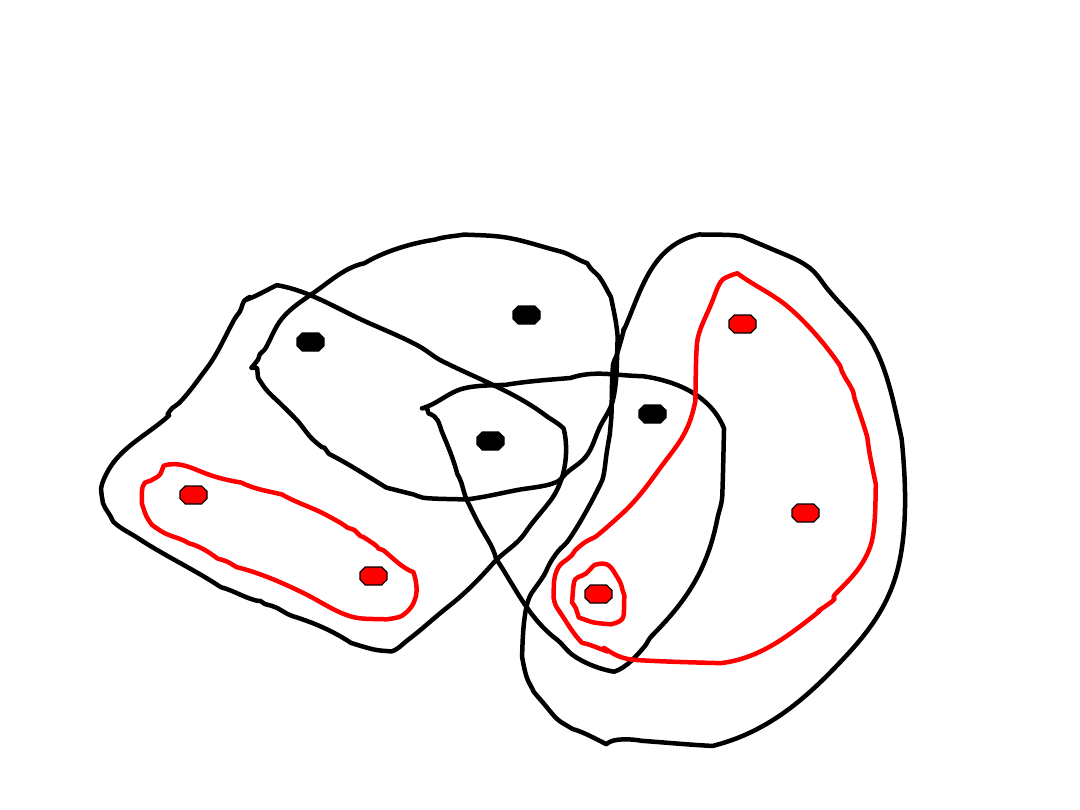
Podhipergraf indukowany