GRAFY PLANARNE

• To grafy, które

można

narysować

na płaszczyźnie tak, by krawędzie
nie przecinały się

(

poza swoimi

końcami

).

• Na przykład K_4, ale nie K_5.

• Formalna definicja prowadzi przez

grafy płaskie.

Grafy płaskie

• G=(V,J)

nazywamy

grafem płaskim

, gdy

V

jest

skończonym podzbiorem punktów płaszczyzny
euklidesowej, a

J

zbiorem (otwartych)

krzywych Jordana o końcach w

V

i takich, że:

1) różne krzywe mają różne pary końców

,

2) „wnętrza” krzywych nie zawierają punktów

innych krzywych zbioru J ani żadnych
punktów zbioru V.

Trzy interpretacje grafu

płaskiego

• Graf płaski

G=(V,J)

często utożsamiamy z

grafem abstrakcyjnym

G=(V,E),

gdzie

E={uv: u i v są końcami pewnej krzywej e z

J}

,

• ale też ze zbiorem punktów na płaszczyźnie

}

:

{

J

e

e

V

G









Ilustracja

Ściany

• jest

otwartym

podzbiorem płaszczyzny,

• jego obszary spójne nazywamy

ścianami

grafu G,

• dokładnie jedna ściana jest

nieograniczona – nazywamy ją

zewnętrzną,

• brzeg ściany

albo

daną krawędź zawiera

albo

jest rozłączny z jej wnętrzem.

G





2

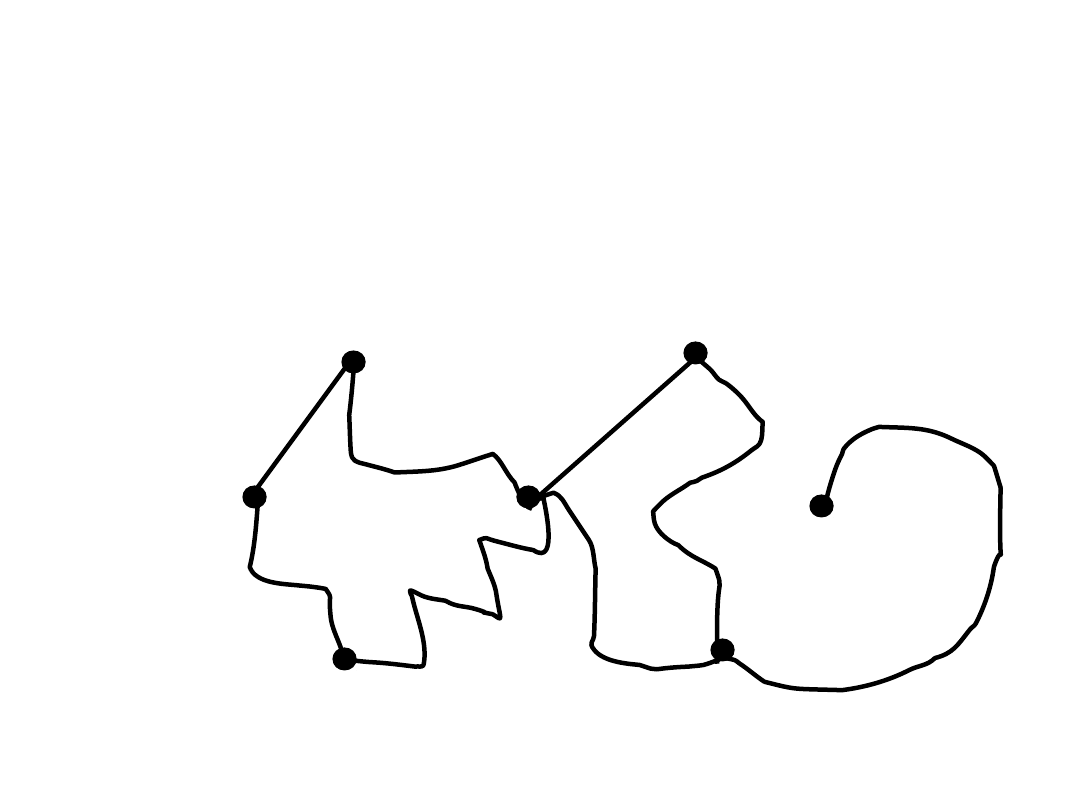
Ilustracja

S1

S2

S3 – ściana zewnętrzna

S3

S3

Mosty i nie-mosty

Niech C będzie cyklem w grafie płaskim G

.

• Jeśli e należy do C, to e leży na brzegu

dokładnie dwóch ścian i te ściany
zawarte są w dwóch różnych ścianach
grafu C.

• Jeśli e jest mostem, to e leży na brzegu

dokładnie jednej ściany

.

• Wniosek

: płaski las ma tylko jedną

ścianę.

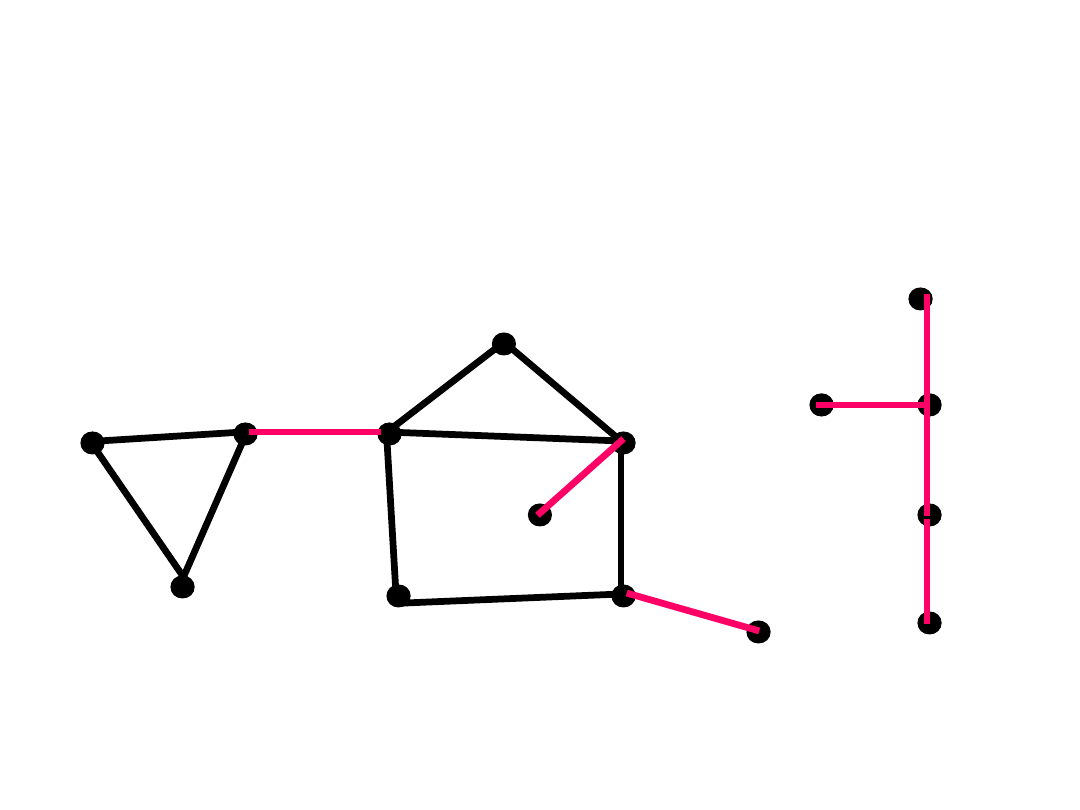
Ilustracja:

mosty,

cykle

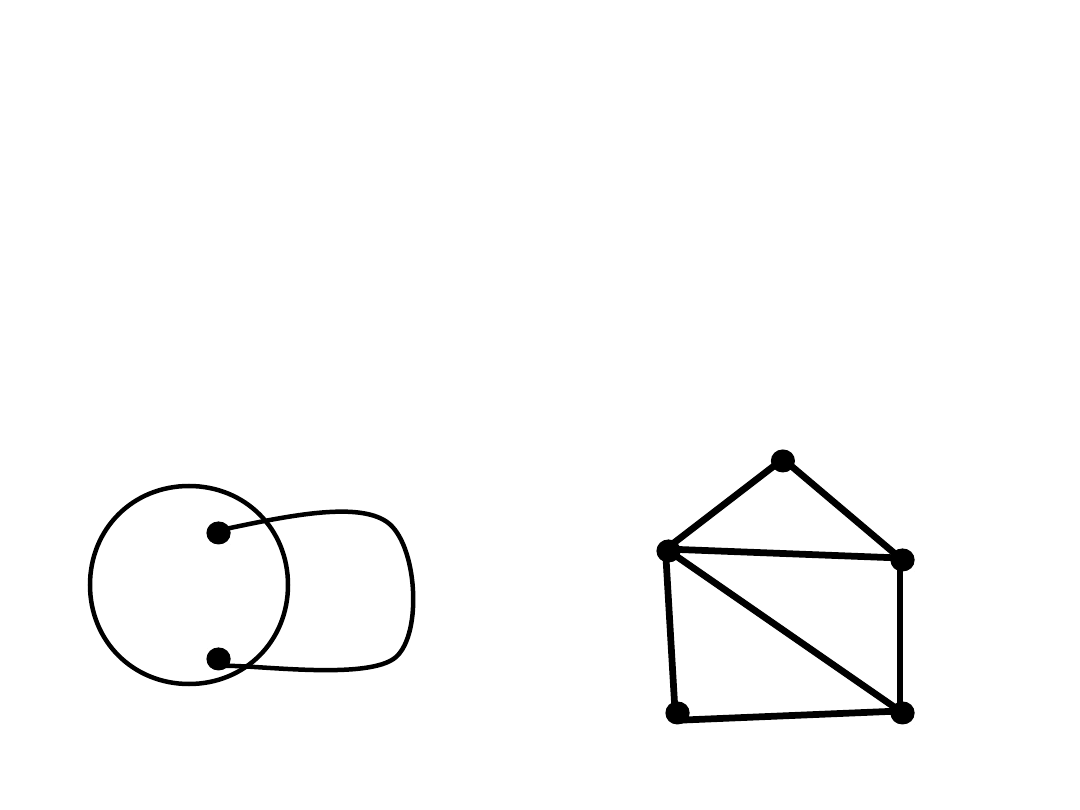
2-spójne grafy płaskie

Fakt

: W

2-spójnym

grafie płaskim brzeg każdej

ściany jest cyklem.

Dowód:

Indukcja z wykorzystaniem konstrukcyjnej

charakterystyki grafów 2-spójnych

(ćw).



H

P

Triangulacje

• Graf płaski nazywamy

maksymalnym

,

gdy żaden jego nadgraf właściwy o tym

samym zbiorze wierzchołków nie jest

płaski.

• Graf płaski nazywamy

triangulacją

, gdy

brzeg każdej ściany jest trójkątem.

Fakt

. Graf płaski o co najmniej 3

wierzchołkach jest maksymalny wgdy

jest triangulacją.

Dowód

 Jeśli każda ściana jest trójkątem, to nie

można dodać krawędzi, która nie naruszałaby

warunków 1) i 2) z def. płaskości.

 G musi być 2-spójny, więc brzeg każdej ściany

jest cyklem. Niech C będzie jednym z nich.

 Skoro G jest maksymalny, to V(C) jest kliką

w G, której wszystkie krawędzie leżą na

zewnątrz ściany C.

 Jest to jednak możliwe tylko, gdy |V(C)|<4
(patrz: rysunek).



Ilustracja dowodu

C

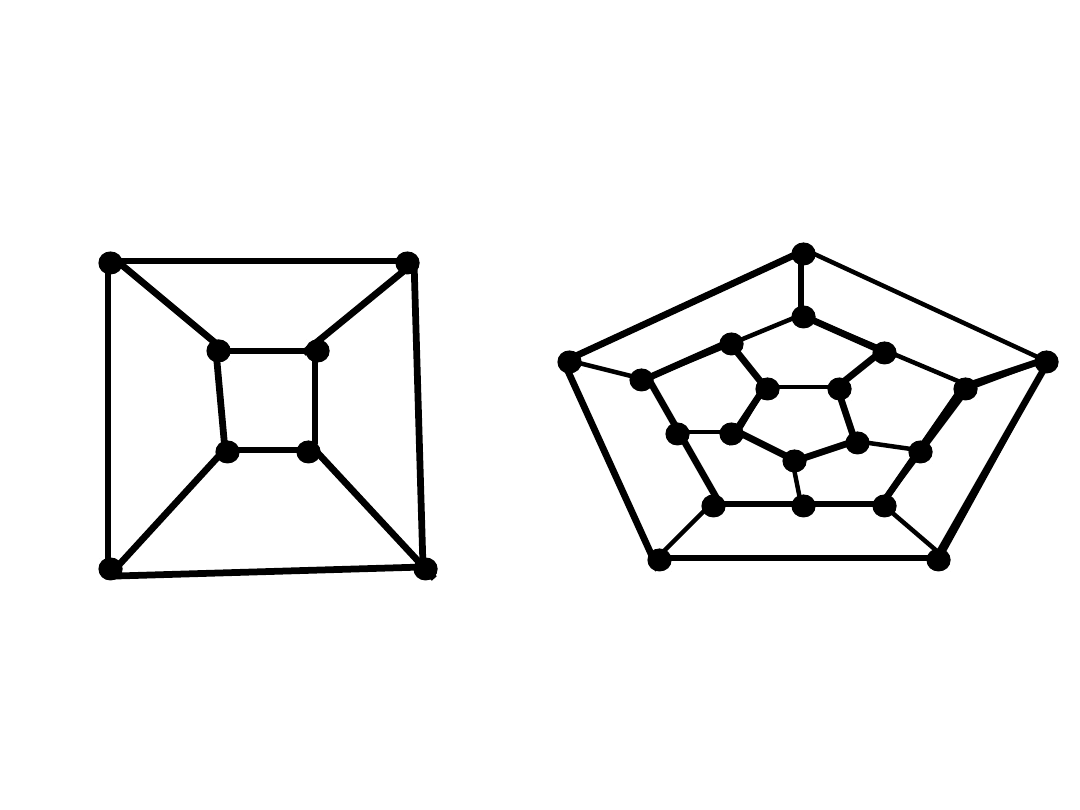
Zajrzyjmy do pudełek

n=8, m=12, l=6

n=20, m=30, l=12

n-m+l=2

Wzór Eulera

Tw. (Euler, 1752)

W każdym

spójnym

grafie

płaskim liczba wierzchołków

n

, liczba

krawędzi

m

i liczba ścian

l

spełniają równość:

n-m+l=2

Dowód:

Indukcja względem m przy ustalonym n.

Jeśli m=n-1, to G jest drzewem i l=1.

Jeśli m>n-1, to G zawiera cykl

.

Usuńmy krawędź e z tego cyklu. Graf G-e ma 1

krawędź mniej i 1 ścianę mniej niż G

.

Stosujemy zał. ind. do G-e

. 

Liczba krawędzi grafu

płaskiego

Wniosek:

Graf płaski o n wierzchołkach

ma nie więcej niż

3n-6

krawędzi,

triangulacja ma ich dokładnie tyle.

Dowód:

Licząc krawędzie wokół każdej

ściany triangulacji i sumując je,
otrzymamy 2m, ale jednocześnie 3l.

Stąd i ze wzoru Eulera pomnożonego

przez 3, 3n-3m+2m=6

.

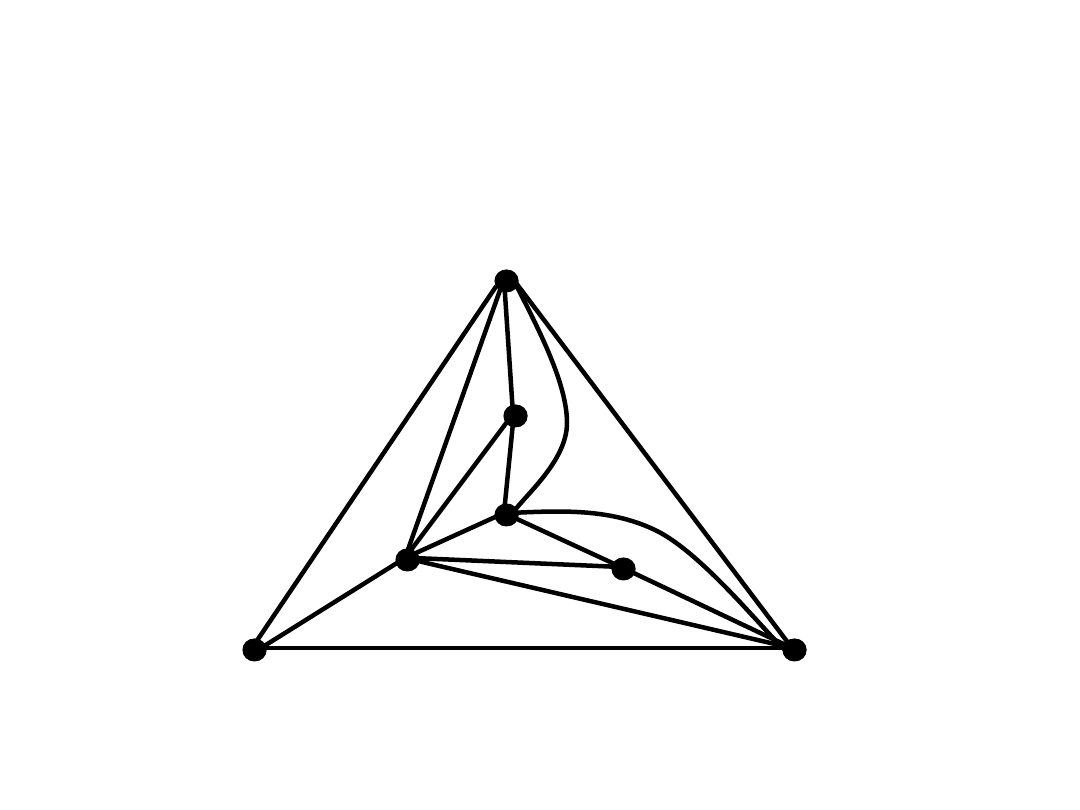
Przykład triangulacji

n=7, m=3n-6=15, l=10

Grafy planarne

• Graf G jest

planarny

, gdy jest izomorficzny z

(abstrakcyjnym) grafem płaskim. Mówimy

wtedy, że można go

zanurzyć w (narysować na)

płaszczyźnie.

• Graf płaski, izomorficzny z G nazywamy

płaskim

rysunkiem G

.

Fakt:

Każdy graf planarny posiada płaski rysunek,

którego krawędzie są odcinkami prostych.

(ćw)

K_4

Równoważność

topologiczna

• Dwa płaskie rysunki tego samego grafu są

topologicznie równoważne

, gdy

(multi)zbiory podgrafów będących brzegami

ścian pokrywają się.

• Przykład:

Dwa top. równoważne rysunki

K_4

Poniższe pary

nie

są

równoważne

6

7

5

4

6

5

5

6

3-spójne grafy planarne

Tw. (Whitney, 1932)

Każde dwa płaskie rysunki

3-

spójnego

grafu planarnego są topologicznie

równoważne.

Lemat:

Cykl C 3-spójnego grafu płaskiego jest

brzegiem ściany wgdy C jest

cyklem

indukowanym

a V(C)

nie

rozspójnia

G.

Dowód Tw.:

Z Lematu, każdy płaski rysunek

3-

spójnego grafu planarnego ma te same cykle na

brzegach ścian. 

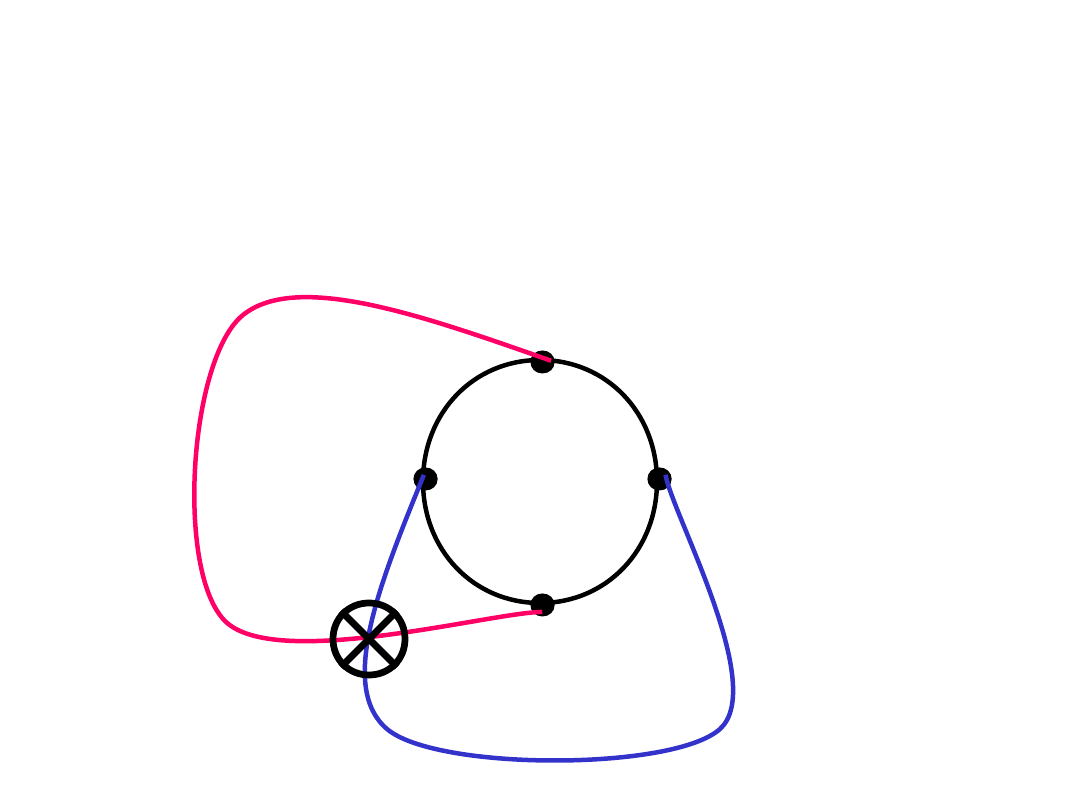
Dowód Lematu:



Skoro V(C) nie rozspójnia G, to

przynajmniej 1 ze ścian C nie zawiera punktów G-

C. Zatem C jest brzegiem ściany.

Dowód Lematu 

• Niech C będzie brzegiem ściany, a x,y

dwoma (niesąsiednimi na C)

wierzchołkami C.

• Z 3-spójności G, w G-{x,y} istnieje ścieżka

P łącząca dwa ścieżki grafu C-{x,y}.

• Gdyby istniała krawędź xy, to przecinałaby

P (bo obie muszą biec przez zewnętrzną

ścianę C) –

sprzeczność!

(bo G jest płaski).

• Zatem C jest cyklem indukowanym

.

Ilustracja

C

x

y

P

Dowód Lematu  c.d.

• Niech x,y należą do V(G)-V(C)

• Z 3-spójności G są między nimi co

najmniej 3 niezależne ścieżki, które
dzielą płaszczyznę na 3 rozłączne
obszary.

• C musi się zawierać w jednym z nich,

a więc jedna ze ścieżek omija C.

• Zatem zbiór V(C) nie rozspójnia x,y.



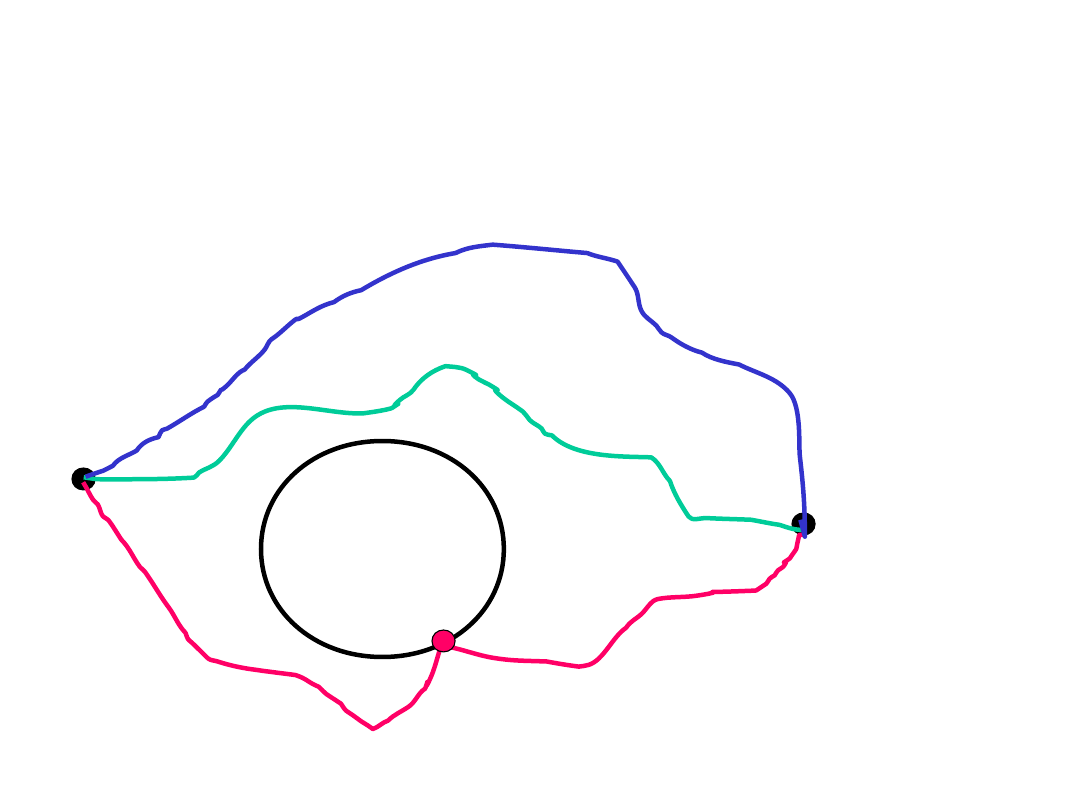
Ilustracja

C

x

y

Maksymalne grafy

planarne

• Graf planarny jest

maksymalny

, gdy żaden

jego nadgraf właściwy o tym samym zbiorze

wierzchołków nie jest planarny.

• Płaski rysunek maksymalnego grafu

planarnego jest triangulacją, i odwrotnie,

każda triangulacja jest maksymalnym grafem

planarnym.

• Zatem, graf planarny o n>2 wierzchołkach

jest maksymalny wgdy ma 3n-6 krawędzi

.

• Dla n>3, triangulacje są 3-spójne

(

dowód na

ćw.

)

Ani, ani

• Wszystkie grafy na 4 wierzchołkach są

planarne (bo K_4 jest planarny)

• Wszystkie grafy na 5 wierzchołkach są

planarne, oprócz K_5

(ćw.)

• Wszystkie grafy dwudzielne na 6

wierzchołkach są planarne, oprócz
K_{3,3}

(ćw.)

•

Ani

K_5,

ani

K_{3,3} nie jest planarny

Dowód dla K_5

: m=10>9=3n-6

Dowód dla K_{3,3}:

na ćwiczeniach!

D1

D2

D3

S1

S2

S3

?

?

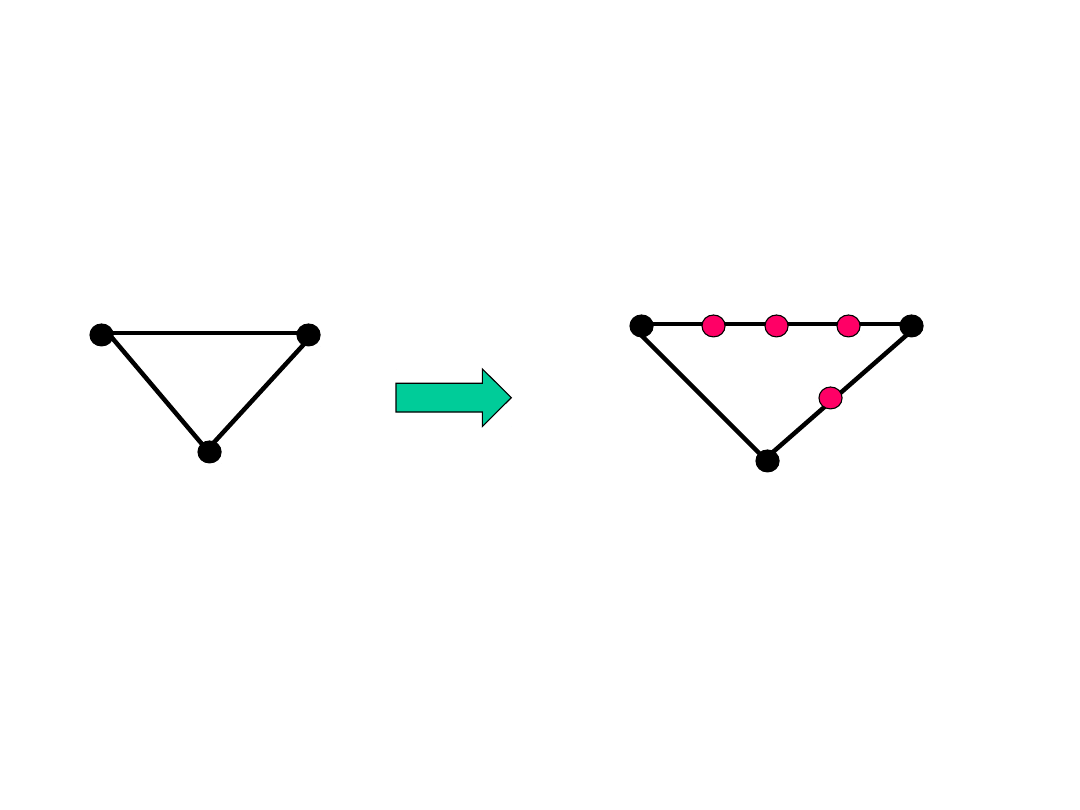
Podziały topologiczne

krawędzi

• Nieformalny zapis

G=TH

oznacza, ze G jest

jednym z grafów, które można otrzymać z grafu

H przez topologiczne podziały krawędzi.

(TH jest więc nieskończoną rodziną grafów)

K_3

G=TK_3

Tw. Kuratowskiego

• Ani TK_5, ani TK_{3,3} nie jest

planarny.

• Żaden graf planarny nie zawiera ich.

Tw. (Kuratowski 1930)

Graf G jest planarny wgdy nie zawiera

ani TK_5 ani TK_{3,3}.

(bez

dowodu.)