1

WYKŁAD Nr 12

PODSTAWY

PROJEKTOWANIA

KONSTRUKCJI

ŻELBETOWYCH

Semestr V , r .ak. 2009/2010

Opracowanie - prof. dr hab. inż. Andrzej Łapko

Obliczanie i konstruowanie

fundamentów z betonu

2

Sposób i warunki posadowienia

fundamentów

Dobór rodzaju posadowienia i konstrukcji
fundamentów z betonu zależy od:

•

Rodzaju i sztywności konstrukcji obiektu,

•

Warunków wykonania i eksploatacji,

•

Właściwości podłoża gruntowego,

•

Zwierciadła wody gruntowej

.

Wyróżniamy:

1. Posadowienia

bezpośrednie

(ławy, stopy, płyty,

ruszty)

2. Posadowienia

pośrednie

(na palach, studniach

lub kesonach

3

Stany graniczne w

projektowaniu fundamentów

z betonu

Wyróżnia się:

•

I

stan graniczny fundamentu (stan nośności

podłoża)

•

II

stan graniczny fundamentu (stan

odkształcalności podłoża).

I stan graniczny nośności podłoża budowli
decyduje
o wymiarach rzutu fundamentu:

O nośności podłoża decyduje wielkość
fundamentu i rozkład naprężeń w gruncie
(funkcja wielu czynników, takich jak sztywność
fundamentu, obciążenie i rodzaju gruntu).

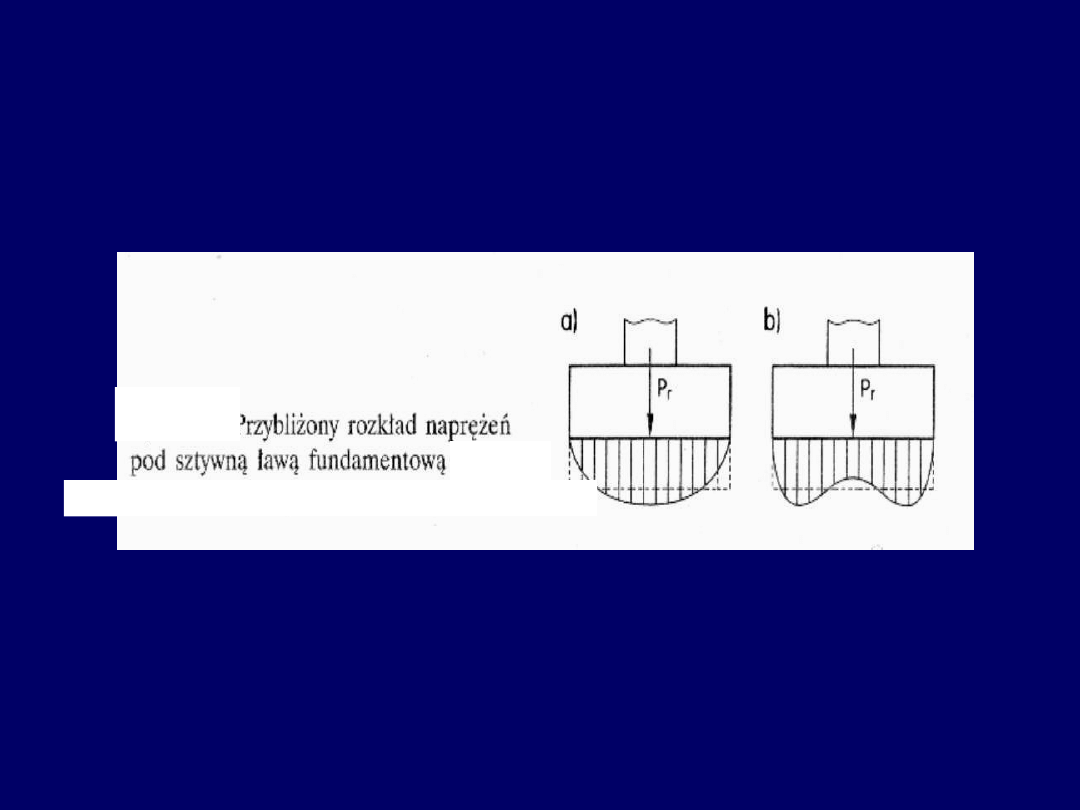
4

I stan graniczny podłoża

budowli

Z badań doświadczalnych wynika, że

rozkład odporu gruntu jest nieliniowy,

jednak do obliczeń

można przyjąć rozkład liniowy

W praktyce przyjmuje się rozkład prostoliniowy

odporu gruntu:

prostokątny, trapezowy lub trójkątny

a– w gruntach sypkich, b– w gruntach spoistych

5

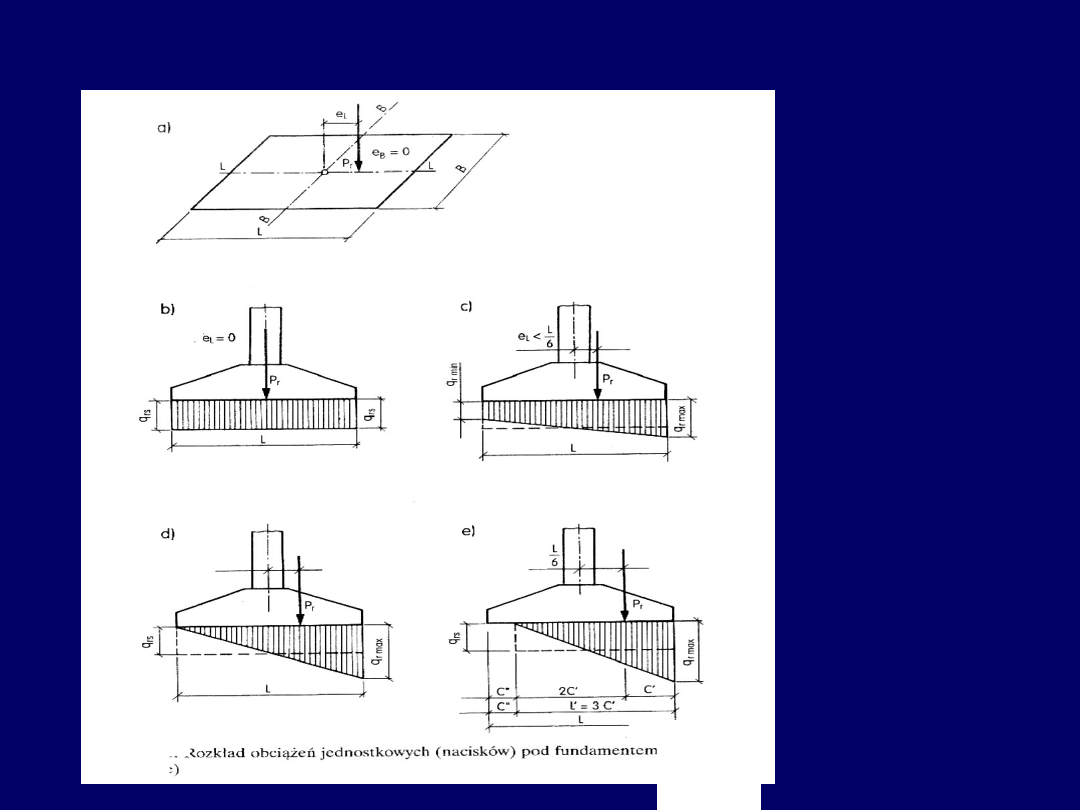
Wykresy naprężeń
pod fundamentem:
a) prostokątny,
b) trapezowy
c), d) trójkątny

Ustalanie wymiarów rzutu fundamentu B x L

e

L

>L/6

e

L

=L/6

6

Ustalenie wymiarów B i L

prostokątnej podstawy

fundamentu

W przypadku ogólnym ustalania wymiarów podstawy
fundamentu
wg I stanu granicznego sprawdzamy warunek (wg PN-
81/B-03020)

f

r

Q

m

N





gdzie: N

r

– obciążenie obliczeniowe (graniczne) fundamentu,

Q

f

– nośność (opór graniczny) podłoża,

m – współczynnik bezpieczeństwa (korekcyjny): m = 0,9 (metoda
A), m = 0,81 (B i C)



gB

N

L

B

gD

N

L

B

c

N

L

B

B

Q

r

B

B

r

D

D

r

u

c

f

)

(

min

)

(

)

(

25

,

0

1

5

,

1

1

3

,

0

1















 





















 













 





gdzie: N

c

, N

B

, N

D

– współczynniki obliczeniowe podłoża, zależne od kąta

tarcia Φ gruntu
c

u

– spójność gruntu (w gruntach sypkich c

u

= 0)

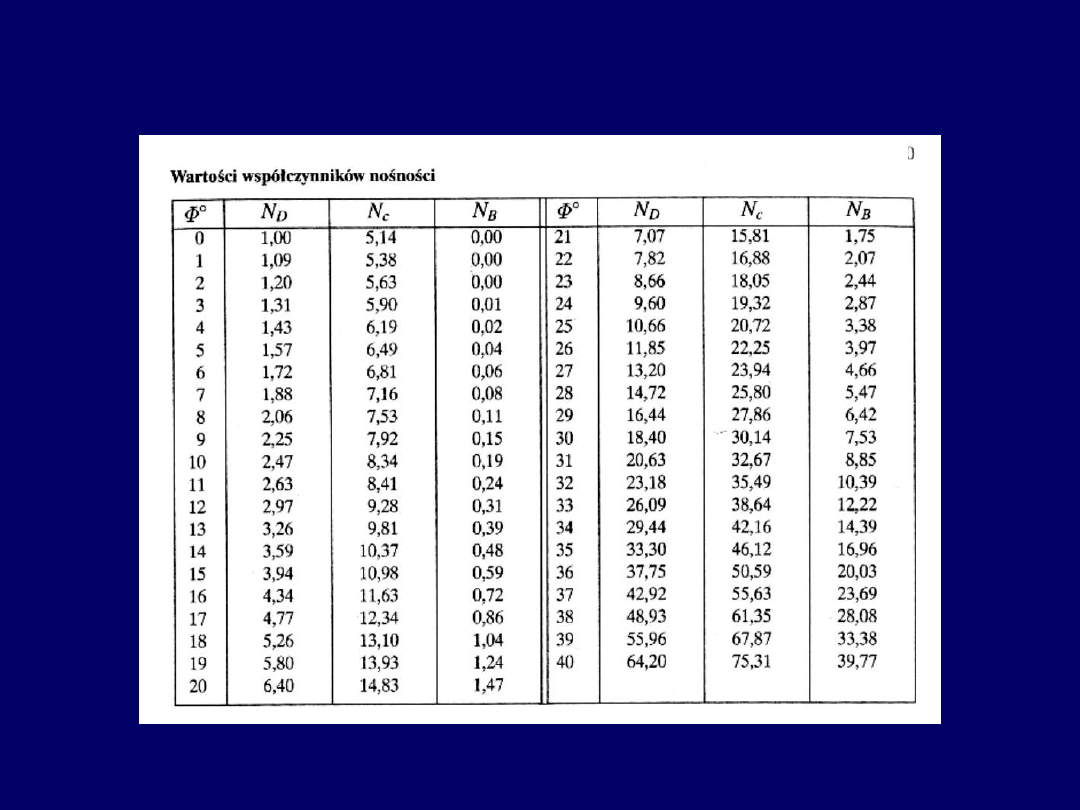
7

Φ –

kąt tarcia wewnętrznego gruntu

Wartości współczynników obliczeniowych nośności podłoża
N

D

, N

c

, N

B

w funkcji kąta tarcia wewnętrznego Φ

8

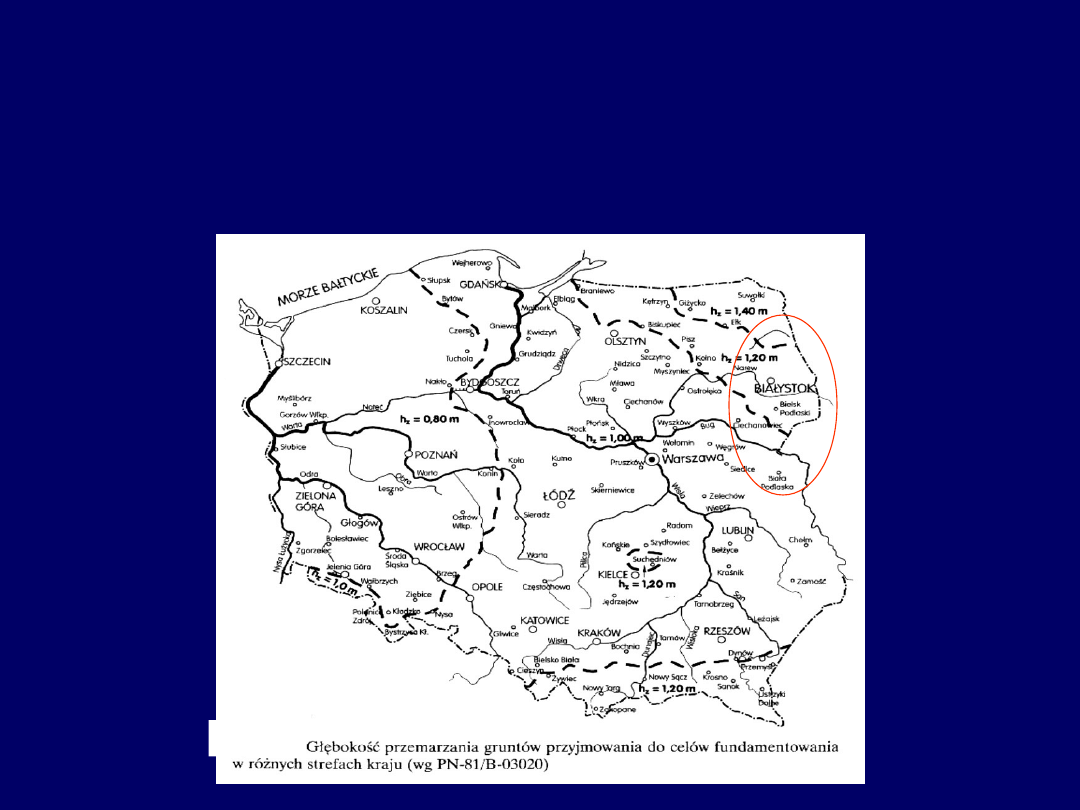
Głębokość posadowienia

fundamentu

Głębokość h poniżej terenu powinna wynosić min. 0,5
m.

W gruntach wysadzinowych głębokość ta zależy od głębokości przemarzania

9

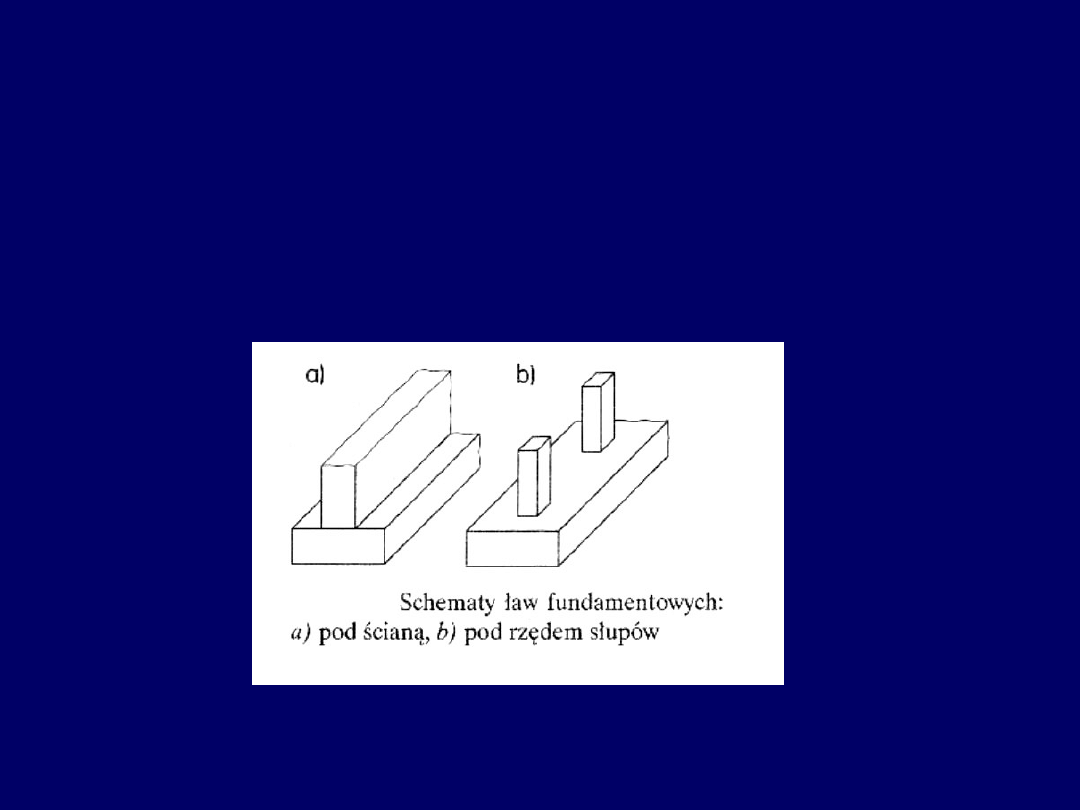
Ławy fundamentowe

Stosuje się powszechnie jako fundamenty pod ściany lub rzędy słupów.

Materiały - to obecnie najczęściej: beton lub żelbet.

10

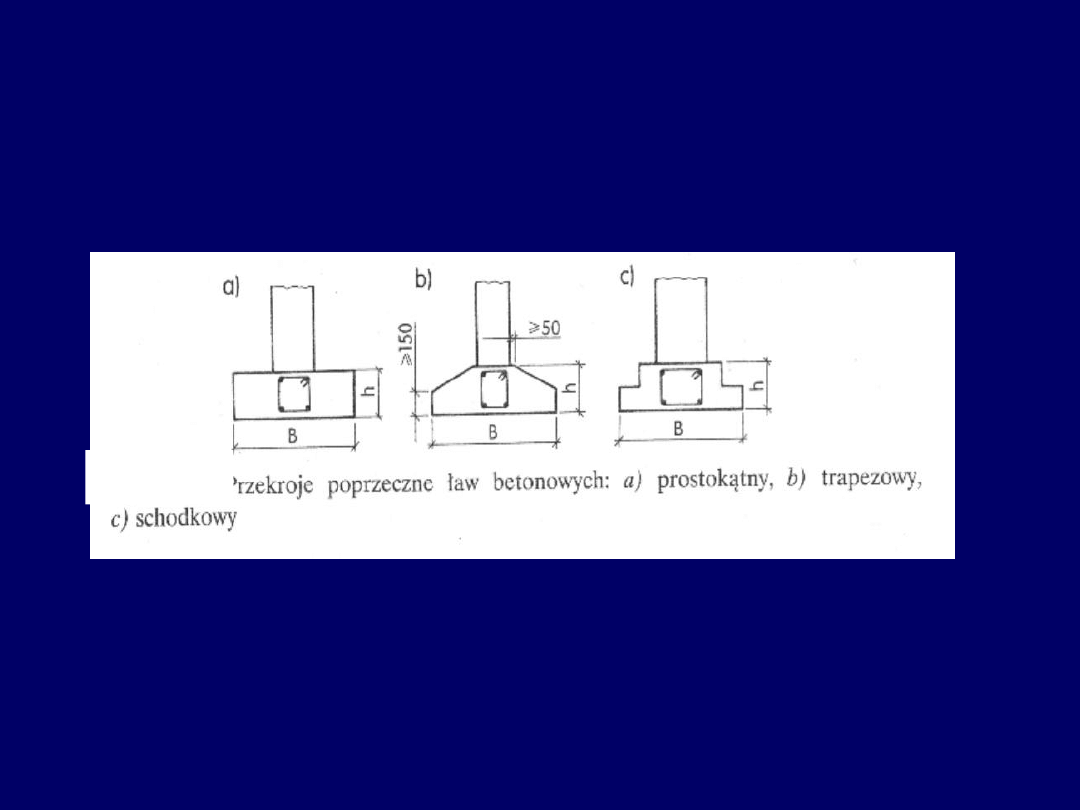
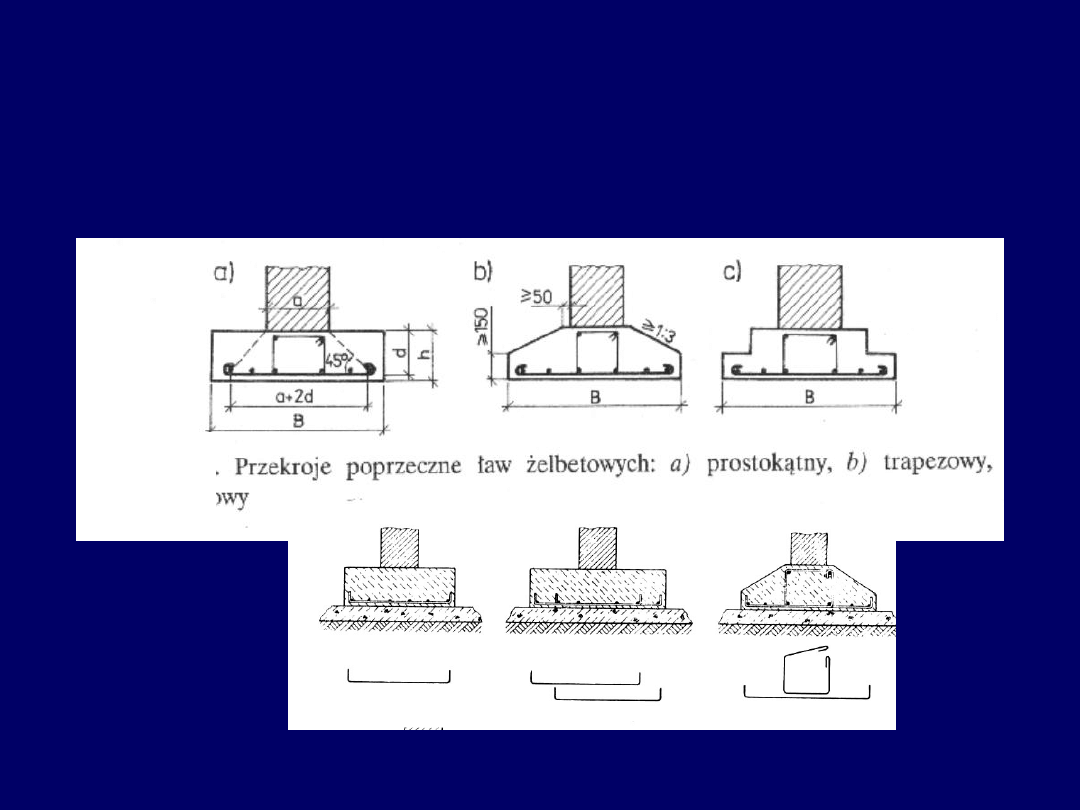
Ławy fundamentowe betonowe –

kształty przekrojów poprzecznych

11

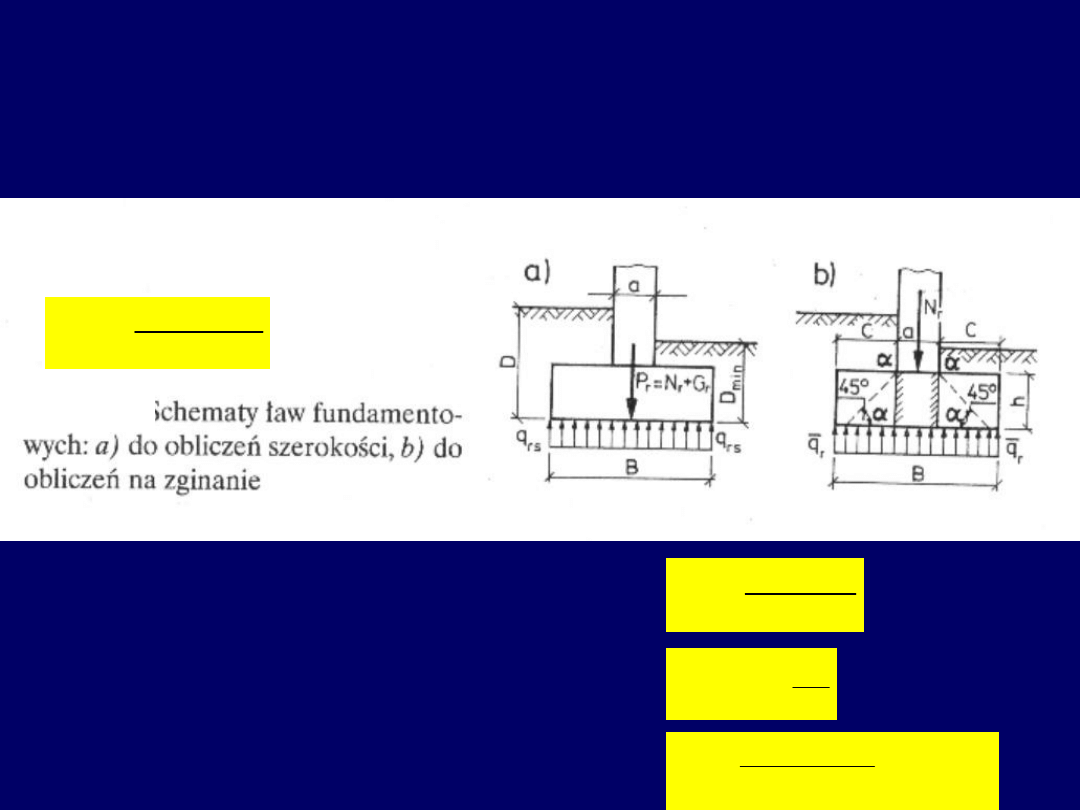
Ławy fundamentowe żelbetowe -

zasady obliczania zbrojenia na zginanie

Naprężenia odporu gruntu pod ławą
przy osiowym działaniu siły

B

G

N

q

r

r

rs







00

,

1

B

N

q

r

r





00

,

1

Odpór gruntu wywołujący poprzeczne zginanie ławy

Moment zginający wspornik odsadzki ławy

2

2

c

q

M

r

r



Pole przekroju zbrojenia na zginanie poprzeczne

min

,

9

,

0

s

yd

r

s

A

f

d

M

A







12

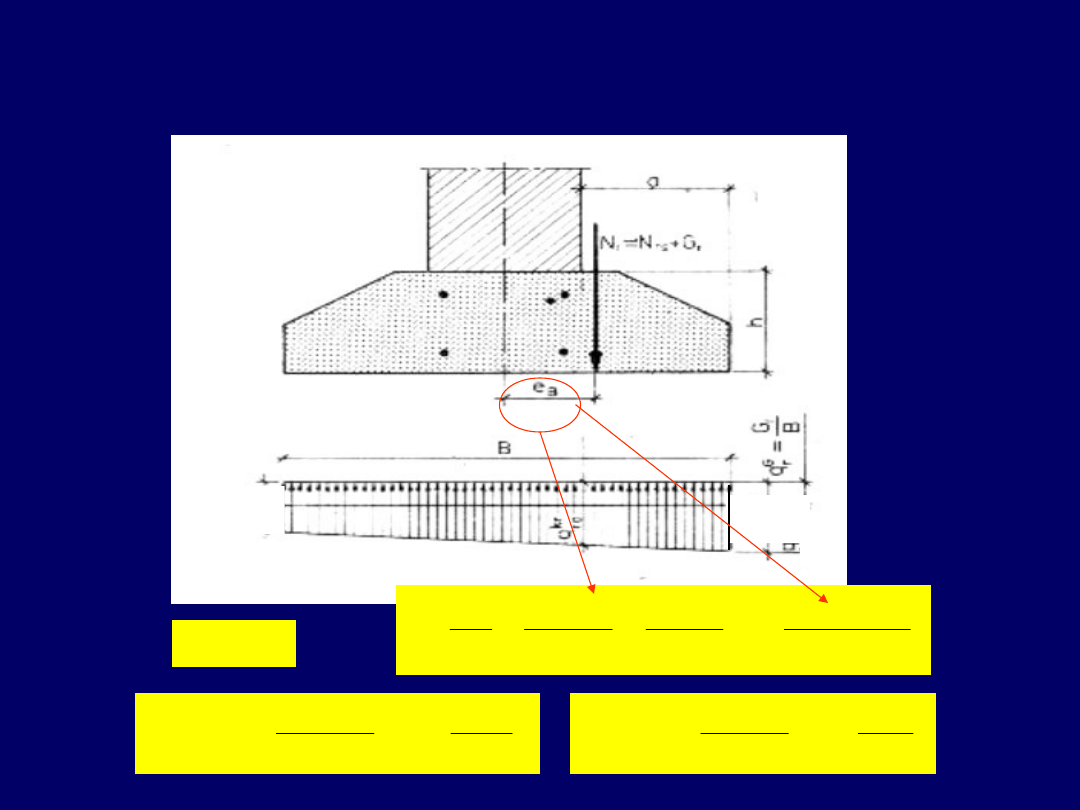
Rozkład naprężeń pod ławą mimośrodowo obciążoną











 





B

e

B

N

q

a

r

r

6

1

0

,

1

min

,











 





B

e

B

N

q

a

r

r

6

1

0

,

1

max

,

Jeżeli

6

/

B

e

a



q

r,min

q

r,max



























6

/

0

,

1

1

0

,

1

2

B

e

B

N

W

e

N

A

N

q

a

r

a

r

r

czyli

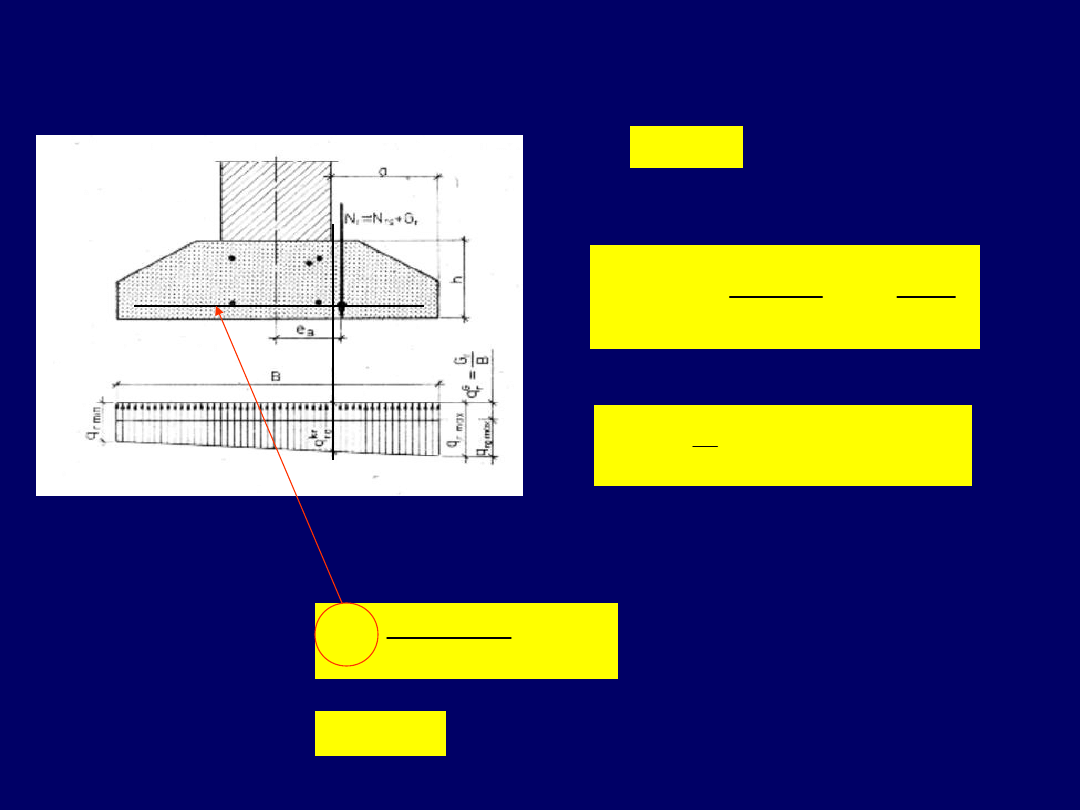
13

Zbrojenie poprzeczne ławy mimośrodowo obciążonej











 





B

e

B

N

q

a

r

r

6

1

0

,

1

max

,

Jeżeli

6

/

B

e

B







kr

r

r

r

q

q

a

M

,

max

,

2

6





min

,

9

,

0

s

yd

r

s

A

f

d

M

A







Moment zginający wspornik ławy

Pole przekroju zbrojenia poprzecznego na zginanie ławy

1

a

h

d





14

Ławy fundamentowe żelbetowe –

kształt zbrojenia poprzecznego na zginanie

Układ zbrojenia poprzecznego ławy

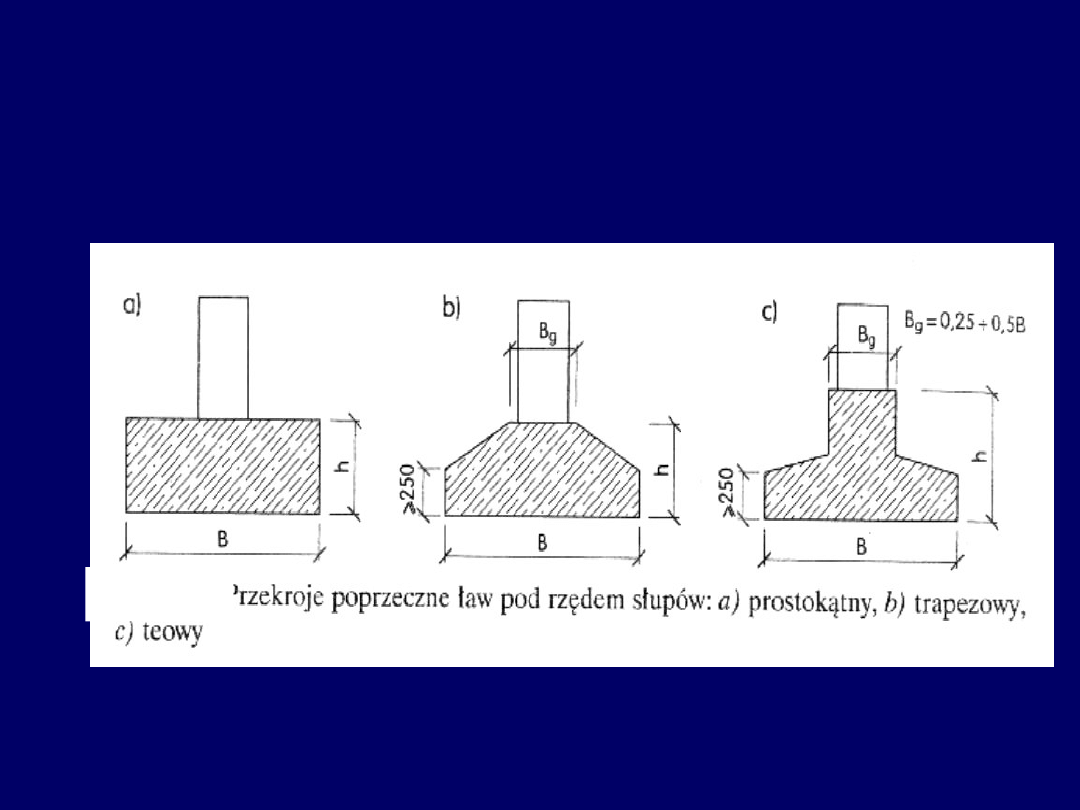
15

Ławy fundamentowe

żelbetowe pod rzędem słupów

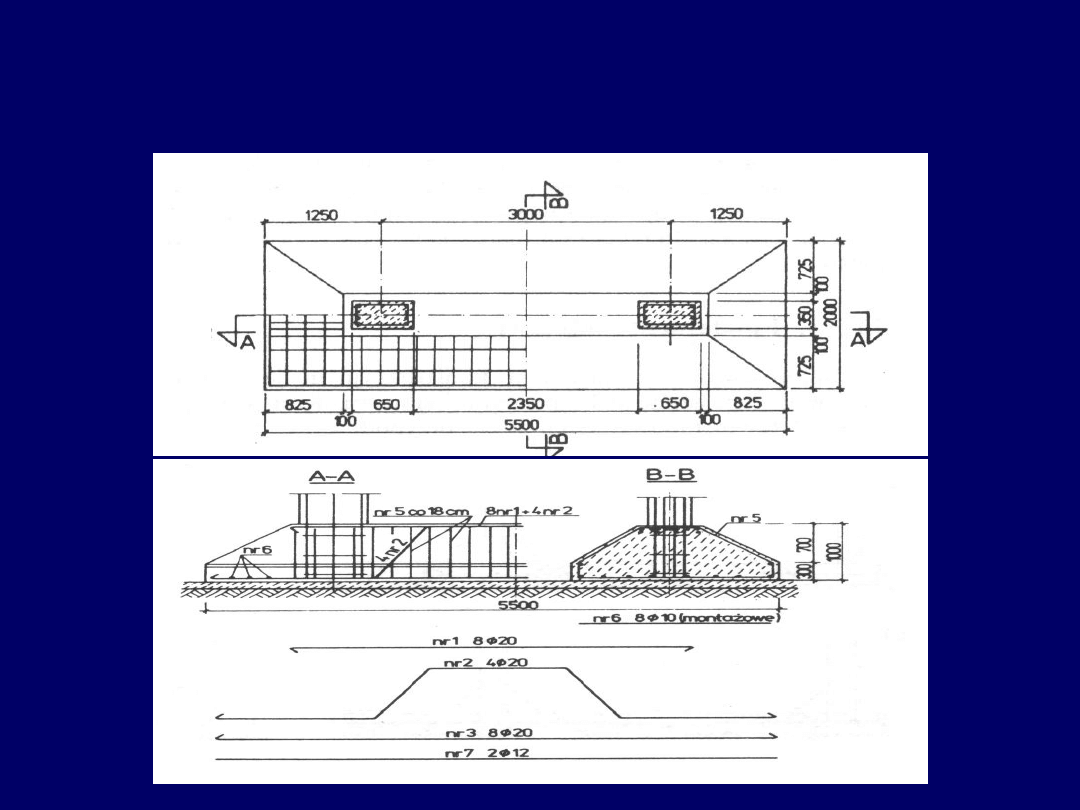
16

Ławy fundamentowe żelbetowe pod

rzędem słupów

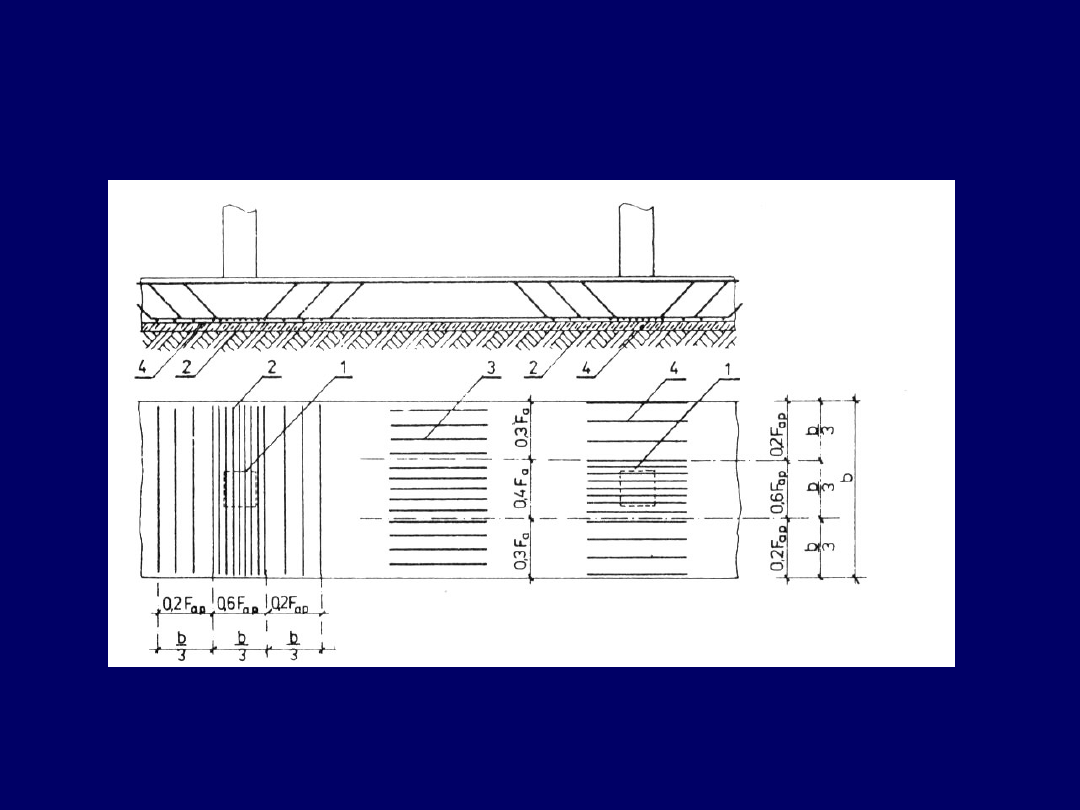
17

Ławy fundamentowe żelbetowe pod rzędem

słupów

Ogólne zasady rozmieszczenia zbrojenia nośnego w ławach o przekroju prostokątnym

1) – słupy, 2- dolne zbrojenie poprzeczne pod słupami, 3 – zbrojenie przęsłowe

4)- podłużne zbrojenie podporowe

18

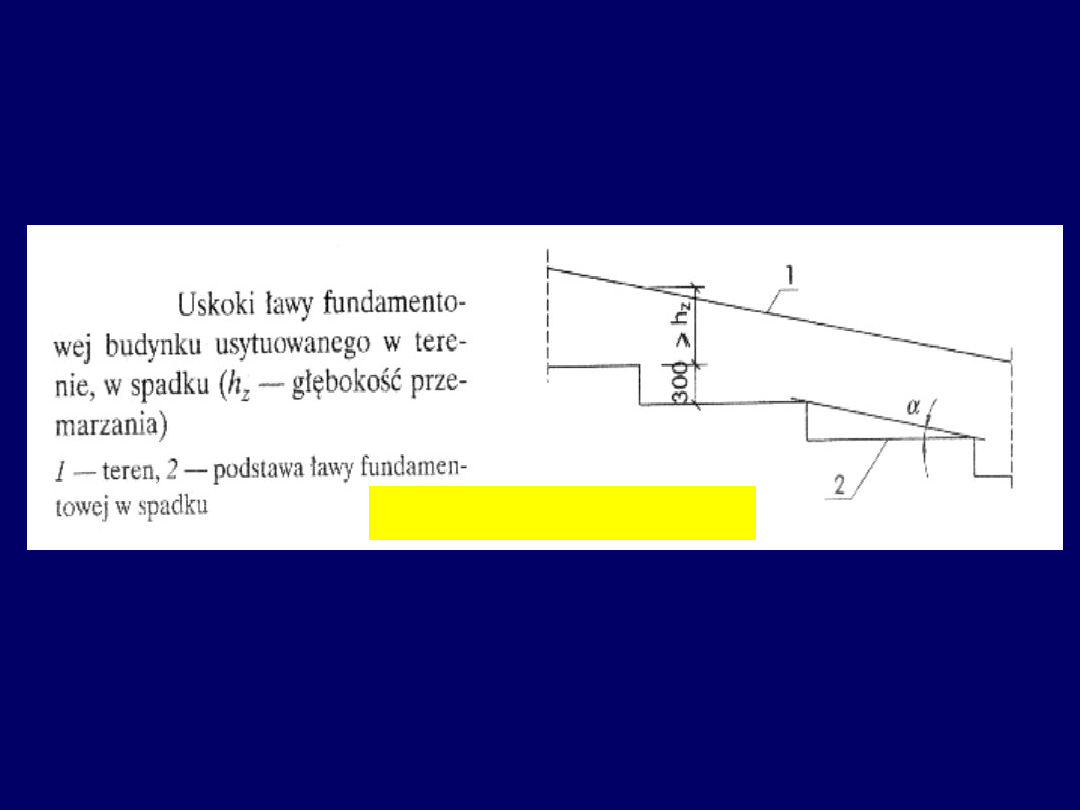
Ławy fundamentowe –

kształt podłużny w terenie pochyłym

)

(

tan

tan

,

6

,

0

tan

r

u











19

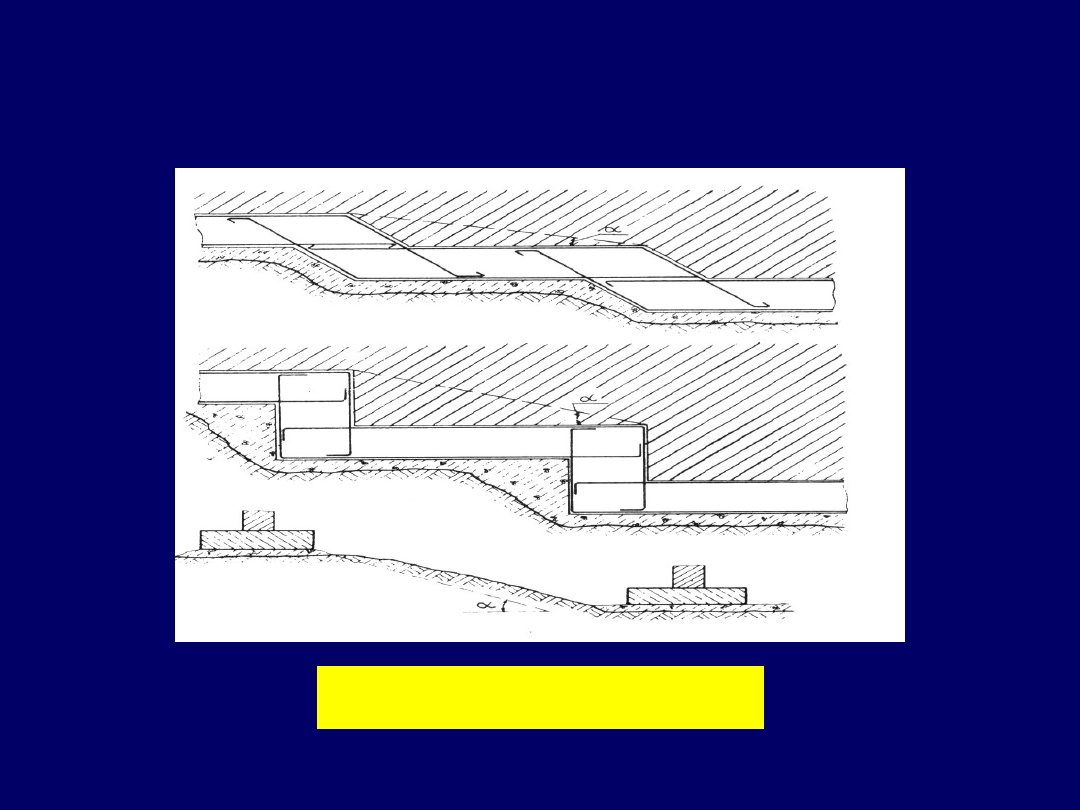
Ławy fundamentowe –

kształt podłużny w terenie pochyłym

)

(

tan

tan

,

6

,

0

tan

r

u











20

Ławy fundamentowe –

poniżej otworów w ścianie piwnicznej

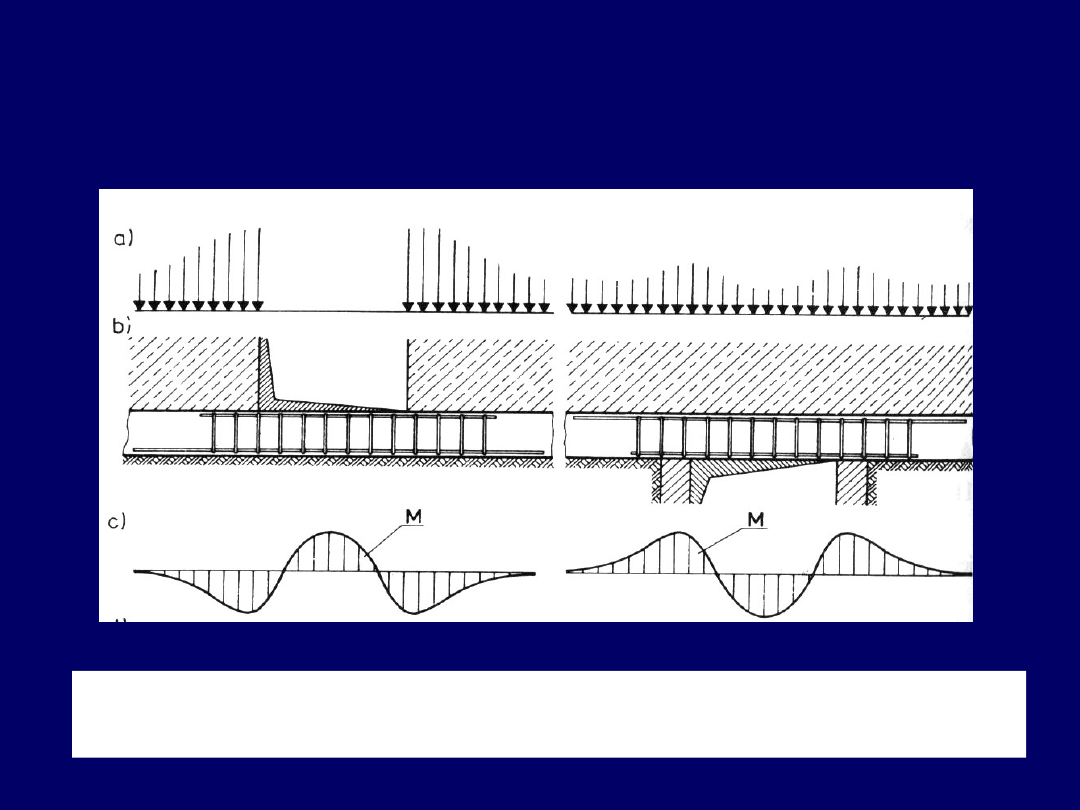
21

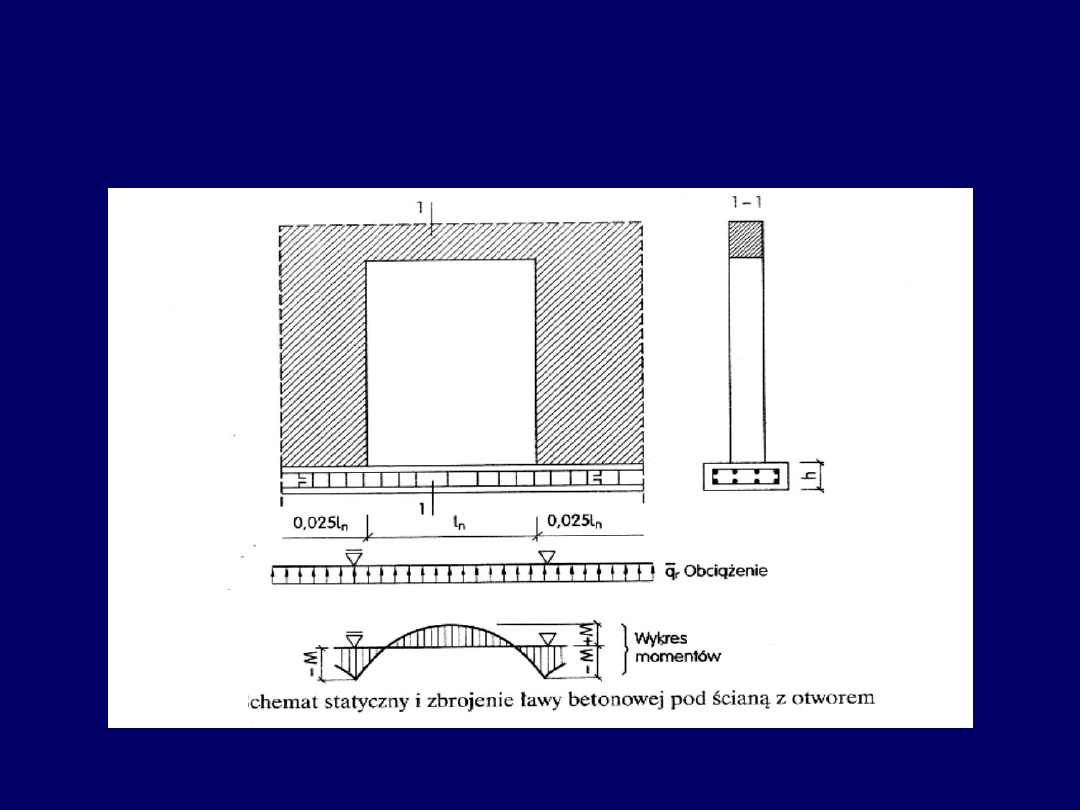
Ławy fundamentowe –

poniżej i powyżej otworów w ścianie piwnicznej

Dozbrojenie podłużne ławy fundamentowej pod i nad otworem

w

ścianie piwnicznej

22

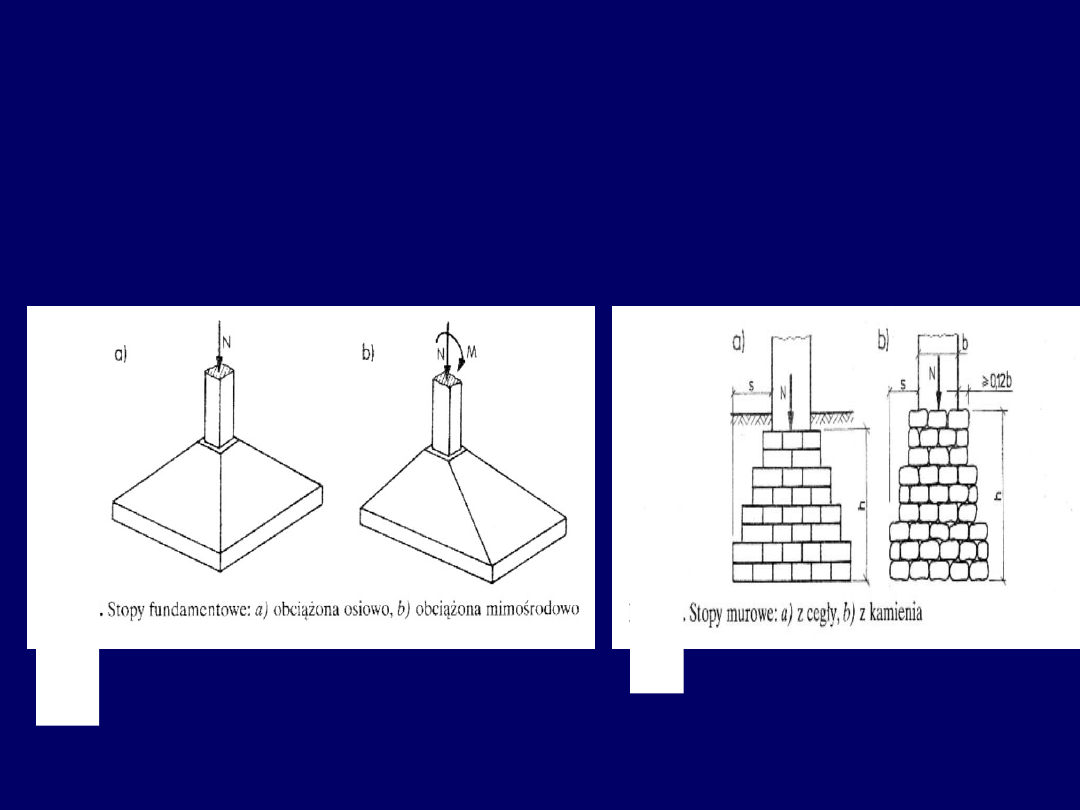
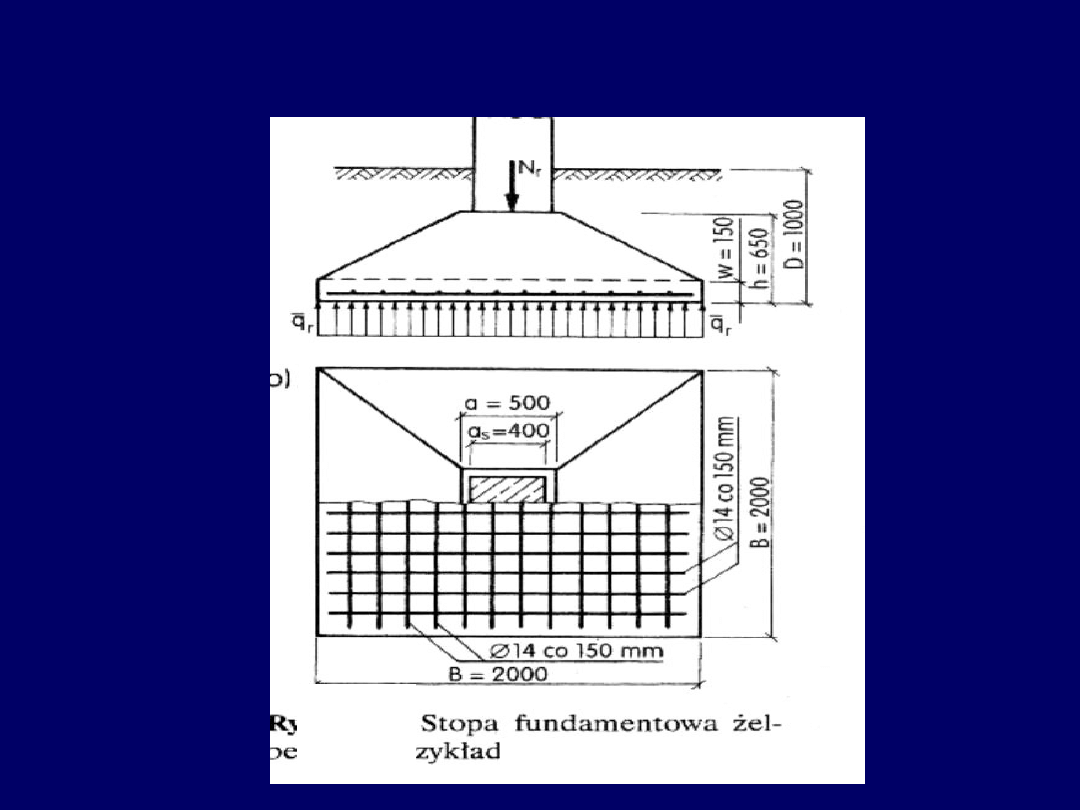
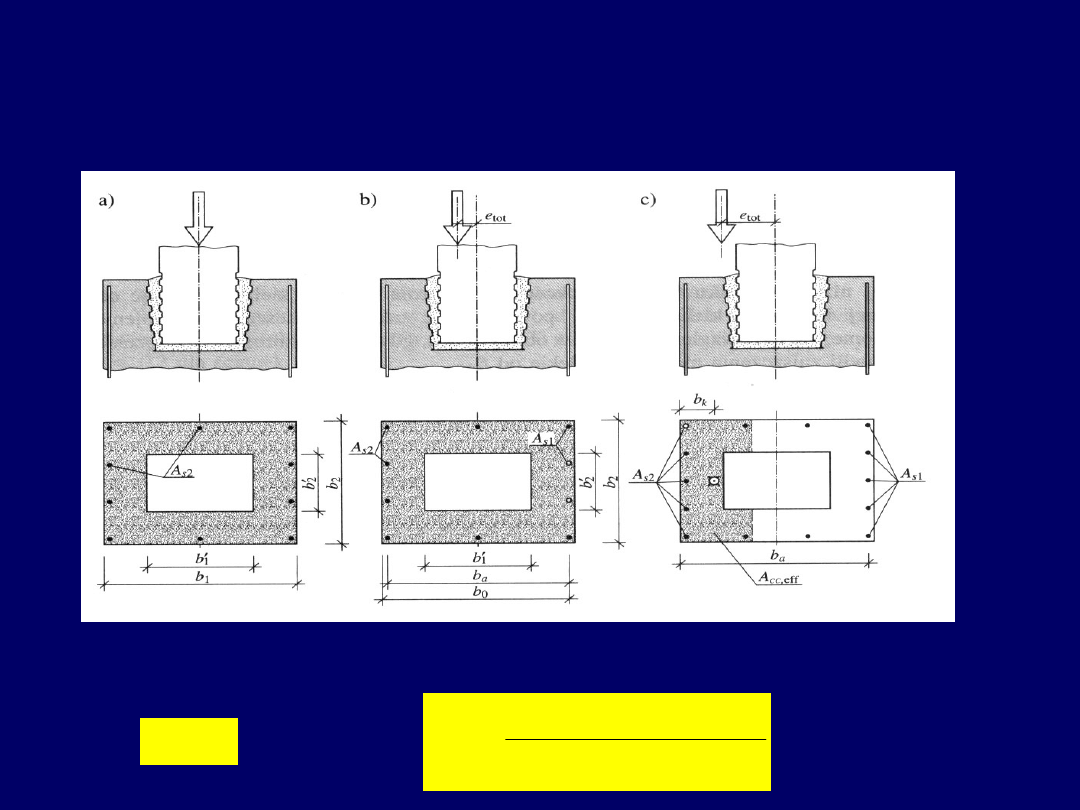
Stopy fundamentowe

Stosuje się powszechnie jako fundamenty pod słupy. Materiały to obecnie najczęściej

beton lub żelbet. W przeszłości wykonywano je często z cegły lub kamienia

23

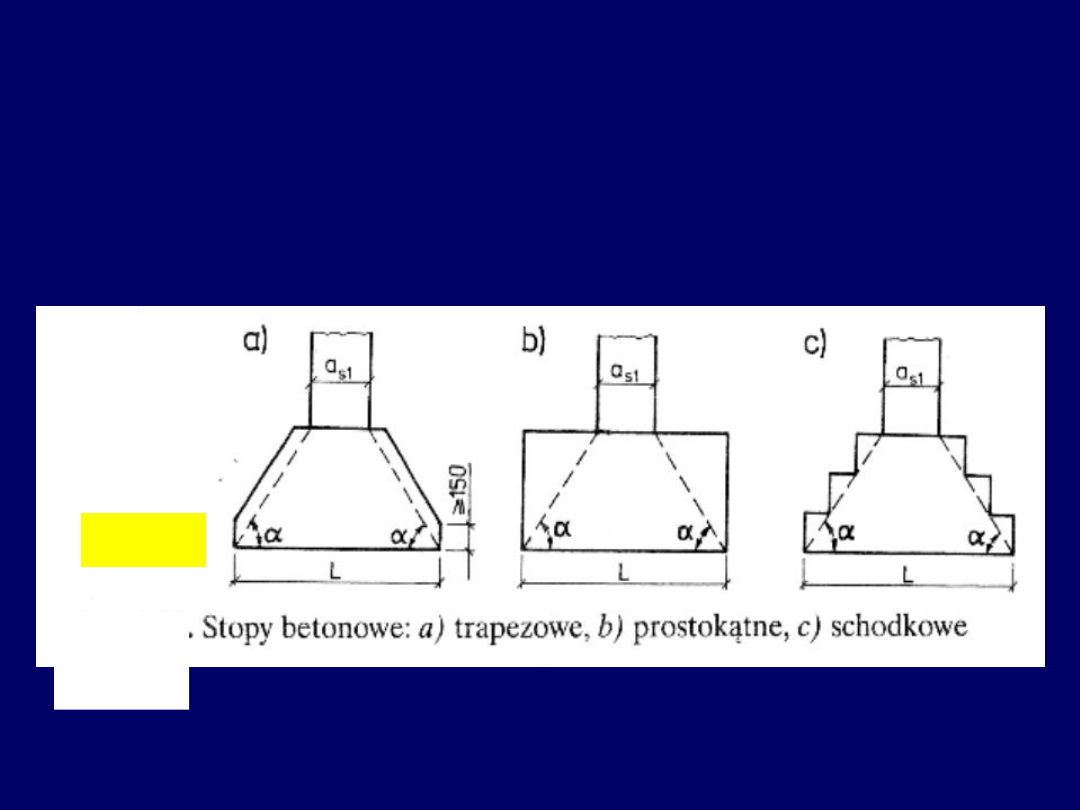
Stopy fundamentowe betonowe (bez zbrojenia)

– kształty przekrojów poprzecznych

0

30





24

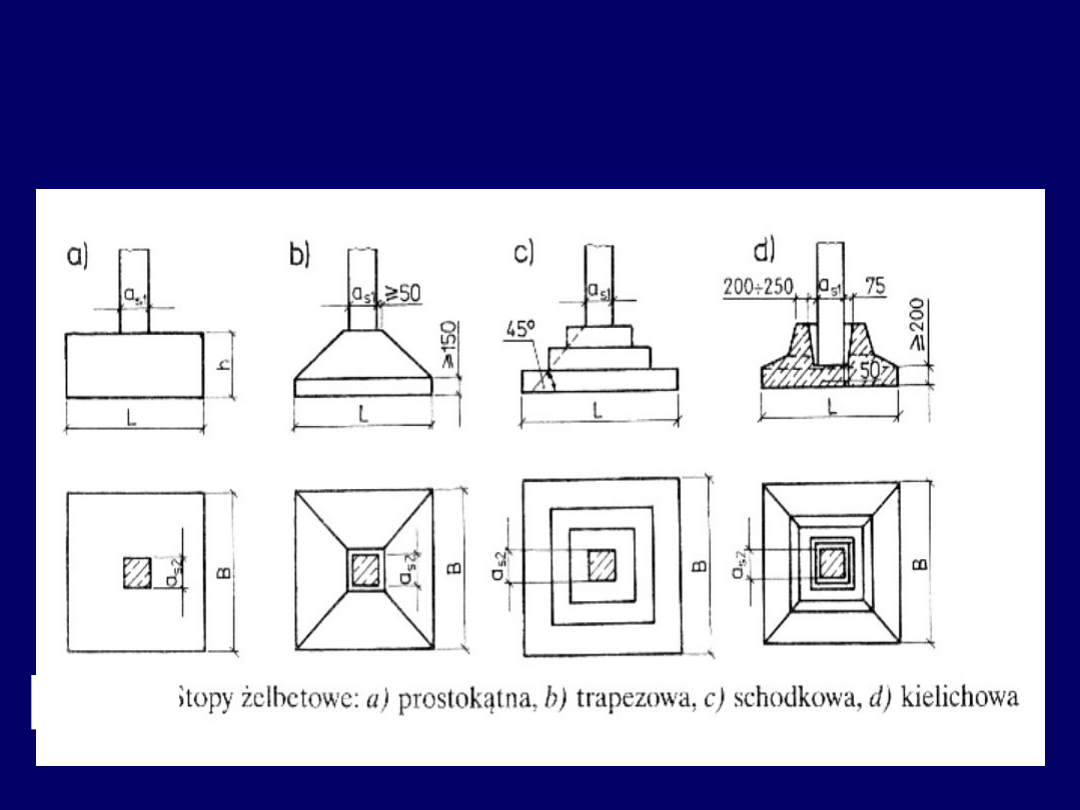
Stopy fundamentowe z betonu –

rodzaje i kształty przekrojów poprzecznych

25

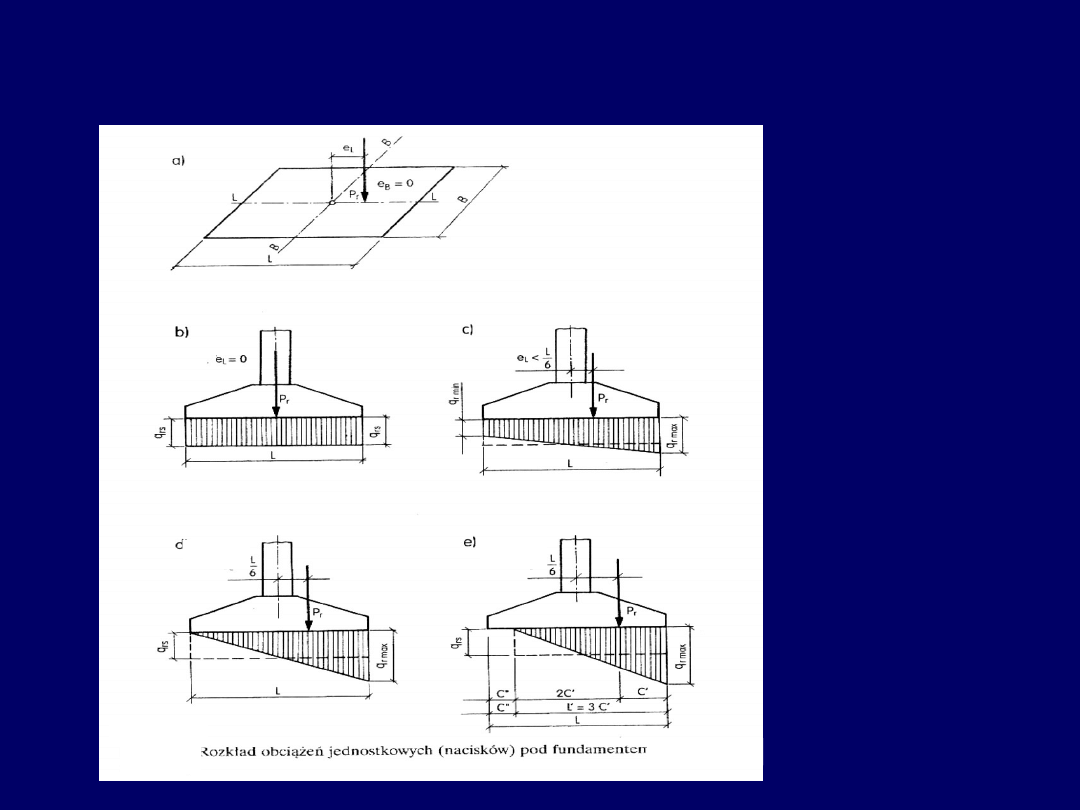
Wykresy naprężeń pod stopą

fundamentową:

a) prostokątny, b) trapezowy, c), d)

trójkątny

e

L

>L/6

e

L

=L/6

26

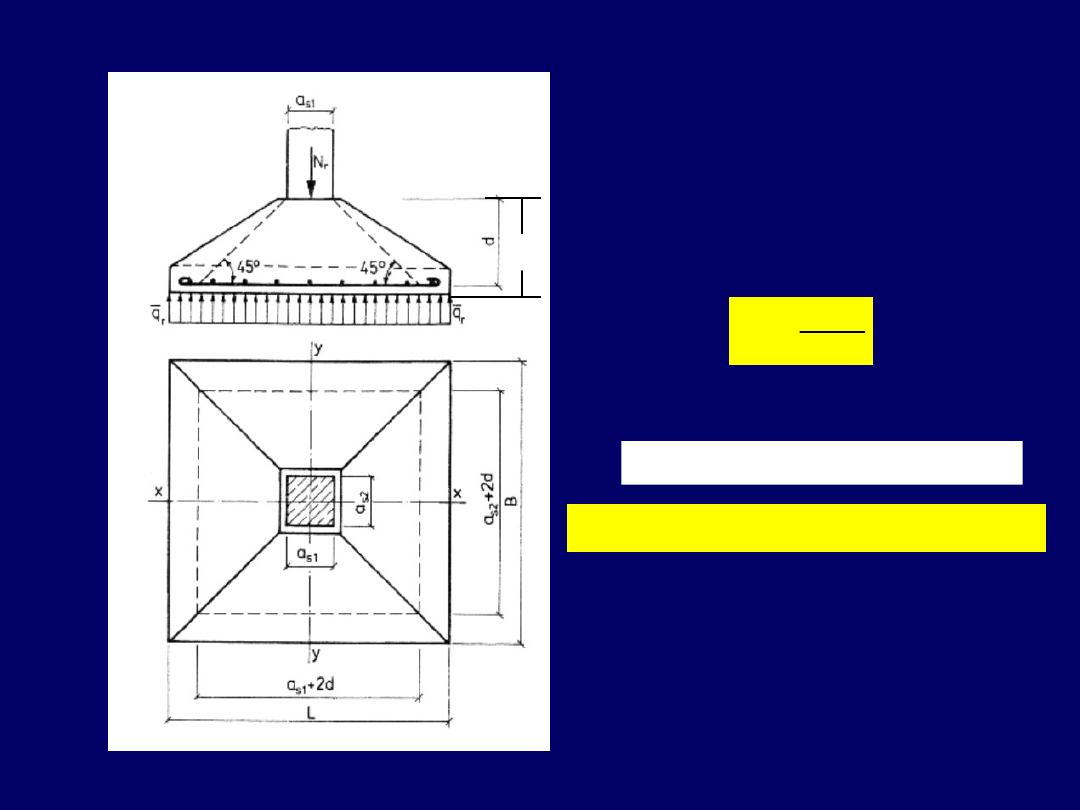
Naprężenia pod stopą

obciążoną osiowo

B

L

N

q

r

r





Wysokość stopy żelbetowej









1

1

5

,

0

3

,

0

s

s

a

L

h

a

L









h

27

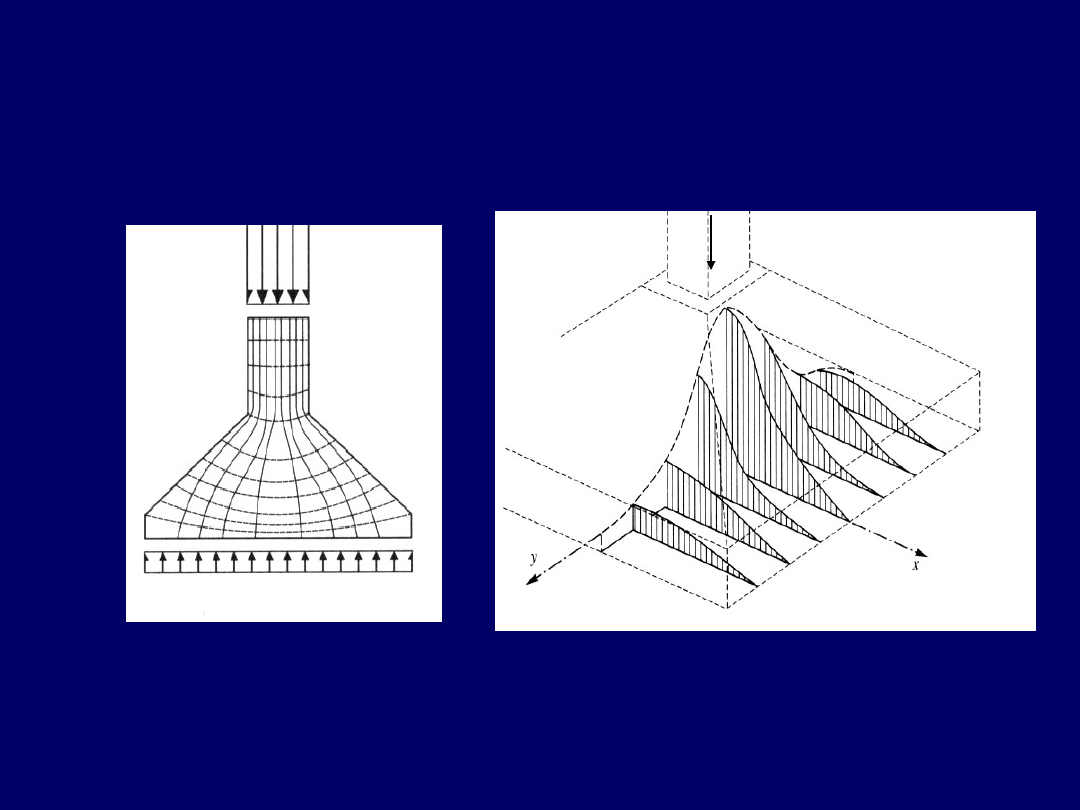
Obliczenie stopy na zginanie

-

zagadnienie przestrzenne

Przebieg trajektorii naprężeń głównych

w stopie obciążonej osiowo

Rozkład momentów M

x

w stopie fundamentowej

28

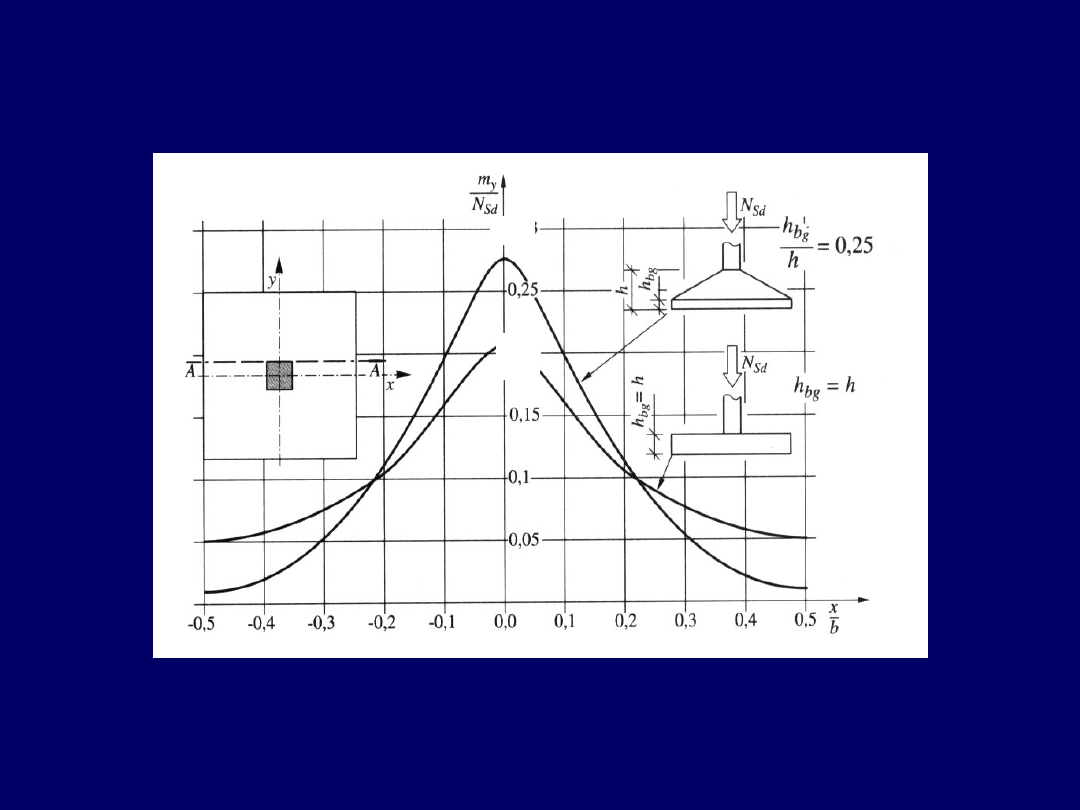
Obliczenie stopy na zginanie

-

zagadnienie przestrzenne

Rozkład momentów M

y

w przekroju A – A stopy fundamentowej

o rzucie kwadratowym, w zależności od stosunku h

bg

/h

0,3

0,

2

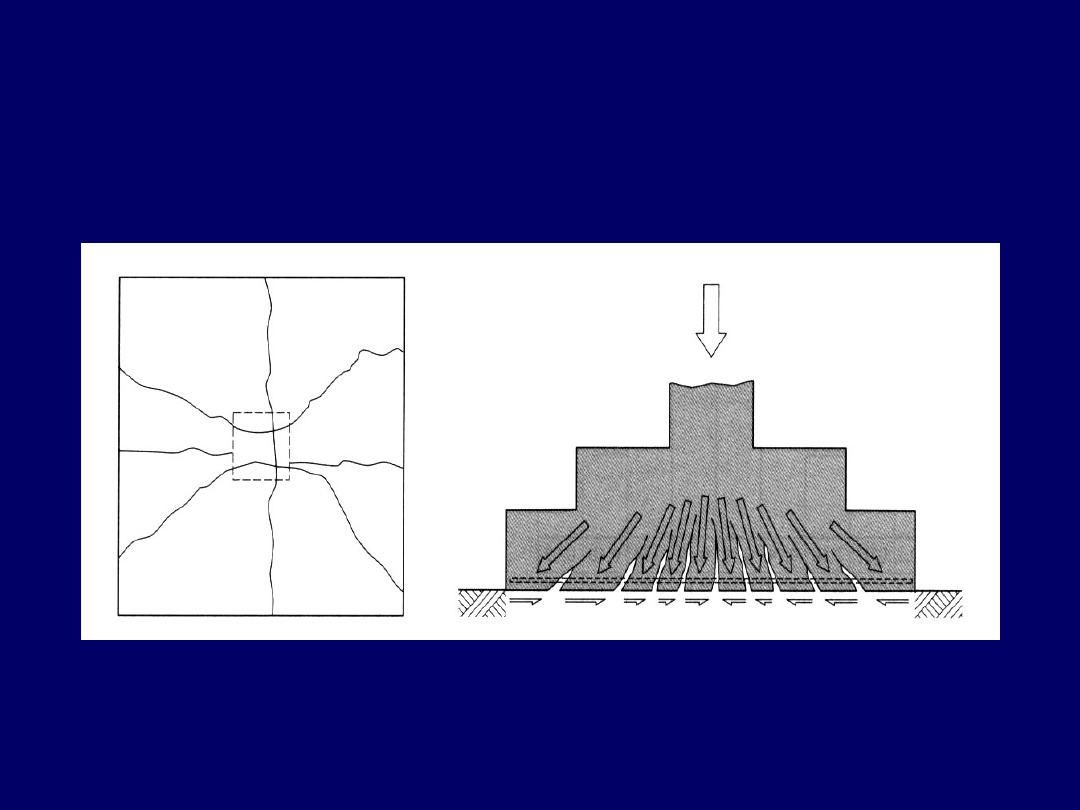
29

Schemat pracy stopy żelbetowej

na zginanie

Widok zarysowań stopy fundamentowej osiowo obciążonej od zginania:

a) – układ rys na spodzie stopy, b) – schemat pracy na zginanie

b)

a)

30

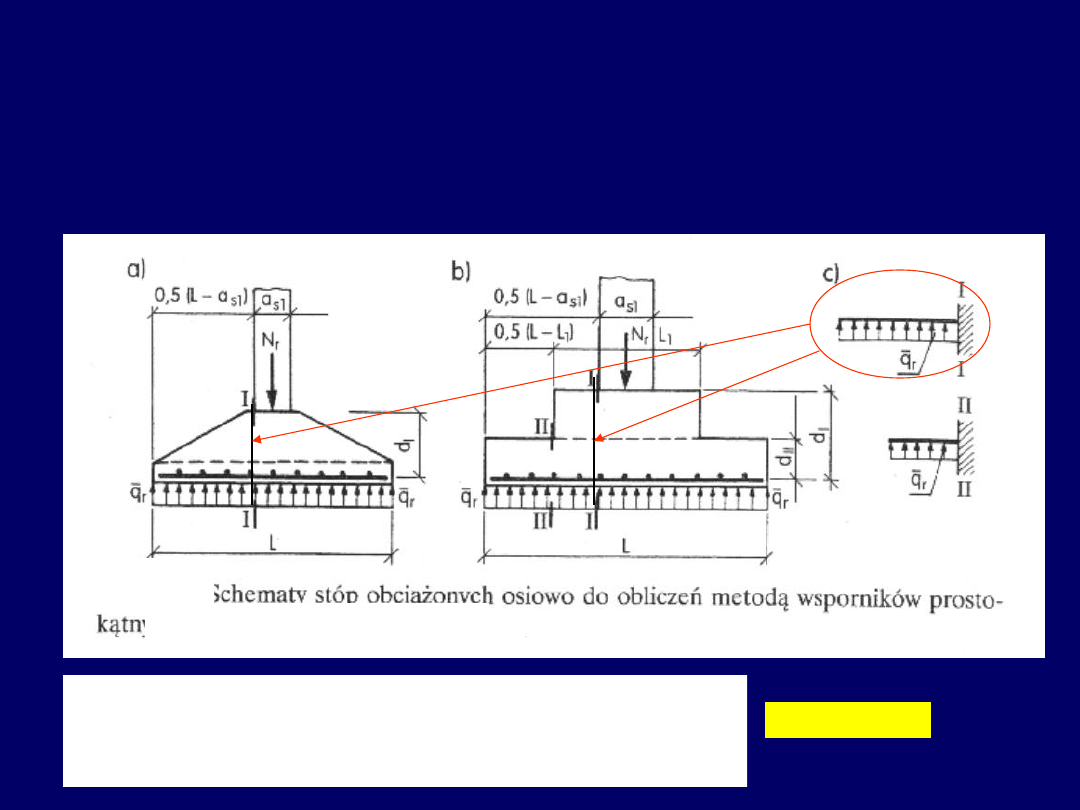
Założenia metody wsporników wydzielonych

podejście tradycyjne

W podejściu tradycyjnym

do obliczeń momentu

zginającego wspornik uwzględnia się wysięg
wspornika

)

(

5

,

0

1

s

a

L 

31

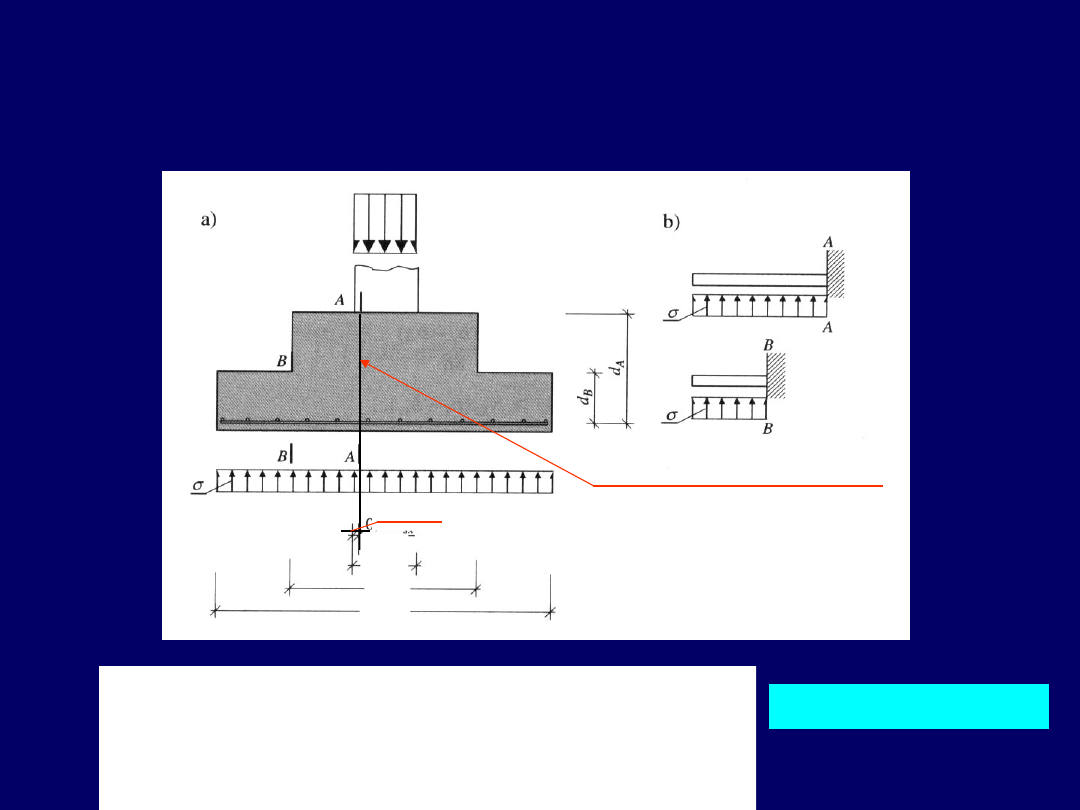
Założenia metody wsporników wydzielonych

Podejście wg Eurokodu 2

W podejściu wg Eurokodu 2

do obliczeń

momentu zginającego wspornik uwzględnia
się wysięg wspornika
przesunięty o odcinek 0,15 a

s1

od lica słupa

1

1

15

,

0

)

(

5

,

0

s

a

L

L





Przekrój utwierdzenia wspornika

L

0,15a

s1

L

1

a

s1

32

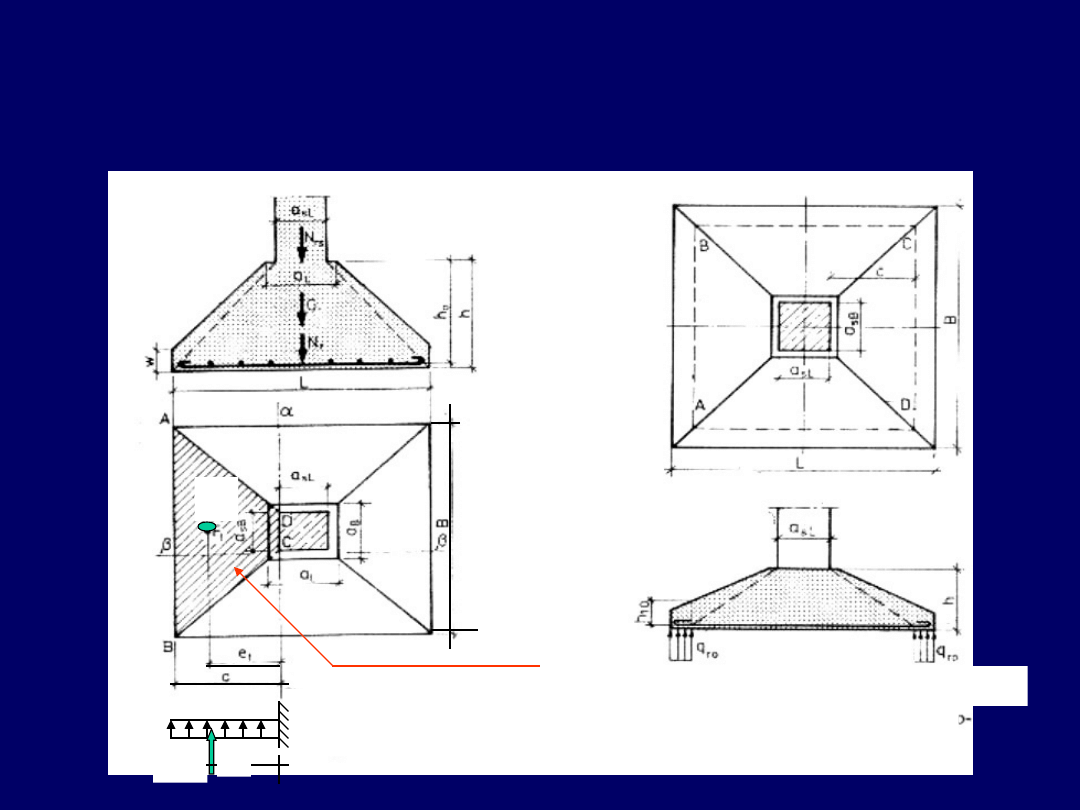
Zasady obliczenia momentu zginającego wspornik o rzucie trapezu

stopa żelbetowa obciążone osiowo

Metoda
wsporników
trapezowych

Schematy pracy stopy obciążonej osiowo

Wspornik trapezowy

F

t

F

t

e

t

Schemat pracy stopy na przebicie

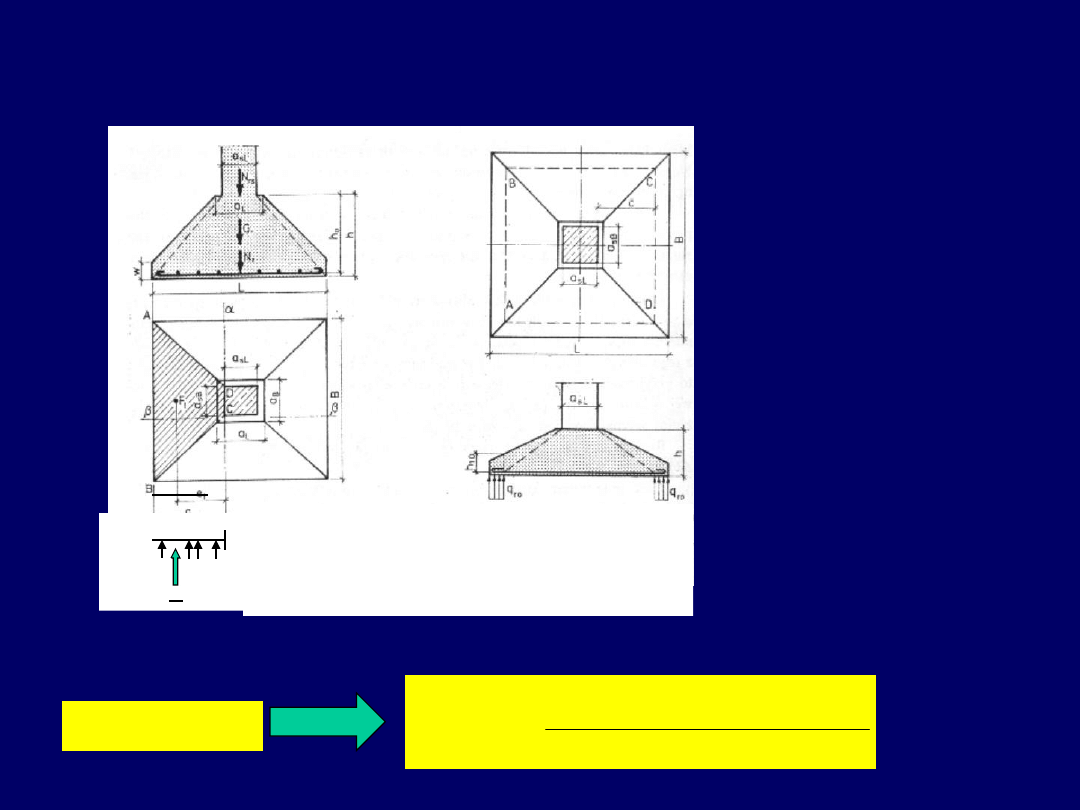
33

Zasady obliczenia zbrojenia na zginanie i przebicie

Metoda
wsporników
trapezowych

Moment zginający wspornik trapezowy ABCD stopy osiowo obciążonej



 



24

2

2

sB

sL

r

r

a

B

a

L

q

M







t

t

r

r

e

F

q

M





C

D

I

F

t

34

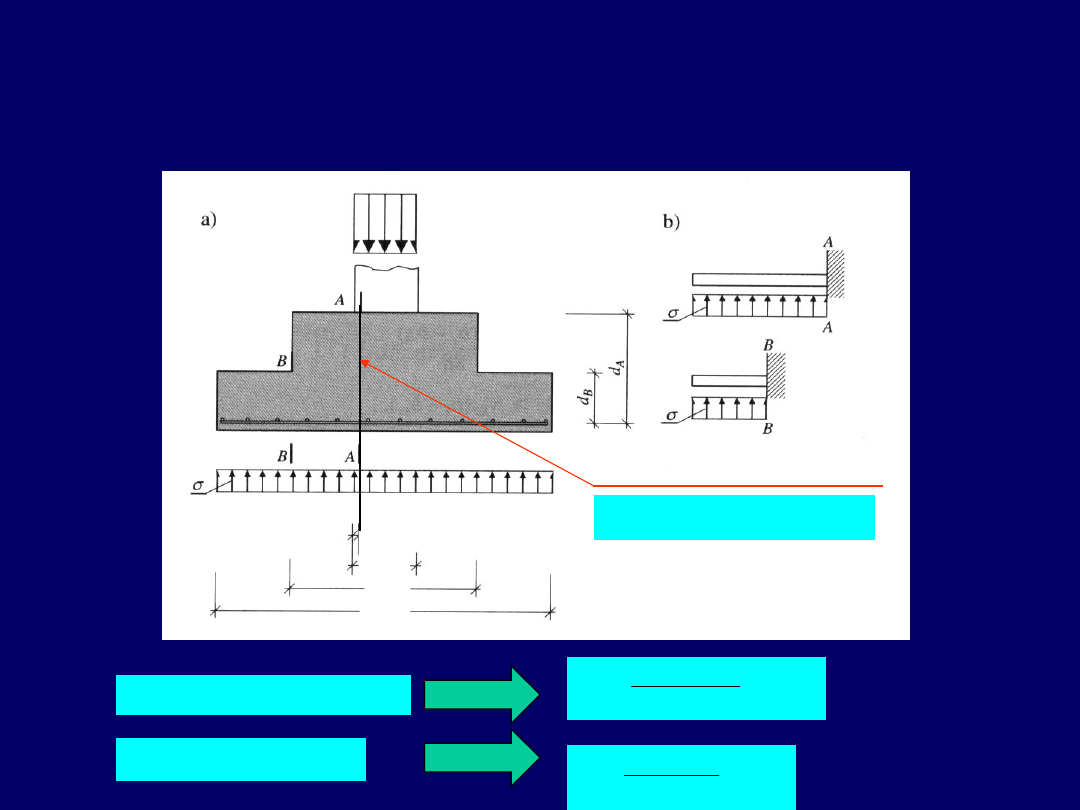
Założenia metody wsporników wydzielonych

Podejście wg Eurokodu 2

1

1

15

,

0

)

(

5

,

0

s

a

L

L





Przekrój utwierdzenia wspornika

w odległości od krawędzi stopy

L

0,15a

s1

L

1

a

s1





B

a

L

M

s

A

Ed

2

1

,

7

,

0

125

,

0











B

L

L

M

B

Ed

2

1

,

125

,

0







min

,

,

9

,

0

s

yd

A

A

Ed

sA

A

f

d

M

A







1

1

15

,

0

)

(

5

,

0

s

a

L

L





min

,

,

9

,

0

s

yd

B

B

Ed

sB

A

f

d

M

A







(w przekroju A)

(w przekroju B)

35

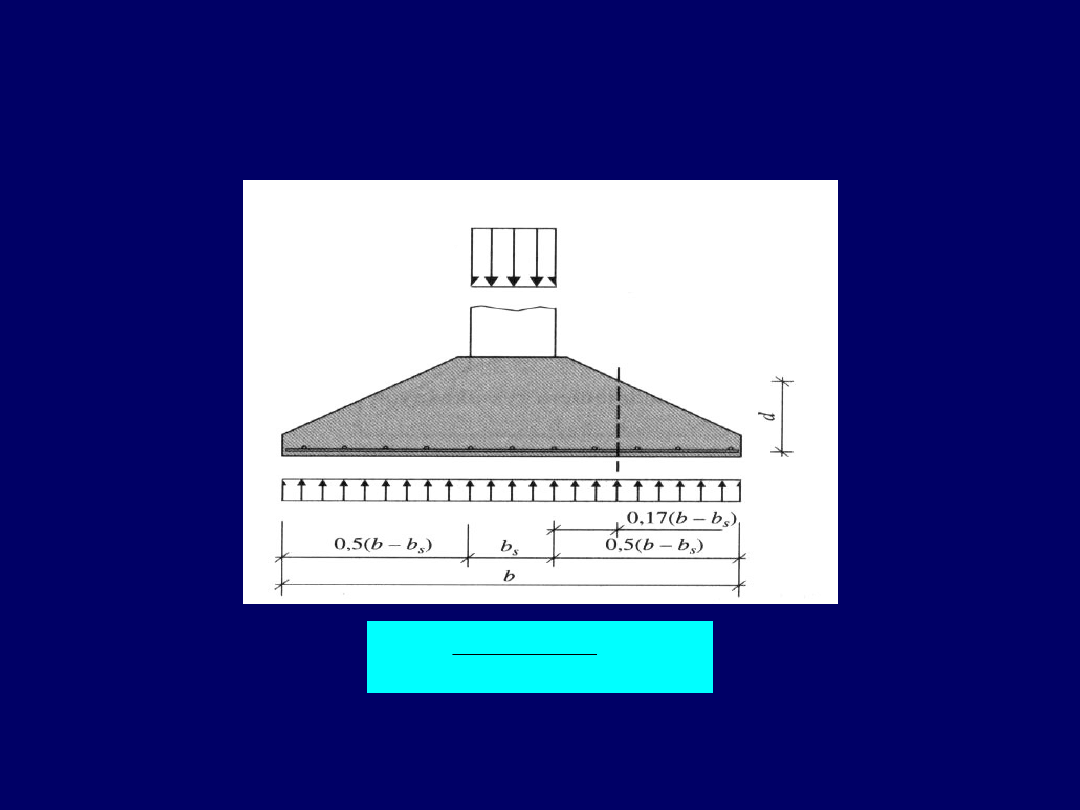
Zasady obliczenia zbrojenia na zginanie i przebicie

Metoda wsporników trapezowych wg podejścia
Eurokodu 2

min

,

,

9

,

0

s

yd

x

A

s

sA

A

f

d

M

A







C

D

Wysokość użyteczną stopy d przyjmuje się w odległości 1/3 od
krawędzi słupa

36

Przykład zbrojenia stopy osiowo obciążonej na zginanie

37

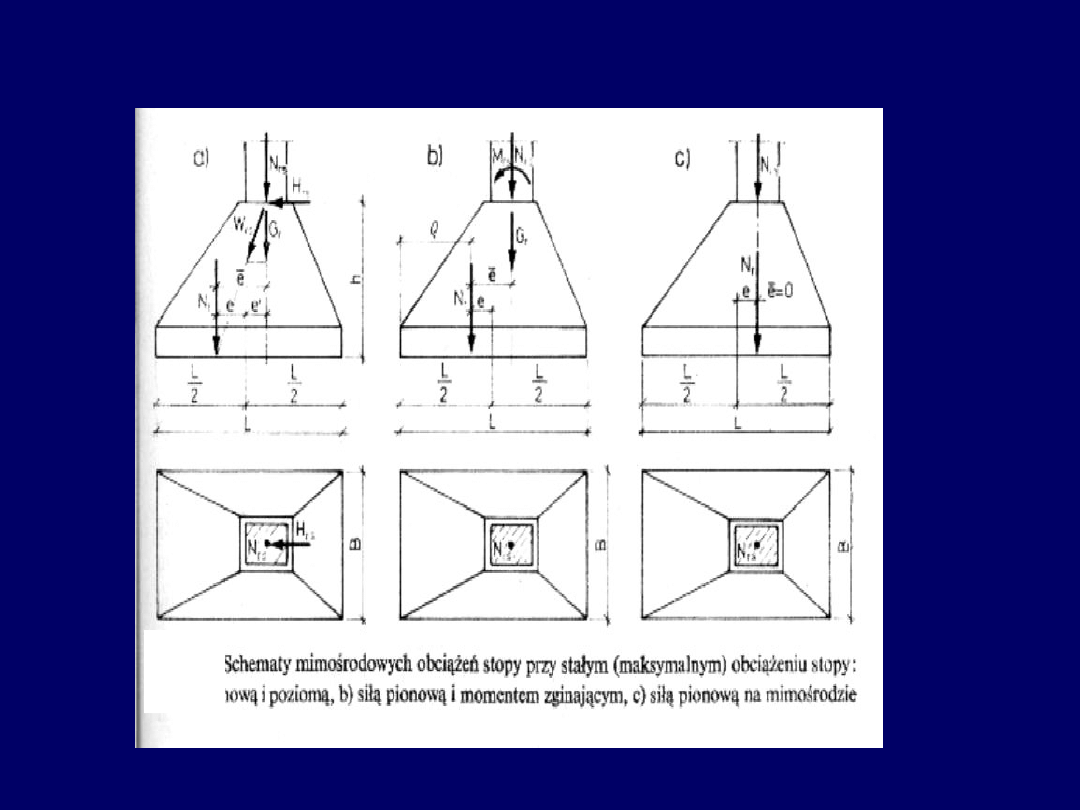
Schematy mimośrodowego obciążenia stóp fundamentowych

38

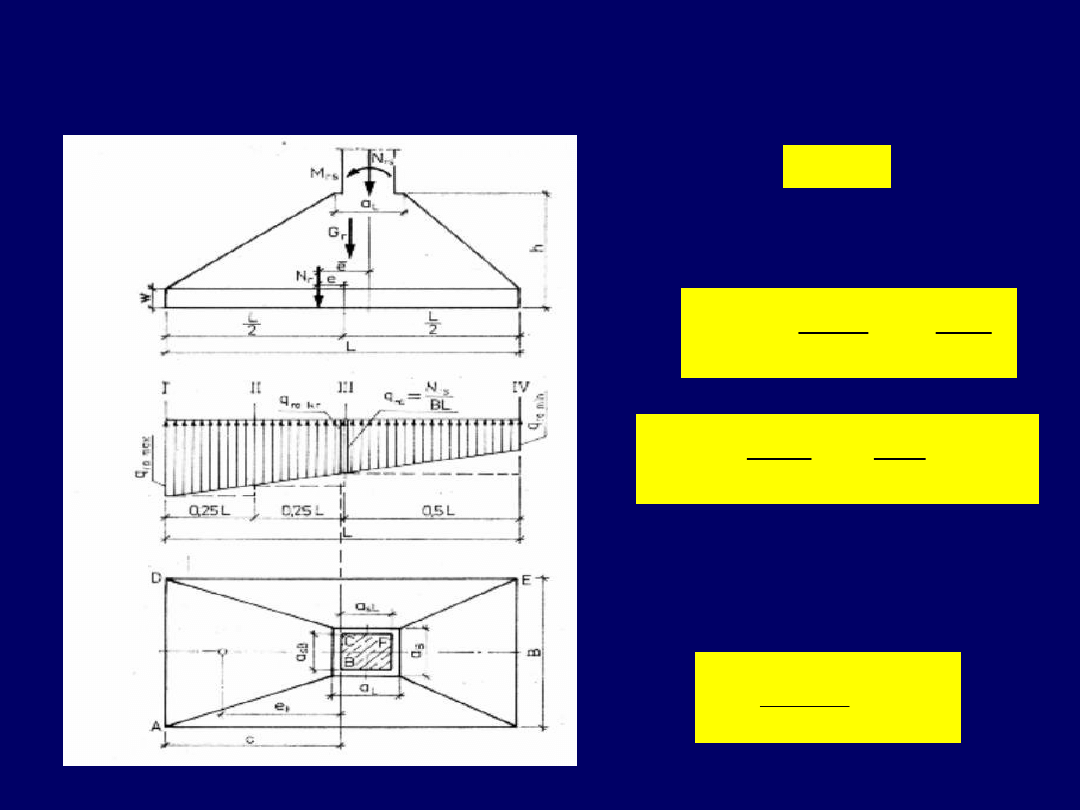
Rozkład naprężeń w stopie mimośrodowo obciążonej











 





L

e

L

B

N

q

L

r

r

6

1

min

,

f

L

r

r

mq

L

e

L

B

N

q













 





6

1

max

,

6

/

L

e

L



Jeżeli





sB

kr

r

r

a

B

c

q

M







2

6

2

,

Moment zginający wspornik trapezowy
ABCD

Naprężenia krawędziowe

39

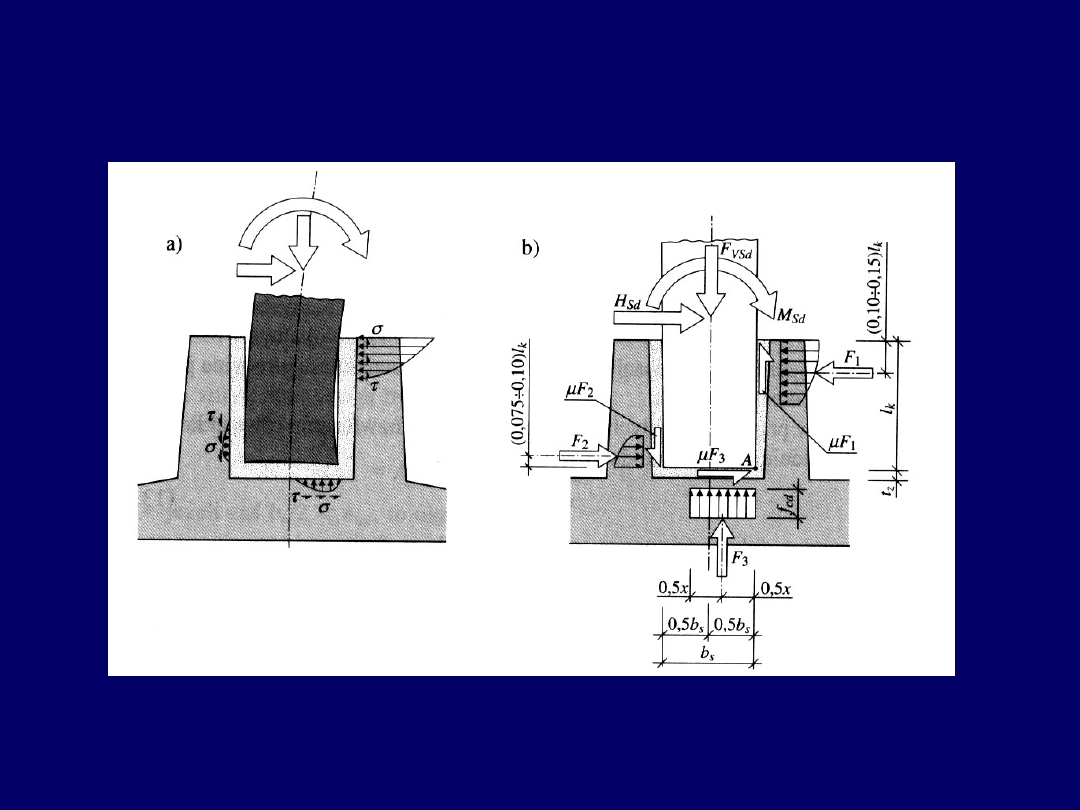
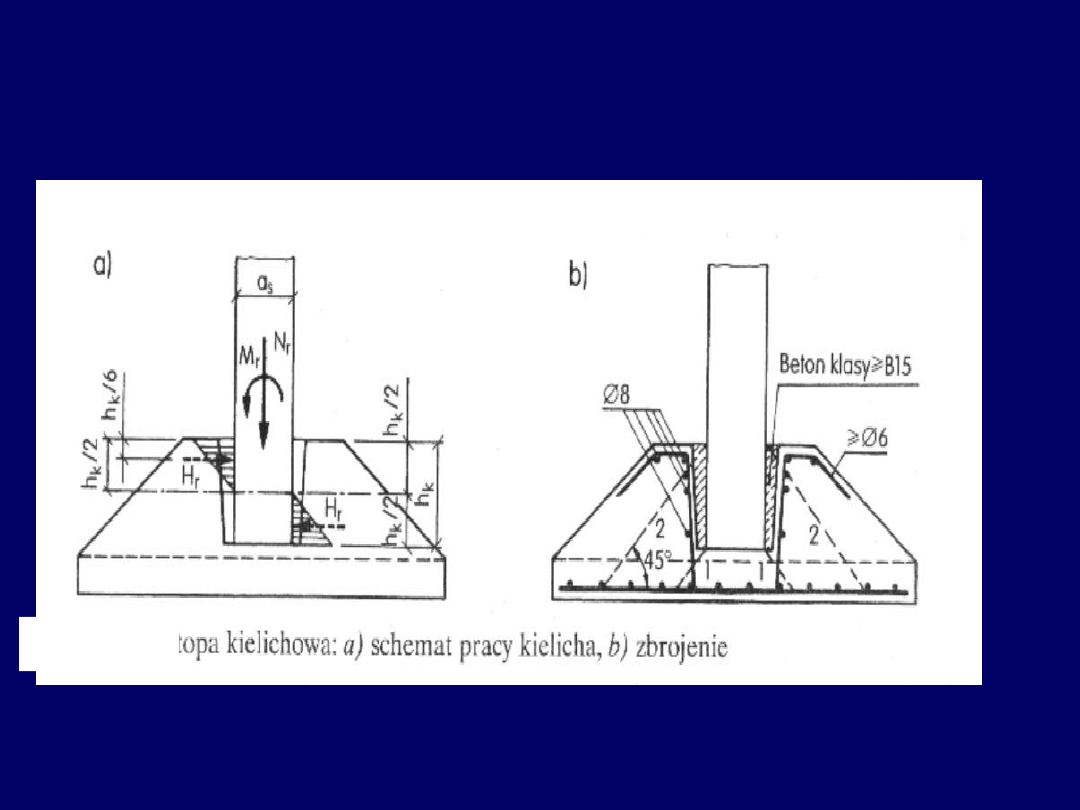
Stopy kielichowe

(pod słupy prefabrykowane)

Schemat obliczeniowy kielicha stopy

40

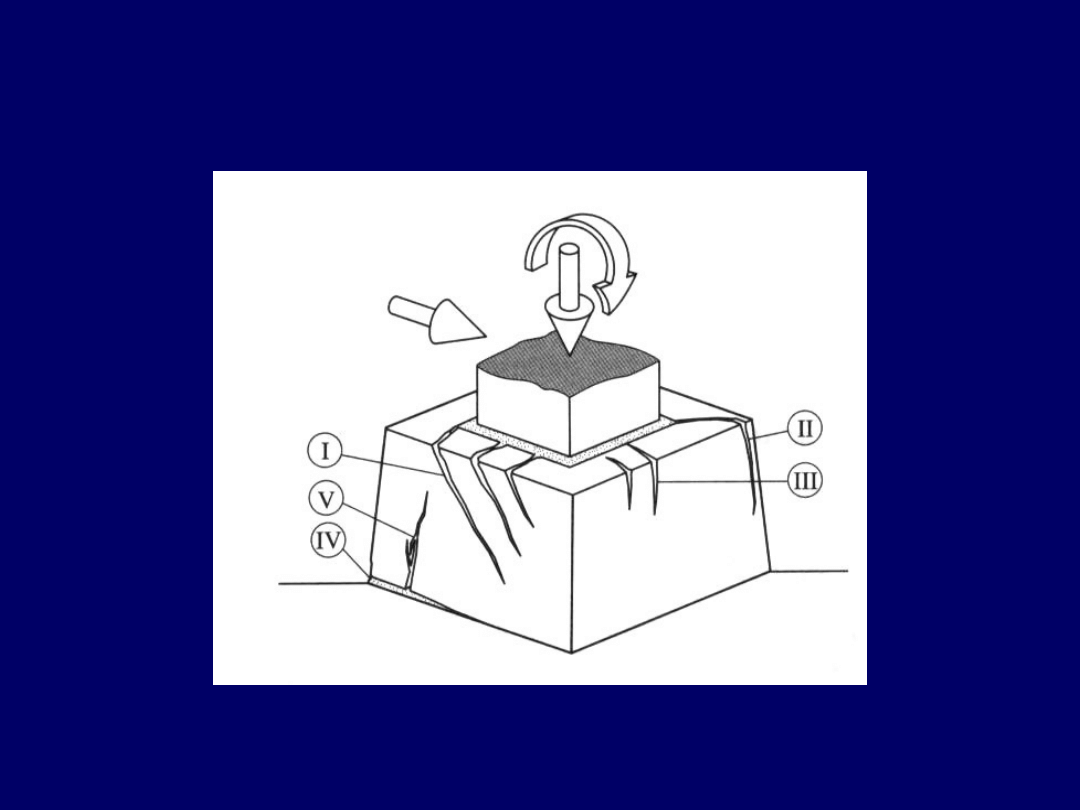
Stopy kielichowe

(pod słupy prefabrykowane)

Widok możliwych uszkodzeń kielicha stopy

41

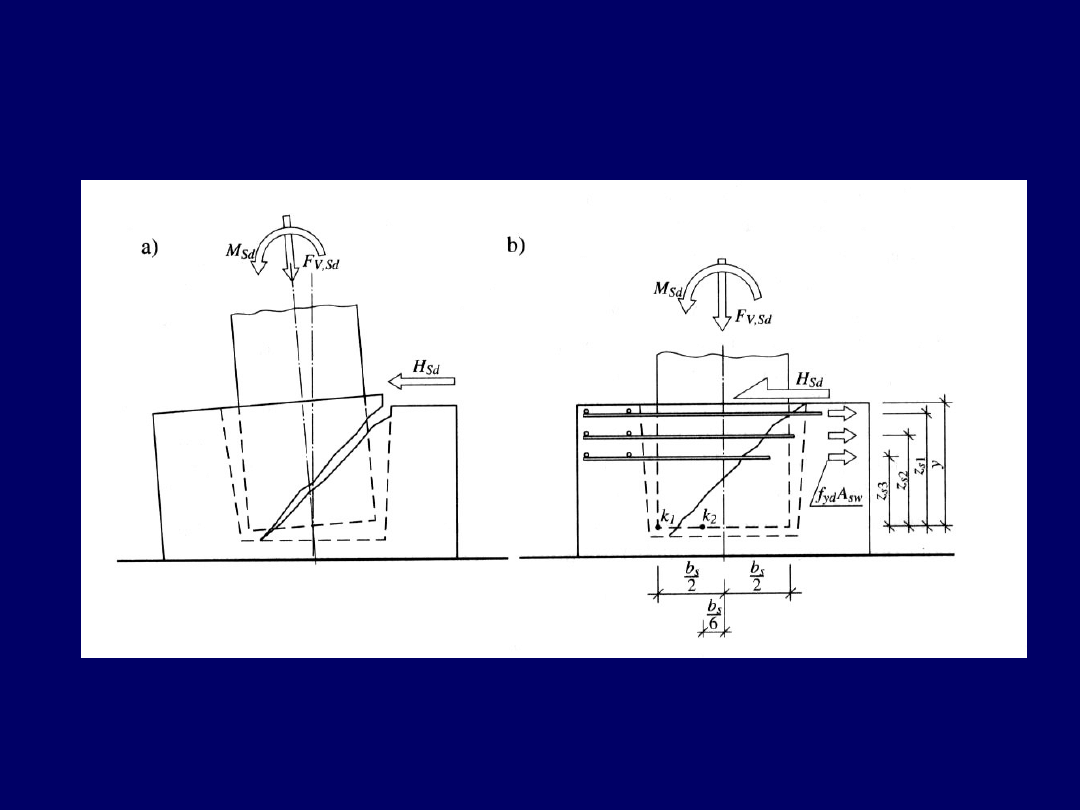
Stopy kielichowe

(pod słupy prefabrykowane)

Siły w strzemionach poziomych w kielichu: a) – obraz zniszczenia

b) – warunki równowagi sił w ściance kielicha

42

Stopy kielichowe

(pod słupy prefabrykowane)

Zasady obliczania zbrojenia pionowego w kielichu

0



tot

e

yd

ef

cc

cd

Sd

v

s

f

A

f

F

A

,

,

2

8

,

0





43

Stopy kielichowe

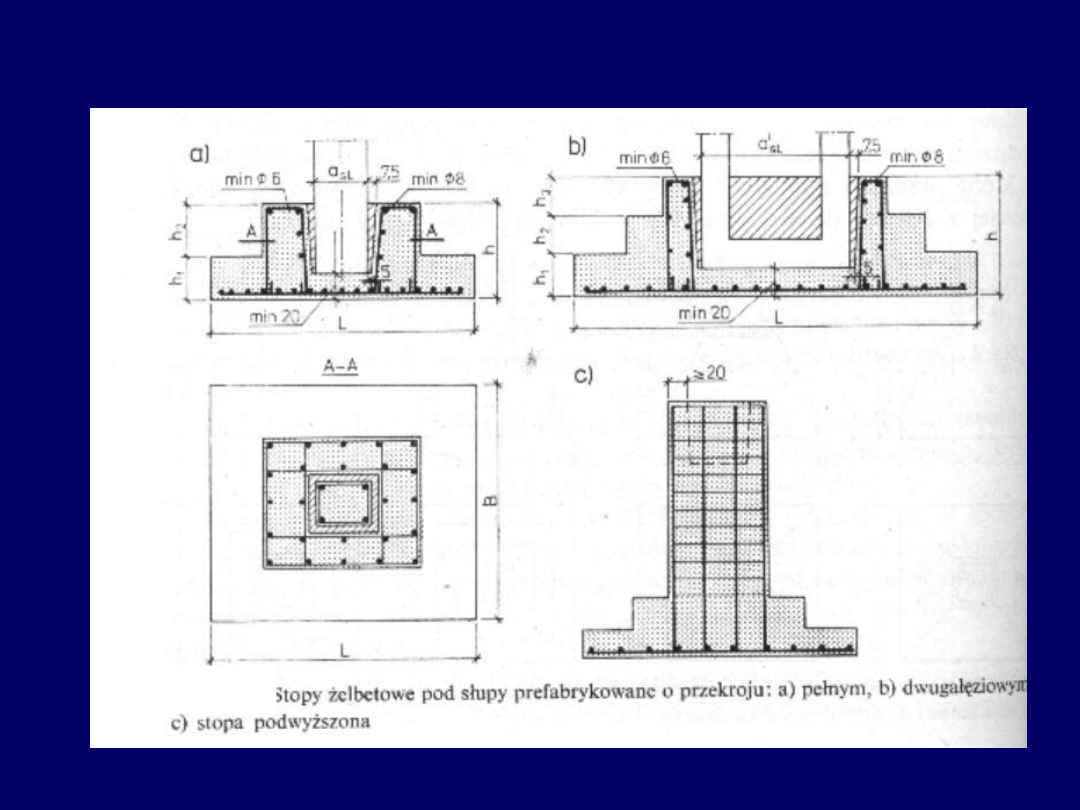
44

Stopy kielichowe prefabrykowane

45

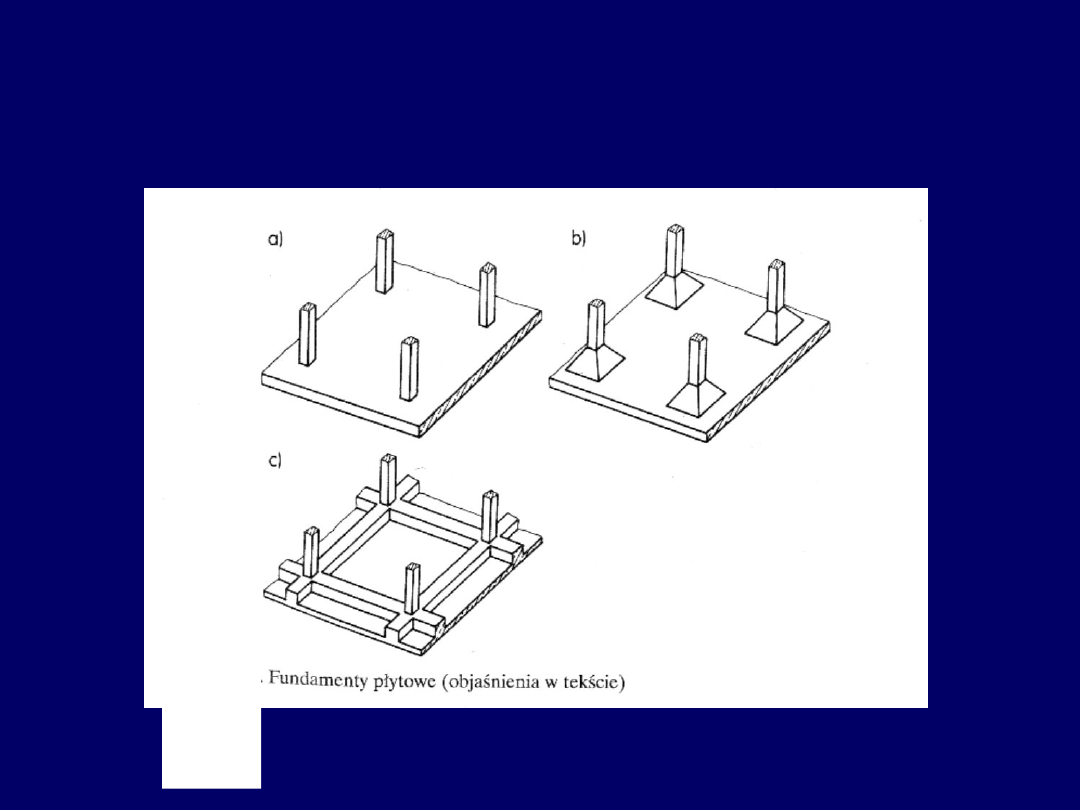
Płyty i ruszty fundamentowe

46

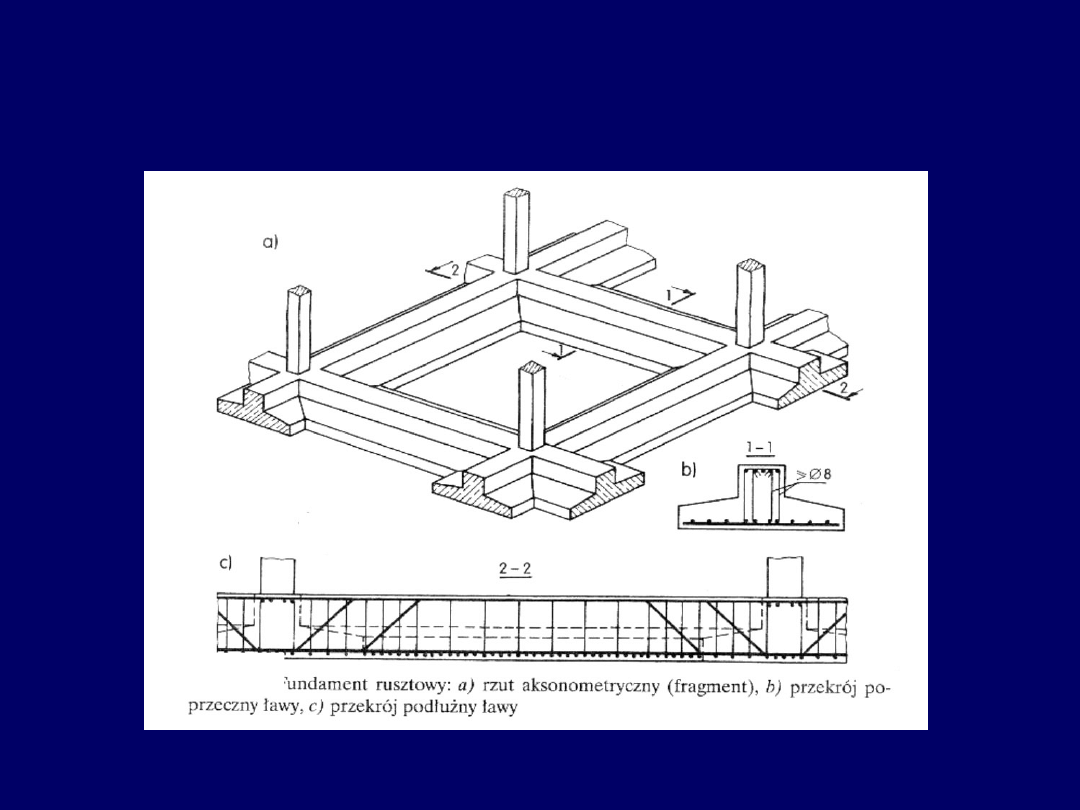
Ruszty fundamentowe

47

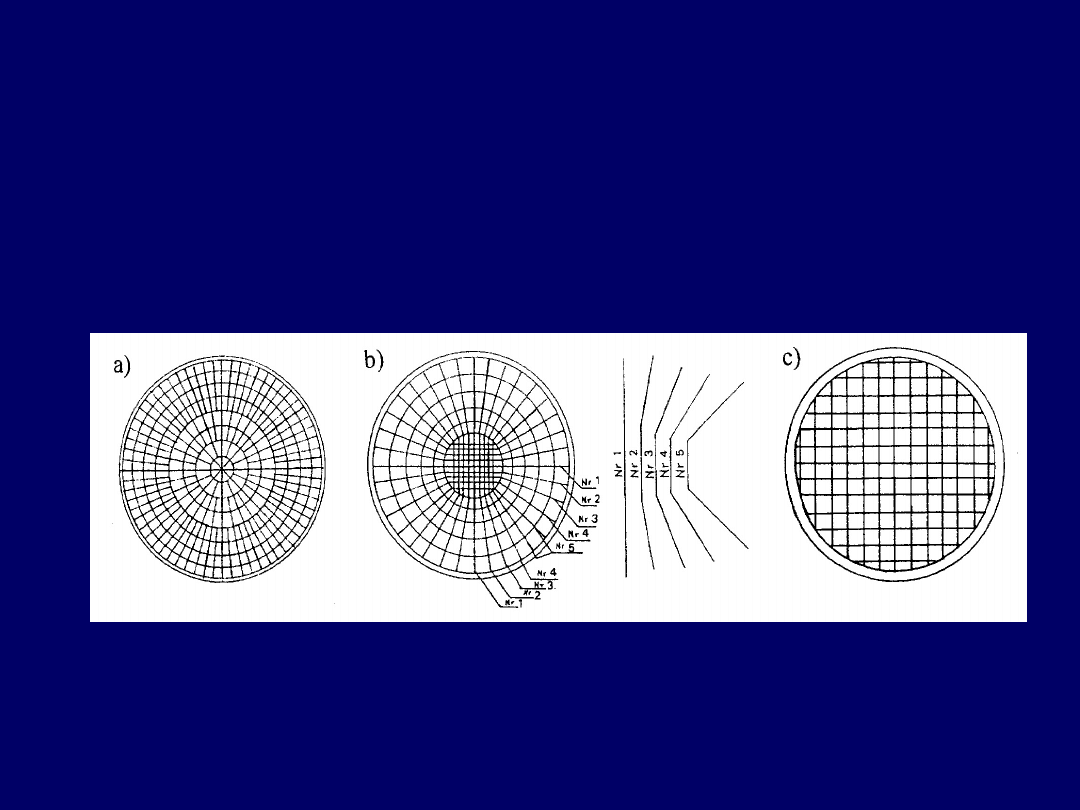
Fundamenty zbiorników

cylindrycznych

48

Koniec
wykładu