ZAWIESZENIA

ZAWIESZENIA

Projektowanie elementów sprężystych

Warszawa, 2007

Andrzej Reński

Elementy sprężyste

Stalowe:
- resory piórowe,
- sprężyny śrubowe,
- drążki skrętne

Naprężenia dopuszczalne

• gnące

• skręcające


gdzie:
• R

e

- granica plastyczności stali,

  - współczynnik bezpieczeństwa;  = 1,05...1,10;
• K

b

 ‑ współczynnik obniżenia naprężeń dopuszczalnych; Kb =

1, gdy grubość h lub średnica d materiału jest mniejsza od

10 mm;

dla większych wymiarów
K

b

= 1,07 - 0,0077 d + 0,000055 d

2







b

e

dop

g

K

R

2

,

1







b

e

dop

s

K

R

63

,

0

• Dopuszczalne naprężenia skrętne przy obciążeniu

oscylacyjnym







b

m

a

dop

s

K

R

24

,

0

gdzie: R

m

- wytrzymałość na

rozciąganie

Resory piórowe

zalety:

• łatwość wykonania,

• zdolność przenoszenia nie tylko sił pionowych, ale także

wzdłużnych i poprzecznych oraz momentu reakcyjnego

od sił napędowych lub hamujących,

• możliwość korzystnego wprowadzenie sił w ramę lub w

nadwozie samochodu.

wady:

• duża masa, w znacznej części wchodząca w skład tzw.

masy nieresorowanej.

• duże tarcie między piórami.

• przyśpieszone na skutek tarcia zużycie powierzchni,

wynikające stąd miejsca koncentracji naprężeń i w

efekcie obniżona trwałość.

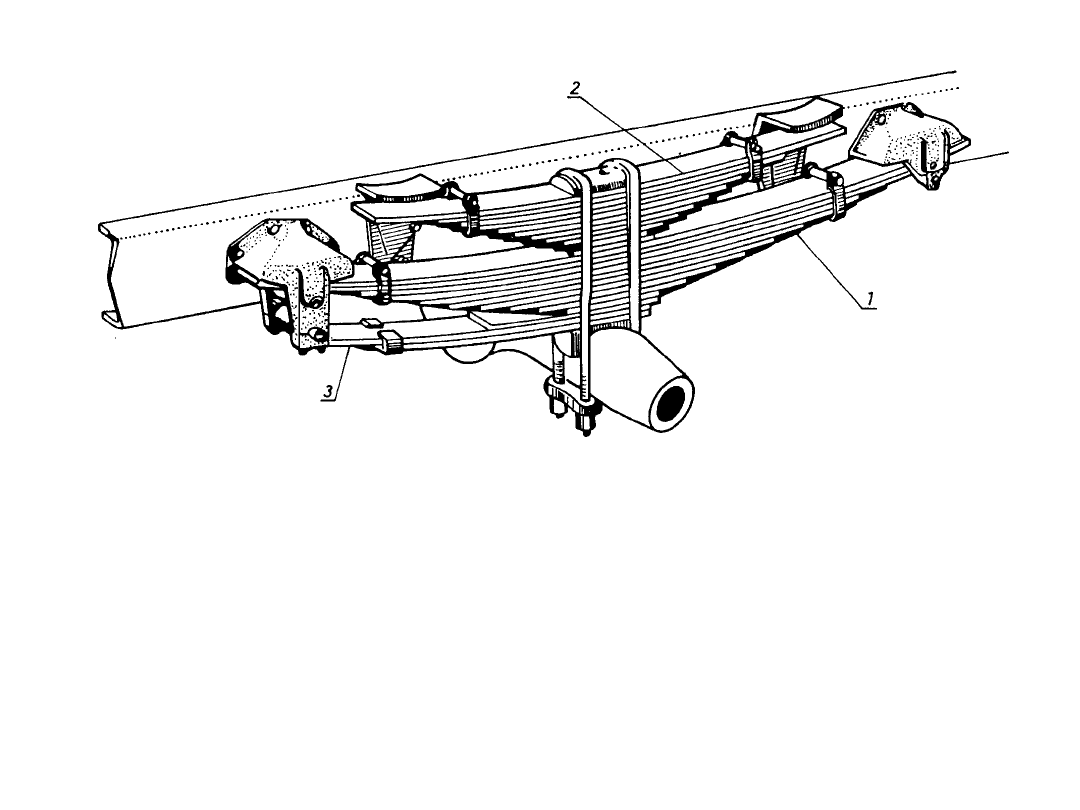
Zawieszenie zależne samochodu ciężarowego: 1 – resor
główny, 2 – resor pomocniczy (umożliwia uzyskanie
charakterystyki progresywnej, 3 – dodatkowe pióro do
przejmowania momentu reakcyjnego

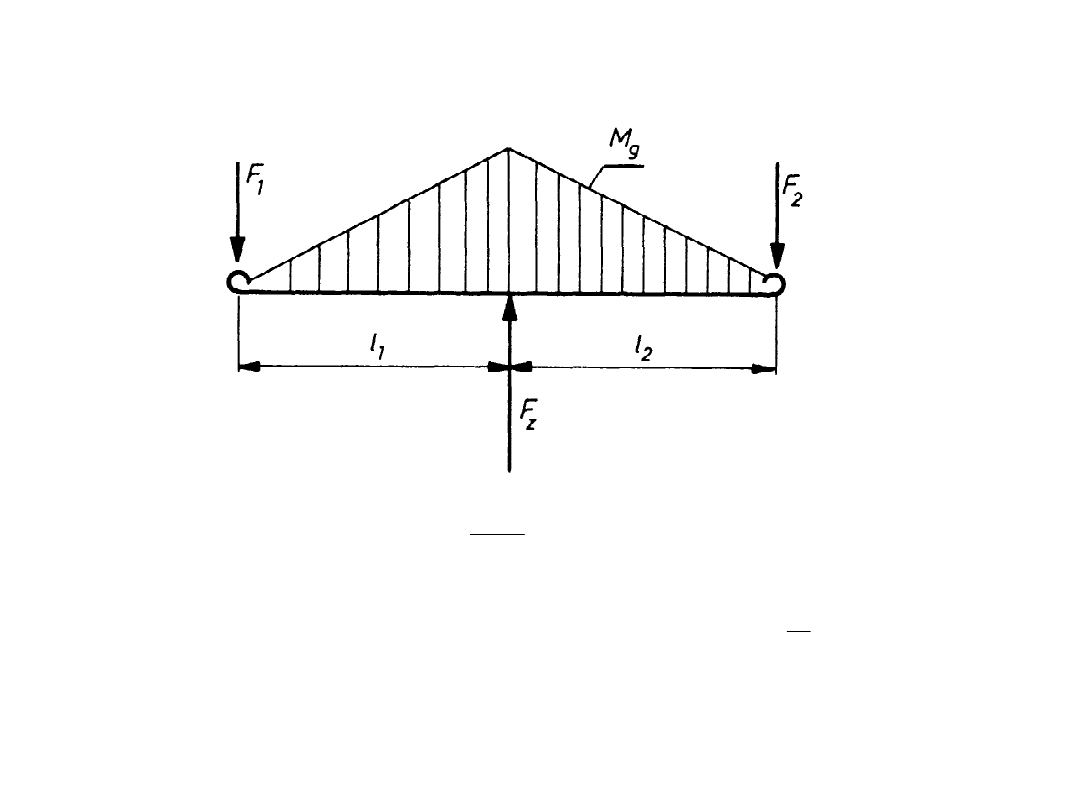
Rozkład momentu gnącego wzdłuż resoru

y

g

g

W

M





2

y

h

b

6

1

W 

b - szerokość belki,
h - grubość belki,

Naprężenia
gnące:

wskaźnik wytrzymałości na
zginanie:

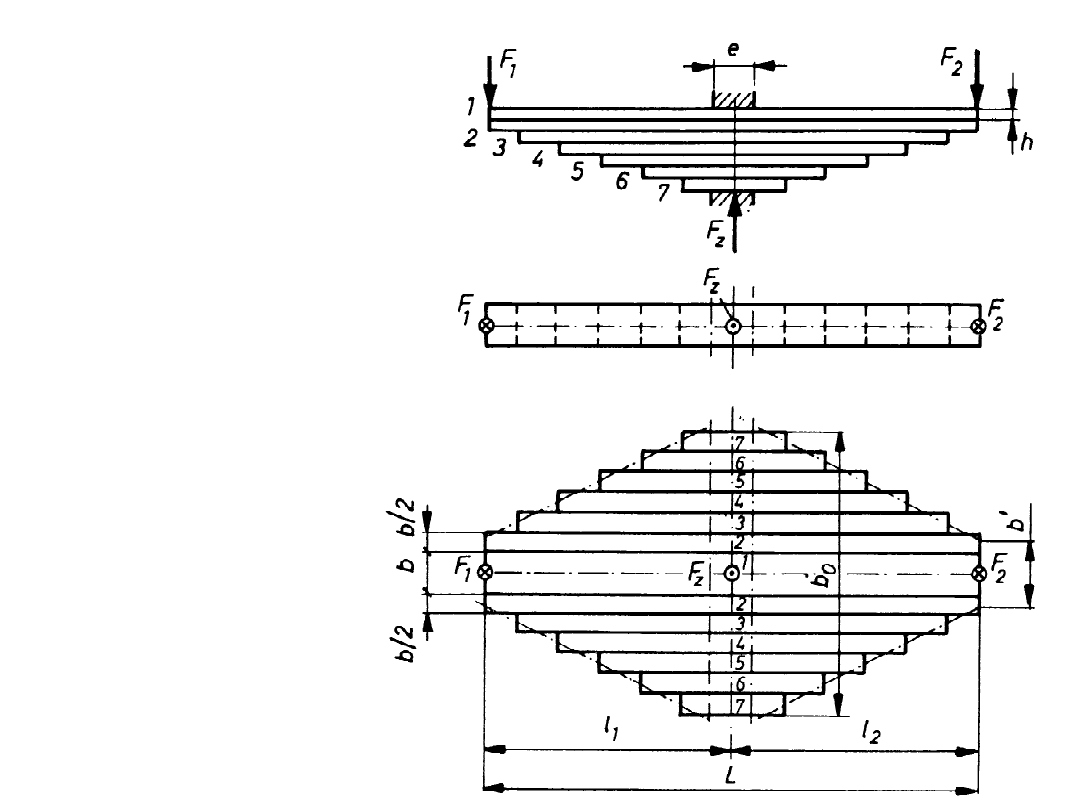
Resor trapezowy

Resor trapezowy
powstały w wyniku
pocięcia na paski
belki o stałej
grubości i
wyrównanych
naprężeniach
gnących

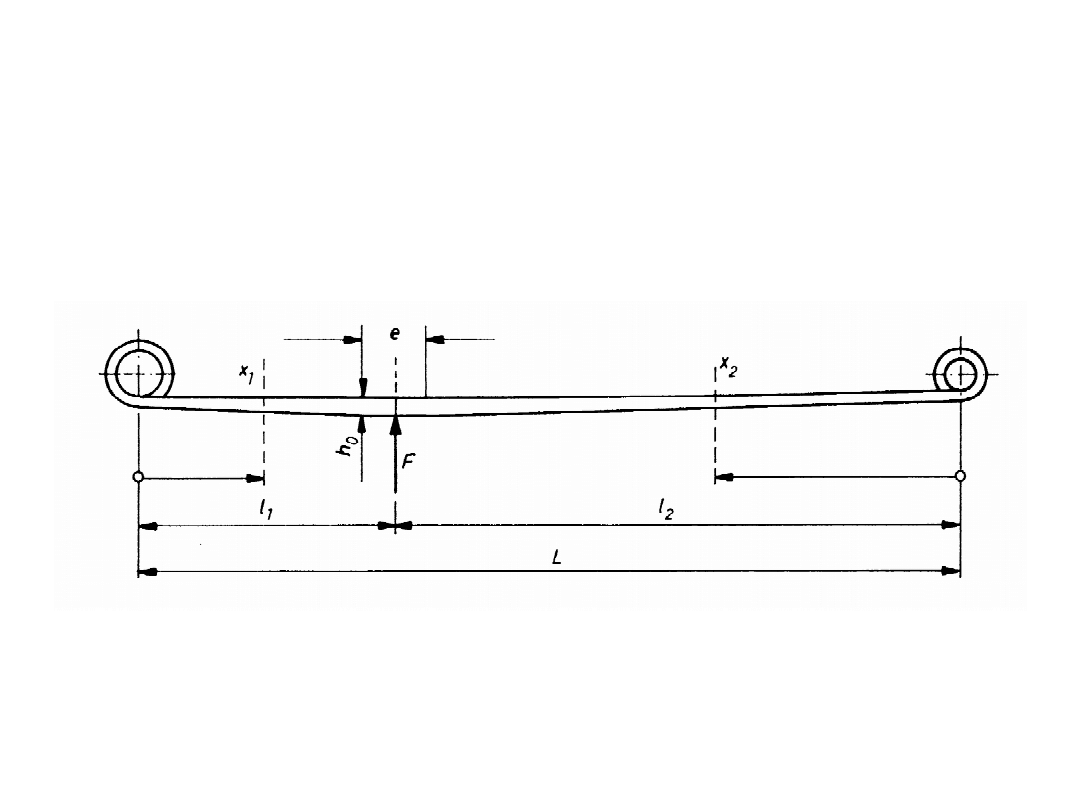
Resor paraboliczny

Resor trapezowy

Średnia obliczeniowa grubość pióra:

gdzie:
• g

1

= l

1

- e/4, g

2

= l

2

- e/4 - efektywne długości

pracujących części resoru,

• k – sztywność resoru
• σ

v

- wstępne naprężenia gnące,

• E - moduł sprężystości (Younga), dla stali E = 2110

4

MPa,

 

0,1

- współczynnik kształtu:



0

= 2,38; 

1

= 2 + n'/n

n - całkowita liczba piór, n' - liczba piór głównych

1

,

0

st

v

2

1

0

E

F

k

g

g

2

h







Resor trapezowy

Wstępne naprężenia gnące σ

v

• na podstawie siły F

max

przy maksymalnym ugięciu

resoru

• na podstawie jednostkowego naprężenia

dopuszczalnego σ*

g dop

(naprężenia przypadającego

na 1 mm ugięcia resoru) przy obciążeniu trwałym
siłą F

st

max

st

dop

g

v

F

F



 

k

F

st

*

dop

g

v



 

σ*

g dop

=

6 MPa/mm - dla resorów parabolicznych,
5,5 MPa/mm - dla resorów trapezowych samochodów osobowych,
5 MPa/mm - dla resorów trapezowych samochodów ciężarowych z
piórami o powierzchniach ulepszonych przez kulkowanie,
4 MPa/mm - dla resorów trapezowych samochodów ciężarowych z
piórami o powierzchniach nieulepszonych.

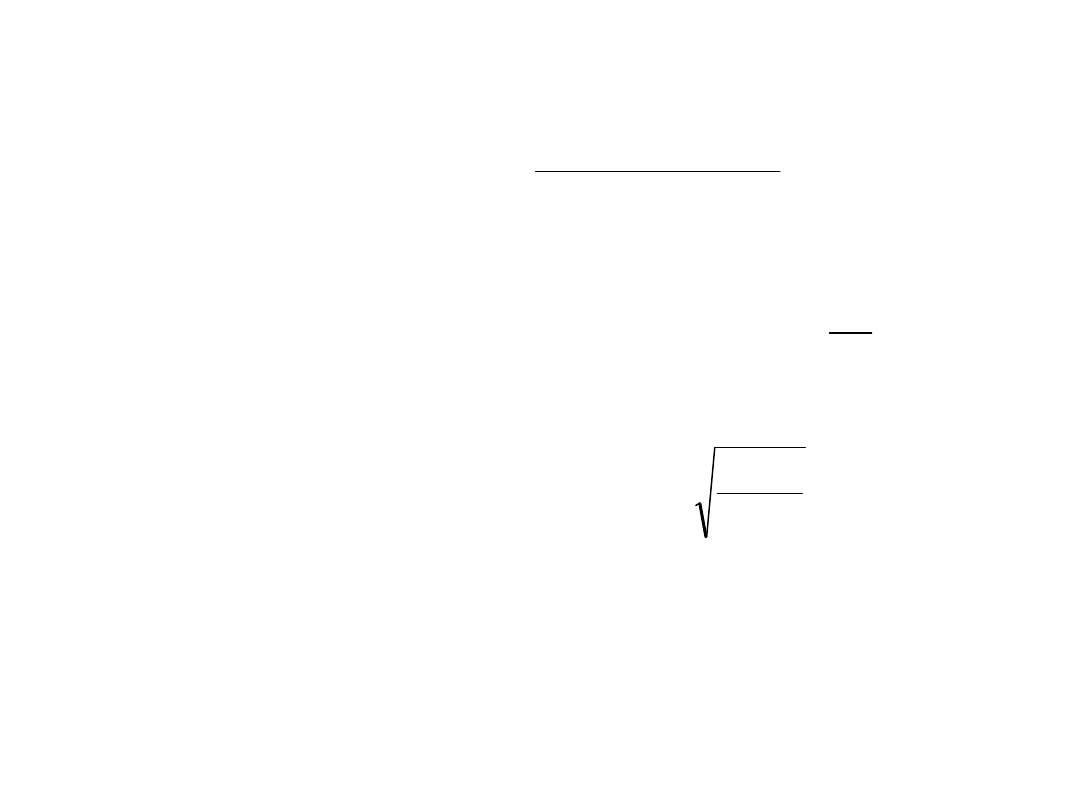
Resor trapezowy

wstępna liczba piór

rzeczywiste grubości piór resoru:

dla piór o jednakowej grubości:

v

2

0

2

1

2

1

max

0

h

b

)

g

g

(

g

g

F

6

n











1

0

3

0

0

3

h

n

h





3

1

0

0

0

n

n

h

h







• ostateczna sztywność resoru

• naprężenia gnące

Resor trapezowy

2

2

2

1

3

2

1

1

g

g

12

h

)

g

g

(

b

E

k















2

2

1

2

1

max

g

h

b

)

g

g

(

g

g

F

6



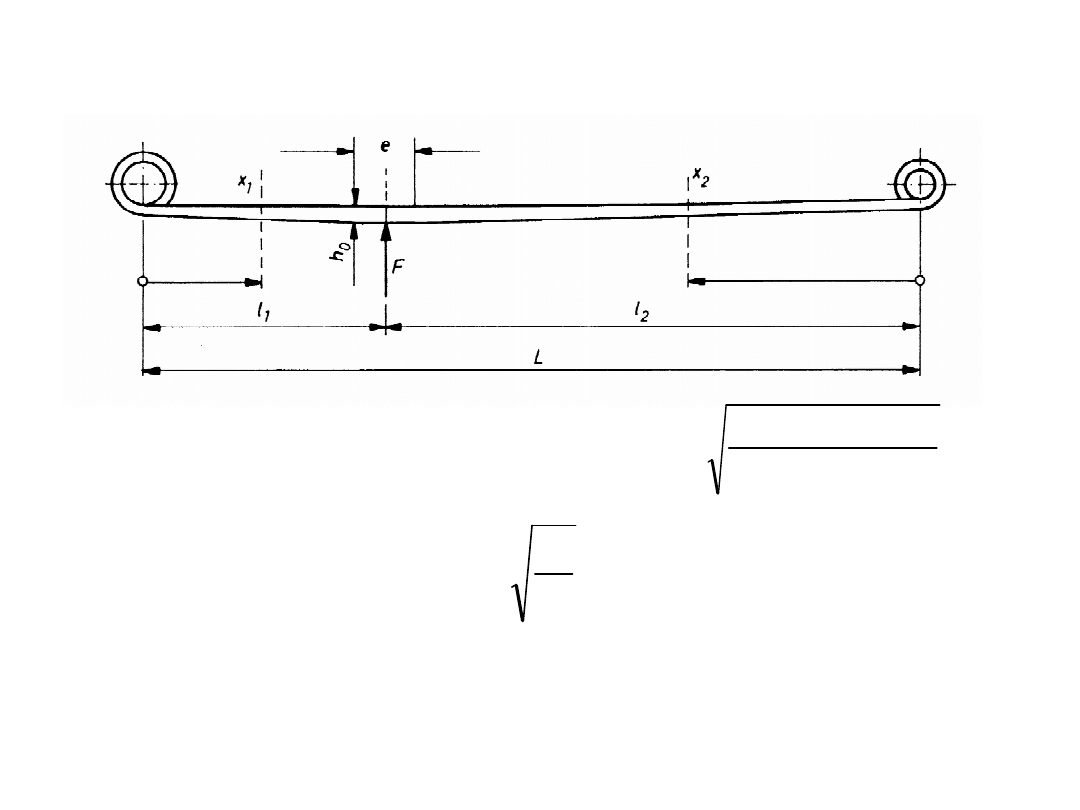
Resor paraboliczny

• nominalna grubość resoru:

• grubość pióra:





2

1

dop

g

2

1

max

0

g

g

b

g

g

F

6

h







1

1

0

1

x

g

x

h

h 

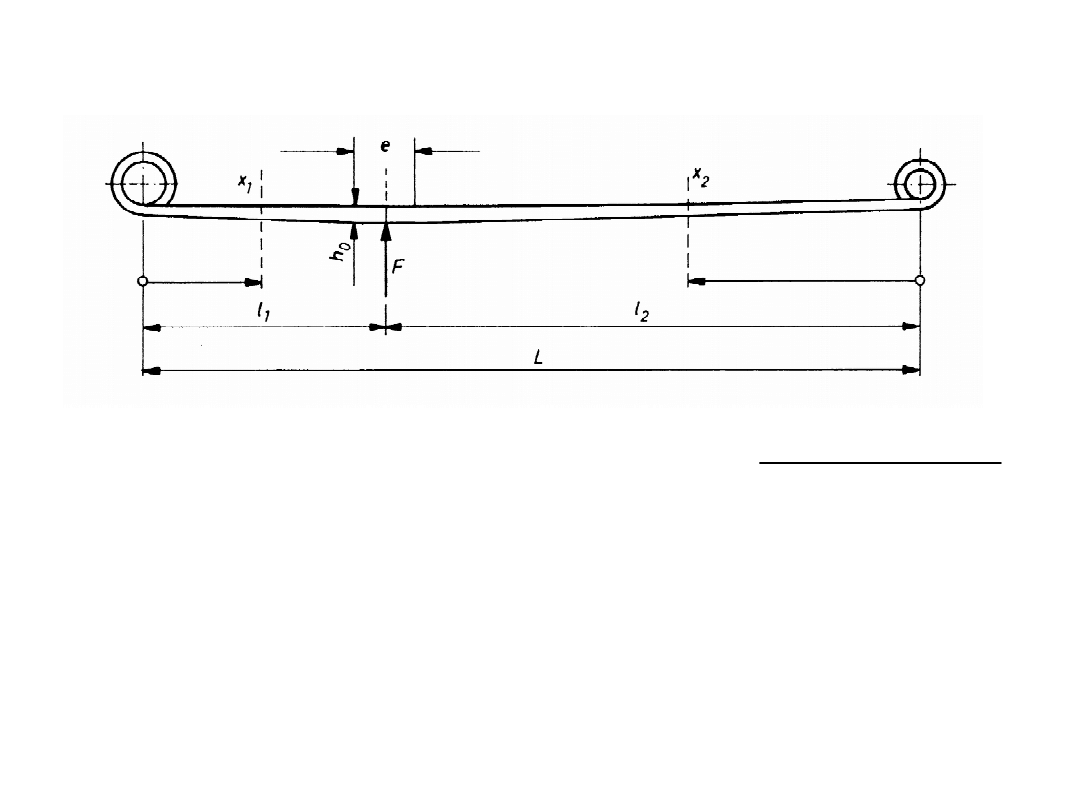
Resor paraboliczny

• Sztywność pionowa resoru

κ = 0,9

.



2

2

2

1

2

1

3

0

g

g

8

)

g

g

(

h

b

E

k





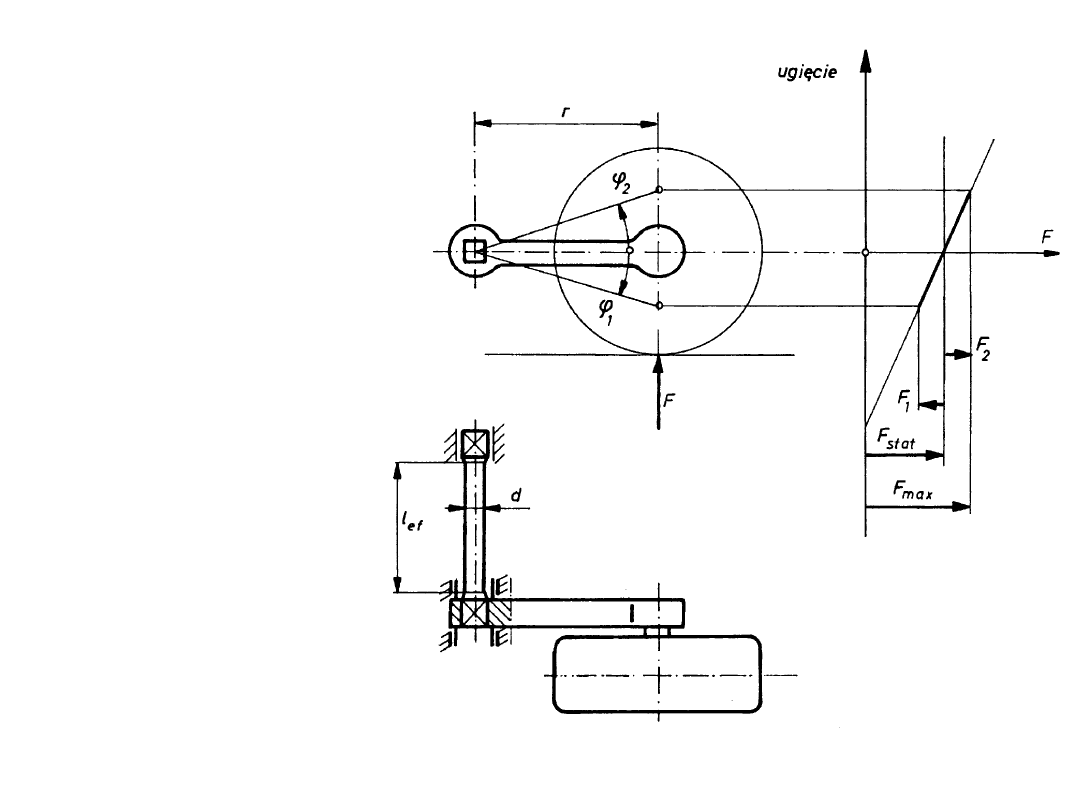
Drążki skrętne

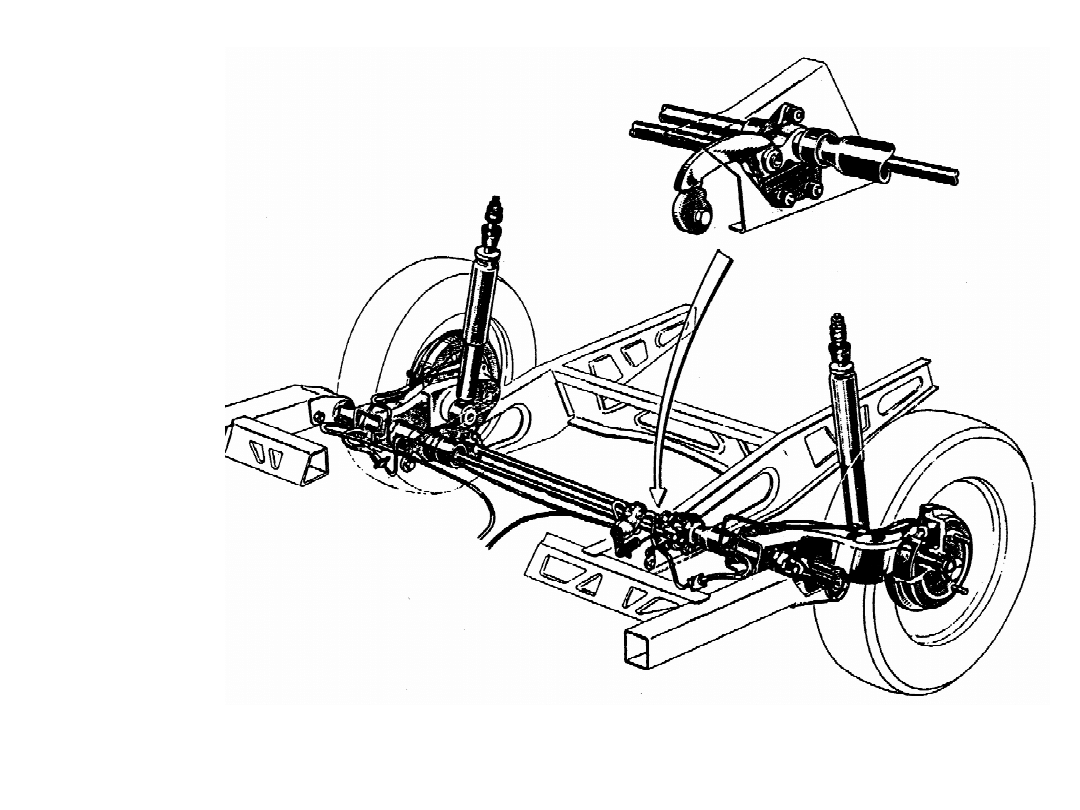
Drążki skrętne

Zawieszenie tylne Renault 5

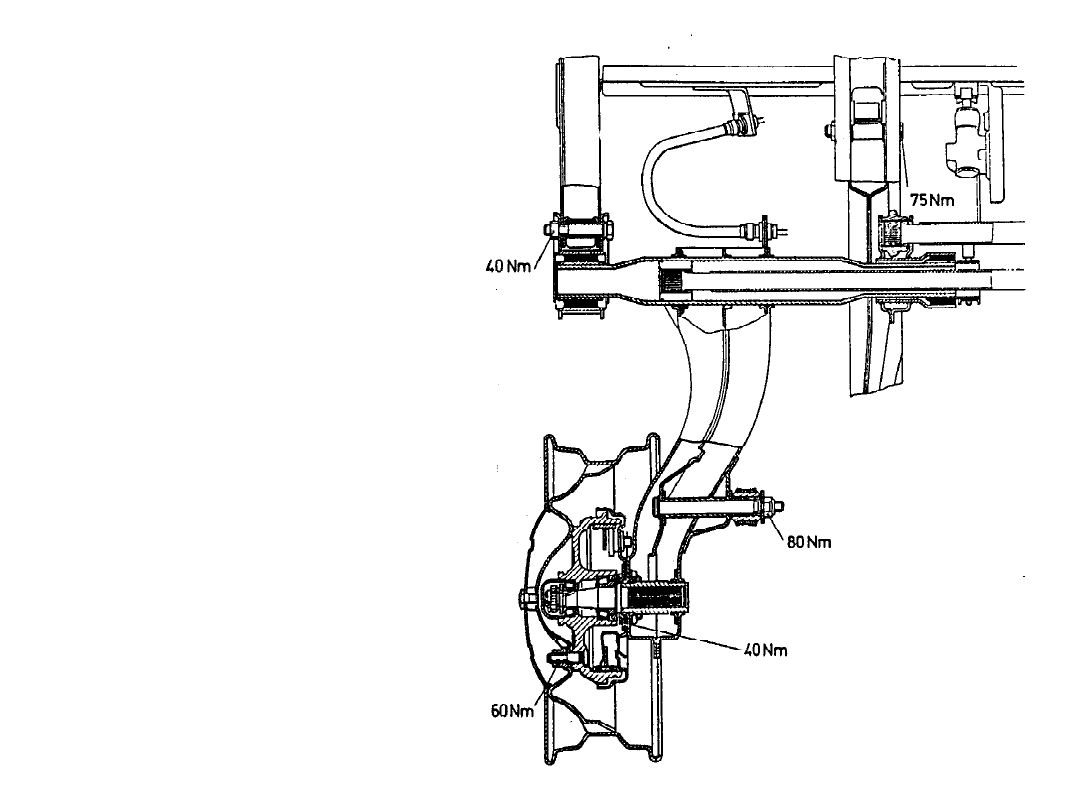
Drążki skrętne

Zawieszenie tylne
Renault 5

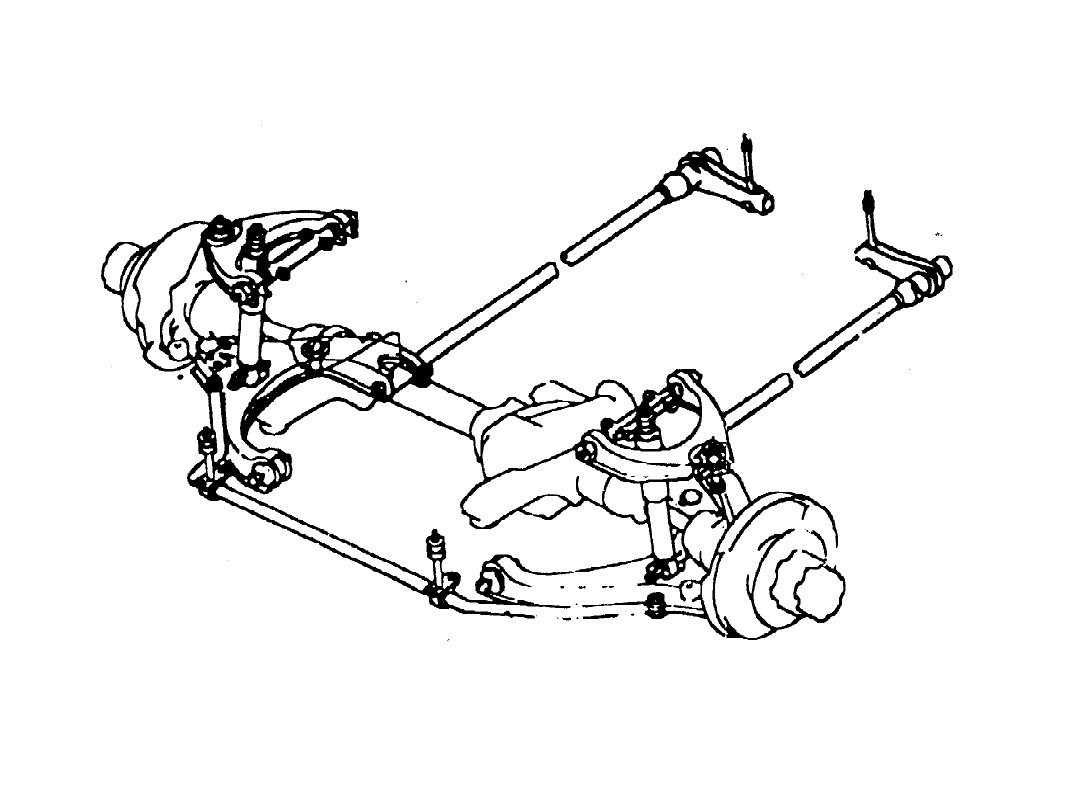
Drążki skrętne

Zawieszenie przednie Mitshubishi Pajero

Drążki skrętne

Zmiany obciążenia zawieszenia F

1

i F

2

w stosunku do obciążenia

statycznego F

st

F

1

= k

z

r φ

1

, F

2

= k

z

r φ

2

Maksymalna siła w zawieszeniu: F

max

= F

st

+ F

2

Obliczeniowa amplituda sił oscylacyjnych:

Minimalną średnicę drążka skrętnego

- z warunku wytrzymałości doraźnej

- z warunku wytrzymałości zmęczeniowej

2

F

F

9

,

0

F

2

1

a





3

dop

s

max

min

r

F

16

d







3

a

dop

s

a

min

r

F

16

d







Drążki skrętne

•

Sztywność skrętna drążka

gdzie:
G - moduł sprężystości postaciowej (dla stali sprężynowych G = 8104

MPa),

- geometryczny moment bezwładności

•

Efektywna długość drążka

związek między sztywnością zawieszenia k

z

a sztywnością skrętną drążka k

skr

k

skr

= k

z

r

2

ef

0

skr

skr

l

J

G

M

k







32

d

J

4

0





2

z

4

ef

r

k

32

d

G

l





Sprężyny śrubowe

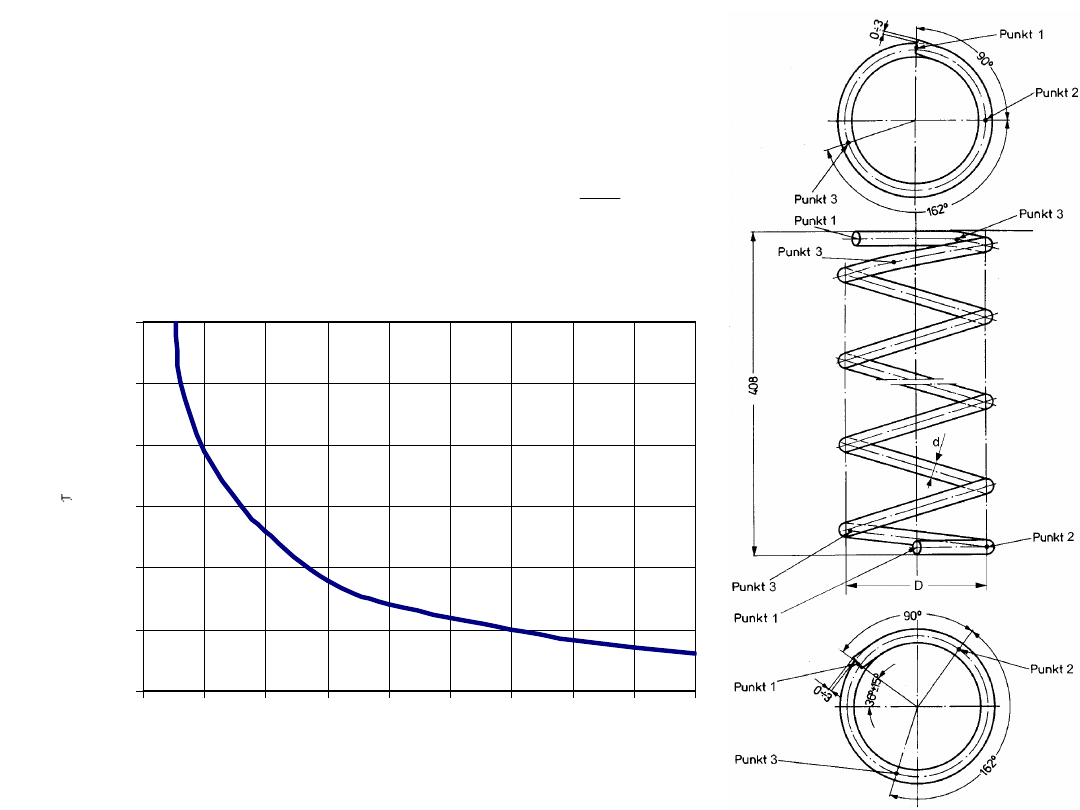
Sprężyny śrubowe

• Naprężenia dopuszczalne

dop

s

'

dop

s

1











1

1,1

1,2

1,3

1,4

1,5

1,6

2

4

6

8

10

12

14

16

18

20

D/d



Sprężyny śrubowe

• Skoki sprężyny liczone od ugięcia statycznego

przy maksymalnym obciążeniu:

f

s1

= f

1

i

ż

przy maksymalnym odciążeniu: f

s2

= f

2

i

ż

• Maksymalne obciążenie sprężyny: F

max

= F

st

/i

z

+ k

s

f

s1

• Obliczeniowa amplituda obciążeń oscylacyjnych:

2

f

f

k

9

,

0

F

2

s

1

s

s

a





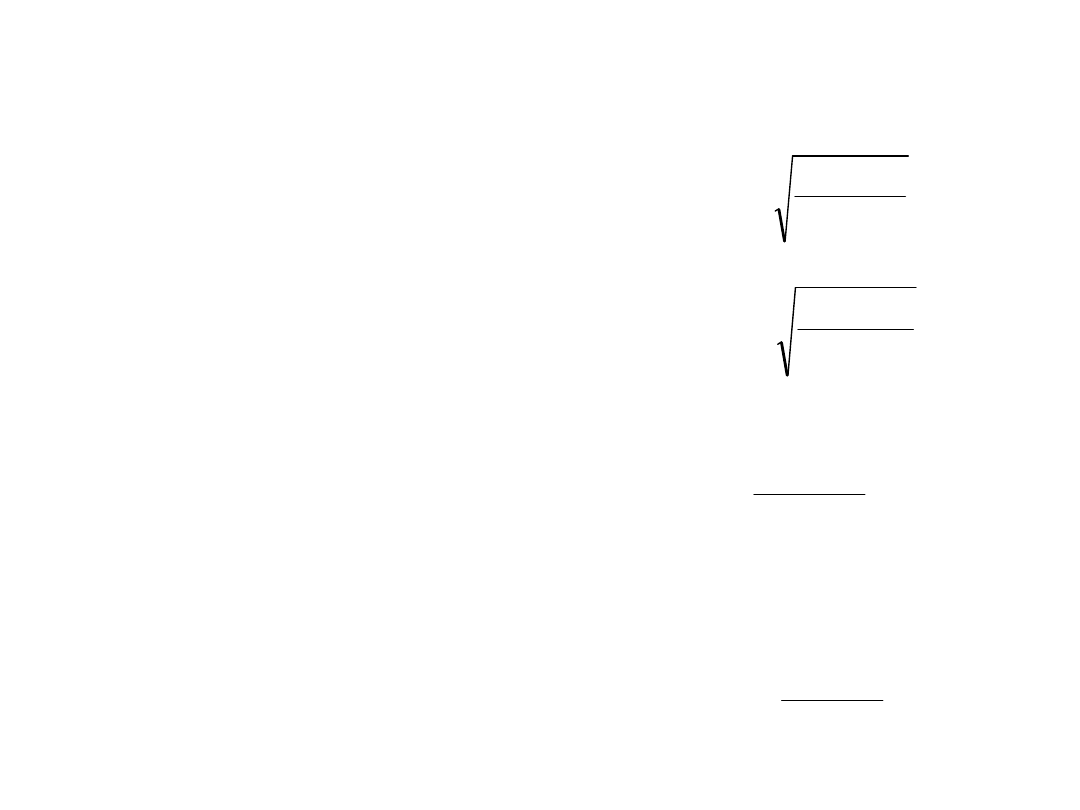
Sprężyny śrubowe

•

Minimalna średnica drutu

sprężyny

z warunku zabezpieczenia przed

powstaniem trwałych odkształceń

plastycznych

z warunku wytrzymałości zmęczeniowej

•

Liczba czynnych zwojów sprężyny

•

Całkowitą liczbę zwoi

n

t

= n + 1,5

•

Sztywność sprężyny

3

dop

s

max

min

'

F

D

8

d







3

a

dop

s

a

min

F

D

8

d







s

3

4

k

D

8

d

G

n 

n

D

8

d

G

k

3

4

s



Sprężyny
śrubowe

walcowa

stożkowa

baryłkow
a

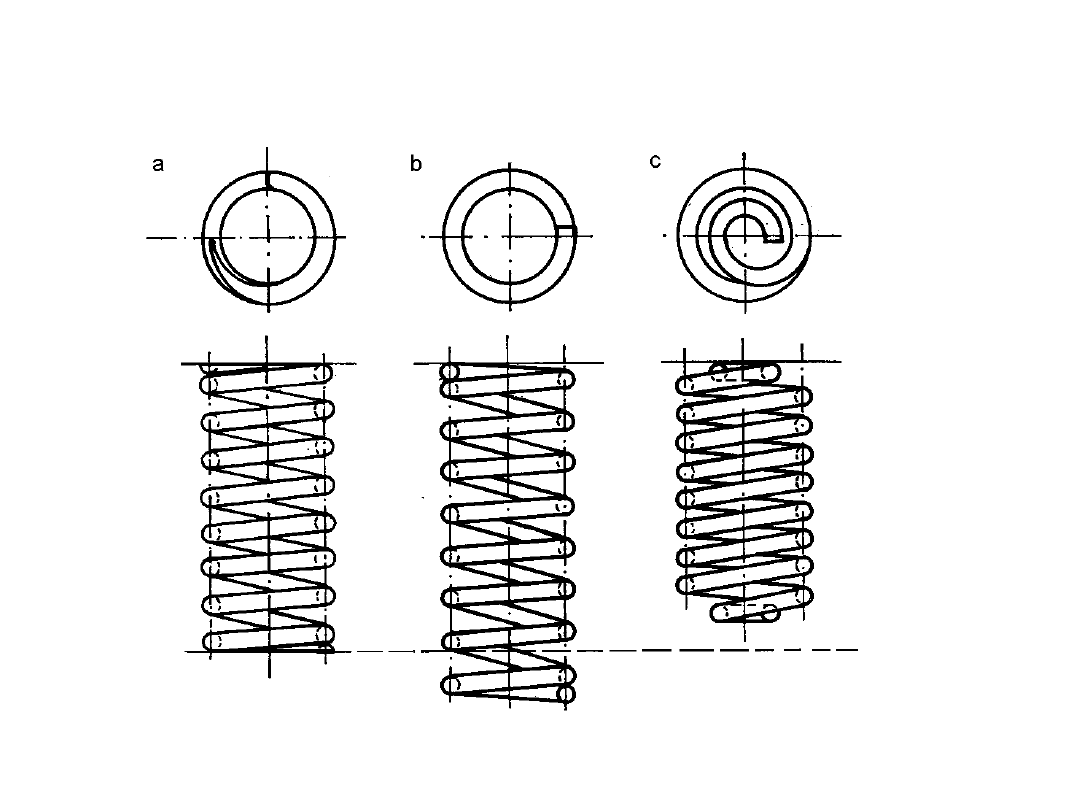
Sprężyny śrubowe

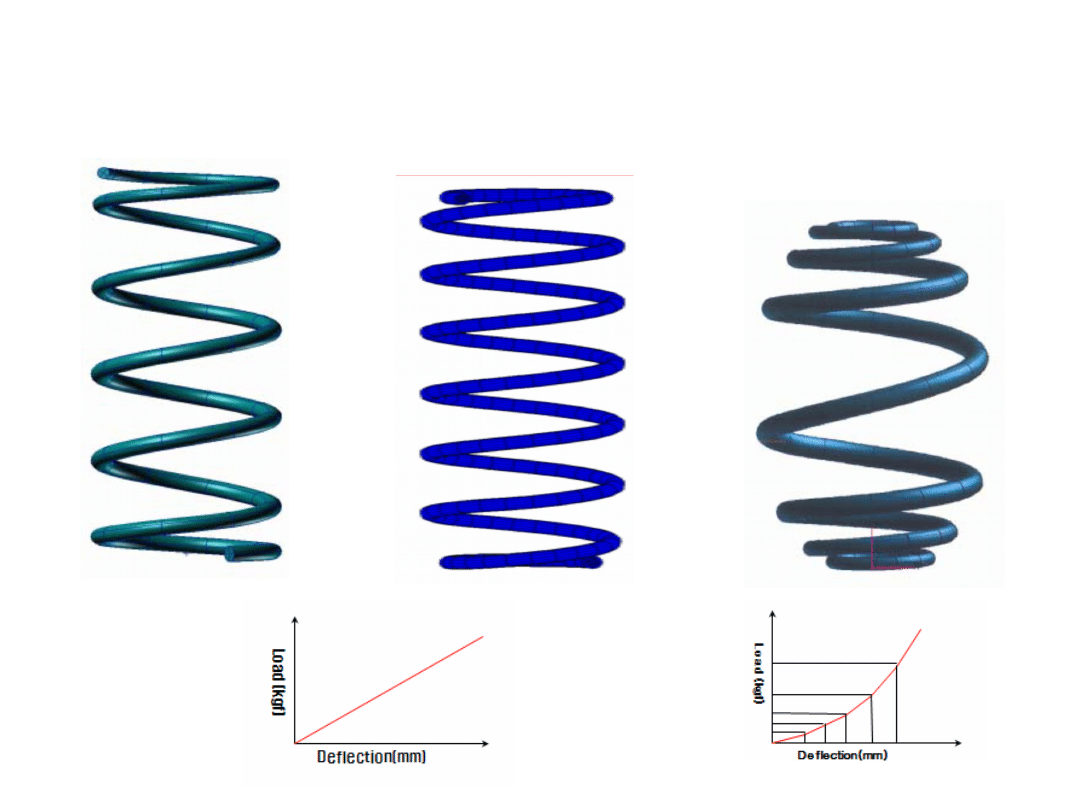
Sprężyny śrubowe

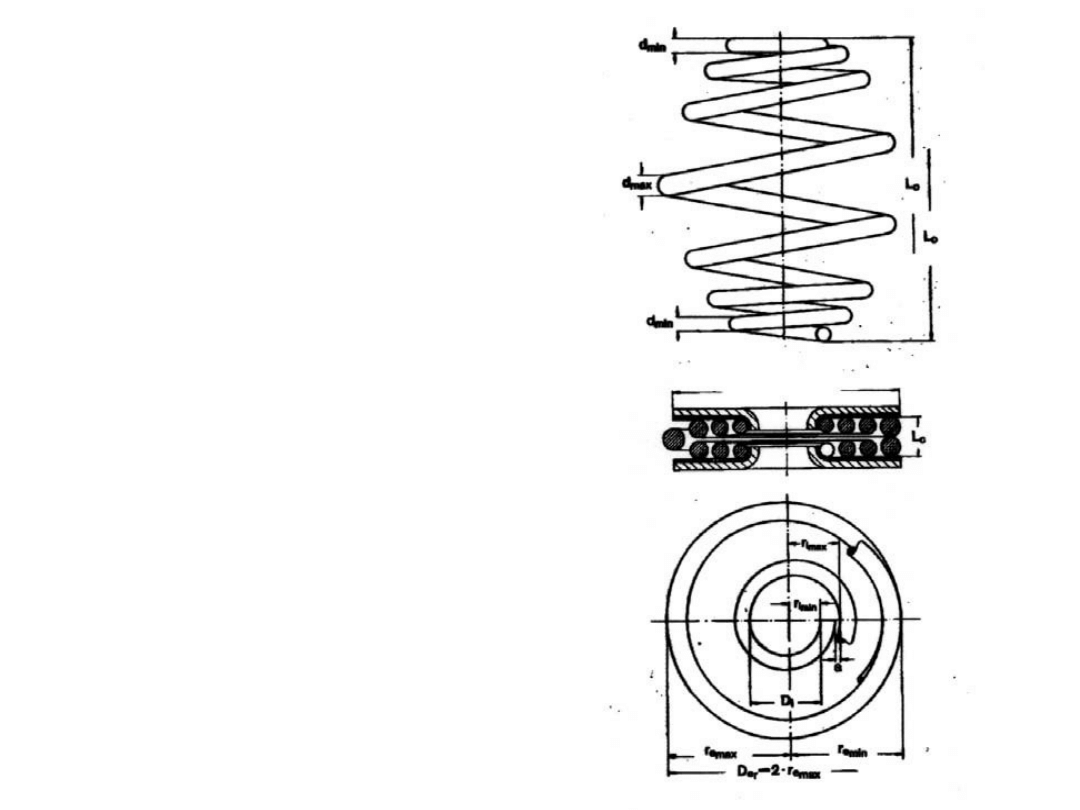
Sprężyna baryłkowa

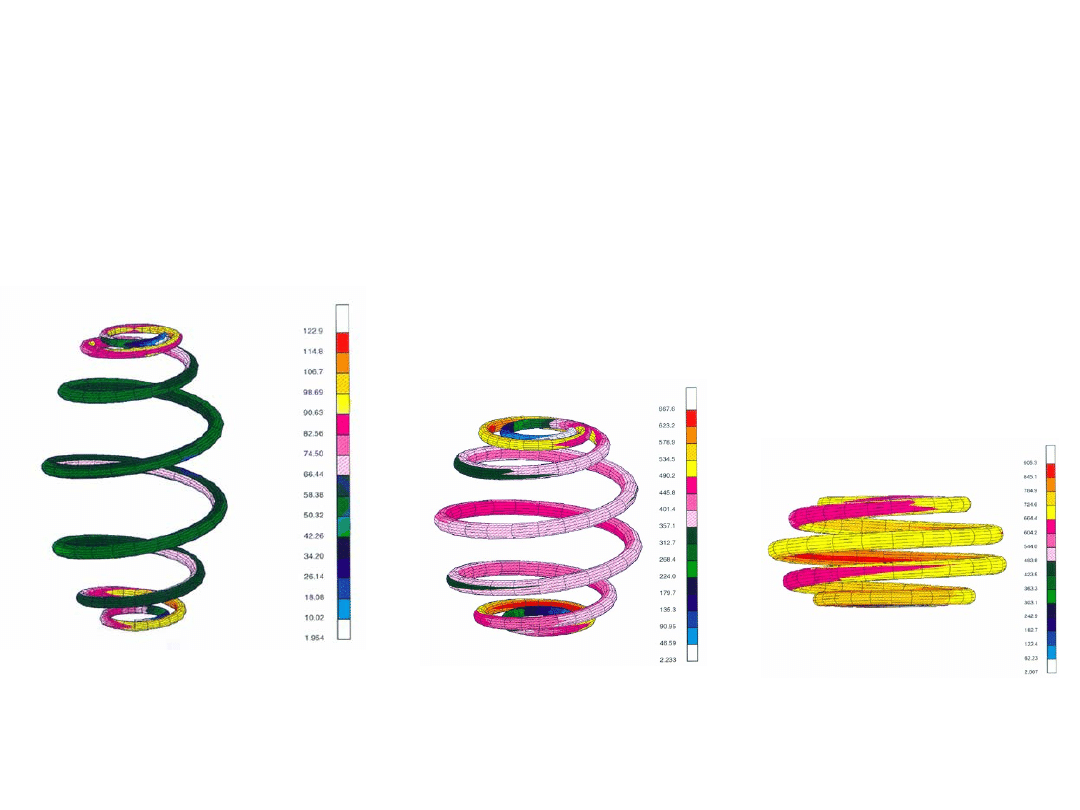
Sprężyna baryłkowa

Sprężyna typu „side load”

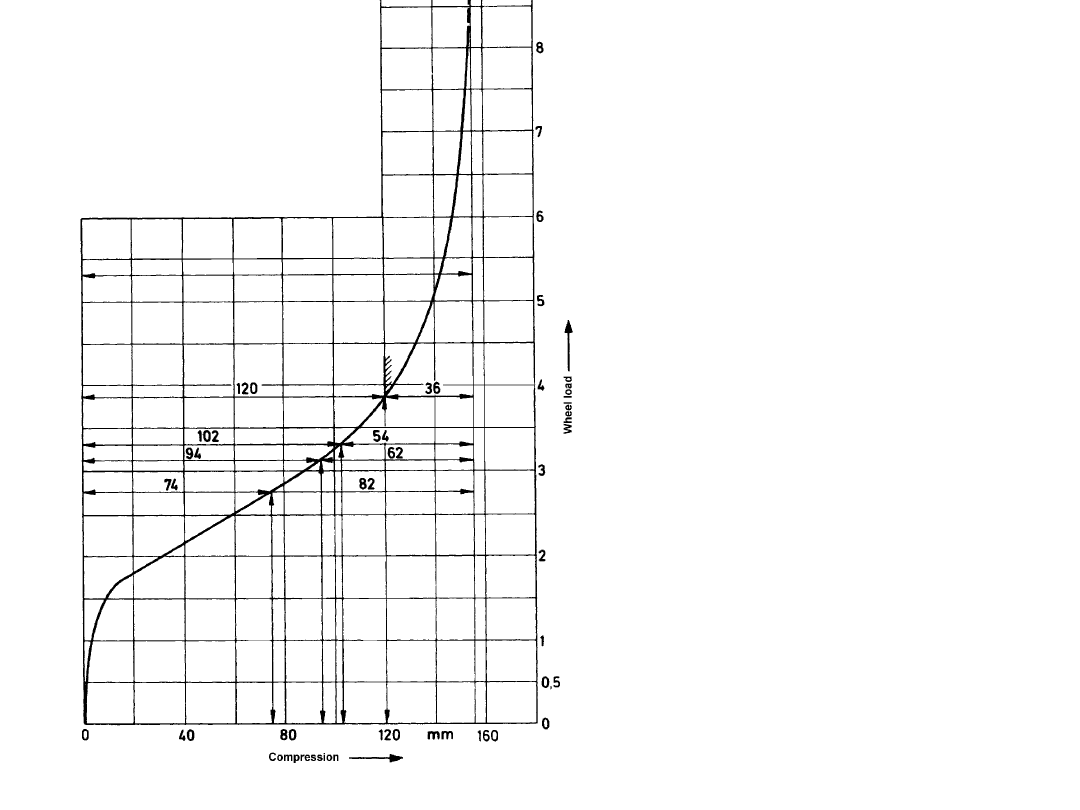
Nieliniowa charakterystyka
zawieszenia:

- Całkowity skok: 158 mm,

- Ugięcie w stanie
nieobciążonym: 74 mm,
pozostały skok: 82 mm,

- Ugięcie przy obciążeniu 3
osobami: 94 mm, pozostały
skok: 72 mm,

- Ugięcie przy obciążeniu 5
osobami: 102 mm, pozostały
skok: 54 mm,

- Ugięcie przy max.
dopuszczalnym obciążeniu osi
(7700 N, w praktyce nie
realizowane, bagaż w bagażniku
odciąza oś przenią): 120 mm,
pozostały skok: 36 mm (za
mały)

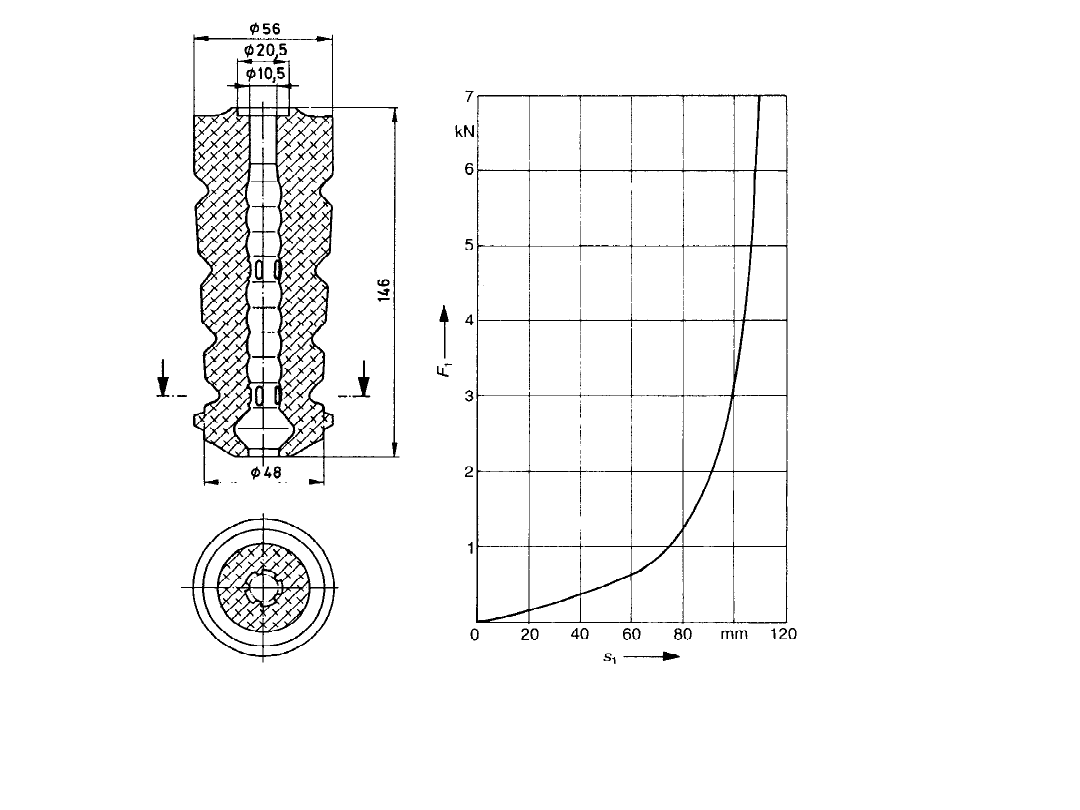
Ogranicznik skoku ze spienionego elastomeru o nieliniowej
charakterystyce

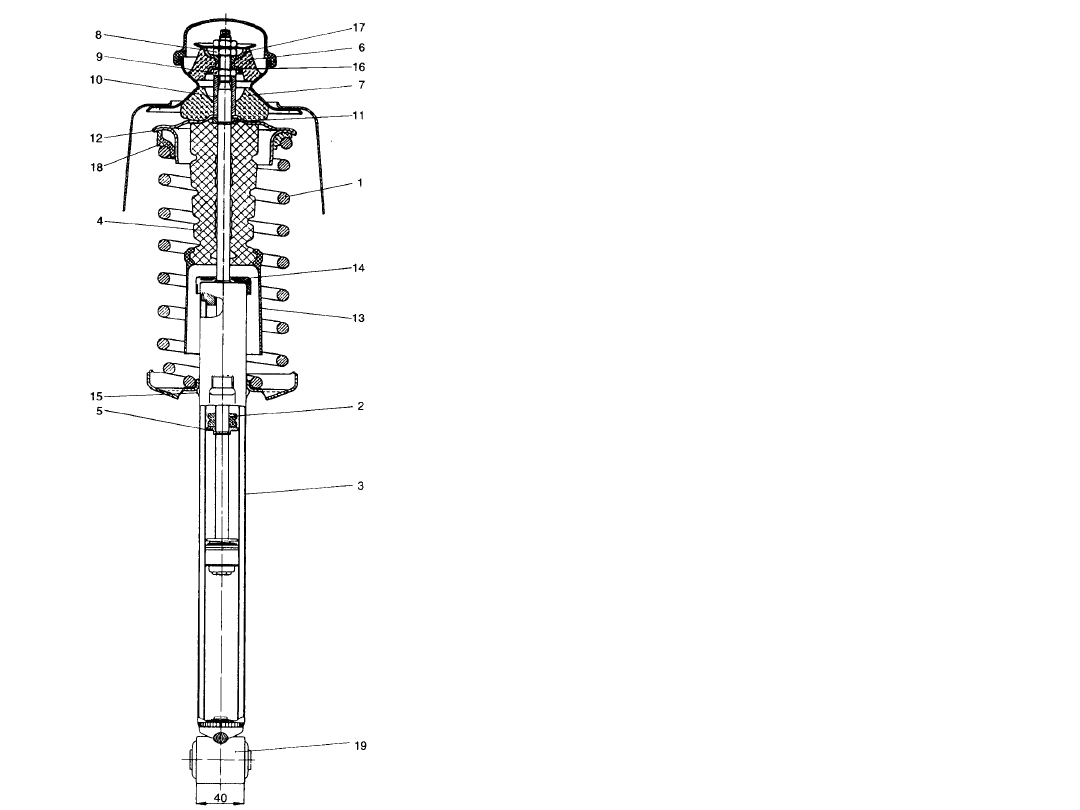
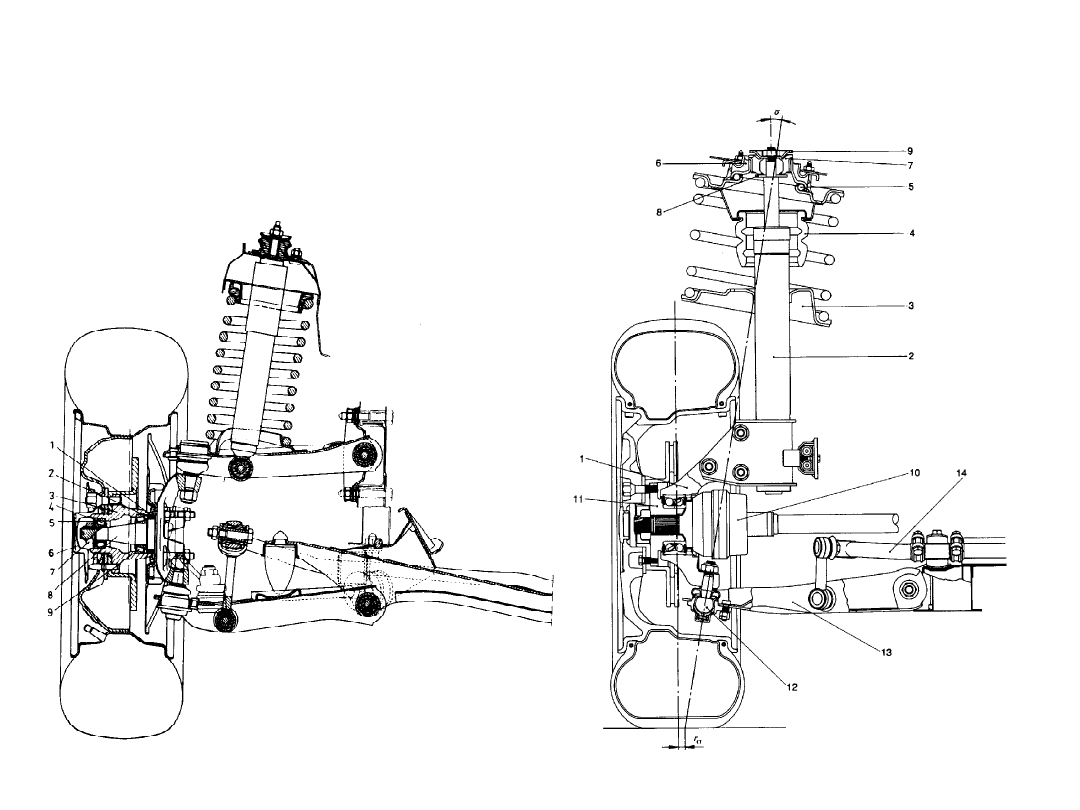
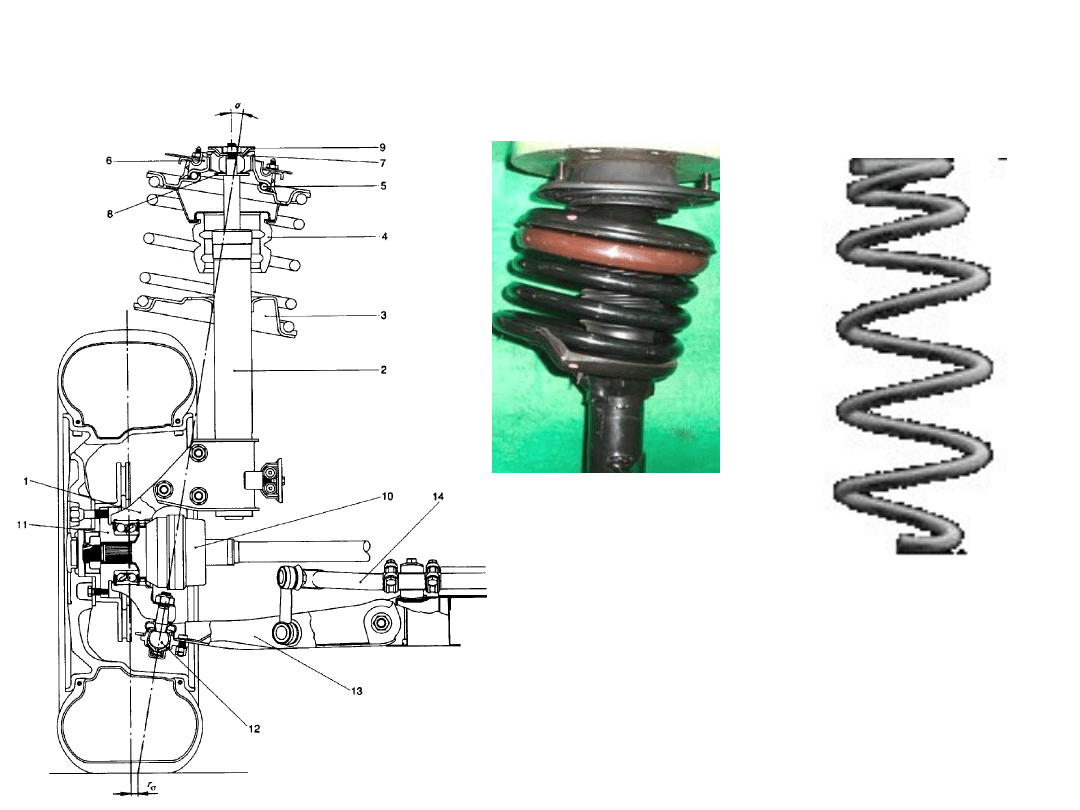
Zespół amortyzatora i sprężyny:
1 – sprężyna śrubowa, 2 – ogranicznik skoku
rozciągania, 3 - amortyzator, 4 – ogranicznik skoku
ściskania, 5 – pierścień zabezpieczający, 6, 7 –
elementy podatne, 8, 9 - nakrętki, 10 – tuleja
dystansowa, 11 – podkładka, 12 – górne gniazdo
sprężyny, 13 - osłona, 14 – pokrywa amortyzatora,
15 – dolne gniazdo sprężyny, 16, 17 - podkładki, 18
– elastyczna podkładka sprężyny, 19 – ucho