Wykład 3-4

Wykład 3-4

Leszek Smolarek

Leszek Smolarek

Akademia Morska w Gdyni

Akademia Morska w Gdyni

2005/2006

2005/2006

Modelowanie procesów

Modelowanie procesów

transportowych

transportowych

Potok ruchu

• Jest to odwzorowanie

przemieszczania się ładunku, ludzi lub
informacji w systemie transportowym.

Potok ruchu mierzy się w jednostkach

transportowych, jeśli towar jest przewożony, jako

liczbę jednostek transportowych na jednostkę czasu.

System oddziaływuje z otoczeniem między innymi poprzez potok ruchu na

wejściu i potok ruchu na wyjściu.

Potok ruchu na wejściu nazywany jest strumieniem wejściowym.

Potok ruchu na wyjściu nazywany jest strumieniem wyjściowym.

Dla każdego strumienia wejściowego wartość średnia liczby
zgłoszeń pojawiających się w jednostce czasu nazywa się
intensywnością strumienia.

Dla każdego strumienia wyjściowego wartość średnia liczby
zgłoszeń opuszczających system w jednostce czasu nazywa się
intensywnością strumienia wyjściowego.

Między dwoma następującymi po sobie zgłoszeniami upływa średni czas.

 

t

e

t

F







1

Strumień wejściowy zgłoszeń, wejście ładunków do systemu, jest

strumieniem Poissona, gdy liczba ładunków

n

n w ustalonym przedziale

czasu pracy systemu ma rozkład Poissona zaś odstęp czasu

t

t

pomiędzy

kolejnymi ładunkami na wejściu systemu ma rozkład wykładniczy.









/

1

1

0











 t

e

td

a

Dla strumienia Poissona średnia liczby zgłoszeń pojawiających
się w czasie

t

t

jest proporcjonalna do długości

t

t przedziału.

Strumień Poissona



  

!

_

Pr

n

t

n

ładunków

Liczba

n







Zastosowanie rozkładu Poissona:
• rozpad promieniotwórczy;
• zderzenia cząstek elementarnych;
• statystyczna kontrola jakości produktów;
• liczba zgłoszeń w centrali telefonicznej;
• liczba przepalonych żarówek;
• ………

Rozkład Poissona

Teoria kolejek

Teoria masowej obsługi

Systemy kolejkowe

Systemy obsługi

MODELE MASOWEJ

OBSŁUGI

Teoria masowej obsługi, zwana także teorią

kolejek, zajmuje się budową modeli

matematycznych, które można wykorzystać w

racjonalnym zarządzaniu dowolnymi

systemami działania, zwanymi systemami

masowej obsługi. Przykładami takich

systemów są: sklepy, porty lotnicze,

podsystem użytkowania samochodów

przedsiębiorstwa transportowe, podsystem

obsługiwania obrabiarek itp.

Wprowadzenie

• Gdzie...

sklepy; hotele; biura; banki;

lotniska; porty; place składowe;

…….

• Po co…

aby opisać zachowanie systemu kolejkowego

aby określić poziom obsługi:

» liczbę stanowisk;
» tryb obsługi

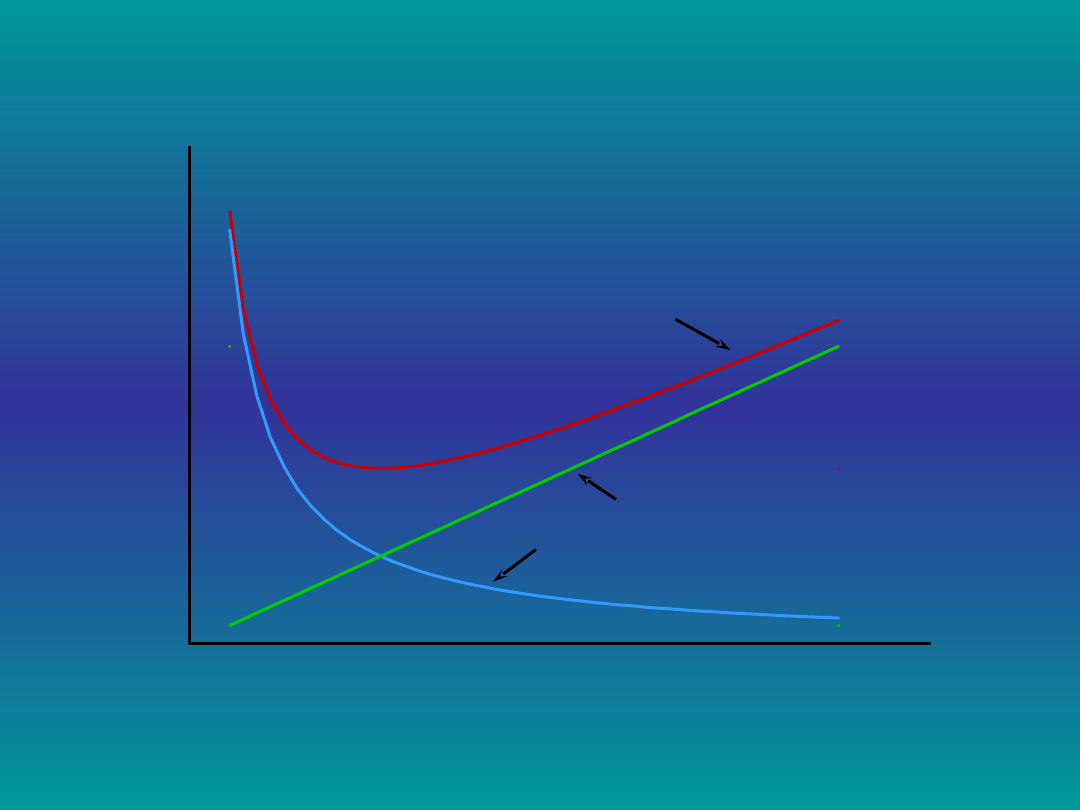
Koszty

$

Poziom obsługi

Calkowity

Obsługi

Niezadowolenia klienta

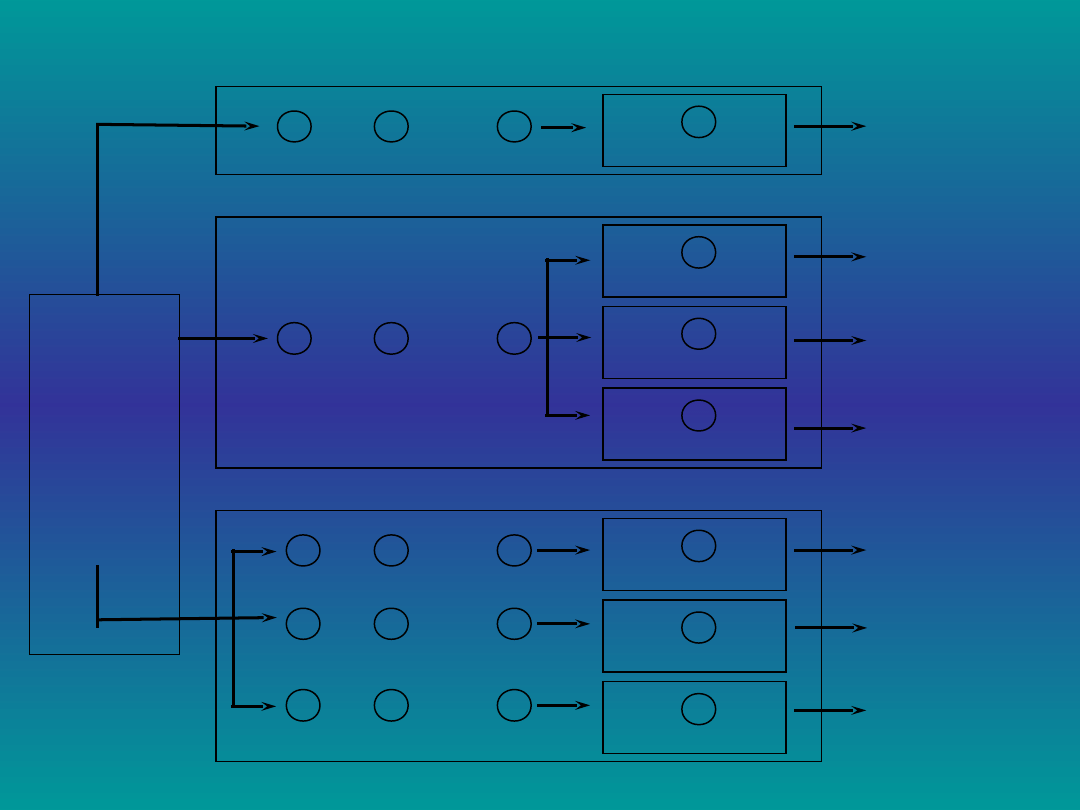
W systemie masowej obsługi mamy do czynienia z napływającymi w miarę
upływu czasu zgłoszeniami 1 (np. uszkodzony pojazd, klient, statek), z kolejką
obiektów 2 oczekujących na obsługę oraz za stanowiskami obsługi 3 (np.
stanowiska diagnozowania pojazdu, sprzedawca, stanowisko wyładunku).

Rozróżnia się systemy masowej obsługi:
-        z oczekiwaniem;
-        bez oczekiwania.

W SMO z oczekiwaniem zgłoszenie (obiekt zgłoszenia) oczekuje w kolejce na
obsługę, zaś w systemie bez oczekiwania, wszystkie stanowiska obsługi są
zajęte i obiekt zgłoszenia wychodzi z systemu nie obsłużony.

Klient

Ładune

k

Przybyc

ie

Do

system

u

...

Kolejka

Stan.

Obsł.

Kolejka

Stan.

Obsł.

...

Kolejka

Stan.

Obsł.

Stan.

Obsł.

Stan.

Obsł.

Kolejka

Kolejka

...

...

...

Stan.

Obsł.

Stan.

Obsł.

Charakterystyki

procent czasu zajętości wszystkich stanowisk obsługi

prawdopodobieństwo, że system nie jest pusty

średnia liczba klientów czekających

średnia liczba klientów czekających i obsługiwanych

średni czas czekania

średni czas czekania i obsługi

prawdopodobieństwo, że przybywający klient czeka

prawdopodobieństwo, że n klientów jest w systemie

Proces wejściowy



intensywność strumienia wejściowego

intensywność

przybywania;



liczba klientów-trend;



czas czekania na klienta.

Proces obsługi

• Czas obsługi (bez czasu czekania w

kolejce)



Rozkład czasu obsługi np.. wykładniczy:

P

for

(

)

,

t

T

t

e

dx

e

e

t

t

x

t

t

ut

t

1

2

1

2

1

2

1

2





























intensywność obsługi



średni czas obsługi 1/.



Przykłady Excel

Notacja Kendalla

• System kolejkowy opisany jest 3

parametrami:

1/2/3

czas przybycia /czas obsługi /liczba stanowisk

czas przybycia /czas obsługi /liczba stanowisk

Parametr 1

M = Markowski czas przybycia
D = Deterministyczny czas
przybycia

Parametr 2

M = Markowski czas obsługi
G = Dowolny czas obsługi
D = Deterministyczny czas
obsługi

Parametr 3

Liczba stanowisk obsługi

System M/M/s



s stanowisk obsługi.



Strumień wejściowy Poisson z
param..



Obsługa wykładnicza z param. .



Dyscyplina obsługi FIFO.



Pojedyncza kolejka.



< s



.

System M/G/1

 Czas obsługi nie musi mieć rozkładu

wykładniczego.

np.:

 Naprawa telewizora
 Badanie wzroku
 Fryzjer

Model :

Strumień wejściowy Poisson z param. .

Czas obsługi o dowolnym rozkładzie, średniej m i
odchyleniu standardowym s.

Jedno stanowisko obsługi.

System M/D/1

 Czas obsługi może być ustalony.

np..

 Taśma produkcyjna.
 Myjnia automatyczna.

 Czas obsługi deterministyczny
 Aby uzyskać system M/D/1 w systemie M/G/1

trzeba przyjąć odchylenie standardowe równe 0
( = 0).

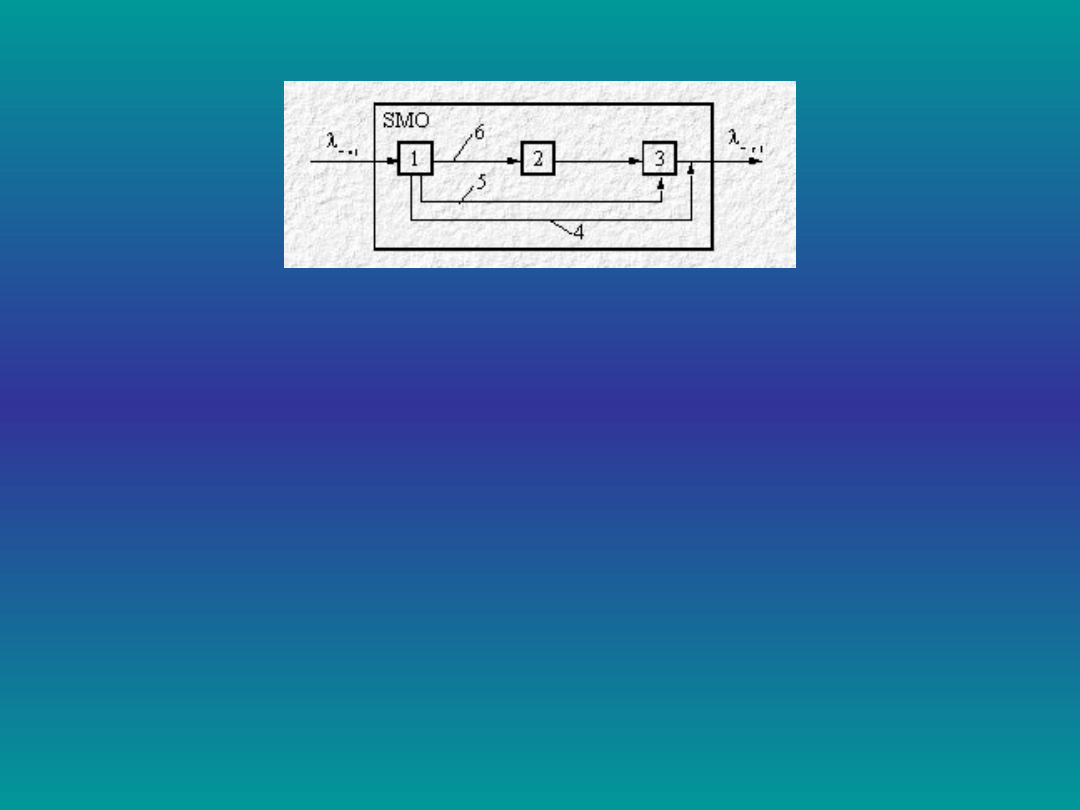
Schemat systemu masowej obsługi

(SMO)

1 – zgłoszenia (obiekty zgłoszenia),
2 – kolejka obiektów,
3 – stanowiska obsługi,
4 – przemieszczenia obiektów w systemie bez

oczekiwania,

5 – przemieszczenia obiektów w systemie z

priorytetem obsługi,

6 – przemieszczenia obiektu w systemie z

oczekiwaniem,



wej

– strumień wejściowy zgłoszeń,



wyj

– strumień wyjściowy obsłużonych obiektów.

• W zależności od dyscypliny obsługi SMO można

podzielić następująco:

• - FIFO (first in first out), czyli kolejność obsługi

według przybycia;

• - SIRO (selection in random order) czyli kolejność

obsługi losowa;

• - LIFO (last in first out), czyli ostatnie zgłoszenie

jest najpierw obsłużone;

• - priorytet dla niektórych obsług (5), np.

bezwzględny priorytet obsługi oznacza, że zostaje

przerwane aktualnie wykonywana obsługa obiektu,

a na jego miejsce wchodzi obiekt z priorytetem.

W modelu tym występują zmienne losowe:

czas upływający między wejściem do systemu dwóch kolejnych

zgłoszeń;

czas obsługi jednego zgłoszenia przez stanowisko obsługi;

liczba stanowisk;

liczebność miejsc w kolejce zgłoszeń oczekujących na obsługę.

Model matematyczny funkcjonowania SMO opiera się na

teorii procesów stochastycznych.

Założenia modelu określają

1)      typ rozkładu prawdopodobieństwa zmiennych

losowych (rozkład deterministyczny – równe

odstępy czasu), rozkład wykładniczy, rozkład

Erlanga, dowolny rozkład;

2)      zależność lub niezależność zmiennych losowych

czasu czekania na zgłoszenie i czasu obsługi;

3)      skończona lub nieskończona wartość liczby

stanowisk obsługi, długości poczekalni;

4)      obowiązującą w systemie dyscyplinę obsługi.

Zastosowanie teorii masowej obsługi umożliwia

wyznaczenie takich wielkości jak: liczba

zgłoszeń, czas oczekiwania dowolnego

zgłoszenia na obsługę, współczynnik zajętości

kanałów obsługi, liczba nie obsłużonych

obiektów.

LITERATURA

Gniadenko B. W., Kowalenko I. N.: Wstęp do teorii obsługi masowej. PWN, Warszawa

1971.

Koźniewska I., Włodarczyk M.: Modele odnowy, niezawodności i masowej obsługi. PWN,

Warszawa 1978.

Leszczyński J. Modelowanie systemów i procesów transportowych, Oficyna wydawnicza

Politechniki Warszawskiej, 1999.

Sienkiewicz P.: Inżynieria systemów. MON, Warszawa 1983.

Smalko Z.: Podstawy eksploatacji technicznej pojazdów. Politechnika Warszawska,

Warszawa 1987.

Smalko Z.: Modelowanie eksploatacyjnych systemów transportowych. ITE, Radom 1996.

Woropay M., Knopik L.: Model matematyczny rzeczywistego procesu eksploatacji

realizowanego w systemie transportowym. I Międzynarodowa Konferencja

„Eksploatacja 97”, SIMP ZG, Warszawa 1997.

Woropay M.: Metoda oceny realizacji procesu eksploatacji w systemie transportowym.

ITE, Radom 1998.

Woropay M., Knopik L., Landowski B.: Modelowanie procesów eksploatacji w systemie

transportowym. Biblioteka Problemów Eksploatacji. ITE, Bydgoszcz-Radom 2001.

Potrzeba synchronizacji transportu

wodnego z transportem lądowym

(kolejowym i drogowym).

Potrzeba likwidacji najsłabszych

ogniw powstających na styku tych

gałęzi transportowych (głównie w

portach).

Potrzeba unifikacji jednostek

ładunkowych, środków transportu

i systemów przeładunkowych.

Dziękuję za uwagę

Dziękuję za uwagę