Seria: Informatyka
Elementy teorii
niezawodności
Wykład 2
Obiekty proste
nieodnawialne
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel.
6-837118
Seria: Informatyka
Elementy teorii
niezawodności
Wykład 2
Obiekty proste
nieodnawialne
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel.
6-837118
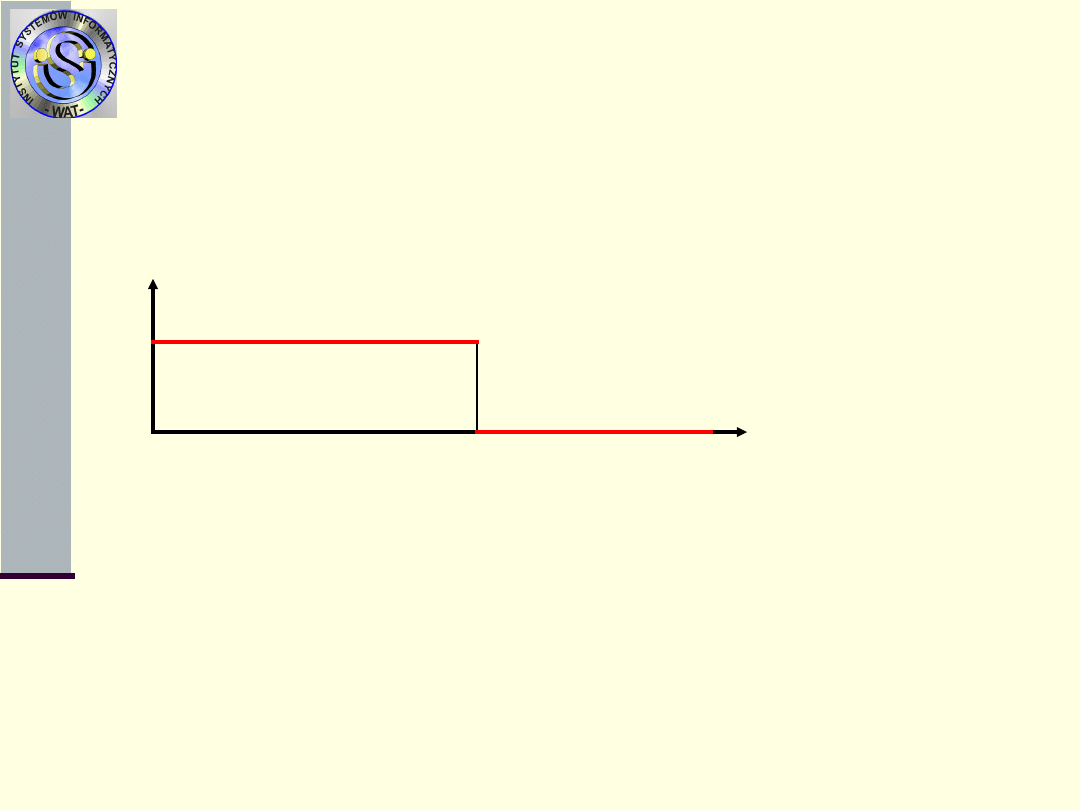
Model niezawodnościowy
Jedynym istotnym zdarzeniem w eksploatacji
obiektu prostego nieodnawialnego jest chwila jego
uszkodzenia. Wtedy traci on własność realizacji
przewidzianych funkcji (zadań).
Zmienna T jest
ciągłą i
dodatnią
zmienną losową
oznaczającą
czas życia
obiektu, zatem czas do jego
uszkodzenia. Jest ona
modelem niezawodnościowym
obiektu prostego nieodnawialnego. Charakterystyki
tej
zmiennej
losowej
są
zatem
miarami
niezawodnościowymi
obiektu.
T
t
t
1
1
0
1- oznacza zdatność obiektu
do
wykonywania funkcji
0 – oznacza jego
niezdatność
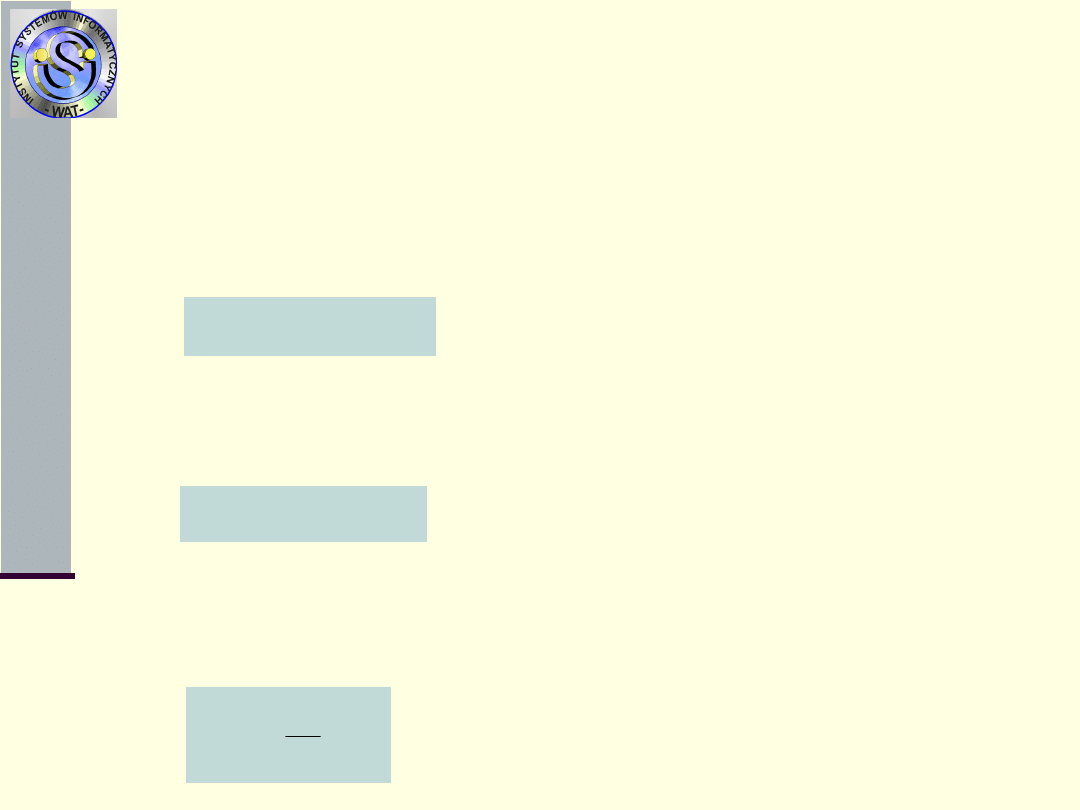
Miary niezawodności
Miary funkcyjne (zależne od upływającego
czasu)
1.
Dystrybuanta F(t) zmiennej losowej T –
prawdopodobieństwo, że czas do
uszkodzenia obiektu jest mniejszy od zadanej
chwili t
2.
Funkcja niezawodności R(t) -
prawdopodobieństwo, że czas do
uszkodzenia obiektu jest większy od zadanej
chwili t
3.
Gęstość zmiennej losowej T – pokazuje
rozłożenie masy prawdopodobieństwa na
posczególnych wartościach zmiennej losowej
t
T
P
)
t
(
F
t
T
P
)
t
(
R
)
t
(
F
dt
d
)
t
(
f
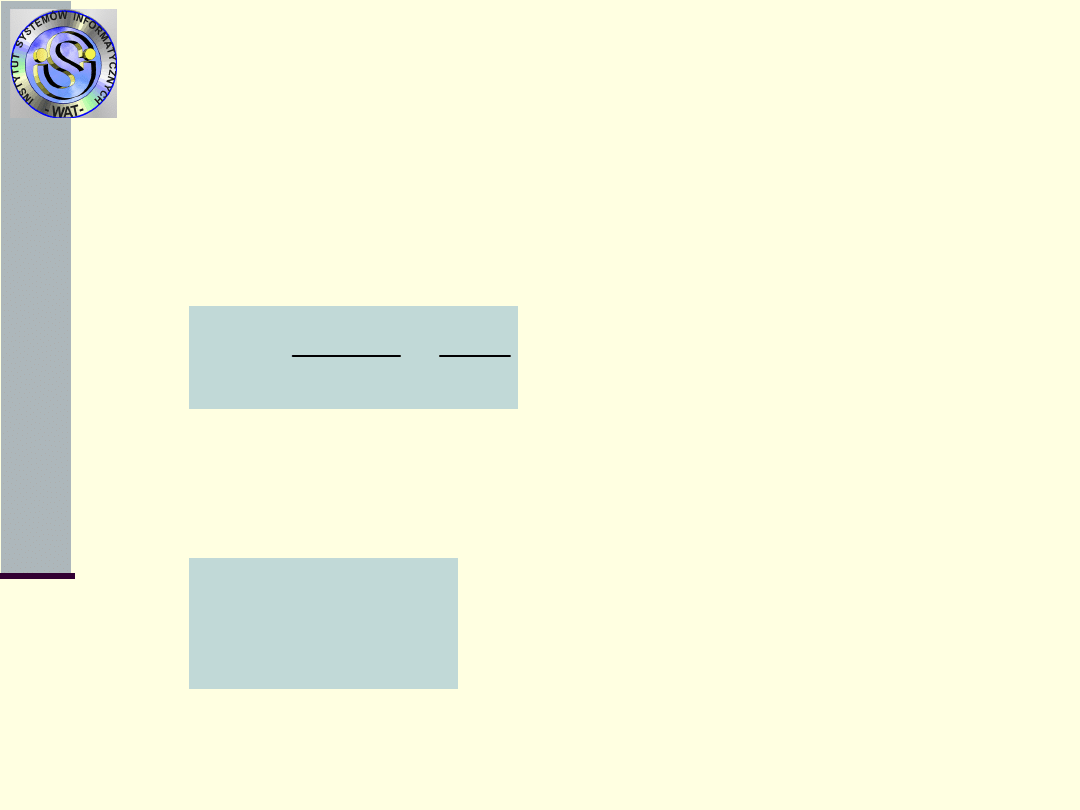
Miary niezawodności
4.
Funkcja (t) intensywności uszkodzeń
zmiennej losowej T – warunkowa
gęstość rozkładu prawdopodobieństwa
czasu powstania uszkodzenia w chwili t
5.
Funkcja wiodąca (t) – skumulowany
wskaźnik bazujący na chwilowej
charakterystyce (t)
t
0
du
)
u
(
)
t
(
)
t
(
R
)
t
(
f
)
t
(
F
1
)
t
(
f
)
t
(
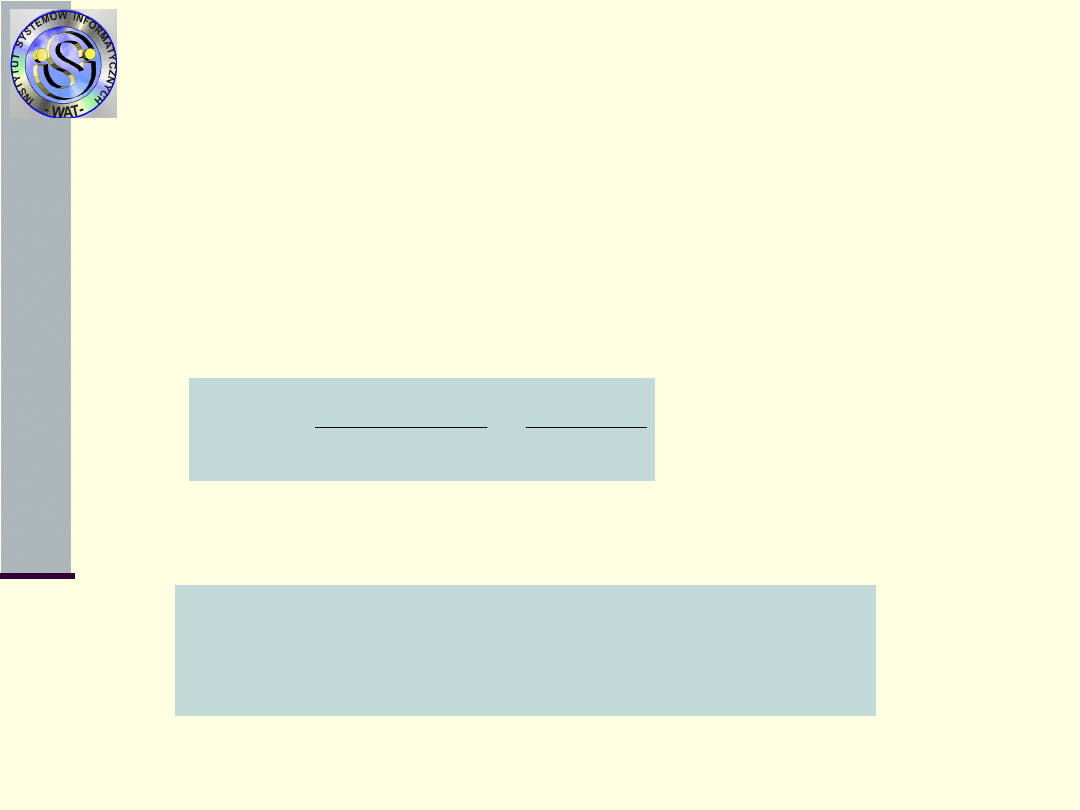
Miary niezawodności
6.
Warunkowa funkcja niezawodności R
t
()
–prawdopodobieństwo warunkowe
zdarzenia polegającego na tym, że
obiekt zachowa stan zdatności jeszcze
przez odcinek czasu o długości co
najmniej pod warunkiem, że do chwili
t nie uszkodził się.
7.
Bezwarunkowe prawdopodobieństwo
P(t,t+ ) braku uszkodzenia w
przedziale czasu (t,t+ )
)
t
(
R
)
t
(
R
1
du
)
u
(
f
)
t
,
t
(
P
t
t
)
t
(
R
)
t
(
R
t
T
P
t
T
P
)
(
R
t
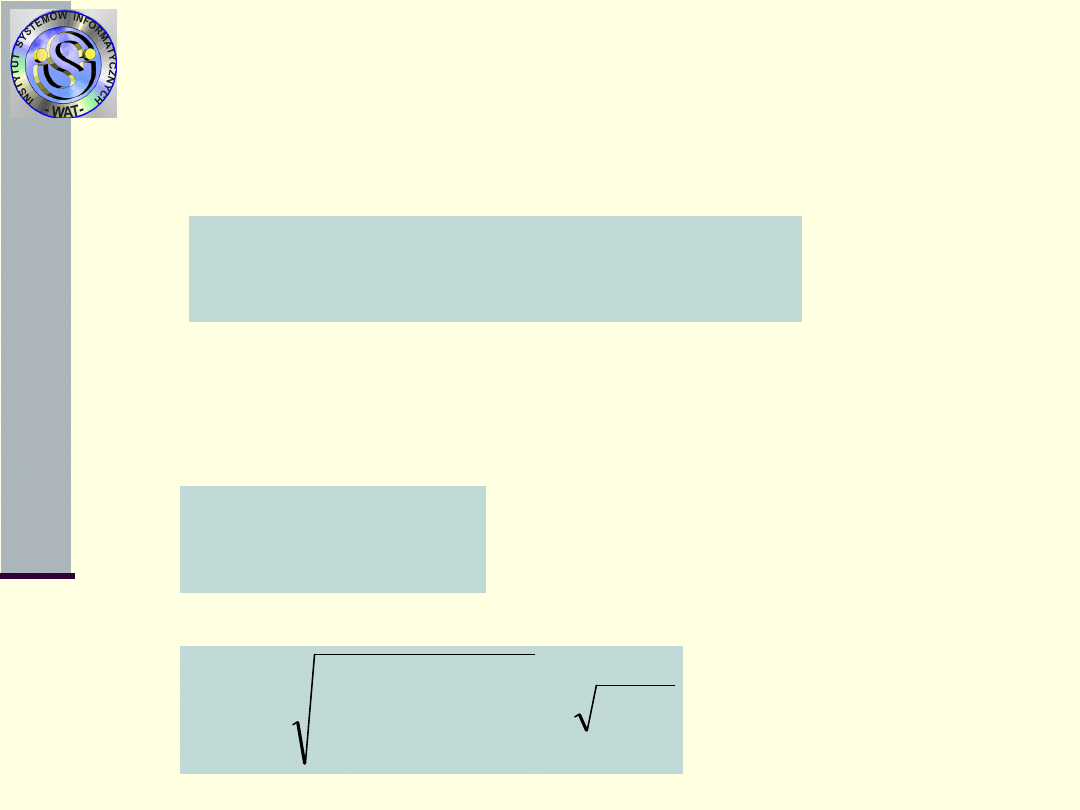
Miary niezawodności
Miary liczbowe (niezależne od
upływającego czasu)
8.
Wartość oczekiwana E{T} zmiennej
losowej T
Uwaga: całkujemy od 0 – dodatnie zmienne losowe
9.
Wariancja zmiennej losowej T – miara
rozrzutu wokół wartości oczekiwanej
10.
Odchylenie standardowe
0
2
dt
)
t
(
f
)
t
(
T
V
0
0
0
dt
)
t
(
R
dt
)
t
(
F
1
dt
)
t
(
f
t
T
E
T
V
dt
)
t
(
f
)
t
(
T
0
2
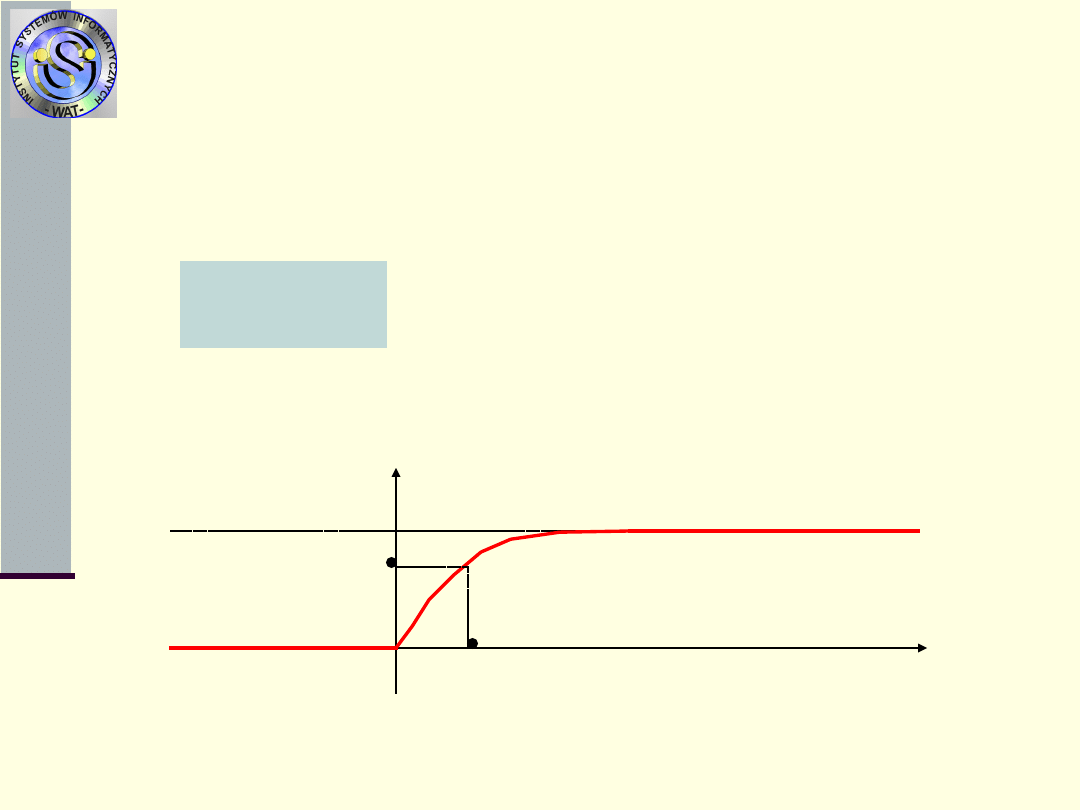
Miary niezawodności
11.
Kwantyl t
p
zmiennej losowej T – jest
chwilą, dla której dystrybuanta F(t)
osiąga wartość p, zatem jest
rozwiązaniem równania:
Interpretacja geometryczna kwantyla
p
t
F
p
t
F(T
)
t
P
p
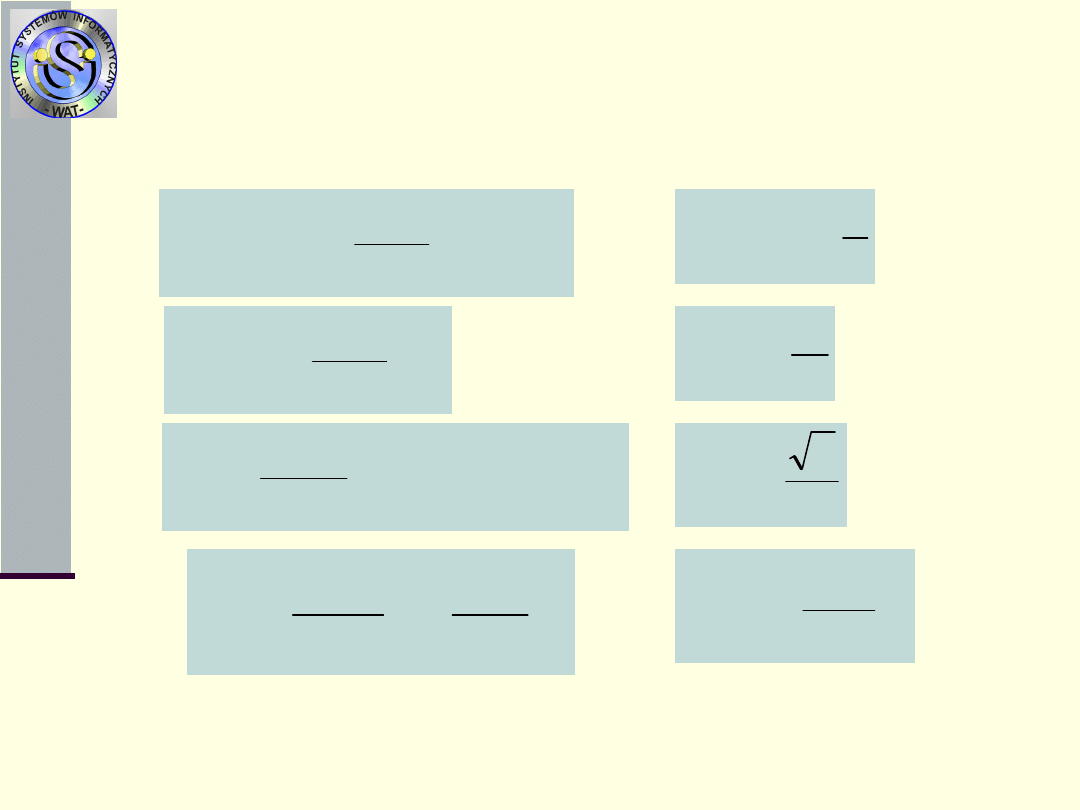
Typowe rozkłady czasów
zdatności
W teorii i praktyce niezawodności obiektów technicznych
rozważa się szereg typowych rozkładów prawdopodo-
bieństw, jakie przyjmuje się dla czasów zdatności obiektów:
1.Rozkład wykładniczy
0
t
,
e
1
)
t
(
F
t
0
t
,
e
)
t
(
R
t
0
t
,
e
)
t
(
f
t
0
t
,
)
t
(
t
t
,
t
)
t
(
0
t
,
e
)
(
R
t
1
T
E
2
1
T
V
1
T
Uwaga: proszę zapoznać się z podstawowymi rozkładami
czasów zdatności ze skryptu Korzana. Pomijać dalej
będziemy fakt, że t0 dla charakterystyk czasowych.
s
s
f
transformata Laplace’a
gęstości zmiennej
losowej
Typowe rozkłady czasów
zdatności
2.Rozkład
Erlanga
n-tego
rzędu
z
parametrem
1
0
( )
( ) 1
,
0
!
i
n
t
i
t
F t
e
t
i
l
l
-
-
=
= -
�
�
1)!
-
(n
(n)
,
e
)
n
(
t
)
t
(
f
t
1
n
n
n
T
E
2
n
T
V
n
T
1
0
( )
( )
!
i
n
t
i
t
R t
e
i
l
l
-
-
=
=
�
n
s
s
f
1
1
1
0
( )
( )
( )
!
n n
i
n
i
t
t
t
n
i
l
l
l
-
-
-
=
�
�
=
�
�
G
�
�
�
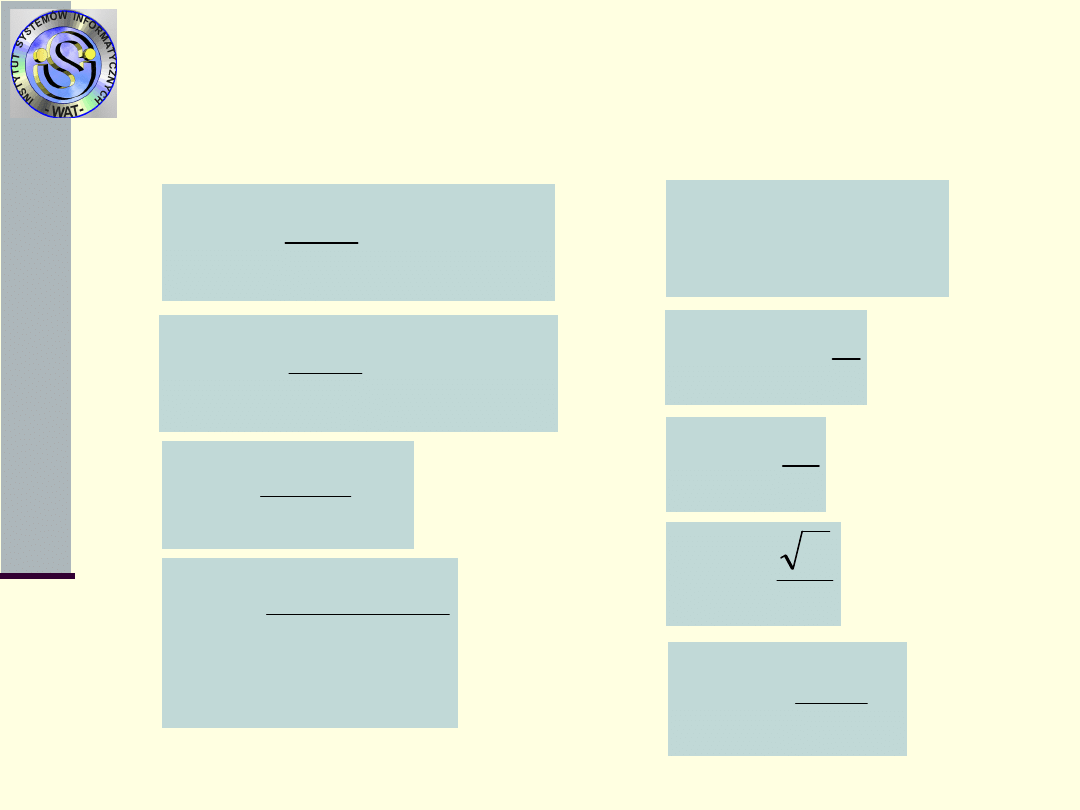
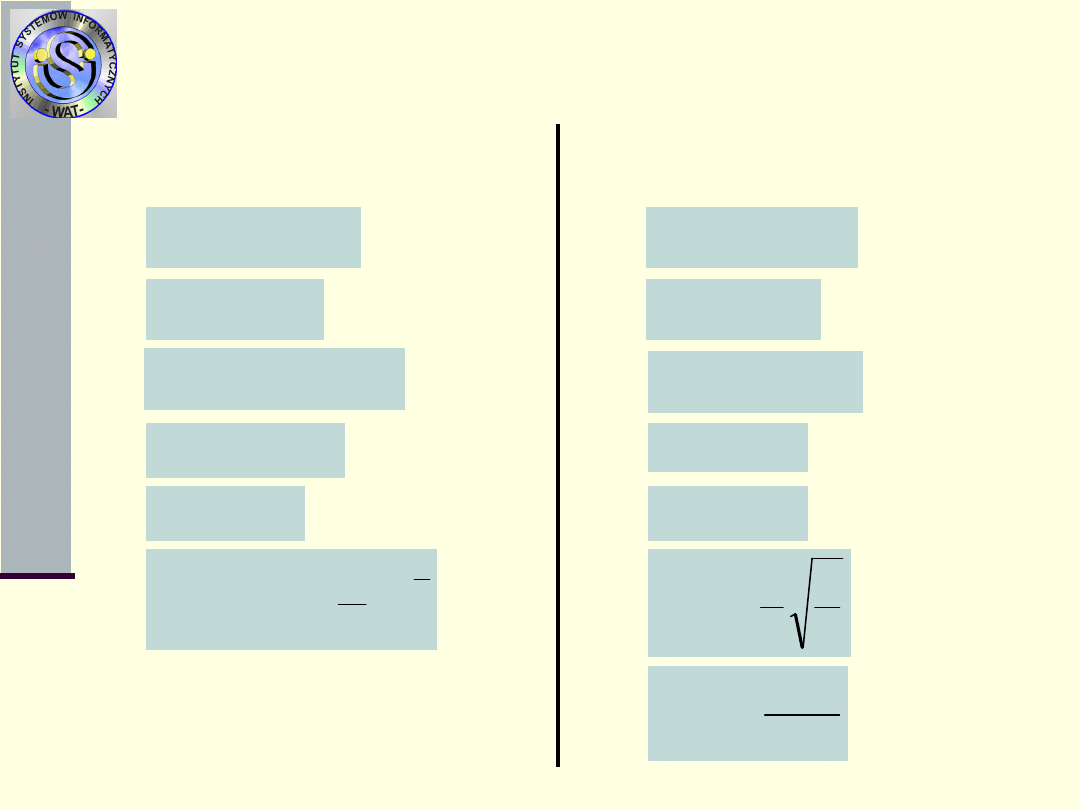
Typowe rozkłady czasów
zdatności
3.Rozkład gamma z parametrami i
dx
e
x
)
n
(
1
)
t
(
F
t
0
x
1
t
1
e
)
(
t
)
t
(
f
T
E
2
T
V
T
s
s
f
dx
e
x
e
t
)
t
(
t
x
1
t
1
dx
e
x
)
n
(
1
)
t
(
R
t
x
1
dx
e
x
)
(
0
x
1
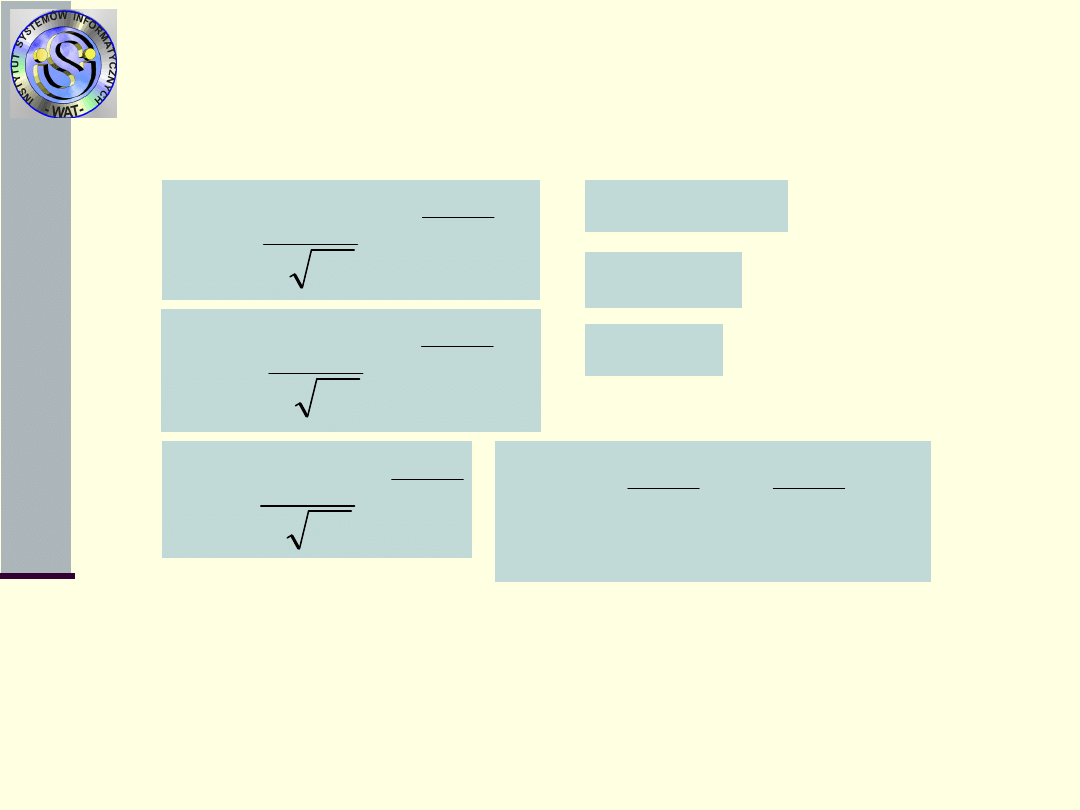
Typowe rozkłady czasów
zdatności
4.Rozkład
Weibulla
(, )
t
e
1
)
t
(
F
t
1
e
t
)
t
(
f
1
t
)
t
(
t
)
t
(
1
)
1
1
(
T
E
t
e
)
t
(
R
5.Rozkład
Rayleigha
()
2
t
e
1
)
t
(
F
2
t
te
2
)
t
(
f
t
2
)
t
(
2
1
T
E
2
t
e
)
t
(
R
2
t
)
t
(
4
4
T
V
Typowe rozkłady czasów
zdatności
6.Rozkład normalny z parametrami (m,)
dx
e
2
1
)
t
(
F
t
2
m
x
2
2
m
T
E
2
T
V
T
2
2
2
m
x
e
2
1
)
t
(
f
dx
e
2
1
)
t
(
R
t
2
m
x
2
2
1
t
2
m
x
2
m
x
dx
e
e
)
t
(
2
2
2
2
Uwaga:
rozkład ten stosować można jedynie wtedy, gdy
m>3. Wtedy ujemne wartości realizacji zmiennej losowej
praktycznie nie występują. W innym przypadku stosujemy
rozkład normalny ucięty w zerze.
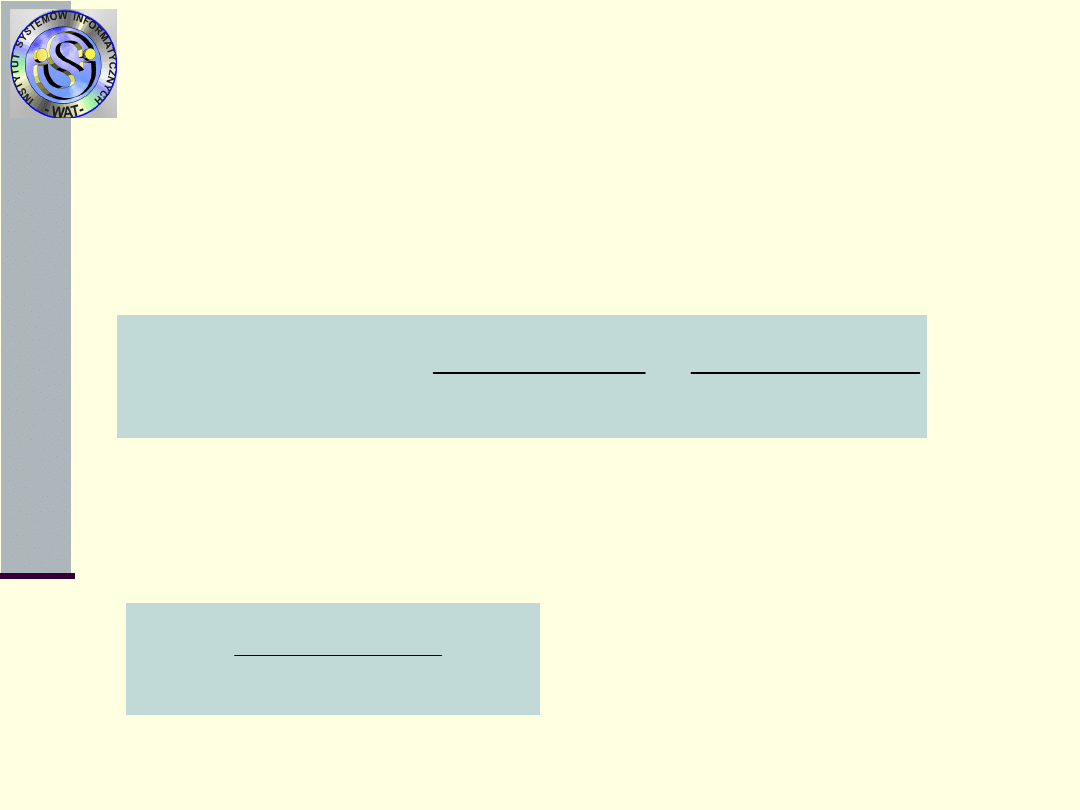
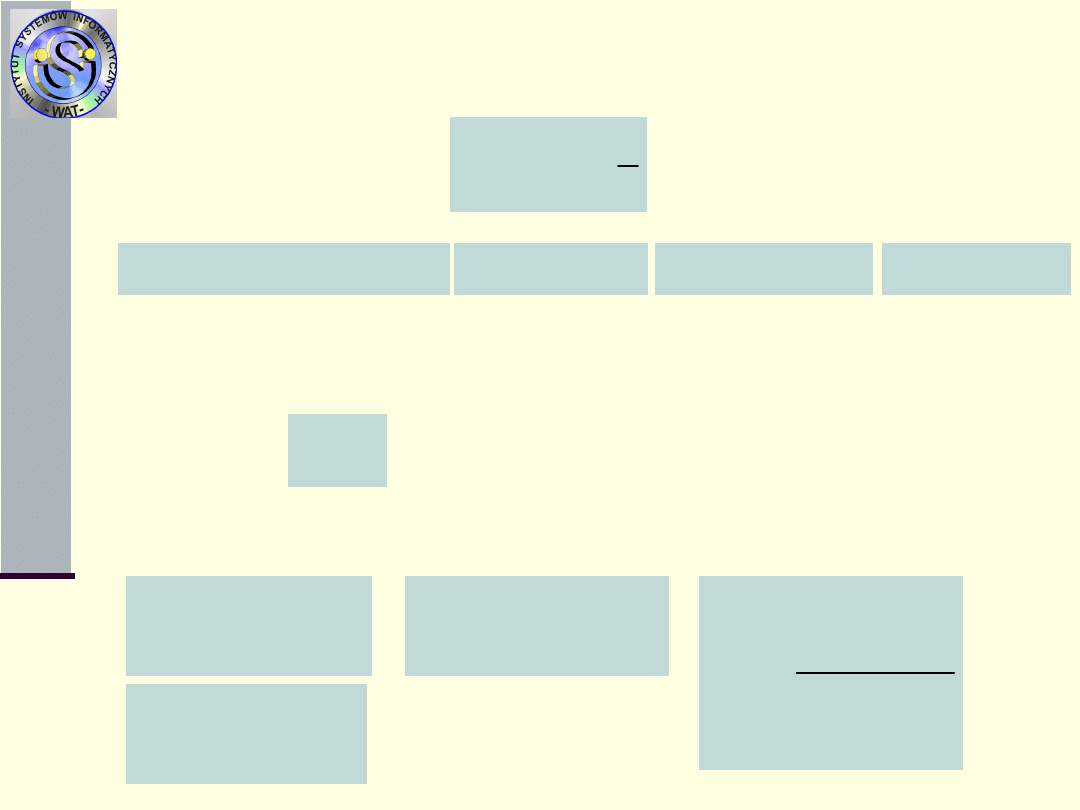
Typowe rozkłady czasów
zdatności
7.Rozkład normalny ucięty w zerze (m,)
Weźmy pod uwagę rozkład warunkowy zmiennej
losowej
X,
o rozkładzie normalnym z dystrybuantą F
X
(x), przy
czym warunek ten jest następujący: X>0. Wtedy
Taka dystrybuanta spełnia warunki dystrybuanty
czasu zdatności T, a rozkład T nazywa się rozkładem
normalnym uciętym w zerze
)
0
(
F
1
)
0
(
F
)
t
(
F
0
X
P
t
X
0
P
0
X
/
t
X
P
X
X
X
0
t
,
)
0
(
F
1
)
0
(
F
)
t
(
F
)
t
(
F
X
X
X
Typowe rozkłady czasów
zdatności
Jeśli przyjmiemy, że
to otrzymujemy dalej
8.
Rozkład mieszaniny
Jeśli mamy n dystrybuant F
k
(t) oraz prawdo-
podobieństwa p
i
takie, że
to mieszaniną zmiennych losowych nazywa się
zmienną losową T o dystrybuancie F(t)
c
1
)
0
(
F
1
X
)
0
(
F
)
t
(
F
c
)
t
(
F
X
X
)
t
(
cf
)
t
(
f
X
)
t
(
cR
)
t
(
R
X
)
t
(
c
)
t
(
X
1
p
n
1
k
k
)
t
(
F
p
)
t
(
F
k
n
1
k
k
)
t
(
f
p
)
t
(
f
k
n
1
k
k
)
t
(
R
p
)
t
(
f
p
)
t
(
k
n
1
k
k
k
n
1
k
k
)
t
(
R
p
)
t
(
R
k
n
1
k
k