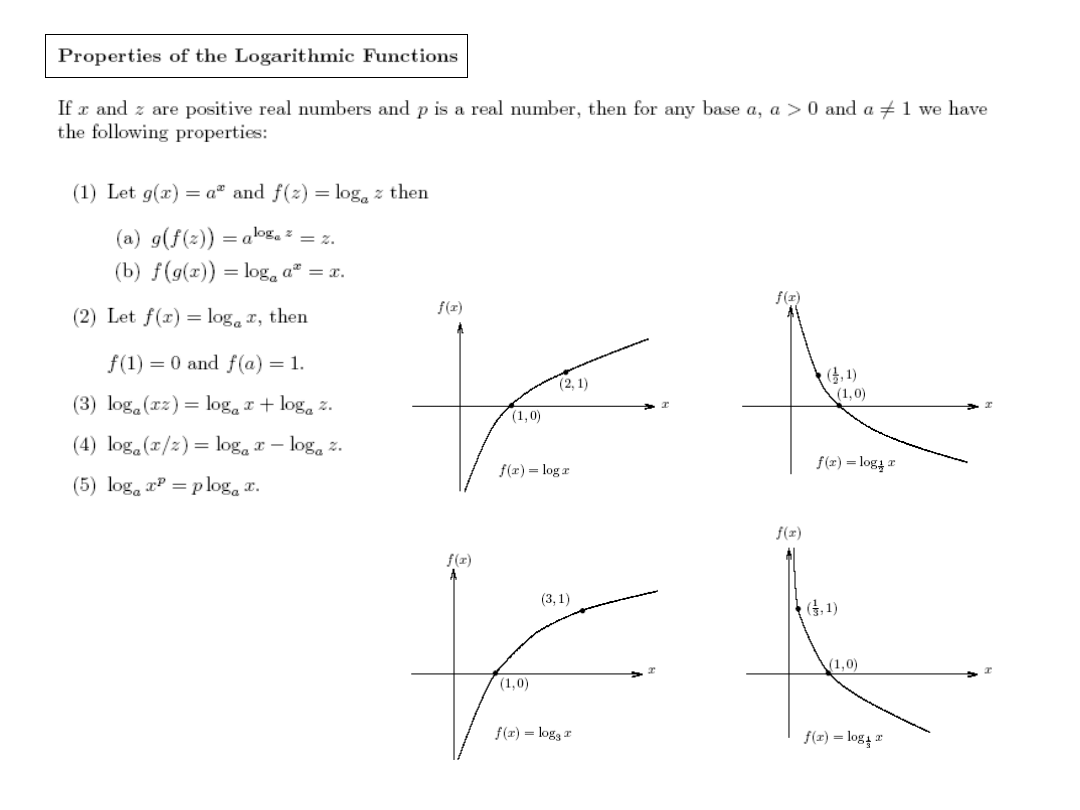
INFINITE SERIES

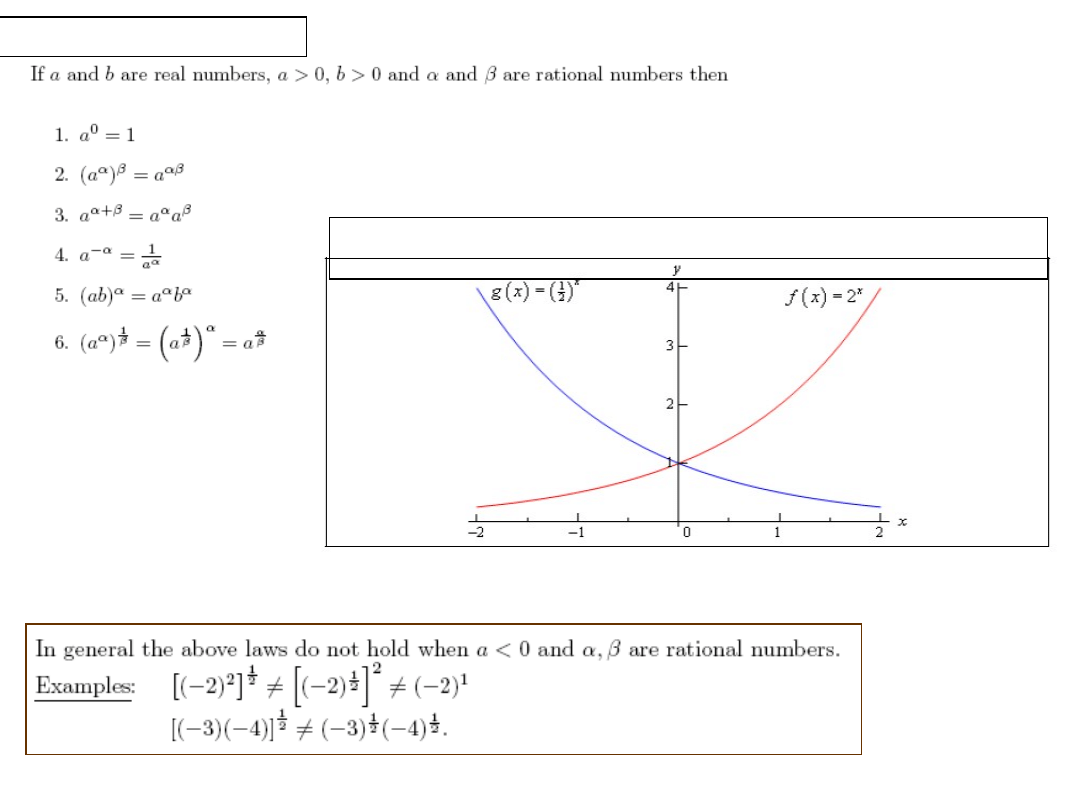
Properties of exponents

Let b>0, . An exponential function is then a function in the
form f(x) = b

x

.

1

b

Napiers bones

Napiers bones

Slide Rules

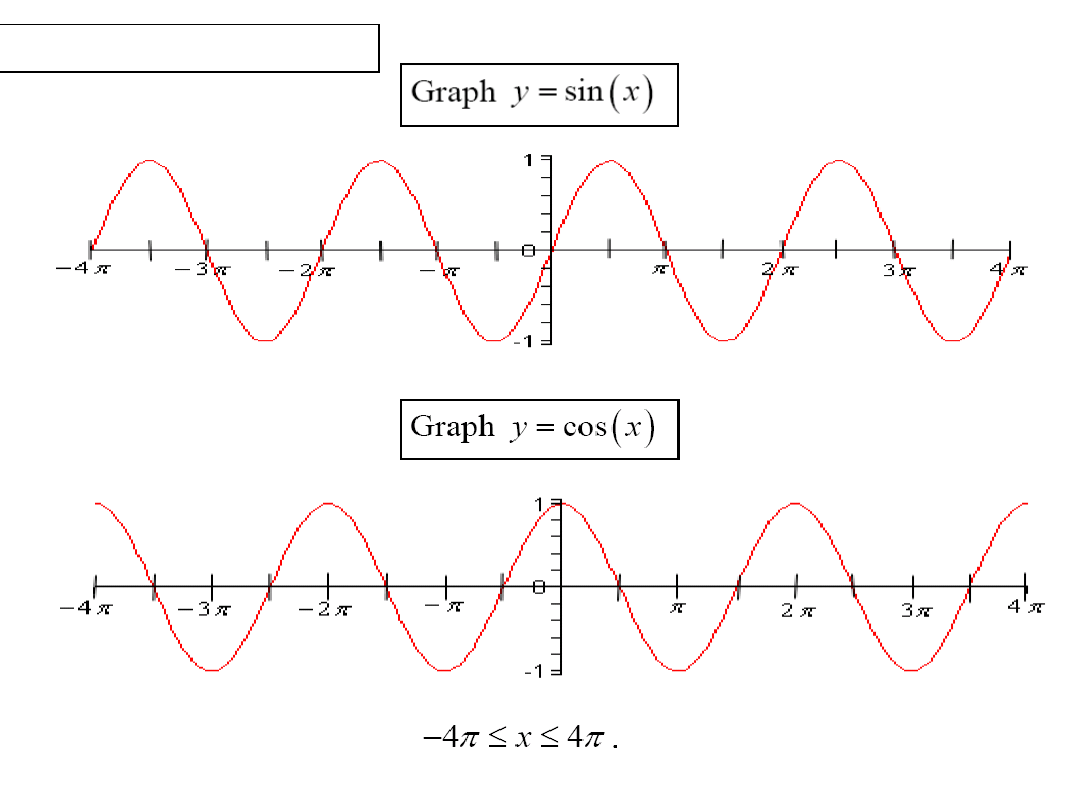
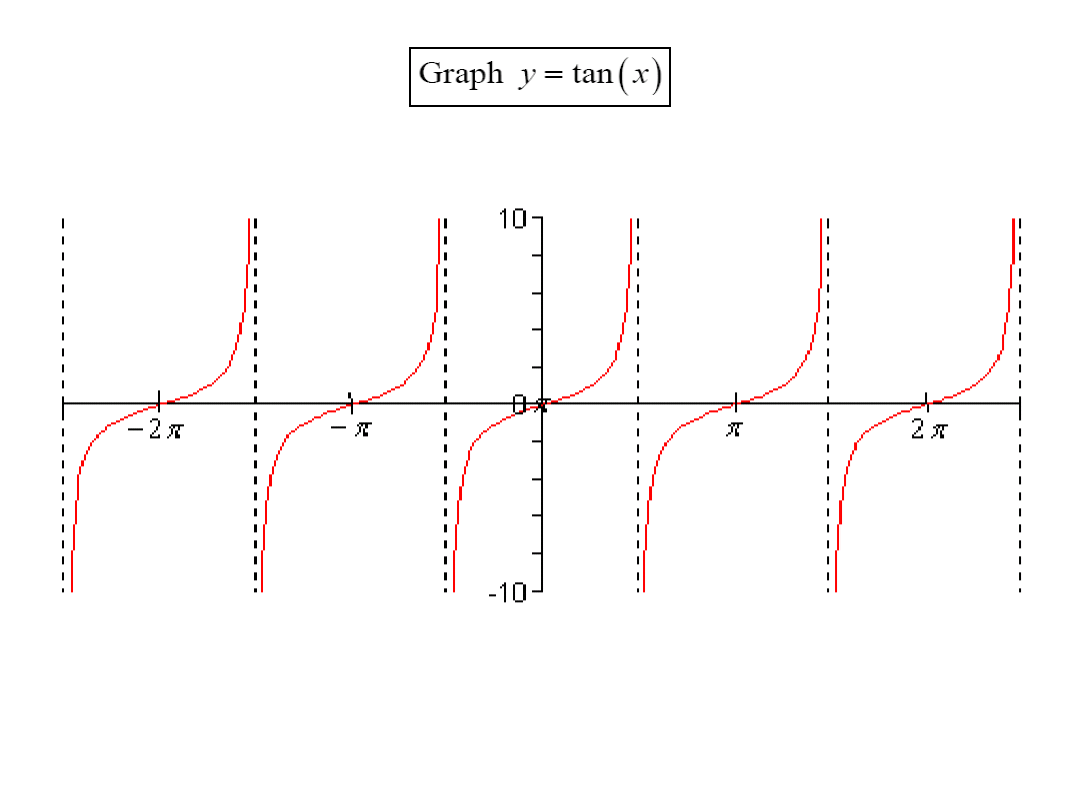
Trigonometric functions

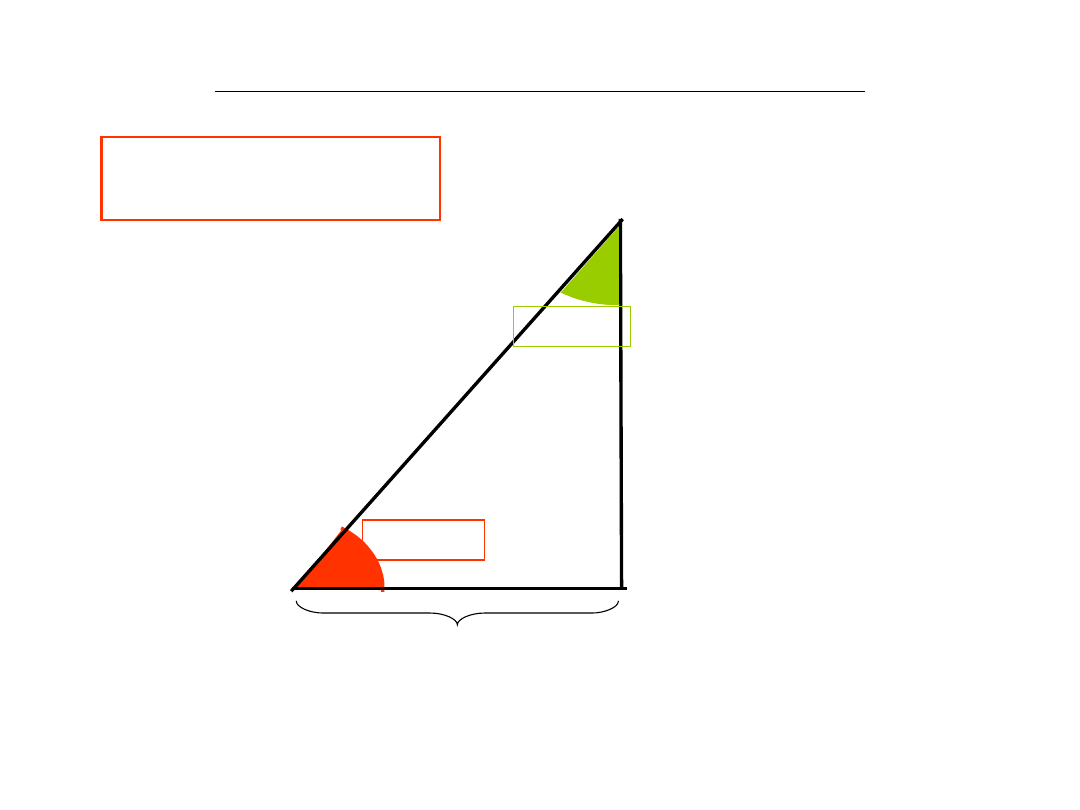
INVERSE TRIGONOMETRIC FUNCTIONS

x = sin α
α = arc sinx = sin

-1

x

1. arc cos(x) + arc sin(x) = π/2

x

arc cosx

arc sinx

1

i.e. cos(arccos(x)) = x

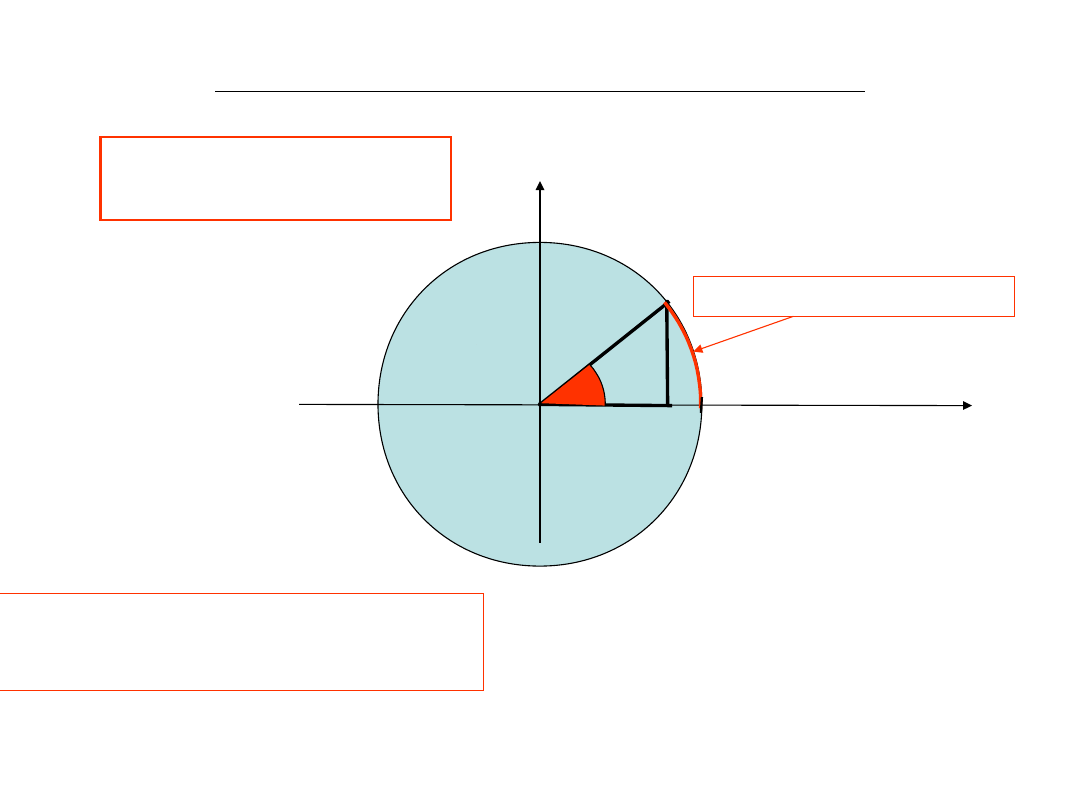
INVERSE TRIGONOMETRIC FUNCTIONS

Unit circle

x

the length of the arc is α

x = cos α
α = arc cosx = cos

-1

x

1

α

From the Figure we can deduce
2. arc cos(x) + arccos(-x ) = π

Name

Usual

notation

Definitio

n

Domain of x

for

real result

Range of typical

principal value

arcsine

y =

arcsin(x)

x =

sin(y)

−1 to +1

−π/2 ≤ y ≤ π/2

arccosine

y =

arccos(x)

x =

cos(y)

−1 to +1

0 ≤ y ≤ π

arctangent y =

arctan(x)

x =

tan(y)

all

−π/2 < y < π/2

arccotange

nt

y =

arccot(x)

x =

cot(y)

all

0 < y < π

Inverse

trigonometric functions

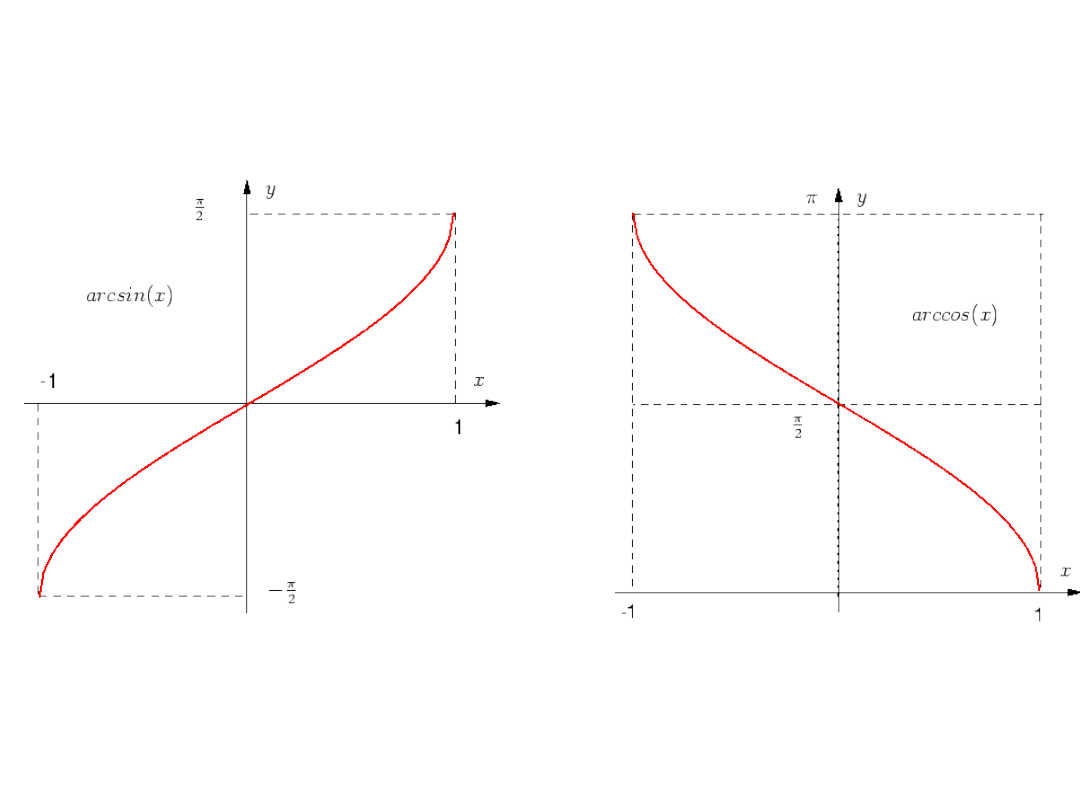
Graph arcsin(x).

Graph arccos(x).

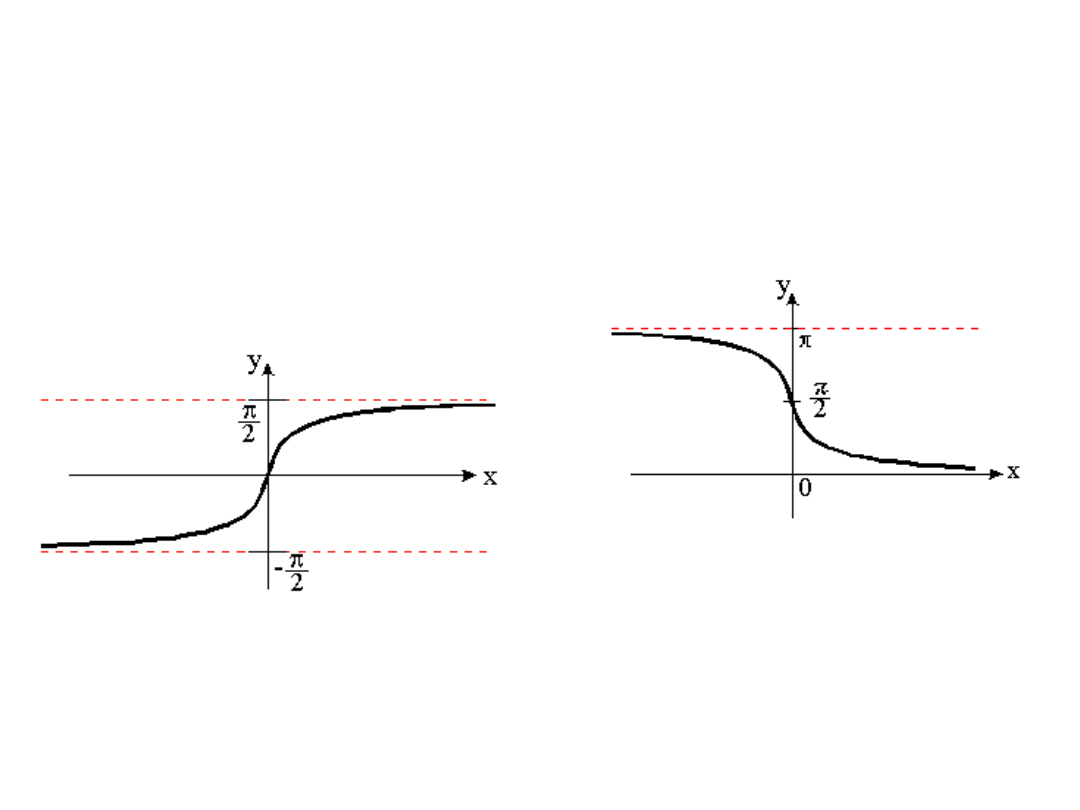
Graph arctan(x)

Graph arcot(x)

NUMBER SERIES

-How much is a drop of lemonade?
-A drop I’ll give you for nothin’!

- Can I get a cupfull of drops?

SERIES
Given a sequence the N-th
partial sum S

N

is the sum of the first N terms

of the sequence, that is,

}

,

a

,

a

,

a

{

3

2

1









N

1

n

n

N

a

S

We say that this series converges to S, or that its sum is S, if the limit

S

a

lim

N

1

n

n

N











exists and is equal to S. If there is no such number,
then the series is said to diverge.

In more formal language, a series converges if there
exists a limit S such that for any arbitrarily small
positive number there is a large integer N

0

such that for all N > N

0

0









 S

S

N

 

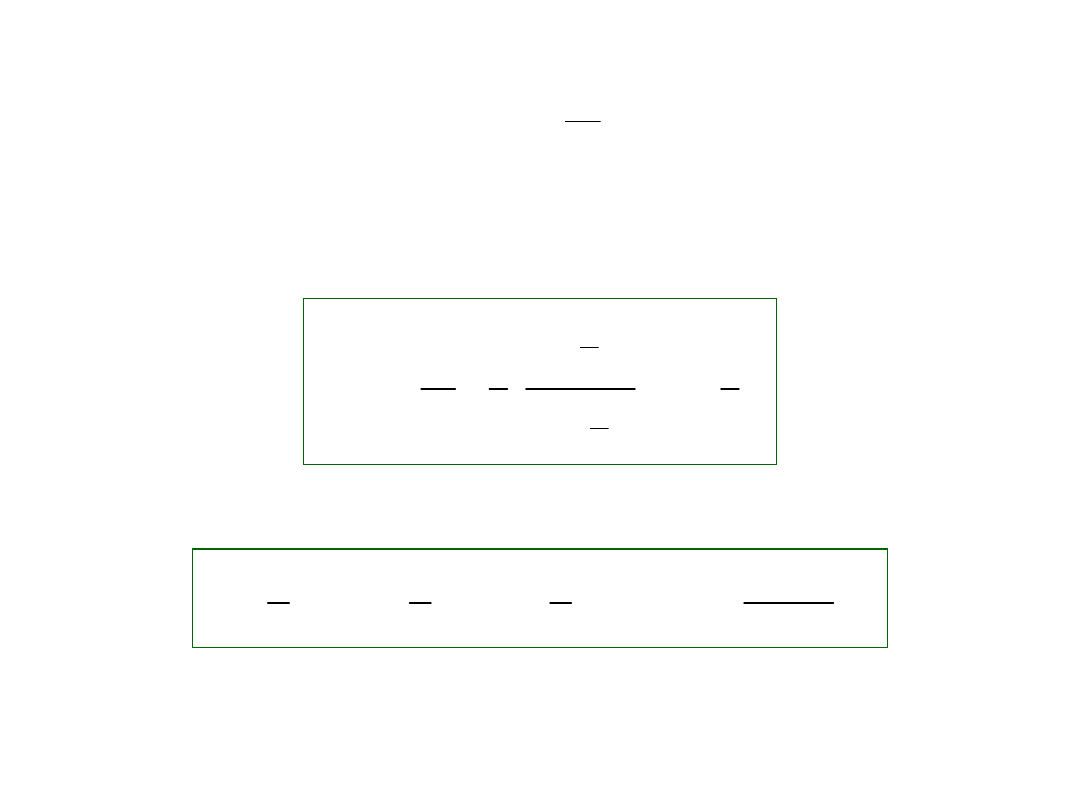
n

n

a

2

1



 

N

S

N

N

N

1

k

k

N

2

1

1

2

1

1

2

1

1

2

1

2

1

S















































,

2

1

2

S

,

,

8

7

S

,

4

3

S

,

2

1

S

N

N

N

3

2

1











Let

EXAMPLE

The N-th partial sum is

so the specific partial sums are

This is only a test for divergence. If the limit is zero you can’t
conclude anything, so you should never use this test to show
that a series converges

n

1

n

n

S

S

a

oof

Pr

























1

n

n

1

n

n

a

k

a

k

























1

n

n

n

1

n

1

n

n

n

)

b

a

(

b

a

0

...

0

0

0

)

)

3

(

)

2

(

)

1

(

(

)

3

2

1

(



































2.

The sum of two divergent series can be convergent!!!

NOTE:

1.

The sum of two convergent series is always convergent

2. The sum of series

1. Multipying a series by a number

We can add a finite number of terms to a series or delete
a finite number of terms without changing the series’
convergence or divergence.

As long as we preserve the order of its terms we can
reindex any any series without altering its convergence,



























h

1

n

3

2

1

h

n

1

n

n

a

a

a

a

a



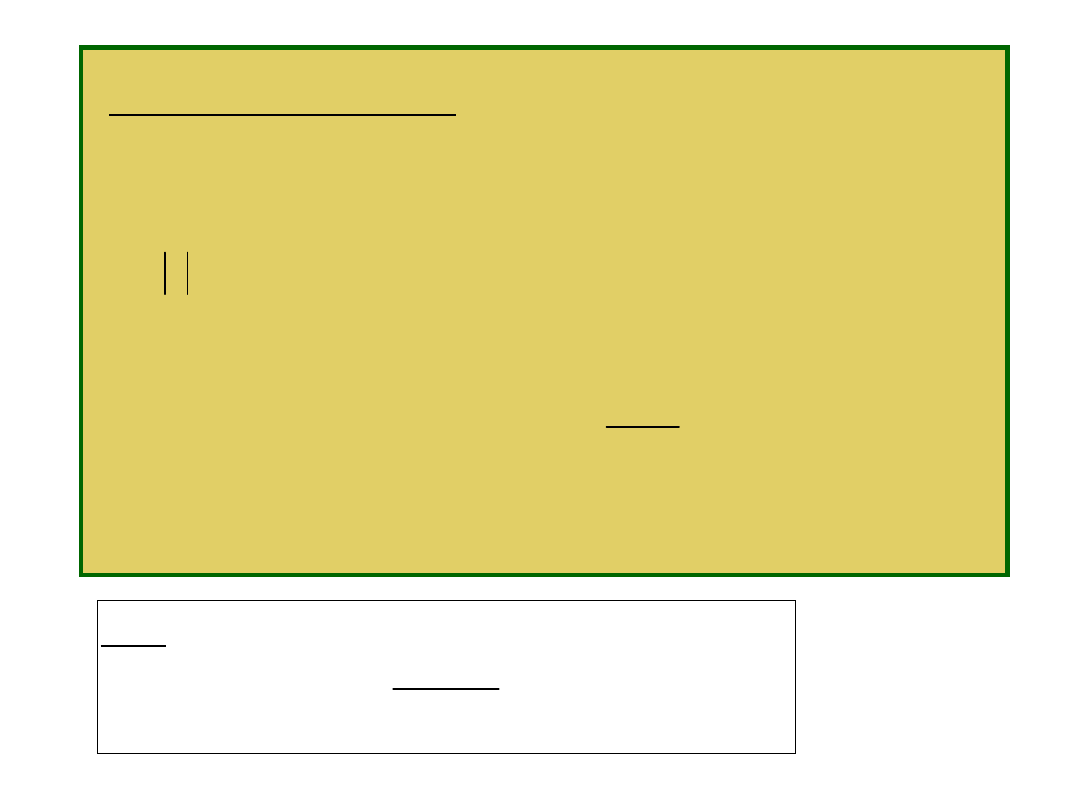
POSITIVE SERIES

a

n

> 0

1

q 











1

n

n

q

1

a

q

a

1

q

1. Geometric Series

the sum of the series is

If

the series diverges .













k

1

n

k

1

n

q

1

q

1

a

q

a





















3

2

1

n

1

n

aq

aq

aq

a

q

a

If

Proof

QED

Express the repeating decimal 5.23232323... as the ratio
of two integrers

99

518

99

23

5

99

100

100

23

5

...

)

100

(

1

)

100

(

1

100

1

1

100

23

5

...

)

100

(

23

)

100

(

23

100

23

5

...

32323232

.

5

3

2

3

2



























































geometric series
a = 1
q = 1/100

99

100

100

1

1

1

...

100

1

100

1

100

1

1















The harmonic series

is divergent



















4

1

3

1

2

1

1

n

1

1

n

If 0 < p  1 then the series diverges, e.g.





1

n

p

n

1





1

n

n

1

3. p-Series Test

Consider the series   

.

If p > 1 then the series converges

For p =1, the harmonic series diverges

Both of the series are convergent or divergent.

1. Examples for Root and Ratio
Tests

2. Inconclusive Root and Ratio Test examples - the tests are useless

convergent

n

1

.

2

divergent

n

1

.

1

1

n

2

1

n













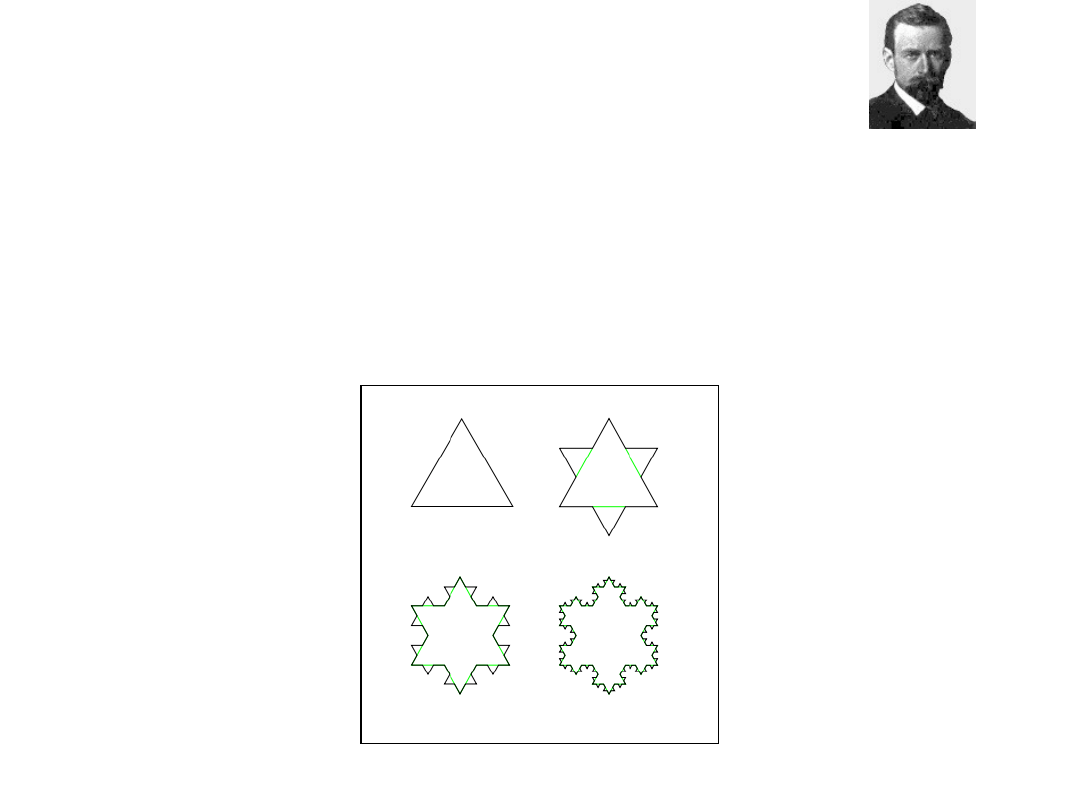
One can imagine that it was created by starting with a line segment, then
recursively altering each line segment as follows:

•divide the line segment into three segments of equal length.

•draw an equilateral triangle that has the middle segment from step 1 as
its base and points outward.

•remove the line segment that is the base of the triangle from step 2.

The Koch curve is the limit approached as the above steps are followed
over and over again.

The Koch snowflake (or Koch star)

The first four iterations of the Koch snowflake.

 

             

von Koch

The first seven iterations in animation.

The Koch curve has an infinite length:at each step the total length increases
by one third and thus the length at step n is (4/3)

n

:

the sum of the lengths is a geometric series with |q| >1, a

n

= 3(4/3)

n

so the sum is infinite.

The area of the Koch curve is

 

                  























n

1

k

k

1

k

9

4

3

1

4

3

here |q|<1 and the series is convergent, the area enclosed by the snowflake is finite.

Wacław Franciszek Sierpiński (March 14, 1882 — October 21, 1969)

Sierpiński curves are a recursively defined sequence of
continuous closed plane fractal curves discovered by Wacław
Sierpiński, which in the limit

 

         completely fill the unit

square: thus their limit curve, also called the Sierpiński curve, is
an example of a space-filling curve.

The length of S

n

is ,

i.e. it is divergent to infnity, whereas the limit of the area
enclosed by S

n

is finite.

Area= (1 - 1/4

n

)/3 + (1/4 + 1/2

2n+3

)/3

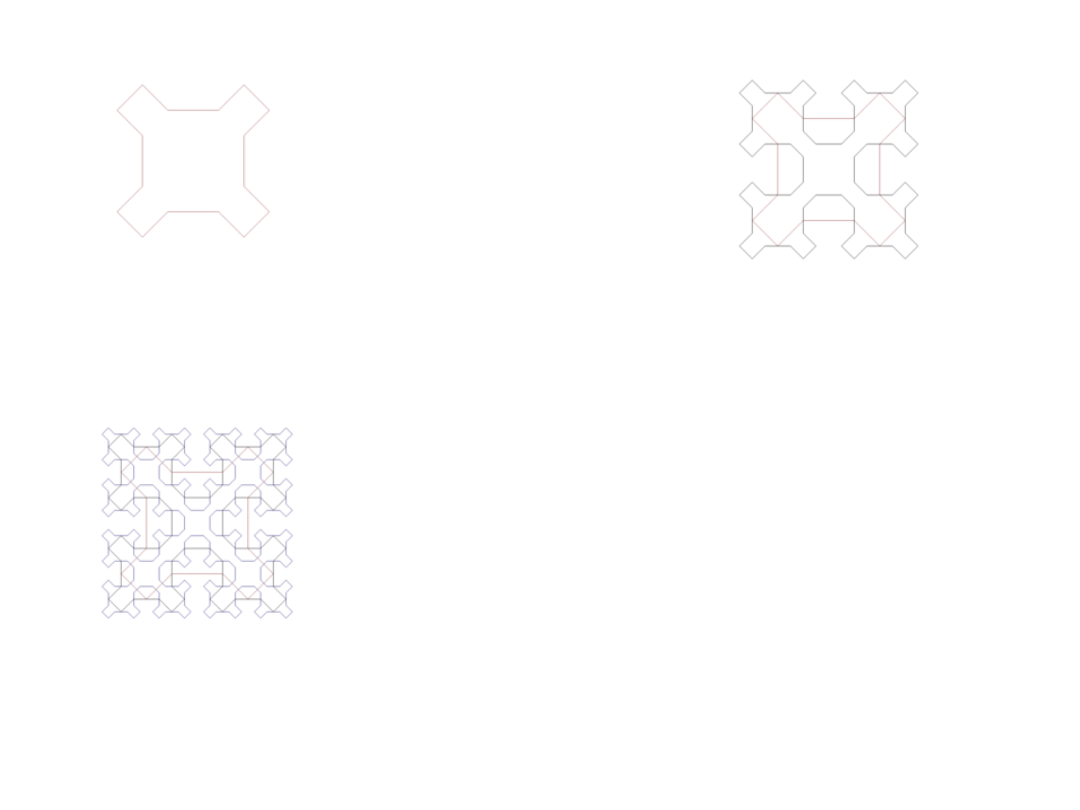
Sierpiński-Curve of first order

Sierpiński-Curves
of orders 1 and 2

Sierpiński-Curves
of orders 1 to 3

The curve grain is obtained by replacing each corner of a
square by a small square placed along the diagonal axis.
Each order of the Sierpinski curve consists of 4 copies of the
curve of the previous order replicated on a smaller scale and
joined at the centre.

http://www.geocities.com/ywhmaths/Fractals/Sierpinski.html

SERIES WITH POSITIVE AND NEGATIVE TERMS

Proof
First notice that |a

n

| is either a

n

or it is −a

n

depending on its sign. This

means that we can then say,

Now, since we are assuming that Σ |a

n

| is convergent then 2 Σ |a

n

| is also

convergent since we can just factor the 2 out of the series and 2 times a
finite value will still be finite. This allows us to use the Comparison Test
to say that Σ a

n

+|a

n

| is also a convergent series.

Finally, we can write,

Σa

n

= Σ(a

n

+|a

n

|) − Σ|a

n

|

and so Σ|a

n

| is the difference of two convergent series and so is also

convergent.

QED





1

n

n

a





1

n

n

a

If

converges,

then

also converges (but not vice-versa).

n

n

n

a

2

a

a

0







If a series converges conditionally, it is possible to rearrange the
terms of the series in such a way that the series converges to
any value, or even diverges.

If is absolutely convergent then it is also convergent





1

n

n

a

We can use the positive series tests to check absolute convergence of a mixed
term series. If the series is absolutely convergent then it is convergent.

Absolute convergence is a “stronger” type of
convergence.
Series that are absolutely convergent are guaranteed to
be convergent.
However, series that are convergent may or may not be
absolutely convergent

n

n

n

n

n

n

n

a

)

a

a

(

a

,

a

2

)

a

a

(

0

oof

Pr













TIPS

1. First make an informal guess as to whether the series
converges or diverges. Is a

100

very small? Try the necessary

condition for divergence.

2. Use limit comparison to find a simpler series you are
familiar with where the terms behave like the terms of the
given series.

3. If you see a factorial (!), use the ratio test.

4. If you see c

n

(where c is constant), try the root or ratio

test.

5. If you see n

c

(n changes, c is constant), try the p-test.

6. If you see that the sign of the terms change try the
alternating series test.

A conditionally convergent series

In standard presentation 1-1/2 + 1/3 -1/4 + 1/5 -...
the alternating harmonic series converges to S = ln(2),

A conditionally convergent series