Jednomiany i sumy
algebraiczne
Przypomnijmy, że wyrażeniami
algebraicznymi nazywamy takie
wyrażenia, w których obok liczb i
znaków działań występują litery.
Na przykład:
10c+19n
15a+7d
Wszystkie wyrażenia algebraiczne
zbudowane są z
jednomianów
, czyli
wyrażeń, które są pojedynczymi
liczbami, pojedynczymi literami lub
iloczynami liczb i liter.
Przykłady jednomianów:
-10xy -28
d
4k 3h
Aby wyrażenie algebraiczne było
czytelne, staramy się jednomiany
uporządkować.
Mnożymy czynniki liczbowe, wynik zwykle
zapisujemy na początku jednomianu.
Iloczyn takich samych czynników
literowych zapisujemy w postaci potęg.
Przykłady:
5ac * 2b²=10ab²c
4c * (-3ab²)=-12ab²c
7yx * 2(-x)y²= -14x²y³
Jeśli w jednomianie występują
pierwiastki, to zwykle te pierwiastki
zapisujemy na końcu.
Na przykład:
b²√5 4d√2
-x³√6
Wyrażenie algebraiczne, które powstaje
przez dodawanie jednomianów,
nazywamy
sumą algebraiczną
.
Jednomiany, które dodajemy, nazywamy
wyrazami sumy
.
Przykłady sum algebraicznych:
-3a³+12a²-5a+1
2x²-xy+2xz
2c-d
Uwaga !
W sumie algebraicznej
-3a³+12a²-5a+1
wyrazami są jednomiany:
-3a³, 12a², -5a, 1
Sumy algebraiczne staramy się
zapisywać w jak najprostszej postaci.
Podkreślamy w jednakowy sposób i
redukujemy wyrazy podobne. My
wyrazy podobne zaznaczyłyśmy takim
samym kolorem.
3x
-
4xy
+
2y
-3-
7x
-
y
+6+
4xy
=-4x+y+3
Przypomnijmy sobie, jak dodajemy i
odejmujemy sumy algebraiczne.
Gdy przed nawiasem jest znak plus,
nawias możemy opuścić.
Przykład:
(4x-y)+(2x+y-7)=4x-y+2x+y-7=6x-7
Gdy przed nawiasem jest znak minus,
opuszczamy nawias, zmieniając
znak każdego wyrażenia z nawiasu
na przeciwny.
Przykład:
(3a+b)-(5a-2b)=3a+b-5a+2b=-
2a+3b
Jaka jest liczba o 6
większą od
kwadratu liczby a
?
Odp. a²=6
Ale to proste ! ;)
Jaka jest liczba 3
razy mniejsza od
połowy liczby c
?
Odp. 0,5c : 3
Brawo ! ;)
Mnożenie jednomianów
przez sumy
Poniższe przykłady pokazują, w jaki
sposób mnożymy jednomian przez
sumę algebraiczną i jak dzielmy sumę
algebraiczną przez liczbę.
Mnożymy jednomian przez każdy
składnik sumy.
-4x*(2x-3)=-8x²+12x
- 4x*2x -4x*(-3)
Dzielimy każdy składnik sumy przez
liczbę.
(12x²=3x=6):6=2x²+0,5x+1
12x²:6 3x:6 6:6
Kolejne przykłady pokazują, jak
wyłączamy przed nawias wspólny
czynnik.
5x²-15xy=5x(x-3y)
5x*x 5x*(-3y)
Zapisz w postaci sumy
algebraicznej:
a) (2x-4xy):2
b) (6a-9ab+1) : (-3)
Odp.
a) x-2xy
b) -2a + 3ab – 1/3
Mnożenie sum
algebraicznych
Na rysunku poniżej przedstawiony jest
prostokąt o bokach a+b i x+y. Pole
tego prostokąta jest równe (a+b)(x+y)
y
x
a
b
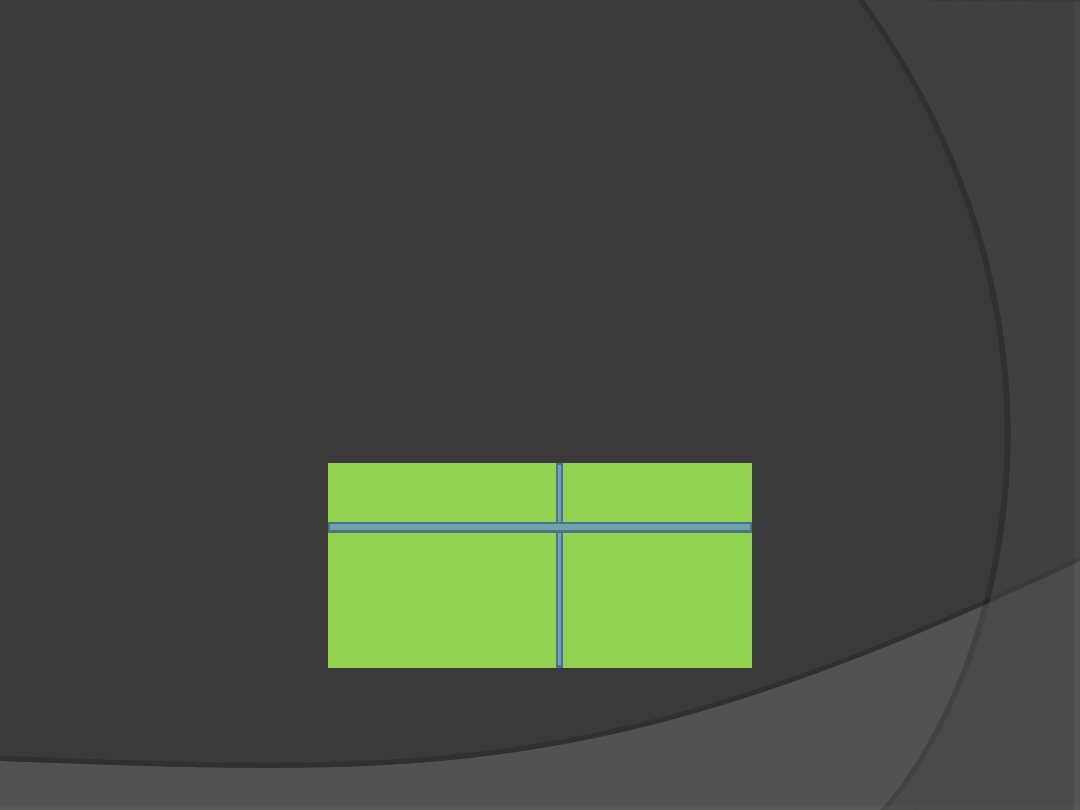
Zauważcie, że pole tego prostokąta jest
sumą pól czterech mniejszych
prostokątów, czyli można je też zapisać
w postaci ax+ay+bx+by.
Otrzymujemy więc równość:
(a+b)(x+y)=ax+ay+bx+by
x
a
b
y
Równość ta pokazuję, w jaki sposób
możemy przekształcać iloczyn
dwóch sum algebraicznych.
( + ) * ( + ) =
= * + * + * + *
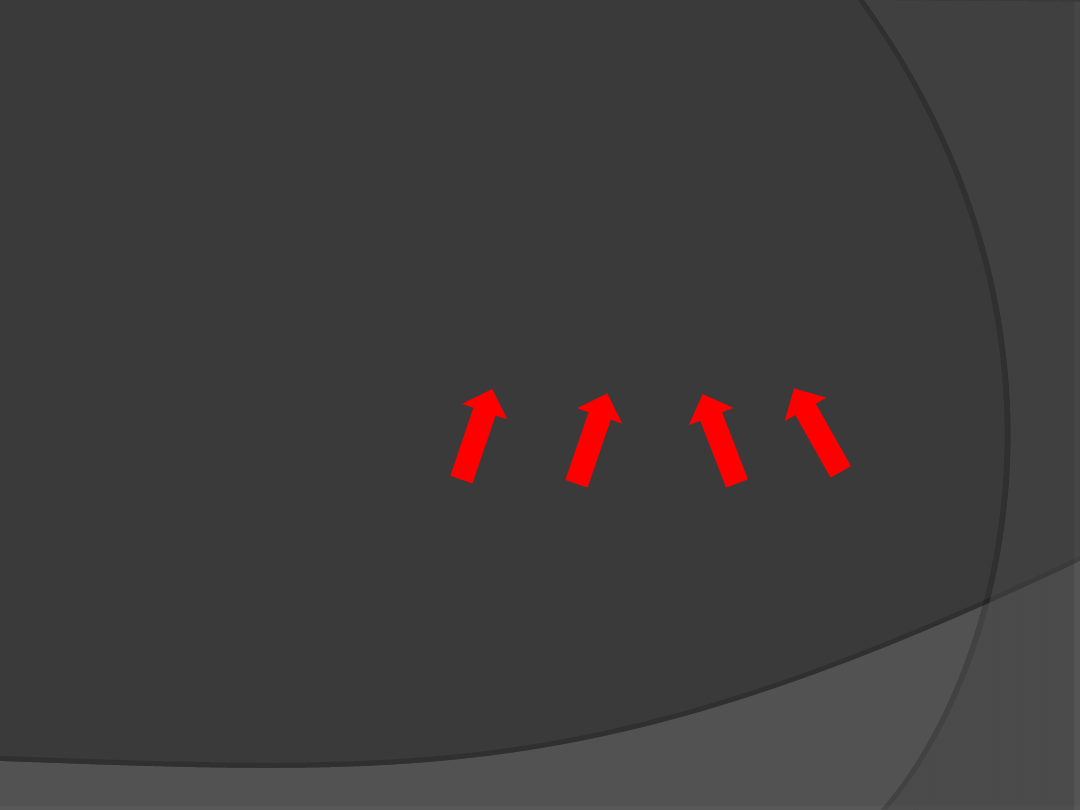
Mnożymy każdy składnik pierwszej
sumy przez każdy składnik
drugiej sumy.
(2a+7)(x+3)=2ax+6a+7x+21
2a*x 2a*3 7*x
7*3
Wzory skróconego
mnożenia
Rysunek przedstawia kwadrat o boku
a+b czyli o polu równym (a+b)².
a
a
b
b
Zauważ, że pole tego kwadratu jest
sumą pól czterech figur: kwadratu o
boku a, dwóch prostokątów o bokach
a i b oraz kwadratu o boku b. Można
je więc zapisać w postaci a²+2ab+b².
Wynika stąd następująca równość:
(a+b)²=a²+2ab+b²
a
a
b
b
Równość tę możemy też uzasadnić
algebraicznie:
(a+b)²=(a+b)(a+b)=a²+ab+ab+b²=
=a²+2ab+b²
Na kolejnych slajdach zapisałyśmy
dwie równości, z których można
skorzystać przy podnoszeniu do
kwadratu sumy oraz różnicy dwóch
liczb. Równości te są nazywane
wzorami skróconego mnożenia.
Kwadrat sumy
dwóch wyrażeń jest
równy kwadratowi pierwszego
wyrażenia plus podwojony iloczyn
pierwszego wyrażenia przez drugie
plus kwadrat drugiego wyrażenia.
(a+b)²=a²+2ab+b²
( + )² = ² + 2* * + ²
Kwadrat różnicy
dwóch wyrażeń jest
równy kwadratowi pierwszego
wyrażenia minus podwojony iloczyn
pierwszego wyrażenia przez drugie
plus kwadrat drugiego wyrażenia.
(a+b)²=a²+2ab+b²
( - )²= ² - 2* * + ²
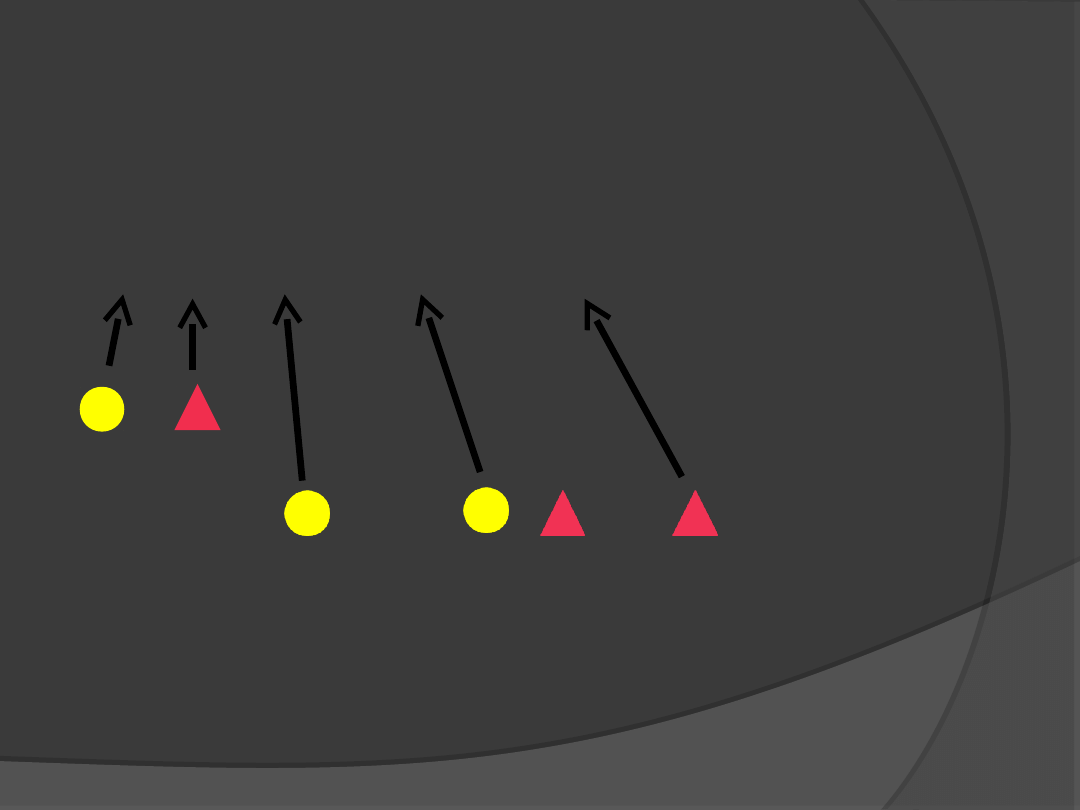
Przykład:
(5+3a)²=5²+2*5*(3a)²+(3a)²=25+30
a+9a²
² 2* * ²
Iloczyn sumy przez różnicę
tych
samych wyrażeń jest równy różnicy
kwadratów tych wyrażeń.
(a+b)(a-b)=a²-b²
( + )( + )= ²- ²
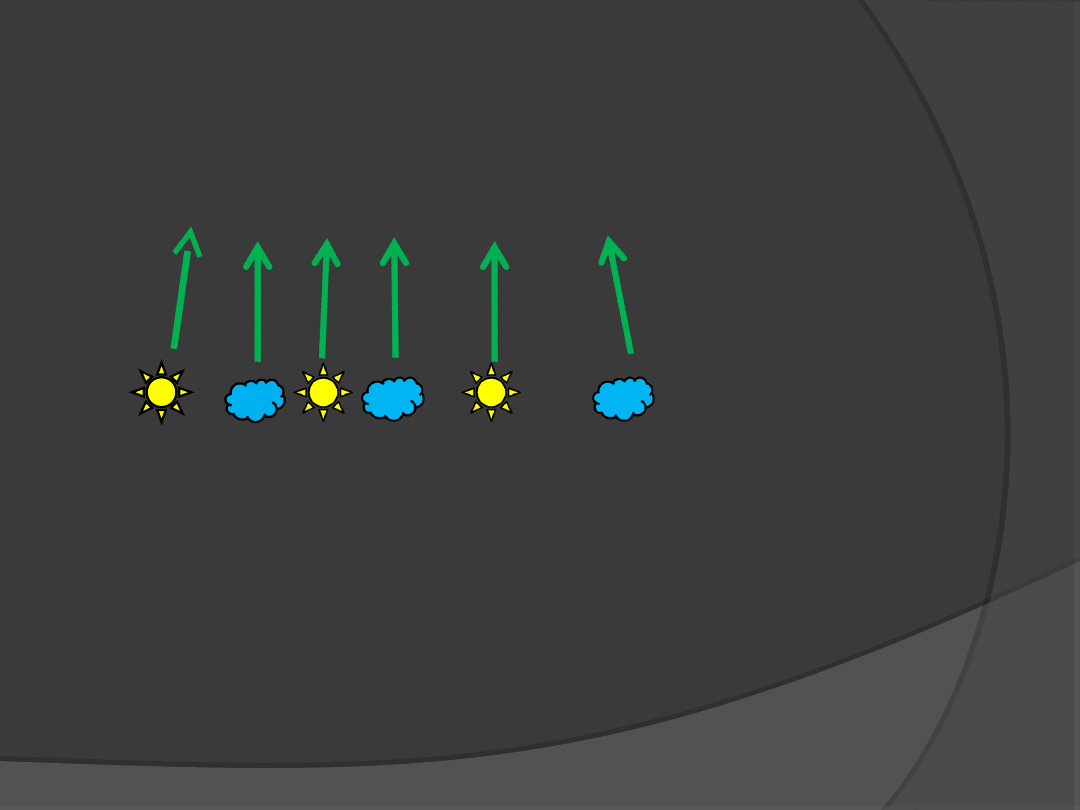
Przykład:
(3x+y²)(3x-y²)=(3x)²-(y²)²=9x²-(y²)²
² ²
Dziękujemy za uwagę !
Pracę wykonały:
Natalia Zwierz
i
Angelika Konopacka