mgr inż. Hieronim Karbowiak

24 godziny lekcyjne zakończone egzaminem pisemnym

24 godziny lekcyjne zakończone egzaminem pisemnym

Literatura:

1.

Podstawowe podręczniki:

Podstawowe podręczniki:

• T. Michalski, Statystyka, WSiP, Warszawa 1994, 2000r.,2004r.;

• A. Komosa, Statystyka – ćwiczenia, Ekonomik s.c.,Warszawa

2006r.

2.

Dodatkowe podręczniki:

Dodatkowe podręczniki:

• Rocznik statystyczny, Mały rocznik statystyczny;

• I. Bąk, Statystyka w zadaniach cz.1 i cz., 2 WNT, Warszawa

2002r.;

• J. Gronek, Statystyka na co dzień, PWN, Warszawa 2003 r.;

• P. Tatarzycki, Statystyka po ludzku, Złote myśli, Gliwice

2007r.;

• J. Czempas, Elementy statystyki – podstawowe mierniki i

metody,Wyższa szkoła biznesu w Dąbrowie Górniczej,

2000r.

• M.Cieciura, J.Zacharski, Metody probabilistyczne w ujęciu

praktycznym, Vizja Press&it sp.z.o.o, Warszawa 2009r.;

• Janina Jóźwiak, Jarosław Podgórski, Statystyka od podstaw,

PWE,

Warszawa 2004r.

1. Wiadomości wstępne;

• Historia, przedmiot, rola, zadania statystyki, służby statystyki, podstawowe pojęcia

statystyczne, źródła wiedzy statystycznej, obowiązki przedsiębiorstw związane ze
statystyką publiczną, praca z rocznikiem statystycznym.

2. Organizacja badania statystycznego

• Pojęcie badania statystycznego, rodzaje badań statystycznych, metody, techniki,

procedury, techniki losowań, sposoby zbierania informacji, formularze statystyczne,
etapy badań itp.

3. Obserwacja statystyczna i opracowanie materiału statystycznego

• Zasady gromadzenia i przechowywania materiału statystycznego, kontrola danych,

porządkowanie i grupowanie danych, zliczanie, poziom dokładności

4. Formy prezentacji danych statystycznych

• Typy prezentacji danych, metody prezentacji, budowa i rodzaje, sposoby prezentacji

5. Analiza danych statystycznych

• Podstawy analizy danych, jednostki statystyczne, analiza struktury, natężenia, miary

klasyczne i pozycyjne, analiz dynamiki itp., interpretacja obliczonych mierników

6. Wnioskowanie statystyczne

• Metody wnioskowania statystycznego, estymacja, weryfikacja hipotez.

Praca kontrolna – zadanie domowe

Temat:

Analiza przeciętnego poziomu zjawiska za pomocą miar

klasycznych (położenia, rozproszenia, zróżnicowania, wskaźników
struktury i kwantyli).

Słuchacz otrzyma kartkę z dokładnym zadaniem:

Tablicę z szeregiem statystycznym, którą będzie musiał

przekształcić w ten sposób, że do liczb podanych w tabeli numery
parzyste z listy dodają numer z listy, a nieparzyste odejmują, a
następnie wykonują uszczegółowione polecenia z treści zadania

Termin oddania pracy

Termin oddania pracy

pierwsze zajęcia w styczniu

pierwsze zajęcia w styczniu

2012 r.

2012 r.

Policealna Szkoła Zawodowa AP – Edukacja

Pracadomowa

Z przedmiotu………………….

Kierunek : ……………………..

Zawód: …………………………

Semestr : (słownie)

Rokszkolny: 2011/2012

Imięi NazwiskoUcznia (słuchacza)

Nr na liście ……………….

Wykładowca: …………………………………………..

Ocena:

Podpiswykładowcy:

Strona tytułowa

Słowo „statystyka” pochodzi od

łacińskiego słowa „status”, które
oznacza stan rzeczy, państwo.

W łacinie średniowiecznej słowa

„status” używano dla wyrażenia
politycznego stanu rzeczy.

USTAWA z dnia 29 czerwca 1995 r. o statystyce publicznej - określa zasady i tworzy
podstawy
rzetelnego, obiektywnego, profesjonalnego i niezależnego prowadzenia badań
statystycznych,
których wyniki mają charakter oficjalnych danych statystycznych, oraz ustala
organizację i tryb
prowadzenia tych badań i zakres związanych z nimi obowiązków.
Przepisy karne z ww. ustawy
Art. 54. Kto narusza tajemnicę statystyczną, podlega karze pozbawienia wolności do lat 3.
Art. 10. Zbierane i gromadzone w badaniach statystycznych statystyki publicznej dane
indywidualne i dane osobowe są poufne i podlegają szczególnej ochronie; dane te mogą być
wykorzystywane wyłącznie do opracowań, zestawień i analiz statystycznych oraz do tworzenia
przez służby statystyki publicznej operatu do badań statystycznych prowadzonych przez te służby;
udostępnianie lub wykorzystywanie danych indywidualnych i danych osobowych dla innych niż
podane celów jest zabronione (tajemnica statystyczna).
Art. 55. Kto w celu osiągnięcia korzyści majątkowej lub osobistej wykorzystuje dane statystyczne,
z którymi zapoznał się w związku z wykonywaniem pracy lub czynności na zlecenie prowadzącego
badanie statystyczne statystyki publicznej,
podlega karze pozbawienia wolności do lat 5.
Art. 56. 1. Kto wbrew obowiązkowi przekazuje dane statystyczne niezgodne ze stanem
faktycznym, podlega grzywnie, karze ograniczenia wolności albo pozbawienia wolności do lat 2.
2. W wypadku mniejszej wagi sprawca podlega grzywnie.
Art. 57. Kto wbrew obowiązkowi odmawia wykonania obowiązku statystycznego albo udzielenia
informacji w spisie powszechnym lub innym badaniu statystycznym, podlega grzywnie.
Art. 58. Kto wbrew obowiązkowi przekazuje dane statystyczne po upływie oznaczonego terminu,
podlega karze grzywny.
Wszystkie powyższe informacje są na stronie http://www.stat.gov.pl/gus oczywiście
zachęcam
do zapoznania się z całą ustawą:) Na tej stronie można znaleźć także roczniki
statystyczne, z
którymi będziemy czasem pracować.

Statystyka

jest dyscypliną naukową,

zajmującą się „konstrukcją metod
liczbowego opisu i wnioskowania o
zjawiskach masowych”.

Z takiej definicji wynika, że należy

wyróżnić tutaj dwa pojęcia: metodę i
zjawisko masowe.

Statystyka

-

określa zbiór informacji liczbowych,

dotyczących celowo wybranej grupy lub kategorii zjawisk

(dostarcza informacji o podstawowych dziedzinach życia i

funkcjonowania państwa), dyscyplina naukowa, traktująca

o metodach liczbowego opisu i wnioskowania o

prawidłowościach występujących w procesach masowych,

nowoczesna statystyka dostarcza metod (narzędzi) do

podejmowania decyzji w warunkach niepewności.

Statystyka matematyczna

- dostarcza

metod wyboru prób losowych i reguł
wnioskowania, czyli pozwala na uogólnienia
wniosków wynikających z obserwacji części
zbiorowości tak aby ryzyko popełnienia
błędu było małe (rachunek
prawdopodobieństwa

)

Statystyka opisowa

- dostarcza metod i

procedur gromadzenia, opracowania i
prezentacji danych statystycznych, celem
jest zwięzły opisy materiału statystycznego.

Statystyka branżowa -

WIEDZA POTOCZNA

WIEDZA NAUKOWA

(socjalizacja itd.) – wiedza zindywidualizowana,
subiektywna, różna, zależna od doświadczeń
życiowych.

Jednolita, systematyczna. Sądy należące do
tzw. korpusu wiedzy w danym momencie,
uznawane są za prawdziwe, zmierzające do
obiektywizacji.

Ma charakter konkretny i praktyczny. Ludzie
posługują się nią w życiu społecznym. Zawiera
(na ogół) sądy jednostkowe, uogólnienia
sprowadzane są do pewnych klas zachowań
człowieka, stosowane do określonych sytuacji.

Ma charakter abstrakcyjny; sądy zawarte w
niej nie są jednostkowe, lecz ogólne. Odnoszą
się do zbiorów ludzi i mają charakter
generalizacji

historycznych

lub

praw

naukowych.

Język – wiedza potoczna operuje językiem
potocznym. Jest to język mało precyzyjny
(niejednoznaczny), nie jest wolny od ocen,
posiada komponenty emocjonalne.

Język nauki jest wolny od ocen. Jest, jak mówi
Osowski, „językiem treści pojęciowych”.

Nie

jest

systematyczna.

Wiedza

pełna

wewnętrznych sprzeczności, mało spójna; a w
związku z tym sądy jej są wewnętrznie
sprzeczne i niespójne

Immanentną cechą nauki jest systematyczność
jej wiedzy. Jest uporządkowana, w sposób
świadomy dąży do eliminacji sprzeczności weń
się pojawiających.

Nie troszczymy się o jej uzasadnienie – działa
ona na zasadzie pewnej oczywistości. Jest to
produkt naszych doświadczeń, życia, naszych
bliskich.

Empiryczne uzasadnienia sądów są sprawą
zasadniczą.

Uzasadnienie

musi

być

uzasadnieniem intersubiektywnym, procedura
badawcza jawna, określony stopień pewności i
generalizacji sądów.

Cel statystyki

Statystyka określa, jak należy zebrać,

porządkować, prezentować, uogólniać i

analizować dane liczbowe o interesujących

nas

zjawiskach

i

procesach.

Wymienione

działania,

stanowiące opis zjawisk są jedną z dwu jej

funkcji.

Drugą funkcją statystyki jest indukcja,

polega ona na formowaniu reguł, które

pozwalają uogólniać wnioski, uzyskane

dzięki badaniom części zbiorowości, na jej

całość.

Z podziałem cech na jakościowe i ilościowe wiąże się
również stosowanie różnych statystycznych metod
badania. Po wytypowaniu cech, które będą nas
interesować w badaniu, musimy podjąć decyzję, jak
będziemy mierzyć wartości tych cech (bądź określać ich
odmiany, jeśli są niemierzalne) w trakcie obserwacji.
Badając liczbę krwinek białych, możemy ją określić jako
"poniżej normy", "w normie" lub "powyżej normy", lub
podać ich liczbę w 1 ml krwi. Podobnie, badając wzrost
pacjentów, możemy podać go w centymetrach albo
używać określeń: "niski", "średni", "wysoki". Wybór
takiego czy innego pomiaru zależy oczywiście od celu
badania. Pamiętajmy jednak, że w trakcie opracowywania
zgromadzonych informacji możemy przejść od bardzo
ścisłych i dokładnych pomiarów do określeń ogólnych,
natomiast odwrotna droga nie jest możliwa

Rola i przedmiot statystyki
Przedmiotem badania statystyki są masowe zjawiska
społeczno-ekonomiczne, oraz procesy zachodzące w tych
zjawiskach. Statystyka bada te zjawiska i procesy,
analizuje ich rodzaje i formy, kierunki i tempo rozwoju,
wykrywając ich właściwości i prawidłowości. Statystyka
jest bardzo ważnym elementem w procesie podejmowania
decyzji. Pozwala ona konsumentowi na zapoznanie się z
aktualnymi cenami, pozycją na rynku oraz innymi
przydatnymi cechami, którymi kierujemy się podczas
zakupów. Dzięki statystyce wiemy jak kształtuje się rynek
produktów i usług. Jak widzimy ta nauka jest nam bardzo
potrzebna w naszym codziennym życiu. Poprzez badania
statystyczne możemy racjonalnie podjąć najlepszą
decyzje np.: w przypadku wyboru szkoły, sklepu,
przedsiębiorstwa, firmy i produktu.

Zadania statystyki:

·Prowadzenie analiz statystyczno-ekonomicznych, które są
nastawione przede wszystkim na kwestię przyczynowości
zjawisk.

·Informacja statystyczna – obejmuje ona kształtowanie się
w czasie i przestrzeni wszystkich zjawisk, które składają
się na proces p produkcji społecznej.

·Opracowywanie prognoz krótkoterminowych,
średnioterminowych i długoterminowych.

P R O C E S D E C Y Z Y J N Y

Teoria decyzji to wspólny obszar zainteresowań wielu
różnych dziedzin nauki, obejmujący analizę i
wspomaganie procesu podejmowania decyzji.

Korzystają z niej i dostarczają metod między innymi:
matematyka, statystyka, psychologia, socjologia,
ekonomia, zarządzanie, filozofia, informatyka,
medycyna.

Metody teorii decyzji wykorzystuje się wszędzie tam, gdzie podjęcie
decyzji jest z pewnych powodów trudne.

Przykładowo przyczynami mogą być:

• duża liczba możliwych wariantów - np. wybór najlepszego
kandydata na dane stanowisko
• skomplikowana sytuacja decyzyjna - np. opracowanie takich tras i
rozkładów jazdy autobusów, aby zapewnić wysoki poziom obsługi
przy jak najniższym koszcie
• możliwość wysokich korzyści lub dużych strat - np. wybór sposobu
ulokowania oszczędności
• skomplikowany proces decyzyjny - np. podejmowanie grupowych
decyzji w dużych organizacjach
• waga problemu decyzyjnego - np. ustalenie okręgów wyborczych w
wyborach prezydenckich
Z powyższych przykładów wynika, że metody teorii decyzji stosujemy
wszędzie tam, gdzie koszt ich zastosowania może przynieść
wymierne korzyści.

Metoda statystyczna

to sposób badania

liczbowego określonych zbiorowości, za
pomocą odpowiednich narzędzi i procedur.

Zjawisko masowe

to takie zjawisko które

często występuje, dotyczy ono więc
wystarczająco dużej liczby jednostek. Dla
odróżnienia, jednostkowym zjawiskiem jest
pojedyncze, lub rzadko występujące
zdarzenia. Niektóre zjawiska mogą być
traktowane jednostkowo jak i masowo, w
zależności od perspektywy z jakiej je
analizujemy.

Zbiorowość statystyczna

Przedmiotem badania statystycznego jest zbiorowość
statystyczna zwana inaczej populacją lub masą
statystyczną.

Zbiorowość statystyczna

to „zespół jednostek

objętych badaniem statystycznym, posiadających jedną
lub kilka cech wspólnych (stałych) oraz wiele cech je
różnicujących”.

Zbiorowość rozumiana jest więc, jako zbiór dowolnych
jednostek (np. istot żywych, przedmiotów,
przedsiębiorstw, obszarów geograficznych, zjawisk),
które mają chociaż jedną wspólną cechę, a różnią się z
innych punktów widzenia.

•skończenie lub nieskończenie liczne,
•statyczne (elementy obserwowane są w
danym momencie) lub dynamiczne (w
określonym przedziale czasu),
•jednowymiarowe (badanie pod względem
jednej cechy), wielowymiarowe (wielu
cech),
•jednorodne lub niejednorodne.

Podział zbiorowości

statystycznych:

Zbiorowości (populacje)

Zbiorowość próbna (próba) - podzbiór
populacji generalnej, obejmujący część jej
elementów - wybranych w określony
sposób. Próba podlega badaniu
statystycznemu, a wynik jest uogólniany na
zbiorowość generalną.

Zbiorowość (populacja) generalna -
wszystkie elementy, będące przedmiotem
badania, co do których formułowane są
wnioski ogólne.

Statystyki w próbie

Często badanie statystyczne całej

populacji jest nieuzasadnione lub

niemożliwe, dlatego zwykle bada się

jedynie wybrane losowo element

populacji, czyli

próbę losową

, a następnie

wnioskuje na podstawie obserwacji cechy

w próbie o możliwych wartościach cechy

w populacji.

Przykład

Zbiorowością statystyczną mogą być np. studenci
określonego województwa, mają oni dwie cechy
wspólne: mieszkają w tym samym województwie i
studiują, różnią się między sobą rodzajem uczelni
do jakich uczęszczają, ocenami, jaki i cechami
osobowości, wyglądem, płcią itd.

Natomiast zbiorowością statystyczną nie są np.
krzesła w auli wykładowczej o takim samie
kształcie, kolorze, stopniu zużycia.

Jednostka statystyczna

Elementy składowe zbiorowości (próby)

nazywane są jednostkami

statystycznymi (jednostki badania,

obserwacji).

liczebność zbiorowości

Suma jednostek statystycznych

ujmowana jest jako liczebność

zbiorowości (oznaczana jest

symbolem N)

Cechy statystyczne

Jednostka statystyczna w ramach zbiorowości
statystycznej, charakteryzuje się wieloma
właściwościami, czyli cechami statystycznymi.

Cechy wspólne dla wszystkich jednostek danej
zbiorowości to cechy stałe (nie podlegają analizie
statystycznej), natomiast cechy różnicujące
jednostki miedzy sobą to cechy zmienne
(podlegają analizie statystycznej).

Cecha statystyczna to właściwość

populacji,

która

jest

przedmiotem

badania

statystycznego.

Zgodnie

z

definicją cecha statystyczna jest to

funkcja

przypisująca

elementom

populacji elementy zbioru wartości cechy

statystycznej.

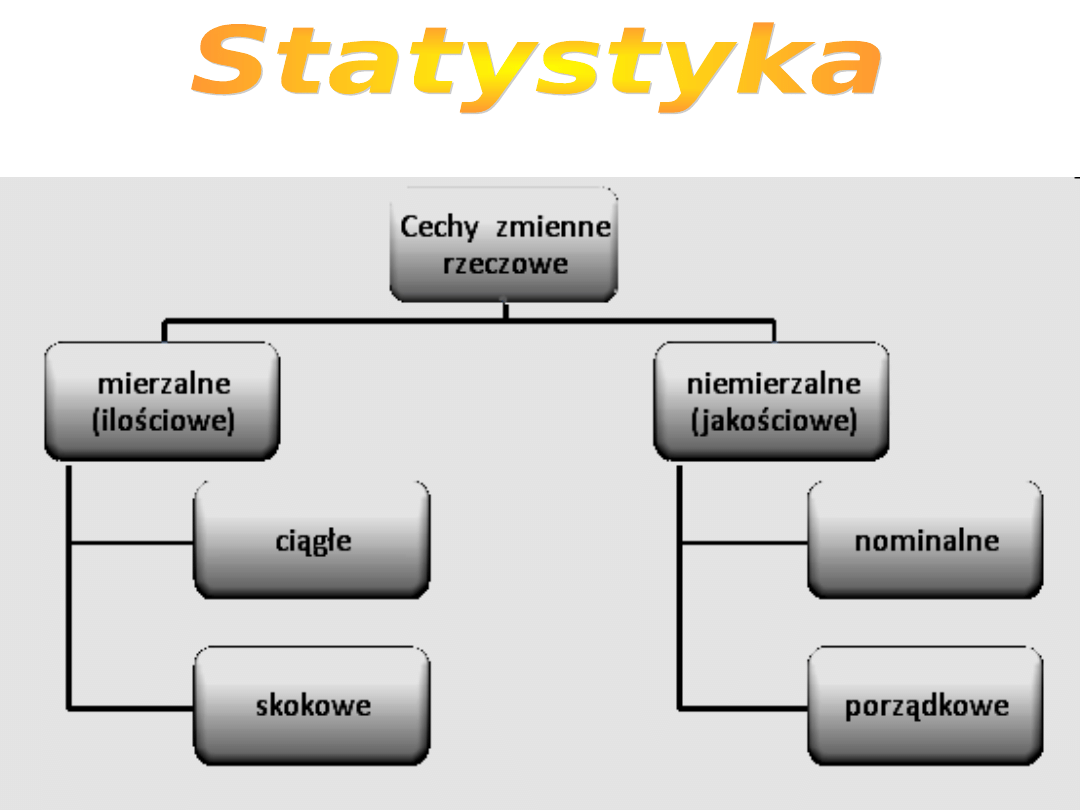
Ilościowe (mierzalne) - np. wzrost, masa,

wiek
Jakościowe (niemierzalne) – np. kolor

oczu, płeć, grupa krwi

Cecha ilościowa ciągła
wzrost, masa wiek

Cechy statystyczne

Cechy stałe

Cechy zmienne

Cecha rzeczowa
(co lub kogo
badamy),

Cecha przestrzenna
(gdzie odbywa się badanie)

Cecha czasowa
(jaki okres jest objęty
badaniem lub w jakiej
chwili ono się odbywa)

Cecha jakościowa
Kolor oczy, płeć, wiek

Cecha ilościowa

Cecha ilościowa skokowa
ilość posiadanych dzieci,
ilość gospodarstw
domowych

Cechy stałe umożliwiają scalenie poszczególnych
jednostek w jednorodną zbiorowość, i odgraniczenie jej od
innych zbiorowości.

Dzielą się na:
• rzeczowe (przedmiotowe) – decyduje o merytorycznej
klasyfikacji jednostek do określonej zbiorowości;
• czasowe – określają jaki moment lub okres dotyczy
obserwacja;
• przestrzenne – ujmuje zbiorowość w przestrzeni bądź
w określonym miejscu.

Cechy stałe czasowe oraz stałe przestrzenne określają
odpowiednio czas i miejsce w którym pojawiają się cechy
rzeczowe jednostek zbiorowości. Cechy stałe służą tylko
do wyodrębnienia zbiorowości statystycznej, nie stanowią
więc przedmiotu badania.

Cechy zmienne, czyli te dzięki którym
pojedyncze jednostki różnią się miedzy
sobą, dzielą się na rzeczowe czasowe i
przestrzenne.

Cechy mierzalne to takie, które mogą być
wyrażane przy pomocy określonych jednostek
miar, czyli mogą przyjmować określone wartości
liczbowe (np. wiek-w latach, wzrost-w cm,
wynagrodzenie-w PLN, a także liczba osób w
gospodarstwie domowym, liczba bezrobotnych w
Polsce).

Cechy ciągłe (o zmienności ciągłej) mogą
przyjmować

wszystkie

wartości

liczb

rzeczywistych

z

określonego

przedziału

liczbowego (np. koszt, wiek, waga), przy czym
ilość miejsca po przecinku uzależniona jest od
dokładności dokonywanych pomiarów.
Cechy skokowe (o zmienności skokowej) mogą
przyjmować skończony lub przeliczalny zbiór
wartości w danej skali liczbowej. Cechy skokowe
mogą, więc być wyrażone tylko liczbami
zmieniającymi się skokami, bez pośrednich
wartości (np. liczba studentów na roku, liczba
pracowników przedsiębiorstwa).

Cechy niemierzalne charakteryzują się tym, że
nie można ich wyrazić za pomocą liczb, a jedynie
można je opisać słownie (np. płeć - kobieta,
mężczyzna; kolor - czarny, biały, zielony, itd.;
wykształcenie

-

podstawowe,

gimnazjalne,

średnie, itd.).

Cechy porządkowe to cechy słownie, dające się
uporządkować

w

pewnej

kolejności

(np.

wykształcenie, oceny egzaminów).

Cechy nominalne nie można ustawić w
odpowiedniej kolejnością (np. płeć, grupa krwi,
kolor oczu).

Cechy jakościowe (niemierzalne)

to takie, których nie

można jednoznacznie scharakteryzować za pomocą liczb
(czyli nie można zmierzyć). Możemy je tylko opisać
słowami. Możliwa jest zatem jedynie zupełna i rozłączna
klasyfikacja zbioru wyników. Podstawową operacją
pomiarową jest identyfikacja kategorii, do której należy
zaliczyć wynik. Prowadzi to do podziału zbioru wyników na
podzbiory rozłączne. Do cech jakościowych zaliczamy np.
płeć, grupę krwi, kolor włosów, zgon lub przeżycie, stan
uodpornienia przeciwko ospie (zaszczepiony lub nie) itp.
W przypadku grupy krwi rezultat pomiaru będzie
następujący: n1 pacjentów ma grupę krwi A, n2 pacjentów
- grupę krwi B, n3 pacjentów - grupę AB i n4 - grupę O.

Informacje o cechach statystycznych i ich
warian-tach dla poszczególnych jednostek
uzyskiwane są w wyniku

badania statystycznego

.

Proces ten umiejętnie zorganizowany i
przepro-wadzony pozwala poznać zjawisko
masowe.

Badania statystyczne polegają na zebraniu
informacji, czyli różnych danych nie koniecznie
liczbowych o określonej zbiorowości, ich
opracowaniu a następnie wyciągnięciu
wniosków.

Cel badania - to użyteczność, którą chcemy poznać, może być ona

praktyczna lub naukowa czy naukowo - poznawcza.

Pierwszym etapem badania statystycznego jest określenie przedmiotu i

zakresu badania zbiorowości, jednostki, jednostek i cech statystycznych

tych, które będziemy badać.

Następnie dokonujemy wyboru metody badania decydującej o jego

jakości. Podstawowym kryterium jest liczba jednostek statystycznych

objęty badaniem statystycznym

TYPY BADAŃ STATYSTYCZNYCH

TYPY BADAŃ STATYSTYCZNYCH

Badania pełne - badanie to obejmuje wszystkie jednostki
statystyczne wchodzące w skład zbiorowości statystycznej. Jest to spis
powszechny (spis statystyczny).

Rejestracja statystycznych - wpisywanie zdarzeń i faktów do
odpowiednich rejestrów np. rejestr do wojska, narodzenia dzieci w
przychodniach
Rejestracja bieżąca np. rejestr handlowy.
Sprawozdawczość statystyczna - podawaniu na specjalnym
folmularzu określonych informacji

Badania częściowe - badaniu poddajemy część jednostek
zbiorowości generalnej, czyli próba.

Badania reprezentacyjne - badaniom podlegają tylko pewne
jednostki ze zbiorowości statystycznej - próba reprezentatywna.

Klasyfikacja badań statystycznych według

Klasyfikacja badań statystycznych według

częstotliwości ich prowadzenia

częstotliwości ich prowadzenia

• Badania okresowe

• Badania ciągłe

• Badania sporadyczne

Przykłady:

–

ruch demograficzny ludności miast o liczbie

mieszkańców przekraczających 50 tys. osób,

–

sprzedaż działek budowlanych w ciągu ostatnich

5 lat przez na terenie danego powiatu,

–

opłaty wnoszone z tytułu dzierżawy przez

mieszkańców,

–

wydawane zlecenia dla prowadzenia

działalności gospodarczej przez urzędy,

–

składane zeznania podatkowe w Izbach

Skarbowych.

Wyróżniamy dwa sposoby wyboru:

Wyróżniamy dwa sposoby wyboru:

Celowy - badający wybiera jednostki w sposób świadomy według swoich
kryteriów

Losowy- polega na tym, że wybór jednostek do próby odbywa się w
sposób przypadkowy

1.

1.

Metoda bezpośrednia:

Metoda bezpośrednia:

• Losowanie zależnie (nie wracaz powrotem do zbiorowości)

• Losowanie niezależne(jednostka wraca z powrotem do

zbiorowości)

2. Losowanie warstwowe

2. Losowanie warstwowe

–

wielopoziomowe

wielopoziomowe

polega na podziale przed losowaniem badanej zbiorowości
statystycznej na jakościowo różniące się części, czyli warstwy i
losowaniu z każdej warstwy jednostki – jednostek do prób

Losowanie wielostopniowe stosowane jest np. w przypadku, gdy
badaną zbiorowość można podzielić kolejno na mniejsze grupy. Np.
wybrano:

• 10 miejscowości

• 10 zakładów

• 10 wydziałów

• 10 osób z każdego wydziału

• 10 osób

Badania monograficzne -

Badania monograficzne - polegają na wszechstronnym opisie i
szczegółowej analizie pojedynczej jednostki, lub niewielkiej liczby
charakterystycznych jednostek badanych zbiorowości statystycznych.

Badania ankietowe

Badania ankietowe - ich istota polega na fakcie, że instytucje
organizujące badania zwracają się do określonej grupy osób z
zaproszeniem do dobrowolnego wypowiedzenia się w określonej
sprawie.

Szacunek statystyczny - stosowany w przypadku, gdy nie możemy
uzyskać interesującej nas zbiorowości lub jej części w sposób
bezpośredni.

Schemat badania statystycznego

obejmuje następujące kroki:

Krok 1. projektowanie BADANIA,

Krok 2. gromadzenie materiału

statycznego,

Krok 3. opracowanie materiału

statycznego,

Krok 4. analiza statyczna.

ETAPY:

ETAPY:



Przygotowanie badania,



Zebranie materiałów statystycznych,



Przygotowanie materiałów statystycznych do opracowania,



Opracowanie materiału statystycznego,



Prezentacja danych statystycznych,



Analiza statystyczna.

Przygotowanie badania.

Przygotowanie badania.

Cel badania



Przedmiot badania w ujęciu rzeczowym, czasowym i terytorialnym



Zakres badania - wybór cech charakterystycznych podlegających
badaniom



Metoda badania (pełne lub częściowe)



Plan badań, czyli harmonogram, formularze, instrukcje
statystyczne



Sposób gromadzenia danych, przez kogo i w jaki sposób np.
(spis,

sprawozdawczość statystyczna, techniki specjalne:

eksperyment,

ankietowanie, wywiad z

kwestionariuszem itd.
Formularze statystyczne, ankiety, druki, programy
komputerowe jest to zbiór spisanych pytań dotyczących
badanych cech rozważanych zbiorowości statystycznych. Formularz
statystyczny składa się z nagłówka (tytuł,nr, adres) z
kwestionariusza właściwego, czyli zasadniczej części formularza, w
którym zawarte są wszystkie pytania formularza statystycznego.
Pytania mogą być w postaci tabelarycznej, tekstowej i mieszanej.
Tabela składa się z boczku i części końcowej.

Każda pozycja formularza jest opisana w instrukcji statystycznej,
która jest niezbędna, aby uniknąć błędnych interpretacji i uzyskać
jednolitą odpowiedź, Powinna zawierać podstawę prawną,
przedmiot badania, terminy, sprawozdania itp.

Materiał statystyczny jest to zbiór informacji o wartościach

Materiał statystyczny jest to zbiór informacji o wartościach

badanych cech w poszczególnych jednostkach statystycznych,

badanych cech w poszczególnych jednostkach statystycznych,

który powstaje w wyniku prowadzonych obserwacji

który powstaje w wyniku prowadzonych obserwacji

Dzielimy go na:



Pierwotny materiał zebrany specjalnie dla naszych celów



Wtórny obejmuje materiały już poprzednio zebrane przez
inne jednostki i wykorzystane dla naszych celów, np. GUS



Kontrola materiału statystycznego



Kontrola formalna, czyli kompletność zebranego materiału,



Kontrola merytoryczna- obejmująca kontrole zgodności
rachunkowej i logicznej poprawności zapisów

Zebranie materiałów statystycznych,

Zebranie materiałów statystycznych,

Przygotowanie materiału statystycznego do
opracowania.

Stosujemy dwa etapy opracowania materiału statystycznego:

1. Grupowanie - polega na podziale całej zbiorowości statystycznej na

mniejsze części



Grupy proste - jedna cecha statystyczna



Grupy złożone - co najmniej dwie cechy statystyczne

Po podzieleniu zbiorowości na grupy według pewnej cechy

ustalamy kolejność oraz nazwy tych grup otrzymujemy
uporządkowane nazwy grup tworzące wykaz klasyfikacyjny.

Wykaz klasyfikacyjny musi być wyczerpujący logiczny i

przejrzysty. W przypadku, gdy badana cecha mierzalna ma charakter
ciągły, warianty cech przedstawiamy w postaci przedziałów
liczbowych (przedziały klasowe).

Opracowanie materiału statystycznego

Opracowanie materiału statystycznego

Metody techniczno-organizacyjne opracowania materiału statystycznego.

Po dokonaniu grupowania statystycznego następuje zliczenie

materiału, czyli ustalenie liczebności poszczególnych grup.

Rozróżniamy np. sposoby zliczenia materiałów:



Bezpośrednie - ręczne



Sposób kreskowy,



Sposób kartkowy,



Sposób maszynowy.

W metodzie maszynowego zliczania poszczególne informacje zawarte w
formularzach statystycznych przenoszone SA za pomocą umownych
znaków cyfrowych na karty maszynowe. Dotyczy to cech mierzalnych i
niemierzalnych.

Prezentacja danych statystycznych.

Rozróżniamy trzy sposoby prezentacji:

Rozróżniamy trzy sposoby prezentacji:



Metoda tabelaryczna,



Metoda graficzna,



Metoda opisowa.

Analiza statystyczna.

Analiza statystyczna.

to przeprowadzenie analizy - oceny uzyskanych danych statystycznych przy

zastosowaniu różnych miar statystycznych. To również opracowanie materiału
diagnostycznego w zrozumiałej dla zamawiającego formie, który to na podstawie tych
danych będzie mógł podjąć decyzję, wyciągnąć wnioski, itp.



analiza struktury zjawisk:



miary zróżnicowania,



pozycyjne,



miary asymetrii,



miary tendencji centralnej,



miary koncentracji.



analiza współzależności zjawisk:



miary korelacji,



miary regresji.



analiza dynamiki zjawisk:



miary tendencji rozwojowej,



miary wahań okresowych,



miary wahań przypadkowych,



indeksy statystyczne.

Ankiety

Ankiety

Rodzaje ankiet:



pocztowa (rozsyłana) wysyłka - zwrot pocztą;



prasowa (publikowana w prasie) - zwrot pocztą;



opakowaniowa (dołączona do sprzedawanych towarów) -
zwrot pocztą;



radiowa (tekst ogłaszany w radiu) - zwrot pocztą;



audytoryjna (rozdawana przy różnych okazjach np.
podczas pokazu) - zbierana osobiście lub wysyłana
pocztą

Błędy statystyczne

Rachunek błędów statystycznych jet to zespół różnych

zagadnień z pogranicza metrologii, statystyki i matematyki.
Obejmuje on zasady opracowywania i prezentacji wyników. Nie
ma wyników, które nie zawierały by żadnych błędów. Błąd
pomiarowy nie powstaje jedynie w wyniku pomyłki.

Mamy następujace typy błędów:

Błąd statystyczny, przypadkowy - wynikajacy z ogółu wpływó
środowiska, których często nie można zidentyfikować.
Charakteryzuje się niewielka wartoscią i znakiem (często
losowym). I eliminuje się go poprzez wykonywanie wielu
pomiarów w tych samych warunkach oraz uśrednianie.
Błąd systematyczny – wynika z zastosowanej metody pomiaru lub
innych przyczyn. Charakteryzuje się stałym znakiem i stałą
wartością czyli powoduje zawyżenie lub zaniżenie wyniku
pomiaru. Dość często nazywany jest popraką.

Wyróżnia się również błąd gruby (pomyłkę), który jest pewną

odmianą błędu przypadkowego, to jest w sensie jego pojawienia się. Ma
on miejsce, wtedy gdy otrzymany wynik pojawia się i znacznie odbiega
od pozostałych danych. Wtedy wyniki take odrzycamy.

Na wyniki pomiarów statystycznych ma ją wpływ różne czynniki,

które są zależne od wykonującego badania oraz zastosowanej np.
aparatury pomiarowej itp. Np.

 Przyrząd pomiarowy. Każdy przyrząd ma określoną dokładność. Np.

linijką centymetrową zmierzymy długość ciała z dokładnością do 1 mm.

 Niedokładne określenie mierzonej wielkości. Wiele wielkości

fizycznych ma charakter statystyczny. Przykładem takiej wielkości jest
temperatura. Wielkości tego rodzaju ze względu na fluktuacje nie mogą
być zmierzone dowolnie dokładnie.

 Niedokładność odczytu.

 Czynniki zewnętrzne. W czasie pomiaru ziemskiego pola

magnetycznego, należy uwzględnić zewnętrzne pole magnetyczne
konstrukcji np. centralnego ogrzewania. W czasie pomiaru oporu żarówki
należy uwzględnić zmianę temperatury.



Błędy tablicowe.

Błędy tablicowe. Są to błędy związane z przyjęciem niewłaściwej
wartości stałej tablicowej.



Błędy przypadkowe.

Błędy przypadkowe. Wszystkie nie uwzględnione przez nas czynniki
wpływają na pomiar w sposób przypadkowy, raz zmniejszając, raz
zwiększając mierzoną wartość.



Błąd pierwszego rodzaju
błąd polegający na odrzuceniu tak zwanej hipotezy zerowej, która w
rzeczywistości jest prawdziwa. Nazywamy go

poziomem istotności

błędu.



Błąd drugiego rodzaju
polegające na nieodrzuceniu hipotezy zerowej, która jest w
rzeczywistości

fałszywa. a jego dopełnienie do jedności nazywane

jest

mocą testu.



Błąd trzeciego rodzaju

błąd trzeciego rodzaju określa się też wszelkie inne błędy, które mogą
wyniknąć przy testowaniu hipotez, np. błąd wynikający z zaokrąglenia

wartości statystyki testowej podczas obliczeń komputerowych.

Unikaj pytań otwartych, czyli takich w których respondent sam wpisuje swoje uwagi i

wnioski. Pytania te są często w badaniu bardzo potrzebne, jednak zbyt wiele takich pytań
uniemożliwia

przeprowadzenie analizy ilościowej, czyli obliczenia statystyk na podstawie

ankiety.
      
Staraj się zadawać jasne i zrozumiałe pytania.
Sugeruj odpowiedzi tak aby można je było łatwo umieścić przynajmniej na skali
pięciostopniowej (Tzw. skali Likerta).
      Przykład:
      " Pytanie 1.  Wykształcenie:
      a) Podstawowe
      b) Zawodowe
      c) Średnie
      d) Wyższe
      e) Stopień doktora"

Lub inny przykład (*):
      "Pytanie 2. Czy jesteś zadowolony z systemu motywacji w twoim przedsiębiorstwie:
      a) Zdecydowanie zadowolony,
      b) Zadowolony,
      c) Umiarkowanie zadowolony,
      d) Trudno mi powiedzieć,
      e) Umiarkowanie niezadowolony,
      f) Niezadowolony,
      g) Zdecydowanie niezadowolony."

Współczynniki jakimi opisujemy zjawiska, cech ststystyczne są
to różnego rodzaju współczynniki matematyczne miedzy
innymi do nich zaliczamy:

Średnie klasyczne:

·średnia arytmetyczna
·średnia harmoniczna
·średnia geometryczna.

Średnia arytmetyczna

– jest wartością, którą otrzymujemy z

podzielenia ogólnej sumy wartości cechy przez ogólną sumę
liczebności.

Średnia harmoniczna

– średniej arytmetycznej nie można stosować

jako miary przeciętnegogo poziomu zjawisk wyrażonych wielkościami
względnymi, tj. uzyskiwanymi jako iloraz dwóch wielkości prostych.

Średnia geometryczna

- Mierząc stosunkowe zmiany zjawiska

często chcemy ustalić średnie tempo tych zmian przypadające na
jednostkę czasu. To średnie tempo ustalamy stosując średnią
geometryczną.
Średnia geometryczna jest to pierwiastek n – tego stopnia z iloczynu
wyrażeń pod pierwiastkiem.

Przykład

Załóżmy, że mamy szereg statystyczny,
zawierający 10 obserwacji dotyczących
wieku studentów II roku, o następującej
postaci: 19, 20, 20, 20, 20, 21, 21, 22, 23,
24.

210

10

1







i

i

x

21

10

/

210



Suma wartości zmiennej

stąd średnia arytmetyczna
wynosi:

Przykład

Wyznaczmy średnią arytmetyczną wieku
studentów na podstawie poniższego szeregu
rozdzielczego:

Numer

klasy

Warianty cechy

(wiek w latach) x

i

Liczebności

n

i

1

19

3

2

20

12

3

21

6

4

22

3

5

23

3

6

24

3



Suma

30

• W celu wyznaczenia średniej

arytmetycznej należy  wyznaczyć
sumę

iloczynów

wartości

zmiennych

x

i

przez

liczbę

studentów będących w konkretnym
wieku n

i

. Następnie dzieląc sumę:

• przez liczbę obserwacji n = 30,

otrzymujemy

średnią

arytmetyczną równą 21 lat. 

630

6

1







i

i

i

n

x

Warto zwrócić uwagę na kilka podstawowych
własności średniej arytmetycznej.

• Jest wypadkową wszystkich wartości badanej cechy,

związku z czym nie może być niższa od najmniejszej
wartości zaobserwowanej w badaniu i nie może być
wyższa od wartości największej.

• Wartość średniej zależy nie od liczebności klas, lecz od

ich wzajemnej proporcji. W praktyce oznacza to, że
można ją również wyznaczyć z takich szeregów, gdzie
zamiast liczebności mamy wskaźniki struktury, a
otrzymane wyniki będą jednakowe.

Nie wyznaczamy średniej

arytmetycznej

• kiedy największe liczebności skupiają się wokół

najniższych lub najwyższych wartości cechy.
Niekiedy średnia arytmetyczna wprowadza po
prostu błąd. Dzieje się tak wówczas, gdy
wyznaczamy średnią ze zbiorów
niejednorodnych oraz gdy występują
obserwacje nietypowe, ponieważ średnia
arytmetyczna zaciera różnice indywidualne.

• Natomiast dla zbiorowości z jednostkami

nietypowymi można policzyć średnią
arytmetyczną odrzucając jednostki nietypowe
pod warunkiem, że nie stanowią one co
najwyżej 5% liczebności całej zbiorowości.

• Zbiory niejednorodne mają rozkłady z kilkoma

ośrodkami dominującymi.

Obserwacja statystyczna - pojedyncza realizacja zmiennej

losowej. W praktyce zwykle jest to wielowymiarowa

zmienna losowa, wówczas obserwacją statystyczną jest

wektor realizacji składowych zmiennych losowych

dotyczących tego samego badanego elementu populacji.

Przykład: obserwacją statystyczną może być wektor

danych o konkretnym noworodku, obejmujący jego

wzrost, masę urodzeniową, płeć i obwód głowy.

Obserwacje statystyczne grupowane są w tabele danych.

Zazwyczaj jedna obserwacja mieści się w jednym wierszu

tabeli, każda kolumna odpowiada jednej zmiennej.

Obserwacje statystyczne

Obserwacje statystyczne dzielimy

według dwu kryterium:

– częstotliwość obserwacji
– kompletność materiałów

Ze względu na pierwsze kryterium
rozróżniamy rejestracje bieżące i
spisy.
Drugim kryterium grupowania
obserwacji statystycznych jest
kompletność materiałów;

Wyróżniamy obserwacje całkowite

i częściowe.

Obserwacje całkowite (wyczerpujące) -

uwzględniają tylko wybraną w określony sposób

część badanej populacji.

Obserwacji częściowe stosowanie determinowane

jest rozlicznymi przyczynami: krótszym okresem

trwania

obserwacji,

możliwością

bardziej

dokładnego

ich

przeprowadzania,

niższymi

kosztami i wreszcie, gdy dokonanie obserwacji

łączy się z niszczeniem badanego przedmiotu,

jedynie stosowanie tej metody jest możliwe.