I rok Farmacji
Statystyka część V

- analiza wariancji (ANOVA)

Czy próby mogą pochodzić z populacji o takich samych średnich?
Czy różnice miedzy nimi są statystycznie istotne?

H

0

: zróżnicowanie między grupami jest nie większe niż wewnątrz grup.

H

1

: pomiędzy grupami różnice są istotne statystycznie.

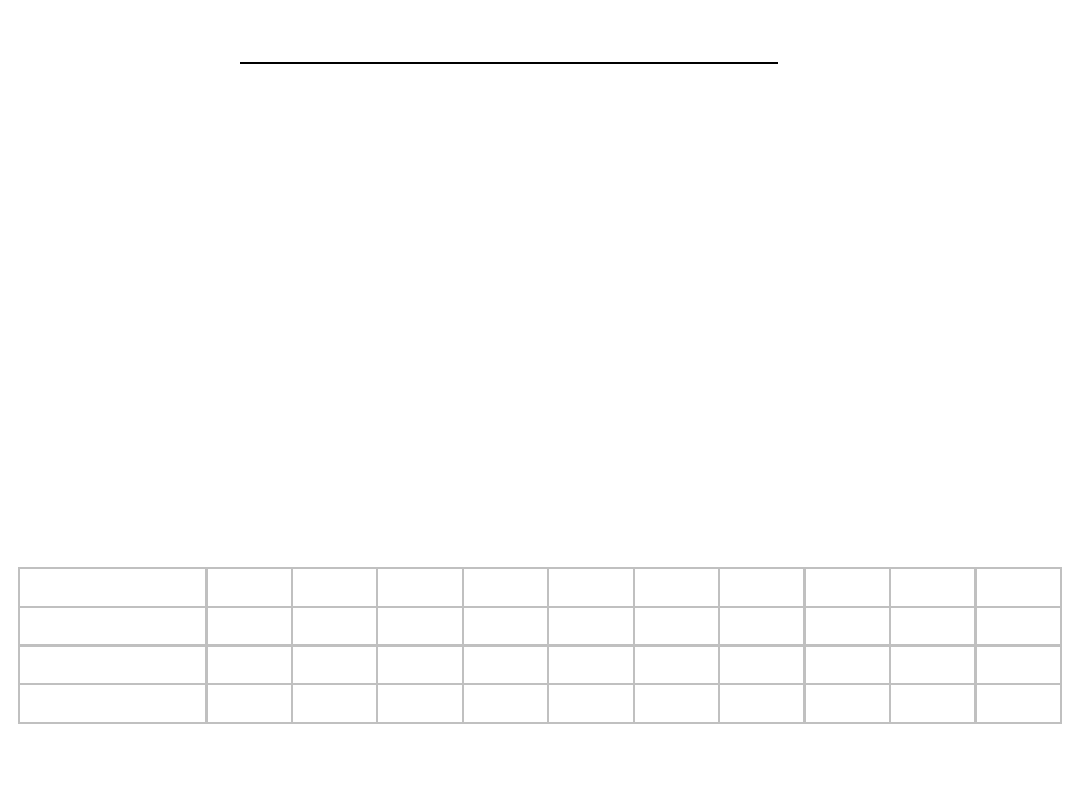
Pobrano cztery próbki.
Czy różnice między nimi są statystycznie istotne?
Czy porównywać metodą każdy z każdym?

Analiza wariancji (ANOVA)

próby

2

3

4

5

6

7

8

9

10

11

porównania

1

3

6

10

15

21

28

36

45

55

0,95 0,95 0,86 0,74 0,60 0,46 0,34 0,24 0,16 0,10 0,06

błąd I rodzaju 0,05 0,14 0,26 0,40 0,54 0,66 0,76 0,84 0,90 0,94

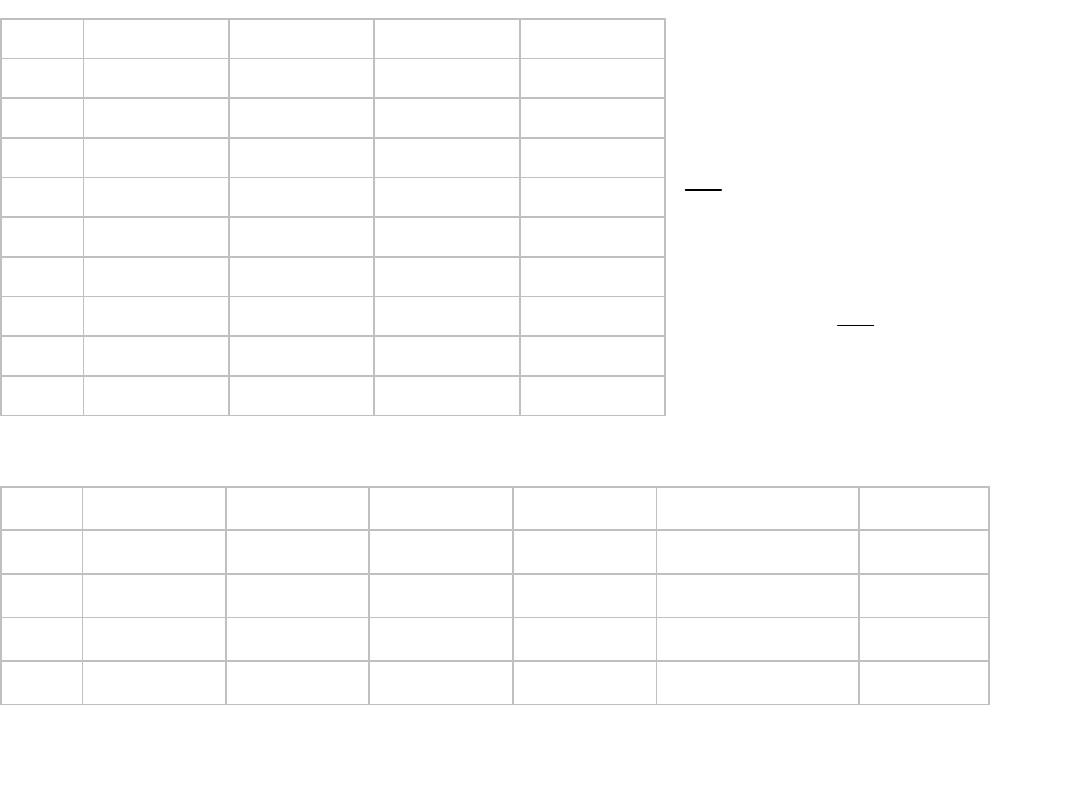
GRUPA 1 GRUPA 2 GRUPA 3 GRUPA 4

1

105

105

103

109

2

106

105

103

104

3

114

106

107

103

4

106

109

101

108

5

115

108

108

104

6

108

106

104

102

7

108

102

103

109

8

112

106

101

106

9

107

107

109

102

Dla całej populacji
(36 próbek):















31

,

388

09

,

11

14

,

106

2

2

X

X

s

X

i

Dla każdej z grup obliczamy: średnią, wariancję i SKO:

GRUPA 1 GRUPA 2 GRUPA 3 GRUPA 4

df

i

8

8

8

8

X

śr

109,00

106,00

104,33

105,22

wariancja

4,1019

s

2

13,75

4,00

8,75

8,19



SKO

110,00

32,00

70,00

65,56

277,56

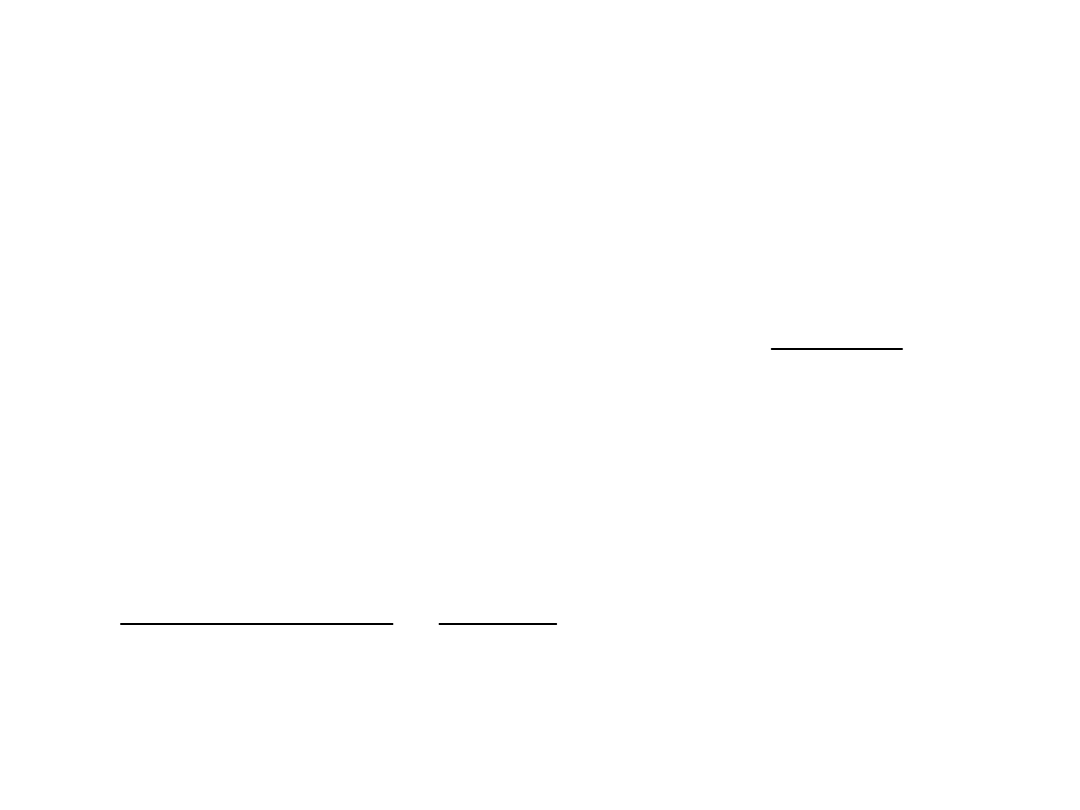
Wewnątrzgrupowa suma kwadratów odchyleń

– SKO dla grup

Wewnątrzgrupowa liczba stopni swobody

– suma stopni swobody dla grup

Wewnątrzgrupowe oszacowanie wariancji

– iloraz (SKO / stopnie swobody)

67

,

8

32

56

,

277

2





w

s

Międzygrupowe oszacowanie wariancji

– wariancja obliczona na podstawie zmienności między grupami.

92

,

36

9

10

,

4

2







m

s

92

,

36

3

75

,

110

3

56

,

277

31

,

388

2









m

s

ale też

Pomiędzy obliczanymi SKO (były trzy różne)
zachodzi następujący związek:

Ogólna SKO = międzygrupowa SKO + wewnątrzgrupowa SKO

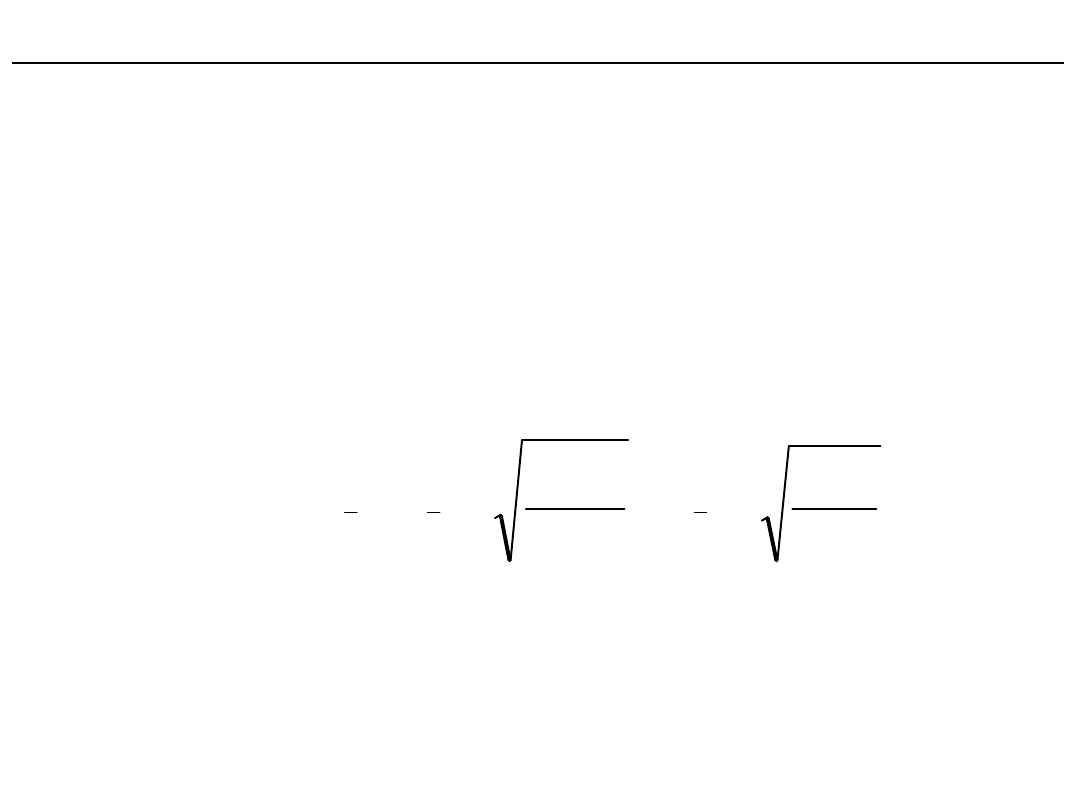
F = wariancja międzygrupowa/wariancja wewnątrz grup

Statystyka:

Wartość graniczna:

26

,

4

67

,

8

92

,

36





F

9

,

2

32

,

3

,

05

.

0



F

Ponieważ statystyka F>2,9
to hipotezę o braku różnic pomiędzy grupami należy odrzucić.

Test a posteriori Tukeya (post-hoc, niezaplanowane)

wersja dla grup o równej liczebności

Wiemy, że pomiędzy grupami występują różnice istotne statystycznie,
nie wiemy jednak różnice pomiędzy którymi grupami są za to
odpowiedzialne. Różne nazwy testu:
- najmniejsza istotna różnica (NIR),
- rozsądna i. r. (RIR).

981

,

0

9

67

,

8

2

.











x

wewn

x

x

krytyczne

s

n

s

s

s

Q

NIR

Q – rozstęp studentyzowany (wartości z tablic).
n=9 – liczba powtórzeń w grupie,
dla N=4 grup i df=32 stopni swobody Q

0,05;4;32

3,83

757

,

3

981

,

0

83

,

3







NIR

x

krytyczne

s

Q

NIR





H

0

- brak różnic pomiędzy średnimi,

odrzucamy gry różnica pomiędzy średnimi porównywanych grup
jest większa od NIR.
H

1

- różnica pomiędzy grupami jest istotna statystycznie.

Różnice pomiędzy średnimi, zaznaczono wartości większe od NIR.

GRUPA 1

GRUPA 2

GRUPA 3

GRUPA 4

GRUPA 1

0

3

4,67

3,78

GRUPA 2

0

1,67

0,78

GRUPA 3

0

-0,89

GRUPA 4

0

Bierzemy pod uwagę wartość bezwzględną różnicy!

Test Kruskala-Wallisa

Analiza wariancji wymaga spełnienia szeregu warunków
- rozkład normalny populacji,
- homogeniczność wariancji
gdy istnieje niepewność co do spełnienia założeń (np. małe próby)
to należy stosować testy nieparametryczne oparte na słabszych
założeniach (tak było w przypadku testu U).

H

0

: pomiędzy grupami nie ma zróżnicowania.

H

1

: pomiędzy grupami występuje zróżnicowanie istotne statystycznie.

Dane z przykładu poprzedniego są przedstawiane w skali porządkowej,
przypisane zostały im rangi. Należy pamiętać o rangach wiązanych!

GRUPA 1 GRUPA 2 GRUPA 3 GRUPA 4

1

14

14

7,5

31,5

2

18,5

14

7,5

11

3

35

18,5

23

7,5

4

18,5

31,5

1,5

27

5

36

27

27

11

6

27

18,5

11

4

7

27

4

7,5

31,5

8

34

18,5

1,5

18,5

9

23

23

31,5

4

suma rang R

j

233

169

118

146

Statystyka:

)

1

(

3

)

1

(

12

2













N

N

R

N

N

H

j

j

j

2082

,

7

37

3

9

146

9

118

9

169

9

233

37

36

12

2

2

2

2































H

W układzie występują rangi wiązane,
należy obliczyć poprawkę:





N

N

t

t

D











3

3

1

t – liczba pomiarów mająca taką samą rangę, np.:

120

5

24

3

3

3













t

t

t

t

t

t





9882

,

0

36

36

552

1

60

120

24

210

24

24

60

24

6

36

36

1

1

3

3



































D

2946

,

7

9882

,

0

2082

,

7









D

H

H

H

p

poprawione

H

p

porównujemy z wartością graniczną z

testu 

2

dla =0,05 i df=4-1=3 stopni swobody.

Ponieważ H

p

<7,815 to hipotezę zerową

należy przyjąć.
Inaczej

niż

w

przypadku

analizy

wariancji!

815

,

7

2

3

;

05

,

0





Analiza wariancji: klasyfikacja prosta
Chcemy ustalić czy pomiędzy kilkoma grupami istnieją różnice
istotne statystycznie, czynnik różnicujący grupy jest czynnikiem
powtarzalnym (pod kontrolą eksperymentatora) a nie ma
charakteru losowego.

H

0

– brak różnic pomiędzy grupami, czynnik różnicujący grupy

nie ma wpływu na nasilenie badanej cechy.
H

1

– występujące różnice są istotne statystycznie, występujące

różnice pomiędzy średnimi można interpretować jako wpływ
czynnika różnicującego.

GRUPA 1 GRUPA 2 GRUPA 3 GRUPA 4 GRUPA 5 GRUPA 6

1

105

112

101

102

104

109

2

106

110

103

104

103

110

3

108

108

101

103

103

111

4

110

106

99

102

104

112

5

108

110

98

104

101

106

6

106

106

100

102

106

107

7

108

107

101

103

102

111

8

108

108

102

100

101

112

9

107

109

103

102

103

111

10

110

102

104

102

109

11

101

104

103

108

12

103

102

111

13

103

112

14

109

średnia

107,33

108,60

101,00

102,75

102,73

109,86

SKO

18,00

34,40

24,00

14,89

23,81

47,71

st. swob.

8

9

10

11

12

13

wariancja

2,25

3,82

2,40

1,35

1,98

3,67

średnia ogólna

105,35

st. swob. wariancja

ogólna SKO

966,8

68

14,218

wewnątrzgrupowa SKO

162,81

63

2,584

międzygrupowa SKO

803,99

5

160,799

Liczba grup N=6,
założony poziom ufności - =0,05
Test F – wartość graniczna dla F

0,05;5;63

=2,361

22

,

62

584

,

2

8

,

160





F

Dla poziomu istotności =0,05 H

0

należy odrzucić. Obliczona

wartość F odpowiada prawdopodobieństwu poniżej p<0,0001,
odrzucając H

0

popełniamy taki błąd I rodzaju. Pomiędzy grupami

istnieją różnice istotne statystycznie, nie wiemy jednak różnice
pomiędzy którymi grupami mają na to wpływ.

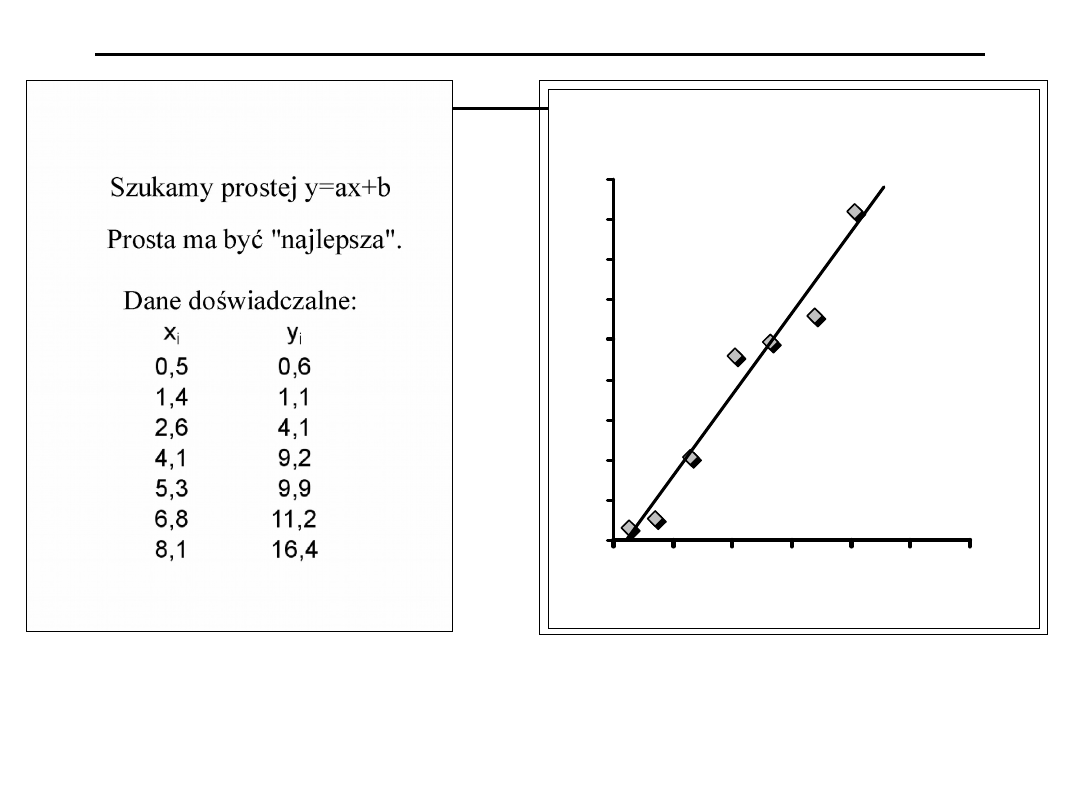
Metoda najmniejszych kwadratów –

regresja liniowa

regresja liniowa

y = 2,03x - 0,84

0

2

4

6

8

10

12

14

16

18

0

2

4

6

8

10

12

x

i

y

i

Szukamy takiej prostej aby suma kwadratów

odległości punktów
od prostej była jak najmniejsza.

Takie a i
b :

 























n

i

i

i

b

x

a

y

b

a

F

1

2

minimum

,

Prosta y=ax+b















 

















  

0

2

1

2

0

)

,

(

0

2

2

0

)

,

(

1

1

1

1

2

1

1

2

1

1

1

2























































































































































n

i

i

n

i

i

n

i

i

i

n

i

i

i

n

i

n

i

i

i

n

i

i

i

n

i

i

i

i

n

i

i

i

n

b

x

a

y

b

x

a

y

b

b

x

a

y

b

b

a

F

x

b

x

a

y

x

x

b

x

a

y

a

b

x

a

y

a

b

a

F

Otrzymujemy układ
równań:



































































n

i

i

n

i

i

n

i

i

i

n

i

n

i

i

i

n

i

i

n

i

i

n

i

n

i

i

i

n

i

i

i

y

n

b

x

a

y

x

x

b

x

a

n

b

x

a

y

x

b

x

a

y

x

1

1

1

1

1

2

1

1

1

1

2

1

0

0





 









 





























































n

i

i

n

i

i

n

i

n

i

n

i

i

n

i

i

i

i

n

i

i

n

i

i

n

i

n

i

n

i

i

i

i

i

x

n

x

y

x

y

x

x

b

x

n

x

y

x

n

y

x

a

i

1

2

2

1

1

1

1

1

2

1

2

2

1

1

1

1

tylko wzory dla:
y=ax+b

n

n

y

x

y

x

y

x

,

,

,

2

2

1

1



n – pomiarów





 































n

i

i

n

i

i

n

i

n

i

n

i

i

i

i

i

x

n

x

y

x

n

y

x

a

1

2

2

1

1

1

1





 



































n

i

i

n

i

i

n

i

n

i

n

i

i

n

i

i

i

i

x

n

x

y

x

y

x

x

b

i

1

2

2

1

1

1

1

1

2

błąd
standardowy:





a

n

n

y

y

n x

x

i

i

i

n

i

i

i

n

i

n































2

2

1

2

1

2

1











































n

i

n

i

i

i

n

i

i

i

n

i

i

x

x

n

y

y

n

x

b

1

2

1

2

1

2

1

2

2

y=a
x











n

i

i

n

i

i

i

x

y

x

a

1

2

1

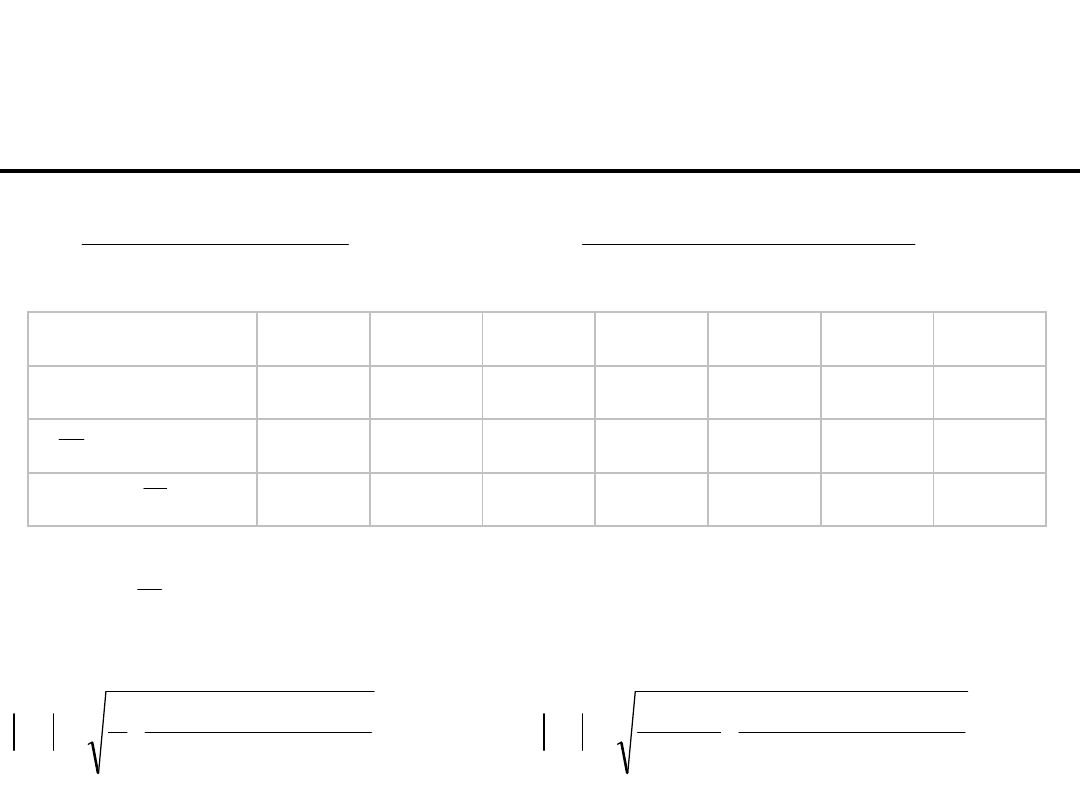
x

i

0,5

1,4

2,6

4,1

5,3

6,8

8,1

y

i

0,6

1,1

4,1

9,2

9,9

11,2

16,4

0,177 2,001 4,432 7,471 9,902 12,942 15,575
0,179 0,811 0,110 2,989 0,000 3,033 0,680

Dla przykładu z pierwszej
strony:



















69

,

311

72

,

165

5

,

52

8

,

28

7

2

i

i

i

i

i

y

x

x

y

x

n









8360

,

0

72

,

165

7

8

,

28

5

,

52

72

,

165

69

,

311

8

,

28

0261

,

2

72

,

165

7

8

,

28

69

,

311

7

5

,

52

8

,

28

2

2































b

a

b

x

a

y

i

i











2

i

i

y

y 





802

,

7

1

2









n

i

i

i

y

y









884

,

0

8

,

28

72

,

165

7

802

,

7

5

72

,

165

182

,

0

8

,

28

72

,

165

7

802

,

7

5

7

2

2

























b

a

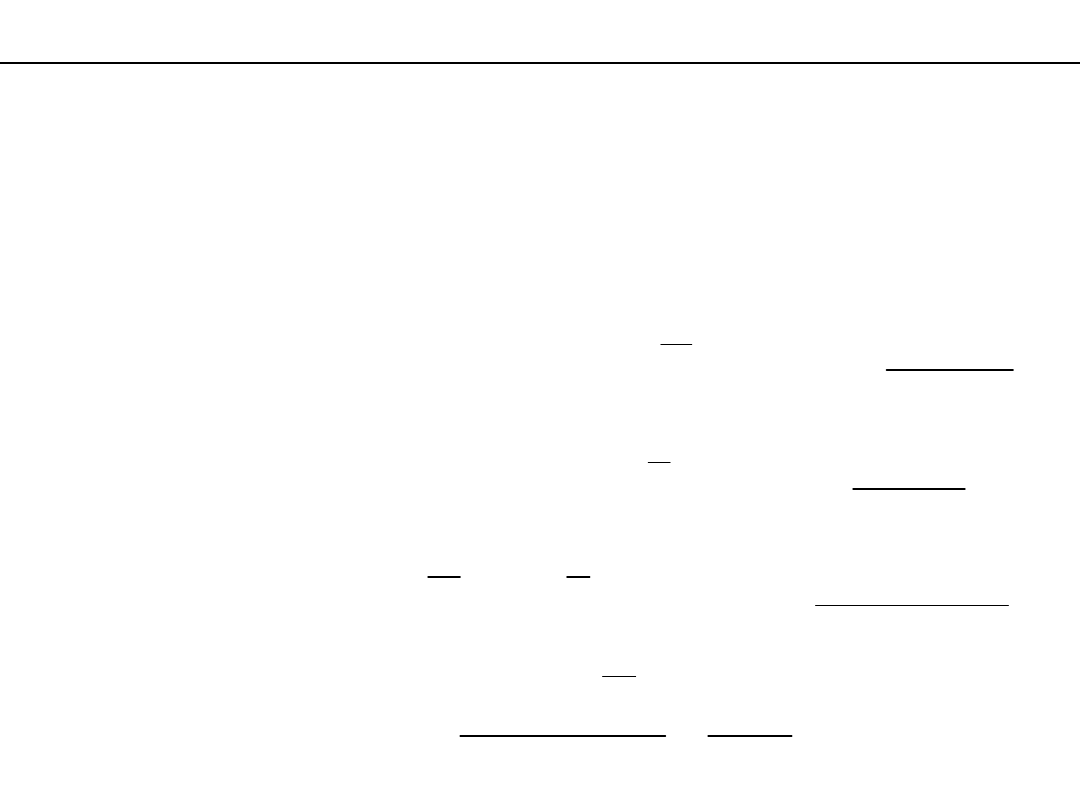
Metoda najmniejszych kwadratów – analiza zależności, test F

Testujemy H

0

: współczynniki korelacji i regresji są równe zeru czyli,

że pomiędzy zmiennymi X i Y nie ma zależności.
H

1

: ?

SKO dla zmiennej X

SKO dla zmiennej Y

























N

X

X

X

X

x

i

i

i

2

2

2

2

























N

Y

Y

Y

Y

y

i

i

i

2

2

2

2



 





























N

Y

X

Y

X

Y

Y

X

X

xy

i

i

i

i

i

i

Wariancja





df

SKO

N

X

X

s

i











1

2

2

X, Y – wartości zmierzone

x, y – odchylenia od średniej

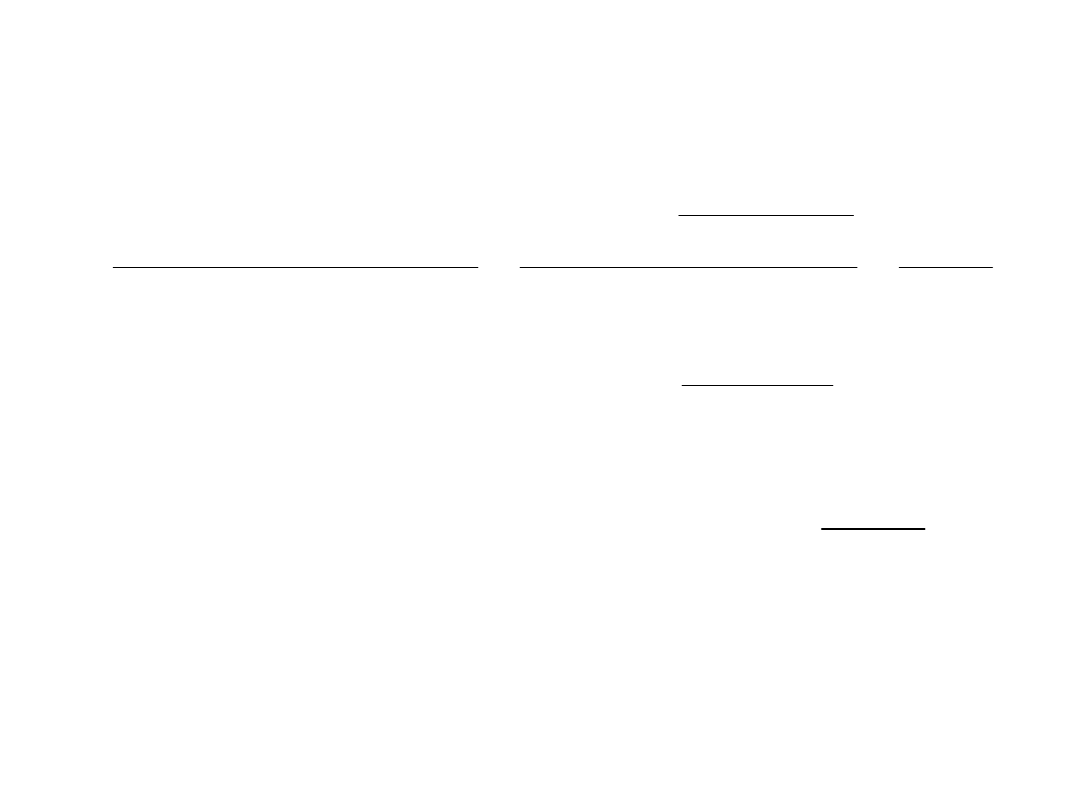
Nachylenie prostej w metodzie najmniejszych kwadratów:









 







 





























































2

2

1

1

2

1

1

1

2

1

1

2

1

1

1

x

xy

N

X

X

N

Y

X

Y

X

X

X

N

Y

X

Y

X

N

a

N

i

i

N

i

i

N

i

N

i

i

i

N

i

i

i

N

i

i

N

i

i

N

i

N

i

i

i

N

i

i

i

Uwaga: gdyby zamienić zmienne X i Y to:







2

/

y

xy

a

Może być regresja: Y względem X
lub X względem Y.

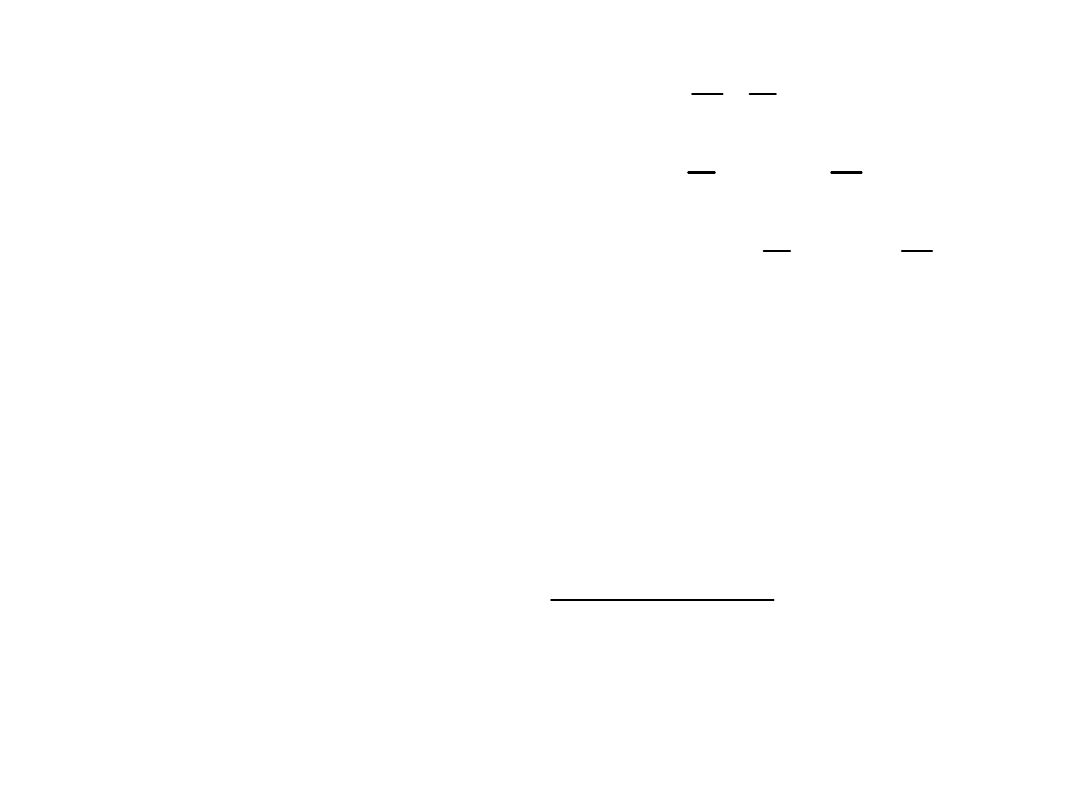
X

a

Y

b

b

X

a

Y

Y

X













;

Prosta regresji przechodzi przez punkt

otrzymujemy więc zależność

z której wyliczamy

Współczynnik korelacji Pearsona:





a

a

y

x

xy

r

















2

2

2

2

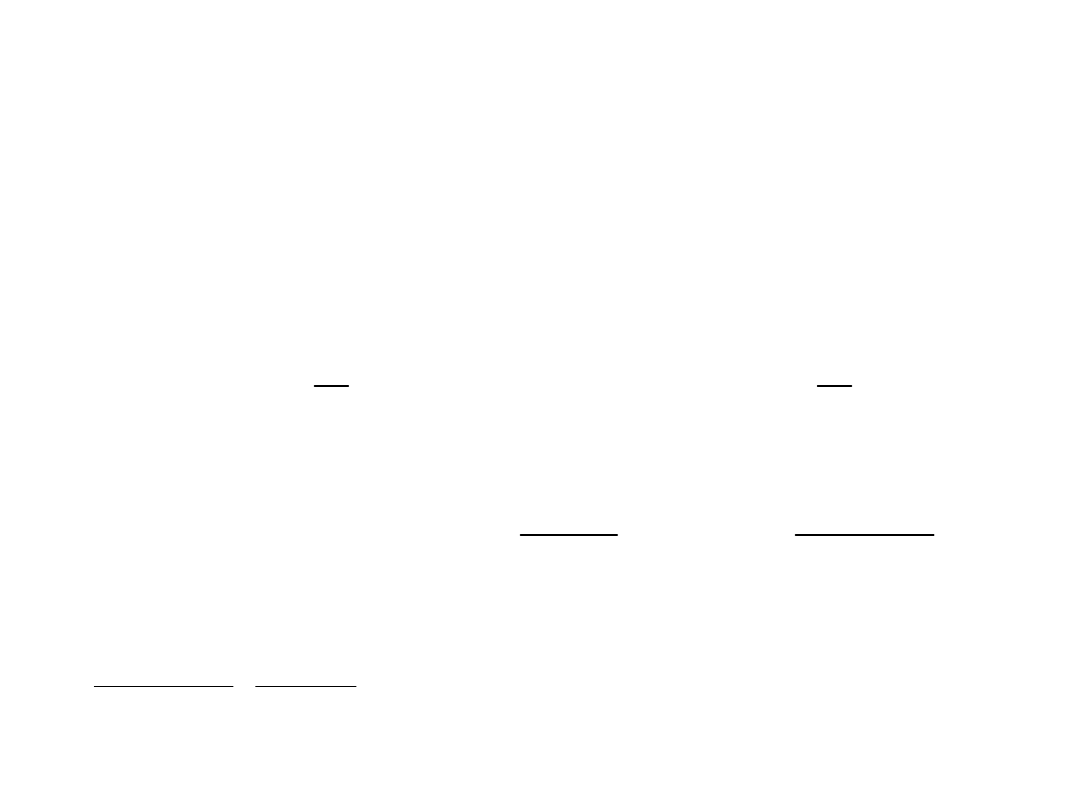
wariancja wyjaśniona = wyjaśniona SKO / st. swobody (df=1)
wariancja niewyjaśniona = niewyjaśniona SKO / st. swobody (df=N-2)

SKO = SKO wyjaśniona + SKO niewyjaśniona











2

2

2

d

y

y

p





















































































































2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

y

r

y

y

x

xy

x

xy

x

x

xy

x

a

x

a

X

X

a

b

X

a

b

X

a

y

i

i

p







2

2

2

y

r

y

p













2

2

2

1

y

r

d

p

p

p

df

y

s





2

2

d

d

df

d

s





2

2

2

1







N

df

df

d

p

Statystyka F:

2

2

d

p

s

s

F 

2

2

1

)

2

(

r

N

r

F







to hipotezę o braku zależności należy odrzucić, czyli przyjąć
hipotezę alternatywną, że istnieje zależność pomiędzy X i Y.

2

,

1

,





N

F

F



Jeżeli

Nieparametryczna alternatywa współczynnika korelacji-

współczynnik korelacji Spearmana

Czy pomiędzy zmiennymi X i Y jest związek statystycznie
istotny
(niekoniecznie liniowy)?
Dane nie muszą być w skali interwałowej, wystarczy
porządkowa.
Każdej wartości X

i

i Y

i

przypisujemy rangi (każdej

zmiennej z osobna).

Dla każdej pary punktów wyznaczamy kwadrat różnicy
rang :

i sumujemy je (

D

i

2

)





2

2

i

i

Y

X

i

R

R

D





Obliczamy współczynnik korelacji rang Spearmana

r

s

:

)

1

(

6

1

2

2













N

N

D

r

s

Jeżeli N>10 obliczamy

statystykę Z i porównujemy

z wartością graniczną

dla rozkładu normalnego.

1







N

r

Z

s

SUMA średnia

X

-3

-1

1

2

3

4

5

6

8

10 11 14

60

5

Y

-1

-4

2

4

17 34 14 35

9

8

47 27

192

16

x

-8

-6

-4

-3

-2

-1

0

1

3

5

6

9

0

y

-17 -20 -14 -12

1

18 -2

19 -7

-8 31 11

0

xy 136 120 56 36 -2 -18 0

19 -21 -40 186 99

571

xx

64 36 16

9

4

1

0

1

9

25 36 81

282

yy 289 400 196 144 1 324 4 361 49 64 961 121 2914

a=2,0248 r

2

=0,3968

SKO

wyjaśn

. 1156,2 df= 1 war wyj = 1156,2

F

obl

=6,58 p= 0,028

SKO

niewyjaśn

. 1757,8 df= 10 war nwyj = 175,8

F

gran

=4,96 p= 0,05

F

obl

>F

graniczne

 H

0

odrzucamy.

Przyjmujemy H

1

i szacujemy błąd I rodzaju.

Współczynnik korelacji Spearmana

Rangi R

X

1

2

3

4

5

6

7

8

9 10 11 12

Rangi R

Y

2

1

3

4

8 10 7 11 6

5 12 9

D

-1 1

0

0 -3 -4 0 -3 3

5 -1 3 SUMA

D

2

1

1

0

0

9 16 0

9

9 25 1

9

80

7203

,

0

143

12

80

6

1

)

1

(

6

1

2

2























N

N

D

r

s

3889

,

2

11

7203

,

0

1













N

r

Z

s

Dla jednostronnego rozkładu normalnego dla Z = 2,3889
prawdopodobieństwo p = 0,0084
czyli H

0

– odrzucamy, błąd I rodzaju - 0,0084.