04. WNIOSKOWANIE STATYSTYCZNE

Wnioskowanie statystyczne polega na wyciąganiu wniosków dotyczących badanej cechy
w populacji generalnej na podstawie badania próby. Opiera się więc na informacji
częściowej, dlatego dostarcza wniosków wiarygodnych, ale nie absolutnie pewnych.

Istnieją dwie formy wnioskowania statystycznego:

 estymacja (ocena nieznanych parametrów lub ich funkcji, które charakteryzują

rozkład badanej cechy populacji),

 weryfikacja postawionych hipotez statystycznych (badanie ich prawdziwości).

1 ESTYMACJA

–

PRZEDZIAŁY

UFNOŚCI

ESTYMACJA – polega na szacowaniu nieznanych wartości parametrów rozkładu populacji
generalnej na podstawie próby z niej wylosowanej. Posiada dwie odmiany:

 estymacja nieparametryczna – szacuje się postać funkcji rozkładu populacji

generalnej,

 estymacja parametryczna – szacuje się tylko wybrane wartości parametru

rozkładu populacji generalnej, dzieli się na:

o

estymację punktową,

o

estymację przedziałową (przedziały ufności).

POPULACJA GENERALNA

m, σ

x, s

_

n-elementowa

PRÓBA

próbkowe oszacowanie
faktycznych wartości parametrów

populacji generalnej

średnia i odchylenie standardowe
z próby – estymatory nieznanych

wartości w populacji generalnej

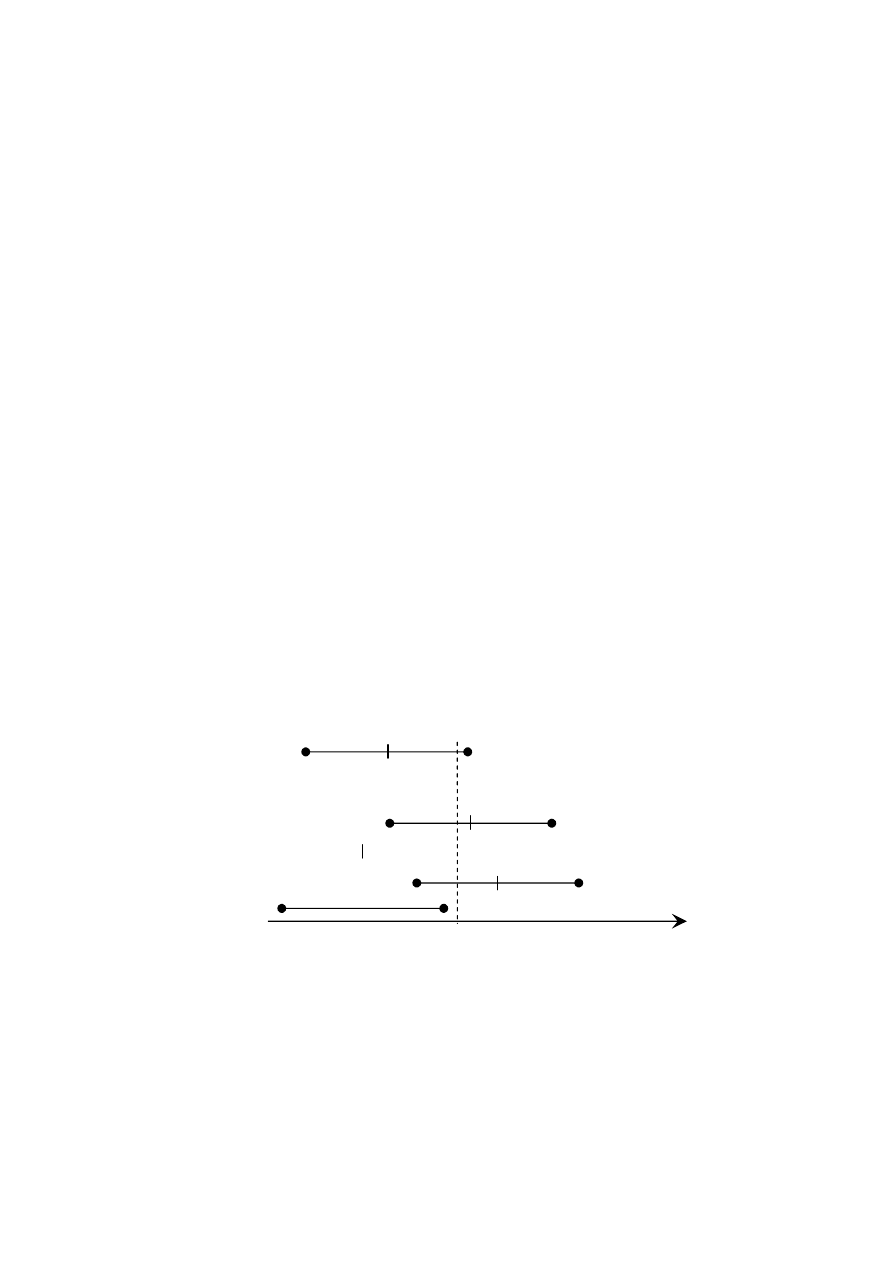
ESTYMACJA PRZEDZIAŁOWA

polega na skonstruowaniu przedziału liczbowego – przedziału ufności – takiego, że z
ustalonym z góry prawdopodobieństwem – poziomem ufności – będzie zawarta w nim

nieznana, prawdziwa wartość szacowanego parametru (np.

m

i

σ

) z populacji generalnej:

















1

.

.

górna

gr

na

dol

gr

P

Przedział ufności – poszukiwany przedział, który z zadanym prawdopodobieństwem
będzie pokrywał nieznaną wartość szacowanego parametru.

Poziom/współczynnik ufności (1–

α

) – prawdopodobieństwo, że skonstruowany

przedział ufności będzie zawierał w sobie szacowany parametr (prawdopodobieństwo
sukcesu). Zwykle przyjmuje wartości: 0,90, 0,95, 0,98, 0,99.

α

– poziom istotności

Końce przedziału ufności są zmiennymi losowymi. Nieznana wartość parametru może
więc znaleźć się w tym losowym przedziale lub nie. Jeśli dla wielu różnych
zaobserwowanych prób losowych zostaną znalezione przedziały ufności, to częstość tych,

które będą zawierać rzeczywistą wartość parametru, będzie w przybliżeniu =

(1–α)

·100%.

Im dłuższy przedział ufności, tym większy współczynnik ufności, ale jednocześnie
mniejsza dokładność oszacowania.

Im większa liczność, tym krótszy przedział ufności, a tym samym większa precyzja
oszacowania.

x

n

_

_

x

3

x

2

_

x

1

_

m

a przedział ufności dla wartości oczekiwanej

m

patrz – tabela poniżej

b przedział ufności dla odchylenia standardowego

σ

patrz – tabela poniżej

c względna precyzja oszacowania

)

(x

B

Określanie względnej precyzji oszacowania na podstawie wartości otrzymanych dla
poszczególnych przedziałów ufności (wzory w tabeli poniżej):



)

(x

B

5% – oszacowanie ma dużą precyzję,

5%





)

(x

B

10% – uogólnienia wyników z próby na populację należy dokonywać z

ostrożnością,



)

(x

B

10% – nie należy przeprowadzać uogólnienia, zbyt mała precyzja

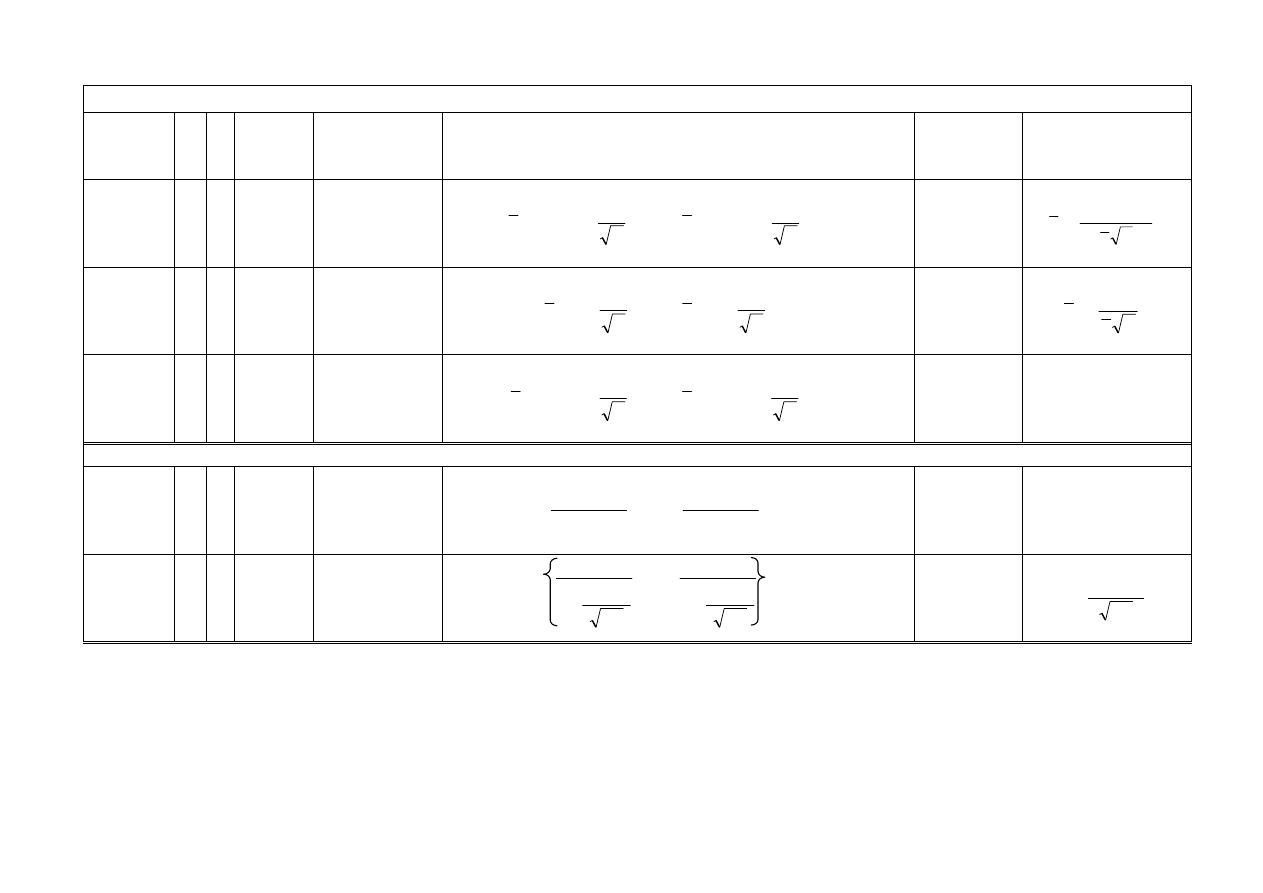
PRZEDZIAŁ UFNOŚCI DLA WARTOŚCI OCZEKIWANEJ

m

ROZKŁAD

CECHY

m σ

n

ROZKŁAD

ESTYMATORA

PRZEDZIAŁ UFNOŚCI UWAGI

WZGLĘDNA

PRECYZJA

OSZACOWANIA

N(

m,σ

)

X √ dowolne

normalny











































1

2

/

1

2

/

1

n

u

x

m

n

u

x

P

długość

przedziału jest

stała, ale

położenie

granic losowe

 

 

%

2

/

1

n

x

u

x

B











N(

m,σ

)

X X

n<30

mała

próba

t-Studenta o

n-1 stopniach

swobody



































1

n

s

t

x

m

n

s

t

x

P

położenie

granic i długość

przedziału są

losowe

 

 

%

n

x

s

t

x

B







X X

√

n≥30

duża

próba

dąży

asymptotycznie

do normalnego











































1

2

/

1

2

/

1

n

u

x

m

n

u

x

P

tylko dla dużej

próby,

dla nieznanego

σ

można

przyjąć

σ = s

PRZEDZIAŁ UFNOŚCI DLA ODCHYLENIA STANDARDOWEGO

σ

N(

m,σ

)

X X n<30

χ

2

(chi-kwadrat)

o n-1 stopniach

swobody























































1

1

1

2

2

/

1

2

2

2

2

/

2

s

n

s

n

P

N(

m,σ

)

X X n≥30

normalny

























1

2

1

2

1

2

/

1

2

/

1

n

u

s

n

u

s

P

 

 

%

2

2

/

1

n

u

s

B







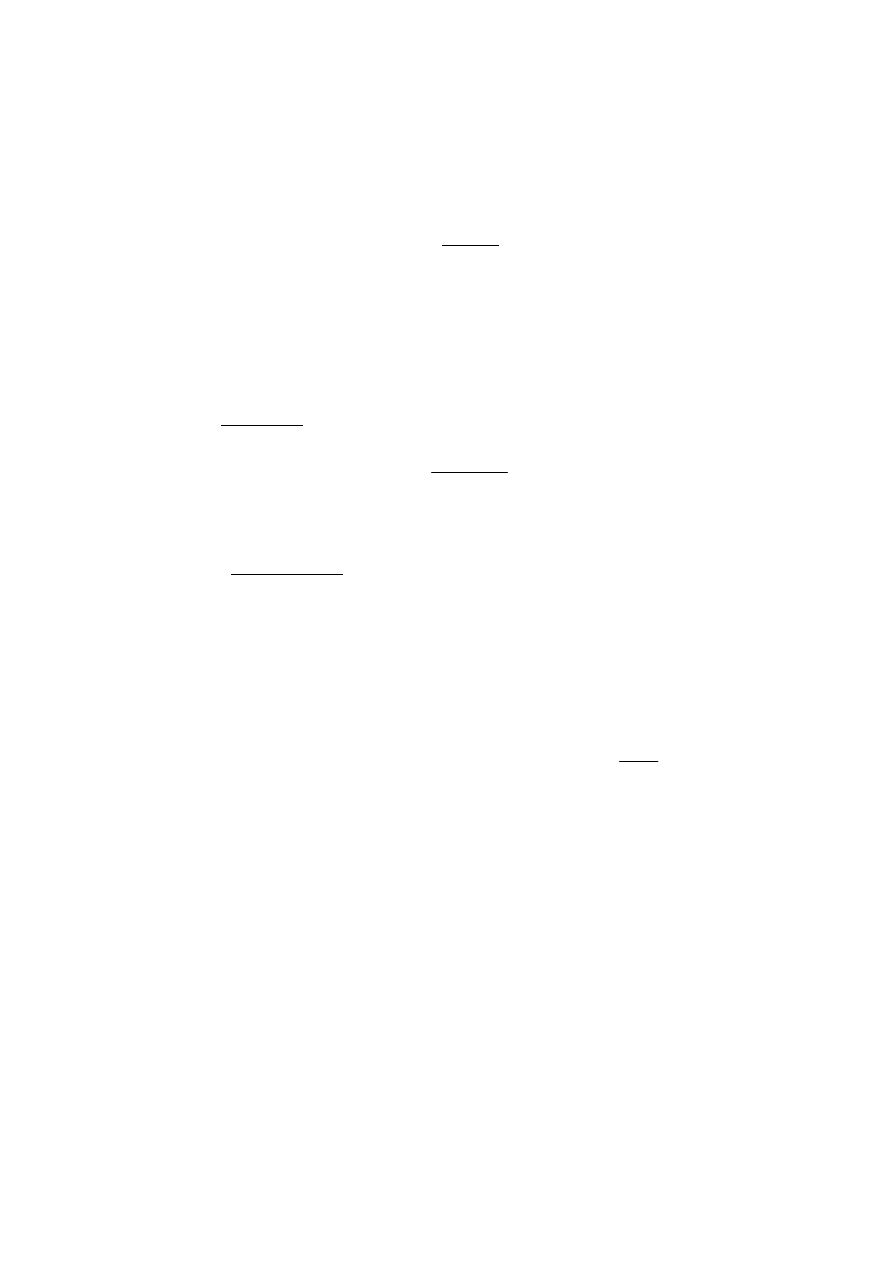
2

MINIMALNA

LICZNOŚĆ

PRÓBY

Niekiedy może zaistnieć sytuacja, że z populacji generalnej trzeba pobrać próbę dla
oszacowania przedziału ufności nieznanej wartości średniej lub frakcji. Minimalną
konieczną liczbę elementów n, które należy pobrać do takiej próby można wyliczyć mając

zadany maksymalny błąd szacowania

d

(=długość przedziału ufności) i poziom ufności

(1–α)

.

Wyliczone ze wzorów liczności minimalne zaokrągla się zawsze w górę do liczby całkowitej.

a minimalna liczność przy szacowaniu wartości średniej

m

– nieznana,

σ

2

– znana, populacja generalna ma rozkład normalny N(

m,σ

) lub zbliżony.

Z przekształcenia przedziału ufności:

2

2

/

1



















d

u

n





b minimalna liczność przy szacowaniu wartości średniej

m

– nieznana,

σ

2

– nieznana, populacja generalna ma rozkład normalny N(

m,σ

) lub

zbliżony

dwustopniowa metoda Steina:

1° Ponieważ nieznana jest wartość wariancji dla populacji, należy przyjąć jej estymator

s

2

wyliczony z wstępnie pobranej bardzo małej próby o liczności

n

0

,

2° Liczność właściwej próby wylicza się na podstawie wzoru:

2

















d

s

t

n



, gdzie

t

– dla

stopni swobody

n

0

-1

.

Jeżeli

to próba wstępna jest wystarczająca, w przeciwnym wypadku do właściwej

próby należy ‘dolosować’ brakującą ilość elementów.

o

n

n 