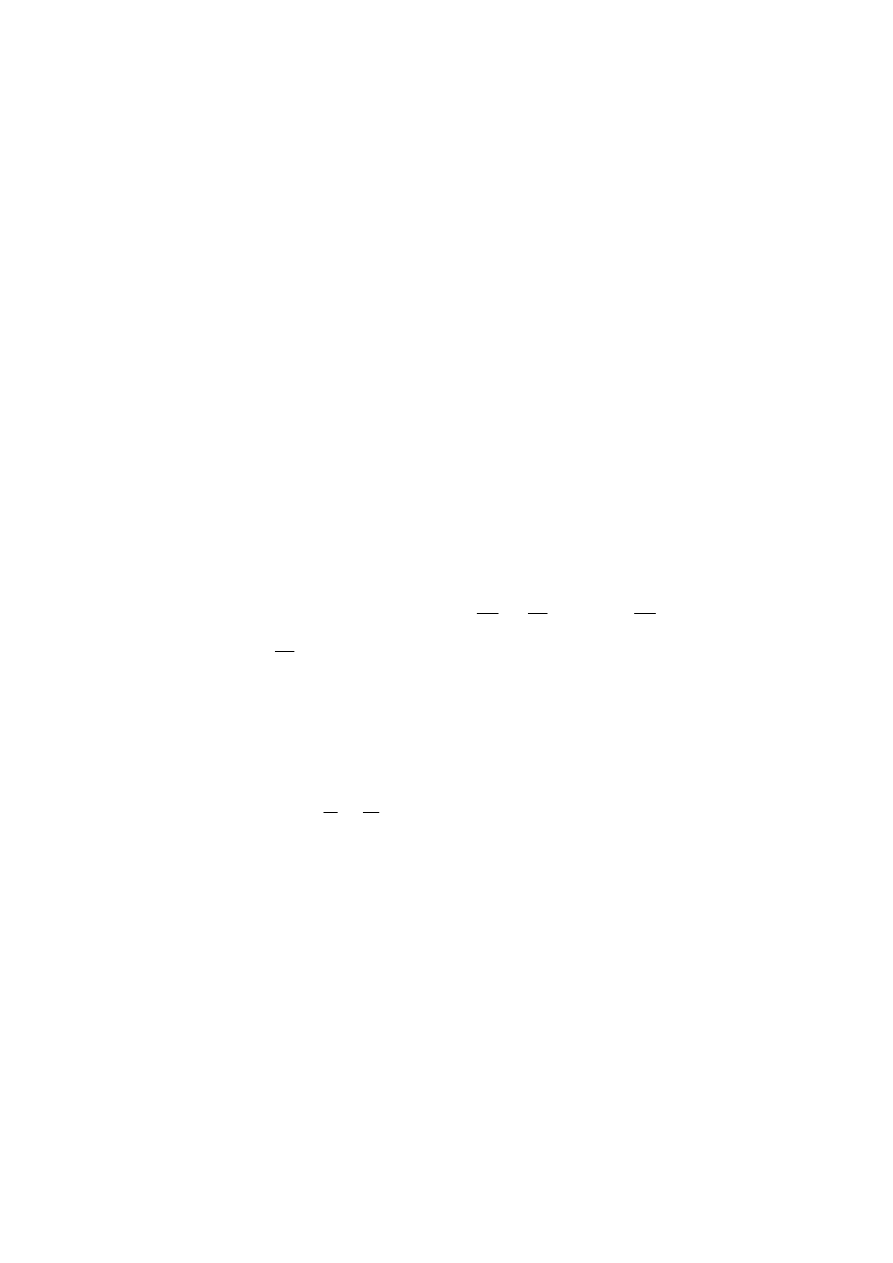
7.3. Wnioskowania statystyczne

Sprawdzenie (weryfikowanie) hipotez statystycznych

Sprawdzanie hipotez statystycznych obywa się zgodnie z następującą procedurą:

Badacz formułuje problem, jako hipotezę. Planuje doświadczenie celem sprawdzenia

słuszności tej hipotezy. Na przykład, wykładowca zauważa, że wyniki osiągane przez stu-

dentów oraz studentki tego samego roku studiów różnią się; podejrzewa, że osiągnięcia

studentów (M) są nie wyższe niż studentek (K). Takie przypuszczenie nazywa się hipotezą

badacza lub hipotezą merytoryczną. Metody weryfikowania hipotez nazywa się testami

istotności. Testy weryfikują nie dowolne hipotezy (hipotezy merytoryczne), lecz tzw. hipo-

tezy statystyczne.

W doświadczeniu dotyczącym wyników studentów każda z grup M, K reprezentuje

populację; wyniki osób z grupy M stanowią jedną próbę, a z grupy K - drugą próbę. W

przypadku obu prób hipoteza statystyczna głosi, że nie ma różnicy między średnimi obu

populacji, tj. że różnica ta jest zerem. Stąd hipotezę tę nazywamy hipotezą zerową i ozna-

czamy symbolem H

0

. Notujemy ją następująco: H

0

:

M

x

-

K

x

= 0, gdzie

M

x

oznacza

ś

rednią w populacji M, a

K

x

- średnią w populacji K.

Charakter danych empirycznych wskazuje, z jakimi zmiennymi losowymi mamy do

czynienia, a więc czy są to zmienne o rozkładzie normalnym, zero - jedynkowym, czy też

innym. Dlatego też, przy założeniu prawdziwości hipotezy statystycznej, wybieramy od-

powiednią zmienną losową. Zmienna ta jest funkcją charakterystyk prób, takich jak wiel-

kości prób n

1

i n

2

, średnich prób

1

x

i

2

x

, wariancji prób

2

1

S

,

2

2

S

a często także niektó-

rych parametrów populacji. Ponieważ omawiana zmienna służy do weryfikowania hipotez

statystycznych, nazywamy ją funkcją testową. Wyznaczywszy wartości charakterystyk

prób: średnie, wariancje itd., obliczamy wartość funkcji testowej.

Następnym punktem w weryfikacji hipotezy statystycznej jest odczytanie z tablic

statystycznych prawdopodobieństwa określającego, jak często występuje wartość zmiennej

równa lub większa od wartości funkcji testowej.

Jeżeli się okaże, że odczytane prawdopodobieństwo jest bardzo małe, np. równe lub

mniejsze niż 0,01 = 1%, to wypowiadamy wniosek z ryzykiem błędu 1 %, że postawiona

hipoteza statystyczna jest fałszywa.

Znając relację między hipotezą statystyczną i merytoryczną przenosimy wniosek na

hipotezę merytoryczną. W ten sposób otrzymujemy informację, czy hipotezę można od-

rzucić z określonym ryzykiem błędu, czy też nie ma podstaw do takiego wniosku. Ten

ostatni przypadek zachodzi wówczas, gdy odczytane prawdopodobieństwo przekracza 5%,

a więc gdy wynosi 10%, 25% itd.

Test istotności t Studenta dla różnicy dwóch średnich normalnych

Niech będą dane dwie próby pobrane losowo z dwu populacji normalnych odpo-

wiednio ze średnimi

1

x

i

2

x

oraz taką samą wariancją

2

S

, czyli Y

1

– N(

1

x

, S) , Y

2

–

N(

2

x

, S). Czytamy to tak: zmienna losowa Y

1

ma rozkład normalny ze średnią

1

x

i od-

chyleniem standardowym S i zmienna losowa Y

2

ma rozkład normalny ze średnią

2

x

i

odchyleniem standardowym S. Parametry

1

x

,

2

x

, S są stałe i nieznane.

Niech n oznacza ilość obserwacji w pierwszej próbie, a m ilość obserwacji w dru-

giej próbie. Wyniki uzyskane z doświadczenia obejmują łącznie n + m obserwacji.

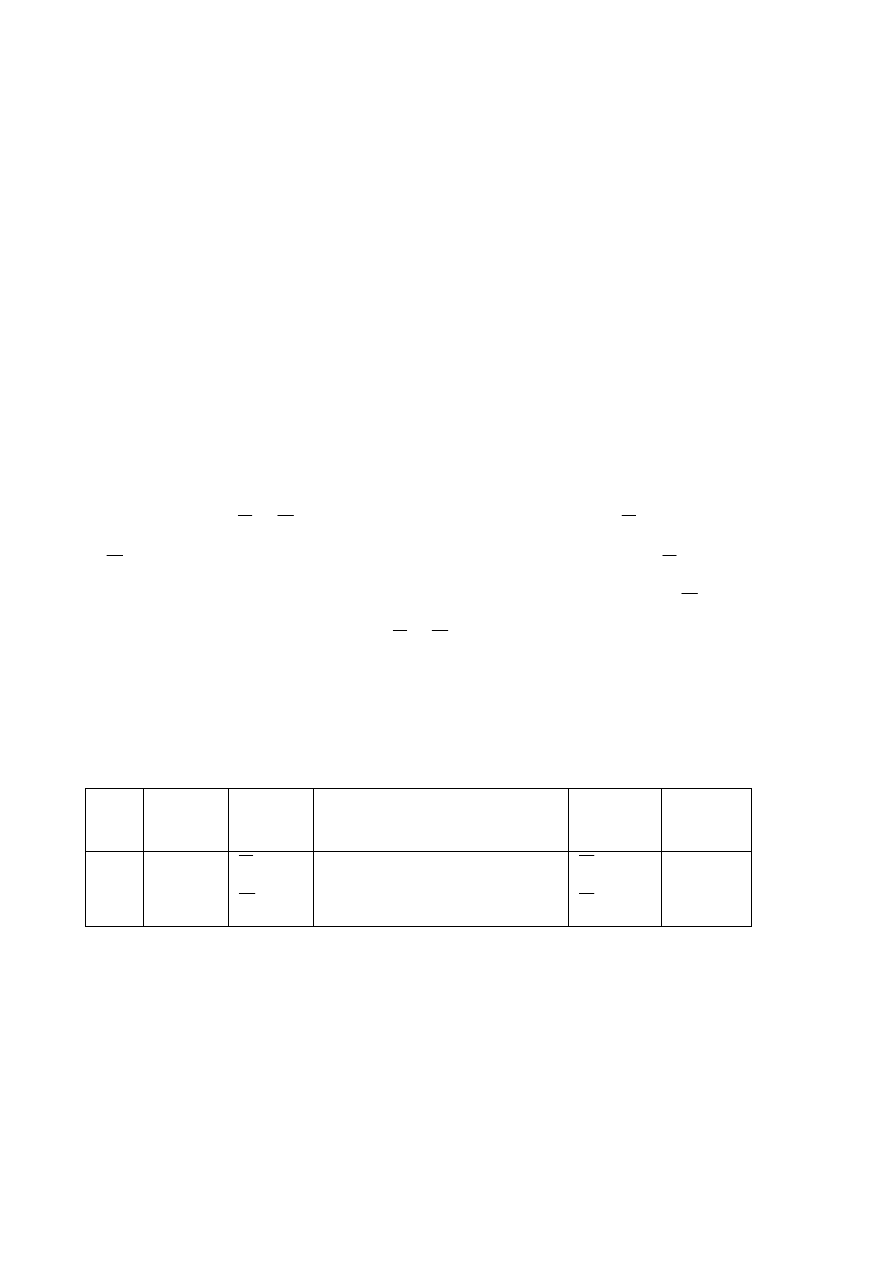
Próba Zmienna

losowa

Ś

rednia

populacji

Wyniki doświadczalne

Ś

rednia

próby

Wariancja

próby

1

2

Y

1

Y

2

1

x

2

x

11

y

,

12

y

,

13

y

, … ,

n

y

1

21

y

,

22

y

,

23

y

, … ,

m

y

2

1

y

1

y

2

1

S

2

2

S

Dla zweryfikowania hipotezy zerowej głoszącej, że nie na różnicy między średnimi

w obu populacjach używamy zmiennej losowej t Studenta zdefiniowanej tak:

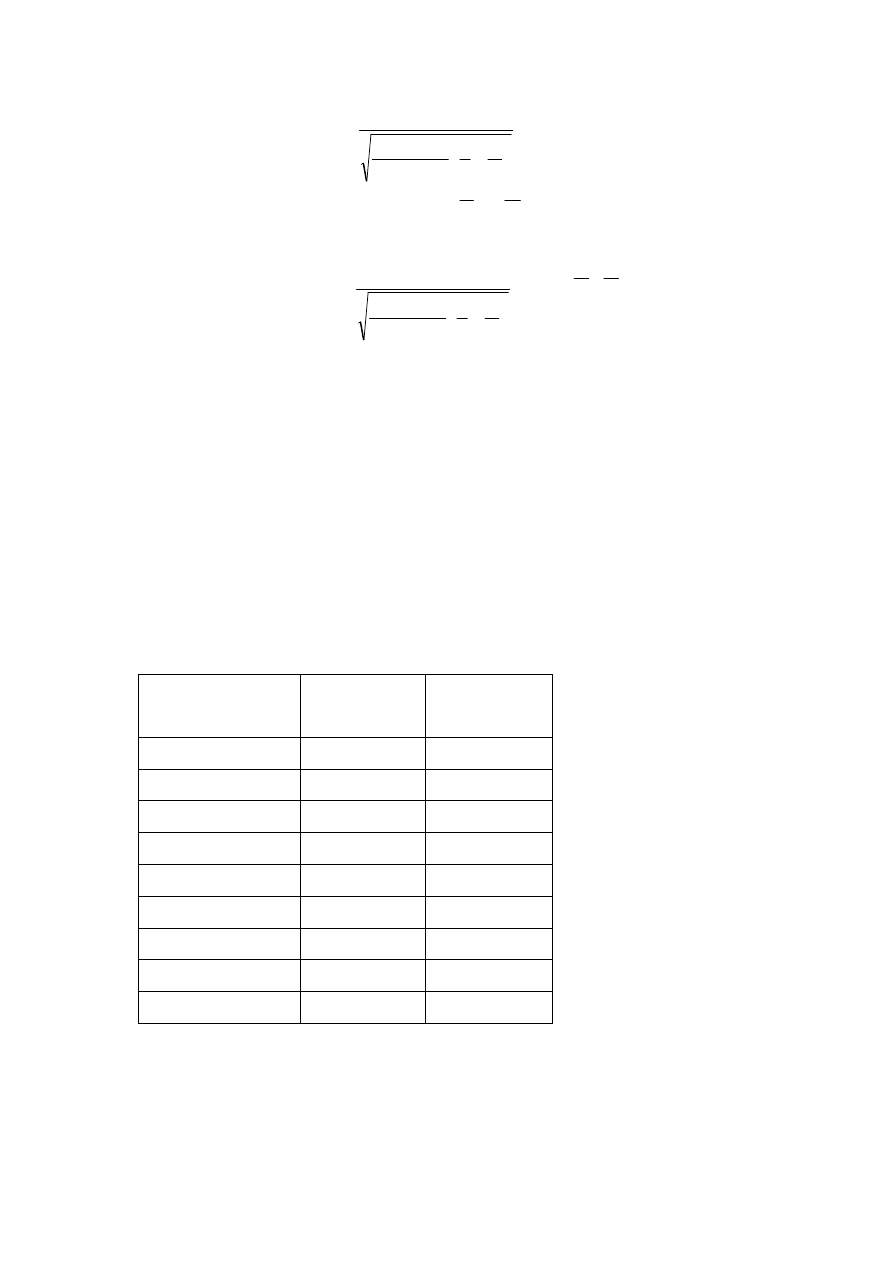
t =













+

−

+

+

−

−

−

m

n

m

n

mS

nS

x

x

y

y

1

1

2

)

(

2

2

2

1

2

1

2

1

W przypadku prawdziwości hipotezy zerowej H

0

:

1

x

-

2

x

= 0 zmienna ta przybiera

postać funkcji testowej dla

ν

= n + m – 2 stopni swobody:

t

0

=













+

−

+

+

−

m

n

m

n

mS

nS

y

y

1

1

2

2

2

2

1

2

1

, gdzie

1

y

,

1

y

oznaczają śred-

nie w pierwszej i drugiej próbie, a

2

1

S

,

2

2

S

są wariancjami pierwszej i drugiej próby.

Ilość stopni swobody wskazuje ten wiersz tablicy t Studenta, z którego przy obranym

ryzyku błędu, np.

α

= 0,05 lub

α

= 0,01 odczytuje się wartość krytyczną t

0,05

lub t

0,01

. Gdy

okaże się, że |t

0

| jest większe od t

0,05

, to hipotezę zerową odrzucamy z 5% ryzykiem błędu i

wnioskujemy o istotności różnicy między średnimi prób.

Zadania do samodzielnego rozwiązywania

Zadanie 1.

Tabela podaje wyniki studentów M oraz studentek K z kolokwiów.

Wyniki kolokwiów

w procentach

Liczba osób

grupy M

Liczba osób

grupy K

0

1

0

10

2

2

20

4

2

30

2

3

40

5

5

50

4

5

60

5

4

70

3

2

80

0

1

90

2

0

100

2

1

liczebność

30

25

ś

rednia

wariancja

a)

Zbuduj tabelę rozkładu częstości prób M, K.

b)

Oblicz średnie i wariacje prób M, K.

c)

Narysuj histogramy obu szeregów.

d)

Sformułuj hipotezę zerową dotyczącą wyników osiąganych przez studentów i

studentki.

e)

Zbadaj tekstem t Studenta istotność różnicy między średnimi obu prób na pozio-

mie 0,05. Sformułuj odpowiedni wiosek merytoryczny.