WNIOSKOWANIE STATYSTYCZNE

 W ZAKRESIE STRUKTURY ZJAWISK

• WPROWADZENIE
Aby móc uogólnić wyniki otrzymane w próbie na całą populację, próba musi być 

losowa.

Próba losowa prosta
Ciąg  n  zmiennych  losowych  X

1

,  X

2

,…,X

n

,  które  są  niezależne  i  mają  jednakowe 

rozkłady, takie jak zmienna X w populacji.

Wnioskowanie  o  parametrach  populacji  na  podstawie  próby  losowej  bazuje  na 

pewnych  funkcjach  zmiennych  losowych  X

1

,  X

2

,…,X

n

,  które  tworzą  próbę. 

Funkcje te nazywa się statystykami z próby.

Przykładami statystyk z próby są następujące funkcje:

Czyli średnia z próby i wariancja z próby.  







n

i

i

X

n

X

1

1















n

i

i

X

X

n

S

1

2

2

1

1

Dysponując wynikami konkretnej próby, tj. ciągiem liczb x

1

, x

2

,…,x

n

, i 

podstawiając do wzoru

Otrzymuje się realizację statystyki, czyli konkretną wartość średniej z 

próby, którą oznacza się       .

Powtarzanie  procesu  pobierania  prób  i  obliczania  na  ich  podstawie 

realizacji  statystyki  prowadzi  do  otrzymania  zbioru  różnych 
wartości  średnich,  który  służy  do  ustalenia  rozkładu  średniej  z 
próby      .

Rozkłady statystyk z próby







n

i

i

X

n

X

1

1

x

x

X

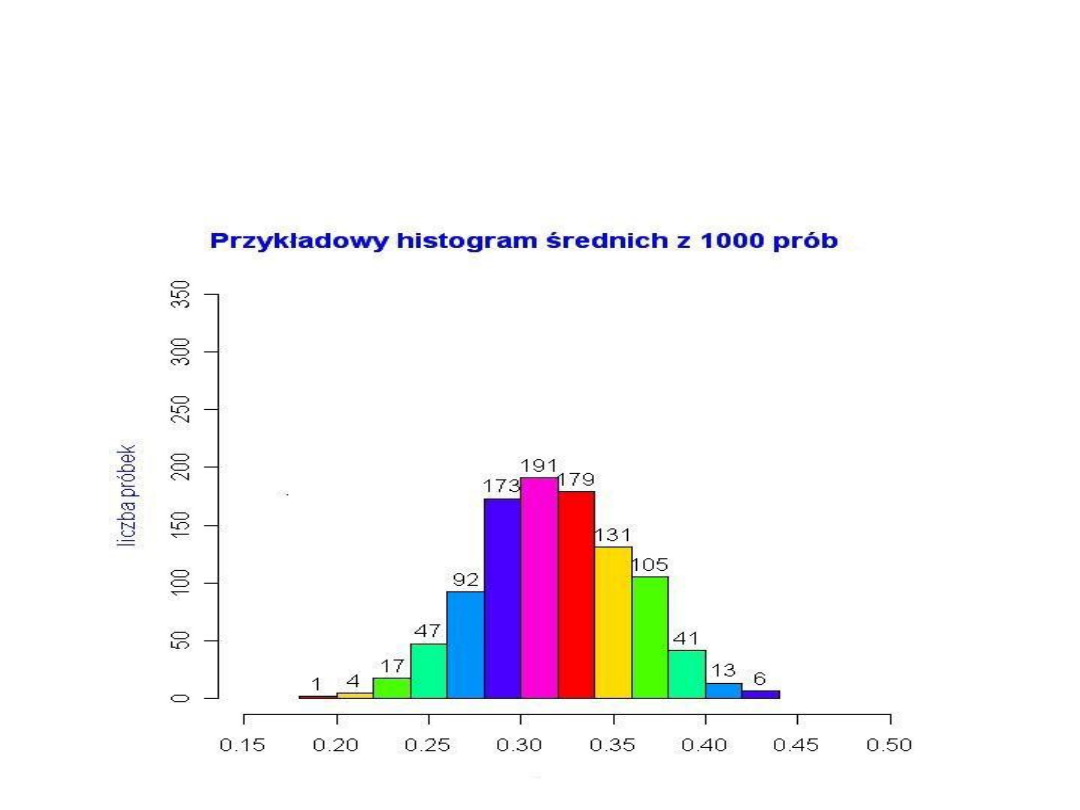
Gdybyśmy  posiadali  wiele  n-elementowych  próbek,  to 

histogram średnich z tych próbek przybliżałby tzw. rozkład 
średniej z próby.

Przykład  histogramu  dla  1000  próbek  (każda  o  liczności  n  = 

150)  przybliżającego  rozkład  średniej  z  próby  przedstawia 
wykres.

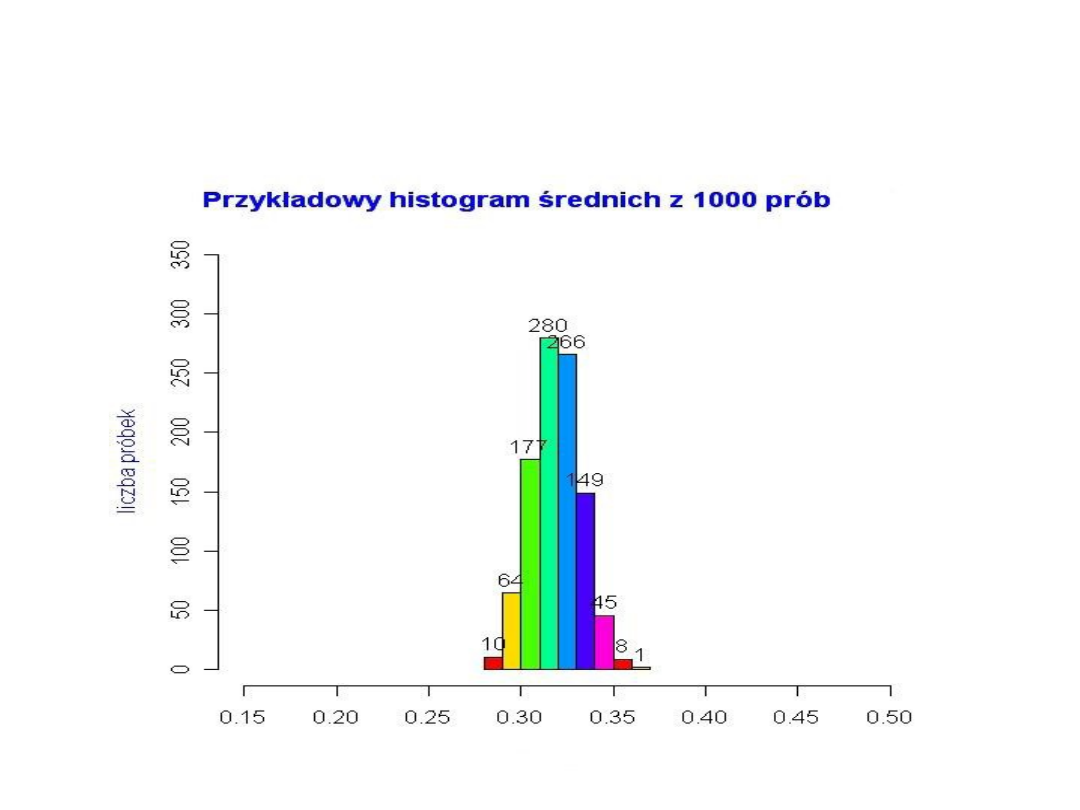
Jeśli  zwiększymy  liczebność  każdej  próbki,  np.  do  n  =  1000, 

wówczas  histogram  średnich  obliczonych  z  tych  próbek 
będzie  bardziej  ”skupiony”  wokół  średniej  z  populacji  (tu 
średnia  z  populacji=  0,32).  Histogram  poniżej  wykonano 
dla 1000 próbek.

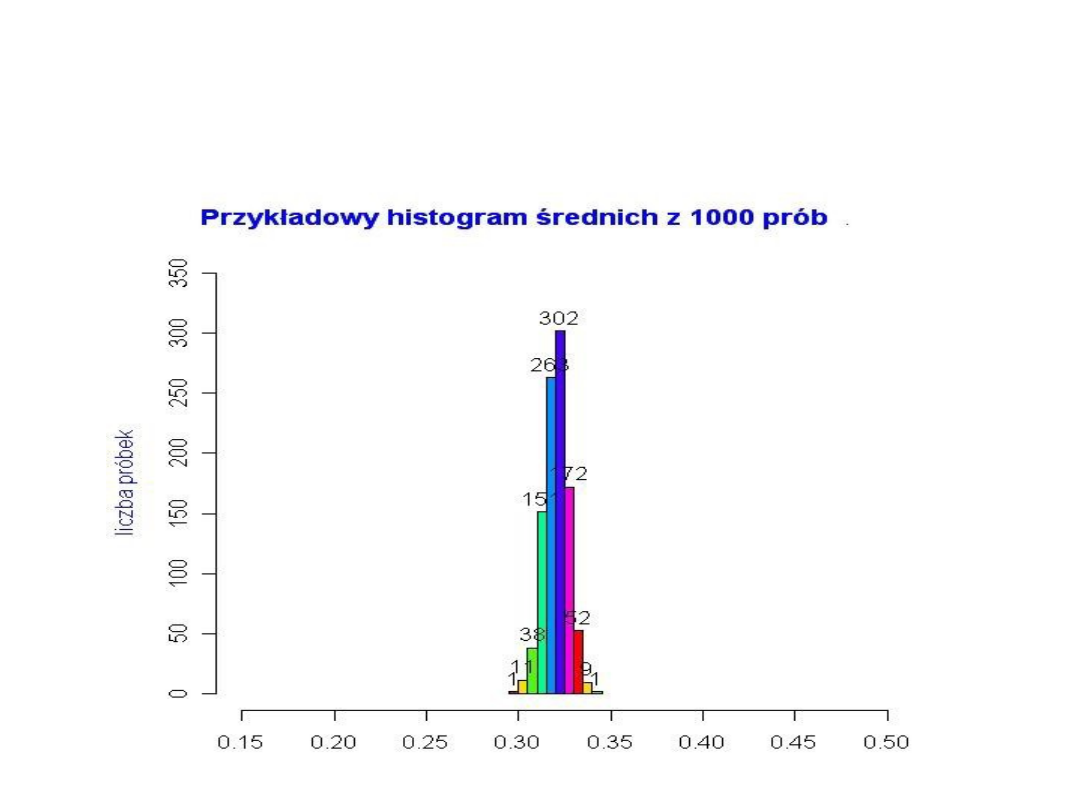
• Załóżmy teraz, że n = 5000. Koncentracja średnich z próbek 

wokół średniej z populacji jest tu jeszcze bardziej wyraźna. 
W tym przypadku średnie dla większości próbek są bardzo 
bliskie  wartości  średniej  dla  całej  populacji  (równej  nadal 
0,32).

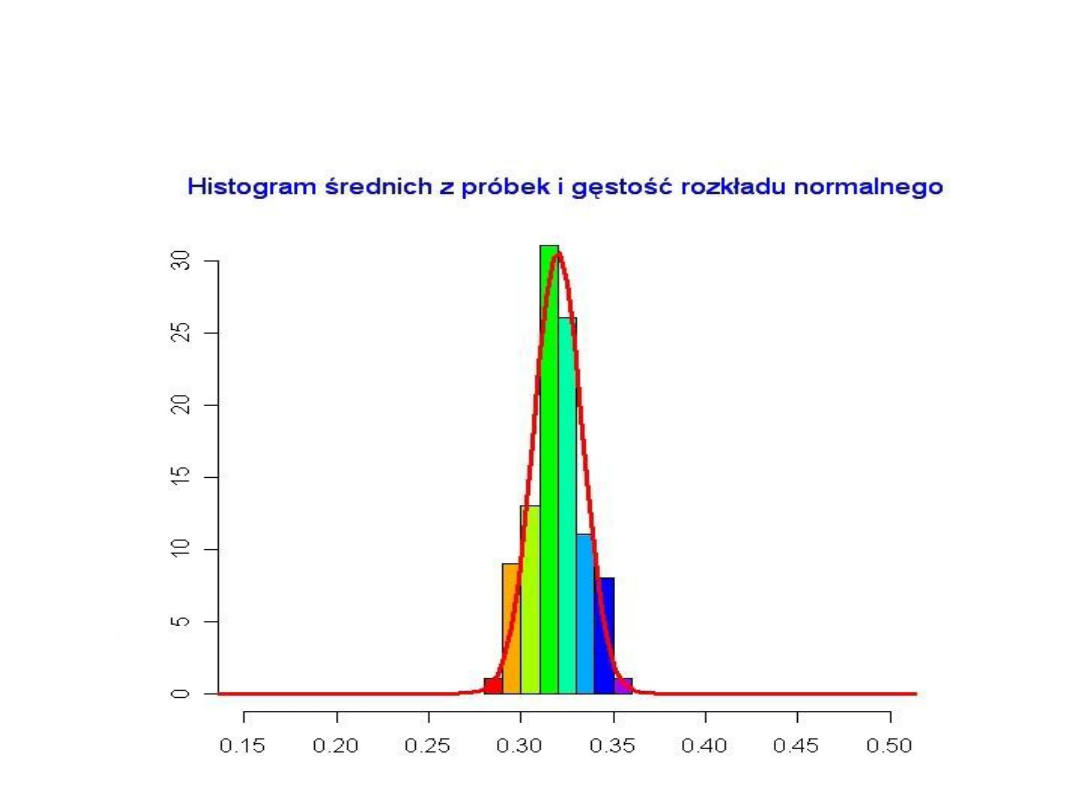
Zauważymy,  że  wykreślona  krzywa  przypomina  krzywą 

gęstości  rozkładu  normalnego.  Wykres  ten  ilustruje  w 
uproszczeniu  sens  centralnego  twierdzenia  granicznego 
przedstawionego dalej.

Centralne 

twierdzenie 

graniczne 

jest 

ważnym 

twierdzeniem    rachunku  prawdopodobieństwa.  W  skrócie 
mówi  ono,  iż  średniej  arytmetycznej  z  próby  dąży  do 
rozkładu  normalnego  N(μ                    ),  gdy  liczebność  n  próby 
dąży do nieskończoności,

Dotychczasowe  rozważania  pokazują,  że  możliwe  jest 

przybliżanie  rzeczywistych  wartości  pewnych  wskaźników 
(parametrów) populacji na podstawie próby losowej.

Prawdopodobieństwo  ”trafienia”  w  prawdziwą  wartość 

parametru  jest  tym  większe,  im  większa  jest  liczność  n 
próby.

Jeśli  szukanym  parametrem  jest  średnia  określonej  cechy  w 

populacji i jeśli dysponujemy dużą próbą (często wystarczy 
n>=30),  wówczas  możemy  odwołać  się  do  własności 
rozkładu  normalnego,  w  celu  wyznaczenia  oszacowania 
szukanej średniej.

n

/

