WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

14. WNIOSKOWANIE

STATYSTYCZNE W SIECI BAYESA

© F.A. Dul 2007

STATYSTYCZNE W SIECI BAYESA

Wnioskowanie statystyczne

Poka

ż

emy, jak zbudowa

ć

model

probabilistyczny

ś

wiata w postaci

tzw. sieci Bayesa, który posłu

ż

y

do efektywnego wnioskowania

do efektywnego wnioskowania
w warunkach niepewno

ś

ci.

© F.A. Dul 2007

• Składnia i semantyka sieci Bayesa

• Przykłady sieci Bayesa

• Wnioskowanie

ś

cisłe i przybli

ż

one w sieciach Bayesa

• Inne rodzaje wnioskowania w warunkach niepewno

ś

ci

Plan rozdziału

© F.A. Dul 2007

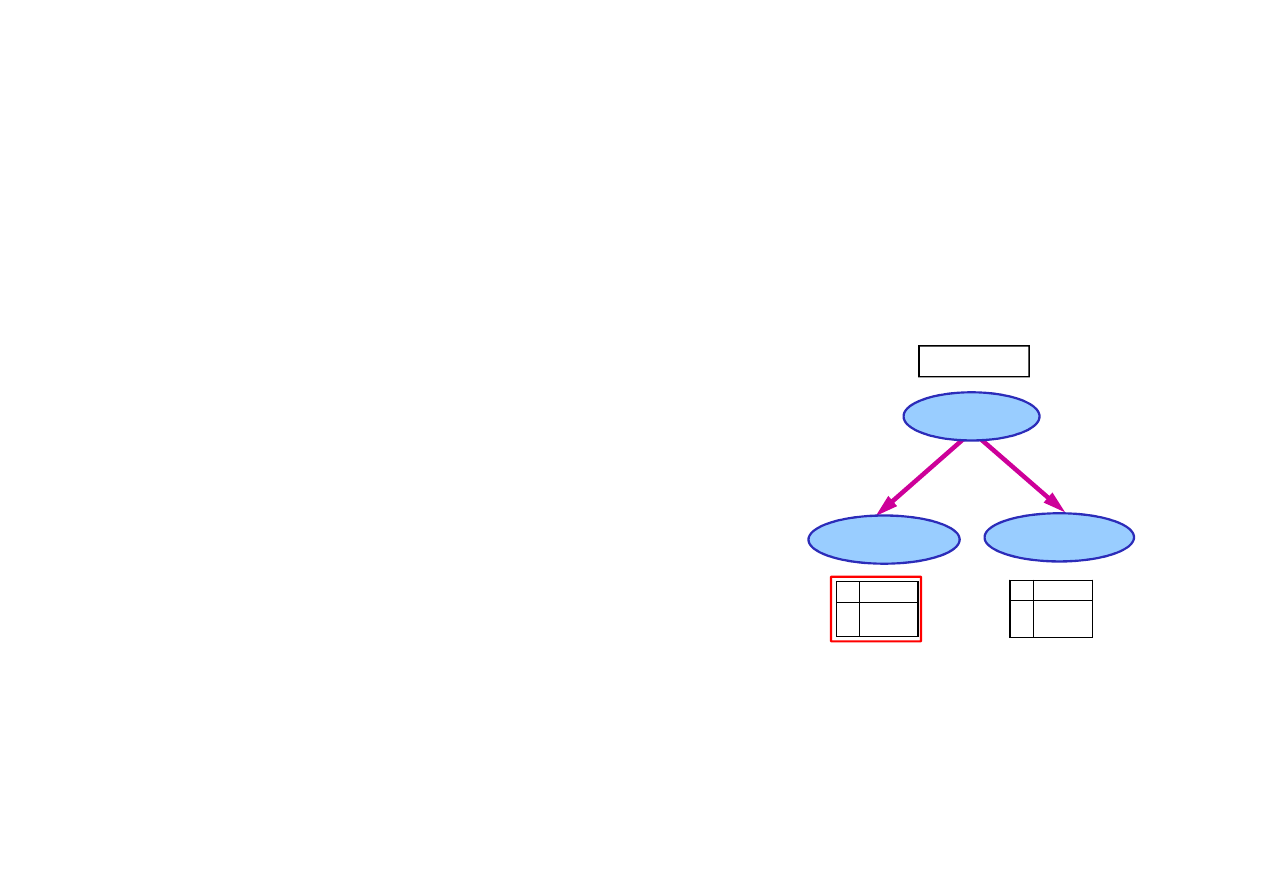
14.1. Sieci Bayesa

Sie

ć

Bayesa jest to graf acykliczny skierowany, który

umo

ż

liwia zapis graficzny zale

ż

no

ś

ci warunkowej zdarze

ń

.

Sie

ć

Bayesa umo

ż

liwia intuicyjne uj

ę

cie zale

ż

no

ś

ci

przyczynowych pomi

ę

dzy zmiennymi.

Sieci Bayesa pozwalaj

ą

przedstawi

ć

zwi

ęź

le rozkład ł

ą

czny

prawdopodobie

ń

stwa.

Składnia sieci Bayesa:

– zbiór w

ę

złów, po jednym dla ka

ż

dej zmiennej

losowej (w

ę

zły grafu),

Z

mienna

1

P(Z

1

)=0.12

© F.A. Dul 2007

losowej (w

ę

zły grafu),

Rozkład warunkowy jest przedstawiany najcz

ęś

ciej w postaci

tablic prawdopodobie

ń

stwa warunkowego

(conditional proba-

bility table, CPT), które podaj

ą

rozkład prawdopodobie

ń

stwa

warunkowego dla X

i

dla ka

ż

dej kombinacji warto

ś

ci rodziców.

Z

mienna

2

Z

mienna

3

– poł

ą

czenia odpowiadaj

ą

ce zale

ż

no

ś

ciom

pomi

ę

dzy zmiennymi (kraw

ę

dzie grafu),

– rozkład prawdopodobie

ń

stwa warunkowego

ka

ż

dego w

ę

zła przy znanych warto

ś

ciach

rozkładu prawdopodobie

ń

stwa rodziców,

P(X

i

| Rodzice(X

i

))

Z

1

P

(Z

2

|Z

1

)

t

f

0.80
0.20

Z

1

P(Z

3

|Z

1

)

t

f

0.45
0.06

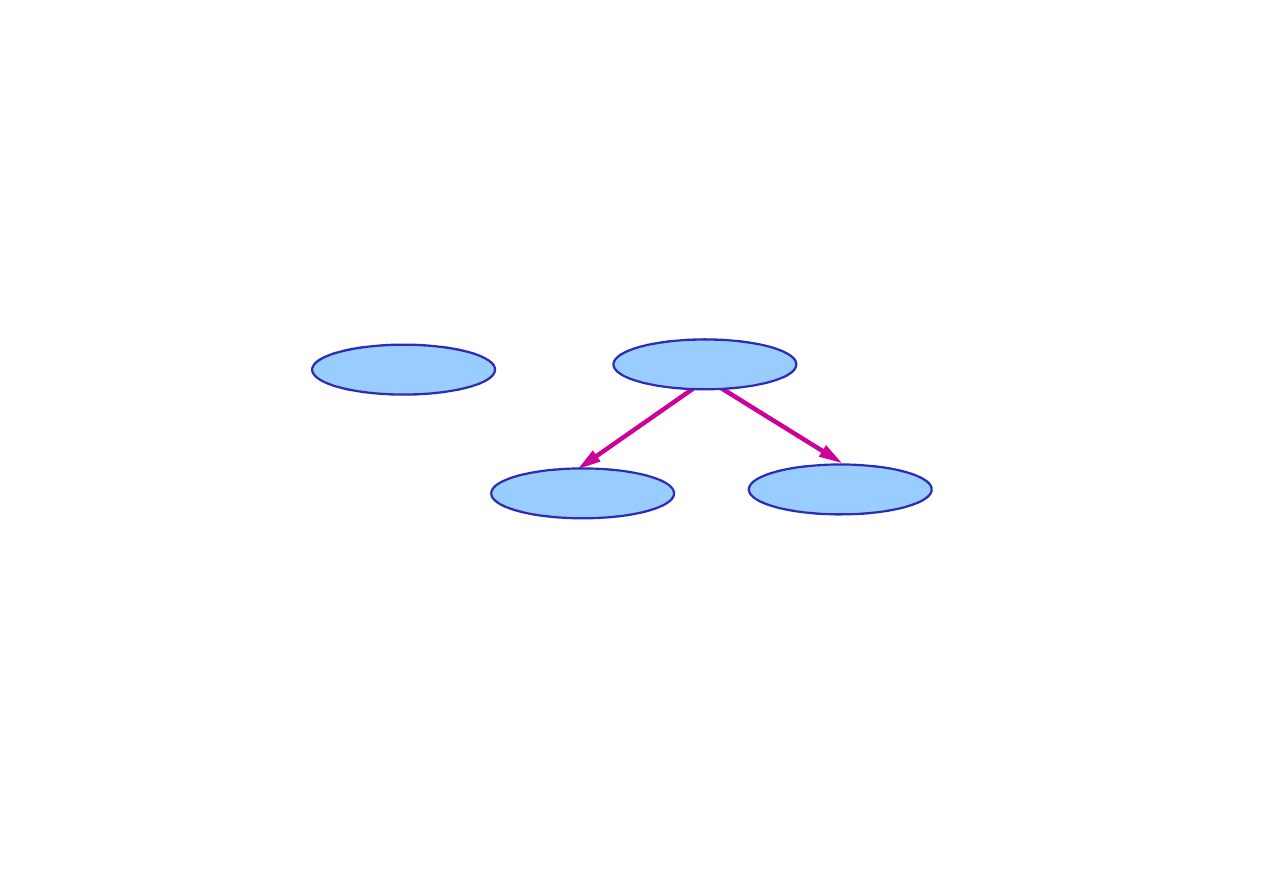
14.1. Sieci Bayesa

Przykład sieci Bayesa

Sie

ć

Bayesa dla modelu opisuj

ą

cego zale

ż

no

ś

ci pomi

ę

dzy

bólem z

ę

ba, ubytkiem, wykryciem ubytku oraz pogod

ą

.

• Zmienne losowe zadania :BólZ

ę

ba, Ubytek, Wykrycie

oraz Pogoda.

Pogoda

Ubytek

© F.A. Dul 2007

BólZ

ę

ba

Wykrycie

Topologia sieci Bayesa pozwala opisa

ć

niezale

ż

no

ść

absolutn

ą

lub warunkow

ą

zmiennych.

• BólZ

ę

ba i Wykrycie s

ą

niezale

ż

ne warunkowo przy danej

warto

ś

ci zmiennej Ubytek.

• Pogoda jest niezale

ż

na od pozostałych zmiennych

(i vice versa).

14.1. Sieci Bayesa

Bardziej zło

ż

ony przykład sieci Bayesa

• Opis problemu

Jestem w pracy. Dzwoni do mnie s

ą

siad Jan z informacj

ą

,

ż

e uruchomił si

ę

alarm w moim domu. Druga s

ą

siadka, Maria,

nie dzwoni. Alarm jest czasami wł

ą

czany przez ró

ż

ne wstrz

ą

sy.

Czy to jest włamanie?

• Zmienne losowe (w nawiasach nazwy skrócone):

Włamanie (W), Wstrz

ą

sy (S), Alarm (A),

MariaDzwoni (M), JanDzwoni (J).

© F.A. Dul 2007

MariaDzwoni (M), JanDzwoni (J).

• Wiedza o zadaniu:

– Alarm mo

ż

e uruchomi

ć

włamywacz.

– Alarm mog

ą

te

ż

uruchomi

ć

wstrz

ą

sy, np. od przelatuj

ą

cego

samolotu.

– Wł

ą

czony alarm mo

ż

e skłoni

ć

Mari

ę

lub Jana do zadzwonienia

do mnie.

• Topologia sieci Bayesa powinna odzwierciedla

ć

powy

ż

sz

ą

wiedz

ę

przyczynow

ą

.

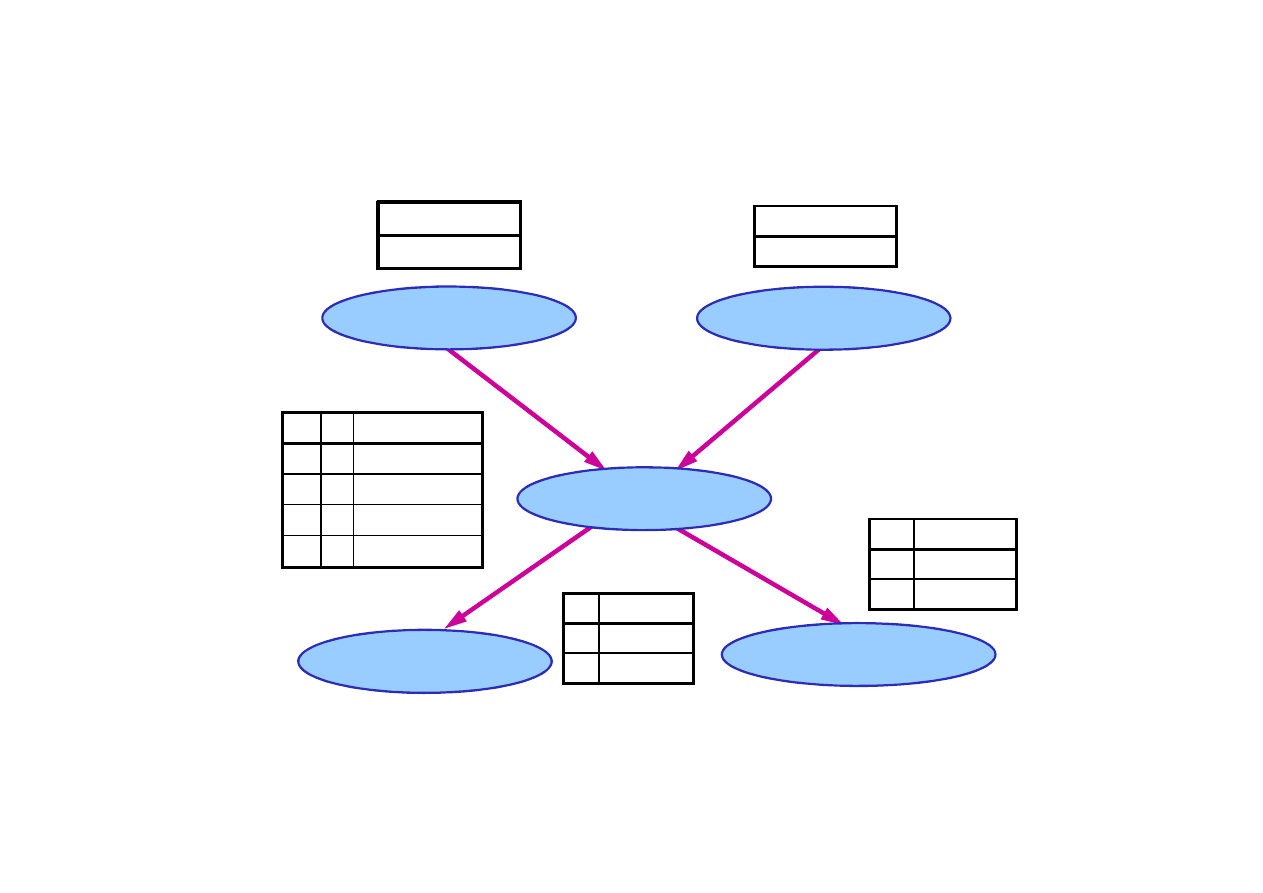
14.1. Sieci Bayesa

Sie

ć

Bayesa dla problemu włamania

P(S)

0.002

P(W)

0.001

W S

P(A|W,S)

T

T

0.95

W

łamanie

W

s

trz

ą

sy

© F.A. Dul 2007

T

T

0.95

T

F

0.94

F

T

0.29

F

F

0.01

J

an Dzwoni

M

aria Dzwoni

A

larm

A P(J|A)
T

0.90

F

0.05

A

P(M|A)

T

0.70

F

0.01

14.1. Sieci Bayesa

Zwarto

ść

reprezentacji za pomoc

ą

sieci Bayesa

• Tablica CPT dla zmiennej losowej boolowskiej X

i

maj

ą

cej k boolowskich rodziców ma 2

k

wierszy

dla wszystkich kombinacji warto

ś

ci zmiennych

rodziców.

• Ka

ż

dy wiersz zawiera prawdopodobie

ń

stwo

p dla X

i

= prawda,

1-p dla X

i

= fałsz.

• Je

ż

eli jest n zmiennych i ka

ż

da zmienna

S

W

A

© F.A. Dul 2007

• Je

ż

eli jest n zmiennych i ka

ż

da zmienna

ma nie wi

ę

cej ni

ż

k rodziców to cała sie

ć

opisana jest za pomoc

ą

O(n

·

2

k

)

liczb.

• Rozmiar ro

ś

nie wi

ę

c liniowo wzgl

ę

dem n, w przeciwie

ń

stwie

do wzrostu wykładniczego

O(2

n

)

dla pełnego rozkładu

ł

ą

cznego.

• Dla problemu włamania jest to 1 + 1 + 4 + 2 + 2 = 10 liczb

(w porównaniu z 2

5

-1 = 31 w przypadku ogólnym).

M

J

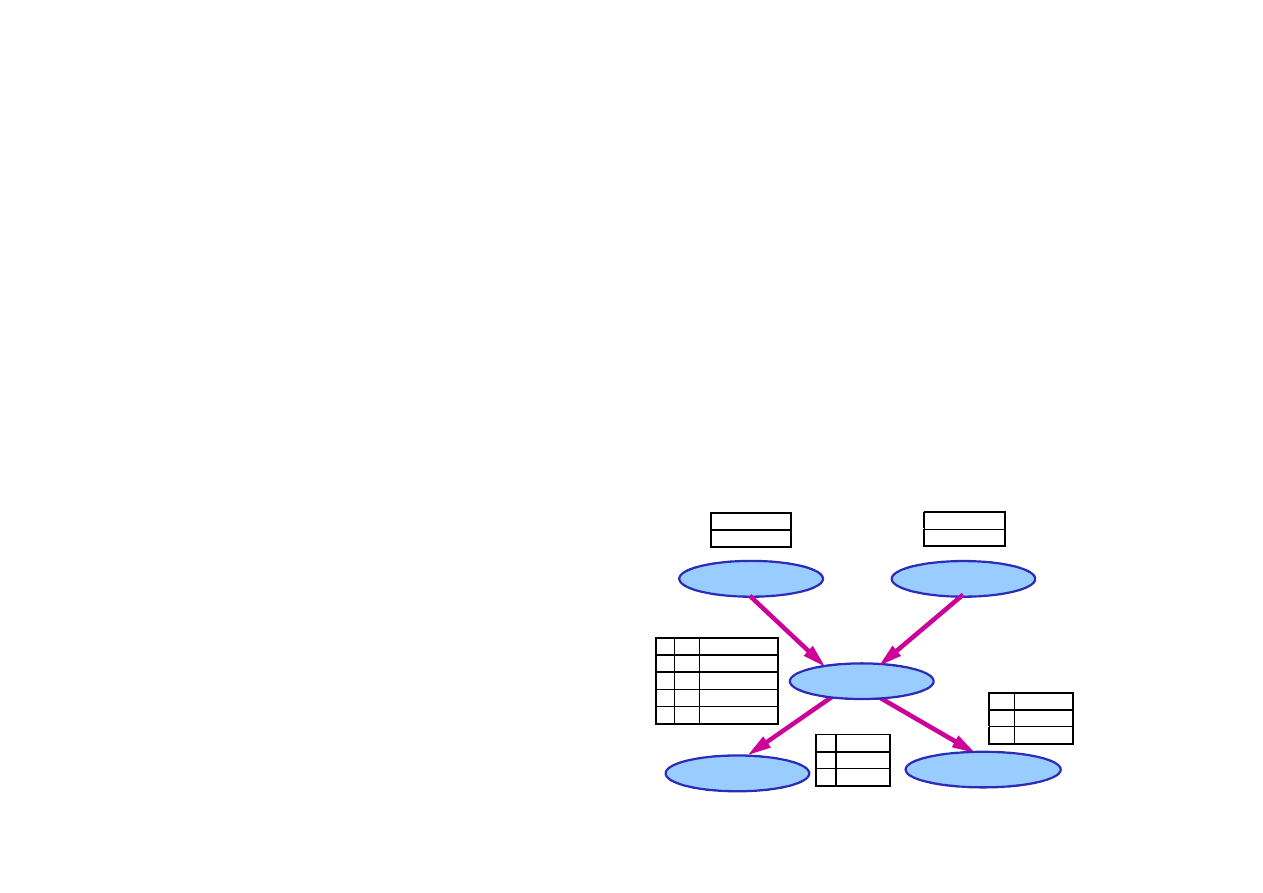
14.2. Semantyka sieci Bayesa

Rozkład ł

ą

czny prawdopodobie

ń

stwa jest iloczynem

rozkładów w

ę

złowych

Wnioskowanie na podstawie sieci Bayesa jest analogiczne
do wnioskowania z rozkładu ł

ą

cznego.

Przykład

W problemie włamania rozkład prawdopodobie

ń

stwa dla zdarzenia

„Jan dzwoni, Maria dzwoni, alarm działa, nie ma włamania i nie ma

∏

=

=

n

i

i

i

n

X

Rodzice

X

X

X

1

1

)

)

(

|

(

)

,...,

(

P

P

© F.A. Dul 2007

„Jan dzwoni, Maria dzwoni, alarm działa, nie ma włamania i nie ma
wstrz

ą

sów” (j

∧

m

∧

a

∧

¬

b

∧

¬

e ) wynosi

P( j

∧

m

∧

a

∧

¬

b

∧

¬

e ) =

= P(j | a)

×

P(m | a)

×

×

P(a |

¬

b,

¬

e)

×

P(

¬

b)

×

P(

¬

e)

= 0.90

×

0.70

×

0.001

×

0.999

×

0.998

= 0.00062

B E

P(A|B,E)

T

T

0.95

T

F

0.94

F

T

0.29

F

F

0.01

Jan Dzwoni

Włamanie

Maria Dzwoni

Alarm

Wstrz

ą

sy

A P(J|A)
T

0.90

F

0.05

A

P(M|A)

T

0.70

F

0.01

P(B)

0.001

P(E)

0.002

14.2. Semantyka sieci Bayesa

Budowanie sieci Bayesa

1. Wybra

ć

porz

ą

dek zmiennych losowych X

1

, … ,X

n

;

2. Dla i = 1, … , n :

–

doda

ć

X

i

do sieci;

–

wybra

ć

spo

ś

ród X

1

, … ,X

i-1

takich rodziców, dla których

P(X

i

| Rodzice(X

i

)) = P(X

i

| X

1

, ... X

i-1

)

© F.A. Dul 2007

Taki wybór rodziców gwarantuje wła

ś

ciwe reprezentowanie

rozkładu ł

ą

cznego:

P(X

1

, … ,X

n

)

=

∏

i =1

P(X

i

| X

1

, … , X

i-1

) (reguła ła

ń

cuchowa)

=

∏

i =1

P(X

i

| Rodzice(X

i

))

(z konstrukcji)

Topologia sieci oraz jej zwarto

ść

zale

żą

od pocz

ą

tkowego

wyboru porz

ą

dku zmiennych.

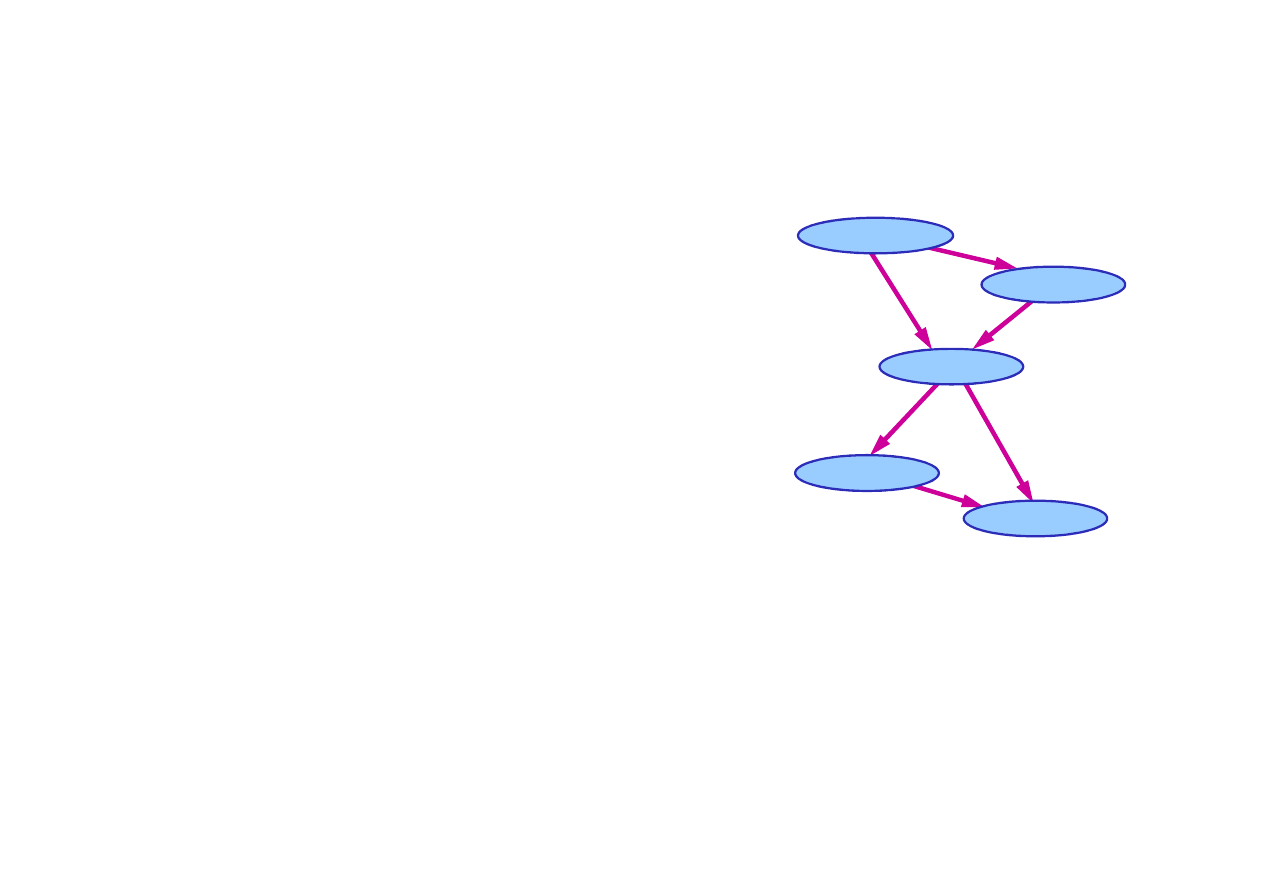
14.2. Semantyka sieci Bayesa

Przykład budowania sieci Bayesa

P(J | M) = P(J)?

Załó

ż

my,

ż

e wybrali

ś

my porz

ą

dek zmiennych: M, J, A, W, S;

J

an Dzwoni

M

aria Dzwoni

A

larm

P(A | J, M) = P(A | J)?

P(A | J, M) = P(A)?

P(W | A, J, M) = P(W | A)?

P(W | A, J, M) = P(W)?

Nie

Nie

Nie

Nie

Tak

© F.A. Dul 2007

• Inny porz

ą

dek zmiennych wprowadził dwie nowe kraw

ę

dzie.

• Sie

ć

jest mniej zwarta ni

ż

poprzednio: trzeba zapami

ę

ta

ć

1 + 2 + 4 + 2 + 4 = 13 liczb.

• Okre

ś

lanie niezale

ż

no

ś

ci warunkowej jest trudne

w kierunkach nieprzyczynowych (noncausal).

• Wydaje si

ę

,

ż

e modele przyczynowe i niezale

ż

no

ść

warunkowa s

ą

“wbudowane” w natur

ę

ludzk

ą

!

W

łamanie

W

s

trz

ą

sy

P(W | A, J, M) = P(W | A)?

P(S | W, A, J, M) = P(S | A, W)?

P(S | W, A ,J, M) = P(S | A)?

Nie

Tak

Tak

14.4. Wnioskowanie

ś

cisłe w sieci Bayesa

∑

=

=

y

y

e

e

e

)

,

,

(

)

,

(

)

|

(

X

X

X

P

P

P

α

α

Prawdopodobie

ń

stwo zmiennej

X

przy danych warto

ś

ciach

zmiennych

E =

e jest równe

Wyznaczmy w zagadnieniu włamania prawdopodobie

ń

stwo

zdarzenia

P(Wlamanie|JanDzwoni=prawda,MariaDzwoni=prawda)

∑∑

=

=

m

j

a

s

W

m

j

W

m

j

W

)

,

,

,

,

(

)

,

,

(

)

,

|

(

P

P

P

α

α

© F.A. Dul 2007

Dla przypadku w = (Włamanie=prawda) otrzymujemy

∑∑

s

a

∑∑

=

s

a

a

m

P

a

j

P

s

w

a

P

s

P

w

P

m

j

w

P

)

|

(

)

|

(

)

,

|

(

)

(

)

(

)

,

|

(

α

gdzie: j = (JanDzwoni=prawda), m = (MariaDzwoni=prawda)

Po przegrupowaniu składników otrzymujemy

∑

∑

=

s

a

a

m

P

a

j

P

s

w

a

P

s

P

w

P

m

j

w

P

)

|

(

)

|

(

)

,

|

(

)

(

)

(

)

,

|

(

α

14.4. Wnioskowanie

ś

cisłe w sieci Bayesa

Wyznaczenie prawdopodobie

ń

stwa dla

w = (Włamanie=prawda)

P(s)
0.002

P(

¬

s)

0.998

P(w)

0.001

+

0.01197

0.592238

P(w|j,m) =

αααα ××××

0.000592238

∑

∑

=

s

a

a

m

P

a

j

P

s

w

a

P

s

P

w

P

m

j

w

P

)

|

(

)

|

(

)

,

|

(

)

(

)

(

)

,

|

(

α

B E

P(A|B,E)

T

T

0.95

T

F

0.94

F

T

0.29

F

F

0.01

Jan Dzwoni

Włamanie

Maria Dzwoni

Alarm

Wstrz

ą

sy

A P(J|A)
T

0.90

F

0.05

A

P(M|A)

T

0.70

F

0.01

P(B)

0.001

P(E)

0.002

© F.A. Dul 2007

P(m|a)
0.70

P(j|a)
0.90

P(m|

¬

a)

0.01

P(j|

¬

a)

0.05

P(a|w,s)

0.95

P(

¬

a|w,s)

0.05

+

P(m|a)
0.70

P(j|a)
0.90

P(m|

¬

a)

0.01

P(j|

¬

a)

0.05

P(a|w,

¬

s)

0.94

P(

¬

a|w,

¬

s

)

0.06

+

0.70

0.63

0.70

0.63

0.01

0.0005

0.01

0.0005

0.59223

0.5985

0.000025

0.598525

0.01197

0.5922

0.00003

0.591041

14.4. Wnioskowanie

ś

cisłe w sieci Bayesa

Wyznaczenie prawdopodobie

ń

stwa dla

¬

w = (Włamanie=fałsz)

P(s)
0.002

P(

¬

s)

0.998

P(

¬

w)

0.999

+

0.000366

0.001493

P(

¬

w|j,m) =

αααα ××××

0.001492

∑

∑

¬

¬

=

¬

s

a

a

m

P

a

j

P

s

w

a

P

s

P

w

P

m

j

w

P

)

|

(

)

|

(

)

,

|

(

)

(

)

(

)

,

|

(

α

B E

P(A|B,E)

T

T

0.95

T

F

0.94

F

T

0.29

F

F

0.01

Jan Dzwoni

Włamanie

Maria Dzwoni

Alarm

Wstrz

ą

sy

A P(J|A)
T

0.90

F

0.05

A

P(M|A)

T

0.70

F

0.01

P(B)

0.001

P(E)

0.002

© F.A. Dul 2007

P(m|a)
0.70

P(j|a)
0.90

P(m|

¬

a)

0.01

P(j|

¬

a)

0.05

P(a|

¬

w,s)

0.29

P(

¬

a|

¬

w,s)

0.71

+

P(m|a)
0.70

P(j|a)
0.90

P(m|

¬

a)

0.01

P(j|

¬

a)

0.05

P(a|

¬

w,

¬

s)

0.001

P(

¬

a|

¬

w,

¬

s)

0.999

+

0.70

0.63

0.70

0.63

0.01

0.0005

0.01

0.0005

0.00113

0.1827

0.000355

0.183055

0.000366

0.00063

0.0005

0.001127

14.4. Wnioskowanie

ś

cisłe w sieci Bayesa

Prawdopodobie

ń

stwo zdarzenia

P(W | j,m)

jest wi

ę

c równe

)

)

,

|

(

,

)

,

|

(

(

)

,

|

(

m

j

w

P

m

j

w

P

m

j

W

¬

=

P

479.8245

0.001492)

0.000592

/(

1

=

+

=

α

=

×

=

)

,

(

)

,

|

(

0.001492

0.000592

479.8245

m

j

W

P

)

0.716

,

0.284

(

=

Oznacza to,

ż

e prawdopodobie

ń

stwo włamania gdy dzwoni

ą

)

0.001492

,

0.000592

(

×

×

=

α

α

© F.A. Dul 2007

Oznacza to,

ż

e prawdopodobie

ń

stwo włamania gdy dzwoni

ą

oboje s

ą

siedzi wynosi ok. 28%

Wady wnioskowania

ś

cisłego w sieciach Bayesa:

• Składniki wyra

ż

enia dla prawdopodobie

ń

stwa s

ą

obliczane

wielokrotnie, np. P(j|a)P(m|a) czy P(j|

¬

a)P(m|

¬

a).

• Zło

ż

ono

ść

obliczeniowa dla sieci z n zmiennymi boolowskimi

jest wykładnicza -

O(2

n

)

ale jest ni

ż

sza ni

ż

w przypadku

ogólnym, w którym

O(n

·

2

n

)

.

14.5. Wnioskowanie przybli

ż

one w sieci Bayesa

Ze wzgl

ę

du na wielk

ą

zło

ż

ono

ść

obliczeniow

ą

wyznaczania

prawdopodobie

ń

stwa na podstawie sieci Bayesa w praktyce

stosuje si

ę

najcz

ęś

ciej wnioskowania przybli

ż

one.

Algorytm Monte Carlo próbkowania zmiennych losowych
Idea: przy du

ż

ej liczbie próbkowa

ń

prawdopodobie

ń

stwo okre-

ś

lone jako liczba próbek danej warto

ś

ci zmiennej w stosunku

do liczby wszystkich próbkowa

ń

d

ąż

y do warto

ś

ci dokładnej,

x

N

)

(

∑

© F.A. Dul 2007

Przykład: rzut monet

ą

, Moneta =

〈〈〈〈

orzeł , reszka

〉〉〉〉

, prawdopo-

dobie

ń

stwo

ś

cisłe P(Moneta) =

〈〈〈〈

0.5 , 0.5

〉〉〉〉

, za

ś

przybli

ż

one

N

x

N

x

P

N

)

(

lim

)

(

∑

=

∞

→

N

orzeł

N

orzeł

P

N

)

(

)

(

∑

≈

...}

,

49

.

0

,

43

.

0

,

55

.

0

,

4

.

0

,

3

.

0

,

0

.

0

{

)

(

=

reszka

P

N

N

reszka

N

reszka

P

N

)

(

)

(

∑

≈

Przykład: kolejne rzuty monet

ą

prowadz

ą

do oszacowa

ń

:

14.5. Wnioskowanie przybli

ż

one w sieci Bayesa

Próbkowanie losowe w sieci Bayesa.

Chmury

P(C)=0.5

Zasada: próbkowanie ka

ż

dej zmiennej w kolejno

ś

ci okre

ś

lonej

przez sie

ć

.

Przykład: sie

ć

Bayesa dla problemu mokrej trawy, uporz

ą

dko-

wana nast

ę

puj

ą

co: [ Chmury, Zraszacz, Deszcz, MokraTrawa ]

© F.A. Dul 2007

Zraszacz

MokraTrawa

Deszcz

C P(Z)

t

f

0.10

0.50

C P(D)

t

f

0.80
0.20

Z D P(D)

t t
t

f

f

t

f

f

0.99
0.90
0.90
0.00

14.5. Wnioskowanie przybli

ż

one w sieci Bayesa

Próbkowanie przykładowe w sieci:

1. Próbkowanie P(Chmury) =

〈〈〈〈

0.5, 0.5

〉〉〉〉

wynik:

prawda

;

2. Próbkowanie P(Zraszacz|Chmury=

prawda

) =

〈〈〈〈

0.1, 0.9

〉〉〉〉

wynik:

fałsz

;

3. Próbkowanie P(Deszcz|Chmury=

prawda

) =

〈〈〈〈

0.8, 0.2

〉〉〉〉

wynik:

prawda

;

4. Próbkowanie P(MokraTrawa|Zraszacz=

fałsz

,Deszcz=

prawda

) =

〈〈〈〈

0.9,0.1

〉〉〉〉

wynik:

prawda

;

Próbkowanie zwróciło wi

ę

c zdarzenie zgodne z sieci

ą

Z

1

= [

prawda

,

fałsz

,

prawda

,

prawda

].

Kolejne próbkowanie mo

ż

e zwróci

ć

inne zdarzenie, np.

© F.A. Dul 2007

Kolejne próbkowanie mo

ż

e zwróci

ć

inne zdarzenie, np.

Z

2

= [

prawda

,

prawda

,

fałsz

,

prawda

].

∏

=

=

n

i

i

i

n

PS

X

rodzice

x

P

x

x

S

1

1

))

(

|

(

)

,...,

(

Ze sposobu próbkowania wynika, ze prawdopodobie

ń

stwo

S

PS

(x

1

,...,x

n

) wybranej próbki [x

1

,...,x

n

] wynosi

i jest równe prawdopodobie

ń

stwu zdarzenia reprezentowanym

przez sie

ć

Bayesa

)

,...,

(

)

,...,

(

1

1

n

n

PS

x

x

P

x

x

S

=

14.5. Wnioskowanie przybli

ż

one w sieci Bayesa

Je

ż

eli N

PS

(x

1

,...,x

n

) jest liczb

ą

wylosowa

ń

próbki [x

1

,...,x

n

], to

W przykładzie mokrej trawy prawdopodobie

ń

stwa zdarze

ń

wylosowanych z sieci Bayesa wynosz

ą

)

,...,

(

)

,...,

(

)

,...,

(

lim

1

1

1

n

n

PS

n

PS

N

x

x

P

x

x

S

N

x

x

N

=

=

∞

→

S

PS

(Z

1

) = 0.5

××××

0.9

××××

0.8

××××

0.9 = 0.324,

S

PS

(Z

2

) = 0.5

××××

0.1

××××

0.2

××××

0.9 = 0.009.

© F.A. Dul 2007

S

PS

(Z

2

) = 0.5

××××

0.1

××××

0.2

××××

0.9 = 0.009.

Przy du

ż

ej liczbie próbkowa

ń

N zdarzenie Z

1

b

ę

dzie wybrane

w 32.4%, za

ś

zdarzenie Z

2

- tylko w 0.9% przypadków.

Koszt C wnioskowania przybli

ż

onego w sieciach Bayesa jest

zazwyczaj du

ż

o ni

ż

szy ni

ż

koszt wnioskowania

ś

cisłego,

C << O(2

n

)

Istniej

ą

równie

ż

inne metody wnioskowania przybli

ż

onego

w sieciach Bayesa, np. metoda

Monte Carlo dla ła

ń

cucha

Markowa

(Markov chain Monte Carlo).

U

ż

yteczno

ść

sieci Bayesa

Sieci Bayesa stanowi

ą

wygodn

ą

form

ę

reprezentacji

zale

ż

no

ś

ci zdarze

ń

.

Pozwalaj

ą

te

ż

znacznie zredukowa

ć

rozmiar

reprezentacji a tak

ż

e koszt wnioskowania

stochastycznego.

Wnioskowanie przybli

ż

one w sieciach Bayesa

cechuje si

ę

niskim kosztem przy zadowalaj

ą

cych

©

F.A. Dul 2007

cechuje si

ę

niskim kosztem przy zadowalaj

ą

cych

dokładno

ś

ciach uzyskiwanych rozkładów

prawdopodobie

ń

stw.

Sieci Bayesa s

ą

równie

ż

wykorzystywane do opisu

dynamicznych zjawisk stochastycznych stanowi

ą

c

podstaw

ę

filtru Kalmana

.

14.7. Inne metody wnioskowania probabilistycznego

Podej

ś

cie stochastyczne jest szeroko stosowane w wielu

dziedzinach wiedzy i praktyki: w fizyce, genetyce, ekonomii,
ubezpieczeniach, bankowo

ś

ci...

W sztucznej inteligencji podej

ś

cie probabilistyczne jest

u

ż

ywane dopiero od lat 70. XX wieku, głównie w systemach

ekspertowych.

Powodem był wykładniczy koszt wnioskowania – wcze

ś

niej

nie znano algorytmów dla sieci Bayesa.

© F.A. Dul 2007

nie znano algorytmów dla sieci Bayesa.

Dlatego do wnioskowania w warunkach niepewno

ś

ci

stosowano podej

ś

cia alternatywne, takie jak:

• Wnioskowanie

domy

ś

lne

,

• Reprezentacja niepewno

ś

ci za pomoc

ą

reguł

,

• Reprezentacja ignorancji (teoria

Dempstera-Shafera

),

• Reprezentacja nieprecyzyjno

ś

ci za pomoc

ą

logiki rozmytej

.

Panuje przekonanie,

ż

e wnioskowanie stochastyczne jest

bardziej uniwersalne ni

ż

powy

ż

sze wnioskowania alternatywne.

14.7. Inne metody wnioskowania probabilistycznego

Metody wnioskowania oparte na regułach
Metody wnioskowania wykorzystuj

ą

ce reguły s

ą

podobne

do metod logiki zda

ń

lub pierwszego rz

ę

du.

Wnioskowanie logiczne jest uzupełnione czynnikiem
okre

ś

laj

ą

cym stopie

ń

wiarygodno

ś

ci

(fudge factor)

, np.

A

25

|

→

0.3

zapewni dojazd na czas;

Uwzgl

ę

dnienie stopnia wiarygodno

ś

ci umo

ż

liwia „sterowanie”

wnioskowaniem logicznym.
Jednak z podej

ś

ciem takim wi

ążą

si

ę

trudno

ś

ci.

© F.A. Dul 2007

Jednak z podej

ś

ciem takim wi

ążą

si

ę

trudno

ś

ci.

Przykład
Czy mokra trawa jest wynikiem deszczu,
czy te

ż

wł

ą

czenia zraszacza?

Zraszacz

MokraTrawa

Deszcz

Mimo takich problemów wnioskowanie z

czynnikiem pewno

ś

ci

jest stosowane z powodzeniem w wielu systemach
ekspertowych (np. MYCIN).

– Zraszacz |

→

0.99

MokraTrawa;

– MokraTrawa |

→

0.7

Deszcz;

Problem: czy zraszacz powoduje deszcz?

14.7. Inne metody wnioskowania probabilistycznego

Teoria Dempstera-Shafera reprezentacji ignorancji

Teoria Dempstera-Shafera opisuje ró

ż

nice pomi

ę

dzy

niepewno

ś

ci

ą

a

ignorancj

ą

.

Funkcja wiarygodno

ś

ci

Bel(X)

opisuje prawdopodobie

ń

stwo

tego,

ż

e obserwacje potwierdzaj

ą

twierdzenie

X

.

Przykład
Dla zdarzenia „Reszka” przy rzucie niepewn

ą

monet

ą

i przy

braku obserwacji zarówno

Bel(Reszka)=0

jak i

Bel(

¬

Reszka)=0

.

Je

ż

eli stwierdzi si

ę

z 90% pewno

ś

ci

ą

,

ż

e moneta jest dobra,

© F.A. Dul 2007

Je

ż

eli stwierdzi si

ę

z 90% pewno

ś

ci

ą

,

ż

e moneta jest dobra,

(

P(Reszka)=0.5

), to

Bel(Reszka) = 0.9

×

0.5 = 0.45

; podobnie

Bel(

¬

Reszka) = 0.45

.

Istniej

ą

ca 10% luka wyra

ż

a niepewno

ść

co do jako

ś

ci monety.

Reguła Dempstera

okre

ś

la sposób wyznaczania warto

ś

ci

funkcji

Bel

na podstawie obserwacji.

Teoria Dempstera-Shafera definiuje przedziały prawdopodo-
bie

ń

stwa, np. dla wyrzucenia reszki przedział prawdopodo-

bie

ń

stwa wynosi [0,1] przed weryfikacj

ą

monety, za

ś

po jej

weryfikacji [0.45,0.55].

14.7. Inne metody wnioskowania probabilistycznego

Logika rozmyta i reprezentacja nieprecyzyjno

ś

ci

Teoria zbiorów rozmytych okre

ś

la

nieprecyzyjno

ść

twierdze

ń

.

Przykład
Czy zdanie „Jan jest wysoki” (wzrost 175cm) jest prawdziwe?
Najcz

ę

stsza odpowied

ź

: Jan jest wysoki

„w pewnym stopniu”

.

UWAGA!

Nieprecyzyjno

ść

nie jest niepewno

ś

ci

ą

(wzrost Jana

jest znany).
Teoria zbiorów rozmytych okre

ś

la stopie

ń

prawdziwo

ś

ci

twierdze

ń

, np. Wysoki(Jan)

∈

[0,1] zamiast Wysoki(Jan)=fałsz.

© F.A. Dul 2007

twierdze

ń

, np. Wysoki(Jan)

∈

[0,1] zamiast Wysoki(Jan)=fałsz.

Stopie

ń

prawdziwo

ś

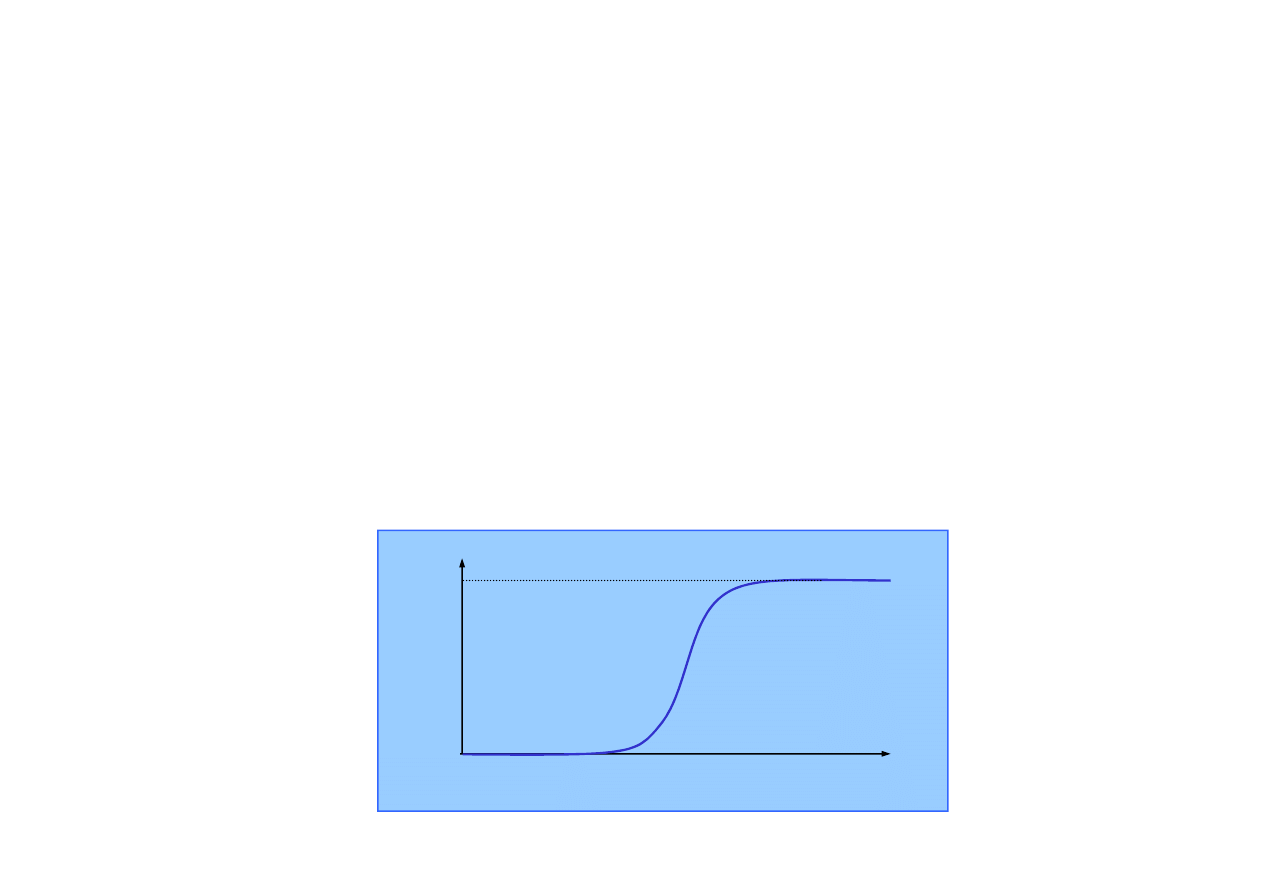
ci opisuje zazwyczaj rozkład typu

probit

1.0 1.5 2.0 m 2.5

1.0

Wysoki

0.0

14.7. Inne metody wnioskowania probabilistycznego

Logika rozmyta i reprezentacja nieprecyzyjno

ś

ci

Logika rozmyta

umo

ż

liwia wnioskowanie z wyra

ż

eniami

logicznymi okre

ś

lonymi w zbiorach rozmytych.

Miara prawdziwo

ś

ci T okre

ś

lona jest regułami:

Problemy: T(Wysoki(Jan)) = 0.6, T(Ci

ęż

ki(Jan)) = 0.4.

T(Wysoki(Jan)

∧

Ci

ęż

ki(Jan)) = 0.4

→

OK.

• T(A

∧

B) = min ( T(A) , T(B) ),

• T(A

∨

B) = max ( T(A) , T(B) ),

• T(

¬

A) = 1 – T(A).

© F.A. Dul 2007

Sterowanie rozmyte

słu

ż

y do syntezy sterowania przy u

ż

yciu

reguł rozmytych.
Sterowanie rozmyte jest szeroko stosowane w wielu
urz

ą

dzeniach, np.: pralkach, kamerach wideo, sprz

ę

cie AGD.

T(Wysoki(Jan)

∧

Ci

ęż

ki(Jan)) = 0.4

→

OK.

T(Wysoki(Jan)

∧

¬

Wysoki(Jan)) = 0.4

???

Podsumowanie

• Sieci Bayesa stanowi

ą

naturaln

ą

reprezentacj

ę

niezale

ż

no

ś

ci warunkowej (indukowanej przyczynowo).

• Topologia sieci i tablice prawdopodobie

ń

stwa warunkowego

(CPT) pozwalaj

ą

na zwart

ą

reprezentacj

ę

rozkładu ł

ą

cznego

prawdopodobie

ń

stwa.

• Sieci Bayesa s

ą

szczególnie przydane i łatwe do zastosowa-

nia w systemach ekspertowych.

• Wnioskowanie

ś

cisłe z u

ż

yciem sieci Bayesa jest kosztowne

© F.A. Dul 2007

• Wnioskowanie

ś

cisłe z u

ż

yciem sieci Bayesa jest kosztowne

~O(2

n

).

• Wnioskowanie przybli

ż

one za pomoc

ą

próbkowania zdarze

ń

pozwala obni

ż

y

ć

koszt oblicze

ń

przy zachowaniu akcepto-

walnej dokładno

ś

ci wyznaczonych prawdopodobie

ń

stw.

• Zwykłe sieci Bayesa maj

ą

cechy logiki zda

ń

, co ogranicza

zakres ich zastosowania.

• Istniej

ą

inne sposoby uwzgl

ę

dniania niepewno

ś

ci: reguły

niepewno

ś

ci, reprezentacja ignorancji, logika rozmyta.