
WPROWADZENIE
DO SZTUCZNEJ INTELIGENCJI
POLITECHNIKA WARSZAWSKA
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
MEL
MEL
NS 586
Dr in
ż
. Franciszek Dul
© F.A. Dul 2007

14. WNIOSKOWANIE
STATYSTYCZNE W SIECI BAYESA
© F.A. Dul 2007
STATYSTYCZNE W SIECI BAYESA

Wnioskowanie statystyczne
Poka
ż
emy, jak zbudowa
ć
model
probabilistyczny
ś
wiata w postaci
tzw. sieci Bayesa, który posłu
ż
y
do efektywnego wnioskowania
do efektywnego wnioskowania
w warunkach niepewno
ś
ci.
© F.A. Dul 2007

• Składnia i semantyka sieci Bayesa
• Przykłady sieci Bayesa
• Wnioskowanie
ś
cisłe i przybli
ż
one w sieciach Bayesa
• Inne rodzaje wnioskowania w warunkach niepewno
ś
ci
Plan rozdziału
© F.A. Dul 2007
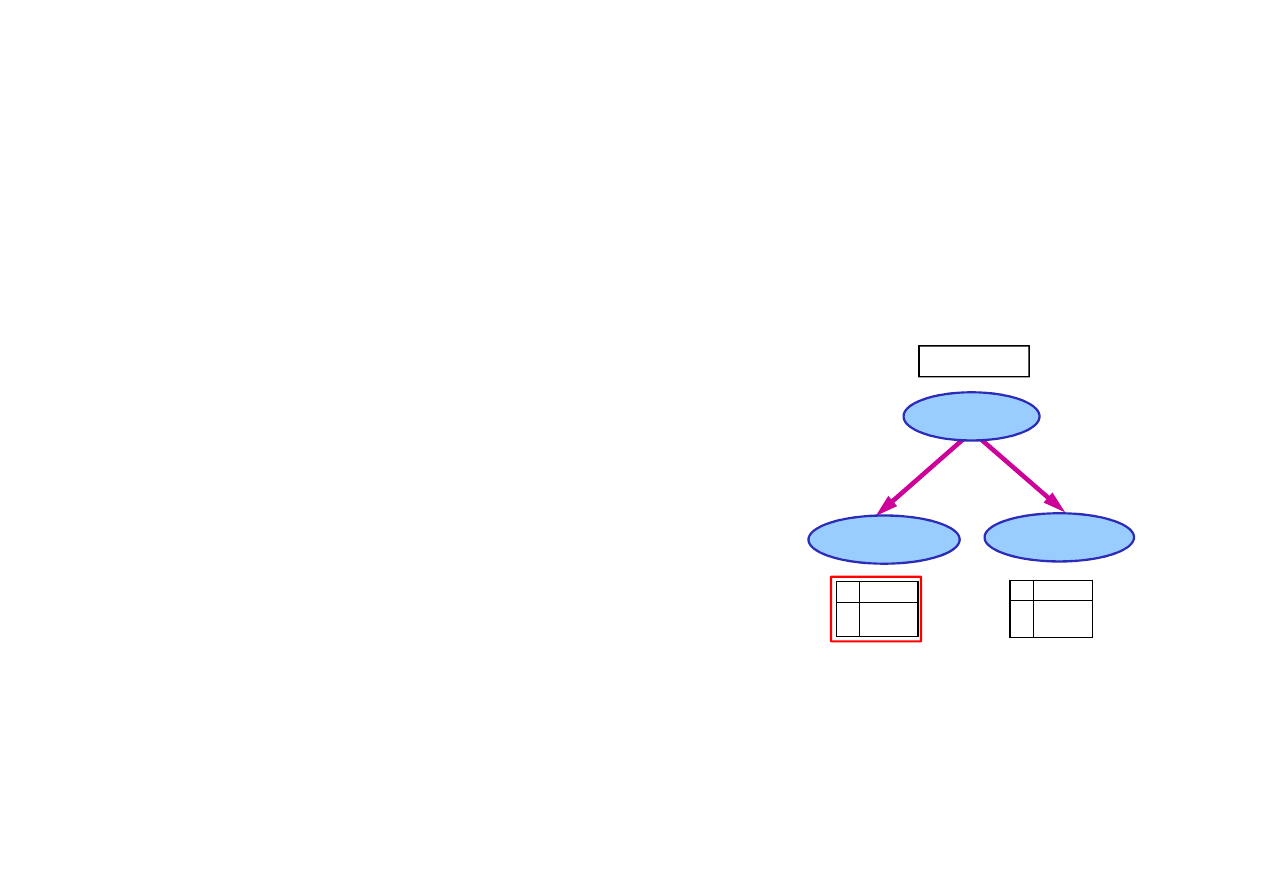
14.1. Sieci Bayesa
Sie
ć
Bayesa jest to graf acykliczny skierowany, który
umo
ż
liwia zapis graficzny zale
ż
no
ś
ci warunkowej zdarze
ń
.
Sie
ć
Bayesa umo
ż
liwia intuicyjne uj
ę
cie zale
ż
no
ś
ci
przyczynowych pomi
ę
dzy zmiennymi.
Sieci Bayesa pozwalaj
ą
przedstawi
ć
zwi
ęź
le rozkład ł
ą
czny
prawdopodobie
ń
stwa.
Składnia sieci Bayesa:
– zbiór w
ę
złów, po jednym dla ka
ż
dej zmiennej
losowej (w
ę
zły grafu),
Z
mienna
1
P(Z
1
)=0.12
© F.A. Dul 2007
losowej (w
ę
zły grafu),
Rozkład warunkowy jest przedstawiany najcz
ęś
ciej w postaci
tablic prawdopodobie
ń
stwa warunkowego
(conditional proba-
bility table, CPT), które podaj
ą
rozkład prawdopodobie
ń
stwa
warunkowego dla X
i
dla ka
ż
dej kombinacji warto
ś
ci rodziców.
Z
mienna
2
Z
mienna
3
– poł
ą
czenia odpowiadaj
ą
ce zale
ż
no
ś
ciom
pomi
ę
dzy zmiennymi (kraw
ę
dzie grafu),
– rozkład prawdopodobie
ń
stwa warunkowego
ka
ż
dego w
ę
zła przy znanych warto
ś
ciach
rozkładu prawdopodobie
ń
stwa rodziców,
P(X
i
| Rodzice(X
i
))
Z
1
P
(Z
2
|Z
1
)
t
f
0.80
0.20
Z
1
P(Z
3
|Z
1
)
t
f
0.45
0.06
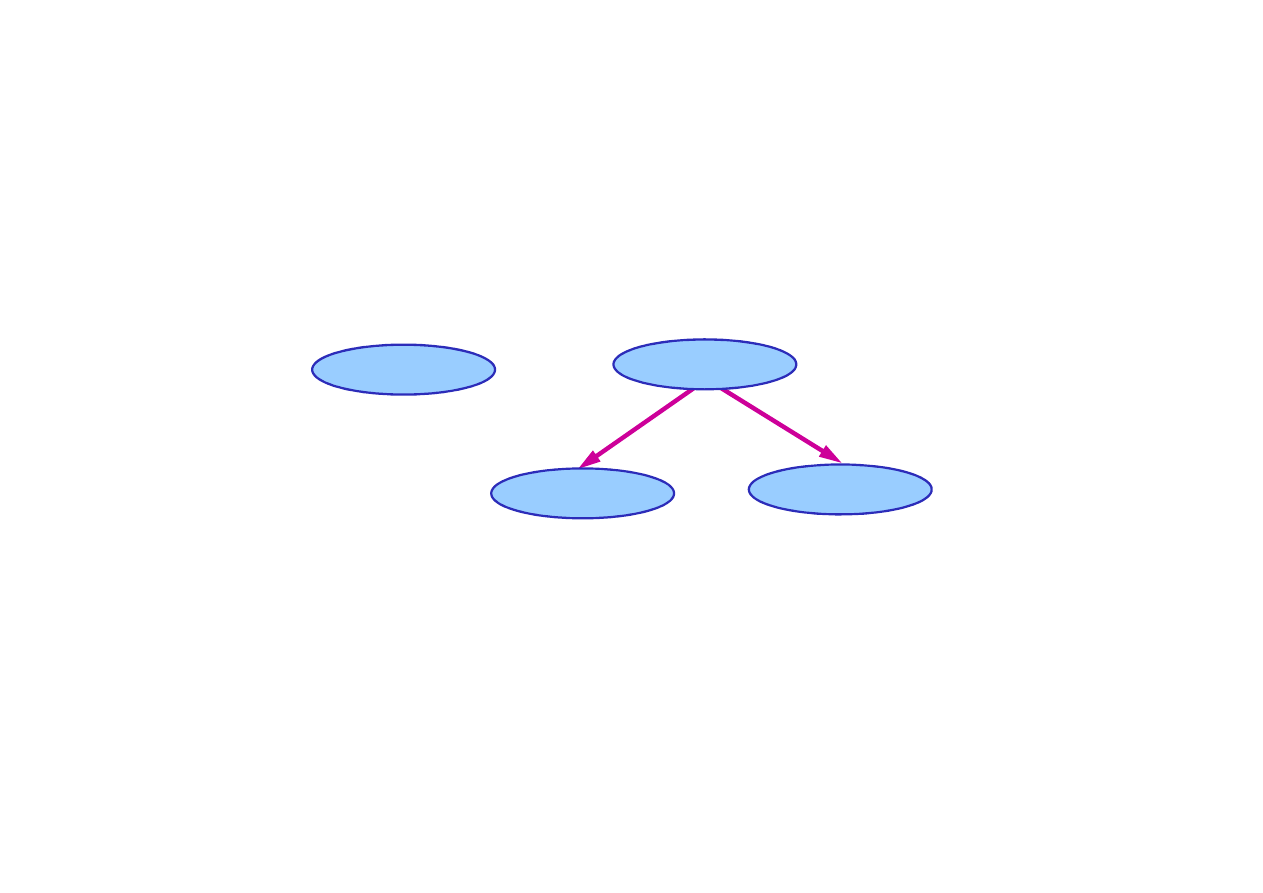
14.1. Sieci Bayesa
Przykład sieci Bayesa
Sie
ć
Bayesa dla modelu opisuj
ą
cego zale
ż
no
ś
ci pomi
ę
dzy
bólem z
ę
ba, ubytkiem, wykryciem ubytku oraz pogod
ą
.
• Zmienne losowe zadania :BólZ
ę
ba, Ubytek, Wykrycie
oraz Pogoda.
Pogoda
Ubytek
© F.A. Dul 2007
BólZ
ę
ba
Wykrycie
Topologia sieci Bayesa pozwala opisa
ć
niezale
ż
no
ść
absolutn
ą
lub warunkow
ą
zmiennych.
• BólZ
ę
ba i Wykrycie s
ą
niezale
ż
ne warunkowo przy danej
warto
ś
ci zmiennej Ubytek.
• Pogoda jest niezale
ż
na od pozostałych zmiennych
(i vice versa).

14.1. Sieci Bayesa
Bardziej zło
ż
ony przykład sieci Bayesa
• Opis problemu
Jestem w pracy. Dzwoni do mnie s
ą
siad Jan z informacj
ą
,
ż
e uruchomił si
ę
alarm w moim domu. Druga s
ą
siadka, Maria,
nie dzwoni. Alarm jest czasami wł
ą
czany przez ró
ż
ne wstrz
ą
sy.
Czy to jest włamanie?
• Zmienne losowe (w nawiasach nazwy skrócone):
Włamanie (W), Wstrz
ą
sy (S), Alarm (A),
MariaDzwoni (M), JanDzwoni (J).
© F.A. Dul 2007
MariaDzwoni (M), JanDzwoni (J).
• Wiedza o zadaniu:
– Alarm mo
ż
e uruchomi
ć
włamywacz.
– Alarm mog
ą
te
ż
uruchomi
ć
wstrz
ą
sy, np. od przelatuj
ą
cego
samolotu.
– Wł
ą
czony alarm mo
ż
e skłoni
ć
Mari
ę
lub Jana do zadzwonienia
do mnie.
• Topologia sieci Bayesa powinna odzwierciedla
ć
powy
ż
sz
ą
wiedz
ę
przyczynow
ą
.
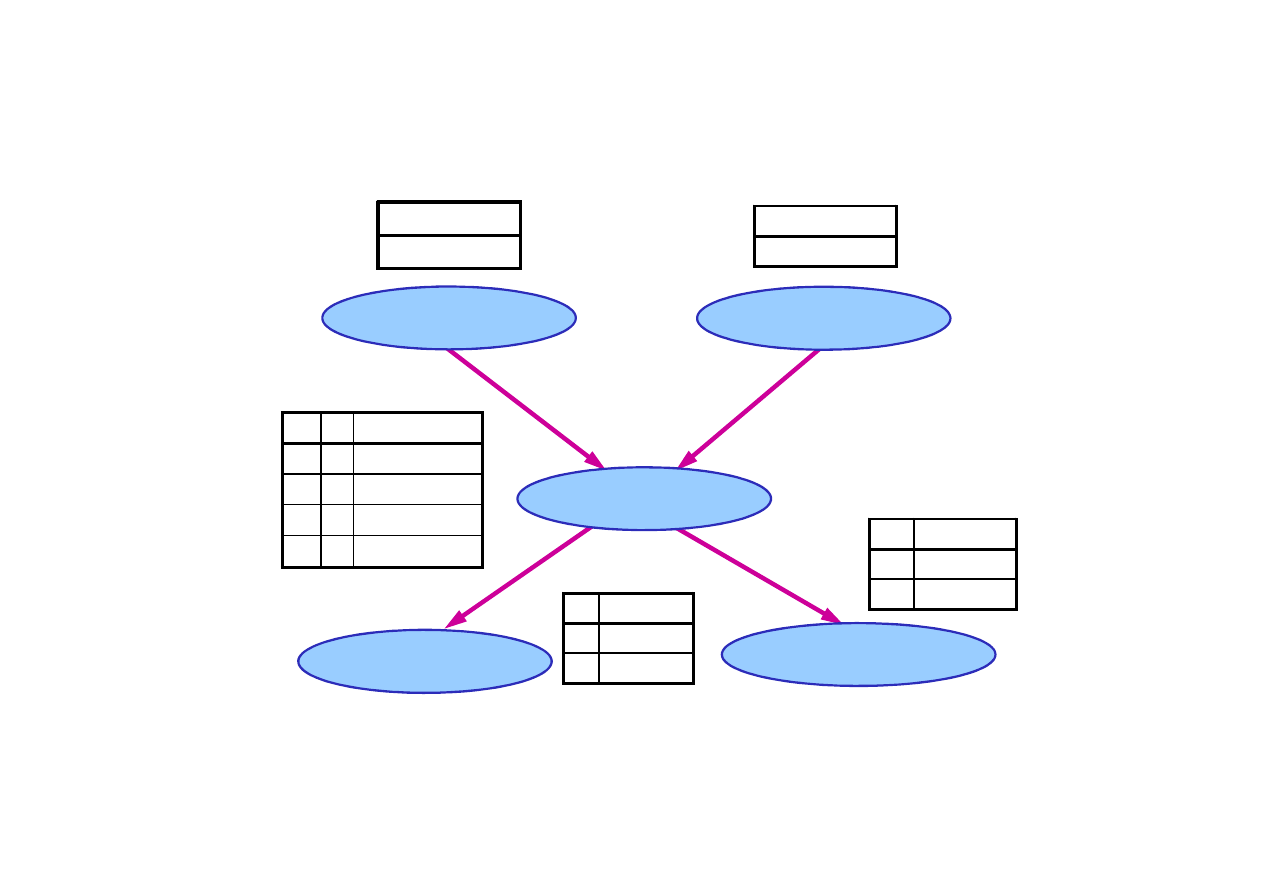
14.1. Sieci Bayesa
Sie
ć
Bayesa dla problemu włamania
P(S)
0.002
P(W)
0.001
W S
P(A|W,S)
T
T
0.95
W
łamanie
W
s
trz
ą
sy
© F.A. Dul 2007
T
T
0.95
T
F
0.94
F
T
0.29
F
F
0.01
J
an Dzwoni
M
aria Dzwoni
A
larm
A P(J|A)
T
0.90
F
0.05
A
P(M|A)
T
0.70
F
0.01
14.1. Sieci Bayesa
Zwarto
ść
reprezentacji za pomoc
ą
sieci Bayesa
• Tablica CPT dla zmiennej losowej boolowskiej X
i
maj
ą
cej k boolowskich rodziców ma 2
k
wierszy
dla wszystkich kombinacji warto
ś
ci zmiennych
rodziców.
• Ka
ż
dy wiersz zawiera prawdopodobie
ń
stwo
p dla X
i
= prawda,
1-p dla X
i
= fałsz.
• Je
ż
eli jest n zmiennych i ka
ż
da zmienna
S
W
A
© F.A. Dul 2007
• Je
ż
eli jest n zmiennych i ka
ż
da zmienna
ma nie wi
ę
cej ni
ż
k rodziców to cała sie
ć
opisana jest za pomoc
ą
O(n
·
2
k
)
liczb.
• Rozmiar ro
ś
nie wi
ę
c liniowo wzgl
ę
dem n, w przeciwie
ń
stwie
do wzrostu wykładniczego
O(2
n
)
dla pełnego rozkładu
ł
ą
cznego.
• Dla problemu włamania jest to 1 + 1 + 4 + 2 + 2 = 10 liczb
(w porównaniu z 2
5
-1 = 31 w przypadku ogólnym).
M
J
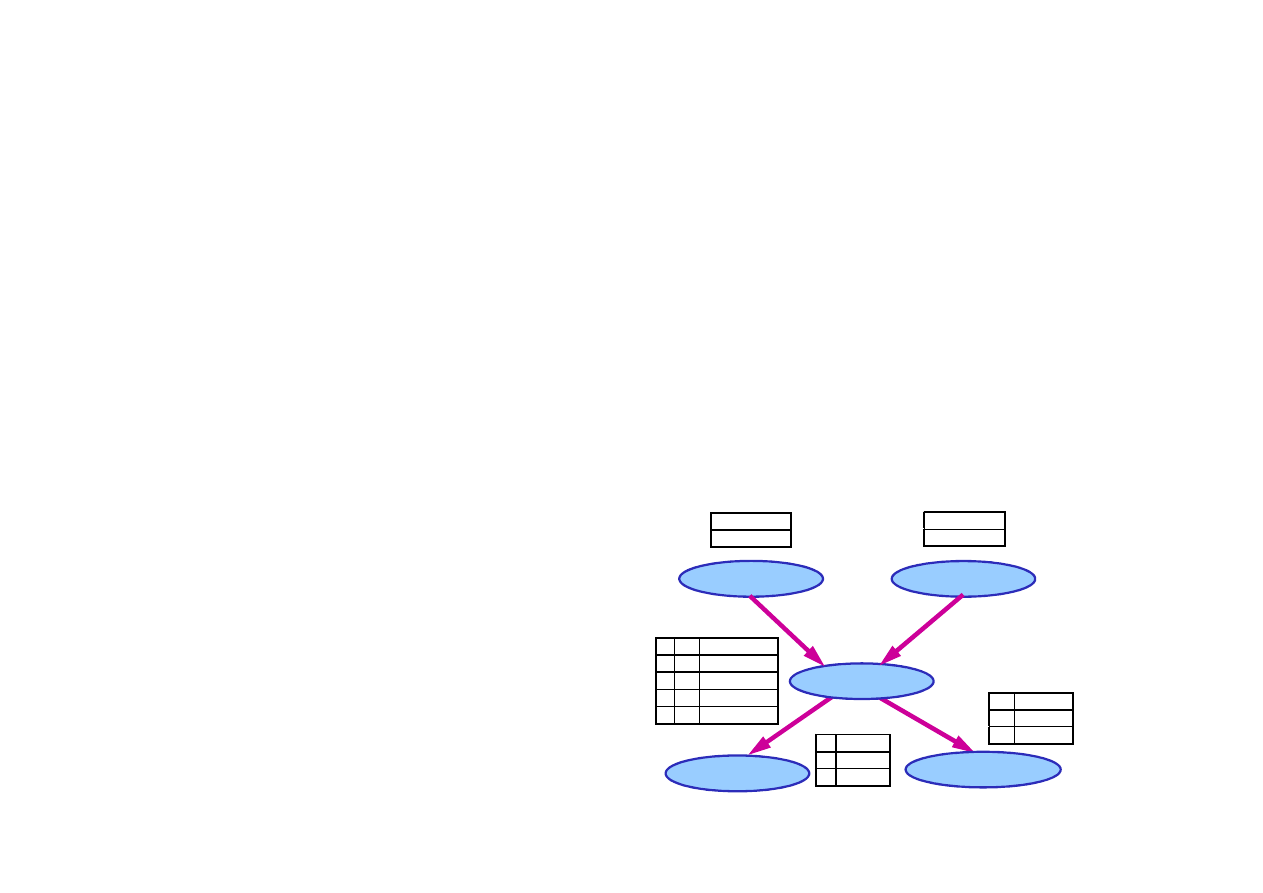
14.2. Semantyka sieci Bayesa
Rozkład ł
ą
czny prawdopodobie
ń
stwa jest iloczynem
rozkładów w
ę
złowych
Wnioskowanie na podstawie sieci Bayesa jest analogiczne
do wnioskowania z rozkładu ł
ą
cznego.
Przykład
W problemie włamania rozkład prawdopodobie
ń
stwa dla zdarzenia
„Jan dzwoni, Maria dzwoni, alarm działa, nie ma włamania i nie ma
∏
=
=
n
i
i
i
n
X
Rodzice
X
X
X
1
1
)
)
(
|
(
)
,...,
(
P
P
© F.A. Dul 2007
„Jan dzwoni, Maria dzwoni, alarm działa, nie ma włamania i nie ma
wstrz
ą
sów” (j
∧
m
∧
a
∧
¬
b
∧
¬
e ) wynosi
P( j
∧
m
∧
a
∧
¬
b
∧
¬
e ) =
= P(j | a)
×
P(m | a)
×
×
P(a |
¬
b,
¬
e)
×
P(
¬
b)
×
P(
¬
e)
= 0.90
×
0.70
×
0.001
×
0.999
×
0.998
= 0.00062
B E
P(A|B,E)
T
T
0.95
T
F
0.94
F
T
0.29
F
F
0.01
Jan Dzwoni
Włamanie
Maria Dzwoni
Alarm
Wstrz
ą
sy
A P(J|A)
T
0.90
F
0.05
A
P(M|A)
T
0.70
F
0.01
P(B)
0.001
P(E)
0.002

14.2. Semantyka sieci Bayesa
Budowanie sieci Bayesa
1. Wybra
ć
porz
ą
dek zmiennych losowych X
1
, … ,X
n
;
2. Dla i = 1, … , n :
–
doda
ć
X
i
do sieci;
–
wybra
ć
spo
ś
ród X
1
, … ,X
i-1
takich rodziców, dla których
P(X
i
| Rodzice(X
i
)) = P(X
i
| X
1
, ... X
i-1
)
© F.A. Dul 2007
Taki wybór rodziców gwarantuje wła
ś
ciwe reprezentowanie
rozkładu ł
ą
cznego:
P(X
1
, … ,X
n
)
=
∏
i =1
P(X
i
| X
1
, … , X
i-1
) (reguła ła
ń
cuchowa)
=
∏
i =1
P(X
i
| Rodzice(X
i
))
(z konstrukcji)
Topologia sieci oraz jej zwarto
ść
zale
żą
od pocz
ą
tkowego
wyboru porz
ą
dku zmiennych.
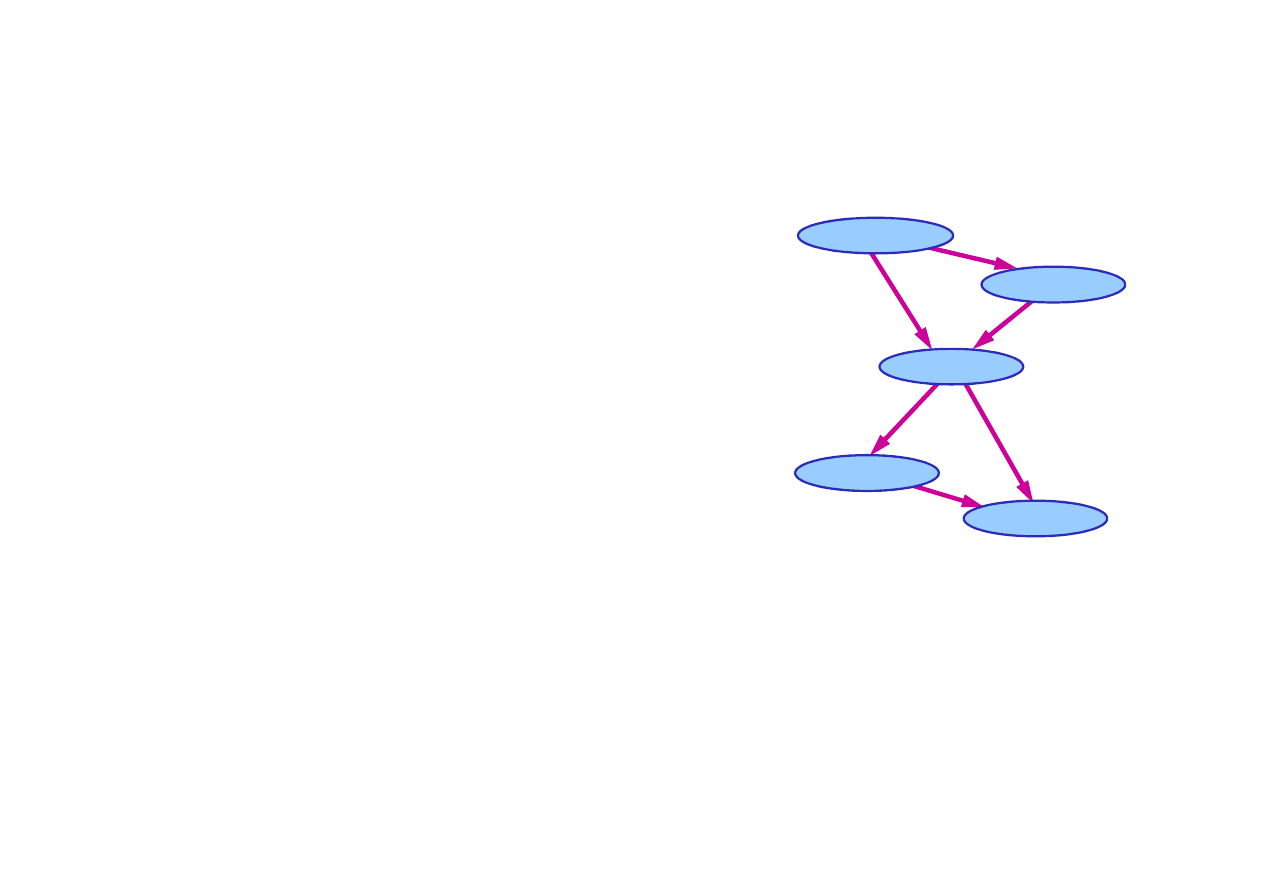
14.2. Semantyka sieci Bayesa
Przykład budowania sieci Bayesa
P(J | M) = P(J)?
Załó
ż
my,
ż
e wybrali
ś
my porz
ą
dek zmiennych: M, J, A, W, S;
J
an Dzwoni
M
aria Dzwoni
A
larm
P(A | J, M) = P(A | J)?
P(A | J, M) = P(A)?
P(W | A, J, M) = P(W | A)?
P(W | A, J, M) = P(W)?
Nie
Nie
Nie
Nie
Tak
© F.A. Dul 2007
• Inny porz
ą
dek zmiennych wprowadził dwie nowe kraw
ę
dzie.
• Sie
ć
jest mniej zwarta ni
ż
poprzednio: trzeba zapami
ę
ta
ć
1 + 2 + 4 + 2 + 4 = 13 liczb.
• Okre
ś
lanie niezale
ż
no
ś
ci warunkowej jest trudne
w kierunkach nieprzyczynowych (noncausal).
• Wydaje si
ę
,
ż
e modele przyczynowe i niezale
ż
no
ść
warunkowa s
ą
“wbudowane” w natur
ę
ludzk
ą
!
W
łamanie
W
s
trz
ą
sy
P(W | A, J, M) = P(W | A)?
P(S | W, A, J, M) = P(S | A, W)?
P(S | W, A ,J, M) = P(S | A)?
Nie
Tak
Tak

14.4. Wnioskowanie
ś
cisłe w sieci Bayesa
∑
=
=
y
y
e
e
e
)
,
,
(
)
,
(
)
|
(
X
X
X
P
P
P
α
α
Prawdopodobie
ń
stwo zmiennej
X
przy danych warto
ś
ciach
zmiennych
E =
e jest równe
Wyznaczmy w zagadnieniu włamania prawdopodobie
ń
stwo
zdarzenia
P(Wlamanie|JanDzwoni=prawda,MariaDzwoni=prawda)
∑∑
=
=
m
j
a
s
W
m
j
W
m
j
W
)
,
,
,
,
(
)
,
,
(
)
,
|
(
P
P
P
α
α
© F.A. Dul 2007
Dla przypadku w = (Włamanie=prawda) otrzymujemy
∑∑
s
a
∑∑
=
s
a
a
m
P
a
j
P
s
w
a
P
s
P
w
P
m
j
w
P
)
|
(
)
|
(
)
,
|
(
)
(
)
(
)
,
|
(
α
gdzie: j = (JanDzwoni=prawda), m = (MariaDzwoni=prawda)
Po przegrupowaniu składników otrzymujemy
∑
∑
=
s
a
a
m
P
a
j
P
s
w
a
P
s
P
w
P
m
j
w
P
)
|
(
)
|
(
)
,
|
(
)
(
)
(
)
,
|
(
α
14.4. Wnioskowanie
ś
cisłe w sieci Bayesa
Wyznaczenie prawdopodobie
ń
stwa dla
w = (Włamanie=prawda)
P(s)
0.002
P(
¬
s)
0.998
P(w)
0.001
+
0.01197
0.592238
P(w|j,m) =
αααα ××××
0.000592238
∑
∑
=
s
a
a
m
P
a
j
P
s
w
a
P
s
P
w
P
m
j
w
P
)
|
(
)
|
(
)
,
|
(
)
(
)
(
)
,
|
(
α
B E
P(A|B,E)
T
T
0.95
T
F
0.94
F
T
0.29
F
F
0.01
Jan Dzwoni
Włamanie
Maria Dzwoni
Alarm
Wstrz
ą
sy
A P(J|A)
T
0.90
F
0.05
A
P(M|A)
T
0.70
F
0.01
P(B)
0.001
P(E)
0.002
© F.A. Dul 2007
P(m|a)
0.70
P(j|a)
0.90
P(m|
¬
a)
0.01
P(j|
¬
a)
0.05
P(a|w,s)
0.95
P(
¬
a|w,s)
0.05
+
P(m|a)
0.70
P(j|a)
0.90
P(m|
¬
a)
0.01
P(j|
¬
a)
0.05
P(a|w,
¬
s)
0.94
P(
¬
a|w,
¬
s
)
0.06
+
0.70
0.63
0.70
0.63
0.01
0.0005
0.01
0.0005
0.59223
0.5985
0.000025
0.598525
0.01197
0.5922
0.00003
0.591041
14.4. Wnioskowanie
ś
cisłe w sieci Bayesa
Wyznaczenie prawdopodobie
ń
stwa dla
¬
w = (Włamanie=fałsz)
P(s)
0.002
P(
¬
s)
0.998
P(
¬
w)
0.999
+
0.000366
0.001493
P(
¬
w|j,m) =
αααα ××××
0.001492
∑
∑
¬
¬
=
¬
s
a
a
m
P
a
j
P
s
w
a
P
s
P
w
P
m
j
w
P
)
|
(
)
|
(
)
,
|
(
)
(
)
(
)
,
|
(
α
B E
P(A|B,E)
T
T
0.95
T
F
0.94
F
T
0.29
F
F
0.01
Jan Dzwoni
Włamanie
Maria Dzwoni
Alarm
Wstrz
ą
sy
A P(J|A)
T
0.90
F
0.05
A
P(M|A)
T
0.70
F
0.01
P(B)
0.001
P(E)
0.002
© F.A. Dul 2007
P(m|a)
0.70
P(j|a)
0.90
P(m|
¬
a)
0.01
P(j|
¬
a)
0.05
P(a|
¬
w,s)
0.29
P(
¬
a|
¬
w,s)
0.71
+
P(m|a)
0.70
P(j|a)
0.90
P(m|
¬
a)
0.01
P(j|
¬
a)
0.05
P(a|
¬
w,
¬
s)
0.001
P(
¬
a|
¬
w,
¬
s)
0.999
+
0.70
0.63
0.70
0.63
0.01
0.0005
0.01
0.0005
0.00113
0.1827
0.000355
0.183055
0.000366
0.00063
0.0005
0.001127

14.4. Wnioskowanie
ś
cisłe w sieci Bayesa
Prawdopodobie
ń
stwo zdarzenia
P(W | j,m)
jest wi
ę
c równe
)
)
,
|
(
,
)
,
|
(
(
)
,
|
(
m
j
w
P
m
j
w
P
m
j
W
¬
=
P
479.8245
0.001492)
0.000592
/(
1
=
+
=
α
=
×
=
)
,
(
)
,
|
(
0.001492
0.000592
479.8245
m
j
W
P
)
0.716
,
0.284
(
=
Oznacza to,
ż
e prawdopodobie
ń
stwo włamania gdy dzwoni
ą
)
0.001492
,
0.000592
(
×
×
=
α
α
© F.A. Dul 2007
Oznacza to,
ż
e prawdopodobie
ń
stwo włamania gdy dzwoni
ą
oboje s
ą
siedzi wynosi ok. 28%
Wady wnioskowania
ś
cisłego w sieciach Bayesa:
• Składniki wyra
ż
enia dla prawdopodobie
ń
stwa s
ą
obliczane
wielokrotnie, np. P(j|a)P(m|a) czy P(j|
¬
a)P(m|
¬
a).
• Zło
ż
ono
ść
obliczeniowa dla sieci z n zmiennymi boolowskimi
jest wykładnicza -
O(2
n
)
ale jest ni
ż
sza ni
ż
w przypadku
ogólnym, w którym
O(n
·
2
n
)
.
14.5. Wnioskowanie przybli
ż
one w sieci Bayesa
Ze wzgl
ę
du na wielk
ą
zło
ż
ono
ść
obliczeniow
ą
wyznaczania
prawdopodobie
ń
stwa na podstawie sieci Bayesa w praktyce
stosuje si
ę
najcz
ęś
ciej wnioskowania przybli
ż
one.
Algorytm Monte Carlo próbkowania zmiennych losowych
Idea: przy du
ż
ej liczbie próbkowa
ń
prawdopodobie
ń
stwo okre-
ś
lone jako liczba próbek danej warto
ś
ci zmiennej w stosunku
do liczby wszystkich próbkowa
ń
d
ąż
y do warto
ś
ci dokładnej,
x
N
)
(
∑
© F.A. Dul 2007
Przykład: rzut monet
ą
, Moneta =
〈〈〈〈
orzeł , reszka
〉〉〉〉
, prawdopo-
dobie
ń
stwo
ś
cisłe P(Moneta) =
〈〈〈〈
0.5 , 0.5
〉〉〉〉
, za
ś
przybli
ż
one
N
x
N
x
P
N
)
(
lim
)
(
∑
=
∞
→
N
orzeł
N
orzeł
P
N
)
(
)
(
∑
≈
...}
,
49
.
0
,
43
.
0
,
55
.
0
,
4
.
0
,
3
.
0
,
0
.
0
{
)
(
=
reszka
P
N
N
reszka
N
reszka
P
N
)
(
)
(
∑
≈
Przykład: kolejne rzuty monet
ą
prowadz
ą
do oszacowa
ń
:
14.5. Wnioskowanie przybli
ż
one w sieci Bayesa
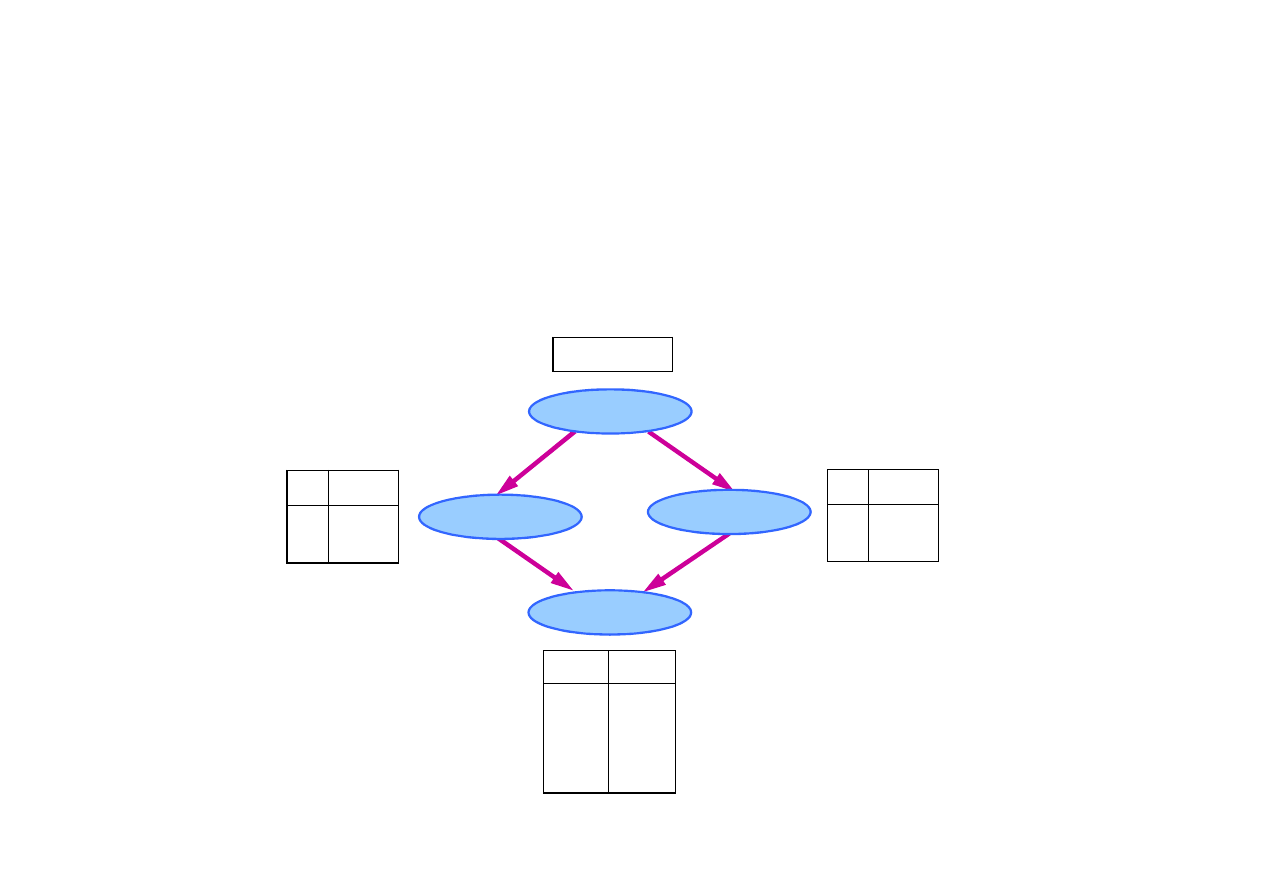
Próbkowanie losowe w sieci Bayesa.
Chmury
P(C)=0.5
Zasada: próbkowanie ka
ż
dej zmiennej w kolejno
ś
ci okre
ś
lonej
przez sie
ć
.
Przykład: sie
ć
Bayesa dla problemu mokrej trawy, uporz
ą
dko-
wana nast
ę
puj
ą
co: [ Chmury, Zraszacz, Deszcz, MokraTrawa ]
© F.A. Dul 2007
Zraszacz
MokraTrawa
Deszcz
C P(Z)
t
f
0.10
0.50
C P(D)
t
f
0.80
0.20
Z D P(D)
t t
t
f
f
t
f
f
0.99
0.90
0.90
0.00

14.5. Wnioskowanie przybli
ż
one w sieci Bayesa
Próbkowanie przykładowe w sieci:
1. Próbkowanie P(Chmury) =
〈〈〈〈
0.5, 0.5
〉〉〉〉
wynik:
prawda
;
2. Próbkowanie P(Zraszacz|Chmury=
prawda
) =
〈〈〈〈
0.1, 0.9
〉〉〉〉
wynik:
fałsz
;
3. Próbkowanie P(Deszcz|Chmury=
prawda
) =
〈〈〈〈
0.8, 0.2
〉〉〉〉
wynik:
prawda
;
4. Próbkowanie P(MokraTrawa|Zraszacz=
fałsz
,Deszcz=
prawda
) =
〈〈〈〈
0.9,0.1
〉〉〉〉
wynik:
prawda
;
Próbkowanie zwróciło wi
ę
c zdarzenie zgodne z sieci
ą
Z
1
= [
prawda
,
fałsz
,
prawda
,
prawda
].
Kolejne próbkowanie mo
ż
e zwróci
ć
inne zdarzenie, np.
© F.A. Dul 2007
Kolejne próbkowanie mo
ż
e zwróci
ć
inne zdarzenie, np.
Z
2
= [
prawda
,
prawda
,
fałsz
,
prawda
].
∏
=
=
n
i
i
i
n
PS
X
rodzice
x
P
x
x
S
1
1
))
(
|
(
)
,...,
(
Ze sposobu próbkowania wynika, ze prawdopodobie
ń
stwo
S
PS
(x
1
,...,x
n
) wybranej próbki [x
1
,...,x
n
] wynosi
i jest równe prawdopodobie
ń
stwu zdarzenia reprezentowanym
przez sie
ć
Bayesa
)
,...,
(
)
,...,
(
1
1
n
n
PS
x
x
P
x
x
S
=

14.5. Wnioskowanie przybli
ż
one w sieci Bayesa
Je
ż
eli N
PS
(x
1
,...,x
n
) jest liczb
ą
wylosowa
ń
próbki [x
1
,...,x
n
], to
W przykładzie mokrej trawy prawdopodobie
ń
stwa zdarze
ń
wylosowanych z sieci Bayesa wynosz
ą
)
,...,
(
)
,...,
(
)
,...,
(
lim
1
1
1
n
n
PS
n
PS
N
x
x
P
x
x
S
N
x
x
N
=
=
∞
→
S
PS
(Z
1
) = 0.5
××××
0.9
××××
0.8
××××
0.9 = 0.324,
S
PS
(Z
2
) = 0.5
××××
0.1
××××
0.2
××××
0.9 = 0.009.
© F.A. Dul 2007
S
PS
(Z
2
) = 0.5
××××
0.1
××××
0.2
××××
0.9 = 0.009.
Przy du
ż
ej liczbie próbkowa
ń
N zdarzenie Z
1
b
ę
dzie wybrane
w 32.4%, za
ś
zdarzenie Z
2
- tylko w 0.9% przypadków.
Koszt C wnioskowania przybli
ż
onego w sieciach Bayesa jest
zazwyczaj du
ż
o ni
ż
szy ni
ż
koszt wnioskowania
ś
cisłego,
C << O(2
n
)
Istniej
ą
równie
ż
inne metody wnioskowania przybli
ż
onego
w sieciach Bayesa, np. metoda
Monte Carlo dla ła
ń
cucha
Markowa
(Markov chain Monte Carlo).

U
ż
yteczno
ść
sieci Bayesa
Sieci Bayesa stanowi
ą
wygodn
ą
form
ę
reprezentacji
zale
ż
no
ś
ci zdarze
ń
.
Pozwalaj
ą
te
ż
znacznie zredukowa
ć
rozmiar
reprezentacji a tak
ż
e koszt wnioskowania
stochastycznego.
Wnioskowanie przybli
ż
one w sieciach Bayesa
cechuje si
ę
niskim kosztem przy zadowalaj
ą
cych
©
F.A. Dul 2007
cechuje si
ę
niskim kosztem przy zadowalaj
ą
cych
dokładno
ś
ciach uzyskiwanych rozkładów
prawdopodobie
ń
stw.
Sieci Bayesa s
ą
równie
ż
wykorzystywane do opisu
dynamicznych zjawisk stochastycznych stanowi
ą
c
podstaw
ę
filtru Kalmana
.

14.7. Inne metody wnioskowania probabilistycznego
Podej
ś
cie stochastyczne jest szeroko stosowane w wielu
dziedzinach wiedzy i praktyki: w fizyce, genetyce, ekonomii,
ubezpieczeniach, bankowo
ś
ci...
W sztucznej inteligencji podej
ś
cie probabilistyczne jest
u
ż
ywane dopiero od lat 70. XX wieku, głównie w systemach
ekspertowych.
Powodem był wykładniczy koszt wnioskowania – wcze
ś
niej
nie znano algorytmów dla sieci Bayesa.
© F.A. Dul 2007
nie znano algorytmów dla sieci Bayesa.
Dlatego do wnioskowania w warunkach niepewno
ś
ci
stosowano podej
ś
cia alternatywne, takie jak:
• Wnioskowanie
domy
ś
lne
,
• Reprezentacja niepewno
ś
ci za pomoc
ą
reguł
,
• Reprezentacja ignorancji (teoria
Dempstera-Shafera
),
• Reprezentacja nieprecyzyjno
ś
ci za pomoc
ą
logiki rozmytej
.
Panuje przekonanie,
ż
e wnioskowanie stochastyczne jest
bardziej uniwersalne ni
ż
powy
ż
sze wnioskowania alternatywne.

14.7. Inne metody wnioskowania probabilistycznego
Metody wnioskowania oparte na regułach
Metody wnioskowania wykorzystuj
ą
ce reguły s
ą
podobne
do metod logiki zda
ń
lub pierwszego rz
ę
du.
Wnioskowanie logiczne jest uzupełnione czynnikiem
okre
ś
laj
ą
cym stopie
ń
wiarygodno
ś
ci
(fudge factor)
, np.
A
25
|
→
0.3
zapewni dojazd na czas;
Uwzgl
ę
dnienie stopnia wiarygodno
ś
ci umo
ż
liwia „sterowanie”
wnioskowaniem logicznym.
Jednak z podej
ś
ciem takim wi
ążą
si
ę
trudno
ś
ci.
© F.A. Dul 2007
Jednak z podej
ś
ciem takim wi
ążą
si
ę
trudno
ś
ci.
Przykład
Czy mokra trawa jest wynikiem deszczu,
czy te
ż
wł
ą
czenia zraszacza?
Zraszacz
MokraTrawa
Deszcz
Mimo takich problemów wnioskowanie z
czynnikiem pewno
ś
ci
jest stosowane z powodzeniem w wielu systemach
ekspertowych (np. MYCIN).
– Zraszacz |
→
0.99
MokraTrawa;
– MokraTrawa |
→
0.7
Deszcz;
Problem: czy zraszacz powoduje deszcz?

14.7. Inne metody wnioskowania probabilistycznego
Teoria Dempstera-Shafera reprezentacji ignorancji
Teoria Dempstera-Shafera opisuje ró
ż
nice pomi
ę
dzy
niepewno
ś
ci
ą
a
ignorancj
ą
.
Funkcja wiarygodno
ś
ci
Bel(X)
opisuje prawdopodobie
ń
stwo
tego,
ż
e obserwacje potwierdzaj
ą
twierdzenie
X
.
Przykład
Dla zdarzenia „Reszka” przy rzucie niepewn
ą
monet
ą
i przy
braku obserwacji zarówno
Bel(Reszka)=0
jak i
Bel(
¬
Reszka)=0
.
Je
ż
eli stwierdzi si
ę
z 90% pewno
ś
ci
ą
,
ż
e moneta jest dobra,
© F.A. Dul 2007
Je
ż
eli stwierdzi si
ę
z 90% pewno
ś
ci
ą
,
ż
e moneta jest dobra,
(
P(Reszka)=0.5
), to
Bel(Reszka) = 0.9
×
0.5 = 0.45
; podobnie
Bel(
¬
Reszka) = 0.45
.
Istniej
ą
ca 10% luka wyra
ż
a niepewno
ść
co do jako
ś
ci monety.
Reguła Dempstera
okre
ś
la sposób wyznaczania warto
ś
ci
funkcji
Bel
na podstawie obserwacji.
Teoria Dempstera-Shafera definiuje przedziały prawdopodo-
bie
ń
stwa, np. dla wyrzucenia reszki przedział prawdopodo-
bie
ń
stwa wynosi [0,1] przed weryfikacj
ą
monety, za
ś
po jej
weryfikacji [0.45,0.55].
14.7. Inne metody wnioskowania probabilistycznego
Logika rozmyta i reprezentacja nieprecyzyjno
ś
ci
Teoria zbiorów rozmytych okre
ś
la
nieprecyzyjno
ść
twierdze
ń
.
Przykład
Czy zdanie „Jan jest wysoki” (wzrost 175cm) jest prawdziwe?
Najcz
ę
stsza odpowied
ź
: Jan jest wysoki
„w pewnym stopniu”
.
UWAGA!
Nieprecyzyjno
ść
nie jest niepewno
ś
ci
ą
(wzrost Jana
jest znany).
Teoria zbiorów rozmytych okre
ś
la stopie
ń
prawdziwo
ś
ci
twierdze
ń
, np. Wysoki(Jan)
∈
[0,1] zamiast Wysoki(Jan)=fałsz.
© F.A. Dul 2007
twierdze
ń
, np. Wysoki(Jan)
∈
[0,1] zamiast Wysoki(Jan)=fałsz.
Stopie
ń
prawdziwo
ś
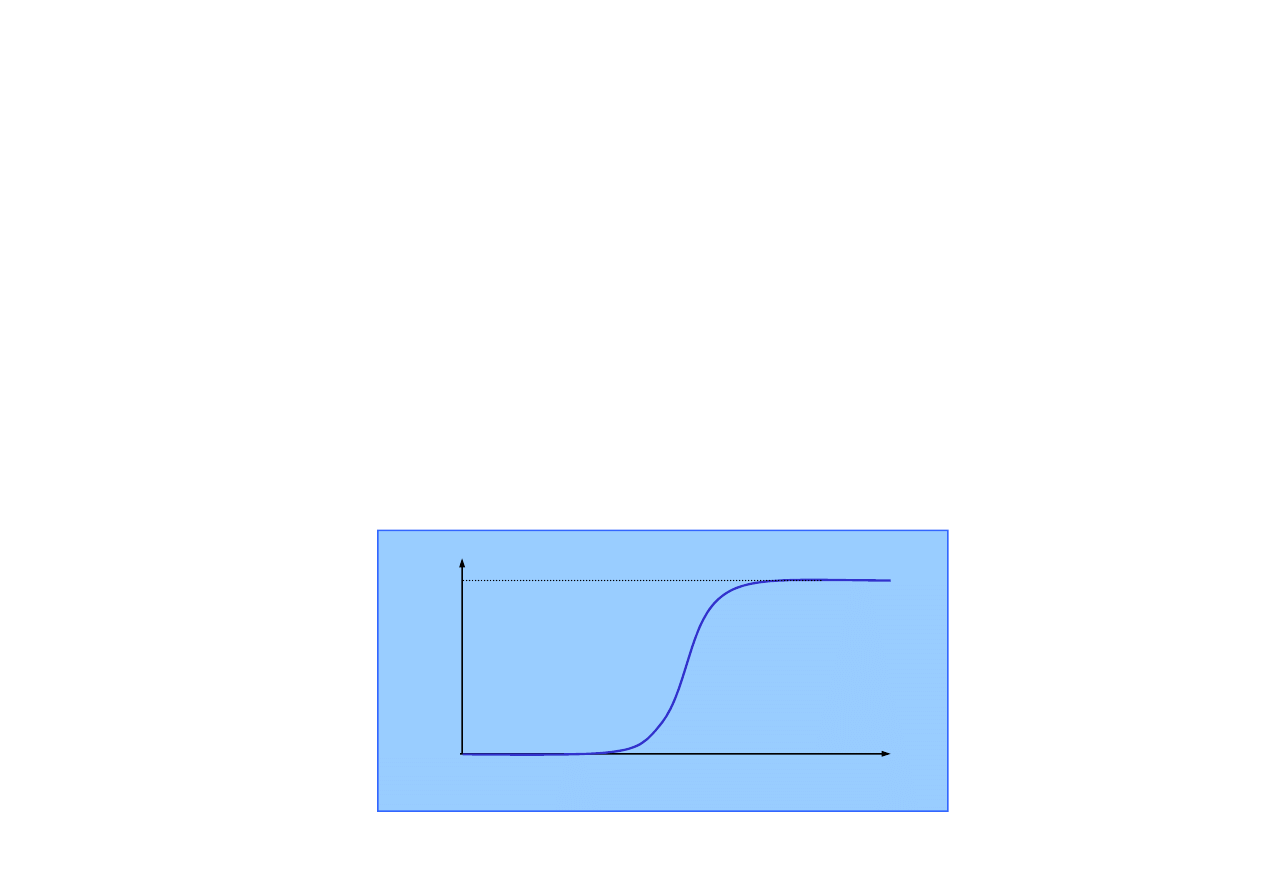
ci opisuje zazwyczaj rozkład typu
probit
1.0 1.5 2.0 m 2.5
1.0
Wysoki
0.0

14.7. Inne metody wnioskowania probabilistycznego
Logika rozmyta i reprezentacja nieprecyzyjno
ś
ci
Logika rozmyta
umo
ż
liwia wnioskowanie z wyra
ż
eniami
logicznymi okre
ś
lonymi w zbiorach rozmytych.
Miara prawdziwo
ś
ci T okre
ś
lona jest regułami:
Problemy: T(Wysoki(Jan)) = 0.6, T(Ci
ęż
ki(Jan)) = 0.4.
T(Wysoki(Jan)
∧
Ci
ęż
ki(Jan)) = 0.4
→
OK.
• T(A
∧
B) = min ( T(A) , T(B) ),
• T(A
∨
B) = max ( T(A) , T(B) ),
• T(
¬
A) = 1 – T(A).
© F.A. Dul 2007
Sterowanie rozmyte
słu
ż
y do syntezy sterowania przy u
ż
yciu
reguł rozmytych.
Sterowanie rozmyte jest szeroko stosowane w wielu
urz
ą
dzeniach, np.: pralkach, kamerach wideo, sprz
ę
cie AGD.
T(Wysoki(Jan)
∧
Ci
ęż
ki(Jan)) = 0.4
→
OK.
T(Wysoki(Jan)
∧
¬
Wysoki(Jan)) = 0.4
???

Podsumowanie
• Sieci Bayesa stanowi
ą
naturaln
ą
reprezentacj
ę
niezale
ż
no
ś
ci warunkowej (indukowanej przyczynowo).
• Topologia sieci i tablice prawdopodobie
ń
stwa warunkowego
(CPT) pozwalaj
ą
na zwart
ą
reprezentacj
ę
rozkładu ł
ą
cznego
prawdopodobie
ń
stwa.
• Sieci Bayesa s
ą
szczególnie przydane i łatwe do zastosowa-
nia w systemach ekspertowych.
• Wnioskowanie
ś
cisłe z u
ż
yciem sieci Bayesa jest kosztowne
© F.A. Dul 2007
• Wnioskowanie
ś
cisłe z u
ż
yciem sieci Bayesa jest kosztowne
~O(2
n
).
• Wnioskowanie przybli
ż
one za pomoc
ą
próbkowania zdarze
ń
pozwala obni
ż
y
ć
koszt oblicze
ń
przy zachowaniu akcepto-
walnej dokładno
ś
ci wyznaczonych prawdopodobie
ń
stw.
• Zwykłe sieci Bayesa maj
ą
cechy logiki zda
ń
, co ogranicza
zakres ich zastosowania.
• Istniej
ą
inne sposoby uwzgl
ę
dniania niepewno
ś
ci: reguły
niepewno
ś
ci, reprezentacja ignorancji, logika rozmyta.
Wyszukiwarka
Podobne podstrony:
14 Wnioskowanie statystyczne w Nieznany (2)
14 Sieci Bayesa poprawione
Analiza sieci bayesa
WNIOSKOWANIE STATYSTYCZNE 12.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
14 Publikowanie dokumentów w sieci Web
LISTA ZADA â 2 WNIOSKOWANIE STATYSTYCZNE
Zagadnienia do egzaminu z wnioskowania statystycznego, wnioskowanie statystyczne
Wnioskowanie statystyczne ściąga D6B4JQ75G5T3M73CHPOI7P6EFHU5KSVYOKQFV3Q
7 3 Wnioskowania statystyczne
WNIOSKOWANIE STATYSTYCZNE 26.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
statystyka 3, WNIOSKOWANIE STATYSTYCZNE - TESTY PARAMETRYCZNE
Statystyki nieparametryczne, PSYCHOLOGIA, I ROK, semestr II, podstawy metodologii badań psychologicz
Centralne Twierdzenie Graniczne, PSYCHOLOGIA, I ROK, semestr II, podstawy metodologii badań psycholo
Wnioskowanie statystyczne, tabelka
04 WNIOSKOWANIE STATYSTYCZNE cz Iid 4877
Analiza i wnioskowanie statysty Nieznany (2)
więcej podobnych podstron