Zaawansowane metody i techniki 

analizy danych

analizy danych

Sieci Bayesa

Plan wykładu

1. Podstawę metody klasyfikacji opartej na rachunku 

Bayesa 

2. Naiwny klasyfikator Bayesa
3. Przykład działania algorytmu

3. Przykład działania algorytmu

Czym jest klasyfikacja?

•

Dane wejściowe: treningowy zbiór krotek 
(przykładów, obserwacji, próbek)

•

Dane wyjściowe: model (klasyfikator), przydziela 

•

Dane wyjściowe: model (klasyfikator), przydziela 
każdej krotce wartość atrybutu decyzyjnego w 
oparciu o wartości pozostałych atrybutów

Klasyfikacja metodą Bayesa

•

Klasyfikacja Bayesowska jest klasyfikacją statystyczną. 
Pozwala przewidzieć prawdopodobieństwo 
przynależności obiektu do klasy. 

•

Opiera się na twierdzeniu Bayesa.

Opiera się na twierdzeniu Bayesa.

•

Z punktu zadania klasyfikacji  chcemy obliczyć 
prawdopodobieństwo a-posteriori p(C|X) tego, że 
obiekt o właściwościach X należy do klasy C

Trochę statystyki

•

Prawdopodobieństwo warunkowe (a posteriori)  
p(C|X) i p(X|C)

•

Prawdopodobieństwo bezwarunkowe (a prori) p(C), 
p(X)

p(X)

•

Prawdopodobieństwo warunkowe uwzględnia więcej 
informacji (wiedza o X)  

•

Twierdzenie Bayesa: 

p(C|X)=p(X|C)*p(C)/p(X)

Naiwny klasyfikator Bayesa 1/4

•

Każdy obiekt/przykład traktowany jest jako wektor X 
(krotka) X=(x

1

, x

2

, ..., x

n

)

•

Niech C

1

, ..., C

m

będą klasami, do których może 

należeć X

należeć X

•

W klasyfikacji Bayesa przykład X przypisujemy do tej 
klasy C

i

, do której prawdopodobieństwo warunkowe

p(C

i

|X) jest największe.

•

Naiwny klasyfikator Bayes’a zakłada, że wartości 
atrybutów w klasach są niezależne.

Naiwny klasyfikator Bayesa 2/4

•

Prawdopodobienstwo p(X) jest stałe dla wszystkich 
klas

•

Wystarczy maksymalizować iloczyn  p(X|C

i

) * p(C

i

)

•

Wartość  p(C

i

) zastępujemy estymatorami: 

•

Wartość  p(C

i

) zastępujemy estymatorami: 

p(C

i

)=s

i

/s 

gdzie: s- oznacza liczbę obiektów/przykładów w 
zbiorze treningowym, s

i  

-liczbę obiektów klasy C

i

Naiwny klasyfikator Bayesa 3/4

•

Przyjmujemy założenie o niezależności atrybutów 
p(X|C

i

) wyznaczamy ze wzoru:

p(X|C

i

)=∏

j=1…n 

p(x

j

|C

i

)

p(X|C

i

)=∏

j=1…n 

p(x

j

|C

i

)

•

Wartość p(x

j

|C

i

) zastępujemy estymatorami:

p(x

j

|C

i

) =s

ij

/s

i 

gdzie: s

ij 

oznacza liczbę obiektów należących do klasy 

C

i

, posiadających wartość x

j 

dla j-tego atrybutu

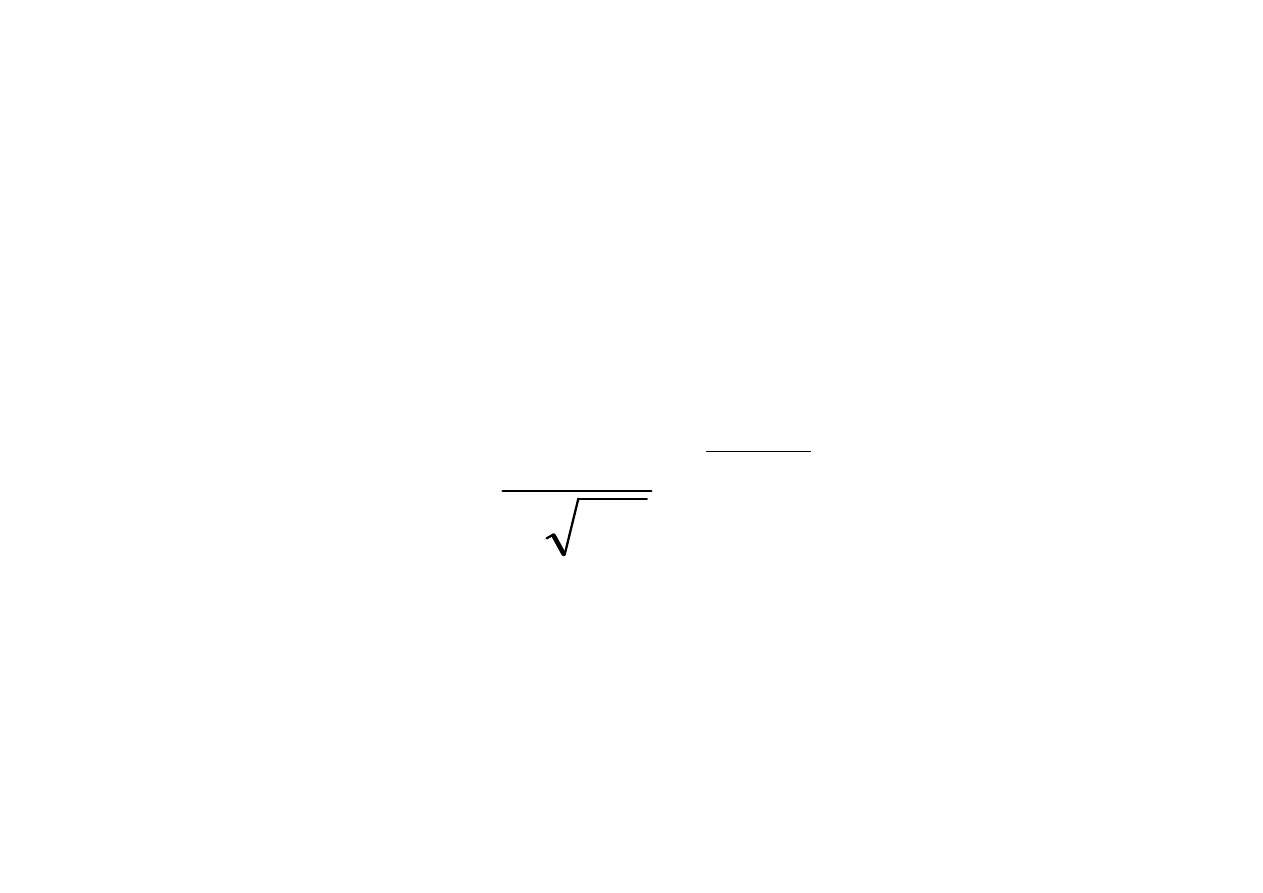
Naiwny klasyfikator Bayesa 4/4

•

Jeżeli j-ty atrybut jest ciągły to p(x

j

|C

i

) estymujemy 

funkcją gęstości Gaussa:

2

)

(

1

µ

−

−

x

(zakładając rozkład normalny wartości atrybutów)

2

2

2

1

)

(

σ

π

σ

−

=

e

x

f

Klasyfikator Bayesa- uwagi

•

Jeżeli założenie niezależności atrybutów  jest 
spełnione, naiwny klasyfikator Bayes’a jest 
optymalny, tzn. zapewnia najlepsza dokładnosc 
klasyfikacji w porównaniu z innymi klasyfikatorami

•

Zalety: 

–

prostota, 

–

dokładność,

–

nadaje się szczególnie do problemów o bardzo wielu 
wymiarach na wejściu

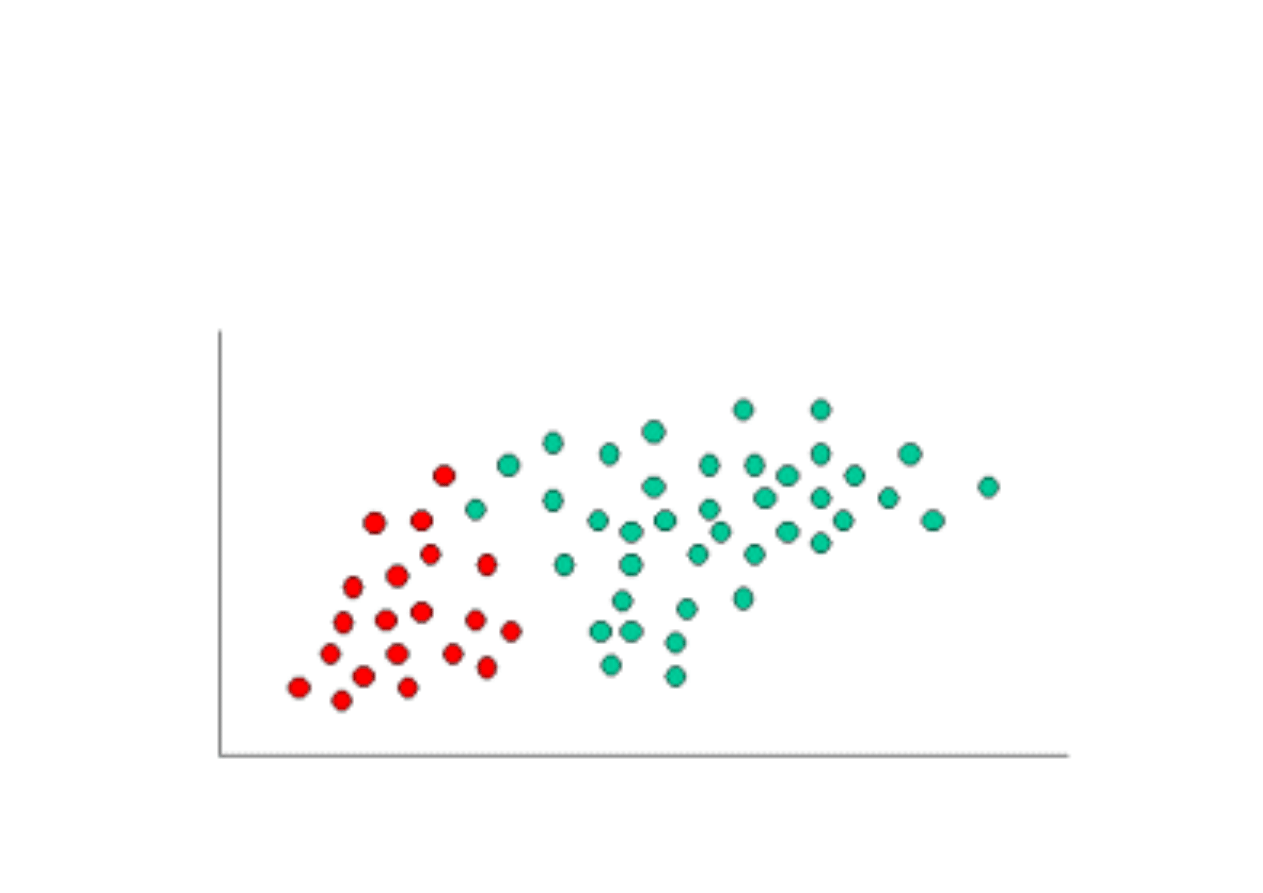
Klasyfikator Bayesa przykład 1 

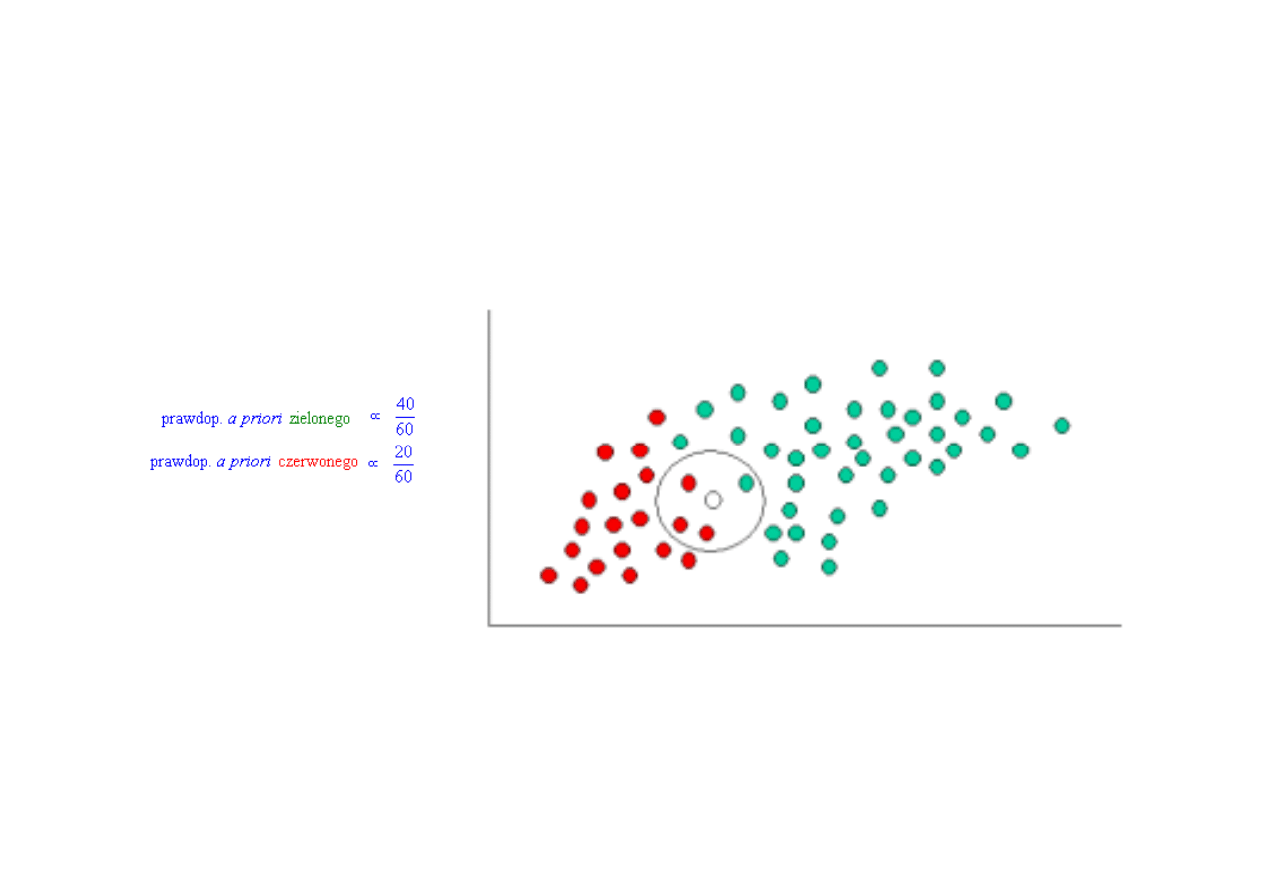
Klasyfikator Bayesa przykład 1 

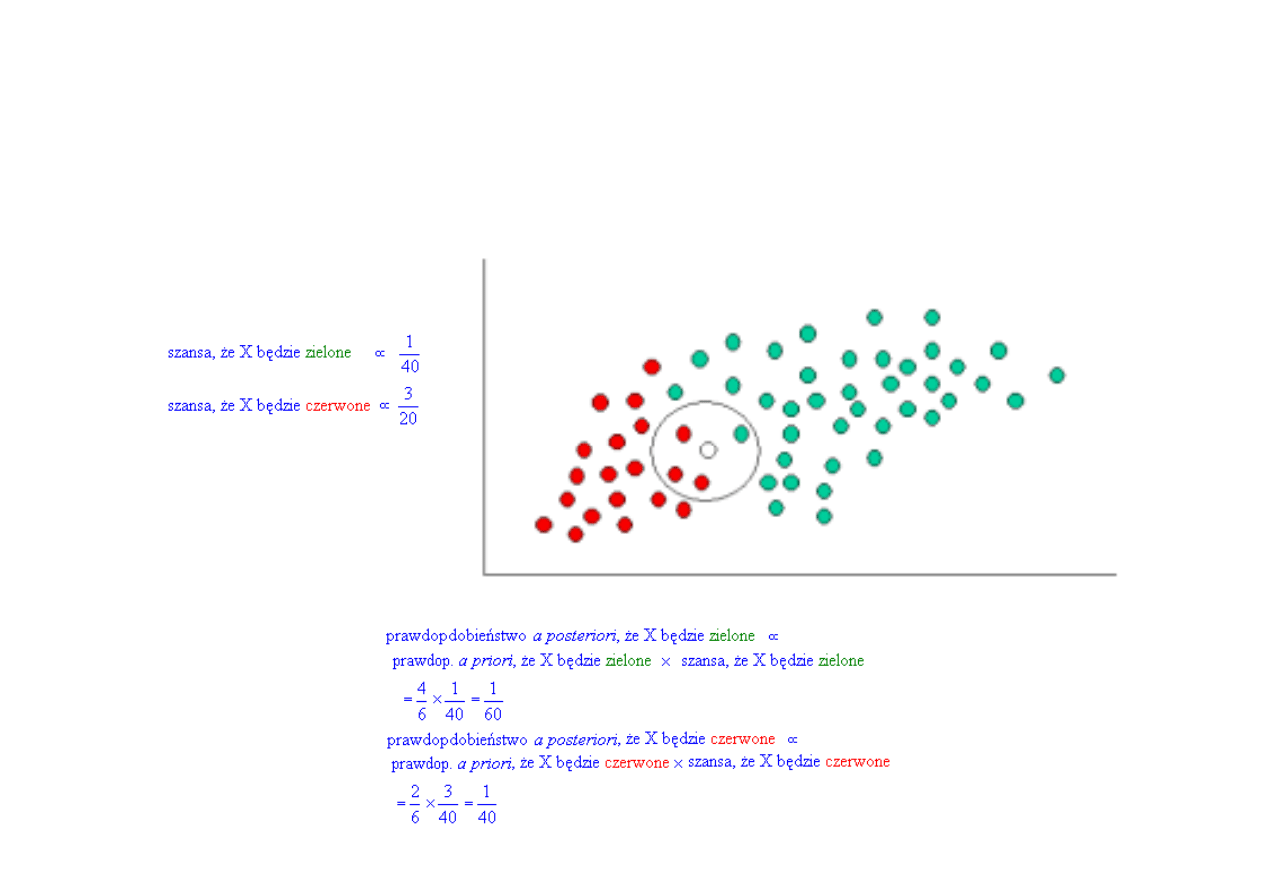
Klasyfikator Bayesa przykład 1 

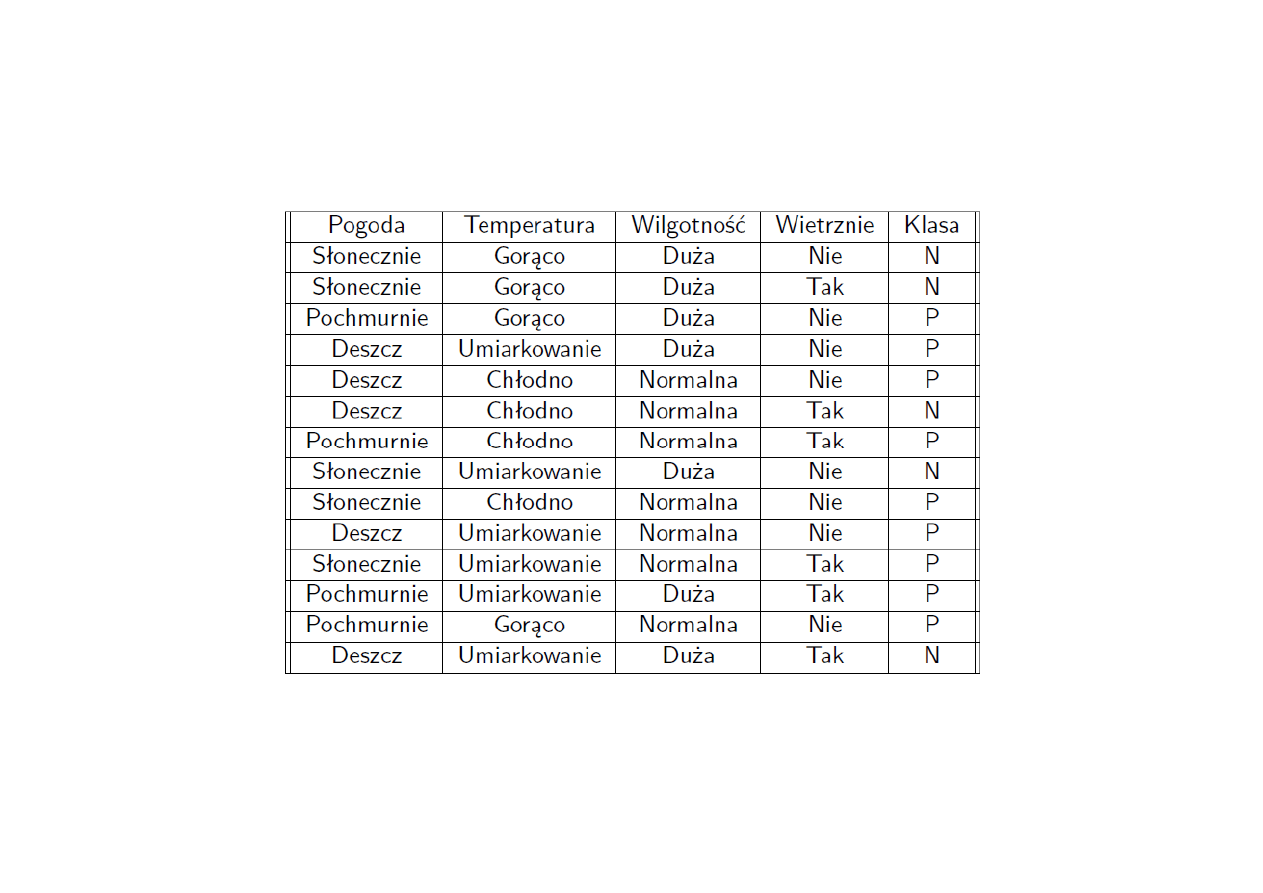
Klasyfikator Bayesa przykład 2

Do jakiej klasy (N czy P) zaklasyfikujemy przypadek: 

<słonecznie, gorąco, duża, tak>?

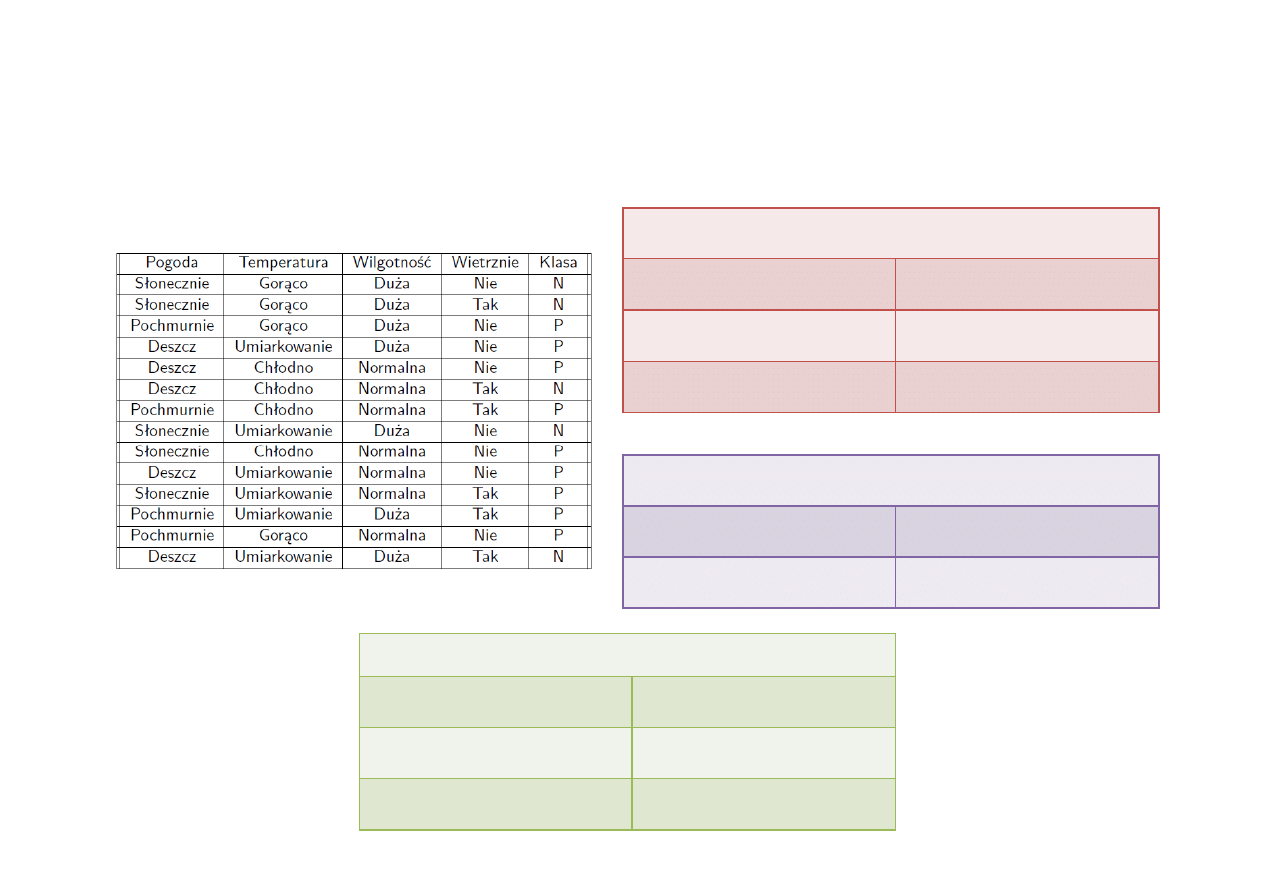
Klasyfikator Bayesa przykład 2

Pogoda

p(słonecznie|P)=2/9

p(słonecznie|N)=3/5

p(pochmurnie|P)=4/9

p(pochmurnie|N)=0

p(deszcz|P)=3/9

p(deszcz|N)=2/5

Wilgotność

p(duża|P)=3/9

p(duża|N)=4/5

p(normalna|P)=6/9

p(normalna|N)=1/5

Temperatura

p(gorąco|P)=2/9

p(gorąco|N)=2/5

p(chłodno|P)=3/9

p(chłodno|N)=1/5

p(umiarkow.|P)=4/9

p(umiarkow.|N)=2/5

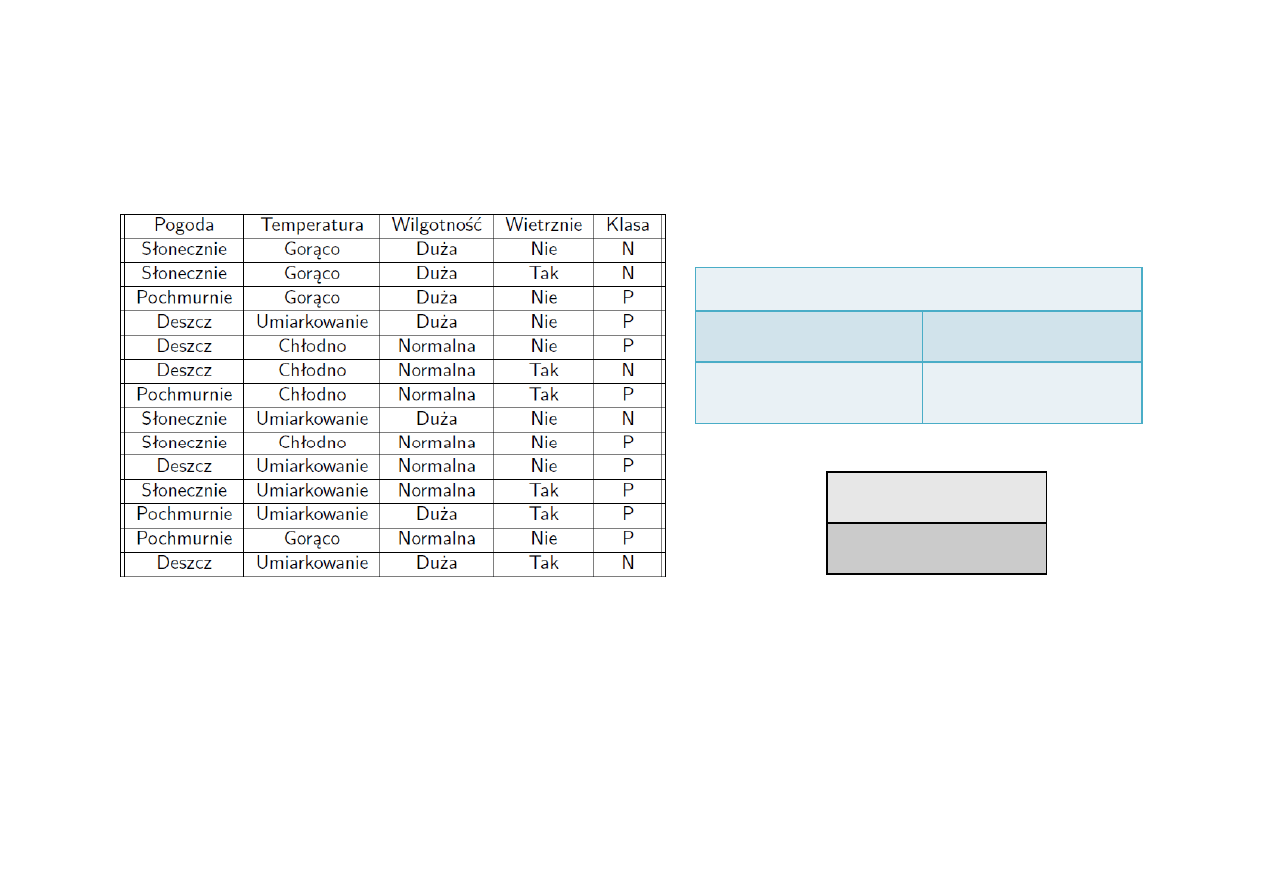
Klasyfikator Bayesa przykład 2

Wiatr

p(tak|P)=3/9

p(tak|N)=3/5

p(nie|P)=6/9

p(nie|N)=1/5

p(P)=9/14

p(N)=5/14

p(P)p(słonecznie|P)p(chłodno|P)p(duża|P)p(tak|P)=0,005

p(N)p(słonecznie|N)p(chłodno|N)p(duża|N)p(tak|N)=0,021

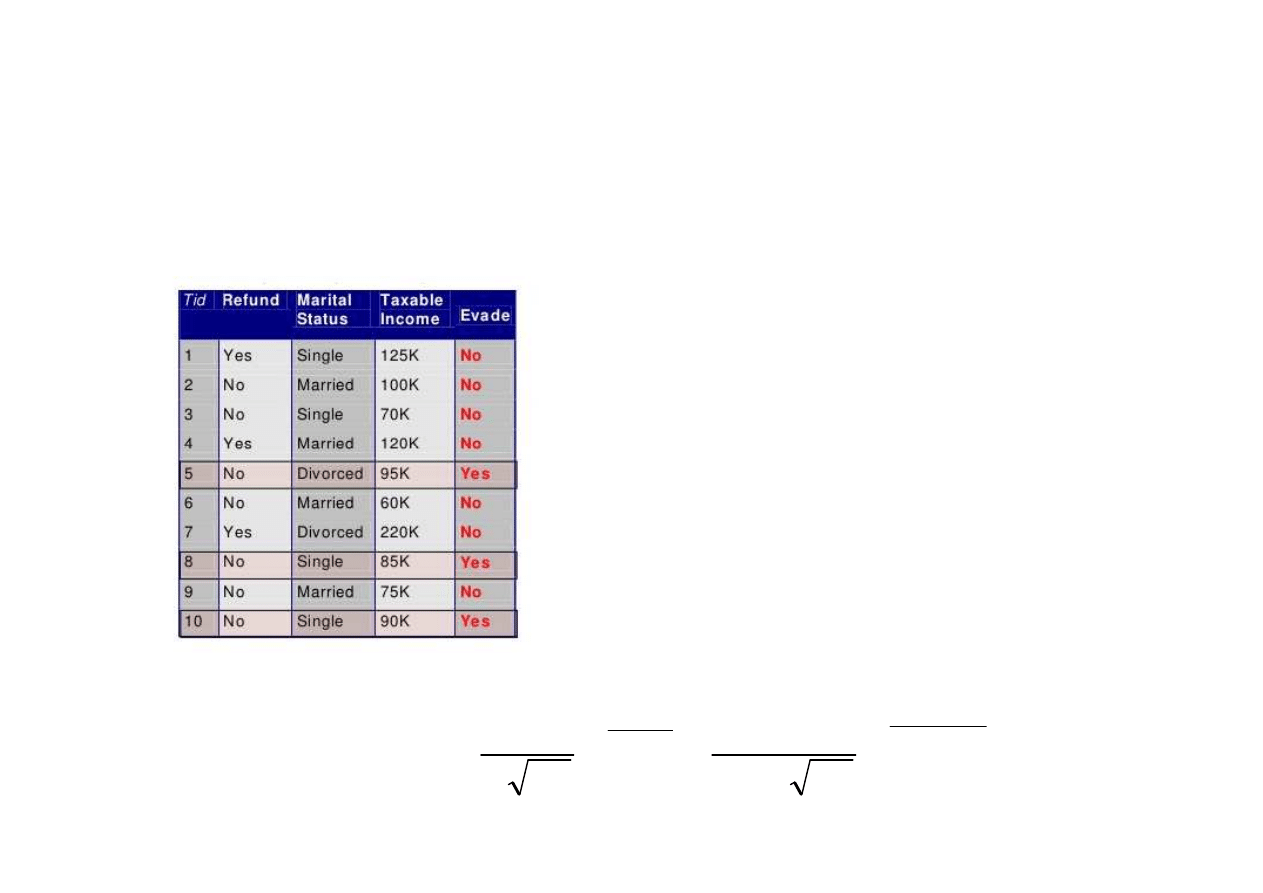
Klasyfikator Bayesa- szacowanie 

prawdopodobieństw

•

Chcemy oszacować 
prawdopodobieństwo 
P(Income|No)

•

Średnia: 110

•

Średnia: 110

•

Odchylenie standardowe: 
54,54

0072

,

0

2

54

,

54

1

2

1

)

|

120

(

2

2

2

2

)

54

,

54

(

2

)

110

120

(

2

)

(

=

=

=

=

−

−

−

−

e

e

No

income

P

x

π

π

σ

σ

µ

Dokładność klasyfikacji 1/2

•

Dokładność klasyfikatora na danym zbiorze 
testowym: 

procent przykładów testowych poprawnie
zaklasyfikowanych przez klasyfikator

zaklasyfikowanych przez klasyfikator

•

Dokładności klasyfikatora nie testujemy na zbiorze 
treningowym!

Dokładność klasyfikacji 2/2

•

W przypadku dużej liczności zbioru:  prosta metoda 
podziału zbioru na dwa niezależne zbiory: treningowy 
(70% przykładów) i testowy (30% przykładów)

•

W przypadku małej liczności zbioru stosujemy 
najczęsciej metodę k-krotnej walidacji krzyżowej

•

Dokładność (walidacja krzyżowa): sumaryczna liczba 
błędów klasyfikacji dla wszystkich k klasyfikatorów,  
podzielona przez liczność n oryginalnego zbioru 
przykładów

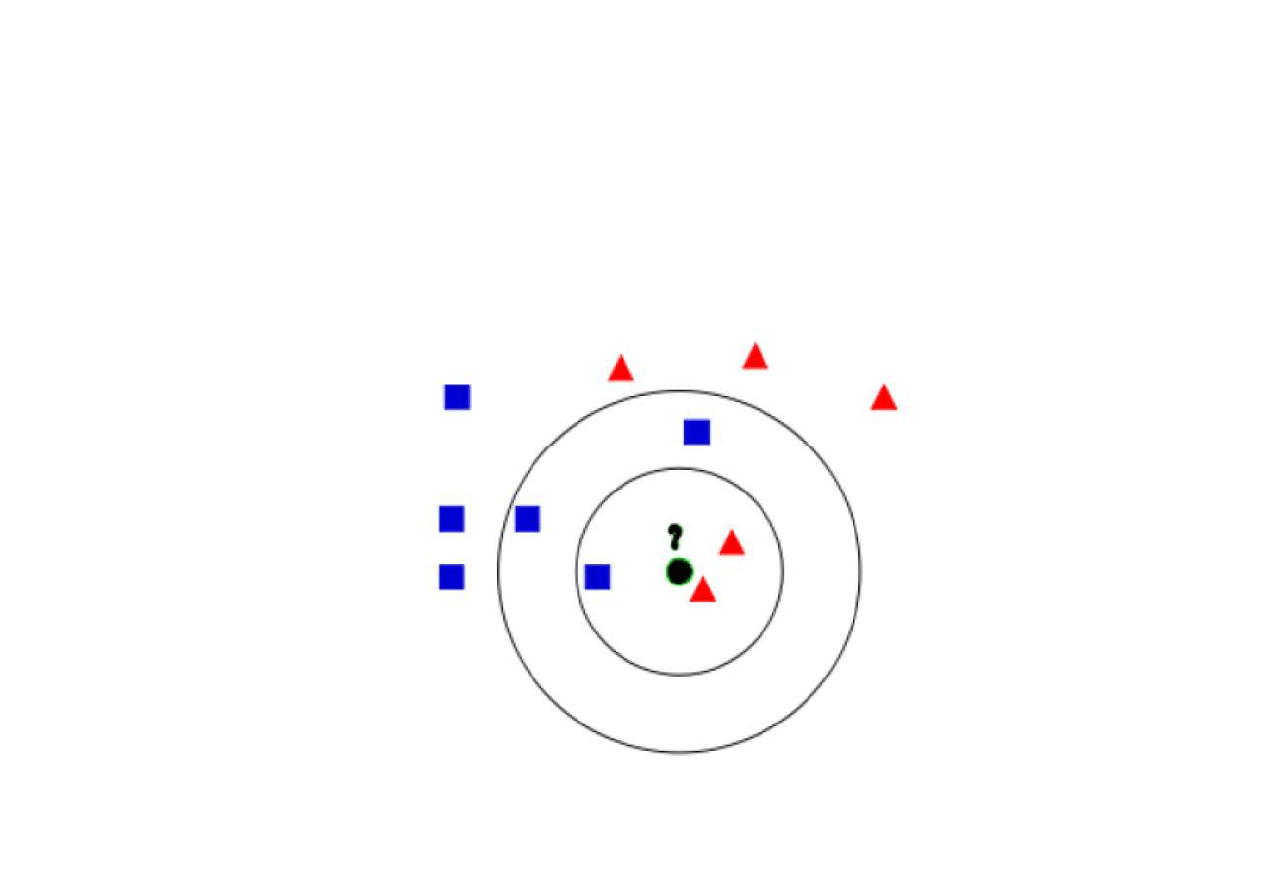
Klasyfikator Bayesa- zadanie 1

Do której klasy zostanie zaklasyfikowany nowy obiekt?

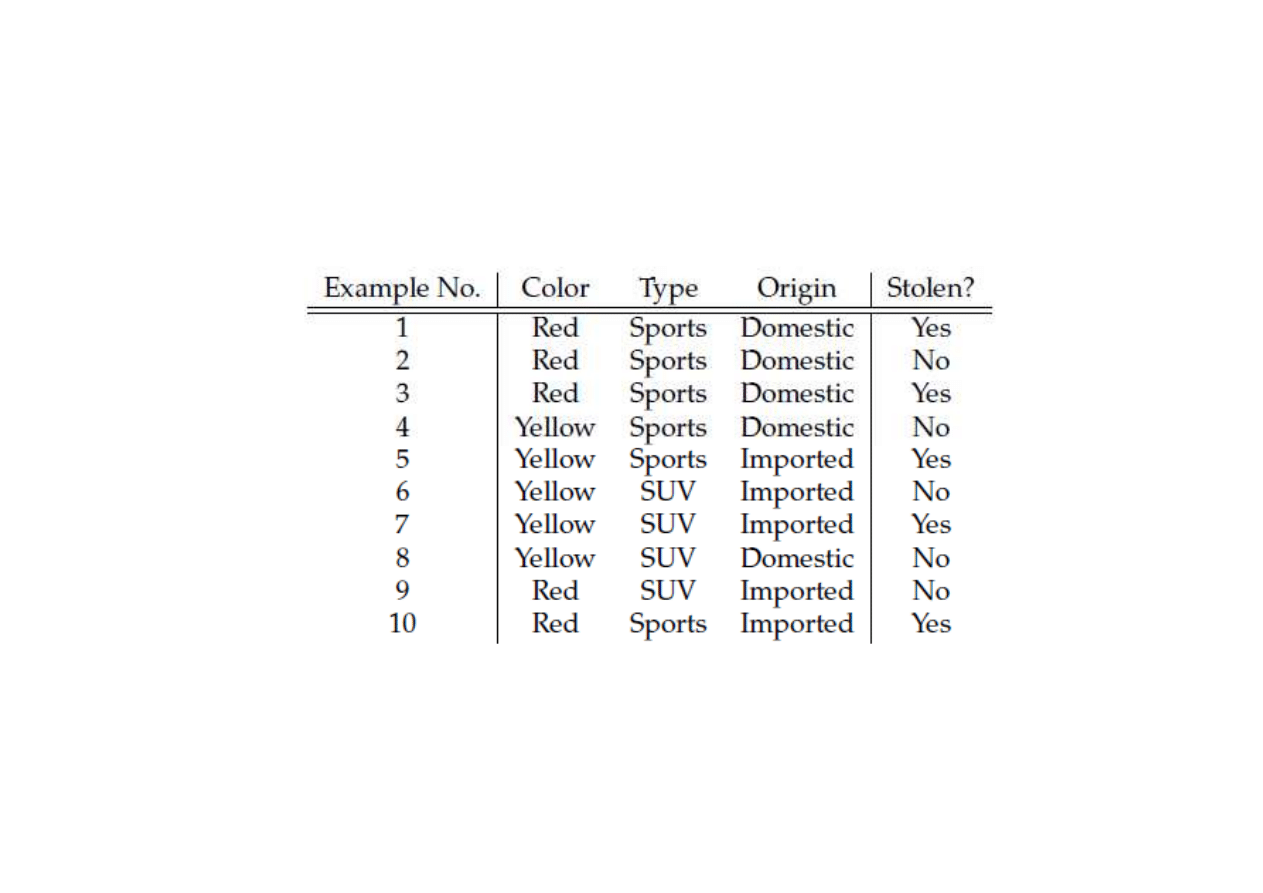
Klasyfikator Bayesa przykład 2

Do jakiej klasy (Y czy N) zaklasyfikujemy przypadek: 

<red, SUV, domestic>?

Klasyfikator Bayesa- zadanie 3

•

Mamy zbiór danych treningowy w postaci: gatunek 
zwierzęcia oraz ilość nóg. W zbiorze danych 
treningowych mamy 30 koni, 50 kotów i 20 kur. 

•

Otrzymaliśmy obiekt testowy o którym wiemy, że ma 
4 nogi. Do jakiej klasy zwierząt go zaklasyfikujemy?