1

Funkcje falowe w atomie wodoru

Wartości przyjmowane przez liczby kwantowe

n,

llll, m

mają wpływ na postać funkcji falowej

)

,

,

(

)

,

,

(

)

,

,

(

ϕ

θ

ϕ

θ

r

r

z

y

x

n,l,m

Ψ

=

Ψ

=

Ψ

)

,

(

Y

)

(

R

)

,

,

(

ϕ

θ

ϕ

θ

l,m

n,l

n,l,m

r

r

⋅

=

Ψ

Funkcja

, która spełnia równanie Schrödingera, nosi nazwę

ORBITALU

ORBITAL ATOMU WODORU

= Funkcja falowa elektronu

w atomie wodoru

Orbitale atomu wodoru (1)

Poboczna liczba kwantowa

ma oznaczenia literowe:

l

l

l

l

0

1

2

3

4

s

s

harp

p

p

rincipal

d

d

iffuse

f

f

unda-

mental

g

Uwaga! Nie kryje się za tym żaden głęboki sens, to
jest po prostu sposób na łatwiejsze pamiętanie ...

Orbitale atomu wodoru (2)

• Orbital 1s: n=1, llll=0, m=0

)

,

(

Y

)

(

R

)

,

,

(

)

,

,

(

00

10

100

100

ϕ

θ

ϕ

θ

⋅

=

Ψ

=

Ψ

r

r

z

y

x

a

h

m e

pm

o

e

0

2

2

52 9

=

=

ε

π

,

0

1

2

3

4

5

r/a

0

r

2

R

2

1 s

Część radialna, R

1,0

(r)

E

1

= -13,6 eV

)

exp(

2

)

(

0

2

/

3

0

a

r

a

r

R

−

⋅

=

−

• Część kątowa

Y(θ,φ)

Orbitale atomu wodoru (3)

ns

1s

wykres łączy punkty o

jednakowej wartości

funkcji kątowej, czyli

jednakowej gęstości

prawdopodobieństwa

znalezienia elektonu

π

ϕ

θ

4

1

)

,

(

=

Y

Orbitale atomu wodoru (4)

•

Orbital 2s: n=2, l=0, m=0

)

,

(

Y

)

(

R

)

,

,

(

)

,

,

(

00

20

200

200

ϕ

θ

ϕ

θ

⋅

=

Ψ

=

Ψ

r

r

z

y

x

0

5

10

r/a

0

r

2

R

2

2 s

E

2

= -3,4 eV

Część radialna, R

2,0

(r)

( )

)

exp(

1

2

1

)

(

0

0

2

2

/

3

0

a

r

a

r

a

r

R

−

⋅

−

⋅

=

−

Orbitale atomu wodoru (5)

ns

2s

E

2

= -3,4 eV

π

ϕ

θ

4

1

)

,

(

=

Y

• Część kątowa

Y(θ,φ)

2

0

5

10

15

r/a

0

r

2

R

2

2 p

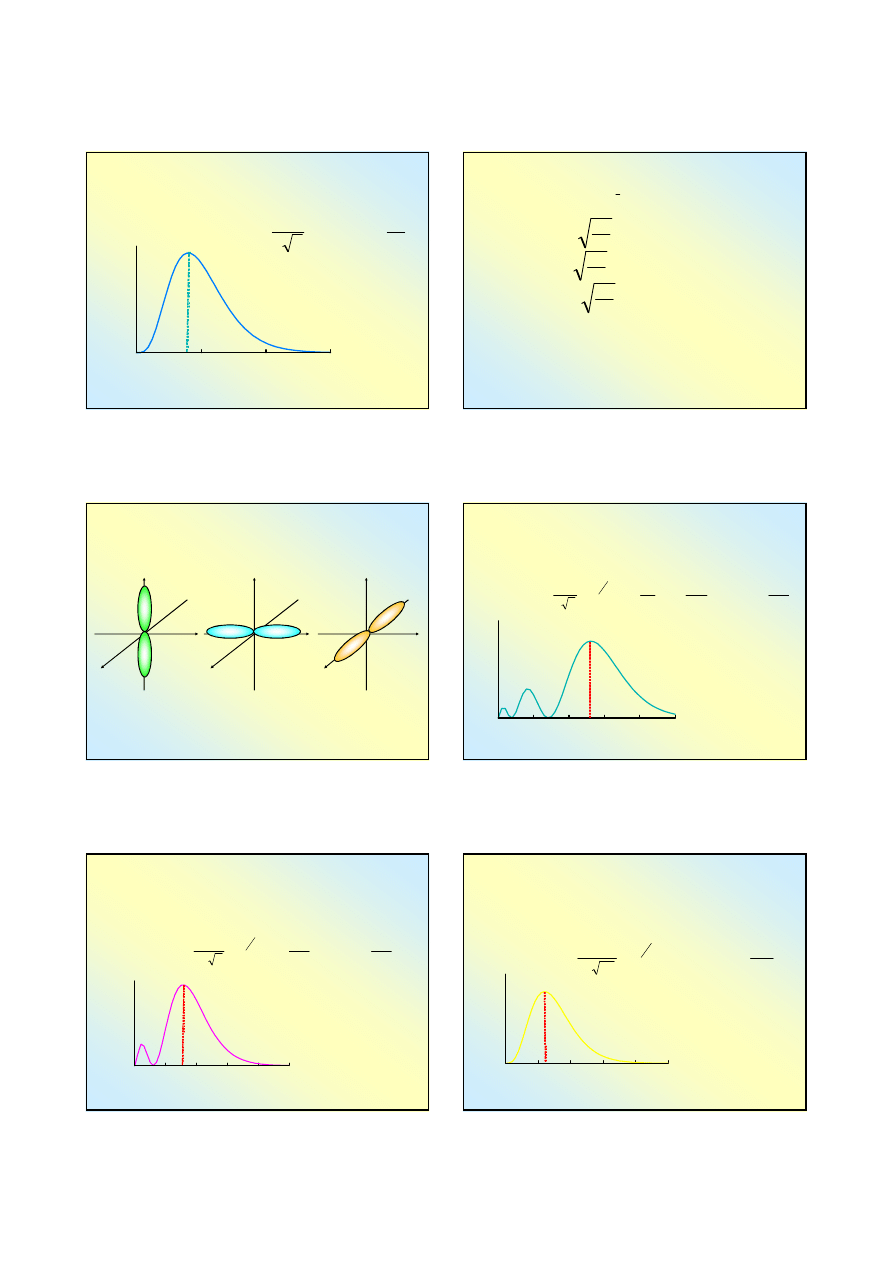
Orbitale atomu wodoru (6)

Orbitale 2p: n=2, l=1, m=0, ±1

Ψ

210

(x,y,z), Ψ

211

(x,y,z), Ψ

21,-1

(x,y,z) ; R

21

(r)

E

2

= -3,4 eV

Część radialna, R

2,1

(r)

( )

0

2

0

1

,

2

exp

6

2

1

)

(

a

r

r

a

r

R

−

⋅

⋅

=

Orbitale atomu wodoru (7)

)

,

(

Y

),

,

(

Y

),

,

(

Y

1

1

11

10

ϕ

θ

ϕ

θ

ϕ

θ

E

2

= -3,4 eV

θ

ϕ

θ

π

cos

)

,

(

4

3

0

,

1

=

Y

2p

z

ϕ

θ

ϕ

θ

π

cos

sin

)

,

(

4

3

1

,

1

=

Y

2p

x

ϕ

θ

ϕ

θ

π

sin

sin

)

,

(

4

3

1

,

1

=

−

Y

2p

y

θ

θ

ϕ

θ

ϕ

cos

sin

sin

sin

cos

⋅

=

⋅

⋅

=

⋅

⋅

=

r

z

r

y

r

x

M

M

M

Orbitale atomu wodoru (8)

orbitale np (np. 2p)

m = 0

m = 1

m = -1

płaszczyzna

węzłowa

xy

płaszczyzna

węzłowa

yz

płaszczyzna

węzłowa

xz

x

y

z

np

z

x

y

z

np

x

x

y

z np

y

Orbitale atomu wodoru (9)

)

,

(

Y

)

(

R

)

,

,

(

)

,

,

(

00

30

300

300

ϕ

θ

ϕ

θ

⋅

=

Ψ

=

Ψ

r

r

z

y

x

•

Orbital 3s: n=3, l=0, m=0

0

5

10

15

20

25

r/a

0

r

2

R

2

3 s

E

3

= -1,5 eV

Część kątowa
jest taka sama
dla wszystkich
orbitali ns

Część radialna, R

3,0

(r)

[

]

( )

0

2

0

2

0

2

3

3

9

2

0

3

9

2

0

,

3

exp

2

3

)

(

a

r

a

r

a

r

a

r

R

−

⋅

+

−

=

−

Orbitale atomu wodoru (10)

Orbitale 3p: n=3, l=1, m=0, ±1

Ψ

310

(x,y,z), Ψ

311

(x,y,z), Ψ

31,-1

(x,y,z) ; R

31

(r)

3p

z

, 3p

x

, 3p

y

0

5

10

15

20

25

r/a

0

r

2

R

2

3 p

Część radialna, R

3,1

(r)

Część kątowa
jest taka sama
dla wszystkich
orbitali np

E

3

= -1,5 eV

[

]

( )

0

0

2

5

3

3

0

6

27

4

1

,

3

exp

2

)

(

a

r

a

r

a

r

R

−

⋅

−

=

−

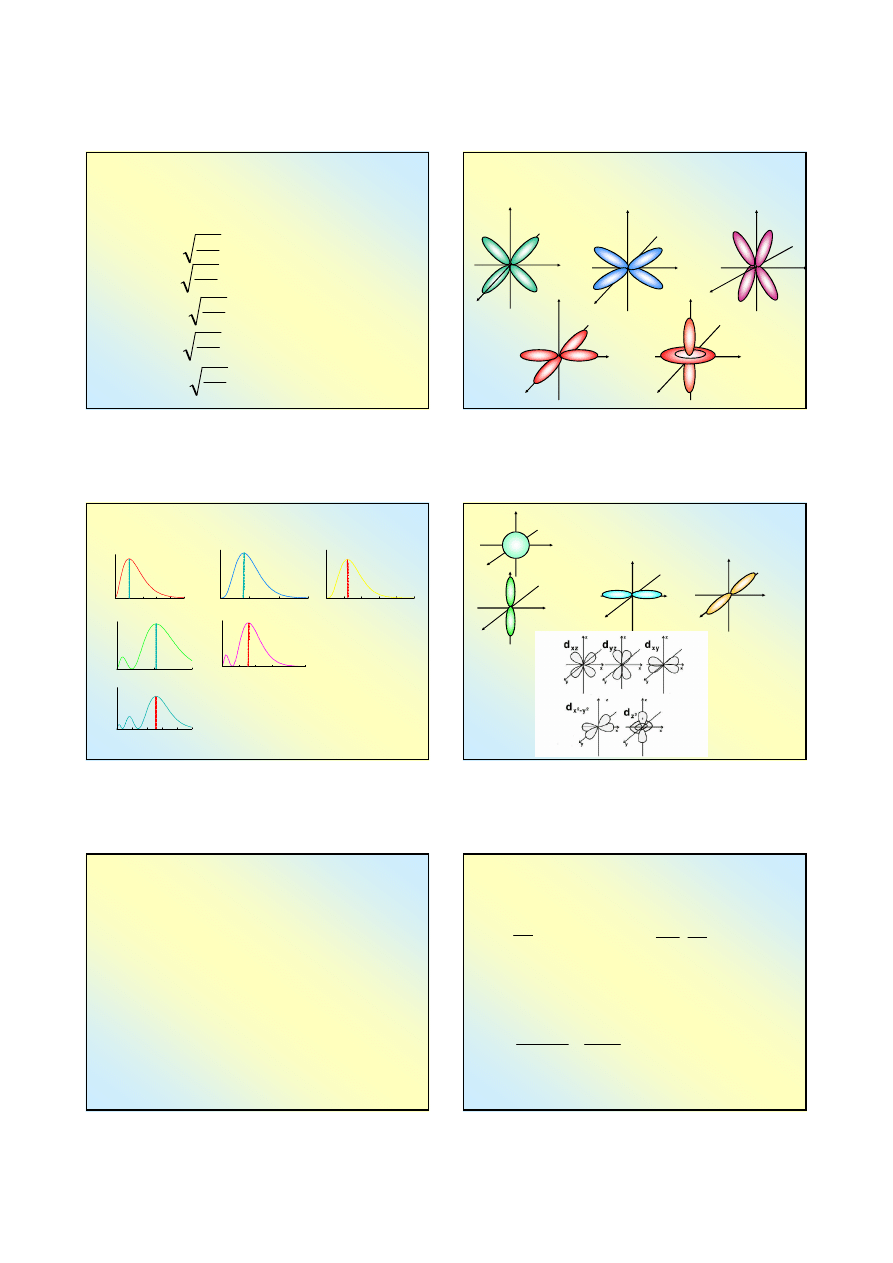
Orbitale atomu wodoru (11)

Orbitale 3d: n=3, l=2, m=0, ±1, ±2

Ψ

320

(x,y,z), Ψ

321

(x,y,z), Ψ

32,-1

(x,y,z), Ψ

322

(x,y,z),

Ψ

32,-2

(x,y,z) ; R

32

(r)

0

5

10

15

20

25

r/a

0

r

2

R

2

3 d

Część radialna, R

3,2

(r)

E

3

= -1,5 eV

( )

0

2

7

3

2

0

30

81

1

2

,

3

exp

)

(

a

r

r

a

r

R

−

⋅

⋅

=

−

3

2

2

2

3

,

3

,

3

,

3

,

3

z

y

x

yz

xz

xy

d

d

d

d

d

−

Orbitale atomu wodoru (12)

część kątowa orbitali 3d

( )

]

1

cos

3

[

,

2

16

45

0

,

2

−

=

θ

ϕ

θ

π

Y

)

3

(

2

z

d

( )

ϕ

θ

ϕ

θ

π

cos

2

sin

,

16

45

1

,

2

⋅

=

Y

)

3

(

xz

d

( )

ϕ

θ

ϕ

θ

π

sin

2

sin

,

16

45

1

,

2

⋅

=

−

Y

)

3

(

yz

d

( )

ϕ

θ

ϕ

θ

π

2

cos

2

sin

,

16

45

2

,

2

⋅

=

Y

)

3

(

2

2

y

x

d

−

( )

ϕ

θ

ϕ

θ

π

2

sin

2

sin

,

16

45

2

,

2

⋅

=

−

Y

)

3

(

xy

d

Orbitale atomu wodoru (13)

część kątowa orbitali 3d

x

z

y

xz

d

3

x

z

y

xy

d

3

x

z

y

yz

d

3

x

z

y

2

2

3

y

x

d

−

x

z

y

2

3

z

d

Orbitale atomu wodoru (14)

część radialna

0

1

2

3

4

5

r/a

0

r

2

R

2

1 s

0

5

10

r/a

0

r

2

R

2

2 s

0

5

10

15

20

25

r/a

0

r

2

R

2

3 s

0

5

10

15

r/a

0

r

2

R

2

2 p

0

5

10

15

20

25

r/a

0

r

2

R

2

3 p

0

5

10

15

20

25

r/a

0

r

2

R

2

3 d

liczba maksimów części radialnej
orbitalu wynosi zawsze n-l;

wysokość maksimów rośnie z r

Orbitale atomu wodoru (15)

część kątowa

ns

x

y

z

np

z

x

y

z

np

x

x

y

z

np

y

płaszczyzna xz

płaszczyzna xy,

na osiach

płaszczyzna xy

płaszczyzna yz

oś z,

w płaszczyźnie xy

Orbitale atomu wodoru

o

Nie oczekuję uczenia się wzorów poszczególnych
funkcji na pamięć – jest to wręcz niewskazane;

o

Oczekuję zapamiętania:

→

jak wygląda atom wodoru i równanie Schrödingera dla
atomu wodoru, i jak się je rozwiązuje (ogólnie);

→

co to są liczby kwantowe i skąd się wzięły, jakie
wielkości są kwantowane;

→

jaki jest związek orbitali z zestawem związanych z nimi
liczb kwantowych;

→

jak wyglądają wykresy części radialnej i kątowej dla
orbitali ns, np i nd (także dla różnych n, czyli kombinacji
n, llll, m);

Jony wodoropodobne

....

,

,

,

,

5

4

3

+

+

+

+

+

+

C

B

Be

Li

He

T

p

m

=

2

2

jak w atomie
wodoru

V

= −

⋅

Z

e

r

o

2

1

4

πε

gdzie Z - liczba
protonów w
jądrze

E

m

e

const

e

o

= −

=

π

ε

Z

2

4

2

2 h n

n

2

2

'

Wyniki:

orbitale jak w atomie wodoru,
energia uwzglednia wyższy ładunek jądra

M, M

z

, s, m

s

jak w atomie wodoru

4

Model atomu wodoru

a rzeczywistość

Doświadczalna weryfikacja wyników

Doświadczalna weryfikacja wyników

Doświadczalna weryfikacja wyników

Doświadczalna weryfikacja wyników

uzyskanych przez mechanikę kwantową

uzyskanych przez mechanikę kwantową

uzyskanych przez mechanikę kwantową

uzyskanych przez mechanikę kwantową

dla atomu wodoru

dla atomu wodoru

dla atomu wodoru

dla atomu wodoru

Spektroskopia

Spektroskopia jest działem fizyki, który zajmuje się

pomiarem (spektrometria) i interpretacją widm
promieniowania różnych substancji;

Spektroskopia emisyjna – widma promieniowania otrzymuje

się wzbudzając substancję (np. termicznie albo w łuku
elektrycznym) i mierzy się otrzymane promieniowanie w
funkcji długości fali (częstotliwości);

Spektroskopia absorbcyjna – substancję poddaje się

działaniu promieniowania obejmującego cały zakres (np.
widzialnego, UV, IR) i bada się, co zostało pochłonięte przez
badaną substancję w funkcji długości fali (częstotliwości);

Spektroskopia opiera się na założeniu Plancka E=h•ν, czyli,

że pochłaniana (emitowana) jest tylko taka energia, która
odpowiada własnym energiom substancji (różnicą poziomów
energii).

Spektroskopia absorbcyjna

monochromator

substancja

badana

źródło

promieniowania

analizator

natężenia

prom.

analizator

natężenia

prom.

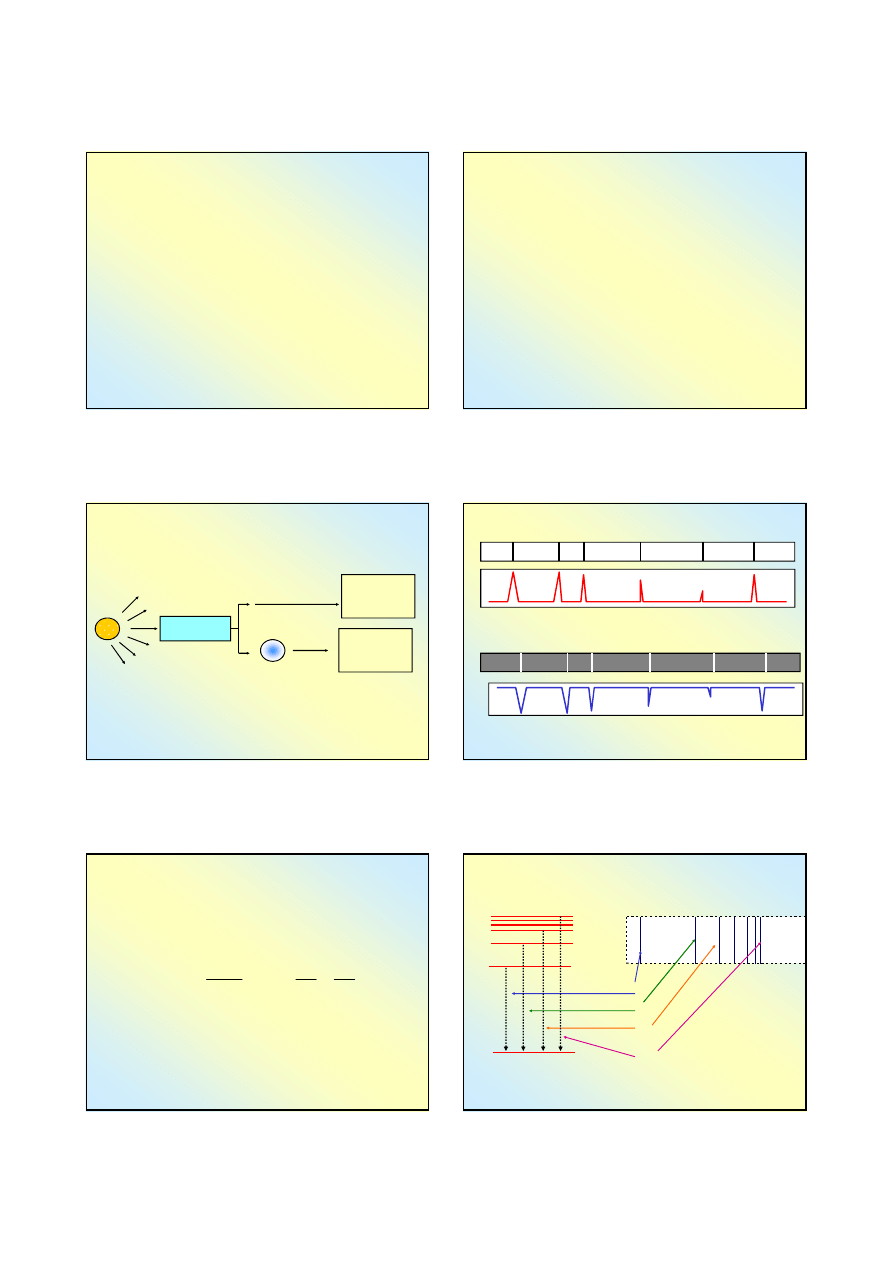
Widmo emisyjne i absorpcyjne

widmo emisyjne

ν→

widmo absorbcyjne

ν→

Weryfikacja modelu

energia elektronu w atomie wodoru

Widmo emisyjne wodoru składa się z serii:

gdzie:

n

- jest numerem kolejnej serii i najniższego

poziomu w danej serii

q

- jest numerem wyższego poziomu

R

H

- stałą Rydberga













−

=

=

−

−

2

2

1

1

q

n

R

h

E

H

n

q

n

q

ν

Poziomy energetyczne w atomie

a widmo promieniowania wodoru

n = 3

n = 4

n = 7

n = 1

n = 2

Poziomy energetyczne elektronu w atomie wodoru,

wynikające z rozwiązania równania Schrödingera

E

1

E

2

E

3

E

4

E

7

21

1

2

1

E

E

E

h

∆

=

−

=

ν

31

1

3

2

E

E

E

h

∆

=

−

=

ν

41

1

4

3

E

E

E

h

∆

=

−

=

ν

71

1

7

6

E

E

E

h

∆

=

−

=

ν

7

4

3

2

1

ν

ν

ν

ν

ν

h

h

h

h

h

→

hv

5

Degeneracja energii w atomie wodoru

Jeśli jednej wartości energii odpowiada kilka funkcji
własnych (orbitali), to mówimy, że ten poziom jest
zdegenerowany:

1s

1

2s

2p

x

2p

y

2p

z

4

3s

3p

x

3p

y

3p

z

xy

d

3

2

2

3

y

x

d

−

2

3

z

d

xz

d

3

yz

d

3

9

dla n=4 jest 1+3+5+

7

=

16 funkcji

dla n=5 jest 1+3+5+7+

9

=

25 funkcji

dla dowolnego n jest 1+3+5+7+

9...

=

n

2

funkcji

Degeneracja energii w atomie wodoru

E

E

E

E

E

E

E

E

E

E

E

E

E

E

s

s

p

p

p

s

p

p

p

d

d

d

d

d

x

y

z

x

y

z

xy

xz

yz

z

x

y

1

2

2

2

2

3

3

3

3

3

3

3

3

3

2

2

2

<

=

=

=

<

=

=

=

=

=

=

=

=

−

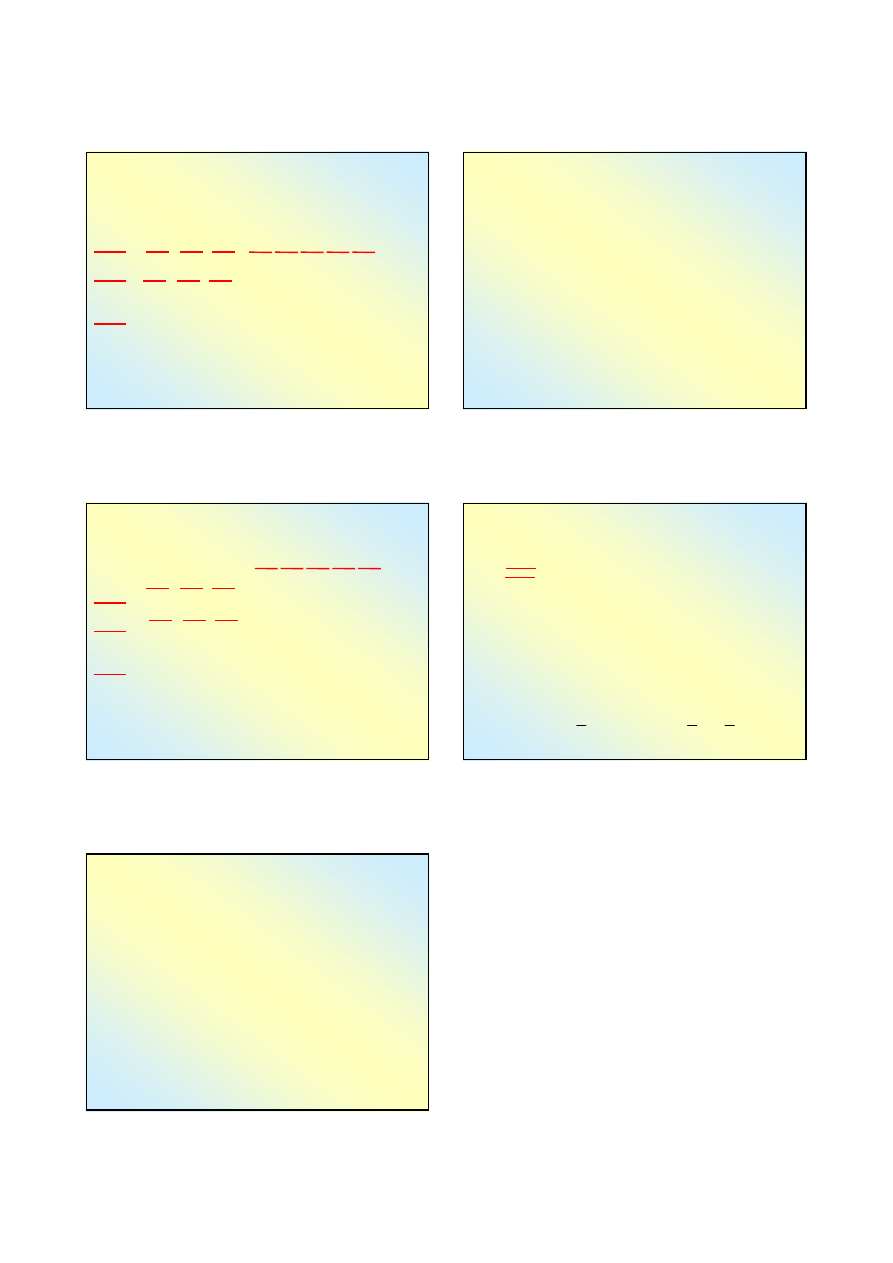
Cofnięcie degeneracji może zachodzić (częściowo
lub całkowicie) w silnym polu :

- elektrycznym (efekt Starka)
- magnetycznym (efekt Zeemana)

Cofnięcie degeneracji można obserwować w widmie
emisyjnym lub absorpcyjnym

E

E

E

E

E

E

E

E

E

E

E

E

E

E

s

s

p

p

p

s

p

p

p

d

d

d

d

d

x

y

z

x

y

z

xy

xz

yz

z

x

y

1

2

2

2

2

3

3

3

3

3

3

3

3

3

2

2

2

<

<

=

=

<

<

=

=

<

=

=

=

=

−

Cofnięcie degeneracji =

rozszczepienie poziomów energii

2s

3s

3p

x

3p

y

3p

z

1s

1

2p

x

2p

y

2p

z

3

xy

d

3

2

2

3

y

x

d

−

2

3

z

d

xz

d

3

yz

d

3

5

Jeśli elektron w atomie wodoru posiada najniższą
możliwą energię, to jego stan opisuje orbital 1s

Nawet poziomy 1s, 2s, .. mogą być

rozszczepione !

1s

w polu elektrycznym
i magnetycznym

Elektron zachowuje sie tak, jakby posiadał
„wewnętrzny moment pędu”
Ta właściwość elektronu nosi nazwę

spinu

(Dirac 1928)
Wartość spinu dla elektronu wynosi zawsze 1/2

s

m

s

=

= − +

1
2

1
2

1
2

,

Stan elektronu w atomie wodoru

Do określenia stanu elektronu w atomie wodoru
niezbędna jest znajomość 4 liczb (bo spin jest stały) -
n, l, m i m

s

W stanie podstawowym (minimum energii) stan
elektronu w atomie wodoru określa orbital 1s

(n=1, l=0, m=0, s=1/2, m

s

=±1/2)

spinowa

funkcja

-

orbital

-

)

,

,

(

,

,

s

s,m

m

l

n

z

y

x

σ

+

Ψ

l

spinorbita

-

)

,

,

(

,

,

,

,

,

,

(x,y,z)

z

y

x

s

s

m

s

m

l

n

s,m

m

l

n

Φ

=

⋅

Ψ

σ