I rok Farmacji
Statystyka część II

- estymatory

- testowanie hipotez

- test znaków

Estymatory obciążone i nieobciążone

Na podstawie znanych statystyk staramy się określić (estymować)
parametry.

Rozważmy doświadczenie w którym pobieramy nie jedną, a bardzo
wiele prób o takiej samej liczności. Dla każdej z nich obliczamy
średnią ( ). Średnia ze średnich powinna być praktycznie równa
średniej z populacji ().

Estymatorem średniej z populacji jest średnia z próby.

X

Obliczając odchylenie standardowe dla populacji ()

korzystamy z wartości średniej dla populacji ().

Rozważając doświadczenie takie jak poprzednio
obliczamy dla każdej z prób odchylenie standardowe (s)
korzystając dla każdym przypadku z innej wartości
średniej.

Chcąc estymować odchylenie standardowe dla populacji
powinniśmy w obliczeniach korzystać z nieznanej (!)
wartości  .

Ponieważ SKO od średniej jest najmniejsza to dla każdej
z prób wartość SKO obliczona od  będzie wieksza lub

równa obliczonej od średniej z próby.

Stąd średnia z odchyleń standardowych dla prób

będzie nieco mniejsza od . To samo dotyczy wariancji.

Dlatego stosujemy
dzielenie przez N-1. Im mniejsza próba (mniejsze N),
tym obciążenie estymatora jest większe.

Testowanie hipotez.

Przyjęcie założeń
– model i hipoteza (o co się pytamy).

Otrzymanie rozkładu z próby
– jakie wyniki są możliwe i z jakim
prwdopodobieństwem

(na podstawie

modelu).

Wyznaczenie poziomu istotności i obszaru
krytycznego
– kiedy mamy przyjąć a kiedy odrzucić
badaną hipotezę,
– czy nie odrzucamy prawdziwej hipotezy

(błąd pierwszego

rodzaju).

Przeprowadzenie badań i obliczenie
statystyki.

Podjęcie decyzji.

Testowanie hipotez

(na przykładzie rozkładu dwumianowego)

Rozkład dwumianowy:





k

N

k

p

1

p

k

N

P(k)



















Jakie jest prawdopodobieństwo, że na N prób dokładnie k
zakończy się sukcesem, jeżeli prawdopodobieństwo sukcesu
w każdej z prób jest takie samo i wynosi p.

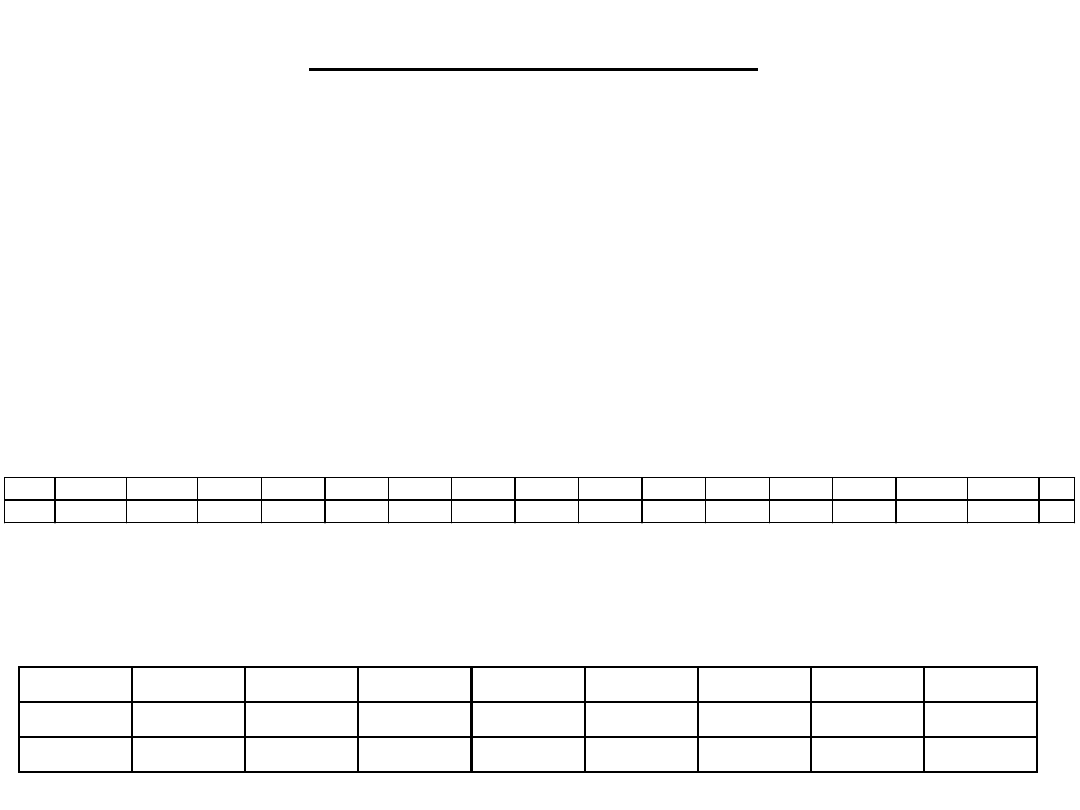
Dla N=14 i p=0,5 otrzymujemy rozkład:

k

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14



P(k) 0,00006 0,00085 0,0056 0,0222 0,0611 0,1222 0,1833 0,2095 0,1833 0,1222 0,0611 0,0222 0,0056 0,00085 0,00006 1

k

0

1

2

3

4

5

6

7

P(k)

0,00006 0,00085 0,00555 0,02222 0,06110 0,12219 0,18329 0,20947

k

14

13

12

11

10

9

8

7

Ponieważ rozkład jest symetryczny (p=0,5) tabelę możemy zapisać
w prostszy sposób:

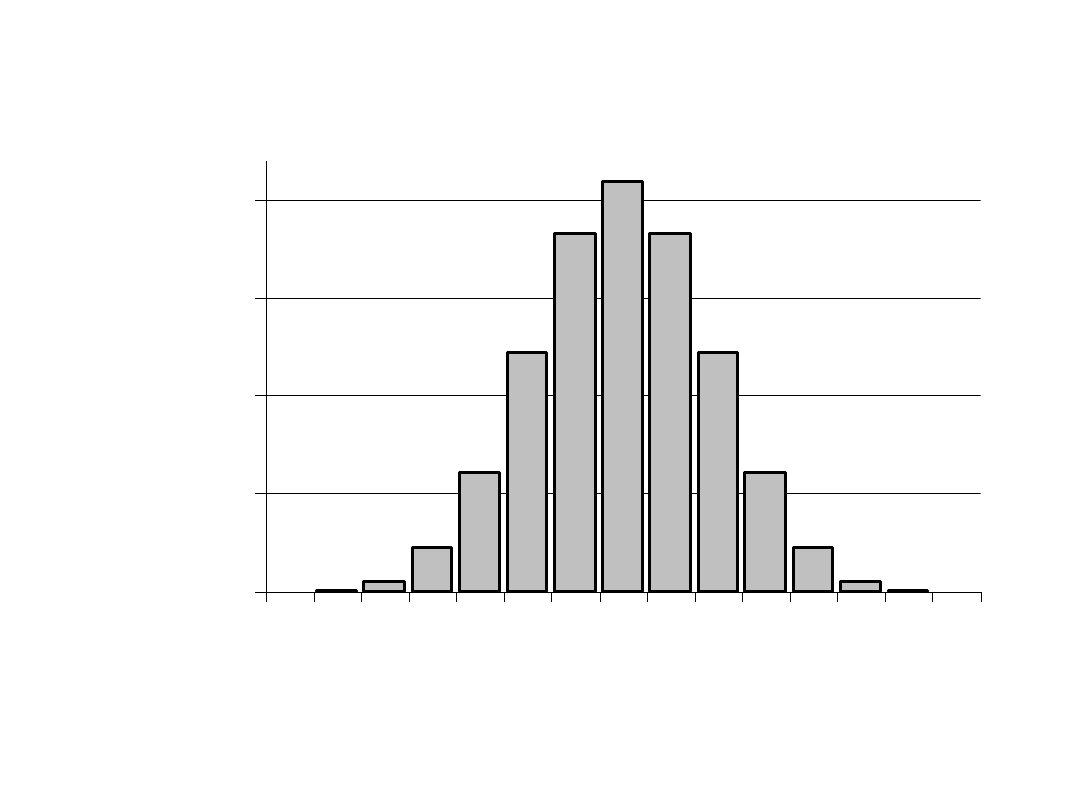
N=14 p=0,5

0,00

0,05

0,10

0,15

0,20

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

liczba sukcesów (k)

P(k)

Histogram rozkładu dwumianowego.

W próbie losowej dokonujemy 14 niezależnych pomiarów (obserwacji):
– losujemy kule z urny (ze zwracaniem),
– odławiamy ptaki (przykład z książki),
– zbieramy rośliny,
– badamy poziom enzymów we krwi po podaniu leków itp.

Za sukces przyjmiemy wystąpienie zdarzenia (A),
za porażkę nie wystąpienie zdarzenia (B).

Przyjmujemy hipotezę, że p=0,5 i oznaczmy jako H

0

. To

znaczy,
że w badanej populacji zdarzenia A i B są równie
prawdopodobne. Jeżeli w wyniku badania nie
przyjmiemy H

0

(czyli odrzucimy ją)

to wówczas przyjmiemy hipotezę alternatywną H

1

,

w tym przypadku p0,5.

Uwaga:

Nie jest to jedyna możliwość! Mogą być inne hipotezy

alternatywne.

Z przyjętych założeń wynika,
że możemy zastosować rozkład dwumianowy dla N=14 i p=0,5.

Czy w badanej populacji i w pobranej z niej
próbce musi
być taka sama proporcja A do B?
Najbardziej prawdopodobny jest wynik k=7 z
P(7)0,21,

ale niewiele mniej prawdopodobne są wyniki
k=6 i k=8
z P(6)=P(8)0,18.

Jeżeli przyjmiemy H

0

tylko dla k=7 to odrzucimy dla pozostałych k.

Inne wartości k są też możliwe P(k7)0,79, czyli z takim

prawdopodobieństwem odrzucimy wynik który moglibyśmy
otrzymać gdy p=0,5.

Prawdopodobieństwo odrzucenia prawdziwej hipotezy
– błąd pierwszego rodzaju
– H

0

jest prawdziwa ale w wyniku losowania otrzymany został wynik

mało prawdopodobny, co czasami może się zdarzyć.

– prawdopodobieństwo, że k7 jest dziełem przypadku p=0,79

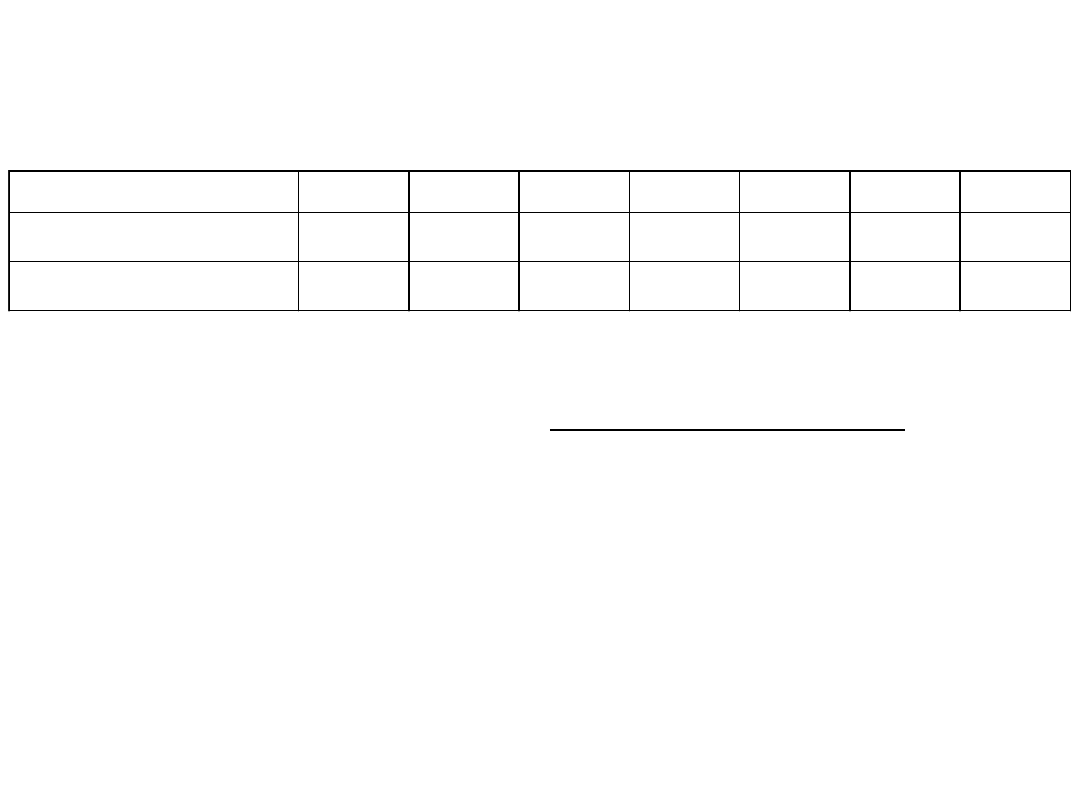
przedział

7

6 - 8

5 - 9

4 - 10 3 - 11 2 - 12 1 -13

prawdopodobieństwo 0,2095 0,5760 0,8204 0,9426 0,9871 0,9982 0,9999

błąd I rodzaju

0,7905 0,4240 0,1796 0,0574 0,0129 0,0018 0,0001

Nawet przyjmując jako możliwy przedział 1–13,
czyli odrzucając hipotezę dla k=0 (tylko B) i dla k=14 (tylko A)
popełniamy błąd I rodzaju (p=0,0001).

Jaki błąd I rodzaju jest do zaakceptowania,
czyli jaki przyjmujemy poziom istotności?

0,05 – biologia, medycyna, rolnictwo
– wartość przyjmowana najczęściej,
– dopuszczamy pomyłkę raz na 20 przypadków,
0,01 ; 0,001 – jesteśmy ostrożni przy odrzucaniu H

0

– medycyna

inne wartości – przyjmowane na podstawie zdobytych doświadczeń,
zwyczaju itp.

Poziom istotności
– dopuszczalne prawdopodobieństwo ryzyka
popełnienia

błędu I rodzaju. Błąd I rodzaju ma być nie

większy od

założonego poziomu istotności.

Obszar krytyczny
– wartości k dla których odrzucimy H

0

,

– najmniej prawdopodobnych przypadków

szukamy po obydwu stronach rozkładu
(test dwustronny)
– otrzymujemy k= 0,1,2 oraz 12,13,14.
– jeżeli w wyniku naszego doświadczenia
otrzymamy
wartości k  

311 to H

0

przyjmujemy.

Przyjmując H

0

stwierdzamy,

że udział zdarzenia A może wynosić 0,5 lub,
że nie udało się pokazać, iż ten udział jest różny od 0,5.

Przykłady – omówienie różnych możliwych wyników.

k= 2 – wynik znajduje się w obszarze krytycznym i H

0

odrzucamy,

przyjmując hipotezę alternatywną H

1

popełniamy błąd I rodzaju z P=0,013.

k=14 – wynik znajduje się w obszarze krytycznym i H

0

odrzucamy,

ale zrobilibyśmy to także dla obszaru krytycznego k=0,14,
wtedy błąd I rodzaju dla takiego obszaru wynosi P=0,0001,
co przy omawianiu wyników należy zaznaczyć.

k=10 – wynik pozwala przyjąć H

0

, nie popełniamy błędu I rodzaju,

ale może być tak, że za prawdziwą przyjęliśmy fałszywą
hipotezę zerową – błąd drugiego rodzaju, rzeczywisty
udział zdarzenia A w populacji może być przecież różny
od 0,5, a wynik jest dziełem przypadku.

Test znaków.

12 kobietom, którym podaje się preparat mający
podwyższać poziom hemoglobiny, podano też inny lek.
Wiadomo, że stosowany preparat jest skuteczny w 2/3
przypadków.
Czy podanie dodatkowego leku wpływa na skuteczność
preparatu?
Zakładamy, że próba jest losowa i niezależna

(może to budzić

wątpliwości).

Przyjmujemy H

0

– poziom hemoglobiny ulegnie podwyższeniu

u 2/3 pacjentek (p=2/3). {H

1

: p2/3}

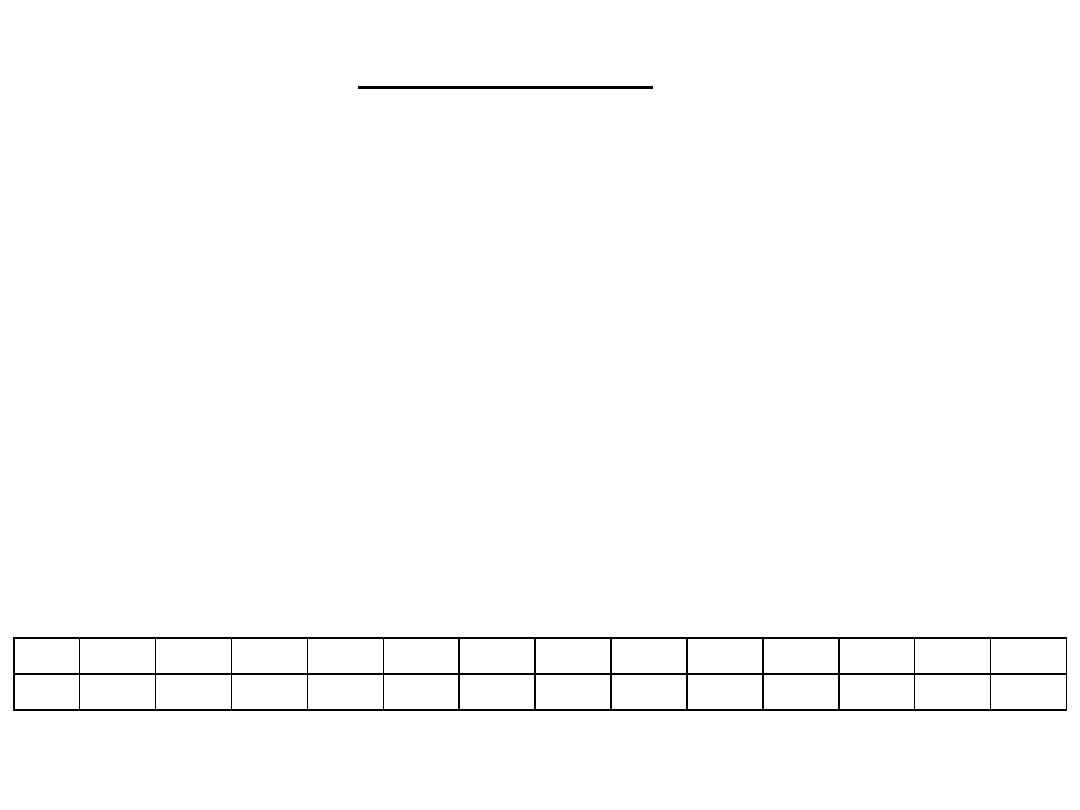
Dla N=12 i p=2/3 otrzymujemy rozkład:

k

0

1

2

3

4

5

6

7

8

9

10

11

12

P(k) 0,000 0,000 0,000 0,003 0,015 0,048 0,111 0,191 0,238 0,212 0,127 0,046 0,008

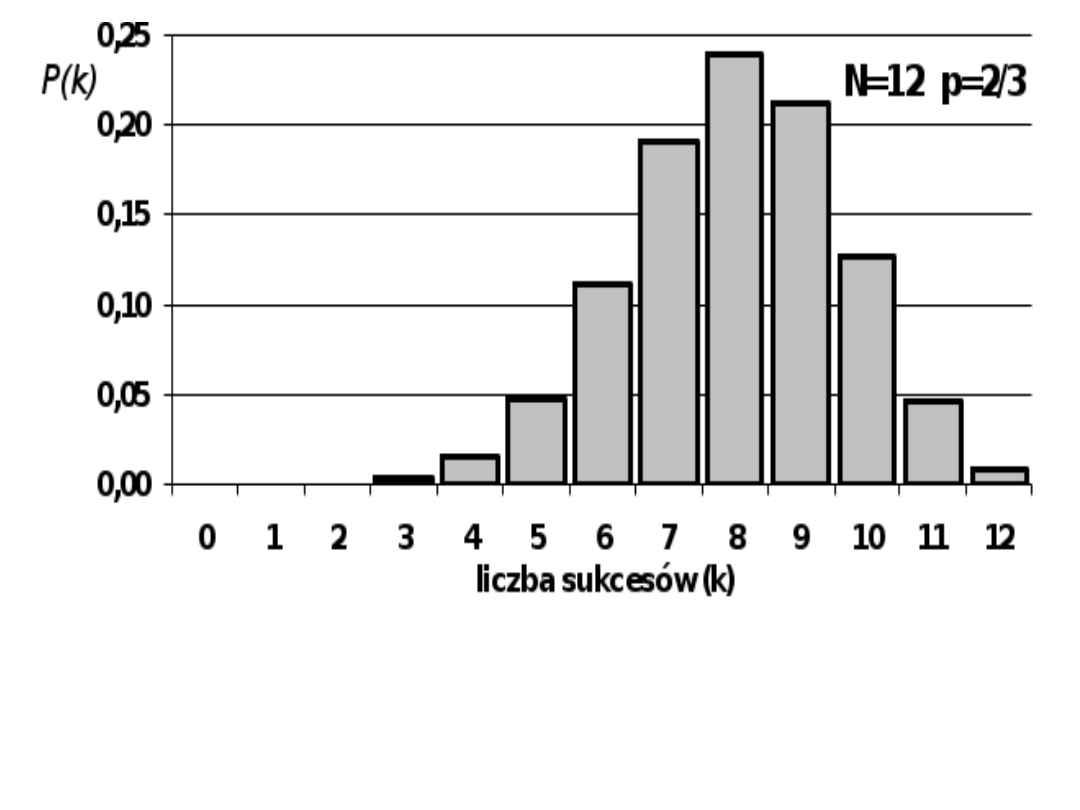
Zakładając poziom istotności na poziomie =0,05

i przedział symetryczny względem wartości przeciętnej H

0

przyjmiemy dla k  

511 , błąd I rodzaju wyniesie wtedy p=0,026.

Przykładowe wyniki testu: + - + - - + + + + - +- [7+; 5-]

+ wzrost poziomu hemoglobiny
- poziom hemoglobiny nie wzrósł

Otrzymane wyniki umożliwiają przyjęcie hipotezy zerowej,
k nie leży w obszarze krytycznym.

Nie stwierdzono wpływu leku na skuteczność preparatu.