I rok Farmacji
Statystyka część I

- populacja generalna i próba

- skale pomiarowe

- statystyka opisowa

Popula
cja
general
na

Prób
a

Próba i populacja generalna.

Zbiór wszystkich
interesujących nas elementów

Elementy wzięte do badania

Ze względów praktycznych zazwyczaj nie

możemy przebadać całej populacji, wybieramy do
badań tylko jej część – próbę.

Populacja w sensie statystycznym i

populacja w sensie ekologicznym czy
genetycznym to nie to samo!

Statystyki i

parametry.

Wielkości obliczane dla pobranej próby –

statystyki,

oznaczane literami łacińskimi, np. średnia z

próby .

 

Wielkości obliczane dla całej populacji –

parametry,

oznaczane literami greckimi, np. średnia z

populacji .

X



Statystyka elementarna – obliczanie statystyk.

Statystyka matematyczna –
wnioskowanie o populacji generalnej na
podstawie próby.

Skale: nominalna, porządkowa i
interwałowa.

Skala nominalna:
– podział populacji na jednoznacznie opisane kategorie
– kryteria podziału.
Skala nominalna dychotomiczna – jw. ale tylko dwa podzbiory.

Skala porządkowa
– elementy zbioru porządkujemy według jednej reguły,
– każdy element ma przypisaną kolejność (rangę).

Skala interwałowa
– wszystkie pomiary uzyskane przez porównanie ze
wzorcem:
długość, objętość, masa, temperatura, czas i
inne,
– dane pochodzące z policzenia:
liczba drzew danego gatunku, liczba
studentów noszących
okulary.

Skala interwałowa:

- skala przedziałowa

~ liczby rzeczywiste
~ istotne są różnice między elementami zbioru
~ np. kalendarz, temperatura w C

- skala ilorazowa

~ j.w.
~ zero bezwzględne
~ stały stosunek (niezależny od jednostek)
~ temperatura w K, masa, odległość

Skale nominalna i porządkowa

– cechy jakościowe

Skala interwałowa

– cechy ilościowe

Zamiana skal:

interwałowa  porządkowa  nominalna

Zamiana w przeciwna stronę jest niemożliwa, mamy za mało danych.
Najdokładniejsza jest skala interwałowa a najmniej skala nominalna.

 

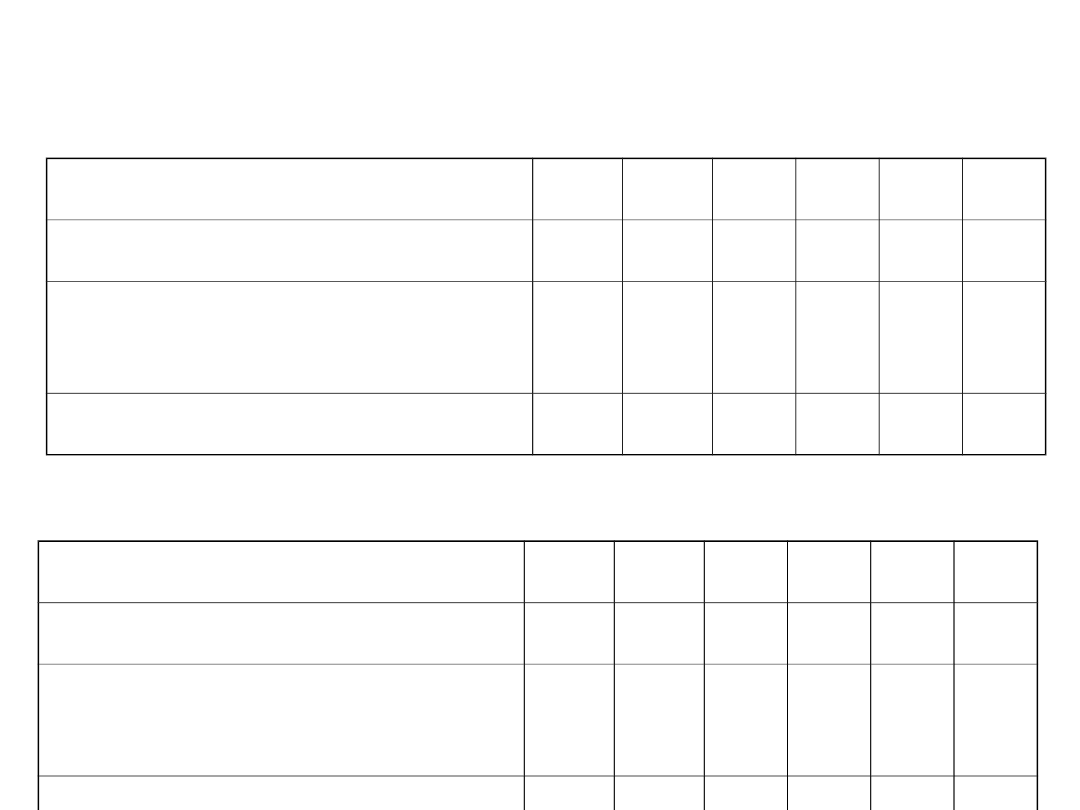
 A

B

C

D

E

F

Skala interwałowa

2

4

9

5

3

7

Skala porządkowa

(rangi)

6

4

1

3

5

2

Skala nominalna (>4) -

-

+ +

-

+

 

 A

B

C

D

E

F

Skala interwałowa

2

4

9

4

3

7

Skala porządkowa

(rangi)

6 3,5 1

3,

5

5

2

Skala nominalna (>4) -

-

+

-

-

+

Rangi wiązane:

Zamiana skal pomiarowych, rangi wiązane.

Procent:

Proporcja:

Stosunek liczbowy

Z

100

A

P





Z

A

P

A

-

Z

A

S

Na 156 studentów farmacji 142 uzyskało zaliczenie z matematyki.

%

3

,

97

156

100

42

1

P







973

,

0

156

42

1

P





Stosunek liczby studentów którzy uzyskali zaliczenie
do liczby tych którzy zaliczenia nie uzyskali wynosi:

1

,

10

14

42

1

S





lub

10,1:1.

Przypomnienie prostych pojęć.

Statystyka opisowa

Obliczanie podstawowych statystyk opisujących pobrana próbę:

- średnie, mediana, moda,

- zmienność (wariancja, odchylenie standardowe),

- charakterystyki kształtu rozkładu,

- zgodność z założona postacią rozkładu,

- przedział ufności.

Graficzne przedstawienie danych:

- histogram.

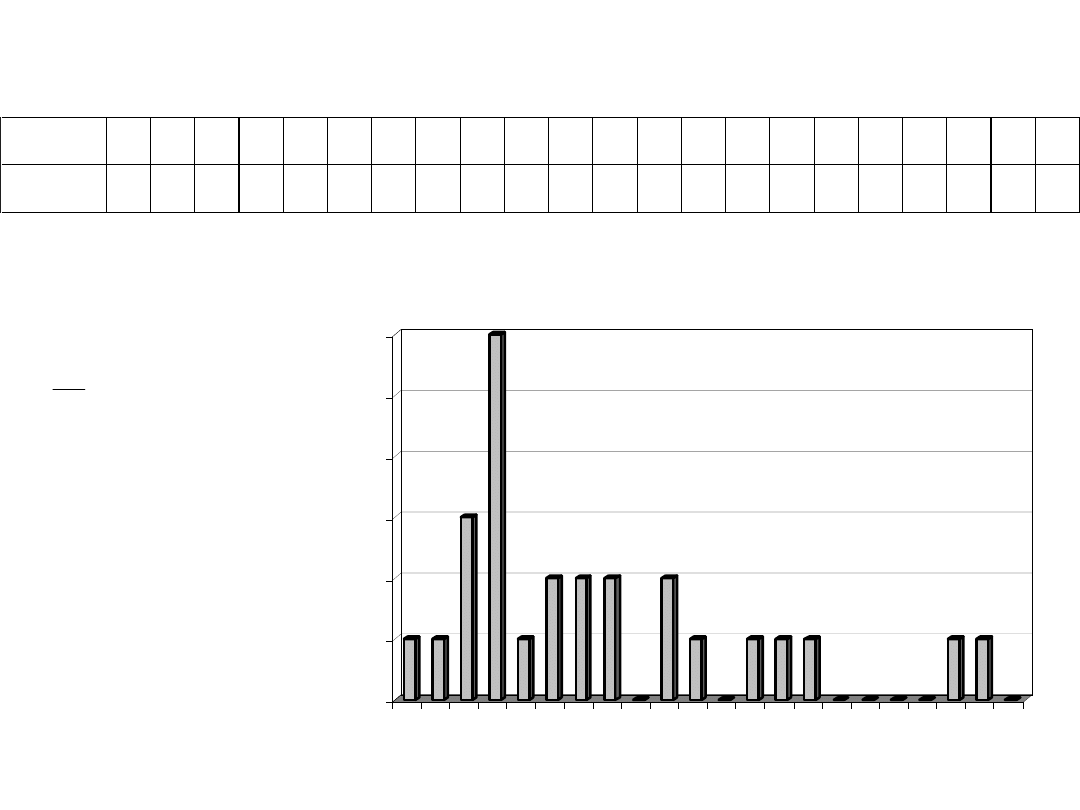
Wyniki semestru zimowego dla grupy 26 studentów.

Dane:

Punkty 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

Osoby 1 1 3 6 1 2 2 2 0 2 1 0 1 1 1 0 0 0 0 1 1 0

N=26 osób

58

,

7



X

0

1

2

3

4

5

6

liczba

osób

1

3

5

7

9

11 13 15 17 19 21

liczba uzyskanych punktów

Wyniki semestru zimowego.

Szereg rozdzielczy. Przedziały klasowe.

Większa liczba pomiarów:
– grupujemy w klasy
– liczba klas zależy od liczebności próby.

Orientacyjnie:

kilkanaście pomiarów - 4-5 przedziałów
setki pomiarów

- 8-10 przedziałów

tysiące pomiarów

- 12 przedziałów

Rozkład prawoskośny
– prawa strona rozkładu ma mniejsze nachylenie,
– więcej pomiarów jest poniżej średniej.
Rozkład lewoskośny
– lewa strona rozkładu ma mniejsze nachylenie,
– więcej pomiarów jest powyżej średniej.

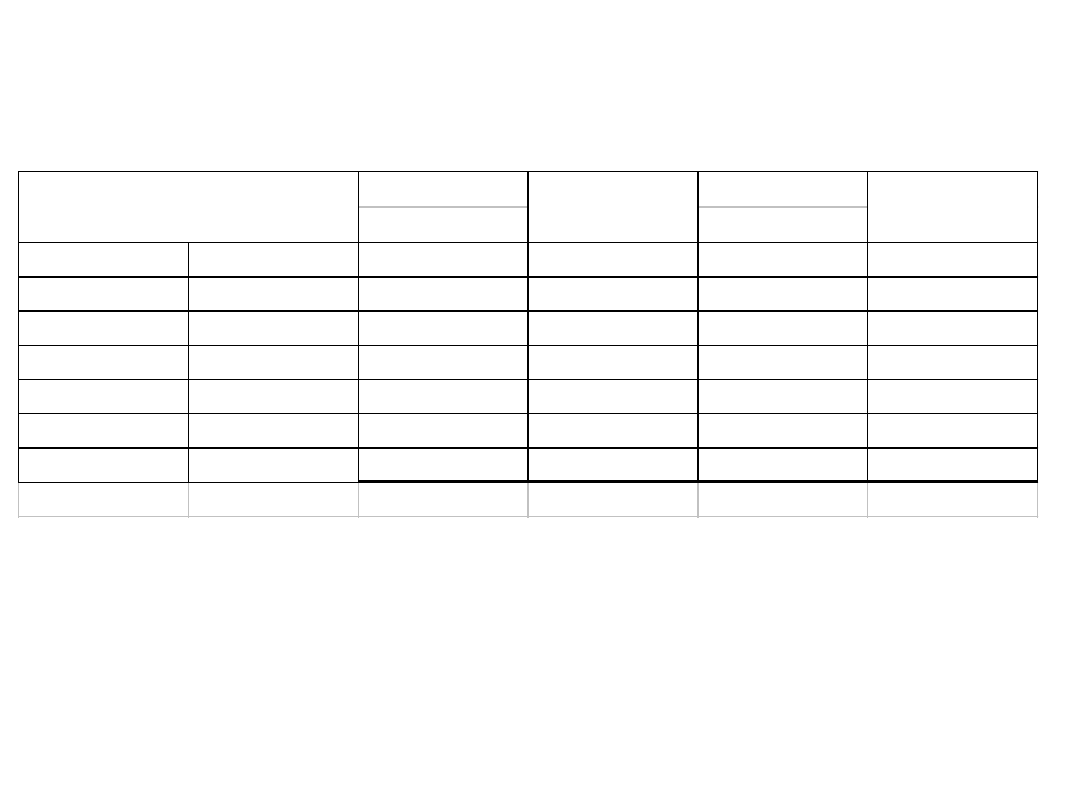
Środek

Liczebność

przedziału

skumulowana

praktyczne

rzeczywiste

1 – 4

0,5 – 4,5

2,5

11

11

0,42

5 – 8

4,5 – 8,5

6,5

7

18

0,27

9 – 12

8,5 – 12,5

10,5

3

21

0,12

13 – 16

12,5 – 16,5

14,5

3

24

0,12

17 – 20

16,5 – 20,5

18,5

1

25

0,04

21 – 24

20,5 – 24,5

22,5

1

26

0,04

Razem

26

1,01

Granice przedziałów

Liczebność

Częstość

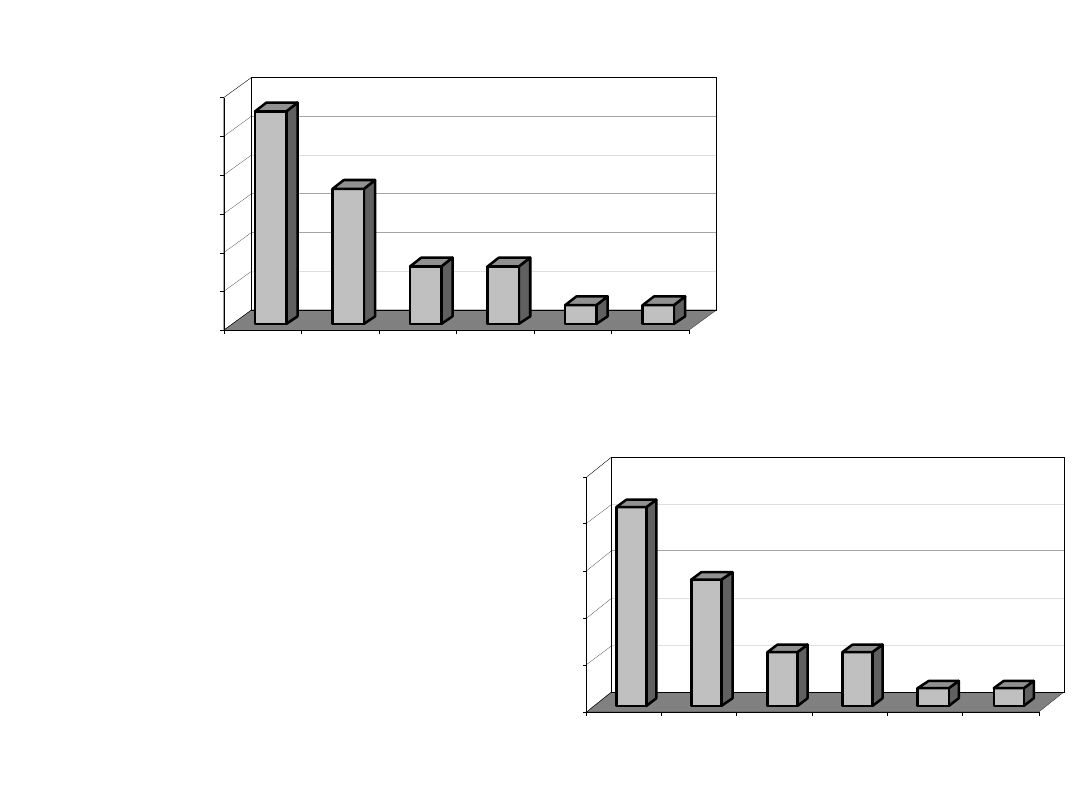
Szereg rozdzielczy otrzymany dla wyników
semestru zimowego.

Jest 6 przedziałów o równej długości.
Granice praktyczne są podane z taką samą dokładnością jak dane.
Granice rzeczywiste są obliczane w przypadku zmiennej ciągłej
(masa, temperatura, czas).

0

2

4

6

8

10

12

Liczebność

2,5

6,5

10,5

14,5

18,5

22,5

Przedziały (środki)

Histogram

0,00

0,10

0,20

0,30

0,40

0,50

Częstość

2,5

6,5

10,5 14,5 18,5 22,5

Przedziały (środki)

Histogram

STATYSTYKA ELEMENTARNA

miary tendencji centralnej i rozproszenia

Liczba pomiarów N – X

1

, X

2

, X

3

, ..., X

i

, ..., X

N

Suma (konwencje) -







N

i

1

i

i

X





N

1

i

i

X



X

Średnia arytmetyczna -

Średnia ważona
– np. dla szeregu rozdzielczego

Średnia geometryczna
– np. średnie tempo wzrostu populacji

Średnia harmoniczna
– liczby dodatnie,
– większe znaczenie dla mniejszych wartości





X

N

1

X









i

i

i

w

w

X

w

X

N

N

1

i

i

G

X

M











X

1

N

1

M

1

H





X

1

N

M

H

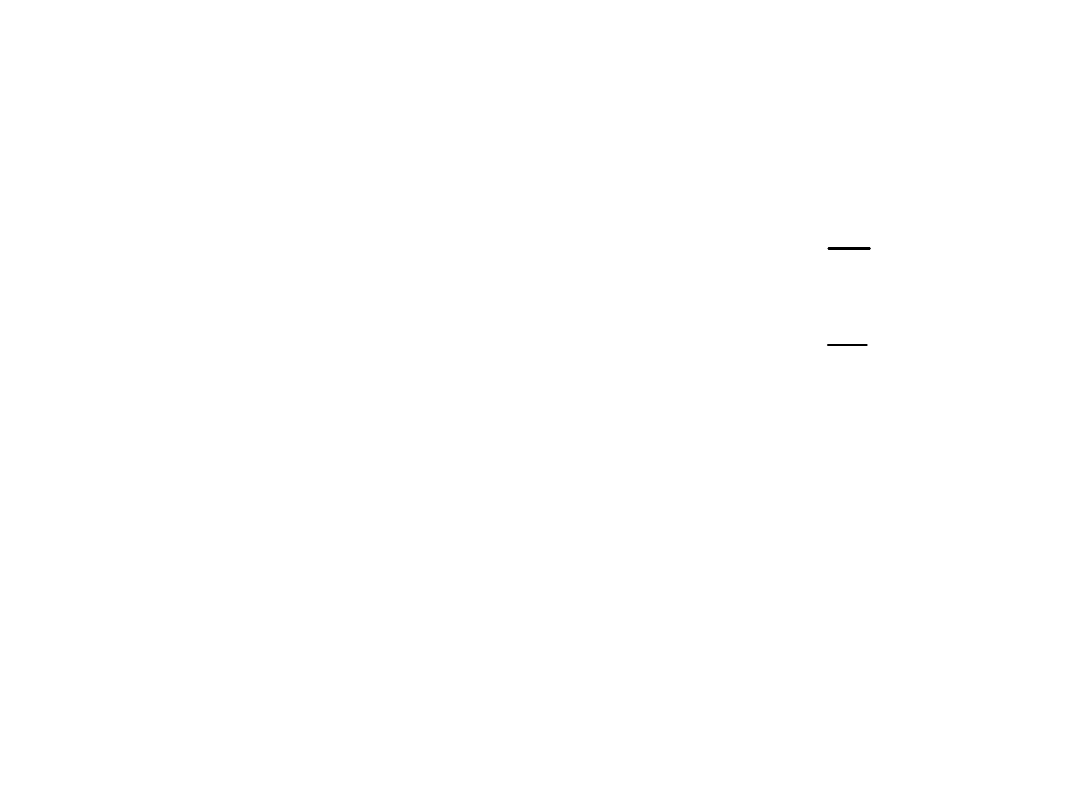
Średnia arytmetyczna –

Średnia ważona (obliczona dla
przedziałów) -

Średnia geometryczna –

Średnia harmoniczna –

Przykładowe obliczenia dla danych z tabel,
wyniki semestru zimowego.

7,6

X 

3

,

7

X

w



6,0

M

G



6

,

4

M

H



Miary tendencji centralnej szeregu statystycznego:

Szereg opisany tabelą ma 26 elementów

2

X

X

Me

14

13







6

2

6

6

Me









~ średnie,
~ mediana – w uporządkowanym szeregu wartość
środkowa,
przy parzystej liczbie elementów średnia
ze środkowych.
~ moda (wartość modalna rozkładu)
– najczęściej występująca wartość,
w podanym rozkładzie Mo = 4,
~ przedział modalny (szeregi rozdzielcze i pomiary
ciągłe)
– dla naszego szeregu jest to przedział 1–4.

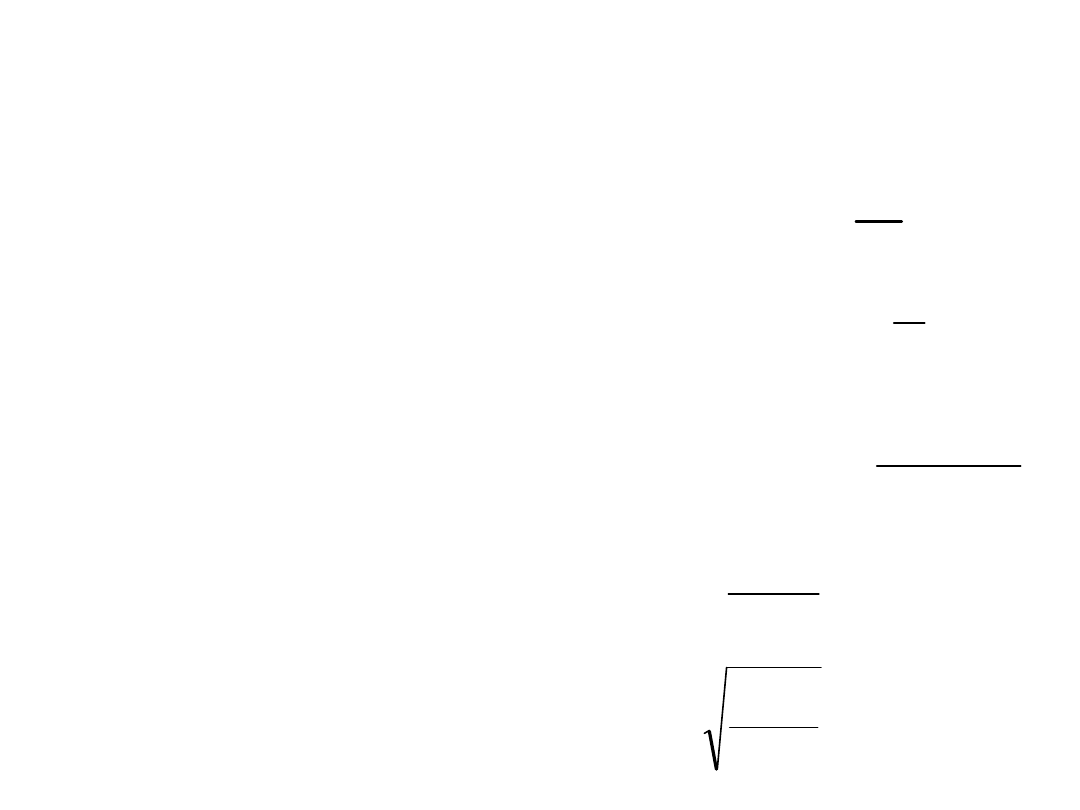
Miary rozproszenia.

Wariancja i odchylenie standardowe.

Stosowane konwencje oznaczeń.

odchylenie od średniej
– obliczane dla każdego pomiaru

suma kwadratów odchyleń (SKO)

można korzystać z wyrażenia
(dużo bardziej praktyczne)

wariancja

odchylenie standardowe

X

X

x

i

i













2

i

2

i

)

X

(X

x





N

X

X

x

2

i

2

i

2

i











1

N

x

s

2

i

2







1

N

x

s

2

i







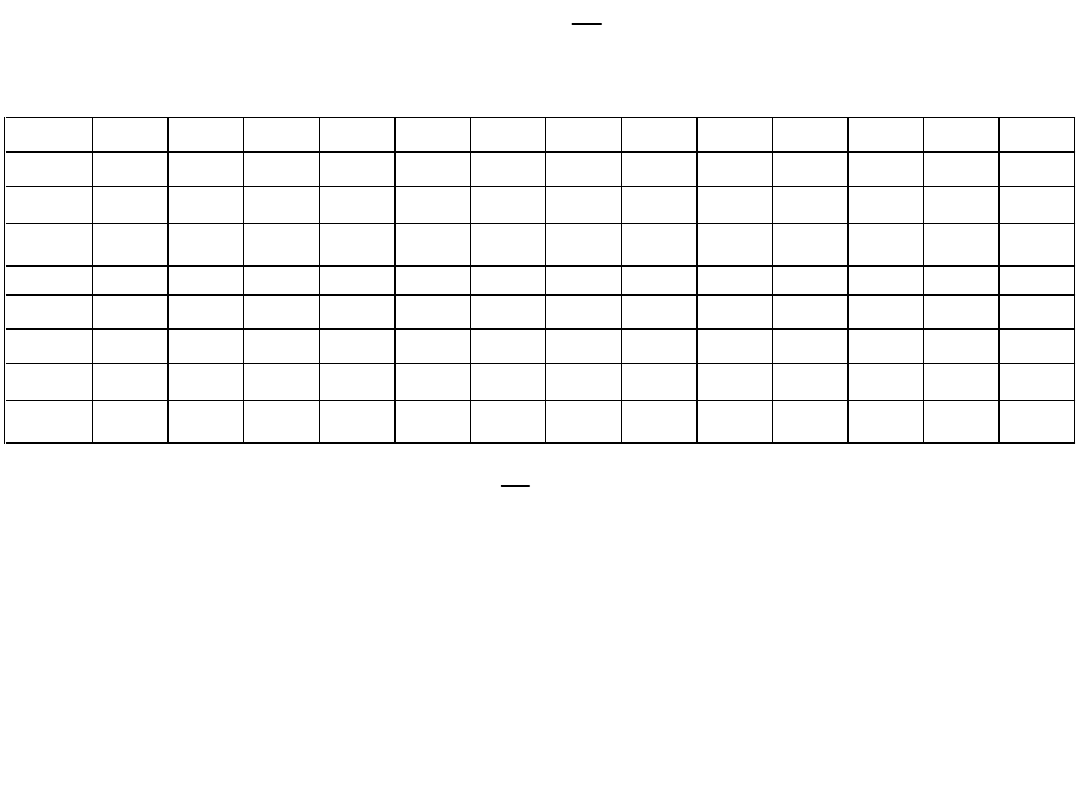
Dane (wyniki semestru zimowego):

osoba

1

2

3

4

5

6

7

8

9

10

11

12

13

punkty

1

2

3

3

3

4

4

4

4

4

4

5

6

x

i

-6,6

-5,6

-4,6

-4,6

-4,6

-3,6

-3,6

-3,6

-3,6

-3,6

-3,6

-2,6

-1,6

x

i

2

43,3 31,1 21,0 21,0 21,0 12,8 12,8 12,8 12,8 12,8 12,8

6,6

2,5

osoba

14

15

16

17

18

19

20

21

22

23

24

25

26

punkty

6

7

7

8

8

10

10

11

13

14

15

20

21

x

i

-1,6

-0,6

-0,6

0,4

0,4

2,4

2,4

3,4

5,4

6,4

7,4

12,4 13,4

x

i

2

2,5

0,3

0,3

0,2

0,2

5,9

5,9

11,7 29,4 41,3 55,1 154,3 180,2

7,6

X 

N=26 N-
1=25



197

X



2203

X

2

7,5769

X 



710,346

x

2

28,41

s

2



33

,

5

s 