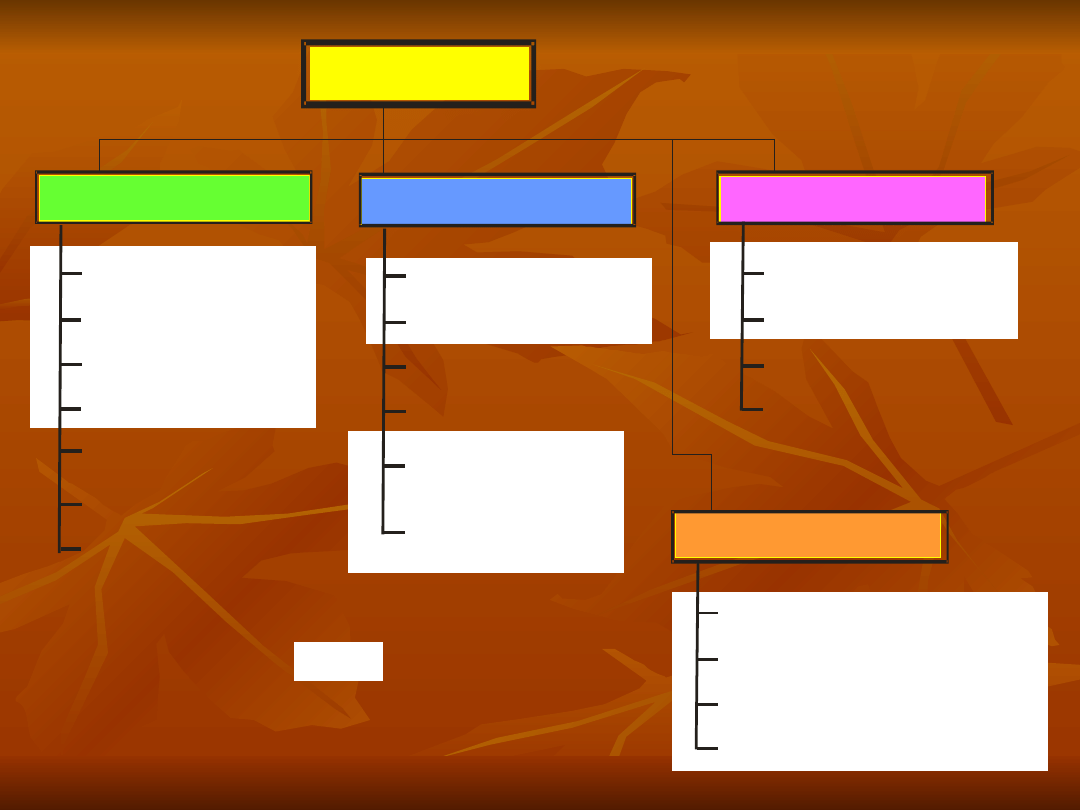
Miary klasyczne

Miary pozycyjne

Miary statystyczne

Miary położenia rozkładu

Miary zróżnicowania

Miary asymetrii

Miary koncentracji

Średnia arytmetyczna

Odchylenie standardowe

Współczynnik skośności

Współczynnik korelacji Giniego

Średnia geometryczna

Wariacja

Współczynnik asymetrii

Współczynnik korelacji Pearson`a

Średnia harmoniczna

Rozstęp

Trzeci moment centralny

Kurtoza

Średnia kwadratowa

Rozstęp ćwiartkowy

Wskaźnik asymertii

Wariacja resztkowa

Mediana

Współczynnik

zmienności

Kwantyl

Moda ( Dominanta)

Średnie odchylenie

bezwzględne

ŚREDNIA ARYTMETYCZNA

ŚREDNIA ARYTMETYCZNA

Średnia arytmetyczna jest to wartość
cechy, którą posiadałaby każda
jednostka zbiorowości, gdyby
u wszystkich jednostek zbiorowości
występowała ta sama wartość cechy.



W przypadku

W przypadku

szeregu szczegółowego

szeregu szczegółowego

korzysta się z relacji:

korzysta się z relacji:



Dla

Dla

szeregu rozdzielczego o przedziałach klasowych

szeregu rozdzielczego o przedziałach klasowych

, w

, w

których zmienna reprezentująca badaną cechę statystyczną

których zmienna reprezentująca badaną cechę statystyczną

jest skokowa, a przedziały klasowe jednojednostkowe

jest skokowa, a przedziały klasowe jednojednostkowe

(

(

punktowe

punktowe

) stosuje się wzór na tzw. średnią ważoną:

) stosuje się wzór na tzw. średnią ważoną:



natomiast w przypadku zmiennych ciągłych występujących w

natomiast w przypadku zmiennych ciągłych występujących w

szeregu

rozdzielczym

o

przedziałach

klasowych

szeregu

rozdzielczym

o

przedziałach

klasowych

wielojednostkowych

wielojednostkowych

, średnią arytmetyczną wyznacza się

, średnią arytmetyczną wyznacza się

jako:

jako:







k

i

i

i

n

x

n

x

1

1









n

i

i

x

n

x

1

1

i

k

i

i

n

x

n

x







1

1







k

i

i

i

n

x

n

x

1

1



i

k

i

i

n

x

n

x







1

1







n

i

i

x

n

x

1

1







k

i

i

i

n

x

n

x

1

1



i

k

i

i

n

x

n

x







1

1

Własności średniej arytmetycznej:
·         nie może być niższa od najmniejszej wartości zaobserwowanej
w badaniu i nie może być wyższa od wartości największej.
·         Wartość średniej zależy nie od liczebności klas, lecz od ich
wzajemnej proporcji.

W praktyce oznacza to, że można ją również wyznaczyć na
podstawie wskaźników struktury
·         Suma odchyleń wartości badanej cechy od średniej
arytmetycznej jest równa zeru.
·         Suma kwadratów odchyleń poszczególnych wartości
zmiennych badanej cechy od średniej arytmetycznej rozkładu jest
najmniejsza.
Średnia arytmetyczna jest wprawdzie najprostszą z miar średnich,
jednak nie zawsze jest ona dobrym miernikiem tendencji centralnej.
Chodzi tu o sytuację, kiedy największe liczebności skupiają się wokół
najniższych lub najwyższych wartości cechy lub występują w
populacji jednostki o nietypowych wartościach cechy, znacznie
odbiegających od pozostałych.
W przypadku, gdy przedziały klasowe (pierwszy i ostatni) są otwarte,
a ich liczebności są stosunkowo małe, można dokonać umownego ich
zamknięcia i ustalić wartości środków przedziałów. Nie można
jednak tak postąpić w przypadku, gdy udział liczebności otwartych
przedziałów w ogólnej sumie liczebności jest znaczny, czyli w tej
sytuacji nie da się wyznaczyć średniej arytmetycznej.

Nie wyznaczamy średniej

arytmetycznej

• kiedy największe liczebności skupiają

się wokół najniższych lub najwyższych
wartości cechy. Niekiedy średnia
arytmetyczna wprowadza po prostu
błąd. Dzieje się tak wówczas, gdy
wyznaczamy średnią ze zbiorów
niejednorodnych oraz gdy występują
obserwacje nietypowe, ponieważ
średnia arytmetyczna zaciera różnice
indywidualne.

• Natomiast dla zbiorowości z jednostkami

nietypowymi można policzyć średnią
arytmetyczną odrzucając jednostki
nietypowe pod warunkiem, że nie
stanowią one co najwyżej 5%
liczebności całej zbiorowości.

• Zbiory niejednorodne mają rozkłady z

kilkoma ośrodkami dominującymi.

• W przypadku, gdy przedziały klasowe

(pierwszy i ostatni) są otwarte, a ich
liczebności są stosunkowo małe, można
dokonać umownego ich zamknięcia
i ustalić wartości środków przedziałów.
Nie można jednak tak postąpić w
przypadku,

gdy

udział

liczebności

otwartych przedziałów w ogólnej sumie
liczebności jest znaczny, oznacza to jeśli
one nie przekraczają 5% liczebności
całej zbiorowości.

Mediana

• jest miarą pozycyjną, która

rozdziela całą populację na
dwie liczebnie równe części w
ten sposób, że w jednej z nich
znajdują się jednostki
o wartościach niższych lub
równych od mediany, a w
drugiej o wartościach
wyższych lub równych od
mediany.

Wynika z tego, że w celu

znalezienia mediany trzeba:

•

najpierw uporządkować zbiorowość

według wielkości jej elementów, tzn.
od ich wartości najmniejszej do
największej (lub odwrotnie).
Przedziały skrajne mogą pozostać
otwarte, gdyż nie mają one
bezpośredniego wpływu na wartość
mediany. W tym m.in. przejawia się
wyższość tej miary nad średnią
arytmetyczną.

• W celu wyznaczenia mediany dla szeregu szczegółowy

należy uporządkować rosnąco i obliczyć:

gdy n jest nieparzyste

gdy n jest parzyste

Me

x

n



1

2

2

2

2

2







n

n

x

x

Me

• Medianę można wyznaczyć nawet z

szeregów, w których przedziały
skrajne są otwarte i nie można ich
umownie zamknąć w celu obliczenia
średniej arytmetycznej. W szeregach
o dużej asymetrii, a także w innych
przypadkach, kiedy nie można
posłużyć się średnią arytmetyczną do
liczbowej charakterystyki
przeciętnego poziomu zjawiska,
należy wykorzystywać medianę.



W sposób przybliżony obliczamy medianę

W sposób przybliżony obliczamy medianę

opierając się na wzorze interpolacyjnym:

opierając się na wzorze interpolacyjnym:

gdzie:

gdzie:

x

x

0

0

   - dolna granica przedziału mediany,

   - dolna granica przedziału mediany,

h

h

0

0

   - rozpiętość przedziału mediany,

   - rozpiętość przedziału mediany,

n

n

0

0

   - liczebność przedziału mediany,

   - liczebność przedziału mediany,

N

N

Me

Me

- numer mediany, (N/2 (a gdy liczba

- numer mediany, (N/2 (a gdy liczba

obserwacji

obserwacji

jest nieparzysta (N+1)/2 – oznacza

jest nieparzysta (N+1)/2 – oznacza

pozycję

pozycję

mediany w szeregu

mediany w szeregu

n

n

sk

sk

-1

-1

 - suma liczebności wszystkich przedziałów

 - suma liczebności wszystkich przedziałów

klasowych poprzedzających przedział mediany.

klasowych poprzedzających przedział mediany.

( suma n

( suma n

i

i

od początku do przedziału z medianą )

od początku do przedziału z medianą )

Me x

h

n

N

n

Me

sk

 





0

0

0

1

(

)

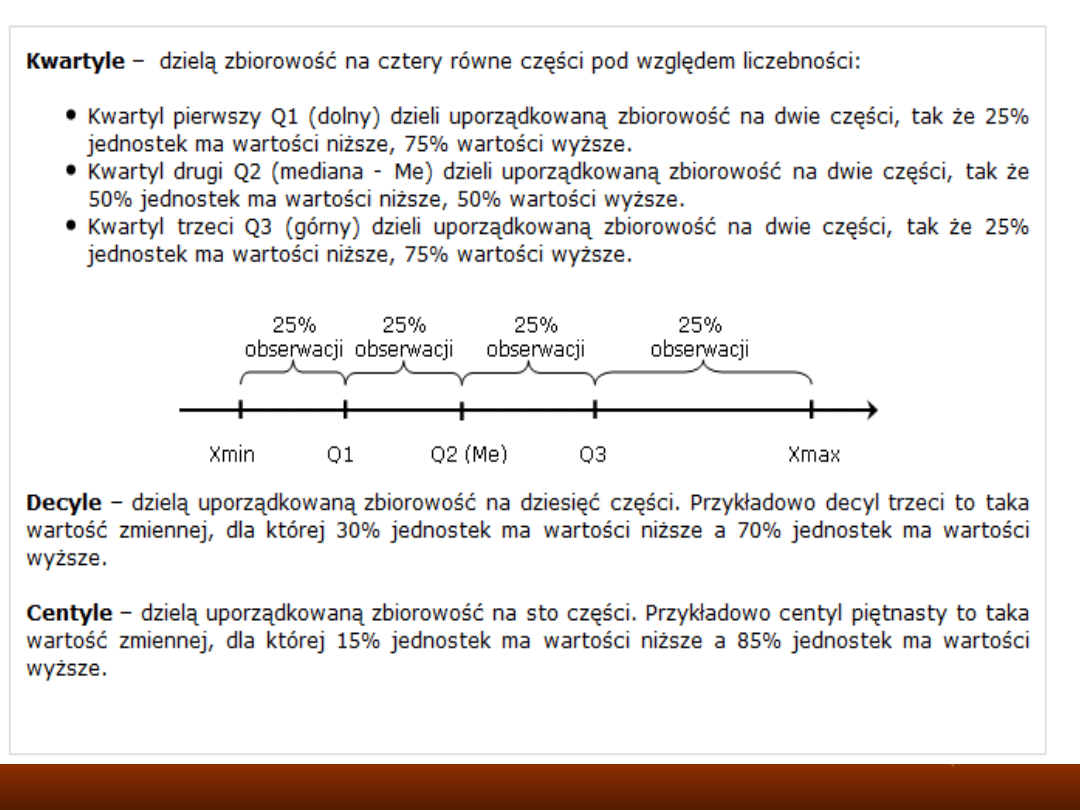
• W podobny sposób jak mediana (kwartyl

drugi) skonstruowane są dwa pozostałe

kwartyle (wartości ćwiartkowe).

• Kwartyl pierwszy (Q

1

) jest to wartość

jednostki, która dzieli szereg w taki sposób,

że 1/4 jednostek ma od niej wartości nie

większe, a 3/4 nie mniejsze.

• Kwartyl trzeci (Q

3

) to taka wartość, od

której 3/4 jednostek zbiorowości ma wartości

nie większe od Q

3

, a 1/4 nie mniejsze.

• Numery odpowiadające kwartylom

znajdujemy według wzorów:

4

1

n

N

Q



4

3

3

n

N

Q



W przypadku liczebnie dużej zbiorowości, ujętej w
szereg rozdzielczy, przy poszukiwaniu mediany
wykorzystuje

się

szereg

skumulowanych

liczebności. Mediana znajduje się wówczas w
grupie, w której skumulowane liczebności
przekraczają lub co najmniej osiągają numer
kolejny jednostki środkowej.

Wyznaczanie mediany komplikuje się, jeśli
wartości cechy są przedstawione w przedziałach
klasowych. Za pomocą kumulacji możemy ustalić,
w którym przedziale znajduje się środkowa
jednostka, natomiast trudno jest ustalić, która
z wartości tego przedziału jest medianą.

Dominanta, moda

• Najpopularniejszą wśród miar

przeciętnych pozycyjnych jest

dominanta, zwana niekiedy wartością

dominującą, modalną (modą).

• Dominantą nazywamy taką wartość

zmiennej, której odpowiada największa

liczba spostrzeżeń, czyli jest ona

najczęściej

występującą

wartością

zmiennej, reprezentującej określony

wariant badanej cechy. Dominanta jest

wygodną charakterystyką zbiorowości.

Można ją stosować zarówno do cech

niemierzalnych jak i mierzalnych.

• Mając

zbiór

indywidualnych

informacji,

łatwo

można

wyznaczyć

dominantę

przez

zliczenie

jednostek

o

danej

wartości cechy. Wariant cechy,

który ma największą częstotliwość

jest

dominantą.

Jeżeli dysponujemy szeregiem z

przedziałami klasowymi, możemy

wówczas łatwo dostrzec, który

przedział

ma

dominującą

liczebność.

• W celu wyznaczenia przybliżonej wartości

dominanty na podstawie szeregu

rozdzielczego o przedziałach klasowych

wielojednostkowych korzysta się z

następującego wzoru:

• gdzie:

x

0

- dolna granica przedziału dominanty,

n

0

- liczebność przedziału dominanty,

n

-1

- liczebność przedziału poprzedzającego przedział

dominanty,

n

+1

- liczebność przedziału następującego po przedziale

dominanty,

h

0

- rozpiętość przedziału dominanty.

o

o

o

h

n

n

n

n

n

n

x

Do

)

(

)

(

1

1

1

o

0



















Miary dyspersji dzieli się

Miary dyspersji dzieli się

na dwie podstawowe

na dwie podstawowe

grupy:

grupy:

–    

–    

bezwzględne

bezwzględne

(absolutne) miary

(absolutne) miary

zmienności, które są wielkościami

zmienności, które są wielkościami

mianowanymi (podobnie jak miary

mianowanymi (podobnie jak miary

średnie)

średnie)

–    

–    

względne

względne

(relatywne) miary

(relatywne) miary

zmienności, które są wielkościami

zmienności, które są wielkościami

niemianowanymi lub mogą być

niemianowanymi lub mogą być

wyrażone w procentach.

wyrażone w procentach.

Najprostszą miarą rozproszenia

Najprostszą miarą rozproszenia

jest

jest

rozstęp,

rozstęp,

nazywany inaczej

nazywany inaczej

obszarem zmienności

obszarem zmienności

,

,

który jest wyznaczany jako różnica

który jest wyznaczany jako różnica

między najwyższą i najniższą

między najwyższą i najniższą

wartością cechy w badanej

wartością cechy w badanej

zbiorowości statystycznej, czyli:

zbiorowości statystycznej, czyli:

min

max

x

x

R





Rozstęp

Rozstęp

jest używany

jest używany

tylko przy wstępnej

tylko przy wstępnej

analizie danych, ponieważ opierając

analizie danych, ponieważ opierając

się na dwóch skrajnych wartościach

się na dwóch skrajnych wartościach

trudno jest określić rzeczywistą

trudno jest określić rzeczywistą

dyspersję występującą w badanej

dyspersję występującą w badanej

zbiorowości.

zbiorowości.

wariancja

wariancja

która nie ma interpretacji ekonomicznej:

która nie ma interpretacji ekonomicznej:



w

w

przypadku szeregu

przypadku szeregu

szczegółowego

szczegółowego



dla szeregu rozdzielczego

dla szeregu rozdzielczego

punktowego

punktowego



dla szeregu rozdzielczego

dla szeregu rozdzielczego

z przedziałami klasowymi

z przedziałami klasowymi

n

)

x

-

x

n

i

(

S

i

2

1

2















k

i= i

n

i

n

)

x

-

x

k

i

(

S

i

1

2

1

2









k

i= i

n

i

n

)

x

-

x

k

i

(

S

i

1

2

1

2



Innym często stosowanym

Innym często stosowanym

miernikiem dyspersji jest

miernikiem dyspersji jest

odchylenie standardowe

odchylenie standardowe

.

.

Wyznacza się je jako pierwiastek

Wyznacza się je jako pierwiastek

kwadratowy z

kwadratowy z

wariancji

wariancji

, będącej

, będącej

średnią arytmetyczną kwadratów

średnią arytmetyczną kwadratów

odchyleń poszczególnych wartości

odchyleń poszczególnych wartości

zbiorowości statystycznej od ich

zbiorowości statystycznej od ich

średniej arytmetycznej.

średniej arytmetycznej.

 

 

Pozycyjną, bezwzględną miarą

Pozycyjną, bezwzględną miarą

dyspersji jest

dyspersji jest

odchylenie

odchylenie

ćwiartkowe

ćwiartkowe

Q

Q

będące połową różnicy między

będące połową różnicy między

kwartylem trzecim a kwartylem

kwartylem trzecim a kwartylem

pierwszym :

pierwszym :

.

.

2

1

3

Q

Q

Q





Odchylenie ćwiartkowe,

Odchylenie ćwiartkowe,

standardowe nie mogą

standardowe nie mogą

być one używane do

być one używane do

porównań dwu

porównań dwu

zbiorowości. Do tych

zbiorowości. Do tych

celów

celów

używa się

używa się

np.

np.

współczynniki zmienności

współczynniki zmienności

.

.

Współczynniki zmienności

Współczynniki zmienności

Definiuje się je jako stosunek

Definiuje się je jako stosunek

wartości miary dyspersji do

wartości miary dyspersji do

średniej.

średniej.

Współczynnik zmienności oparty

Współczynnik zmienności oparty

na odchyleniu standardowym

na odchyleniu standardowym

postaci:

postaci:

Współczynnik zmienności oblicza się

Współczynnik zmienności oblicza się

również dla odchylenia

również dla odchylenia

ćwiartkowego

ćwiartkowego

x

S

=

s

V

e

Q

M

Q

=

V

Ich wartość, wyrażona w procentach,

Ich wartość, wyrażona w procentach,

należy do przedziału 15 - 35 %.

należy do przedziału 15 - 35 %.

Jeżeli wartość współczynnika zmienności

Jeżeli wartość współczynnika zmienności

osiąga 60%, mówimy, że zmienność jest

osiąga 60%, mówimy, że zmienność jest

ogromna, co dowodzi, iż mamy do czynienia

ogromna, co dowodzi, iż mamy do czynienia

ze zbiorowością względnie niejednorodną z

ze zbiorowością względnie niejednorodną z

punktu

widzenia

badanej

cechy.

punktu

widzenia

badanej

cechy.

Miary asymetrii

Miary asymetrii



Wskaźnik asymetrii (zwany również

Wskaźnik asymetrii (zwany również

miernikiem skośności) dla szeregu

miernikiem skośności) dla szeregu

symetrycznego jest równy zero. W

symetrycznego jest równy zero. W

szeregach asymetrycznych miernik

szeregach asymetrycznych miernik

skośności może być większy lub

skośności może być większy lub

mniejszy od zera, mówimy wówczas o

mniejszy od zera, mówimy wówczas o

asymetrii prawostronnej (dodatniej)

asymetrii prawostronnej (dodatniej)

lub asymetrii lewostronnej (ujemnej).

lub asymetrii lewostronnej (ujemnej).

Współczynnik skośności

Współczynnik skośności

określa

określa

zarówno kierunek, jak i siłę

zarówno kierunek, jak i siłę

asymetrii i wyznacza się go:

asymetrii i wyznacza się go:

dla miar klasycznych

dla miar klasycznych

dla miar pozycyjnych

dla miar pozycyjnych

)

(

)

(

)

(

)

(

1

3

1

3

Q

Me

Me

Q

Q

Me

Me

Q

A

s















S

Do

x

W

s





Współczynniki skośności

Współczynniki skośności



są miarami niemianowanymi i

są miarami niemianowanymi i

unormowanymi, co umożliwia porównywanie

unormowanymi, co umożliwia porównywanie

asymetrii różnych rozkładów. Poza

asymetrii różnych rozkładów. Poza

przypadkami skrajnej asymetrii wartości

przypadkami skrajnej asymetrii wartości

współczynników asymetrii

współczynników asymetrii

W

W

s

s

,

,

A

A

s

s

wahają się

wahają się

w przedziale <-1, 1>, w przypadku szeregu

w przedziale <-1, 1>, w przypadku szeregu

symetrycznego przyjmują one wartość zero.

symetrycznego przyjmują one wartość zero.

 

 

Miary asymetrii

Miary asymetrii



Wskaźnik asymetrii (zwany również

Wskaźnik asymetrii (zwany również

miernikiem skośności) dla szeregu

miernikiem skośności) dla szeregu

symetrycznego jest równy zero. W

symetrycznego jest równy zero. W

szeregach asymetrycznych miernik

szeregach asymetrycznych miernik

skośności może być większy lub

skośności może być większy lub

mniejszy od zera, mówimy wówczas o

mniejszy od zera, mówimy wówczas o

asymetrii prawostronnej (dodatniej)

asymetrii prawostronnej (dodatniej)

lub asymetrii lewostronnej (ujemnej).

lub asymetrii lewostronnej (ujemnej).

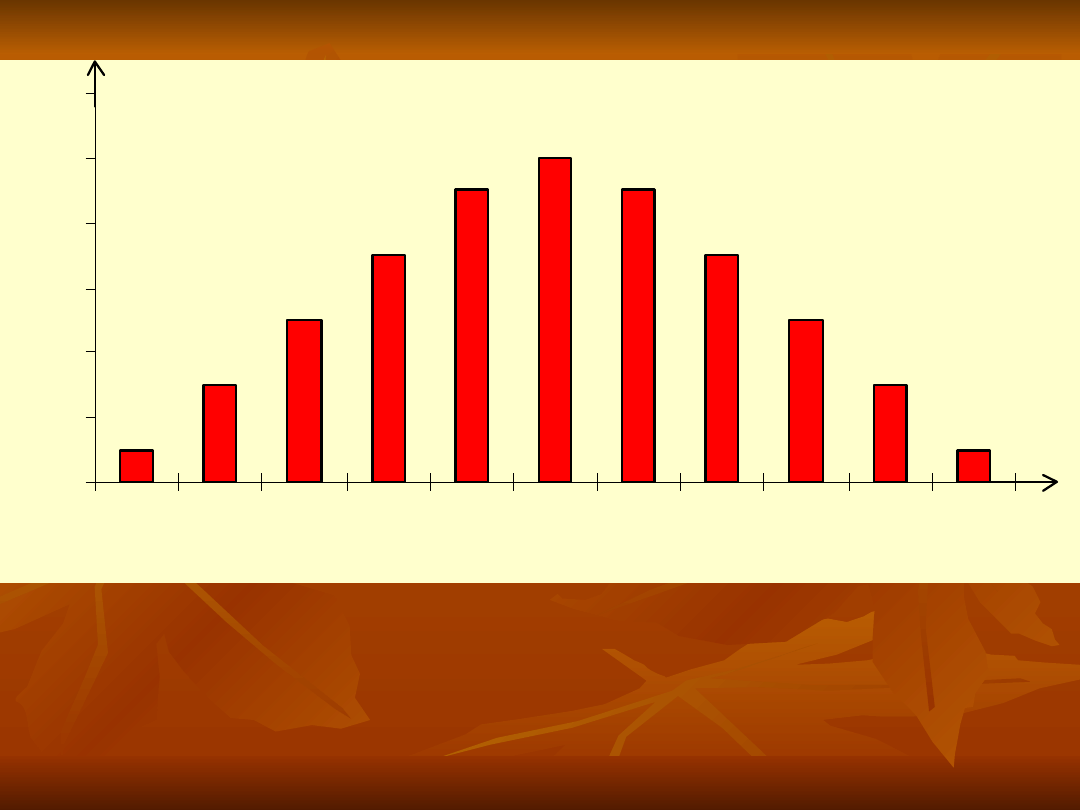
Przykład

Przykład

szeregu symetrycznego

szeregu symetrycznego

0

2

4

6

8

10

12

1

2

3

4

5

6

7

8

9

10

11

Wartość cechy X

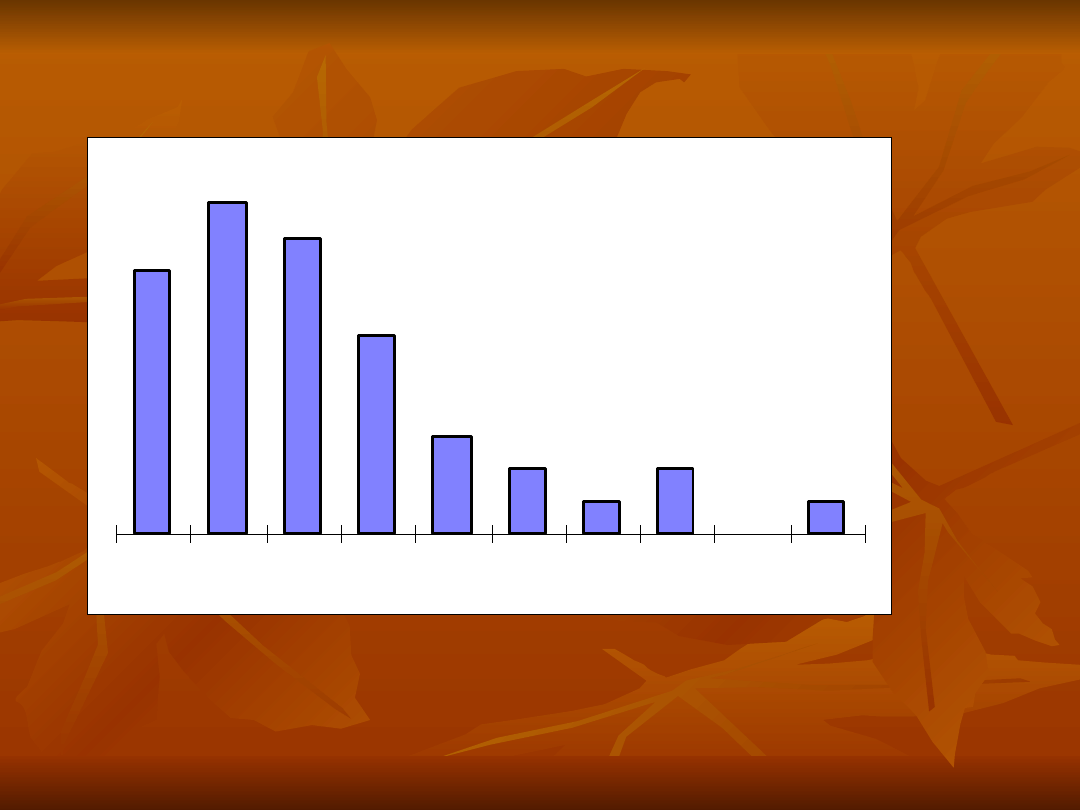
Szereg o asymetrii dodatniej (prawostronnej)

Szereg o asymetrii dodatniej (prawostronnej)

1

2

3

4

5

6

7

8

9

10

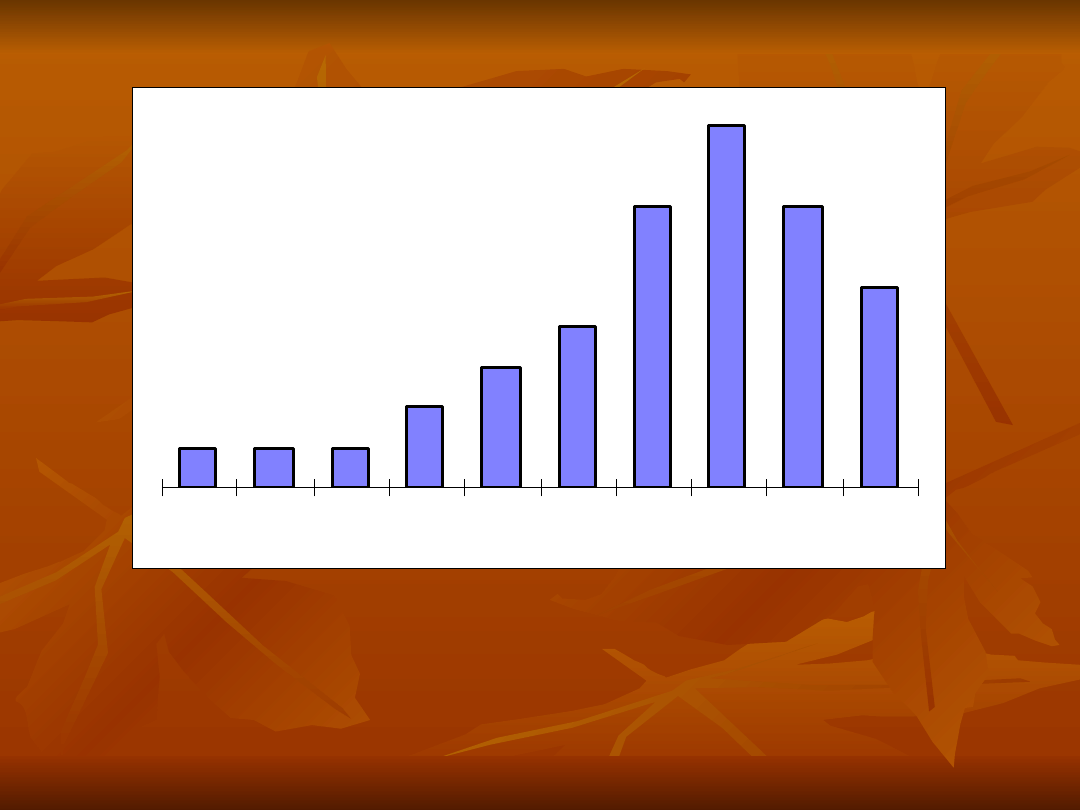
Szereg asymetryczny ujemnie (lewostronnie)

Szereg asymetryczny ujemnie (lewostronnie)

1

2

3

4

5

6

7

8

9

10

W szeregu symetrycznym

W szeregu symetrycznym

przy asymetrii lewostronnej

przy asymetrii lewostronnej

przy prawostronnej  

przy prawostronnej  

 

 

0

D

x

D

Me

x

o









0













s

M

Do

x

Do

Me

x

0













s

M

Do

x

Do

Me

x