Kiniuś™
Statystyka
Dr Elżbieta Grabowska
(notatki z wykładu 6)
24.05.2009
MIARY KONCNTRACJI
Miary koncentracji w podstawowym znaczeniu dotyczą stopnia skupienia wartości cechy
wokół średniej.
Wskaźnik:
![]()
m4 - 4 moment centralny
S4 - odchylenie standardowe do 4 potęgi
4 moment centralny dla danych indywidualnych:
( i ) ![]()
( p ) ![]()
( k ) ![]()
Im wyższa jest wartość K tym większa koncentracja wokół średniej, czyli krzywa jest
bardziej wysmukła.
Przyjmuje się, że jeżeli K=3 to zbiorowość ma rozkład normalny.
Dla ułatwienia interpretacji stosuje się, więc współczynnik koncentracji:
![]()
K' = 0 - rozkład jest normalny
K' > 0 - rozkład bardziej wysmukły
K' < 0 - rozkład bardziej spłaszczony
Wskaźniki :
Absolutne
Względne
Kiniuś™
BADANIE ZALEŻNOŚCI CECH ILOŚCIOWYCH
Współczynnik korelacji liniowej r - Persona
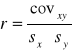
Sy - odchylenie standardowe cechy y
( i ) ![]()
( p ) ![]()
( k ) ![]()
Dla danych indywidualnych wygodniej jest korzystać ze wzoru:
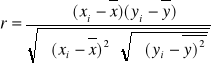
r przyjmuje wartości ściśle od ![]()
r informuje o kierunku i sile zależności cech.
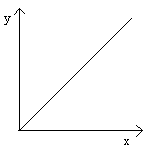
r = +1
zależność dodatnia
obie cechy zmieniają się w tą samą stronę,
jeśli jedna maleje to druga rośnie.
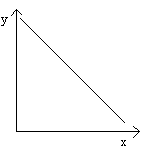
r = -1
zależność ujemna
jak jedna cecha rośnie to druga spada
np. Im szybciej jedzie tym krótszy czas przejazdu.
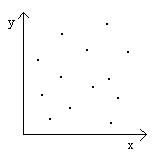
Kiniuś™
r=0
r nadaje się tylko do mierzenia zależności liniowych i w przybliżeniu liniowych.
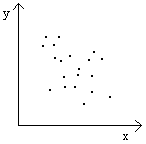
r = +0,8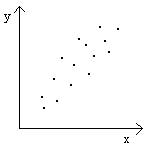
r = -0,4
Nie można stosować r do zależności typowo krzywoliniowych.
r zależy od liczebności próby.
INTERPRETACJA SIŁY ZALEŻNOŚCI
r |
siła zależności |
0 0,01 - 0,2 0,21 - 0,4 0,41 - 0,6 0,61 - 0,8 0,81 - 0,99 1 |
brak bardzo słaba słaba umiarkowana dość silna bardzo silna pełna |
np.
= -0,89 - zależność bardzo silna ujemna
!!! Przy porównywaniu siły zależności nie liczymy (-)
czyli np. :
- 0,89 > 0,19
Aby można było policzyć r musza być spełnione 3 warunki:
Obie cechy powinny być ilościowe (wyrażone na skali stosunkowej lub przedziałowej) ciągłe lub w przybliżeniu ciągłe.
Zależność musi być uzasadniona logicznie
Obie cechy musza być zależne linowo, bądź w przybliżeniu liniowo z całkowitym wykluczeniem zależności ewidentnie krzywoliniowej, dlatego każdorazowo przed przystąpieniem do liczenia r robi się najpierw wykres korelacyjny, z którego ustala się czy zależność w ogóle istnieje.
Kiniuś™
zad.
W 5 os. grupie zaliczających sprawdzian ustalono dla każdej osoby czas wykonania w minutach: 30, 18, 25, 12, 5 oraz liczbę popełnionych błędów: 1, 2, 6, 7, 9. Ustal siłę i kierunek zależności tych cech.
W praktyczny sposób (dla małych danych), aby ustalić czy cecha jest wystarczająco ciągła do liczenia r wyznaczamy rozstęp.
Warunek drugi, sprawdzamy czy zależność ma sens….
Sprawdzamy…
rozstęp |
|
N-2 |
30 - 5
9 - 1 |
> lub = jeżeli jest większe lub równe jest wystarczająco ciągłe |
5-2
5-2 |
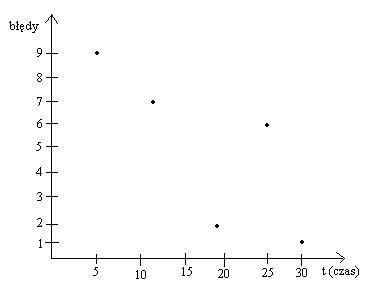
Na podstawie wykresu stwierdzamy, że:
- zależność istnieje
- jest ujemna
- jest w przybliżeniu liniowa
Liczenie r:
Lp. |
|
|
|
|
|
|
|
1 2 3 4 5 |
30 18 25 12 5 |
1 2 6 7 9 |
12 0 7 -6 -13 |
144 0 49 36 169 |
-4 -3 1 2 4 |
16 9 1 4 16 |
-48 0 7 -12 -52 |
N=5 |
90 |
25 |
0 |
398 |
0 |
46 |
-105 |
![]()
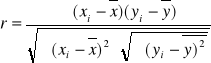
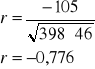
Wniosek:
W badanej grupie 5 osób, wystąpiła silna ujemna zależność między czasem napisania egzaminu a liczba popełnionych błędów. Zależność ta wskazuje, że im dłuższy czas pisania egzaminu tym mniej popełnionych błędów.
Kiniuś™
Obliczenie innym sposobem: 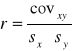
![]()
![]()
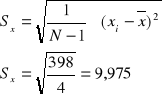

![]()
Możemy również wyznaczyć współczynnik determinacji ![]()
Informuje on nas, w jakim stopniu zmienna zależna (skutek) zależy od zmiennej niezależnej (przyczyny).
![]()
Ostatecznie popełniona liczba błędów 60,2 % zależała od czasu wykonania zadania i w 39,8% od wszystkich zmiennych towarzyszących.
Jeżeli mamy stwierdzona zależność cech to zwykle przeprowadza się analizę regresji w celu wyjaśnienia mechanizmu stwierdzonej zależności.
Analiza regresji pozwala także na prognozę (predykcję) jednej przyszłej wartości cechy, gdy znamy wartość drugiej, zazwyczaj wyznacza się dwa równania regresji.
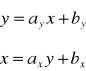
Chociaż bywa, że tylko jedno z nich ma sens logiczny.
Z reguły wyznacza się ![]()
Parametry regresji można wyznaczyć pośrednio z następujących wzorów:
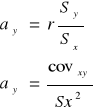
![]()
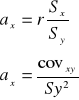
![]()
![]()
![]()
Kiniuś™
Parametr
ay - o ile jednostek wzrośnie (lub spadnie, gdy -a) wartość zmiennej zależnej y, gdy x wzrośnie o 1 jednostkę.
by - jaka jest wartość y niezależna od wpływów x, czyli ile wynosiłaby wartość y gdyby x=0.
Zad.
Badamy zależność między wysokością pensji (x) w tysiącach i miesięcznych wydatków na kosmetyki (y) w zł.
![]()
gdy wysokość pensji wzrośnie o 1 tys. To miesięczny wydatek na kosmetyki wzrośnie przeciętnie o 50 zł.
Wydatek niezależny od wysokości pensji wynosi 20 zł.
Zad.
Badamy zależność między długością wyprodukowanej serii produktów w sztukach (x) a kosztem jednostkowym wyprodukowania 1 sztuki w zł. (y)
![]()
Koszt wyprodukowania 1 sztuki spada przeciętnie p 0,5 zł, gdy długość serii wzrasta o 1, koszt niezależny od długości serii wynosi 1500 zł.
Na podstawie podstawowego równania regresji można dokonać prognozy:
![]()
ile przeciętnie będzie wydane na kosmetyki przy wysokości pensji 3 tys.?
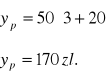
xp=3
6
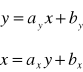
Wyszukiwarka
Podobne podstrony:
analityka Ocena stanu zdrowia w stadzie krów mlecznych cz I i II wersja 24 05 2009
Statystyka opisowa VI wykład 16.05.2009, Statystyka opisowa 16
24 elektrostatyka 07 05 2009 r
Podobno złapali szefa irackiej al Kaidy (24 04 2009)
07 05 2009
Irak będzie respektować kalendarz wojsk USA (04 05 2009)
inormatyzacja przedsiebiorstw(na 6.05.2009), Studia, IP- projekt
wprowadzenie 24-05-09, Wprowadzenie do psychologii
teorie socjalizacji -material uzupelniajacy z zajec 16.05.2009, socjologia, soc małych gr i rodziny
MPLP 268 24.11.2009, lp
Zarządzanie Jakością10 05 2009
24 05 2010 B&K, Bazy Danych 10 11 12
21 05 2009 GIEŁDA MED RAT
Księga 1. Proces, ART 479(9) KPC, III CZP 127/08 - z dnia 24 lutego 2009 r
Psychologia 31.05.2009
wyklad od p kasza, 04.05.2009
histologia 25.05.2009, kosmetologia licencjat
więcej podobnych podstron