Metoda podziału i

ograniczeń

Janusz Papliński

Przykład wprowadzający

Znaleźć największą ilość różnych dodatnich liczb całkowitych, tak by ich suma była
równa 7

Opis matematyczny:

7

*

7

1







i

i

i

a

max

7

1







i

i

a

gdzie









0

1

i

a

Ograniczenie dolne





















max

max

7

1

i

i

a

n

Ograniczenie górne

Dla warunku

7

*

7

1







i

i

i

a

Dokonujemy relaksacji (osłabienia)

7

*

7

1







i

i

i

a

dla którego





















max

min

7

1

i

i

a

n

0

1

0

a

1

3

7

4

3

2

0

1















n

a

4

7

4

3

2

1

1

1

















n

a

3



n

4



n

0

1

0

a

1

3



n

4



n

a

2

1

0

3

7

4

3

1

0

,

1

2

1

















n

a

a

3



n

4

7

4

3

2

1

1

,

1

2

1



















n

a

a

4



n

0

1

0

a

1

3



n

4



n

a

2

1

0

3



n

4



n

1

0

a

3

4

7

4

3

2

1

1

,

1

,

1

3

2

1





















n

a

a

a

4



n

n

n

a

a

a





















3

7

4

2

1

0

,

1

,

1

3

2

1

n

n



3

0

1

0

a

1

3



n

4



n

a

2

1

0

3



n

4



n

1

0

a

3

4



n

n

n



3

Metoda podziału i ograniczeń

•Generuje trajektorię fragmentami

•Stosuje procedury powrotu

•Niektóre procedury są odrzucane, jeśli nie prowadzą do rozwiązania optymalnego

•Wyznacza się ograniczenie górne i dolne

Idea metody:

Dzielenie generowanych trajektorii na pozostawiane i odrzucane, oraz
posługiwanie się ograniczeniami do oceny perspektywiczności

29.10.09

29.10.09

Metoda podziału i ograniczeń

Generowanie stanów

Generowanie stanów obejmuje

Reguły podziału
Reguły wyboru
Procedury generowania stanów

Stan aktywny – stan pozwalający wygenerować stan następny

Stany aktywne umieszczone są na liście stanów aktywnych

Stan z którego generuje się stany jest usuwany z listy stanów aktywnych

Na listę wpisuje się każdy wygenerowany stan aktywny

Metoda podziału i ograniczeń

Reguły wyboru – określają stan wybrany z listy stanów aktywnych do
generowania dalszych stanów.

FIFO – first in, first out

Bardzo dużo stanów generowanych

LIFO – last in, first out

Poszukiwania w głąb.

LLB – least lower bound

Daje nadzieje na szybkie znalezienie rozwiązania bliskiego

optymalnemu

Metoda podziału i ograniczeń

Eliminowanie stanów

Cel – pomijanie w obliczeniach trajektorii nie prowadzącej do rozwiązania

optymalnego

Reguła wyczerpywania

Pozwala sprawdzić, czy ze stanu P



,



nie da się uzyskać żadnego rozwiązania

dopuszczalnego

Gdzie  - nr stanu;

 - stopień rozbicia

Należy wykazać, że w stanie P



,



jest operacja



n

która przekracza przyjęte

ograniczenia

Metoda podziału i ograniczeń

Reguły sondowania

Dla każdego stanu P



,



nie wyeliminowanego regułami wyczerpywania

oblicza się dolne V

d



,



i górne

V

g



,



ograniczenie funkcji celu

.

Ograniczenia górne V

g



,



(dla szukania minimum) – pewne dopuszczalne

rozwiązanie uzyskane ze stanu P



,



, np. za pomocą heurystyki

Ograniczenie dolne V

d



,



(dla szukania minimum) – wyznacza się przez relaksację

(osłabienie) ograniczeń obszaru dopuszczalnego

Ze stanu P



,



nie można uzyskać lepszego rozwiązania niż

V

g



,



jeżeli spełniony jest

warunek

Metoda podziału i ograniczeń

(1)









,

,

g

d

V

V



W obliczeniach zapamiętuje się najlepszy w danej chwili stan końcowy P

*

o

wartości V

*

.

Ze stanu P



,



nie można uzyskać lepszego rozwiązania niż P

*

jeżeli

(2)



,

*

d

V

V 

1. Jeżeli jest spełniony warunek (2), to stan P



,



eliminujemy z dalszych obliczeń

2. Jeżeli jest spełniony warunek (1), a nie jest (2), to stan otrzymany ze stanu jest

w danej chwili najlepszym stanem końcowym

3. Jeżeli warunki (1) i (2) nie są spełnione, to stanu nie da się wyeliminować za

pomocą reguł sondowania.

Reguły dominacji
Wygenerowany stan porównuje się ze stanami aktywnymi. Stany zdominowane
eliminuje się z listy stanów aktywnych

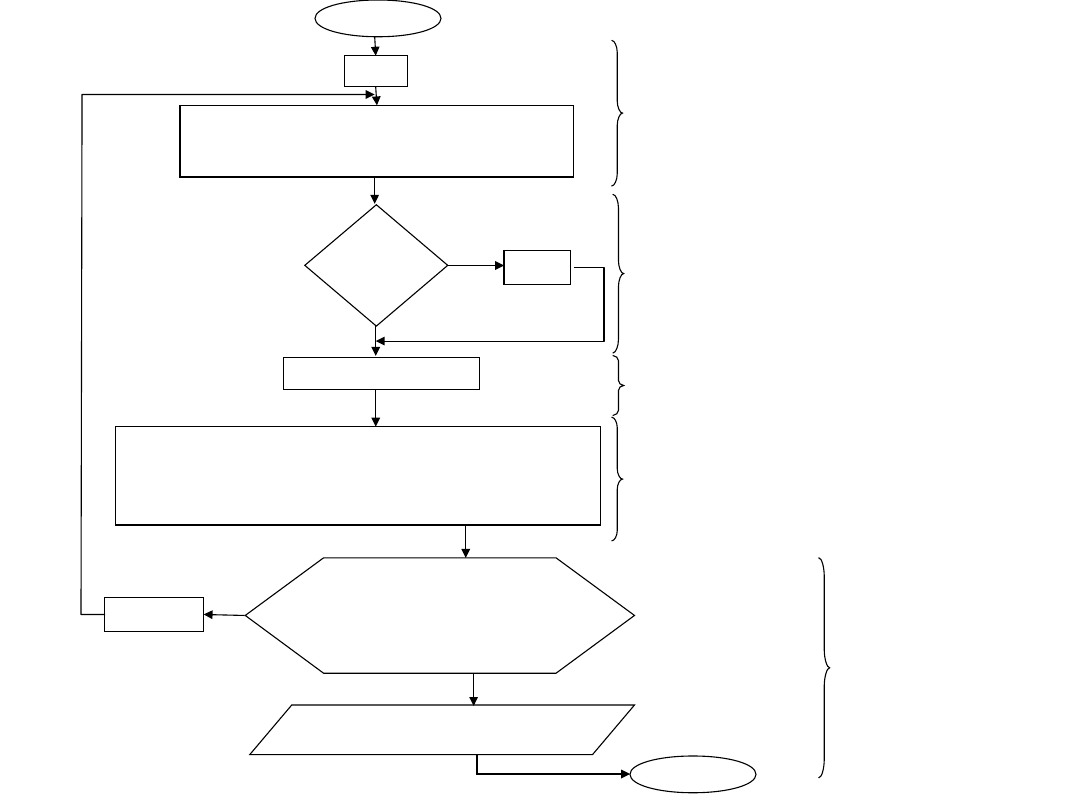
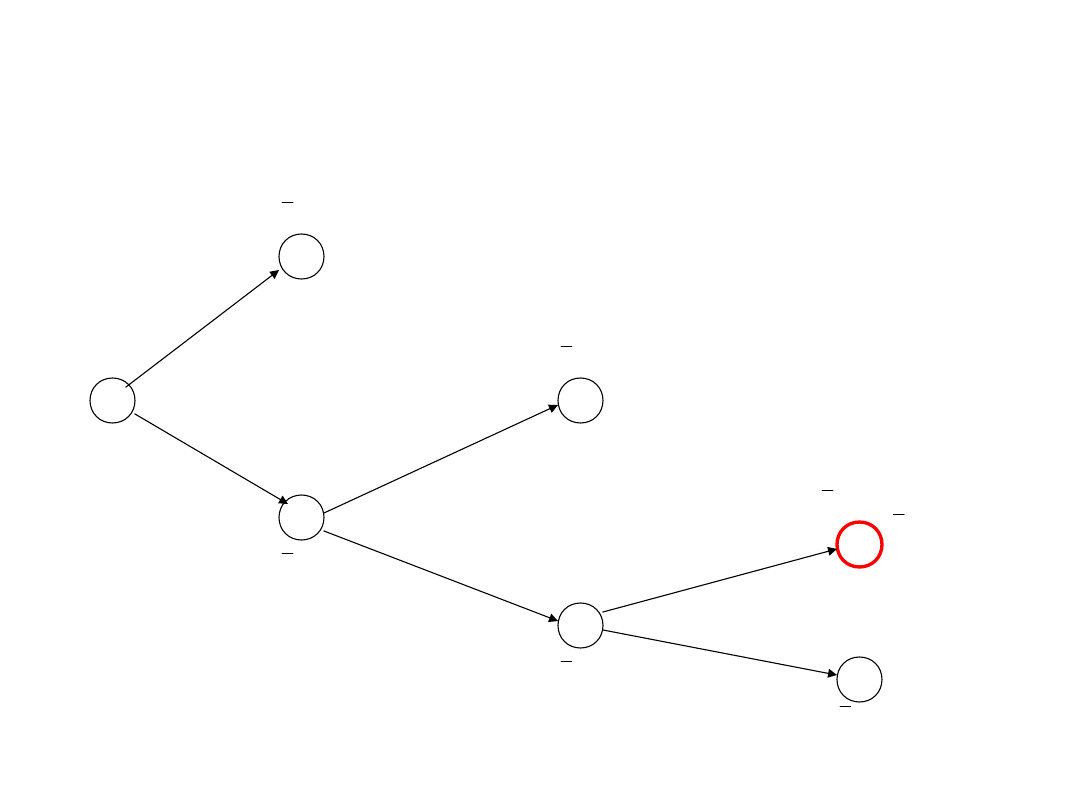
r=1

Dokonaj rozbicia zbioru wszystkich

rozwiązań na n podzbiorów (stanów), w

których na pierwszym miejscu znajduje

się jeden z n wyrobów.

START

If n – r =
1

r =

n

LB(N

r

) = ...

Wybierz stan o minimalnej wartości dolnego

ograniczenia LB.

Dla kilku wierzchołków o tej samej wartości LB,

wybierz ten który ma największy stopień rozbicia

r.

If r = n

i wartość dolnego ograniczenia
rozważanego stanu jest nie
mniejsza od LB innych stanów
aktywnych

Znaleziono rozwiązanie

optymalne

STOP

r = r +

1

N

T

N

T

KROK 1

KROK 2

KROK 3

KROK 4

KROK 5

Przykład
Algorytm metody podziału i ograniczeń dla zagadnienia harmonogramowania w
systemie przepływowym

Wartość dolnego ograniczenia dla zbioru N

r

utworzonego z r zadań wybranych

spośród n zadań w sekwencji (J

(1)

, J

(2)

, ..., J

(r)

)

 













k

N

E

k

N

F

N

LB

r

r

m

k

r

,

,

max

,

1







gdzie

m – ilość maszyn

J

(r )

J

(r-1)

J

(r )

M

k-1

M

k

F(N

r-1

,k)

F(N

r

,k-

1)

F(N

r

,k)

J

(r )

J

(r-1)

J

(r )

M

k-1

M

k

F(N

r

,k-

1)

F(N

r-1

,k)

F(N

r

,k)





 

 





 

k

r

k

r

k

r

r

t

F

F

k

N

F

,

1

,

,

1

,

max

,









czas ukończenia zadania J

(r )

z sekwencji (J

(1)

, J

(2)

, ..., J

(r)

), wykonanego na k-tej

maszynie

5.11.09

5.11.09

 













k

N

E

k

N

F

N

LB

r

r

m

k

r

,

,

max

,

1







ocena czasu wykonania pozostałych R

r

zadań na k-tej maszynie, oraz czasy

wykonania pozostałych zadań na maszynach M

k+1

, M

k+2

, ..., M

n





















m

k

R

R

k

r

t

t

k

N

E

r

r

1

min

,











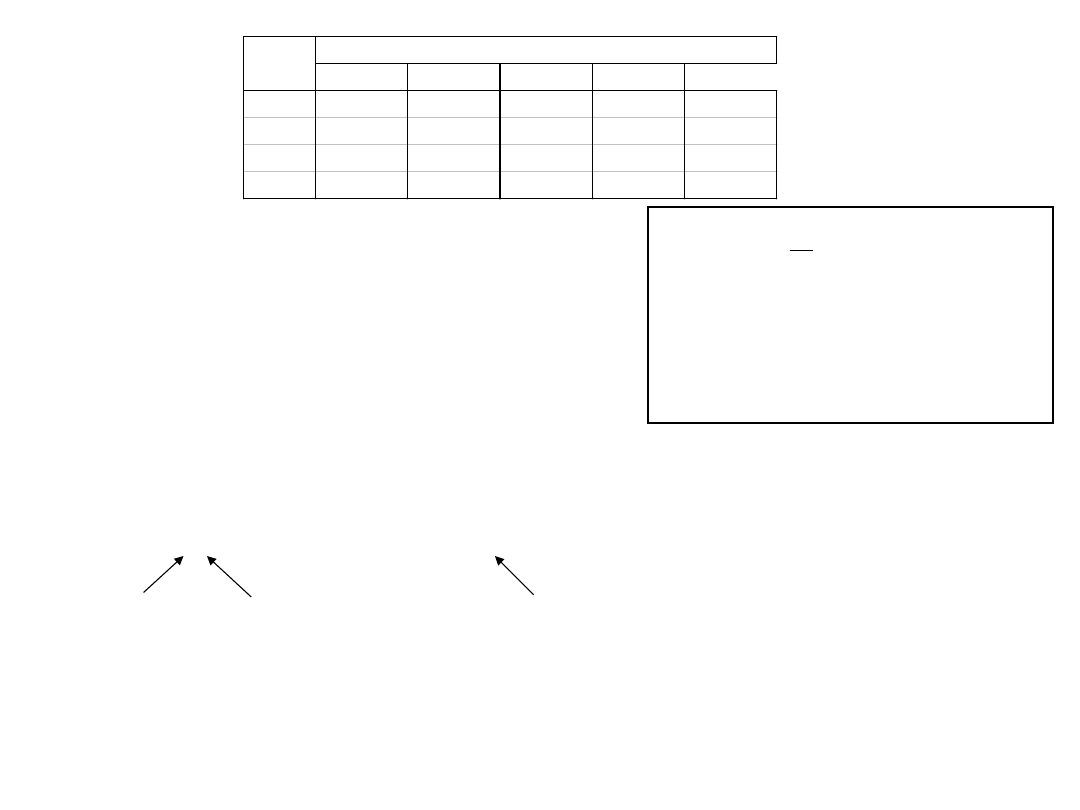
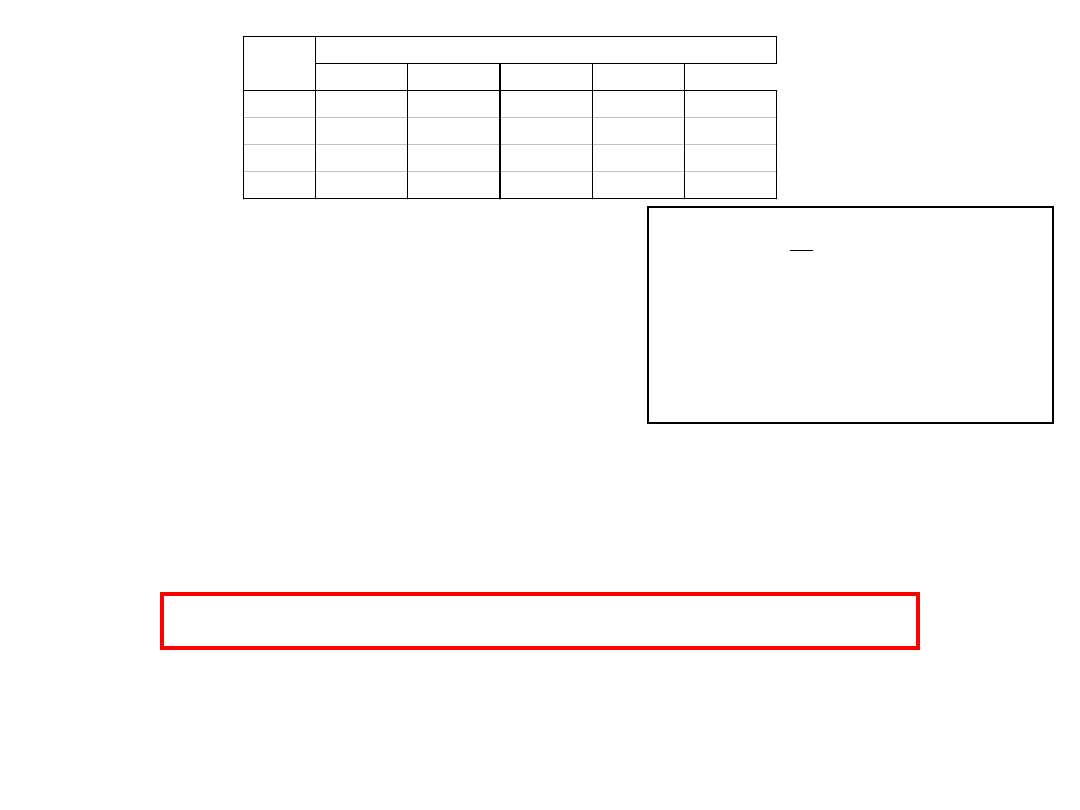
Maszyna M1

Maszyna M2

Maszyna M3

Maszyna M4

Maszyna M5

1

5

8

20

5

13

2

2

5

3

20

4

3

30

4

5

3

21

4

6

30

6

14

8

Zadanie

jednostkowe czasy wykonania operacji

KROK 1
r = 1
Stany aktywne: {J

1

}, {J

2

},{J

3

},{J

4

},

Dla stanu {J

2

}:

J

(1)

= J

2

R

r

= {1, 3, 4}

Wyznaczamy LB(N

1

={J

2

)):

Czasy zakończenia 1-wszego zadania na poszczególnych maszynach

F(N

1

,1) = t

(1)1

= t

21

= 2 F(N

1

,2) = F(N

1

,1) + t

(1)2

= t

21

+ t

22

= 2 +5 = 7

1-wsze
wykonywane
zadanie

Na 1-wszej
maszynie

2 – ga
maszyna

F(N

1

,3) = 10;

F(N

1

,4) = 30;

F(N

1

,5) = 34

 













k

N

E

k

N

F

N

LB

r

r

m

k

r

,

,

max

,

1











 

 





 

k

r

k

r

k

r

r

t

F

F

k

N

F

,

1

,

,

1

,

max

,





























m

k

R

R

k

r

t

t

k

N

E

r

r

1

min

,











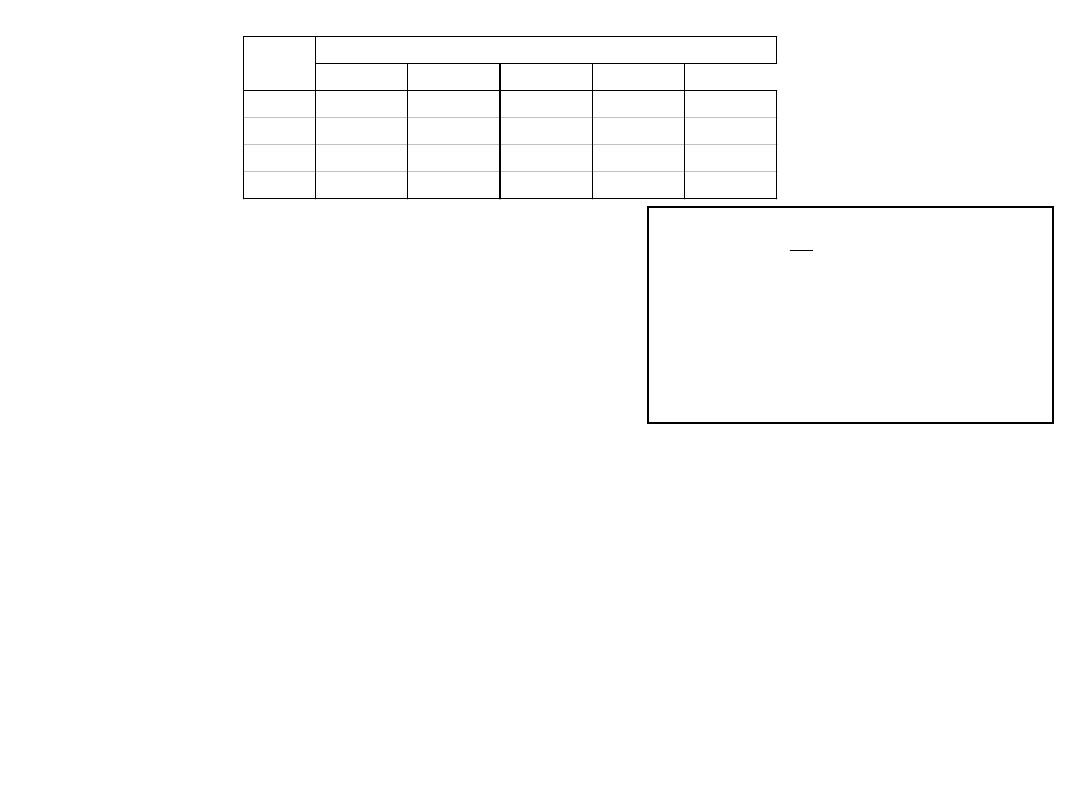
Maszyna M1

Maszyna M2

Maszyna M3

Maszyna M4

Maszyna M5

1

5

8

20

5

13

2

2

5

3

20

4

3

30

4

5

3

21

4

6

30

6

14

8

Zadanie

jednostkowe czasy wykonania operacji

F(N

1

,1) = 2

F(N

1

,2) = 7

F(N

1

,3) = 10;

F(N

1

,4) = 30;

F(N

1

,5) = 34

 













k

N

E

k

N

F

N

LB

r

r

m

k

r

,

,

max

,

1











 

 





 

k

r

k

r

k

r

r

t

F

F

k

N

F

,

1

,

,

1

,

max

,





























m

k

R

R

k

r

t

t

k

N

E

r

r

1

min

,



























74

58

,

33

,

46

min

41

,

,

min

min

1

,

45

44

43

42

35

34

33

32

15

14

13

12

41

31

11

5

2

1

1



















































t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

N

E

n

R

R

r

r





















70

,

,

min

min

2

,

45

44

43

35

34

33

15

14

13

42

32

2

,

1

5

3

2

1







































t

t

t

t

t

t

t

t

t

t

t

t

t

t

N

E

r

r

R

R











E(N

1

,3)=48; E(N

1

,4)=29;

E(N

1

,5)=42

J

(1)

= J

2

R

r

= {1, 3, 4}

Maszyna M1

Maszyna M2

Maszyna M3

Maszyna M4

Maszyna M5

1

5

8

20

5

13

2

2

5

3

20

4

3

30

4

5

3

21

4

6

30

6

14

8

Zadanie

jednostkowe czasy wykonania operacji

F(N

1

,1) = 2

F(N

1

,2) = 7

F(N

1

,3) = 10;

F(N

1

,4) = 30;

F(N

1

,5) = 34

 













k

N

E

k

N

F

N

LB

r

r

m

k

r

,

,

max

,

1











 

 





 

k

r

k

r

k

r

r

t

F

F

k

N

F

,

1

,

,

1

,

max

,





























m

k

R

R

k

r

t

t

k

N

E

r

r

1

min

,















74

1

,

1



N

E





70

2

,

1



N

E

E(N

1

,3)=48;

E(N

1

,4)=29;

E(N

1

,5)=42

 









77

42

34

,

29

30

,

48

10

,

70

7

,

74

2

max

2

1















 J

N

LB

 





 





 





104

,

104

,

83

4

1

3

1

1

1













J

N

LB

J

N

LB

J

N

LB

Maszyna M1

Maszyna M2

Maszyna M3

Maszyna M4

Maszyna M5

1

5

8

20

5

13

2

2

5

3

20

4

3

30

4

5

3

21

4

6

30

6

14

8

Zadanie

jednostkowe czasy wykonania operacji

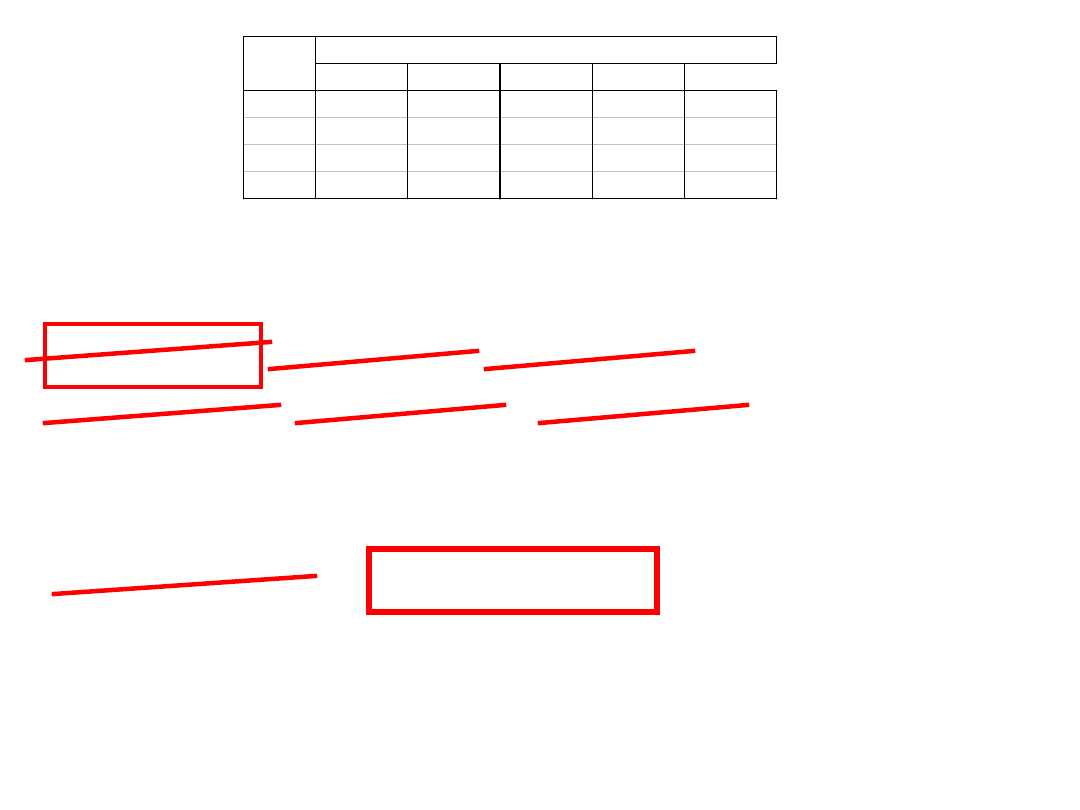
KROK 2

r = 3

n – r = 4 – 3 =1 stąd

r = n = 4

Stany aktywne: {J

2

,J

1

J

3

J

4

}, {J

2

,J

1

J

4

J

3

},

 





 





 





104

,

104

,

83

4

1

3

1

1

1













J

N

LB

J

N

LB

J

N

LB

KROK 3

r = 2
Nowe stany aktywne: {J

2

,J

1

}, {J

2

J

3

}, {J

2

J

4

},

















94

,

101

3

4

1

2

4

4

3

1

2

4









J

J

J

J

N

LB

J

J

J

J

N

LB

























95

,

102

,

81

4

2

2

3

2

2

1

2

2













J

J

N

LB

J

J

N

LB

J

J

N

LB

KROK 4

















100

,

101

4

3

2

1

2

4

3

2

1

4









J

J

J

J

N

LB

J

J

J

J

N

LB

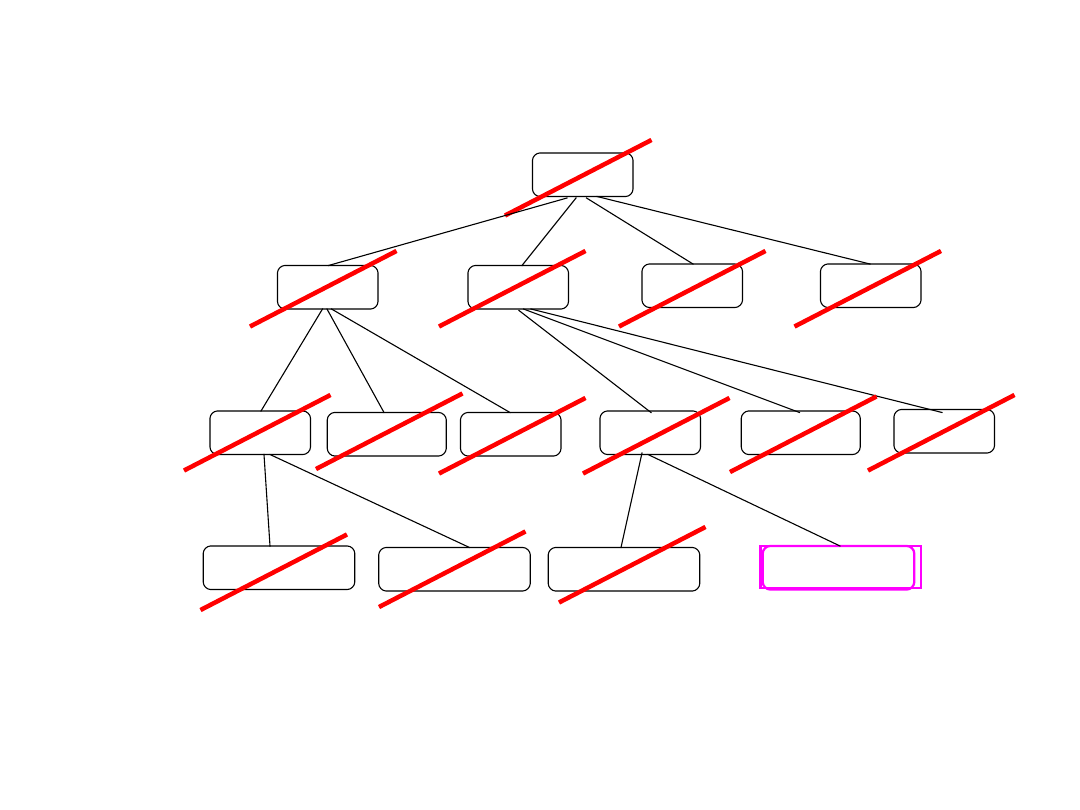
J

1

(83)

J

2

(77)

J

3

(104)

J

4

(102)

J

2

J

1

(95)

J

2

J

1

(102)

J

2

J

1

(81)

J

2

J

1

J

3

J

4

(101)

J

2

J

1

J

4

J

3

(94)

J

1

J

4

(96)

J

1

J

3

(101)

J

1

J

2

(90)

J

1

J

2

J

3

J

4

(101)

J

1

J

2

J

4

J

3

(100)