MANIPULATOR ROBOTA

W ASPEKCIE

KINEMATYKI CIAŁA

SZTYWNEGO

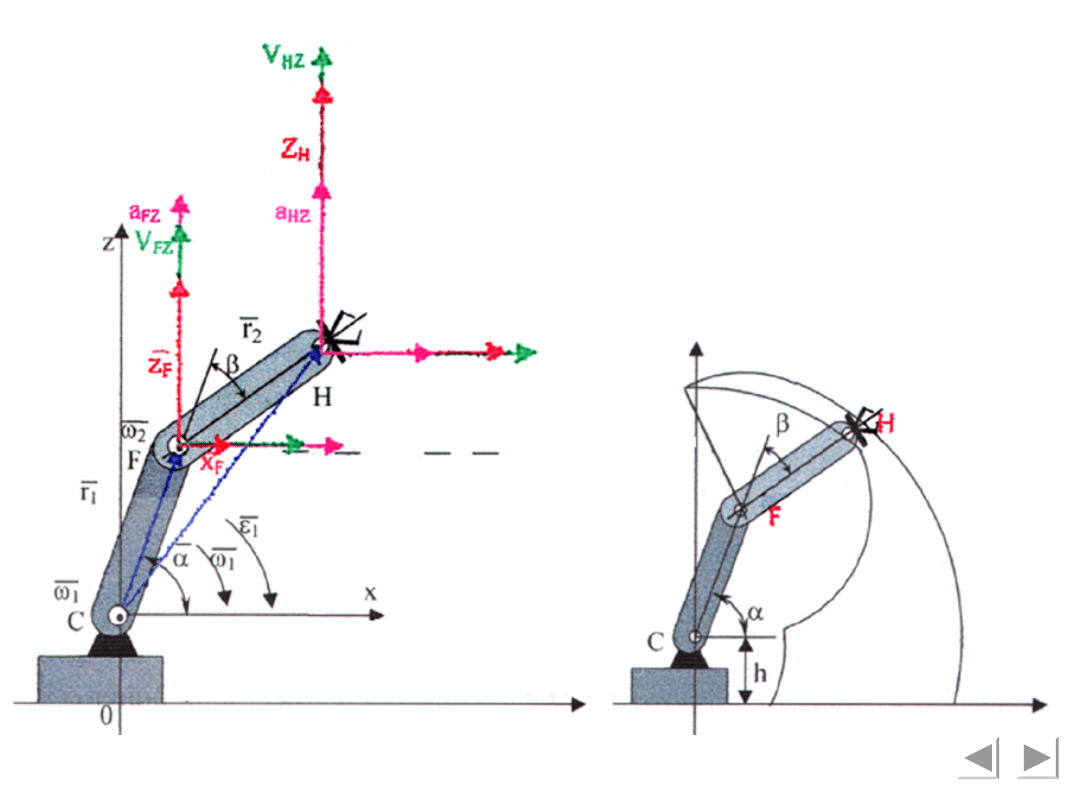
Wyznaczenia: toru, prędkości i

przyspieszenia punktu H, metodą

wyznaczania kolejnych różniczek

równania ruchu.

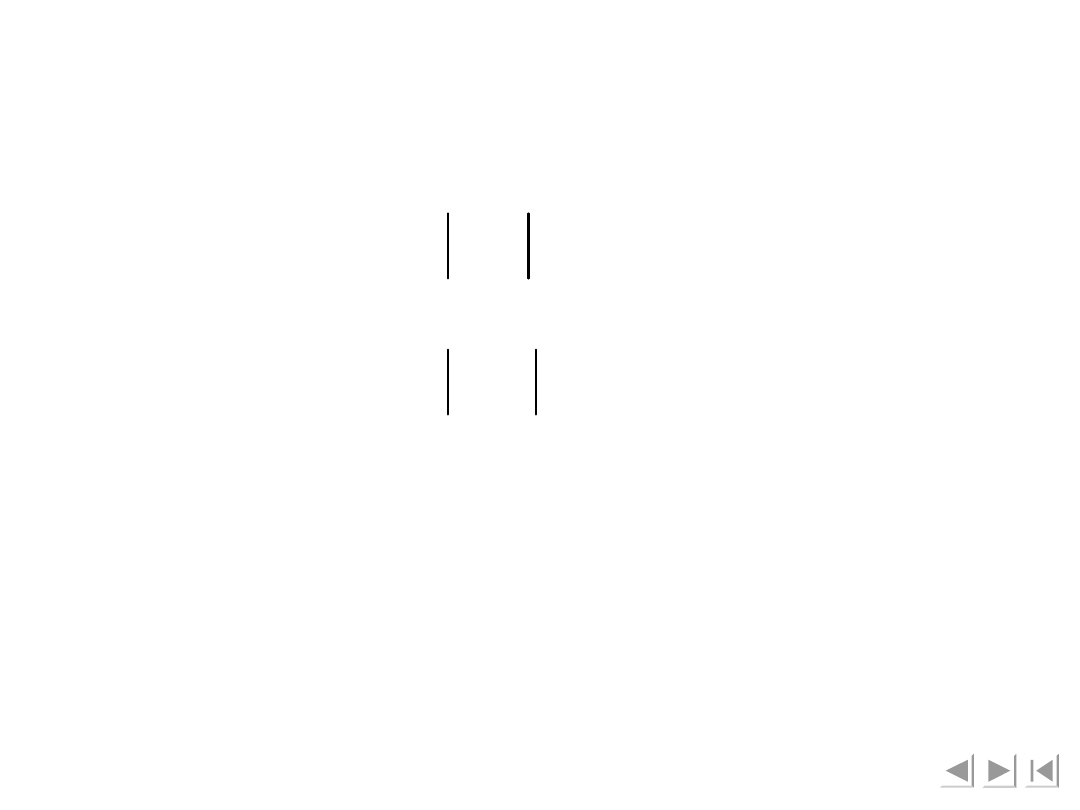
Przyjmując

jednoczesny

ruch

dwóch

ogniw

wyznaczymy

ich

tory

ruchu,

prędkości

i

przyspieszenia.

Niech

1

r

CF 

a

2

r

FH 

Składowe wektora położenia punktu F:

x

F

= r

1

cosα

z

F

= h + r

1

sinα

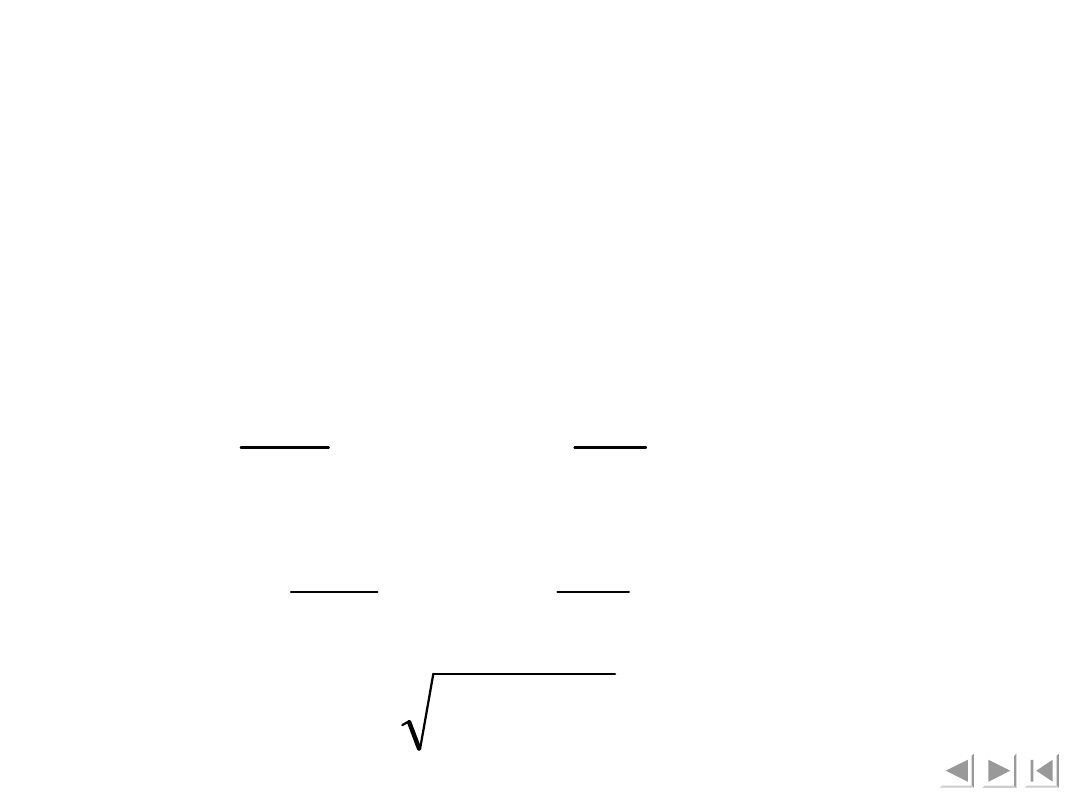
wyłączając z tego kąt

α

otrzymujemy





2

2

2

r

h

z

x

F

F







Jak widać torem punktu F jest okrąg o środku w
punkcie C(0,h) i promieniu r

1

. Prędkość punktu F

poprzez

różniczkowanie

składowych

wektora

położenia punktu F:







sin

d

d

sin

d

d

1

1

ω

r

t

r

t

x

V

F

x



















cos

d

d

cos

d

d

1

r

t

t

z

V

F

z







1

1

2

2



r

V

V

V

z

x

F







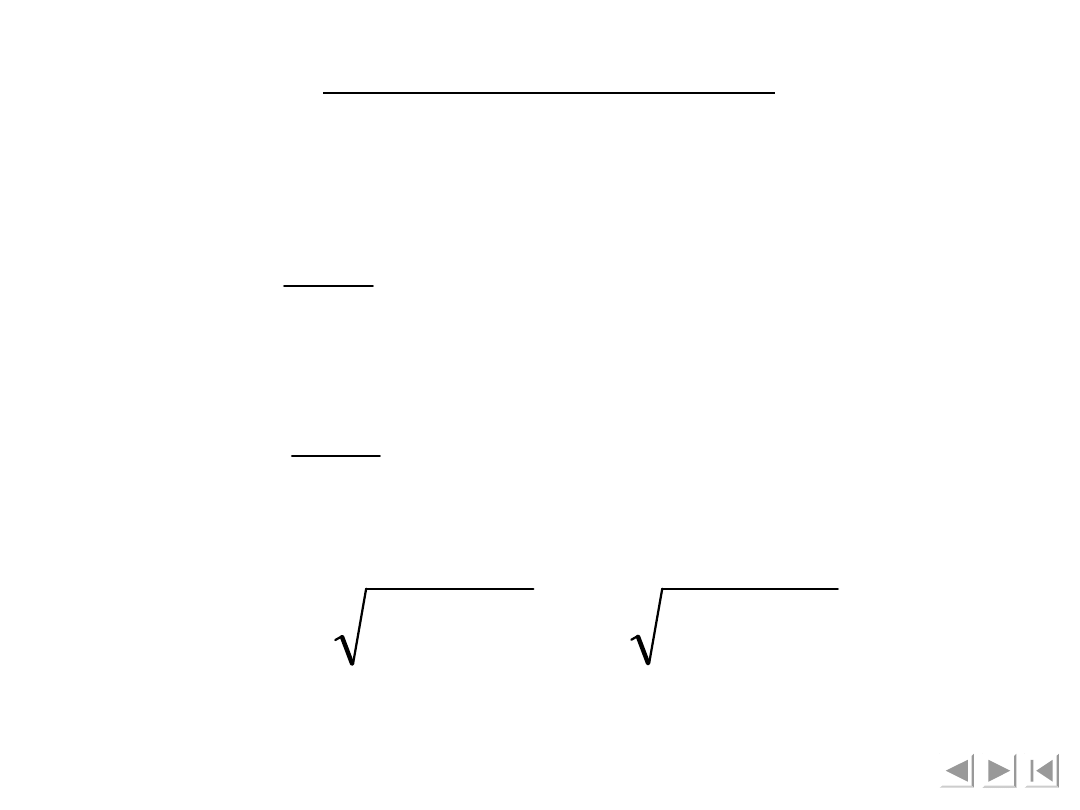
Przyśpieszenie punktu F:

- układ kartezjański









cos

sin

d

d

2

1

1

1

1

r

r

t

V

a

x

x

















sin

cos

d

d

2

1

1

1

1

r

r

t

V

a

z

z







4

1

2

1

1

2

2













r

a

a

a

z

x

F

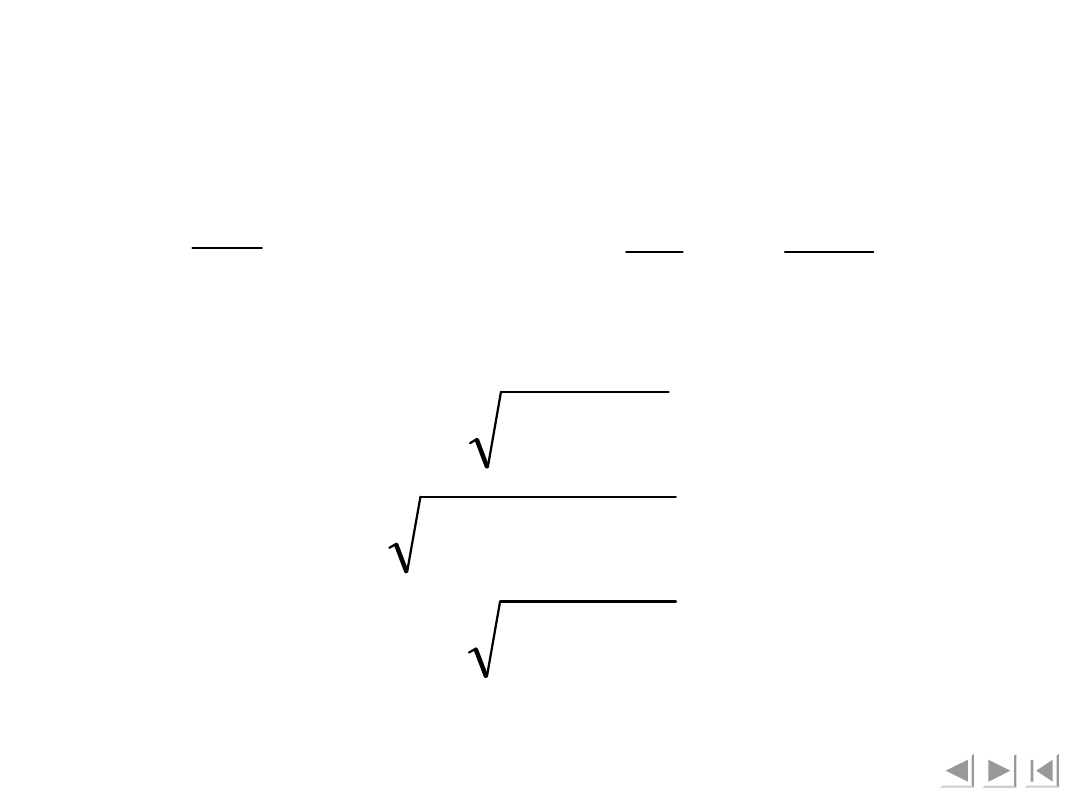
- układ naturalny (wg stycznej i normalnej)

1

1

1

1

d

d

d

d





r

t

r

t

v

a

t







2

1

1

1

2



r

r

V

a

n









4

1

2

1

1

4

1

2

1

2

1

2

2

























r

r

a

a

a

n

t

F

Równanie ruchu punktu H:

Równania toru punktu H

















cos

cos

2

1

r

r

x

H



















sin

sin

2

1

r

r

h

z

H

Przy ustalonej wartości kąta β torem punktu H jest
okrąg o równaniu:







 



2

2

2

2

2

1

2

2

sin

cos

CH

r

r

r

h

z

x

H

H





















- ruch członu 2

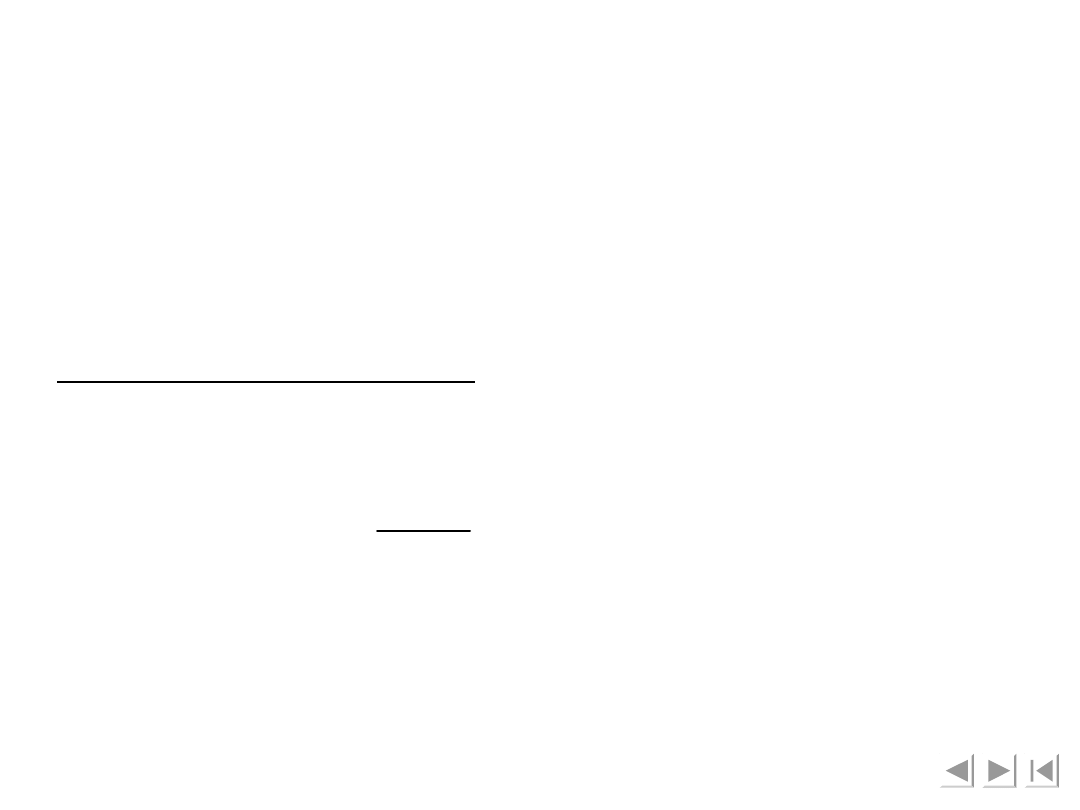
Natomiast przy ustalonej wartości kąta α torem
punktu H jest okrąg o równaniu:



 



2

2

2

1

2

1

sin

cos

r

r

h

x

r

x

H

H















(ruch członu 1)

Prędkość punktu H otrzymamy różniczkując
równania ruchu punktu H względem czasu



 





























sin

sin

d

d

2

1

2

1

1

r

r

t

x

V

H

x



 

























cos

cos

d

d

2

1

2

1

1

r

r

t

z

V

H

z









2

2

1

2

2

2

1

1

2

1

2

1

2

1

2

2

2

cos

2

ω

ω

r

β

ω

ω

ω

r

r

ω

r

V

V

V

z

x

H

















Podobnie różniczkując równania ruchu punktu H
względem czasu otrzymamy jego przyspieszenie:







 

 

























































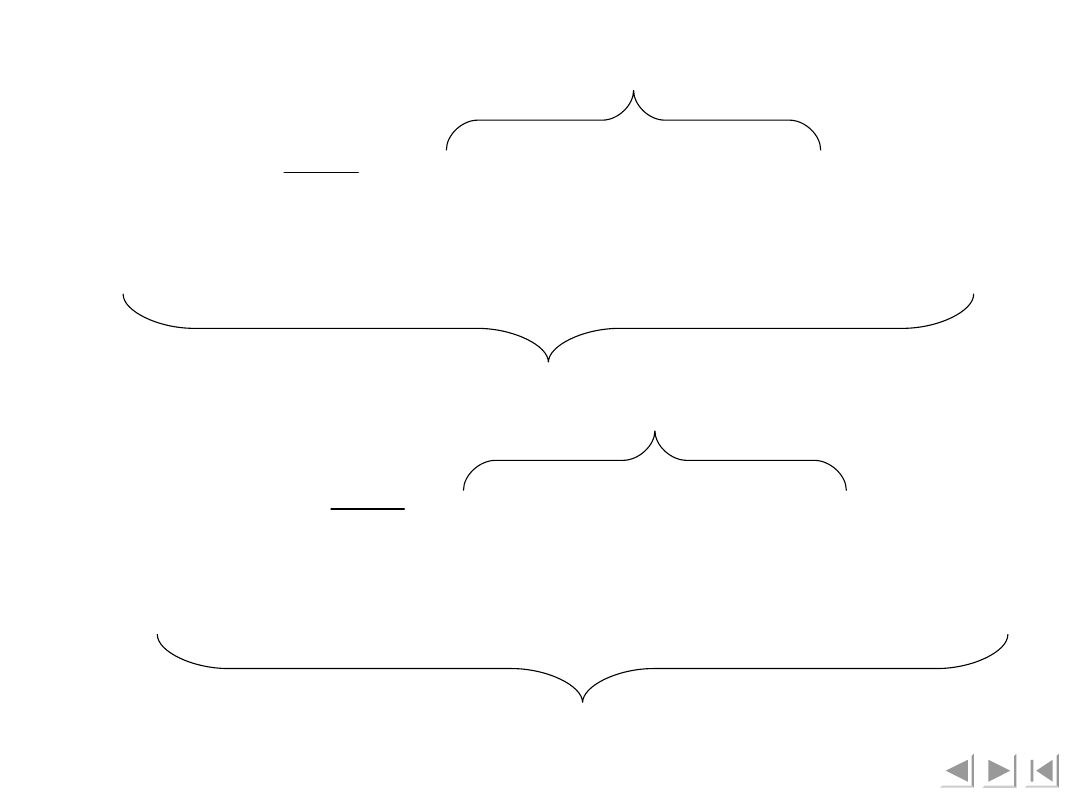
cos

sin

cos

sin

d

d

2

2

1

2

1

2

2

1

1

1

r

r

t

V

a

x

x

a

b







 

 























































sin

cos

sin

cos

d

d

2

2

1

2

1

2

2

1

1

1

r

r

t

V

a

z

z

c

d













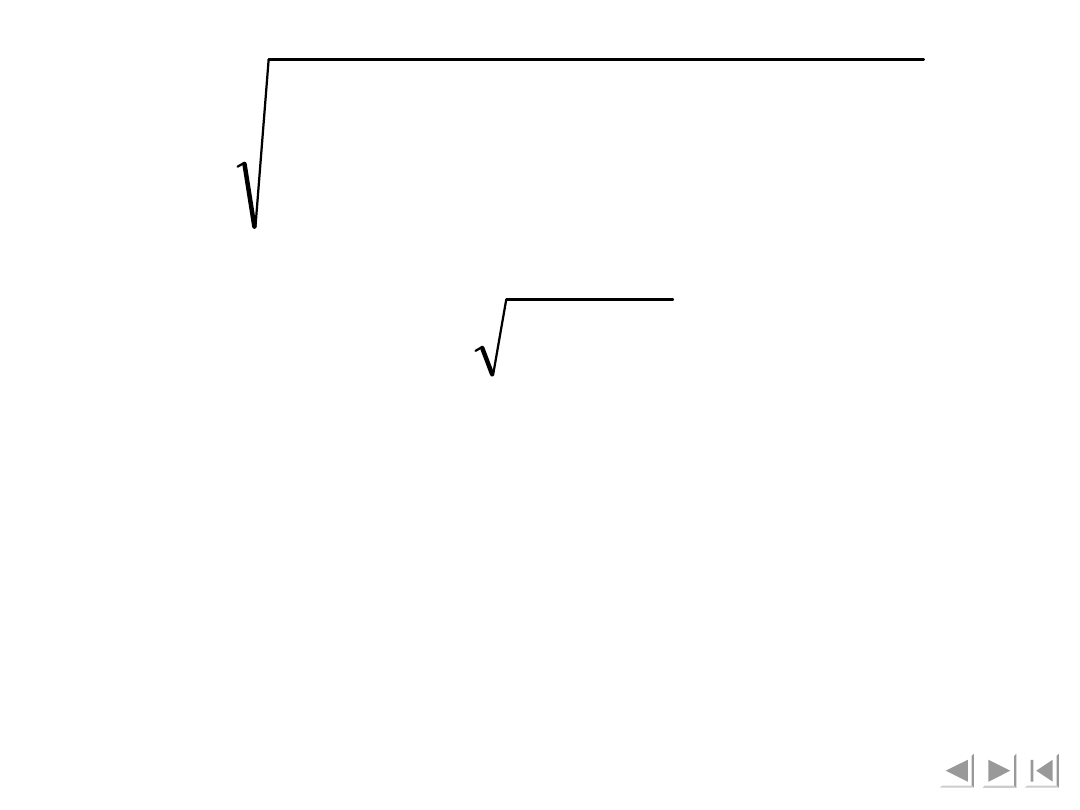
4

2

1

2

2

1

2

2

4

1

2

1

2

1

2

2

2





































r

cd

ab

r

a

H

2

2

z

x

H

a

a

a





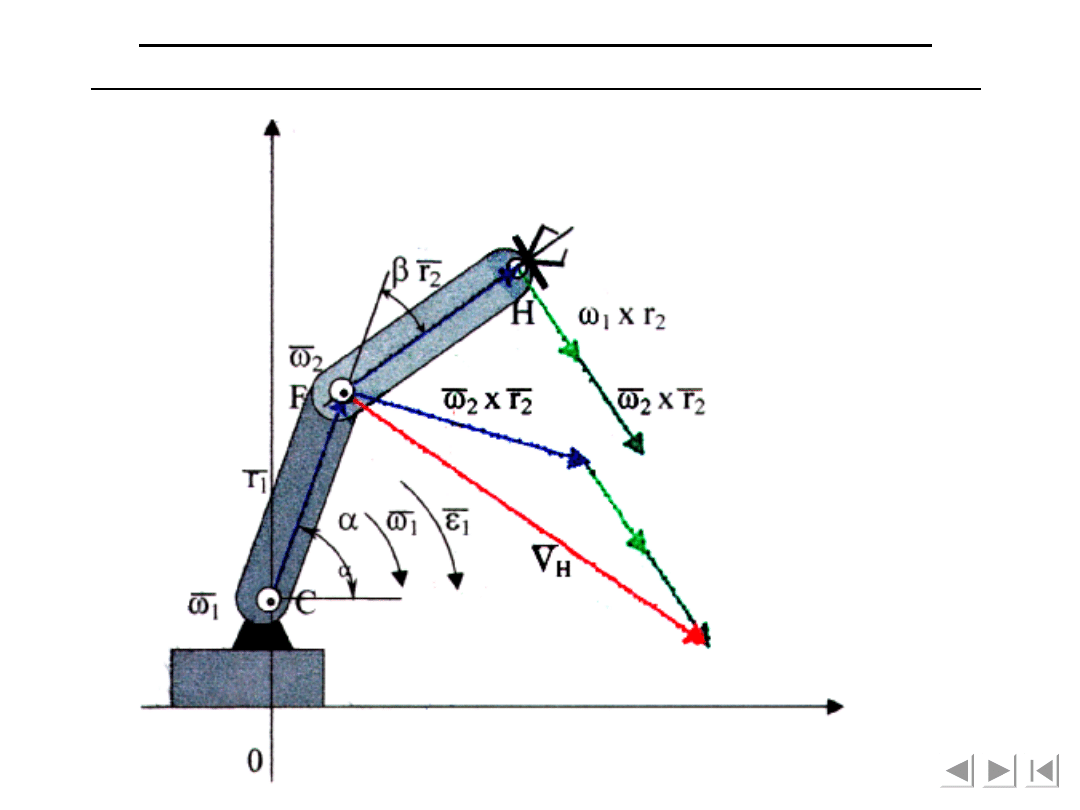
Rozwiązanie klasyczne do wyznaczania

prędkości i przyspieszeń punktu H

jako ruch złożony

Przyjmując

jednoczesny

ruch

dwóch

ogniw

wyznaczamy

ich

prędkości

i

przyspieszenia

rozkładając ruch punktu H na ruch unoszenia i
względny:

1

1

r

V

F







2

1

1

1

2

1

r

r

r

V

V

F

U





















3

2

r

V

W















2

2

1

2

2

2

1

1

2

1

2

1

2

1

2

cos

2





























r

r

r

r

V

H

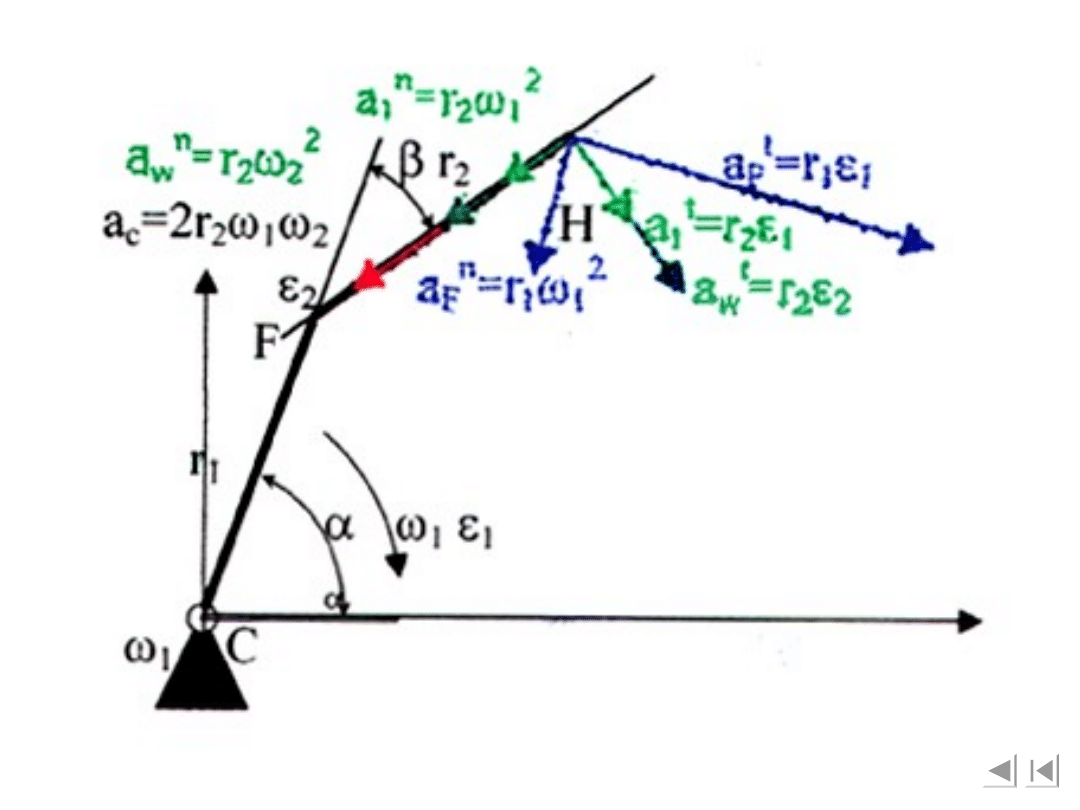
Przyspieszenia punktu H wyznaczymy rozpatrując
ruch złożony punktu H oraz ruch płaski ramienia:





W

W

F

H

V

a

r

r

a

a























1

2

1

1

2

1

2









gdzie:

n

F

t

F

F

a

a

a





1

1



r

a

t

F



2

1

1



r

a

n

F



n

W

t

W

W

a

a

a





2

2



r

a

t

W



2

2

2



r

a

n

W



2

2

1

1

2

2

r

V

a

W

C

















W

H

V

ω

ω

r

ε

r

r

ω

ω

r

ε

ω

r

ε

r

a



























1

2

2

2

2

2

2

1

1

2

1

2

1

1

1

1

2

Przyspieszenie punktu H względem punktu F
można wyznaczyć też z zależności:

t

HF

n

HF

n

F

t

F

HF

F

H

a

a

a

a

a

a

a













1

1



r

a

t

F



2

1

1



r

a

n

F







2

1

2









r

a

t

HF





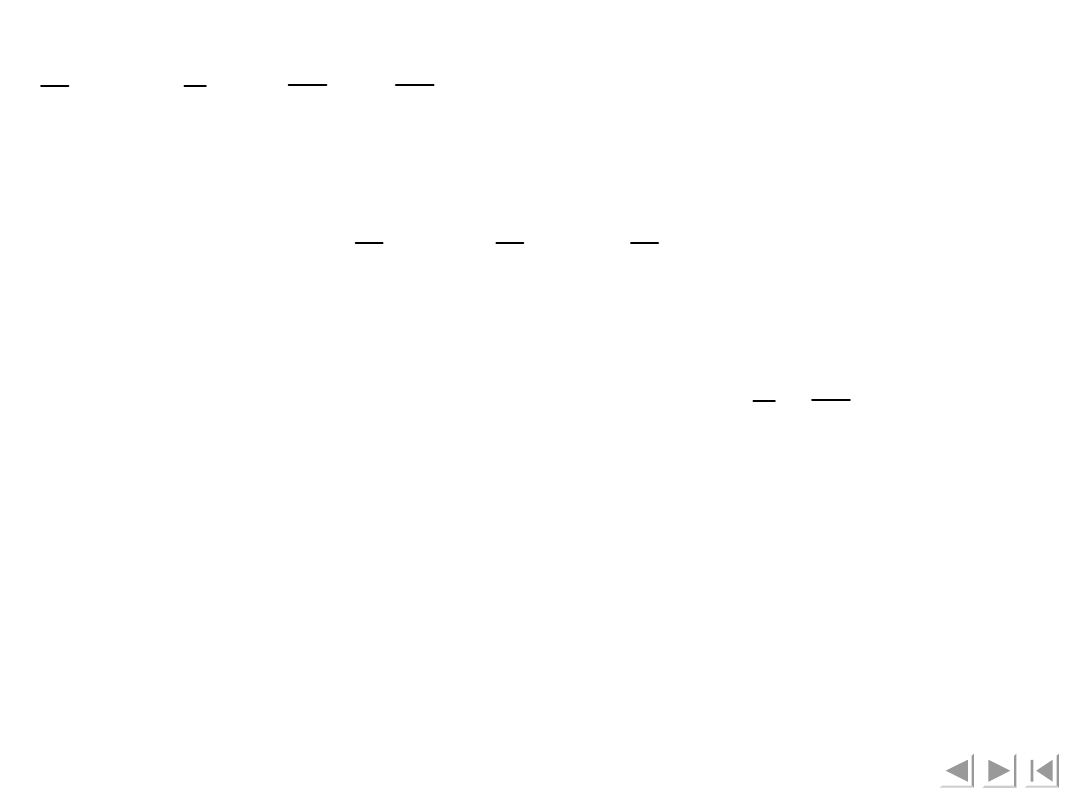
2

1

2

2

2

2

2

1

2

2

2

1

2

2













r

r

r

r

a

n

HF













t

HF

n

HF

HF

a

a

a













2

2

1

2

2

1

2

2

1

1

1

1

























r

r

r

r

a

H

Moduł przyspieszenia a

H

obliczymy, rzutując

wszystkie jego składowe na prostą F

H

i prostopadła

do niej:













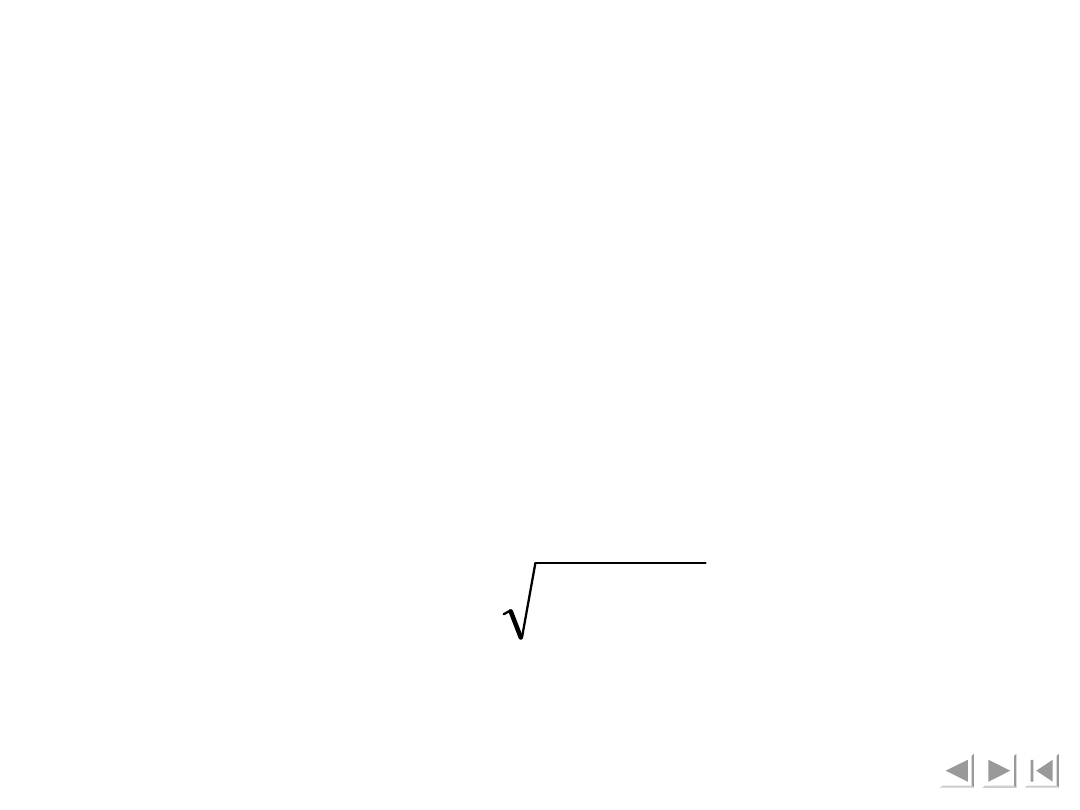
sin

cos

2

1

1

1

1

2

2

1

2

2

r

r

r

r

a









2

2

2

1

a

a

a

H





















cos

sin

2

2

1

1

1

1

2

1

2

2

2

2

2

1

2

1

r

r

r

r

r

a











