04 Kinematyka.doc
39
KINEMATYKA
CIAŁA SZTYWNEGO
KINEMATYKA
: opis ruchu ciał bez wnikania w związki mię-
dzy ruchem a
jego przyczyną (opis geometryczny).
RUCH CIAŁA: zjawisko zmiany położenia ciała w czasie
względem innego ciała, umownie przyjętego za nieruchome
RUCH JEST POJĘCIEM WZGLĘDNYM
UKŁAD ODNIESIENIA
Z I E M I A
MECHANIKA KLASYCZNA: ruch ciała odbywa się z prędko-
ściami bardzo małymi w porównaniu z prędkością światła
PRZESTRZEŃ EUKLIDESOWA
CZAS: pojęcie pierwotne
CZAS JEST NIEZALEŻNY OD MATERII I PRZESTRZENI.
CZAS JEST NIEODRACALNY.
JEDNOSTKI MIARY W KINEMATYCE: metr, sekunda
04 Kinematyka.doc
40
KINEMATYKA PUNKTU
OPIS RUCHU PUNKTU W FUNKCJI CZASU
1.
Współrzędne prostokątne (kartezjańskie).
2.
Wektor wodzący.
3. Naturalny
– współrzędna łukowa wzdłuż toru.
4. Inny
– współrzędne biegunowe, walcowe, sferyczne.
PODSTAWOWE POJĘCIA
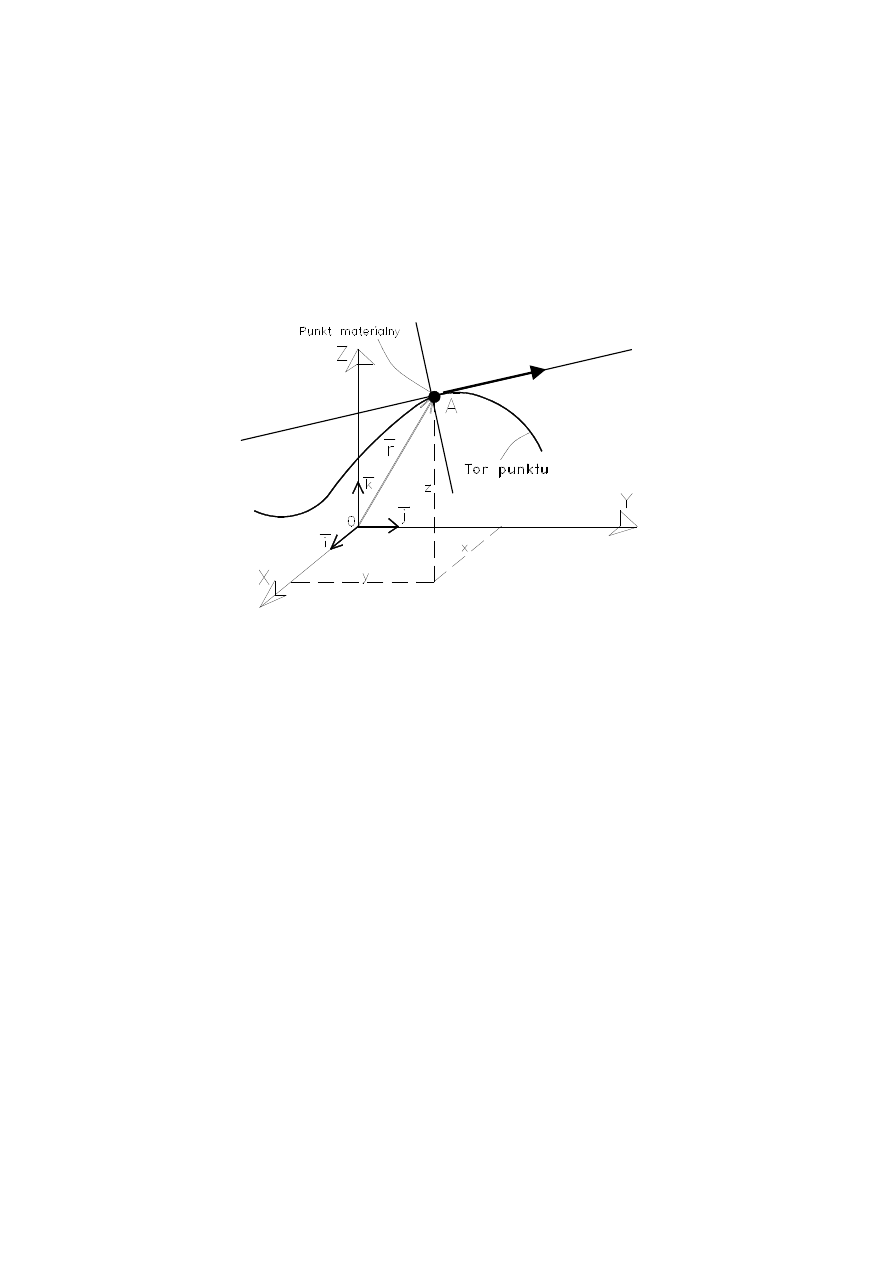
– TOR PUNKTU (trajektoria): linia ciągła, będąca miejscem
geometrycznym kolejnych położeń ruchomego punktu w
przestrzeni.
– RÓWNANIA RUCHU PUNKTU: x = x(t) y = y(t) z = z(t).
– promień (wektor) wodzący: r = r(t), r = x(t) i + y(t) j + z(t) k
r
x
= x(t)
r
y
= y(t)
r
z
= z(t).
– RÓWNANIE TORU PUNKTU: równanie krzywej otrzymanej z
równań ruchu po wyeliminowaniu czasu t.
–
CHWILOWOŚĆ RUCHU: badanie parametrów ruchu (po-
łożenie, droga, prędkość, przyspieszenie w określonej chwili
czasu t).
Styczna do toru
Normalna do toru
Wektor prędkości
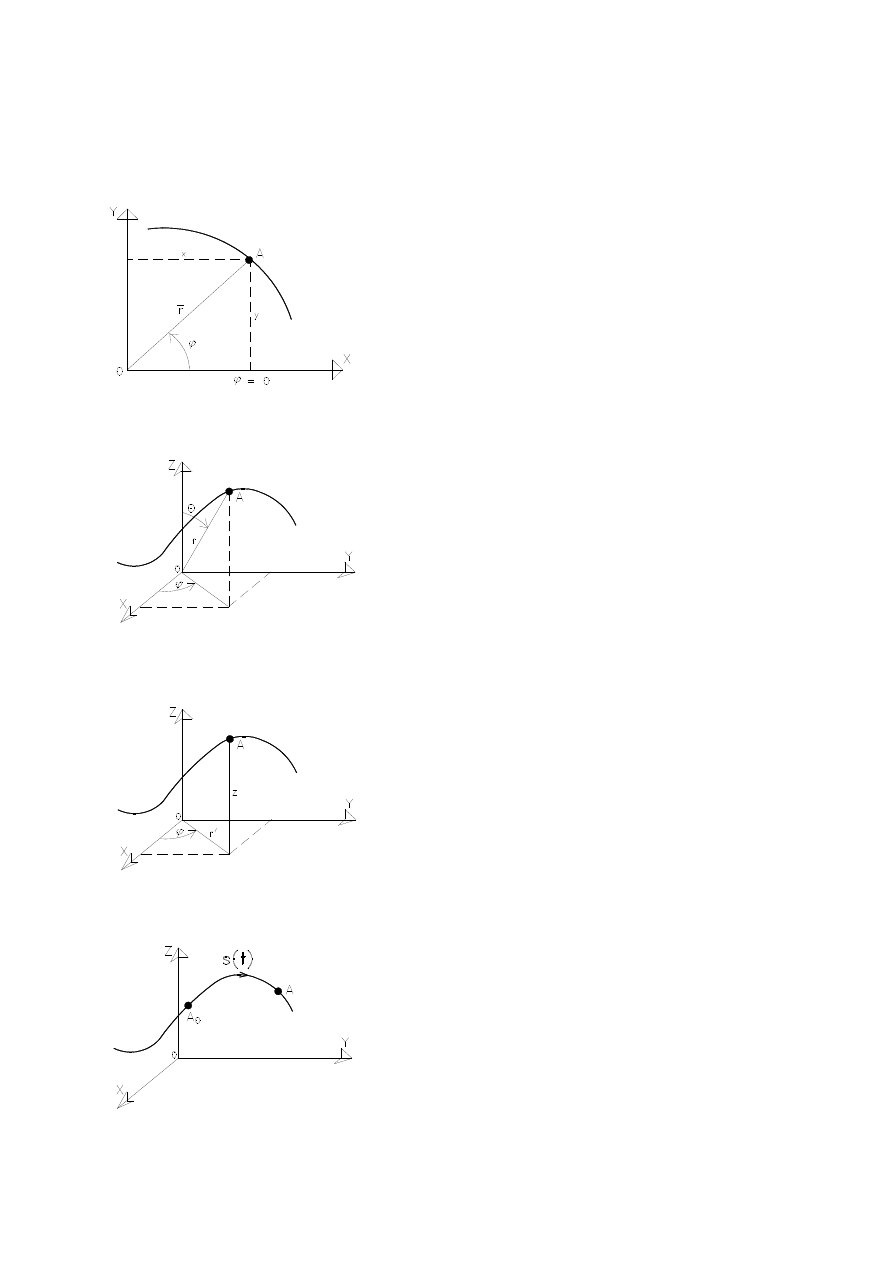
04 Kinematyka.doc
41
MOŻLIWOŚCI OPISU RUCHU PUNKTU W PŁASZCZYŹNIE
Współrzędne biegunowe na płaszczyźnie
r = f
1
(t)
= f
2
(t)
x = r cos
y = r sin
Współrzędne biegunowe w przestrzeni
r = f
1
(t)
= f
2
(t)
= f
3
(t)
x = r sin
cos
y = r sin
cos
z =r cos
Współrzędne walcowe
r' = f
1
(t)
= f
2
(t)
z = f
3
(t)
x = r' cos
y = r' sin
z
z
Równanie ruchu punktu na torze
s = f(t)
A
0
t = 0, s = 0
s(t)
– droga
04 Kinematyka.doc
42
Z równanie ruchu w prostokątnym układzie współrzędnych obli-
cza się współrzędne wektora prędkości i przyspieszenia.
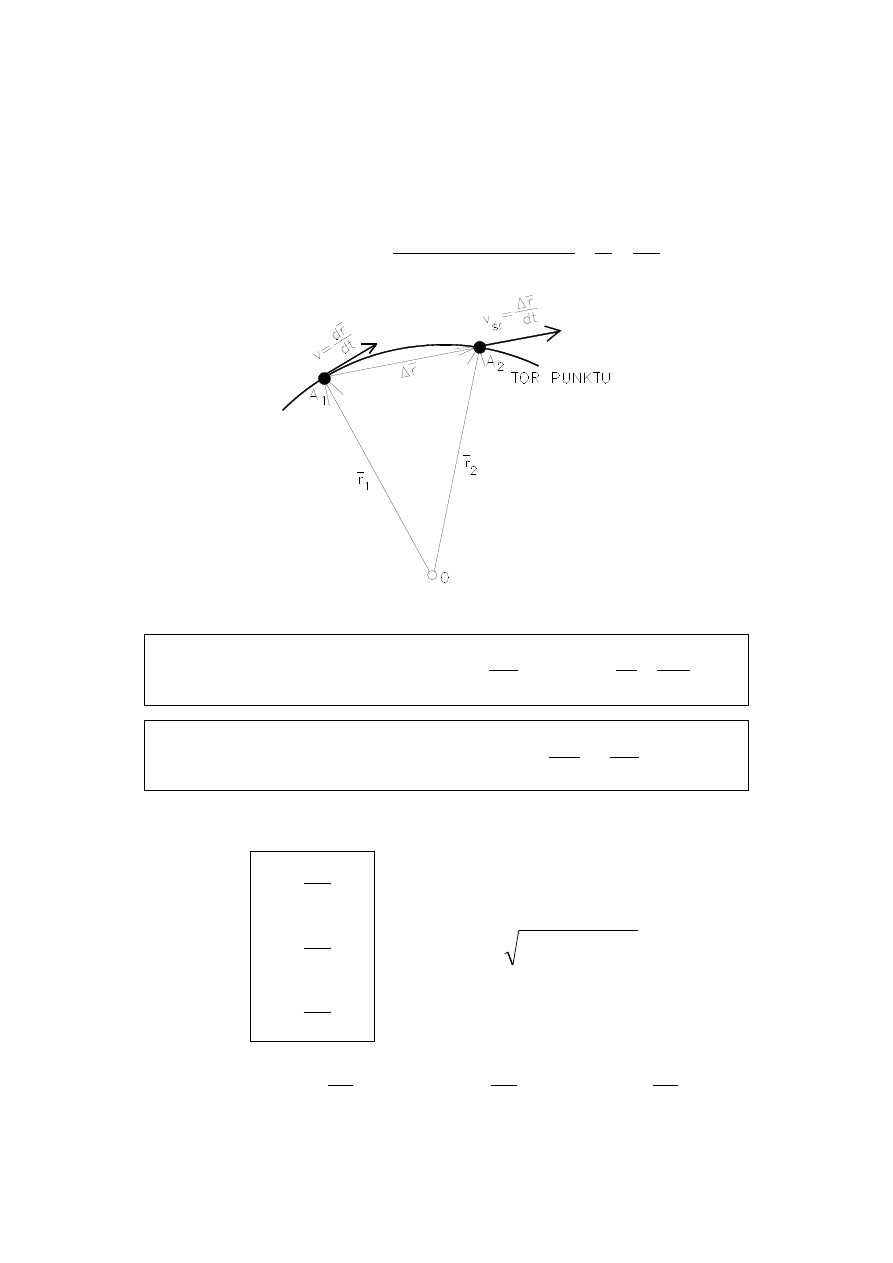
PRĘDKOŚĆ PUNKTU
PRĘDKOŚĆ =
h
km
s
m
CZASU
PRZYROST
DROGI
PRZYROST
Przyrost promienia
– wektora (droga)
)
t
(
r
)
t
(
r
r
1
1
2
2
Prędkość średnia:
h
km
,
s
m
t
r
v
sr
Prędkość chwilowa:
)
t
(
r
dt
r
d
t
r
lim
v
0
t
Zapis wektorowy:
v = v
x
i + v
y
j + v
z
k
z
dt
dz
v
y
dt
dy
v
x
dt
dx
v
z
y
x
2
z
2
y
2
x
v
v
v
v
v
v
)
z
,
v
cos(
,
v
v
)
y
,
v
cos(
,
v
v
)
x
,
v
cos(
z
y
x
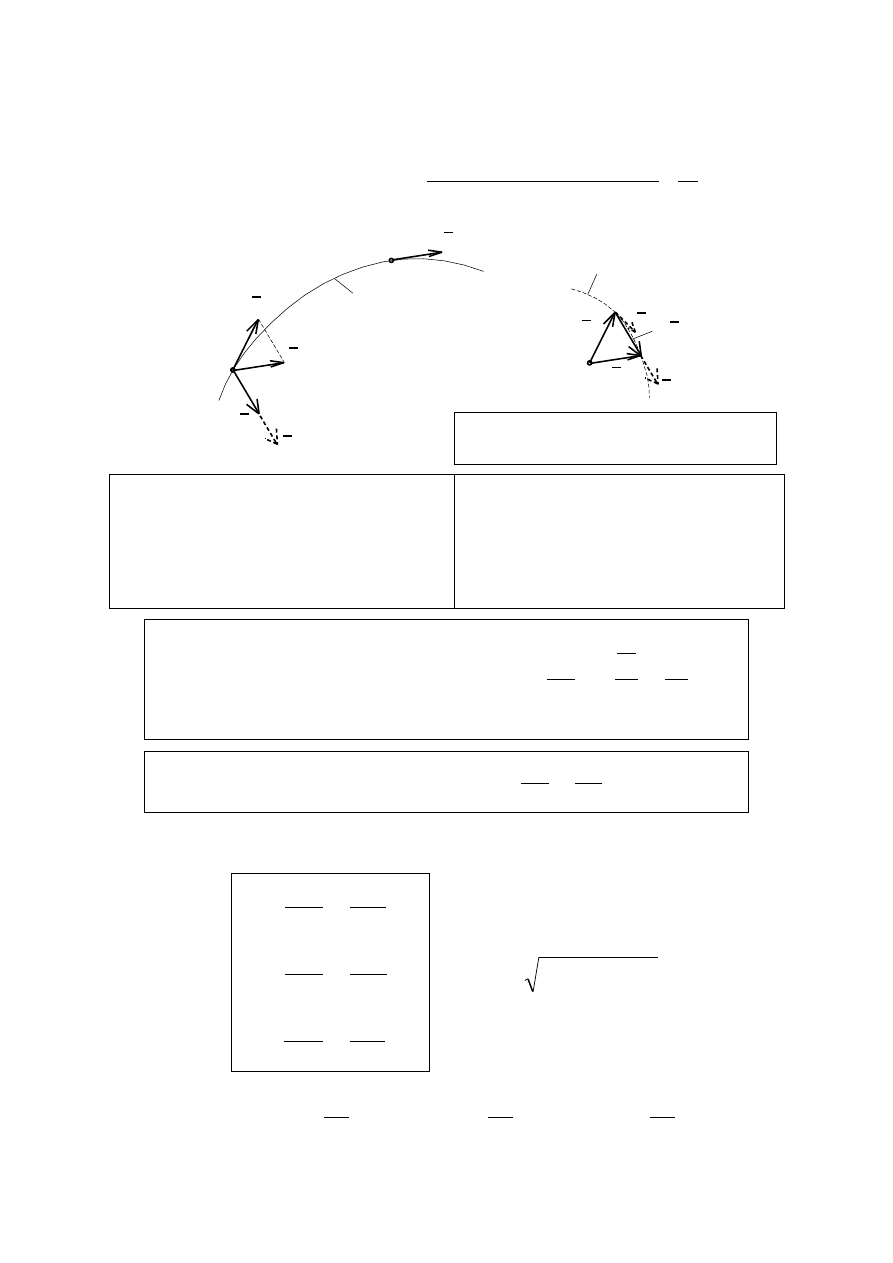
04 Kinematyka.doc
43
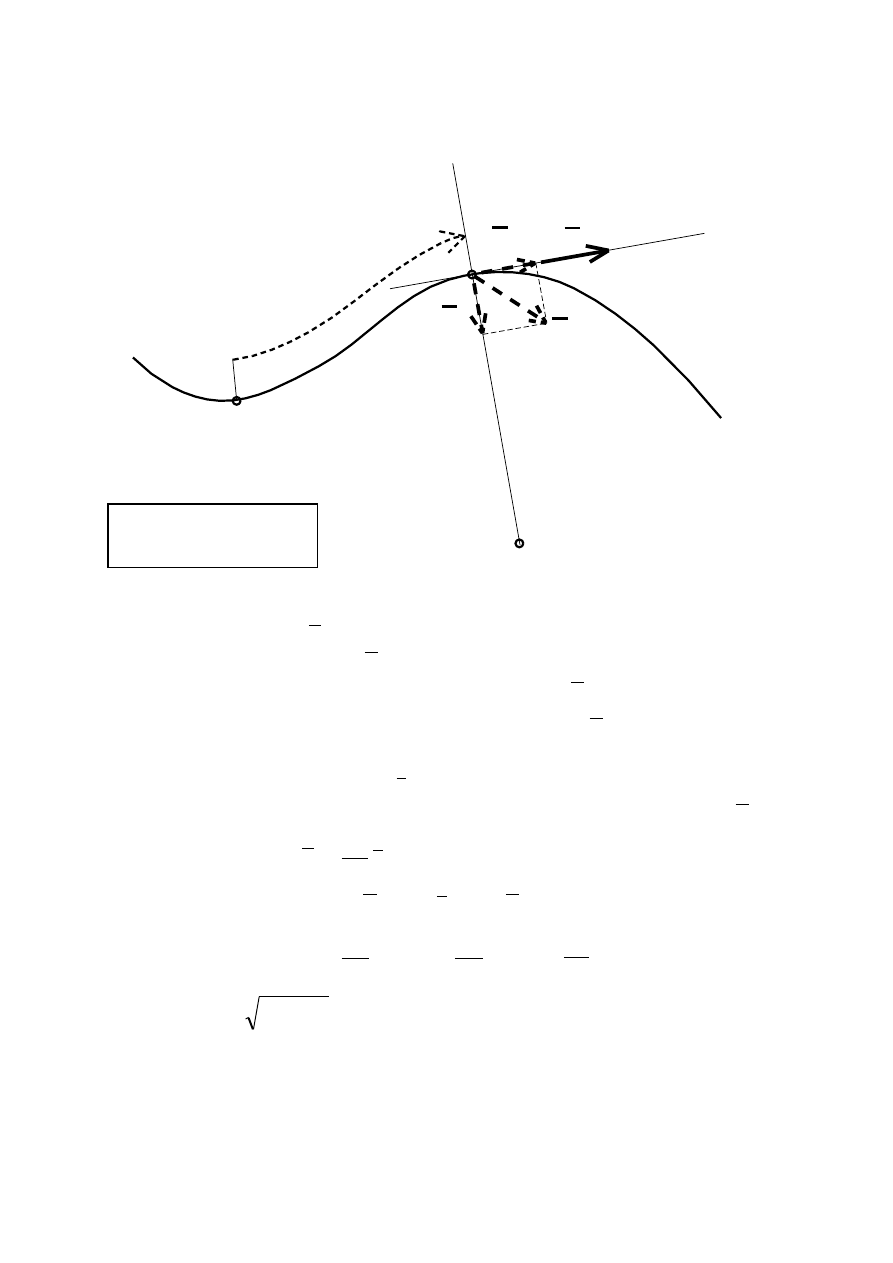
PRZYSPIESZENIE PUNKTU
PRZYSPIESZENIE =
2
s
m
CZASU
PRZYROST
PRĘDKOŚCI
PRZYROST
1
A
śr
O
A
1
2
M
1
v
2
v
a
1
v
2
v
śr
a
1
v
v
a
Tor punktu
Hodograf
v
2
Przyspieszenie:
– zmiana wartości prędkości
– zmiana kierunku wektora
prędkości
1
2
v
v
v
Przyspiesze
nie średnie:
2
sr
s
m
s
s
m
t
v
a
Przyspieszenie chwilowe:
)
t
(
r
)
t
(
v
dt
v
d
t
v
a
lim
0
t
a = a
x
i + a
y
j + a
z
k
z
dt
z
d
dt
dv
a
y
dt
y
d
dt
dv
a
x
dt
x
d
dt
dv
a
2
2
z
z
2
2
y
y
2
2
z
x
2
z
2
y
2
x
a
a
a
a
a
a
)
x
,
a
cos(
,
a
a
)
x
,
a
cos(
,
a
a
)
x
,
a
cos(
z
z
z
.
Hodograf
– krzywa wyznaczana
przez położenie końca wektora pręd-
kości
04 Kinematyka.doc
44
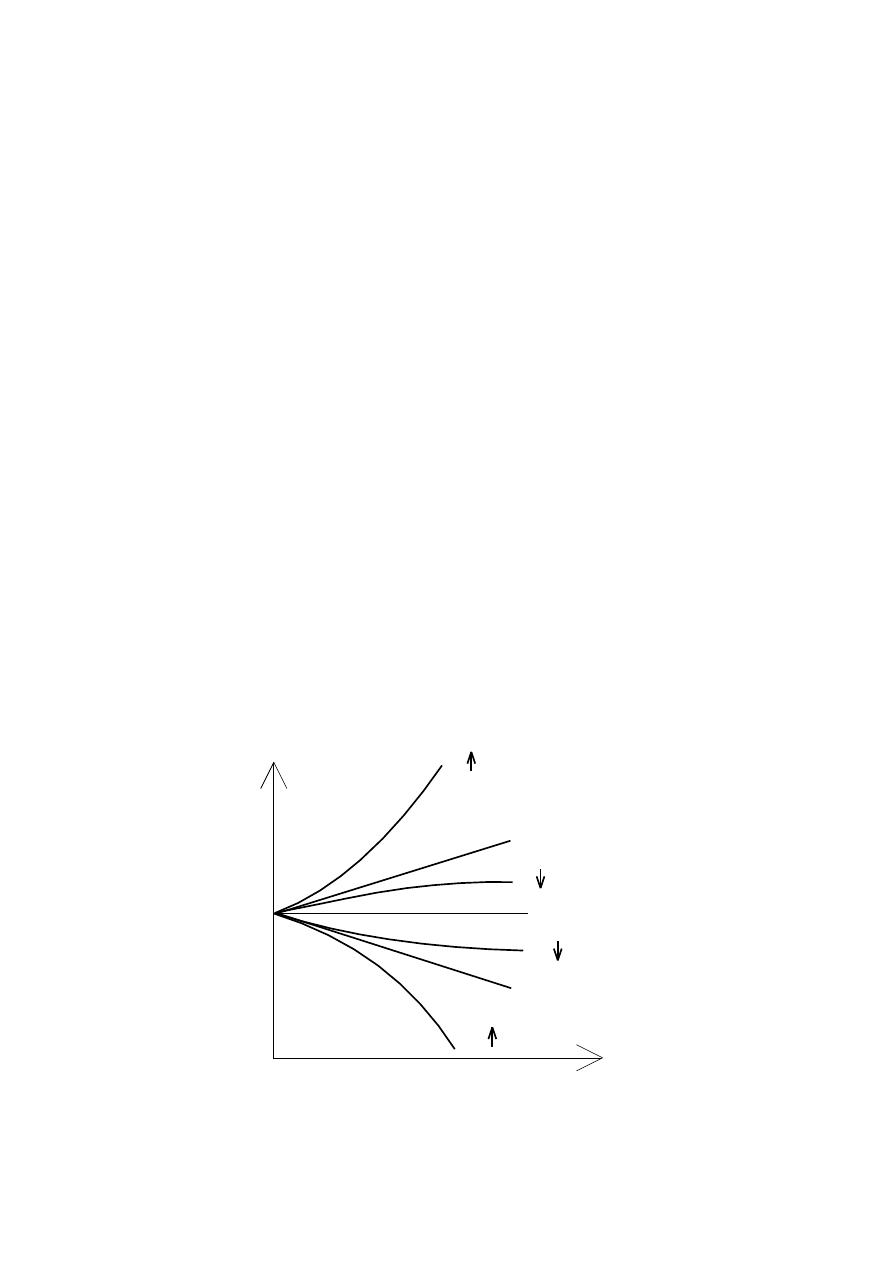
Opis ruchu za pomocą współrzędnej łukowej
Chwila początkowa t = 0
Tor punktu
0
A
s(t)
Współrzędna łukowa
Środek krzywizny
P
ro
m
ie
ń k
rz
yw
izn
y
t
a
a
a
n
v
Styczna
do toru
Normalna do toru
Współrzędna łukowa: s(t)
Wektor prędkości: v
Wektor przyspieszenia: a
Składowa styczna wektora przyspieszenia:
t
a
Składowa normalna wektora przyspieszenia:
n
a
Wektor jednostkowy stycznej do toru, skierowany zgodnie z na-
rastającymi wartościami s:
Wektor jednostkowy normalnej do toru (normalna główna): n
Prędkość punktu:
dt
ds
v
Przyspieszenie punktu:
n
a
a
a
n
t
dt
ds
v
,
dt
dv
a
t
,
2
v
a
n
2
2
n
t
a
a
a
,
0
n
a
ruch prostoliniowy
Współrzędna łukowa:
t
s
dt
)
t
(
v
s
0
0
,
)
t
(
s
s
0
0
.
Równanie ruchu:
s = s(t)
04 Kinematyka.doc
45
PODZIAŁ RUCHU:
RUCH PUNKTU:
– prostoliniowy
– po okręgu (ruch harmoniczny prosty)
– dowolny (krzywoliniowy
RUCH BRYŁY:
– postępowy
– obrotowy
– płaski
– kulisty
– ogólny
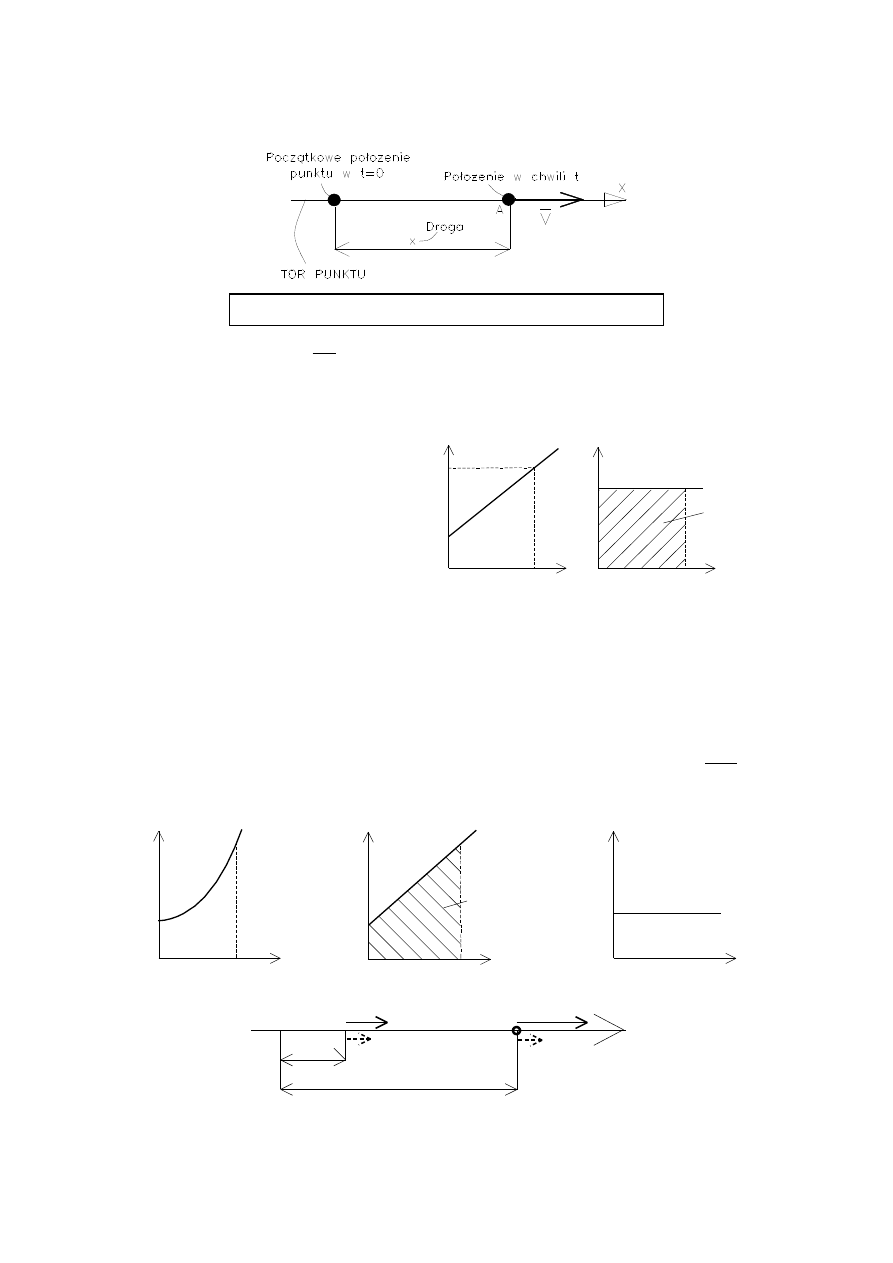
Każdy z w/w ruchów może być:
1. przyspieszony niejednostajnie (a
lub a
)
2. przyspieszony jednostajnie (a = const)
3. jednostajny (v = const)
4.
opóźniony jednostajnie (-a = const)
5.
opóźniony niejednostajnie (-a
lub -a
)
t [czas]
v
v
0
v = const, a = 0
a = const
-a = const
a
-a
a
-a
P
rę
dk
oś
ć
po
cz
ąt
ko
w
a
04 Kinematyka.doc
46
RÓWNANIA RUCHU PROSTOLINIOWEGO
Równanie ruchu: x = x(t)
)
t
(
x
)
t
(
v
a
a
)
t
(
x
dt
dx
v
v
x
x
RUCH JEDNOSTAJNY:
v = const
a = 0
1
t
0
t
0
C
t
v
dx
v
dx
v
x
Warunek początkowy:
t = 0
x = x
0
C
1
= x
0
x = x
0
+ v
t
x
x
0
t
1
x
1
t
t
1
t
v
v = const
droga przebyta
w czasie (0, t1)
RUCH JEDNOSTAJNIE PRZYSPIESZONY:
a = const
v
v
t
0
0
0
at
v
v
dt
a
dv
dt
a
dv
t
0
t
0
2
0
0
0
x
x
2
at
t
v
x
x
dt
)
at
v
(
vdt
dx
dt
v
dx
0
x
t
x
0
t
1
t
v
t
1
v
0
droga przebyta
w czasie (0, t1)
a
t
a = const
0
A
x
x
0
x(t)
v
a
0
a
0
v
0
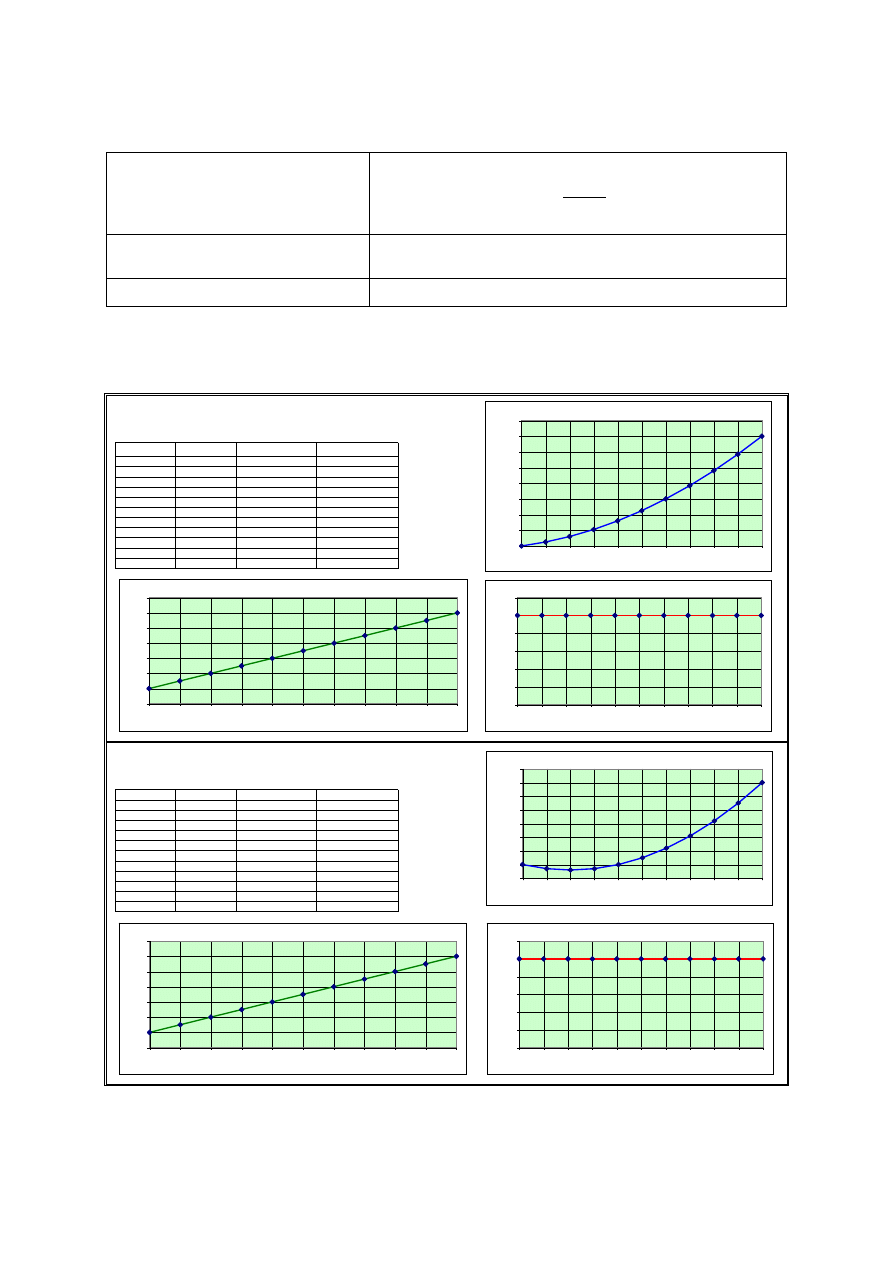
a > 0
ruch jednostajnie przyspieszony,
a < 0
ruch jednostajnie opóźniony.
04 Kinematyka.doc
47
Równania ruchu jednostajnie przyspieszonego:
Droga:
2
at
t
v
x
x
2
0
0
Prędkość:
at
v
v
0
Przyspieszenie:
a = const
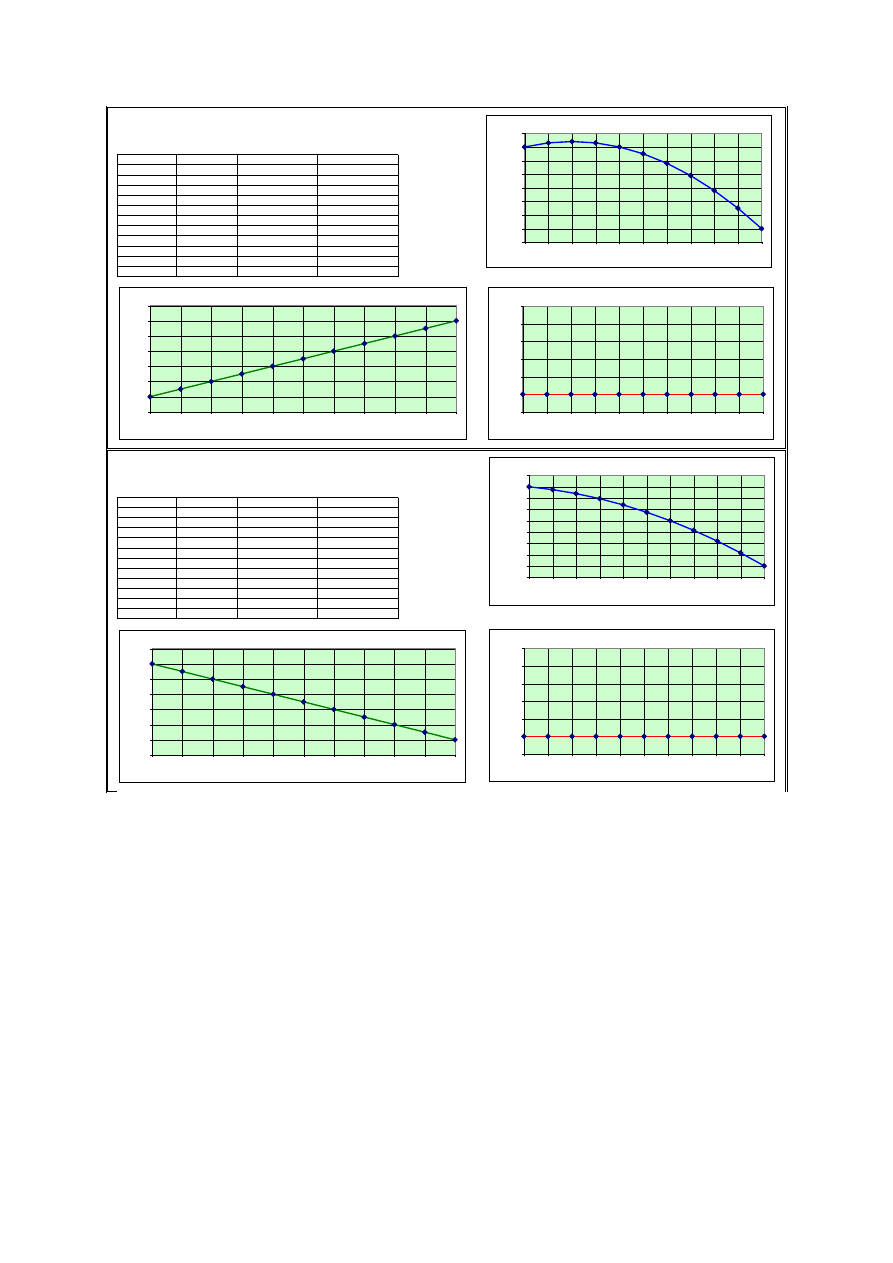
Wykresy ruchu punktu materialnego przedstawiono za pomocą programu Excel.
x
0
=
0
[m]
v
0
=
2
[m/s]
a
0
=
1
[m/s
2
]
t [s]
Droga x
Prędkość v
Przyspieszenie a
0
0,0
2
1
1
2,5
3
1
2
6,0
4
1
3
10,5
5
1
4
16,0
6
1
5
22,5
7
1
6
30,0
8
1
7
38,5
9
1
8
48,0
10
1
9
58,5
11
1
10
70,0
12
1
x
0
=
0
[m]
v
0
=
-2
[m/s]
a
0
=
1
[m/s
2
]
t [s]
Droga x
Prędkość v
Przyspieszenie a
0
0,0
-2
1
1
-1,5
-1
1
2
-2,0
0
1
3
-1,5
1
1
4
0,0
2
1
5
2,5
3
1
6
6,0
4
1
7
10,5
5
1
8
16,0
6
1
9
22,5
7
1
10
30,0
8
1
WYKRESU RUCHU JEDNOSTAJNIE PRZYSPIESZONEGO
Wykres prędkości [m/s]
0
2
4
6
8
10
12
14
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
P
ręd
koś
ć [m
/s
]
Wykres drogi
0,0
10,0
20,0
30,0
40,0
50,0
60,0
70,0
80,0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Dr
og
a [
m]
Wykres przyspieszeń [m/s2]
0
0,2
0,4
0,6
0,8
1
1,2
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prz
y
s
pies
z
enie
[m
/s
2]
Wykres prędkości [m/s]
-4
-2
0
2
4
6
8
10
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prędk
oś
ć
[m
/s
]
Wykres drogi
-5,0
0,0
5,0
10,0
15,0
20,0
25,0
30,0
35,0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Dr
og
a [
m]
Wykres przyspieszeń [m/s
2
]
0
0,2
0,4
0,6
0,8
1
1,2
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prz
y
s
pies
z
enie
[m
/s
2
]
04 Kinematyka.doc
48
x
0
=
0
[m]
v
0
=
2
[m/s]
a
0
=
-1
[m/s
2
]
t [s]
Droga x
Prędkość v
Przyspieszenie a
0
0,0
2
-1
1
1,5
1
-1
2
2,0
0
-1
3
1,5
-1
-1
4
0,0
-2
-1
5
-2,5
-3
-1
6
-6,0
-4
-1
7
-10,5
-5
-1
8
-16,0
-6
-1
9
-22,5
-7
-1
10
-30,0
-8
-1
x
0
=
50
[m]
v
0
=
-2
[m/s]
a
0
=
-1
[m/s
2
]
t [s]
Droga x
Prędkość v
Przyspieszenie a
0
50,0
-2
-1
1
47,5
-3
-1
2
44,0
-4
-1
3
39,5
-5
-1
4
34,0
-6
-1
5
27,5
-7
-1
6
20,0
-8
-1
7
11,5
-9
-1
8
2,0
-10
-1
9
-8,5
-11
-1
10
-20,0
-12
-1
Wykres prędkości [m/s]
-4
-2
0
2
4
6
8
10
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prędk
oś
ć
[m
/s
]
Wykres drogi
-35,0
-30,0
-25,0
-20,0
-15,0
-10,0
-5,0
0,0
5,0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Dr
og
a [
m]
Wykres prędkości [m/s]
-1,2
-1
-0,8
-0,6
-0,4
-0,2
0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prz
y
s
pies
z
enie
[m
/s
2
]
Wykres prędkości [m/s]
-14
-12
-10
-8
-6
-4
-2
0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prędk
oś
ć
[m
/s
]
Wykres drogi
-30,0
-20,0
-10,0
0,0
10,0
20,0
30,0
40,0
50,0
60,0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
D
rog
a [
m]
Wykres prędkości [m/s]
-1,2
-1
-0,8
-0,6
-0,4
-0,2
0
0
1
2
3
4
5
6
7
8
9
10
Czas [s]
Prz
y
s
pies
z
enie
[m
/s
2
]
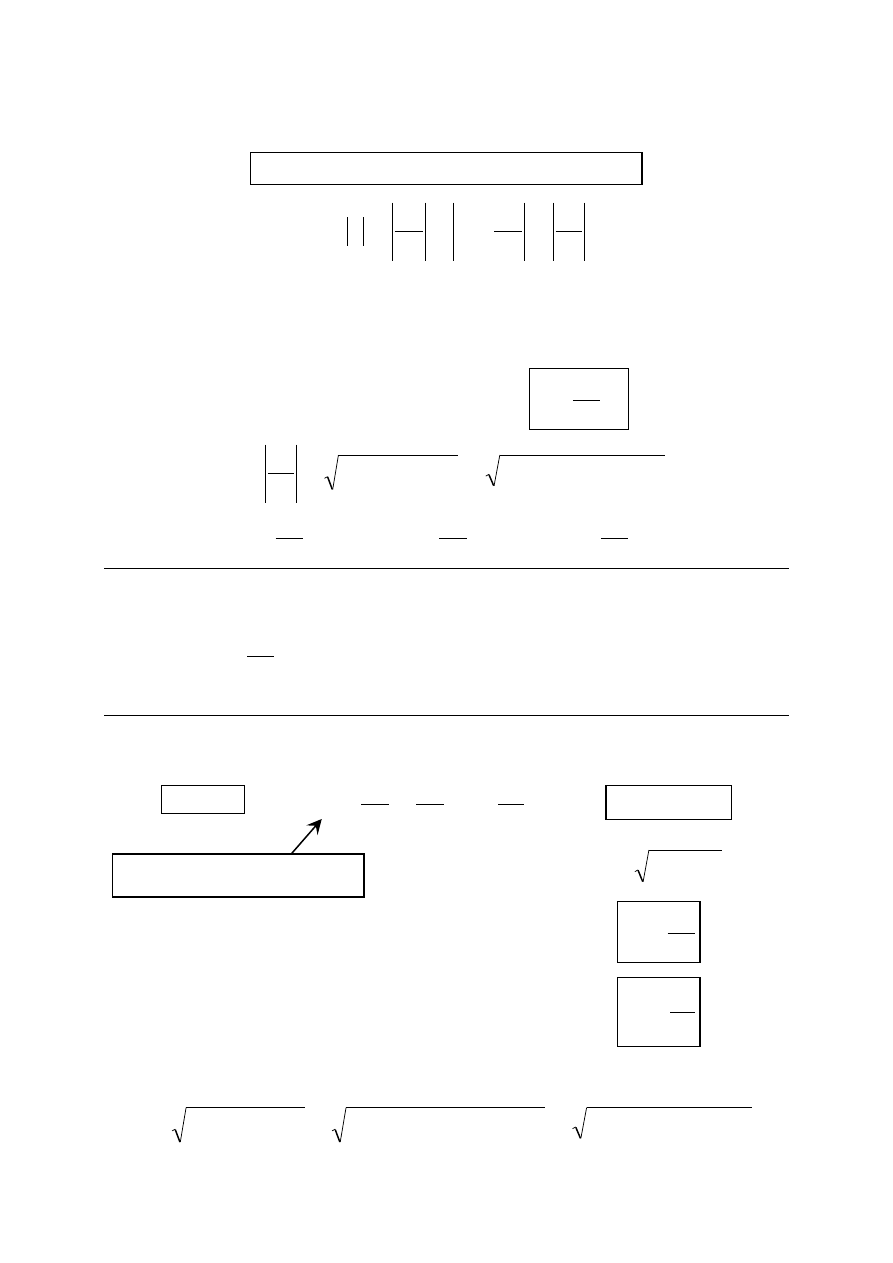
04 Kinematyka.doc
49
RUCH KRZYWOLINIOWY
RÓWNANIE RUCHU:
s = s(t)
dt
ds
t
s
t
s
v
v
lim
0
t
– wektor jednostkowy stycznej do toru, skierowany
zgodnie z narastającymi wartościami s
n
– wektor jednostkowy normalnej głównej
PRĘDKOŚĆ PUNKTU:
dt
ds
v
2
2
2
2
y
2
y
2
x
)
z
(
)
y
(
)
x
(
v
v
v
dt
ds
v
z
dt
dz
v
y
dt
dy
v
x
dt
dx
v
z
y
x
WSPÓŁRZĘDNA ŁUKOWA DLA DANEJ PRĘDKOŚCI v(t):
t
0
0
s
dt
)
t
(
v
s
dt
v
ds
dt
ds
v
s
0
= s(0)
w chwili t = 0
PRZYSPIESZENIE PUNKTU:
v
v
dt
d
v
dt
dv
dt
v
d
a
n
a
a
a
n
t
2
n
2
t
a
a
a
PRZYSPIESZENIE STYCZNE:
dt
dv
a
t
PRZYSPIESZENIE DOŚRODKOWE:
2
n
v
a
Ruch prostoliniowy
a
n
= 0
2
2
2
2
z
2
y
2
x
2
z
2
y
2
x
)
z
(
)
y
(
)
x
(
)
v
(
)
v
(
)
v
(
a
a
a
a
.
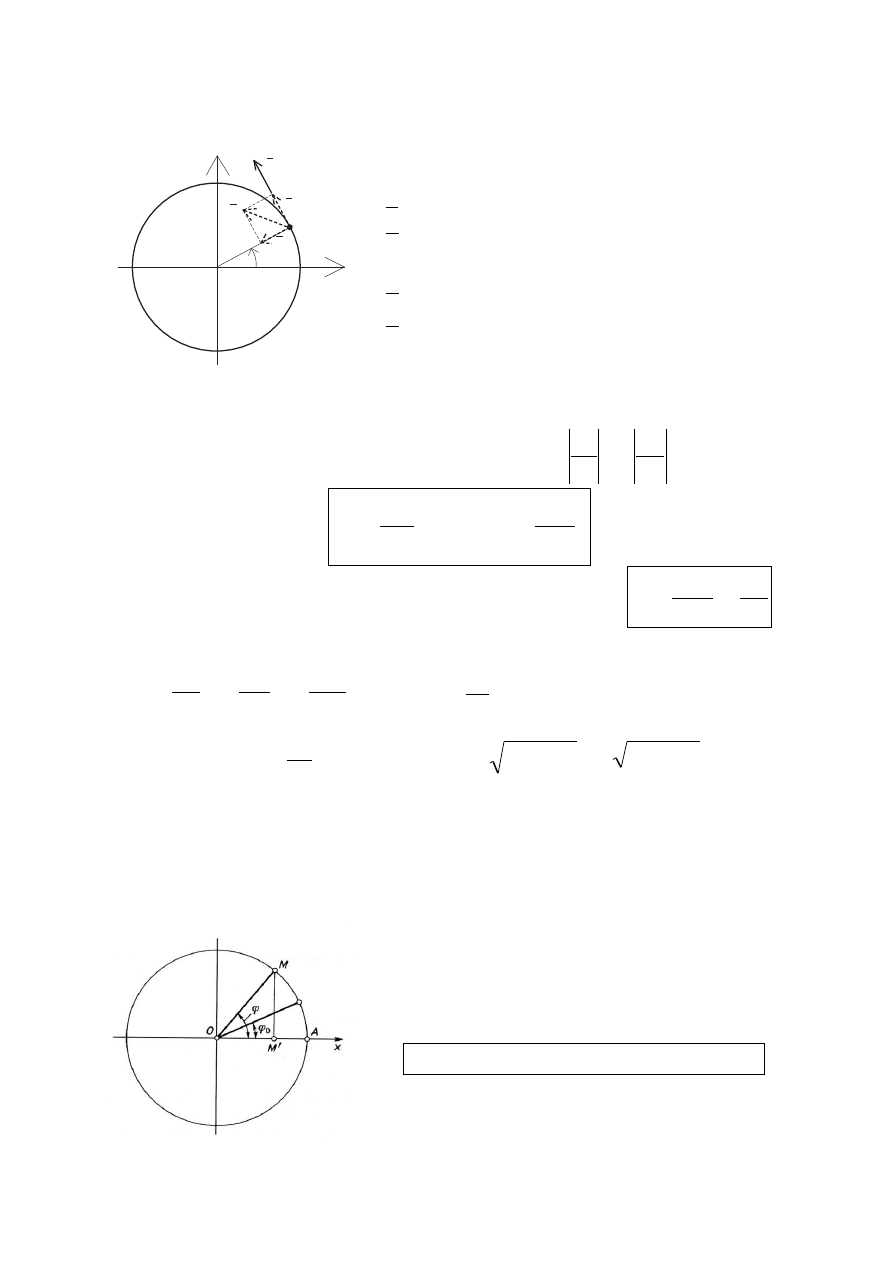
Pochodna funkcji wektorowej
zmiennej skalarnej t (czas)
04 Kinematyka.doc
50
RUCH PUNKTU PO OKRĘGU
X
Y
t
n
r
v
a
a
a
A
0
Parametry punktu A:
v
– prędkość liniowa, styczna do toru
n
a
– przyspieszenie dośrodkowe
(normalne)
t
a
– przyspieszenie styczne
a - przyspieszenie wypadkowe
Równanie ruchu: s = f(t), droga: s = r
s = r
(t)
Prędkość punktu po okręgu:
dt
d
r
dt
ds
v
Prędkość kątowa:
s
rad
dt
d
r
v
Prędkość kątowa w funkcji obrotów n [obr/min]:
30
n
60
n
2
Przyspieszenia w ruchu po okręgu dla
= r = const:
r
dt
d
r
dt
d
r
dt
dv
a
2
2
t
,
2
s
1
– przyspieszenie kątowe
r
r
v
a
2
2
n
,
4
2
2
n
2
t
r
a
a
a
.
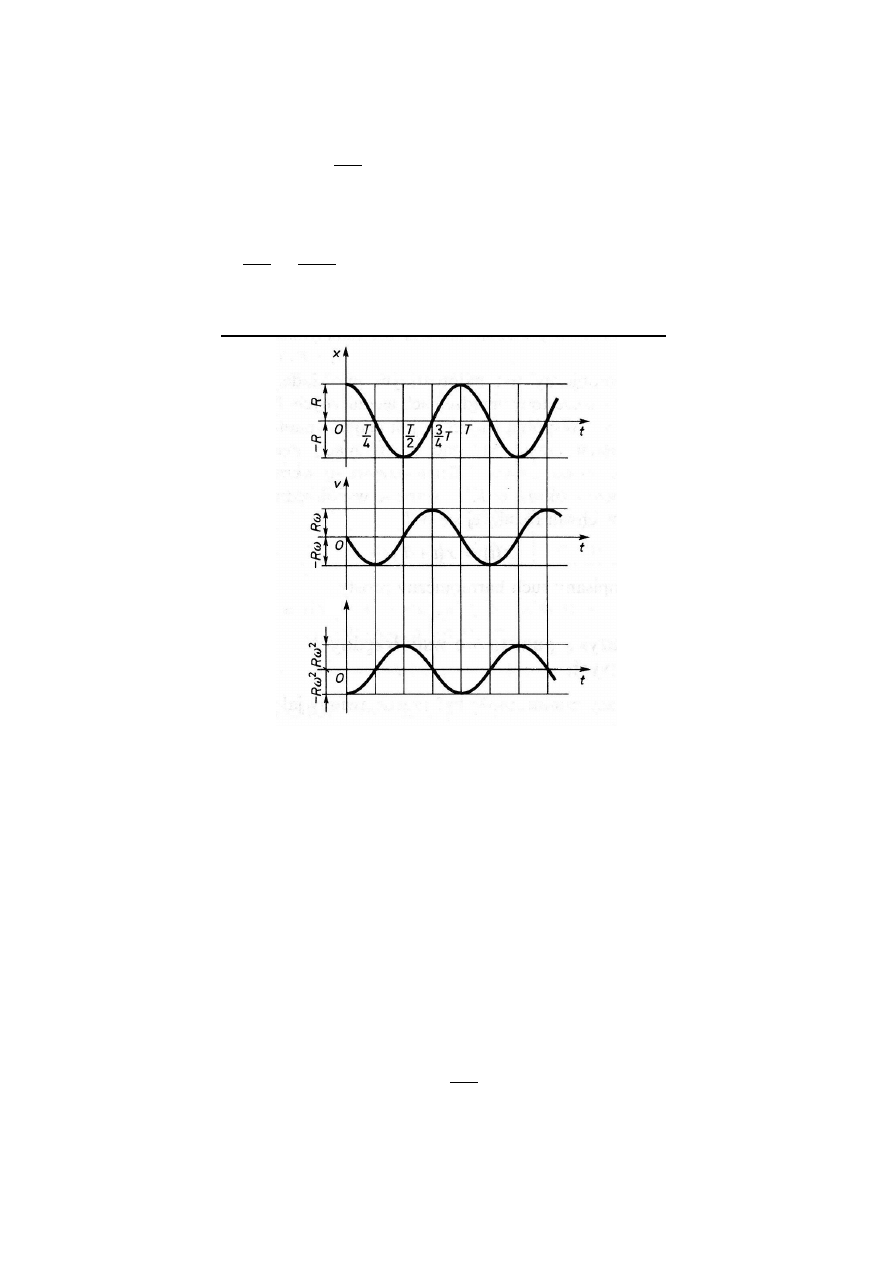
RUCH HARMONICZNY PROSTY
Punkt M
– ruch jednostajny po okręgu
Badan
ie ruchu punktu M’ – rzutu punktu M na oś X
Ruch punktu M’ – ruch prostoliniowy
po torze X. Równanie ruchu M’
w czasie t, liczonym od t = 0 (punkt
w
położeniu A):
x = R
·cos(φ +φ
0
) = R
·cos(
t +
φ
0
).
Jest to równanie
ruchu harmonicznego prostego.
0
04 Kinematyka.doc
51
Prędkość ruchu harmonicznego prostego:
)
sin(
R
dt
dx
v
0
t
.
Przyspieszenie ruchu harmonicznego prostego:
x
ω
)
t
cos(ω
ω
R
dt
dx
dt
dv
a
2
0
2
2
2
.
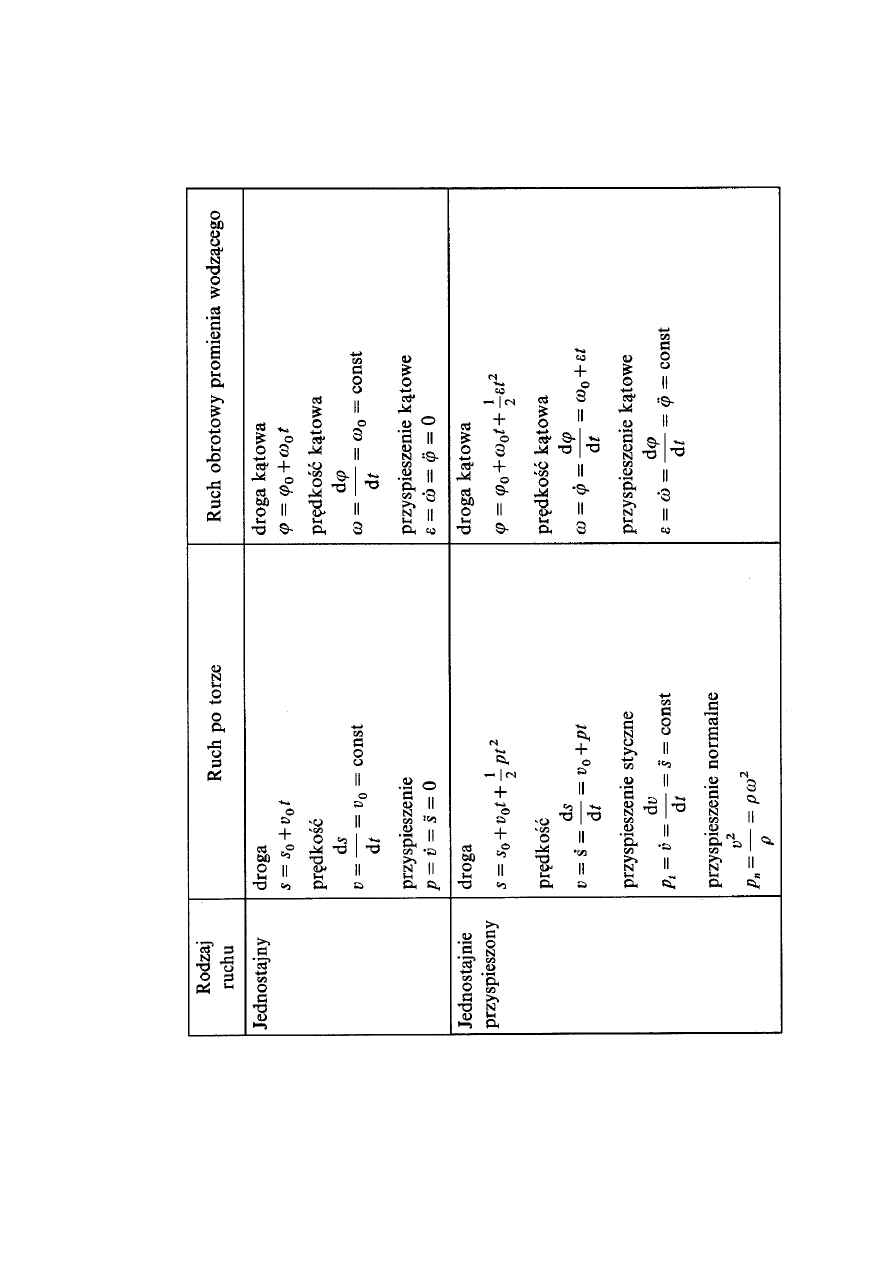
Wykresy drogi, prędkości i przyspieszenia:
Ruch punktu M’ jest ruchem okresowym. Ruch, w którym na-
stępuje okresowa zmiana współrzędnej w zakresie od +R do –R
nazywa się ruchem drgającym.
Punkt 0 wokół którego odbywają się drgania – środek drgań.
Amplituda drgań – największa odległość punktu od środka
drgań (tutaj: – R).
Okres drgań – przedział czasu T, w którym punkt wychodzący
z punktu M
0
wraca do niego.
Faza drgań – kąt φ =
·t.
Stałą
określająca zmiany fazy w jednostce czasu – częstość
kątowa (kołowa) drgań.
2
T
.
Ruch harmoniczny prosty jest ruchem niejednostajnie zmiennym.
a
04 Kinematyka.doc
52
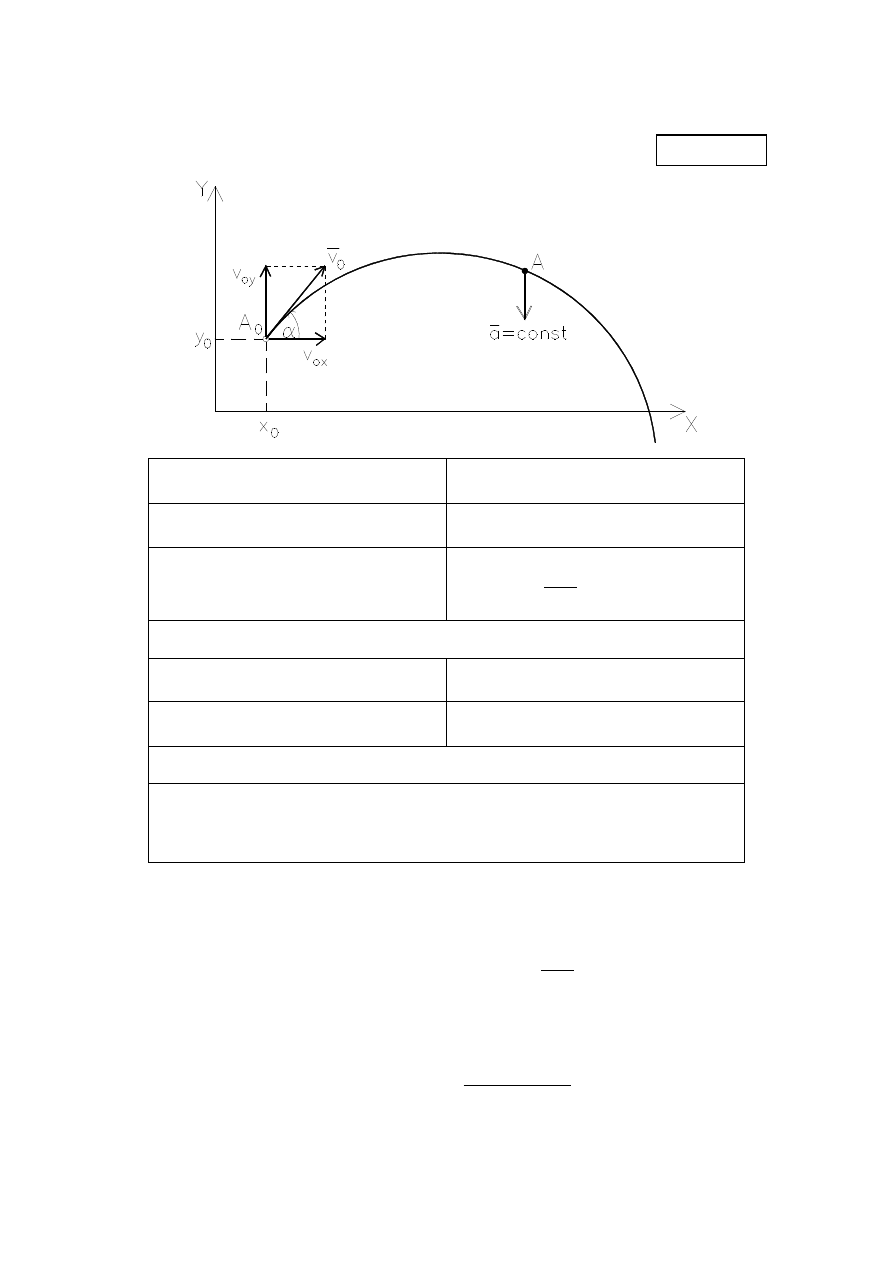
W
z
ory na
ruch po
torze i
na ruc
h obr
o
towy
promi
eni
a wodz
ą
c
ego OA
04 Kinematyka.doc
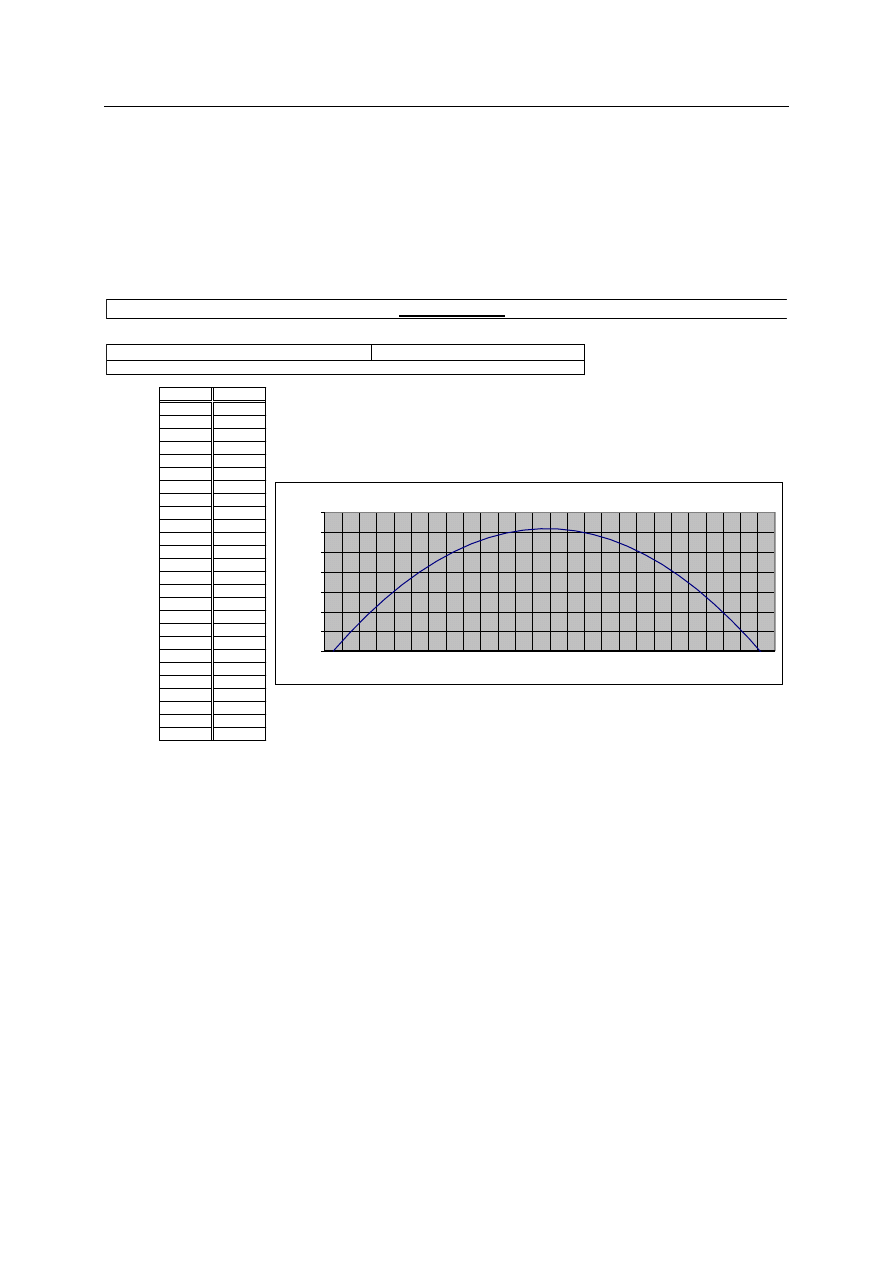
53
RUCH KRZYWOLINIOWY
ZE STAŁYM PRZYSPIESZENIEM (rzut ukośny)
const
a
0
x
a
x
a
y
a
y
1
x
C
x
v
2
y
C
at
y
v
3
1
C
t
C
x
4
2
2
C
t
C
2
at
y
Warunki brzegowe:
0
0
t
x
)
x
(
0
0
t
y
)
y
(
cos
v
)
x
(
)
v
(
0
0
t
0
t
x
sin
v
)
y
(
)
v
(
0
0
t
0
t
y
Stałe całkowania:
0
4
0
3
0
2
0
1
y
C
x
C
sin
v
C
cos
v
C
Równania ruchu:
2
at
t
)
sin
v
(
y
y
t
)
cos
v
(
x
x
2
0
0
0
0
Równanie toru (parabola):
2
0
2
2
0
0
0
)
x
x
(
cos
v
2
a
tg
)
x
x
(
y
y
04 Kinematyka.doc
54
Przypadki szczególne:
rzut ukośny (poziomy)
rzut pionowy
Przykład rzutu ukośnego przedstawiony za pomocą programu Excel:
DANE WEJŚCIOWE:
22
m/s;
9,81
m/s
2
45
0
=
0,785398
rad
x
y
0
0,00
2
1,92
4
3,68
6
5,27
8
6,70
10
7,97
12
9,08
14
10,03
16
10,81
18
11,43
20
11,89
22
12,19
24
12,33
26
12,30
28
12,11
30
11,76
32
11,24
34
10,57
36
9,73
38
8,73
40
7,57
42
6,25
44
4,76
46
3,11
48
1,30
50
-0,67
kąt rzutu
przyspieszenie =
RZUT UKOŚNY
prędkość początkowa v
0
=
RZUT UKOŚNY
0,00
2,00
4,00
6,00
8,00
10,00
12,00
14,00
0
2
4
6
8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50
[m]
[m]
04 Kinematyka.doc
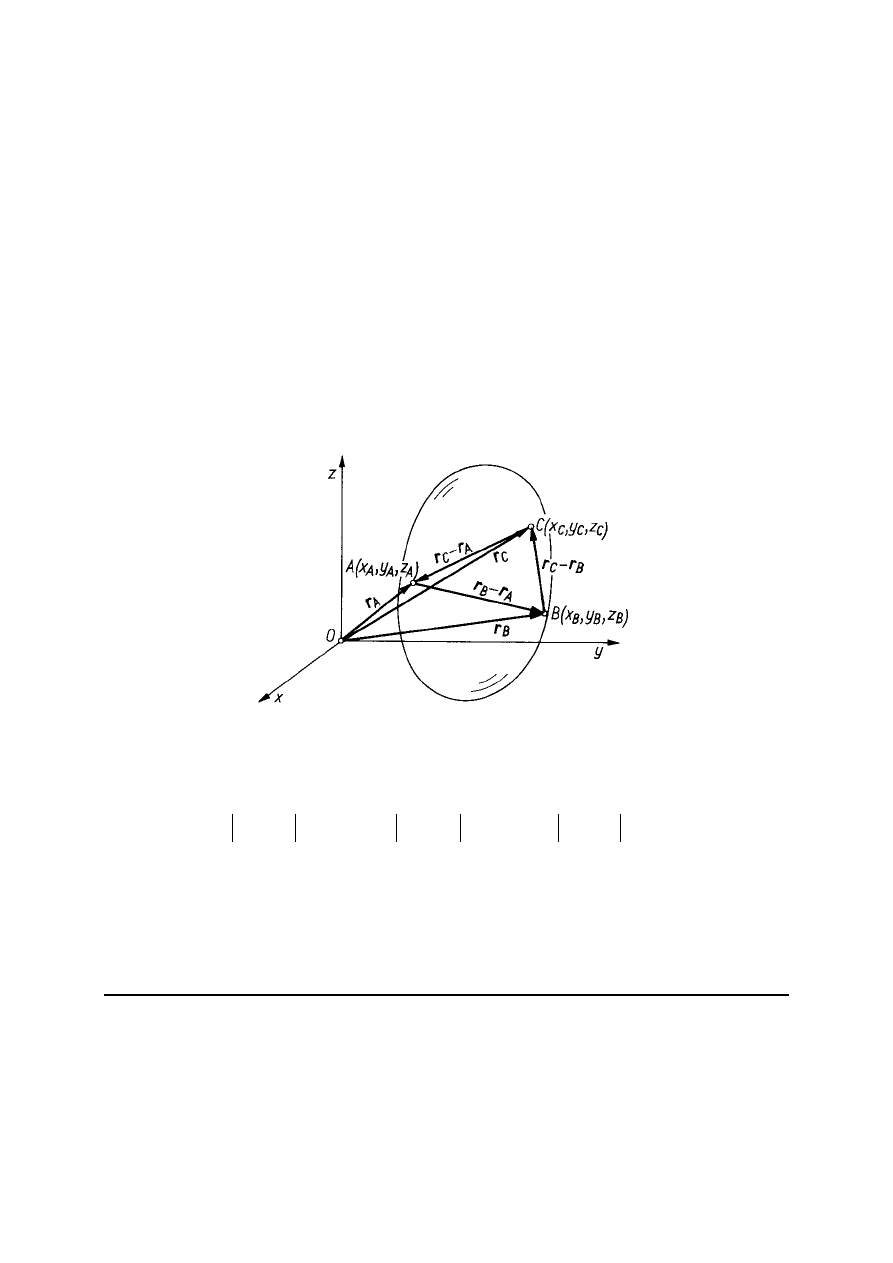
55
KINEMATYK
A CIAŁA SZTYWNEGO
RUCH POSTĘPOWY
RUCH OBROTOWY
RUCH PŁASKI
RUCH KULISTY
RUCH ŚRUBOWY
CIAŁO SZTYWNE W PRZESTRZENI
)
t
(
r
r
)
t
(
r
r
)
t
(
r
r
C
C
B
B
A
A
Z warunku aby 3 punkty nie leżały na jednej prostej:
d
r
r
c
r
r
b
r
r
B
C
A
C
A
B
2
2
C
B
2
C
B
2
C
B
2
2
C
A
2
C
A
2
C
A
2
2
B
A
2
B
A
2
B
A
d
)
z
z
(
)
y
y
(
)
x
x
(
c
)
z
z
(
)
y
y
(
)
x
x
(
b
)
z
z
(
)
y
y
(
)
x
x
(
x
A,B,C
, y
A,B,C,
z
A,B,C
współrzędne punktów A, B, C (9)
Więzy:
3 równania (b, c, d = const)
CIAŁO SZTYWNE W PRZESTRZENI
MA 6 STOPNI SWOBODY (9
– 3 = 6)
04 Kinematyka.doc
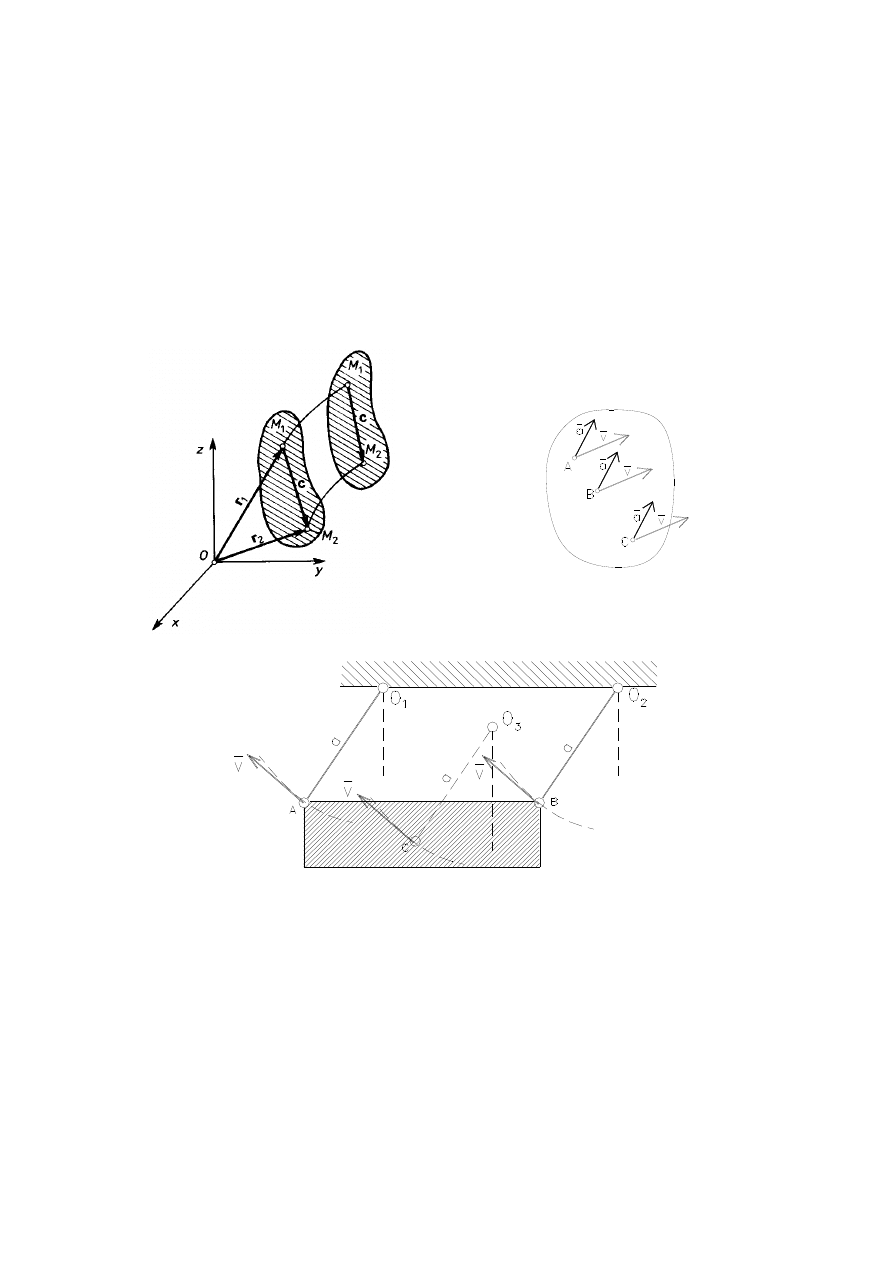
56
RUCH POSTĘPOWY
W ruchu postępowym wszystkie punkty ciała poruszają się po
identycznych torach, w każdej chwili posiadają takie same
prędkości i przyspieszenia (wartość, kierunek i zwrot).
Dla analizy ruchu postępowego wystarczy
określenie ruchu jednego punktu ciała.
Przykłady ruchu postępowego
Inne przykłady:
– ruch tłoka w cylindrze,
– ruch klatki dźwigu,
– nieruchomo siedzący pasażer autobusu (pociągu).
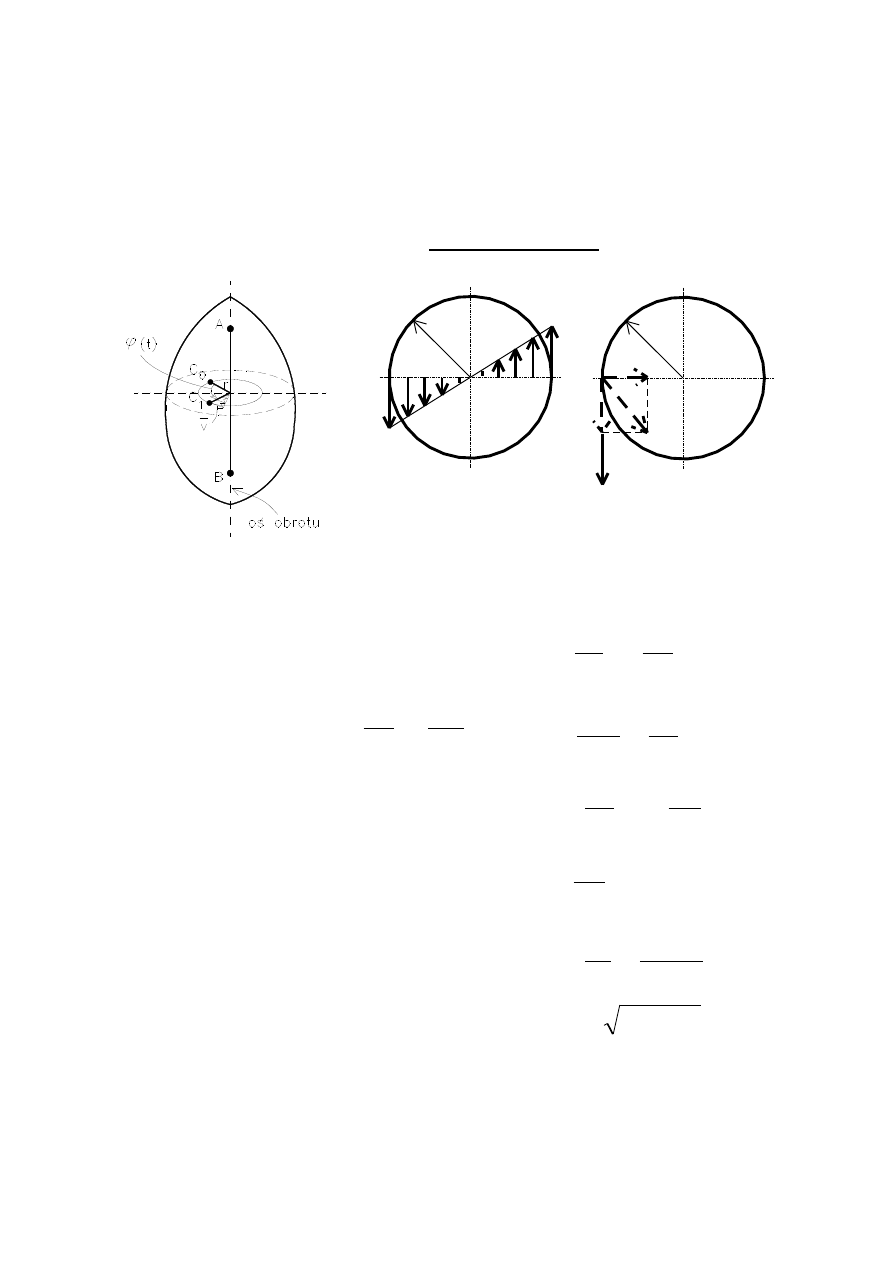
04 Kinematyka.doc
57
RUCH OBROTOWY
W ruchu obrotowym dwa punkty sztywno związane
z cia
łem pozostają nieruchome wyznaczając
nieruchomą oś obrotu ciała.
C
1
r
v
C
1
r
v
a
n
t
a
a
Rozkład prędkości i przyspieszeń w płaszczyźnie pro-
stopadłej do osi obrotu ciała.
Dla punktu C:
równanie ruchu:
)
t
(
r
s
Prędkość punktu:
)
t
(
r
dt
d
r
dt
ds
v
.
Prędkość kątowa:
s
rad
dt
d
30
n
60
n
2
.
Przyspieszenie styczne:
r
dt
d
r
dt
dv
a
t
.
Przyspieszenie kątowe:
2
s
rad
dt
d
.
Przyspieszenie dośrodkowe:
r
r
r
r
v
a
2
2
2
2
n
Przyspieszenie wypadkowe:
4
2
r
a
(Porównaj ruch punktu po okręgu)
04 Kinematyka.doc
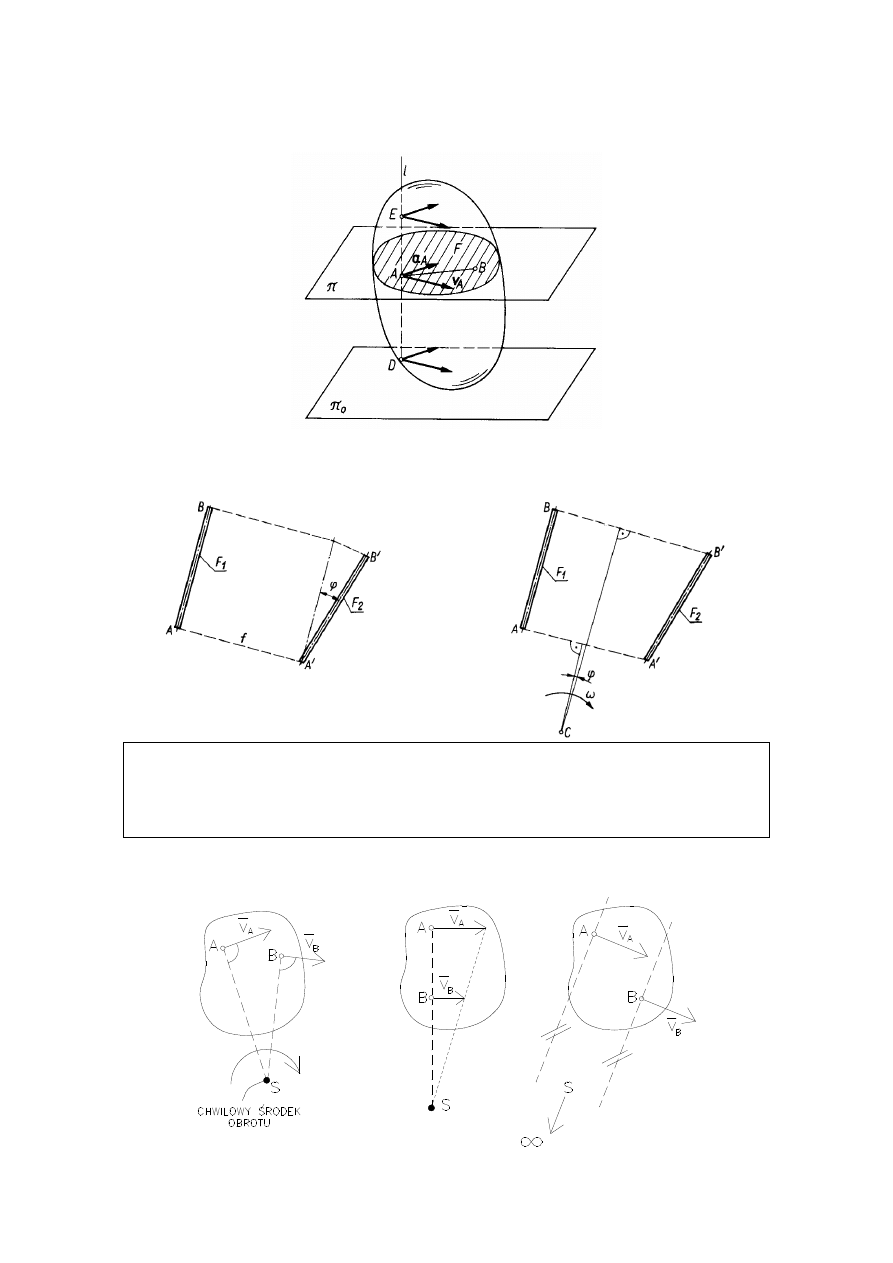
58
RUCH PŁASKI
Analiza ruchu płaskiego sprowadza się do badania ruchu
jednego przekroju ciała, będącego figura płaską.
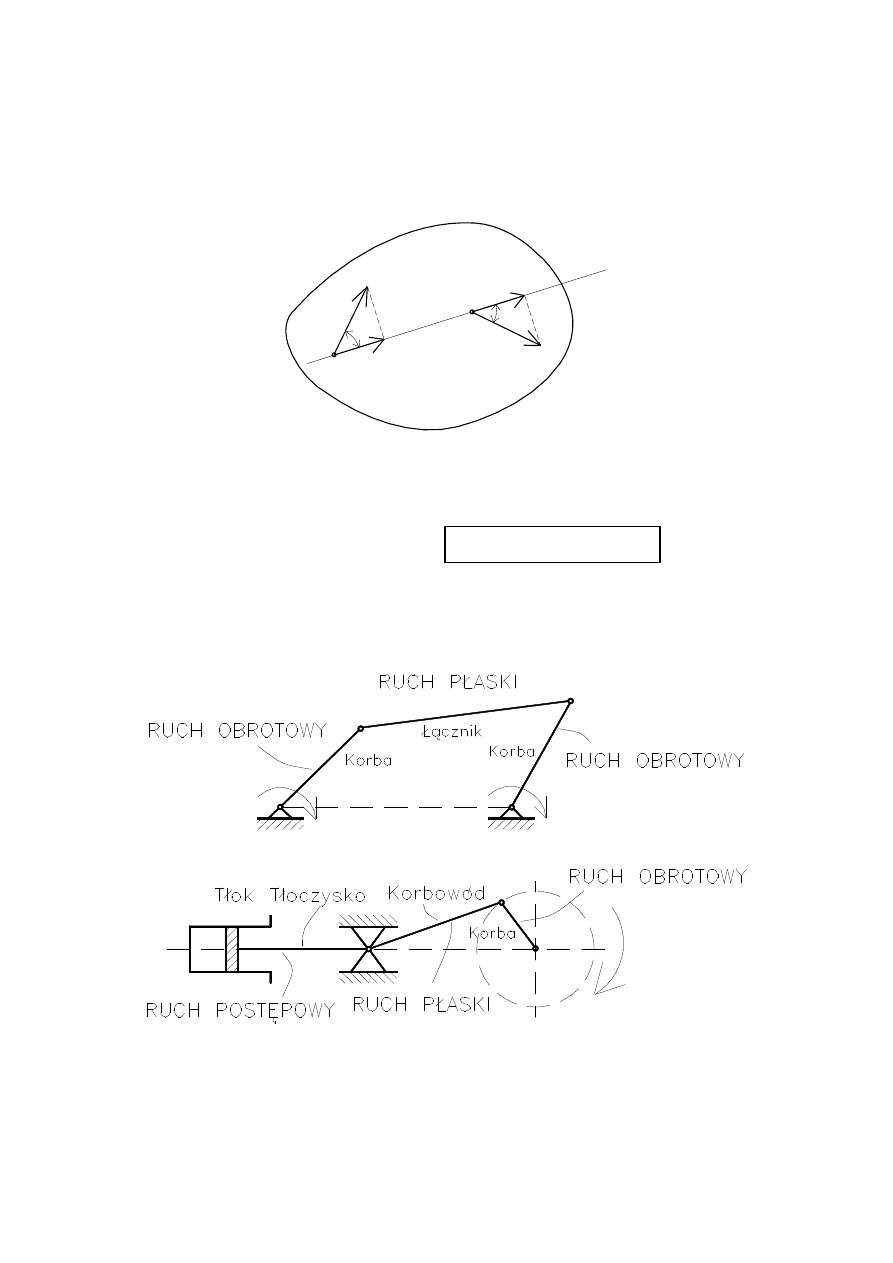
Dowolne przemieszczeni figury płaskiej może być dokona-
ne za pomocą obrotu wokół punktu zwanego chwilowym
środkiem obrotu.
RUCH PŁASKI JAKO CHWILOWY RUCH OBROTOWY
04 Kinematyka.doc
59
TWIERDZENIE O RZUTACH PRĘDKOŚCI
Rzuty prędkości dwóch punktów A i B ciała sztywnego
na pro
stą łączącą te punkty są sobie równe.
A
B
v
Z
AZ
BZ
v
A
B
v
v
W każdej chwili t rzut prędkości v
A
na prostą AB
równa się rzutowi prędkości v
B
na tą prostą.
BZ
AZ
v
v
→
cos
v
cos
v
B
A
Przykłady ruchu płaskiego
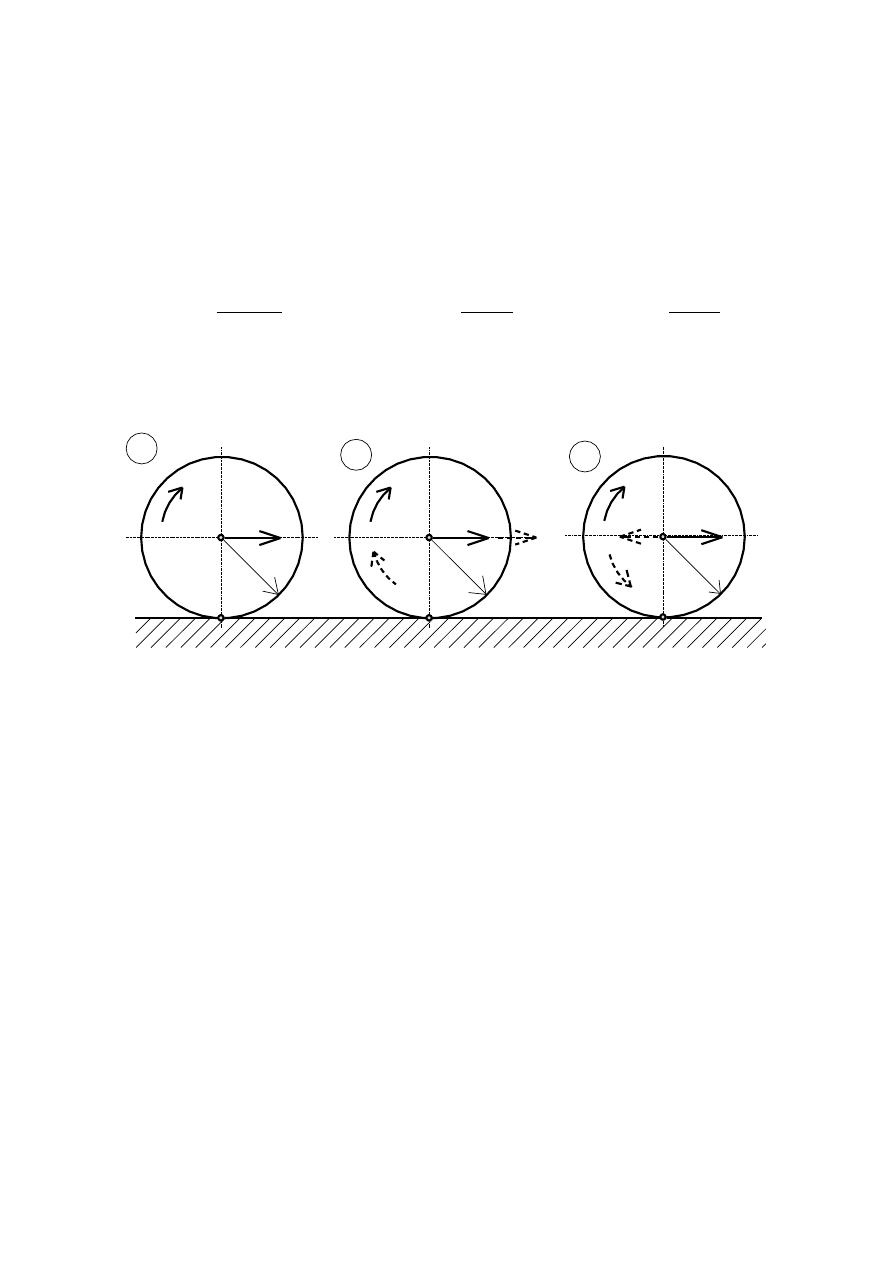
04 Kinematyka.doc
60
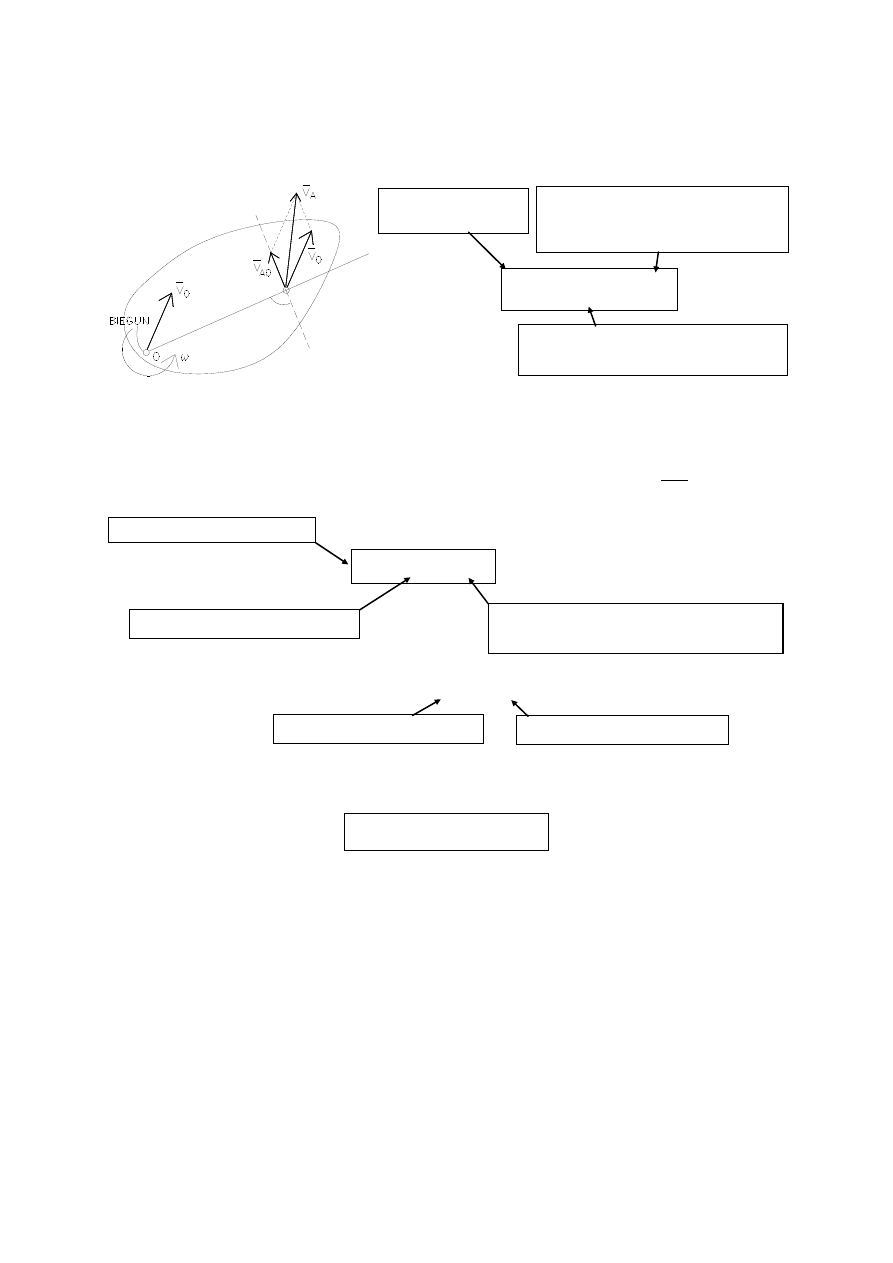
TOCZENIE SIĘ KOŁA PO LINII POZIOMEJ BEZ POŚLIZGU
Koło (tarcza) o promieniu r toczy się bez poślizgu po poziomej
linii. Środek koła A jest w ruchu jednostajnym, punkt styku C
jest chwilowym środkiem obrotu.
Dla danej prędkości v
A
(t) otrzymuje się:
.
r
)
t
(
a
)
t
(
)
t
(
,
r
)
t
(
v
)
t
(
),
t
(
v
dt
)
t
(
dv
a
A
A
A
A
A
A
Dla znanych funkcji ω(t) oraz ε(t) otrzymuje się:
.
r
)
t
(
)
t
(
a
,
r
)
t
(
)
t
(
v
A
A
C
v
A
a
A
(t)
(t)
r
r
r
A
A
C
C
(t)
v
A
(t)
v
A
a
A
A
3
2
1
Trzy
przypadki toczenia się krążka bez poślizgu:
1. Ruch jednostajny (rys. 1):
.
0
a
,
r
v
0
)
t
(
,
const
)
t
(
A
A
2. Ruch jednostajnie przyspieszony (rys. 2):
.
r
a
,
r
t
v
,
const
)
t
(
,
t
)
t
(
A
0
A
0
3.
Ruch jednostajnie opóźniony (rys. 3):
.
r
a
,
r
t
)
(
v
,
const
)
t
(
,
t
)
(
)
t
(
A
0
A
0
Prędkości punktów na obwodzie koła wyznacza się metodą superpozycji
(wyznaczając składową postępową wektora v
A
) lub metodą chwilowego
środka obrotu. Przyspieszenia wyznacza się metodą superpozycji (skła-
dowa postępowa wektora a
A
).
W przypadku toczenia się koła z poślizgiem, w punkcie styku koła z linią
pozioma należy uwzględnić „prędkość poślizgu”
0. Powoduje to zmia-
nę położenia chwilowego środka obrotu C.
04 Kinematyka.doc
61
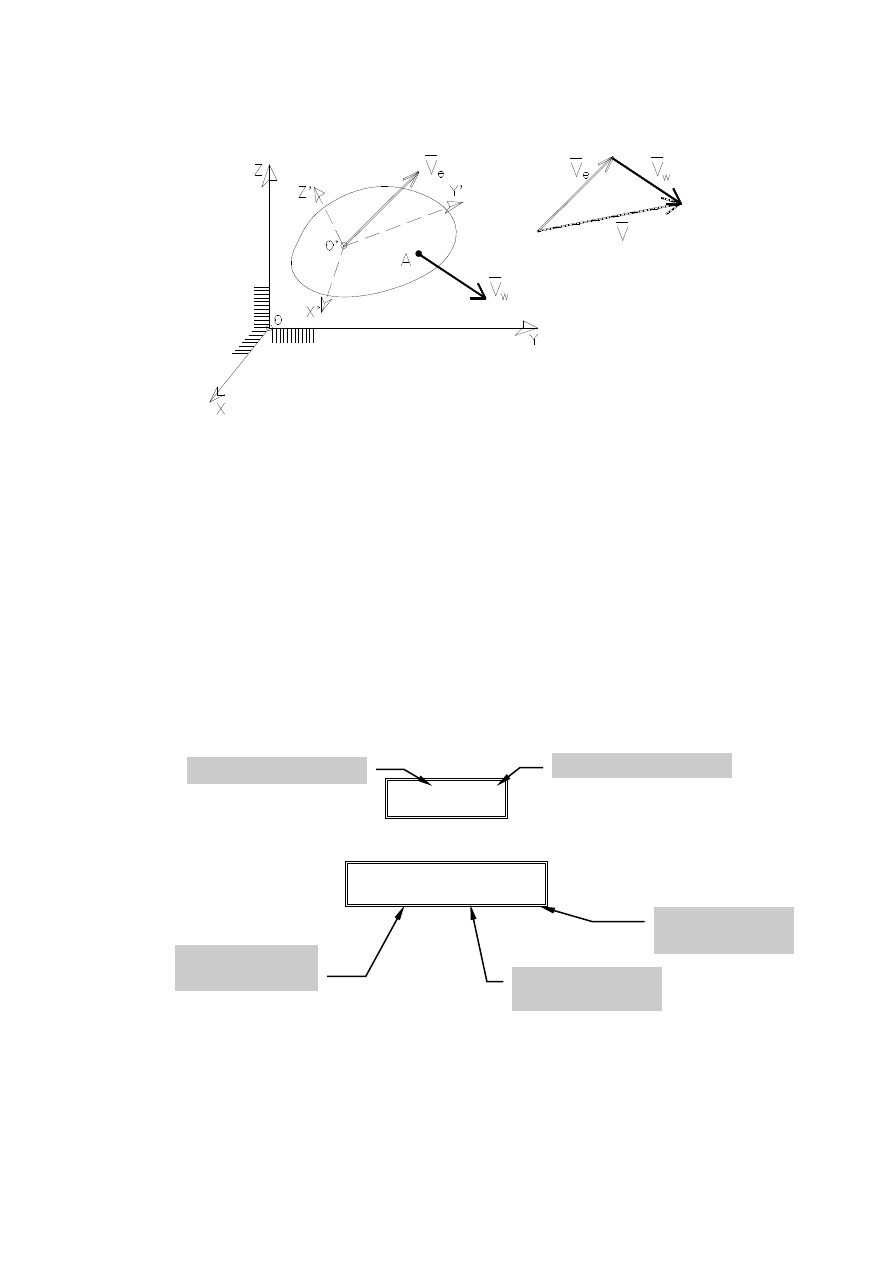
RUCH PŁASKI SKŁADA SIĘ Z CHWILOWEGO RUCHU POSTĘ-
POWEGO ORAZ CHWILOWEGO RUCHU OBROTOWEGO
0
A
0
A
v
v
v
OA
v
v
0
A
0
A
OA
Chwilowa prędkość kątowa względem bieguna
dt
d
= const
AO
O
A
a
a
a
n
AO
t
AO
AO
a
a
a
Całkowite przyspieszenie punktu A:
n
AO
t
AO
O
A
a
a
a
a
Prędkość dowol-
nego punktu A
Prędkość bieguna 0
(prędkość ruchu postępowego)
Prędkość punktu A
względem bieguna 0
(prędkość ruchu obrotowego)
Przyspieszenie punktu A
Przyspieszenie bieguna O
Przyspieszenie w chwilowym ruchu
obrotowym wokół bieguna A
Przyspieszenie styczne
Przyspieszenie normalne
04 Kinematyka.doc
62
RUCH ZŁOŻONY PUNKTU
OXYZ
– nieruchomy układ osi współrzędnych
O’X’Y’Z’ – ruchomy układ osi współrzędnych
Ruch bezwzględny punktu A względem OXYZ:
V
Ruch wzg
lędny punktu A względem O’X’Y’Z’:
w
V
Ruch unoszenia punktu
układu ruchomego O’X’Y’Z’
względem nieruchomego OXYZ:
u
V
Prędkość bezwzględna punktu A w ruchu złożonym jest wypad-
kową prędkości unoszenia
V
u
i prędkości względnej
V
w
.
u
w
V
V
V
Przyspieszenie w ruchu złożonym:
C
u
w
a
a
a
a
Przyspieszenie Coriolisa
– dodatkowe przyspieszenie, wynika-
jące z jednoczesności ruchu względnego i ruchu unoszenia.
Przyspieszenie Coriolisa
C
a
= 0 w ruchu unoszenia prostolinio-
wym oraz gdy wektor
jest równoległy do wektora
w
v
.
Przyspieszenie
względne
Przyspieszenie
unoszenia
Przyspieszenie
Coriolisa
Prędkość względna
Prędkość unoszenia
Wyszukiwarka
Podobne podstrony:
10 Manipulator robota w aspekcie kinematyki ciala sztywnego
kinematyka ciała sztywnego
7 KINEMATYKA CIAŁA SZTYWNEGO
7 Kinematyka 2, Wybrane przypadki ruchu ciala sztywnego
7 Kinematyka 2 Wybrane przypadki ruchu ciala sztywnego
5 dynamika ciala sztywnego id Nieznany (2)
Precesja regularna ciała sztywnego
Wyznaczanie elipsoidy bezwładności bryły, FIZYKA 1, WYZNACZANIE ELIPSOIDY BEZWŁADNOŚCI CIAŁA SZTYWNE
Wyznaczanie elipsoidy bezwładności bryły, FIZYKA 1, WYZNACZANIE ELIPSOIDY BEZWŁADNOŚCI CIAŁA SZTYWNE
fizyka 4 MECHANIKA CIAŁA SZTYWNEGO
Pomiar bezwladnosci ciala sztywnego za pomoca wahadla skretn, Księgozbiór, Studia, Mechnika Doświadc
Odkształcenie ciała sztywnego pod wpływem sił zewnętrznych polega na przemieszczaniu się cząsteczek
ZAGADNIENIA RÓWNOWAGI CIAŁA SZTYWNEGO
7. Wybrane przypadki ruchu ciala sztywnego
Wyprowadzić wzór na prędkość punktu ciała sztywnego poruszającego się ruchem płaskim, WAT, LOTNICTWO
więcej podobnych podstron