
Metoda Gaussa-Seidela
n
1
1
1
n
Gx
D
L
b
D
L
x
Przykład:
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1
0
1
2
0
0
0
0
2
.
0
0
0
0
1
0
0
0
0
D
4
0
0
0
0
10
0
0
0
0
5
0
0
0
0
4
L
0
0
0
0
1
0
0
0
2
0
0
0
0
2
.
0
1
0
G
25
.
0
0
0
0
0
1
.
0
0
0
0
0
2
.
0
0
0
0
0
25
.
0
L
1
A=(L+D)
-1
n
1
n
Gx
A
Ab
x
A
0.25
0.05
5 10
3
0.026
0
0.2
0
0.1
0
0
0.1
0.025
0
0
0
0.25
lub w postaci równań
1
n
,
3
1
n
,
2
1
n
,
4
n
,
4
1
n
,
1
1
n
,
3
n
,
4
1
n
,
1
1
n
,
2
n
,
3
n
,
2
1
n
,
1
x
25
.
0
x
5
.
0
25
.
1
x
x
1
.
0
x
02
.
0
1
x
x
4
.
0
x
2
.
0
x
x
05
.
0
x
25
.
0
5
.
7
x

x
1
7.5
1.5
0.85
1.788
x
2
7.832
2.282
0.665
2.225
x
5
8.109
2.573
0.6
2.386
x
10
8.115
2.579
0.599
2.39
0
0
0
0
x
0
Zerowe przybliżenie

x
10
8.11476764
2.57884338
0.59873219
2.38973864
x
11
8.11477423
2.57885030
0.59873065
2.38974249
x
12
8.11477604
2.57885220
0.59873023
2.38974354
x
15
8.11477671
2.57885291
0.59873007
2.38974394
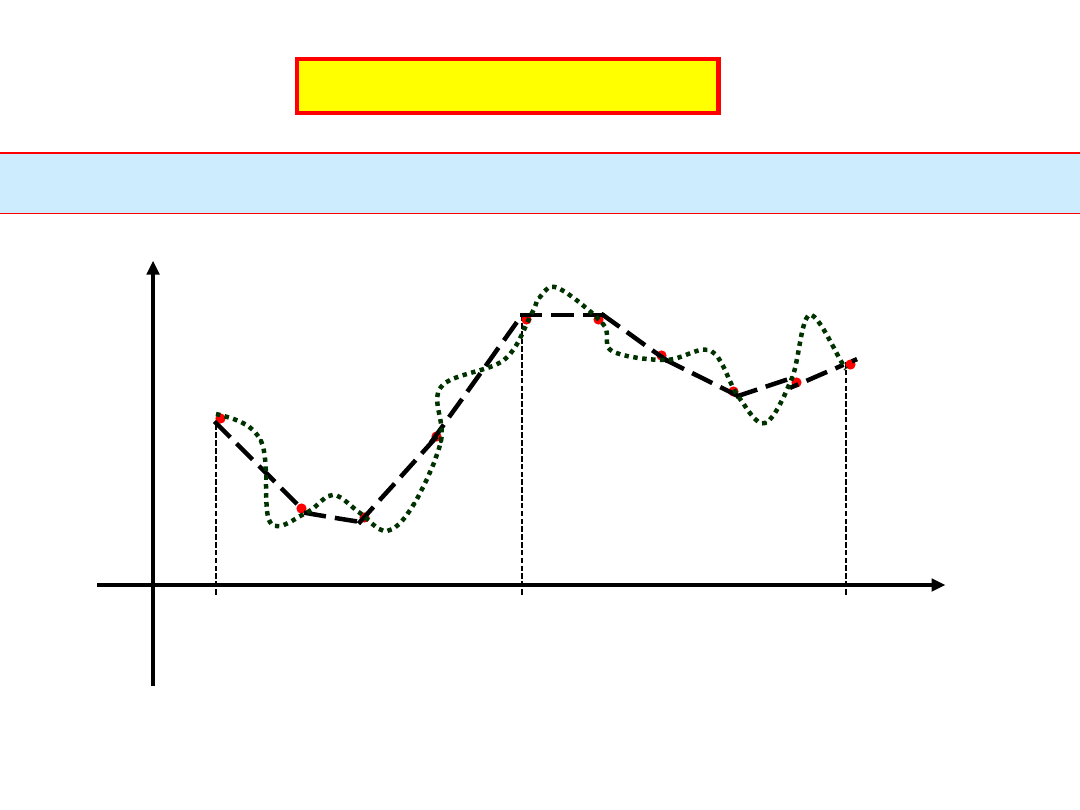
Interpolacja funkcji
Dane wartości funkcji y
n
w punktach x
n
, gdzie n=0,1,2, ....N-1.
x
y
x
0
y
0
x
n
y
n
x
N-1
y
N-1
Interpolacja wielomianowa
Twierdzenie
Istnieje dokładnie jeden wielomian stopnia co najwyżej N (N>=0),
który w punktach x
0
, x
1
,...,x
N-1
przyjmuje wartości y
0
,y
1
,...,y
N-1
.
Wzór interpolacyjny Lagrange'a:
)
x
(
y
....
)
x
(
y
)
x
(
y
)
x
(
W
1
N
1
N
1
1
0
0
n
gdzie
1
-
0,1,...N
=
k
dla
)
x
(
k
jest wielomianem stopnia co najwyżej N.
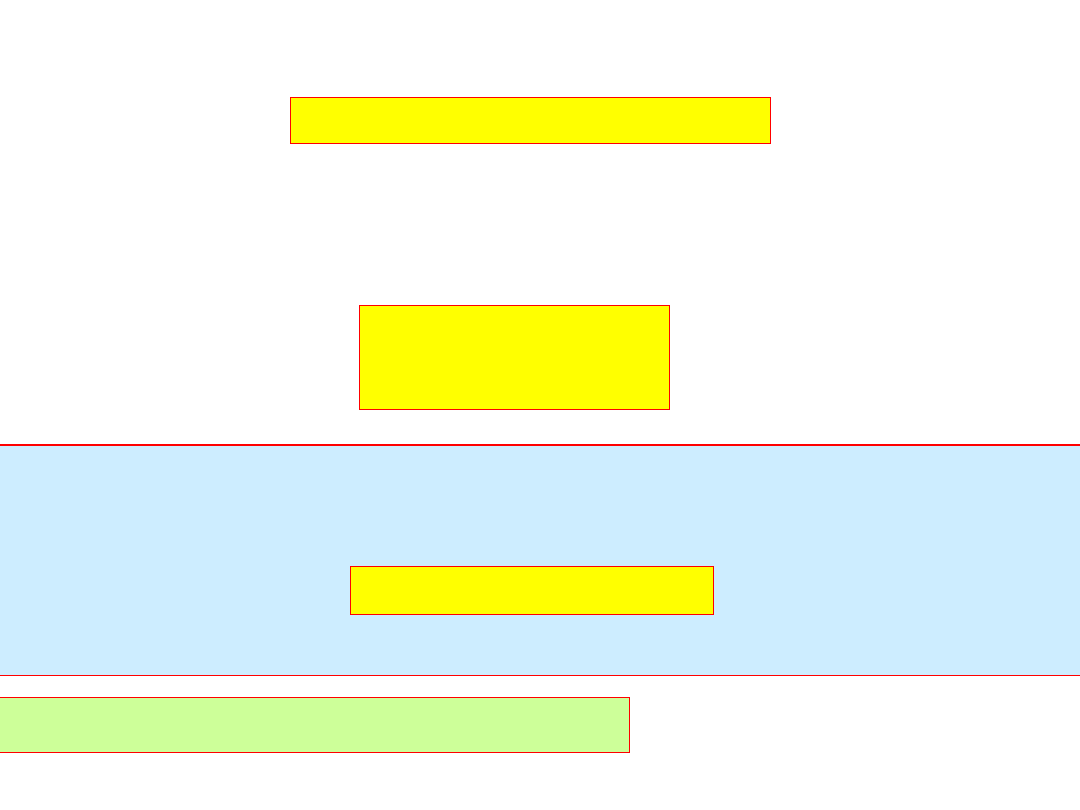
Z warunku interpolacyjnego:
1
-
N
0,1,....,
=
k
dla
y
)
x
(
W
k
k
N
powyższy układ N równań można najprościej rozwiązać
przyjmując dla wielomianów
k
(x) następujące warunki :
i
k
dla
1
i
k
dla
0
)
x
(
i
k
jako wielomian
k
(x) należy wybrać taki, który ma miejsca
zerowe we wszystkich punktach interpolacji
z wyjątkiem punktu x
k
, w którym funkcja ma wartość 1
,
1
N
1
k
1
k
1
0
x
,...,
x
,
x
,...,
x
,
x
Rozwiązaniem jest wielomian :

Rozwiązaniem jest wielomian:
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
A
)
x
(
1
N
1
k
1
k
1
0
k
z warunku:
otrzymuje się:
1
)
x
(
k
k
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
1
A
1
N
k
k
1
k
k
1
k
1
k
0
k
Wielomian Lagrange'a przyjmuje postać:
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
y
)
x
(
W
1
N
k
1
k
k
1
k
k
1
k
0
k
1
N
1
k
1
k
1
0
k
N
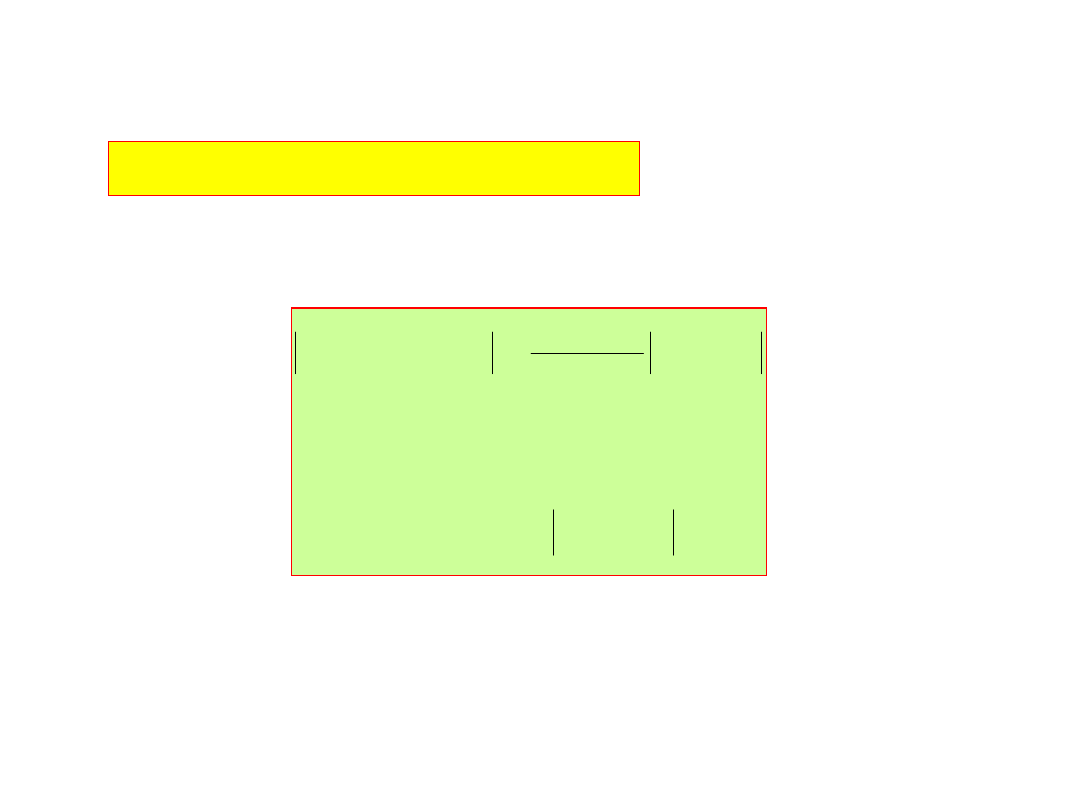
Ocena błędu interpolacji:
)
x
(
f
sup
M
)
x
x
(
)
x
(
gdzie
)
x
(
)!
1
N
(
M
)
x
(
W
)
x
(
f
)
1
N
(
]
b
,
a
[
x
1
N
N
k
0
k
k
1
N
1
N
1
n
N
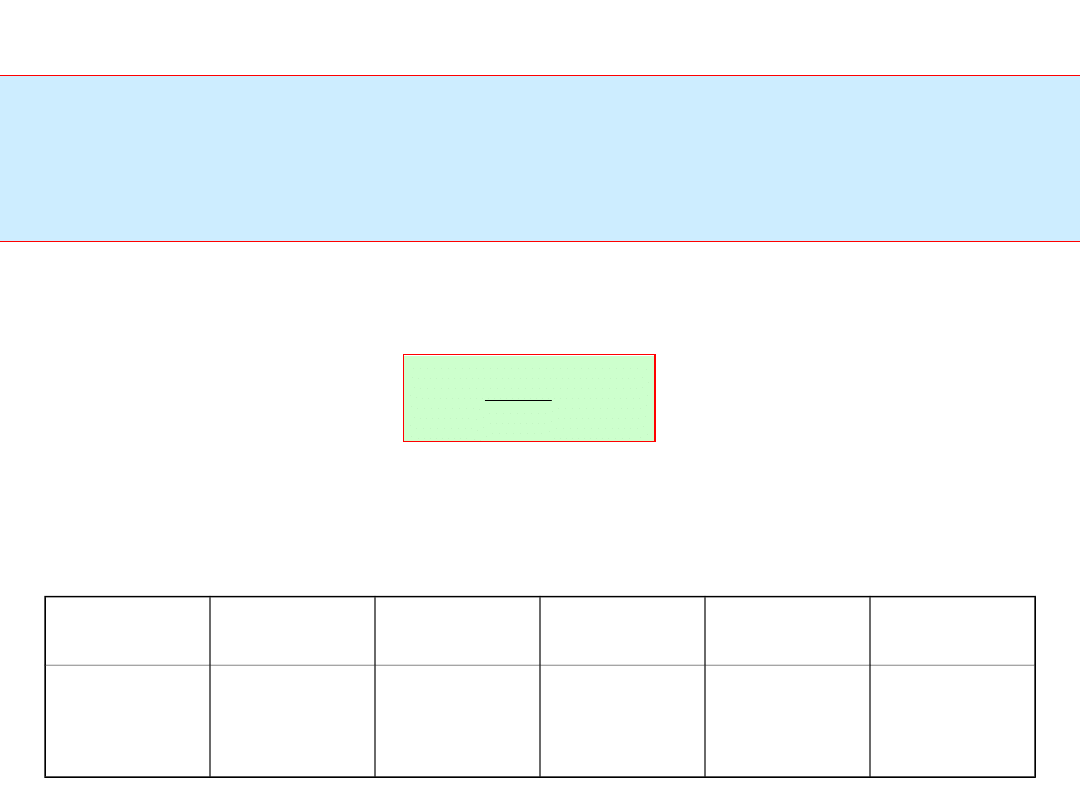
Przykład 1.
Zbudować wielomian interpolacyjny dla funkcji exp(x)
w przedziale [1,2] bazując na 5 węzłach interpolacyjnych.
Wybierzmy węzły równomiernie czyli
25
.
0
4
1
2
x
x
i
1.0
1.25
1.50
1.75
2.0
y
i
2.718
28
3.490
34
4.481
69
5.754
6
7.389
06
mamy:
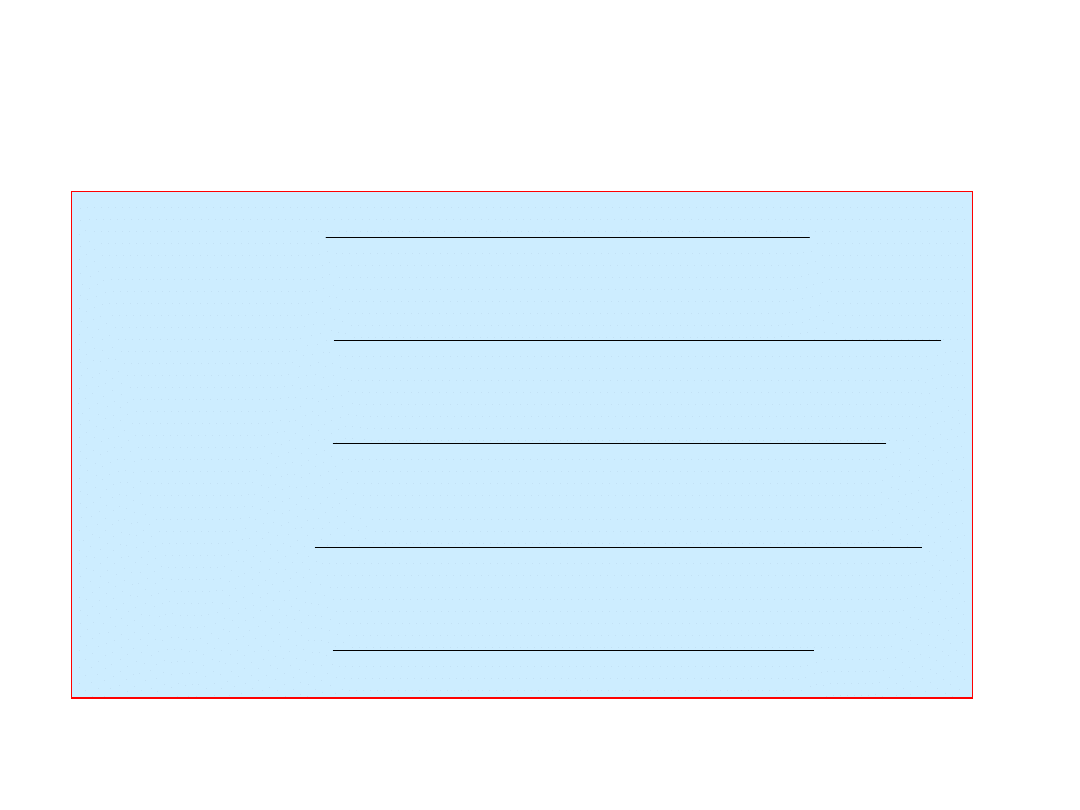
Wielomian Lagrange’a jest:
75
.
1
2
5
.
1
2
25
.
1
2
1
2
75
.
1
x
5
.
1
x
25
.
1
x
1
x
38906
.
7
2
75
.
1
5
.
1
75
.
1
25
.
1
75
.
1
1
75
.
1
2
x
5
.
1
x
25
.
1
x
1
x
7546
.
5
2
5
.
1
75
.
1
5
.
1
25
.
1
5
.
1
1
5
.
1
2
x
75
.
1
x
25
.
1
x
1
x
48169
.
4
2
25
.
1
75
.
1
25
.
1
5
.
1
25
.
1
1
25
.
1
2
x
75
.
1
x
5
.
1
x
1
x
49034
.
3
2
1
75
.
1
1
5
.
1
1
25
.
1
1
2
x
75
.
1
x
5
.
1
x
25
.
1
x
71828
.
2
)
x
(
W
4

lub
75
.
1
x
5
.
1
x
25
.
1
x
1
x
817
.
78
2
x
5
.
1
x
25
.
1
x
1
x
53
.
245
2
x
75
.
1
x
25
.
1
x
1
x
83
.
286
2
x
75
.
1
x
5
.
1
x
1
x
92
.
148
2
x
75
.
1
x
5
.
1
x
25
.
1
x
995
.
28
)
x
(
W
4
Wyniki obliczeń przedstawiono na wykresie:
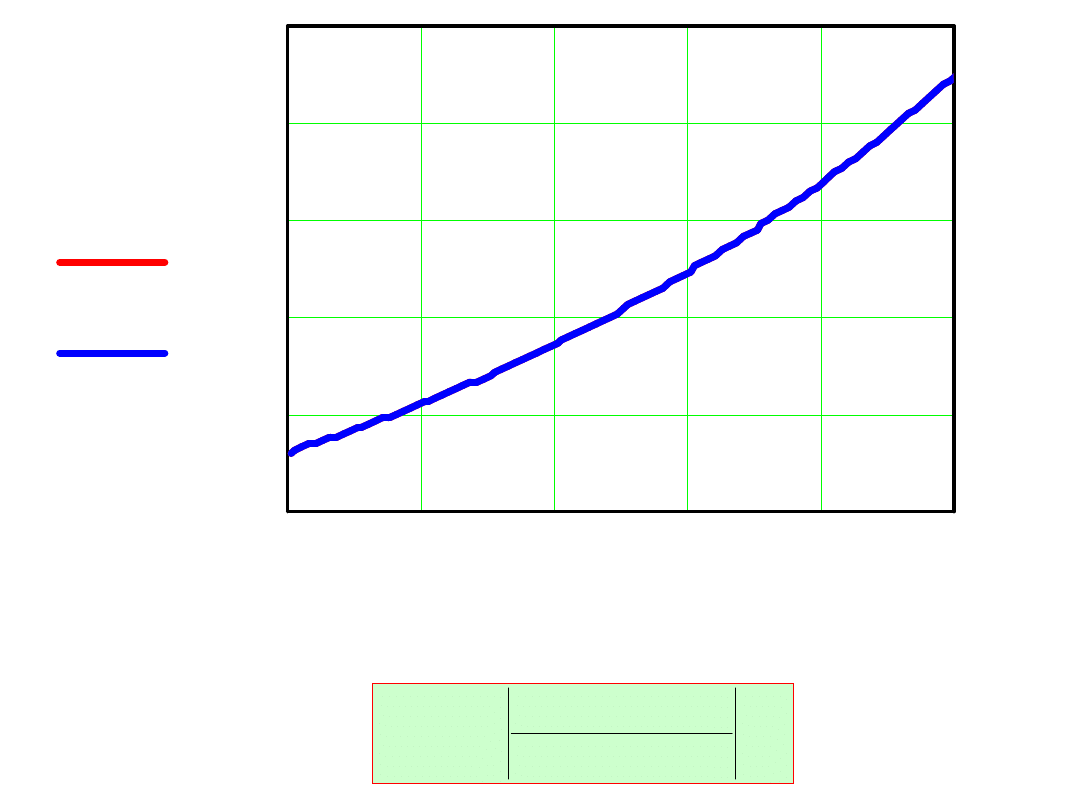
1
1.2
1.4
1.6
1.8
2
2
3.2
4.4
5.6
6.8
8
w x
( )
expx
( )
x
Dla lepszej oceny wykres błędu względnego:
100
)
x
exp(
)
x
exp(
)
x
(
w
)
x
(
eps
4
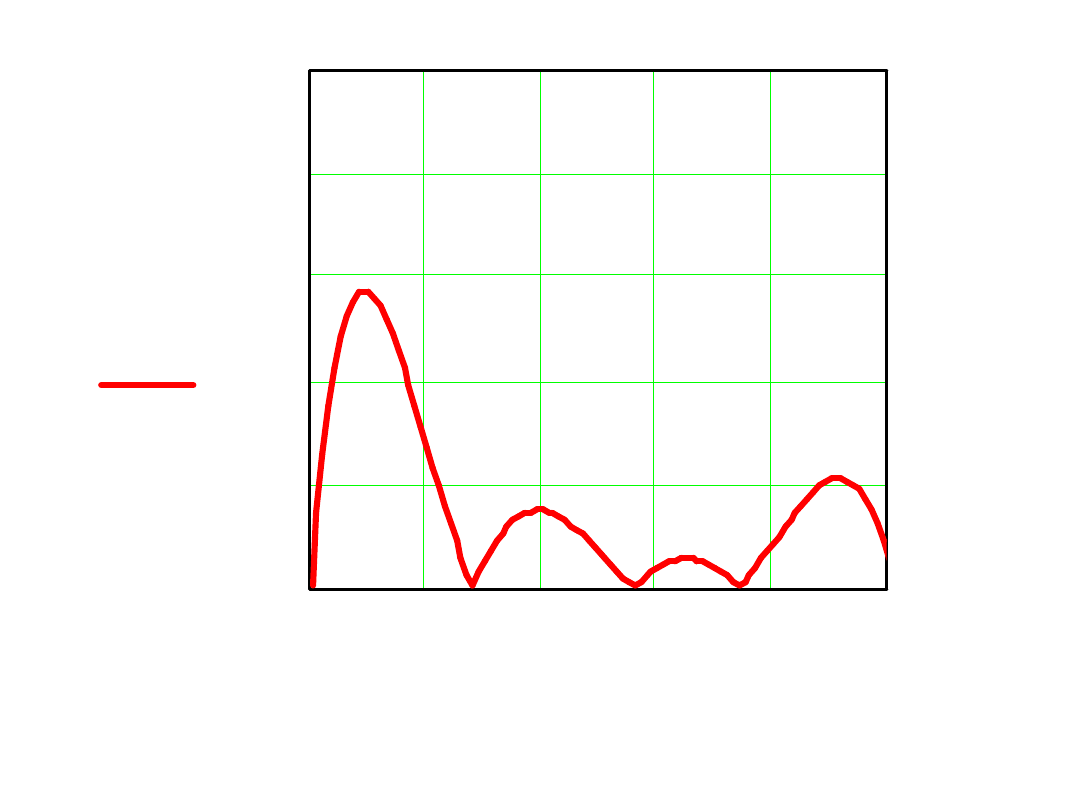
1
1.2
1.4 1.6
1.8
2
0
0.002
0.004
0.006
0.008
0.01
eps x
( )
x
Przykład 2.
W wyniku pomiarów zdjęto pierwotną krzywą magnesowania
B=F(H). Zbudować wielomian interpolacyjny Lagrange'a
dla zakresu 0<=H <=3000A/m.
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
Kolejne wielomiany
k
(H) dla k=0,1,...8 są:
3000
0
2000
0
1500
0
1000
0
3000
H
2000
H
1500
H
1000
H
500
0
200
0
100
0
50
0
500
H
200
H
100
H
50
H
H
0
lub po obliczeniu mianownika mamy:

3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
10
2222
.
2
H
22
0
3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
H
10
4784
.
7
H
22
1
3000
H
2000
H
1500
H
1000
H
500
H
200
H
50
H
H
10
2019
.
7
H
22
2
3000
H
2000
H
1500
H
1000
H
500
H
100
H
50
H
H
10
1198
.
2
H
22
3
3000
H
2000
H
1500
H
1000
H
200
H
100
H
50
H
H
10
9753
.
1
H
23
4
3000
H
2000
H
1500
H
500
H
200
H
100
H
50
H
H
10
924
.
2
H
24
5
3000
H
2000
H
1000
H
500
H
200
H
100
H
50
H
H
10
7366
.
6
H
25
6
3000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
9965
.
9
H
26
7
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
8554
.
1
H
26
8
i wielomian aproksymacyjny jest
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
0
H
B
8
7
6
5
4
3
2
1
0
lub
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
B
8
7
6
5
4
3
2
1
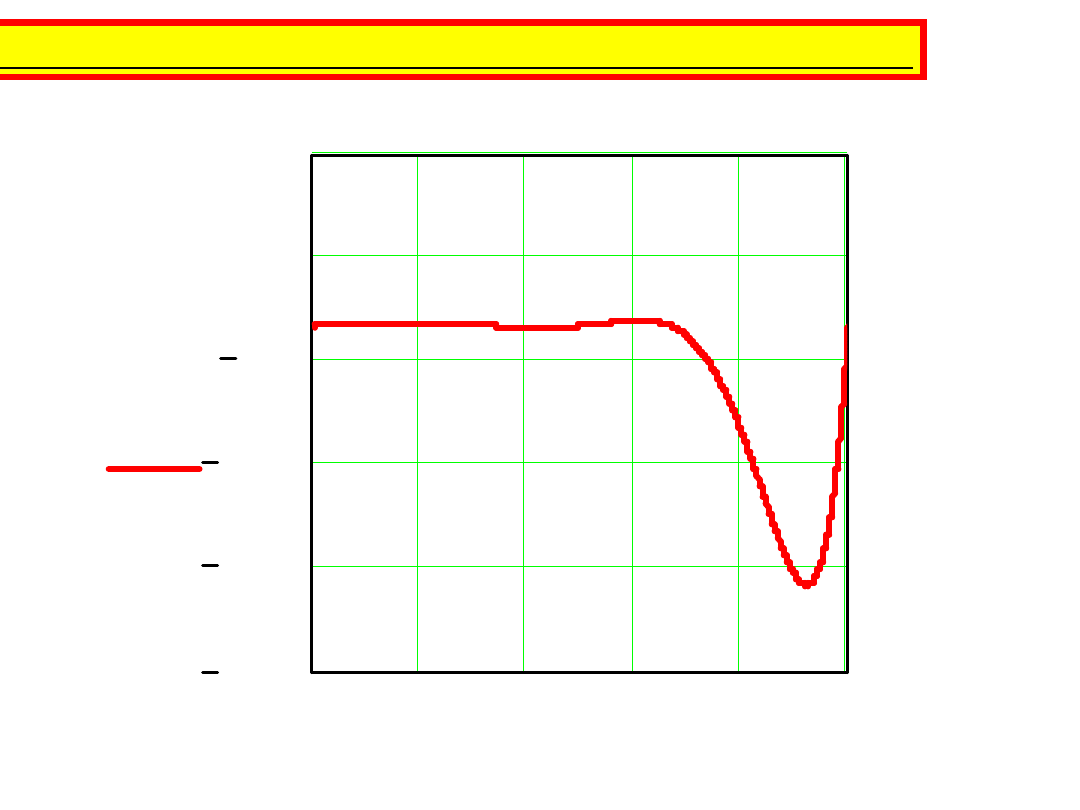
0
600 1200 1800 2400 3000
4000
2800
1600
400
800
2000
B H
( )
H
Otrzymany wynik jest niemożliwy do przyjęcia!!!
Interpolacja liniowa odcinkami:
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
0
50
0
H
75
.
0
50
0
50
H
0
H
B
1
dla
50
H
0
lub po wykonaniu działań:
H
015
.
0
H
B
1
50
H
0
dla
i podobnie:
50
H
03
.
0
100
H
015
.
0
H
B
2
dla
100
H
50
100
H
018
.
0
200
H
015
.
0
H
B
3
dla
200
H
100
200
H
0065
.
0
500
H
006
.
0
H
B
4
500
H
200
dla
500
H
004
.
0
1000
H
0039
.
0
H
B
5
dla
1000
H
500
1000
H
00404
.
0
1500
H
004
.
0
H
B
6
dla
1500
H
1000
1500
H
00406
.
0
2000
H
00404
.
0
H
B
7
dla
2000
H
1500
2000
H
002035
.
0
3000
H
00203
.
0
H
B
8
dla
3000
H
2000
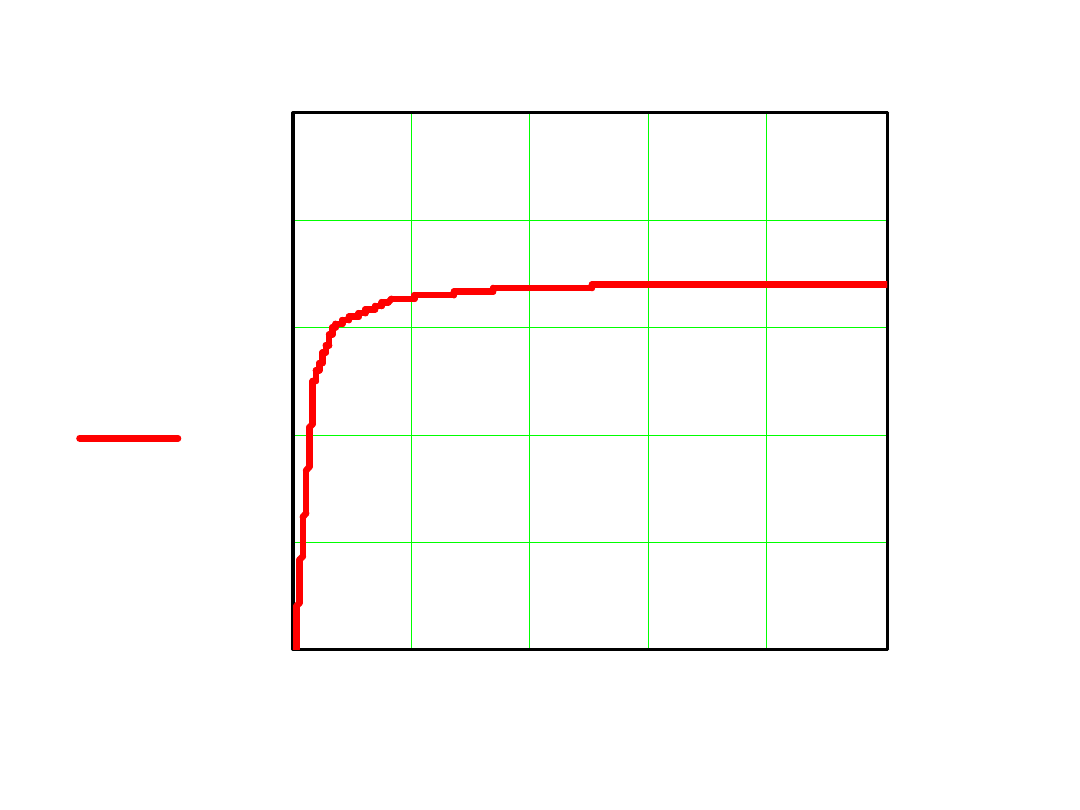
0
600 1200 1800 2400 3000
0
0.6
1.2
1.8
2.4
3
BaH
( )
H
B(H)
0
100 200 300 400 500
0
0.4
0.8
1.2
1.6
2
BaH
( )
B H
( )
H
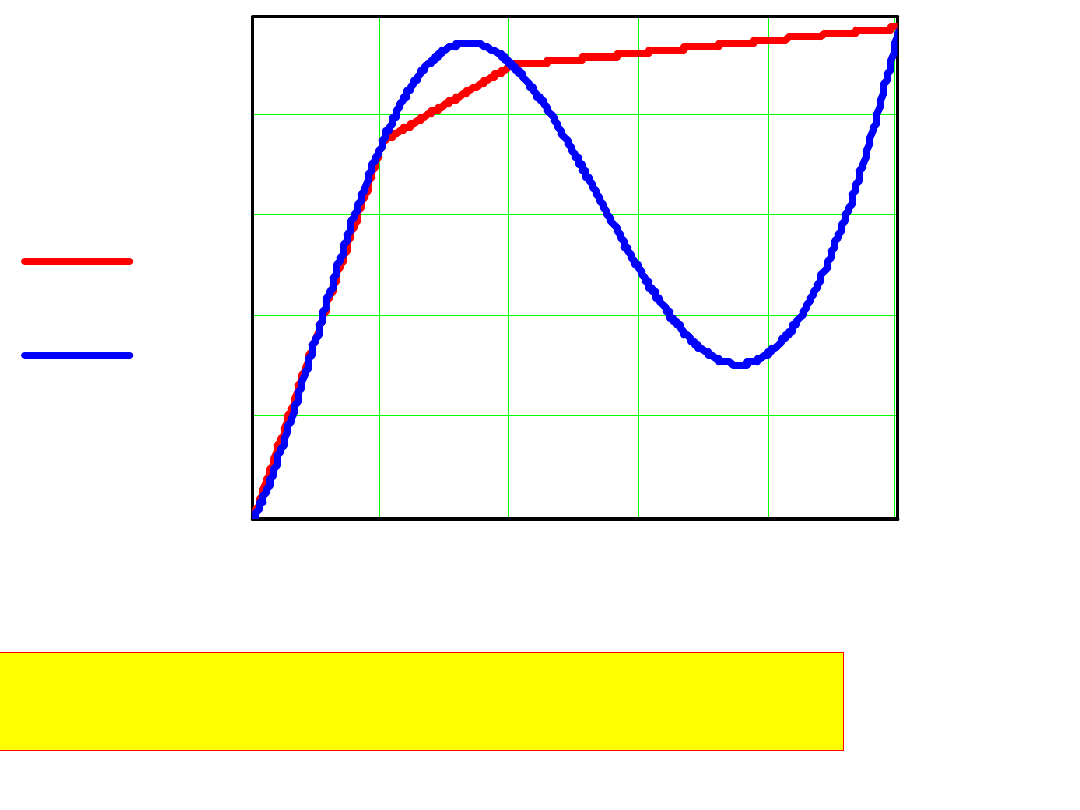
Porównanie Ba(H) – interpolacja liniowa
B(H) – wielomian 8-go stopnia
Optymalny dobór węzłów interpolacji.
Dobrać węzły interpolacji tak aby kres górny wielomianu
)
x
(
sup
1
n
]
b
,
a
[
x
był jak najmniejszy.
Rozwiązanie otrzymuje się za pomocą wielomianów Czebyszewa.
Są to wielomiany zdefiniowane na przedziale x [-1,1]
i są zdefiniowane :
)
x
arccos
n
cos(
)
x
(
T
n
Przykładowe wykresy dla n=1,2,3,4:
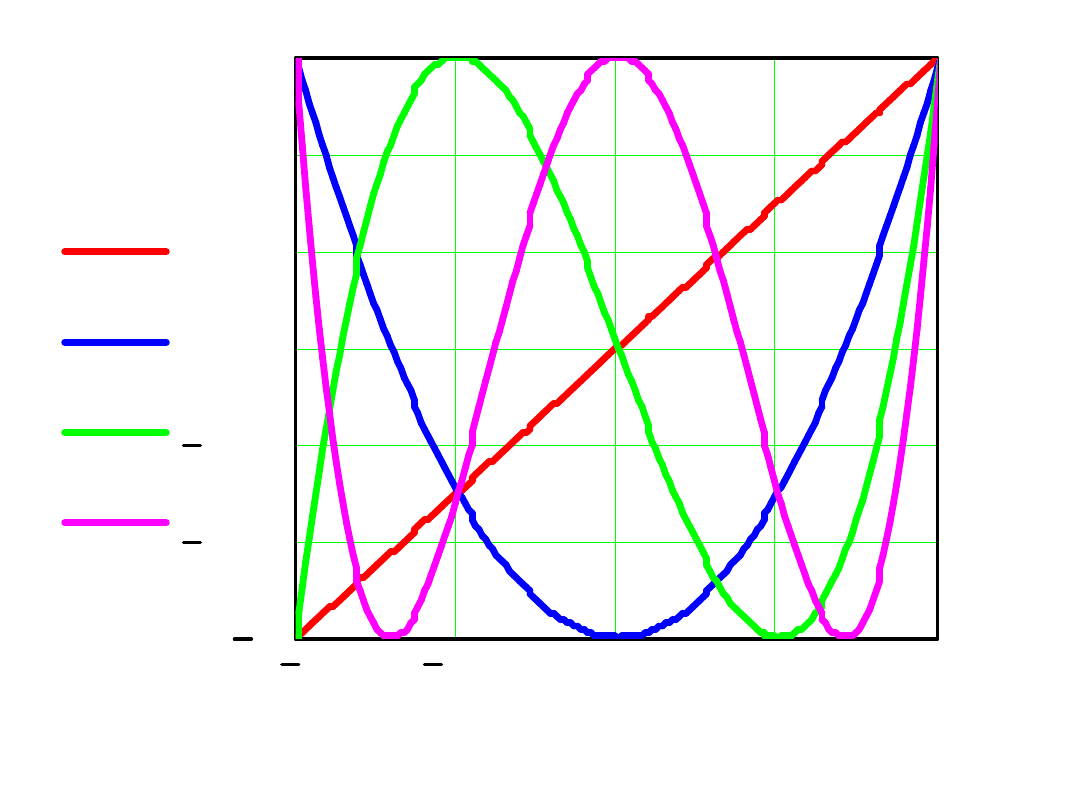
1
0.5
0
0.5
1
1
0.67
0.33
0
0.33
0.67
1
T 1 x
(
)
T 2 x
(
)
T 3 x
(
)
T 4 x
(
)
x

Wielomiany spełniają następujące związki:
x
3
x
4
)
x
(
T
1
x
2
)
x
(
T
.
2,3,4,....
=
n
dla
)
x
(
T
)
x
(
xT
2
)
x
(
T
x
)
x
cos(arccos
)
x
(
T
1
)
x
(
T
3
3
2
2
2
n
1
n
n
1
0
Każdy z wielomianów ma n różnych pierwiastków określonych
zależnością:
1
-
n
0,1,2,...,
=
m
gdzie
)
n
2
1
m
2
cos(
x
m
w przedziale [-1,1].

Współczynnik przy najwyższej potędze x we wielomianie
wynosi 2n-1.
Dowodzi się, że jeżeli dla przedziału [-1,1] dobrać pierwiastki
zgodnie z zależnością
określającą pierwiastki wielomianu Czebyszewa to zachodzi:
)
n
2
1
m
2
cos(
x
m
n
1
n
]
1
,
1
[
x
1
n
n
1
n
2
1
)
x
(
sup
)
x
(
T
2
1
)
x
(
stąd wynika
czyli ocena błędu w przedziale [-1,1] jest:
)!
1
n
(
2
M
)
x
(
W
)
x
(
f
n
1
n
n
Problem jest rozwiązany w przedziale [-1,1].
Aby go rozwiązać w przedziale [a,b] należy dokonać odwzorowania
przedziału [a,b] na przedział [-1,1].
Niech
]
1
,
1
[
z
a
]
b
,
a
[
x
otrzymujemy
a
b
a
x
2
1
z
-1
1
z
a
b
x
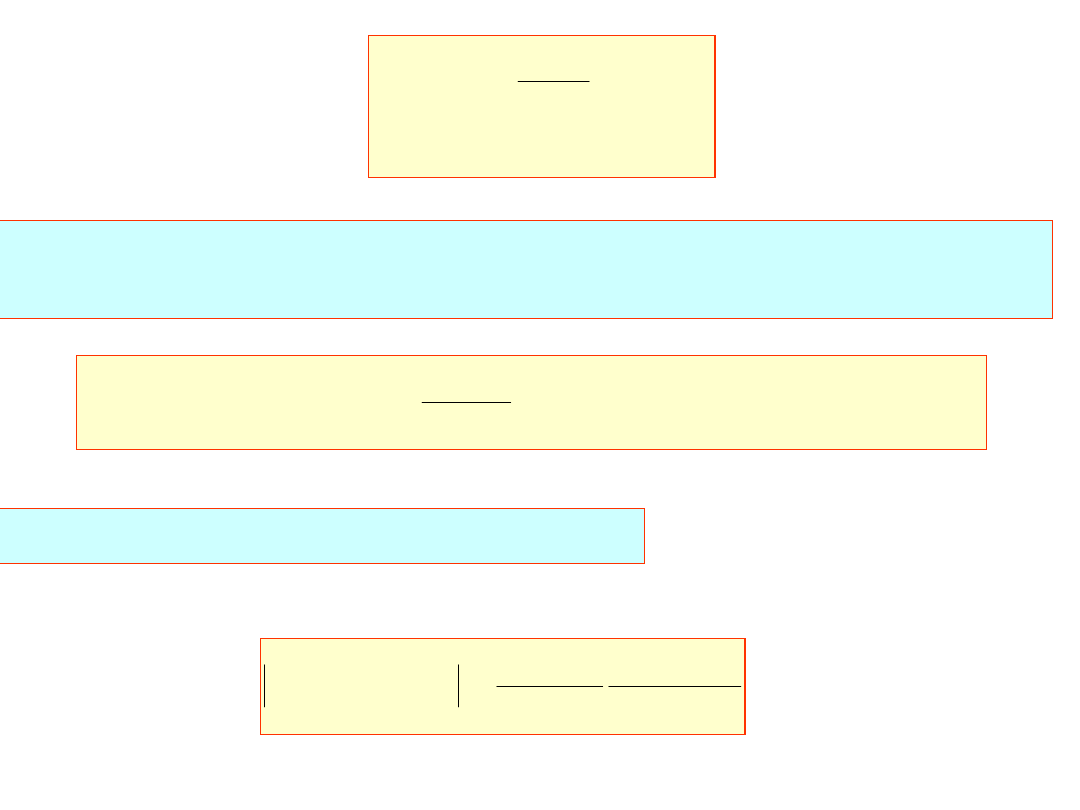
i stąd mamy:
)
1
z
)(
a
b
(
5
.
0
a
x
a
b
a
x
2
1
z
Dla przedziału [a,b] należy dla optymalnej interpolacji
wybrać punkty według zależności:
1
-
n
0,1,2,...,
=
k
dla
1
)
n
2
1
k
2
cos(
)
a
b
(
5
.
0
a
x
k
Ocena błędu przyjmuje postać:
1
n
2
1
n
1
n
n
2
)
a
b
(
)!
1
n
(
M
)
x
(
W
)
x
(
f
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
Wyszukiwarka
Podobne podstrony:
Wyklad mn 2
Wyklad mn 9
Wyklad mn no 8 piątek
Wyklad mn 16
Wyklad mn 9
Wyklad mn 3
Wyklad mn no 7 piątek
Wyklad mn 6
Wyklad mn no 4 piątek
Wyklad mn 12
Wyklad mn 10
Wyklad mn 6
Wyklad mn 15
Wyklad mn no 5 piątek
Wyklad mn 8
Wyklad mn no 6 piątek
Wyklad mn 5
Wyklad mn 8
Wyklad mn no 3 piątek
więcej podobnych podstron