Wyznaczanie obszaru stabilności bezwzględnej

Przekształćmy równanie charakterystyczne

0

z

b

z

a

z

p

1

i

i

p

i

p

0

i

i

p

i

1

p

























do postaci:

























p

1

i

i

p

i

p

0

i

1

p

i

1

p

z

b

z

a

z

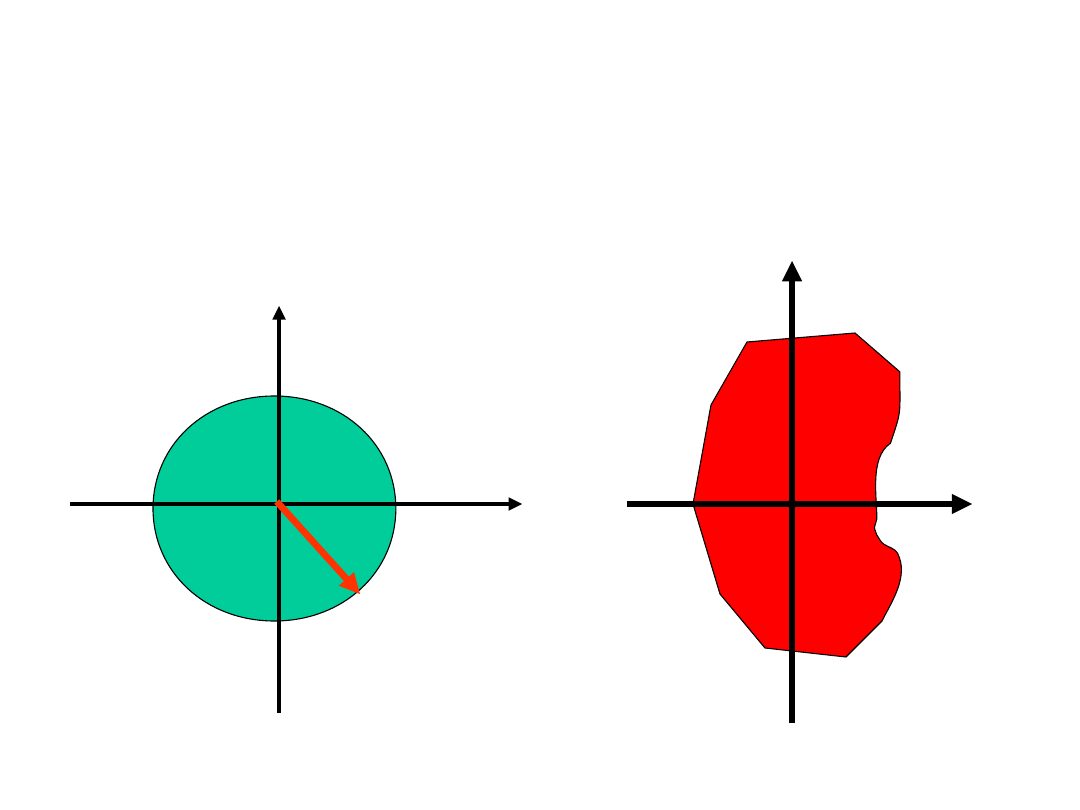
i stawiamy pytanie odwrotnie:
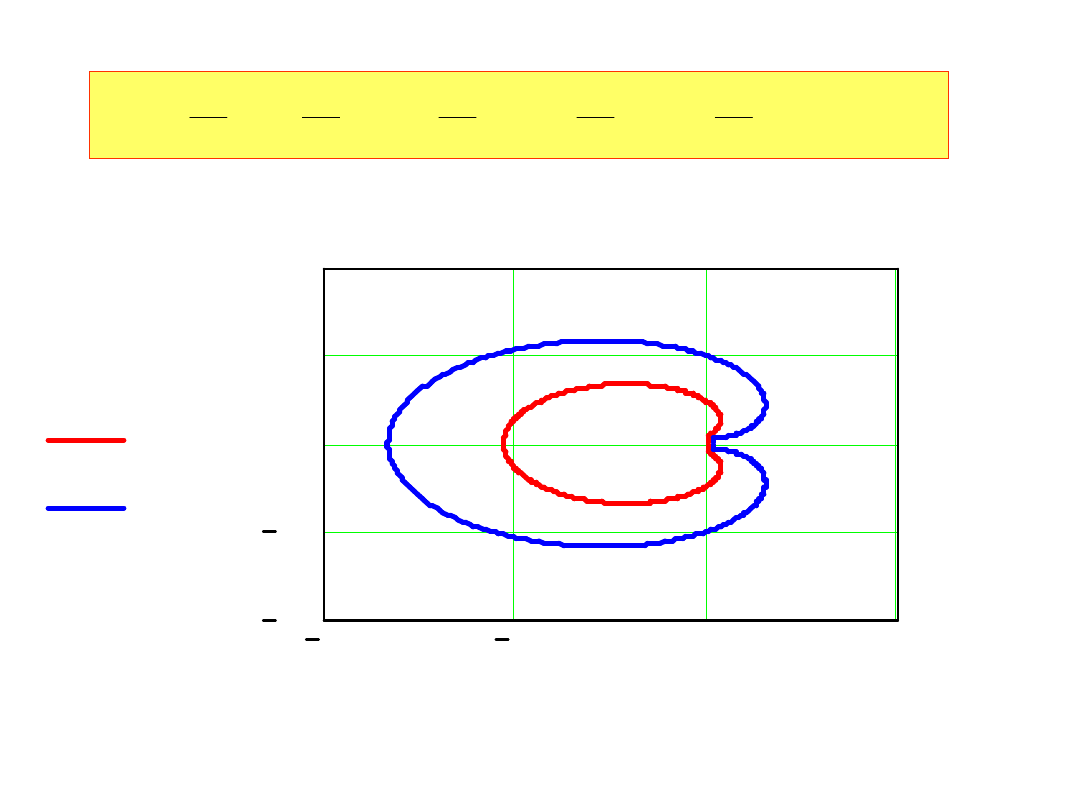
Jeżeli z leży wewnątrz lub na kole jednostkowym
to gdzie będzie leżało 

x

iy





i

e

z

płaszczyzna z

płaszczyzna 

Re()

Im()

Przykłady metoda jawna Adamsa - Bashfortha
schemat Eulera





n

n

n

1

n

t

,

x

hf

x

x







Przyjmując, że z leży na okręgu jednostkowym





i

e

z

i podstawiając do równania:

























p

1

i

i

p

i

p

0

i

1

p

i

1

p

z

b

z

a

z

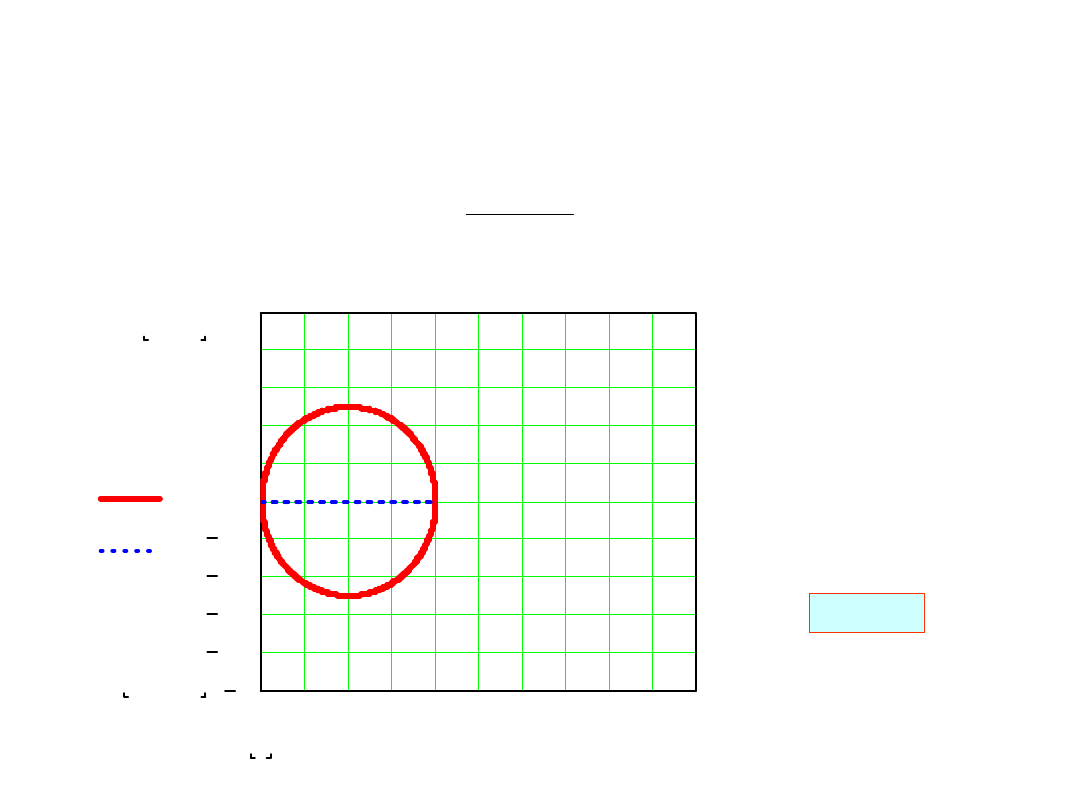
dla metody Eulera otrzymujemy:

 

















i

i

e

1

1

e

1

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

2

1.6

1.2

0.8

0.4

0

0.4

0.8

1.2

1.6

2

2.386

2.386



Ims 

 





Ims 0

( )

(

)

5

0

Res 

 





Wnętrze
koła i dla
rzeczywistych 

mamy:

2

h



Algorytm Adamsa – Bashfortha II-go rzędu





























1

n

1

n

n

n

n

1

n

t

,

x

f

2

1

t

,

x

f

2

3

h

x

x

i po odpowiednich przekształceniach mamy:

 

2

1

e

2

3

e

e

i

i

2

i

















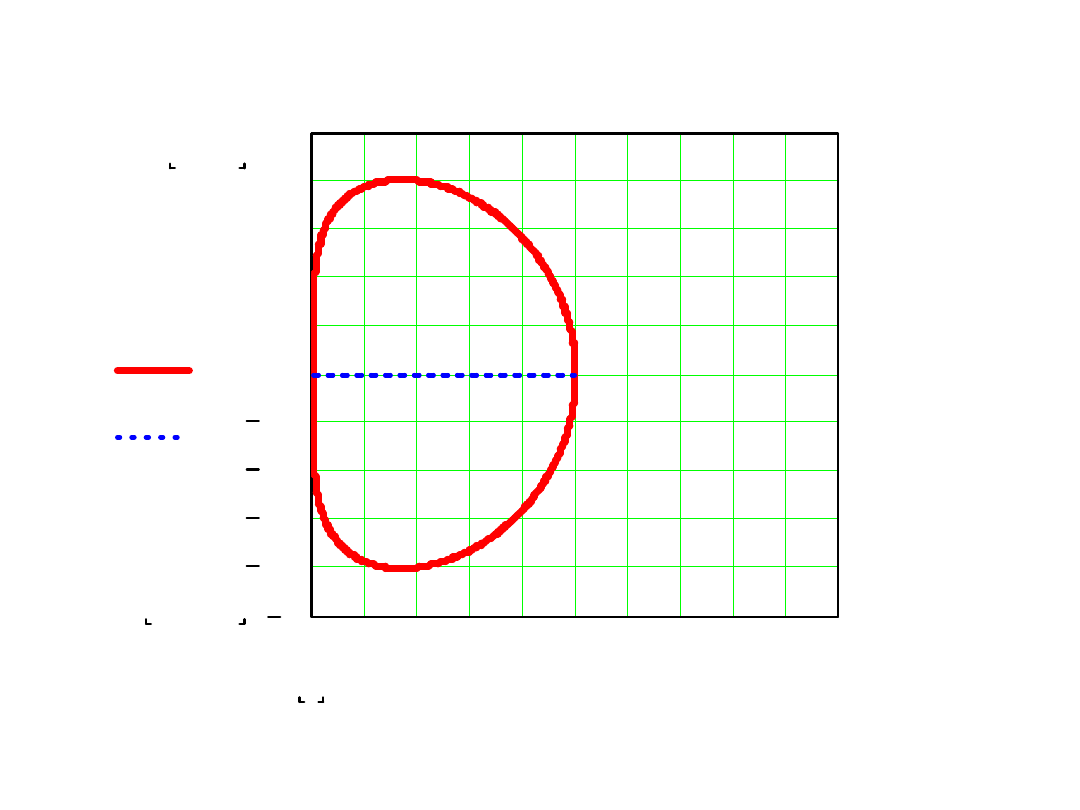
Odwzorowanie koła jednostkowego jest

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

0.955

0.955



Ims 

 





Ims 0

( )

(

)

2

0

Res 

 





1

h 



Jeżeli 

rzeczywiste

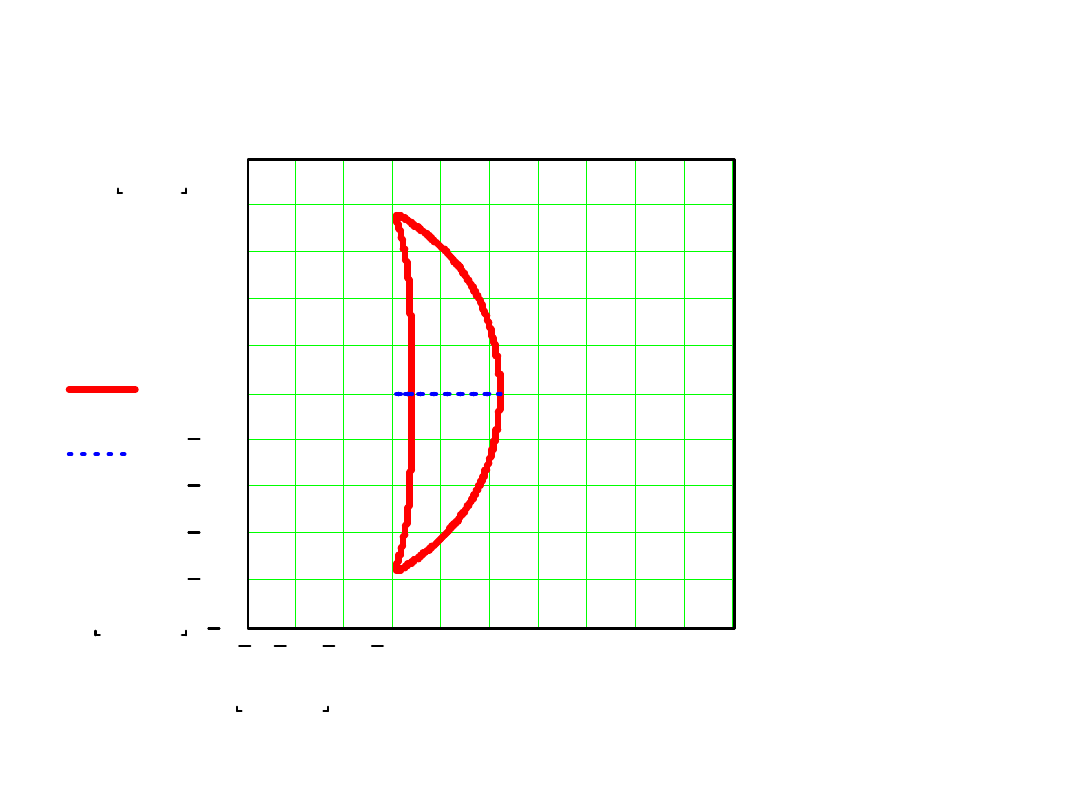
Dla rzędu III-go

1 0.7 0.4 0.10.2 0.5 0.8 1.1 1.4 1.7 2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

1.001

1.001



Ims 

 





Ims 0

( )

(

)

2

0.097



Res 

 





Dla rzeczywistych



5

.

0

h



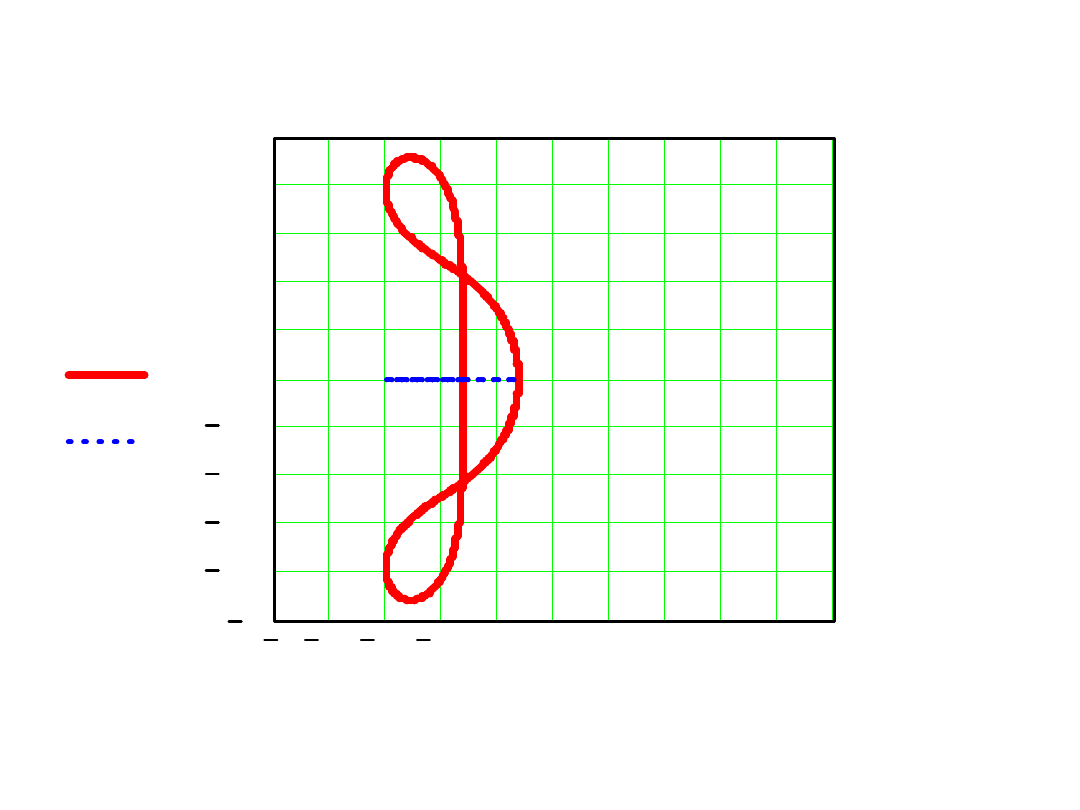
Dla czwartego rzędu

1 0.7 0.4 0.10.2 0.5 0.8 1.1 1.4 1.7 2

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

Ims 

 





Ims 0

( )

(

)

Res 

 





h jeszcze mniejsze niż dla metody rzędu trzeciego

Metody niejawne Adamsa – Moultona
metoda niejawna Eulera





1

n

1

n

n

1

n

t

,

x

hf

x

x











Obszar stabilności określa równanie:

 













i

e

1

Jest to równanie okręgu o środku w punkcie –1
i promieniu 1. Obszar stabilności na zewnątrz
tego okręgu.

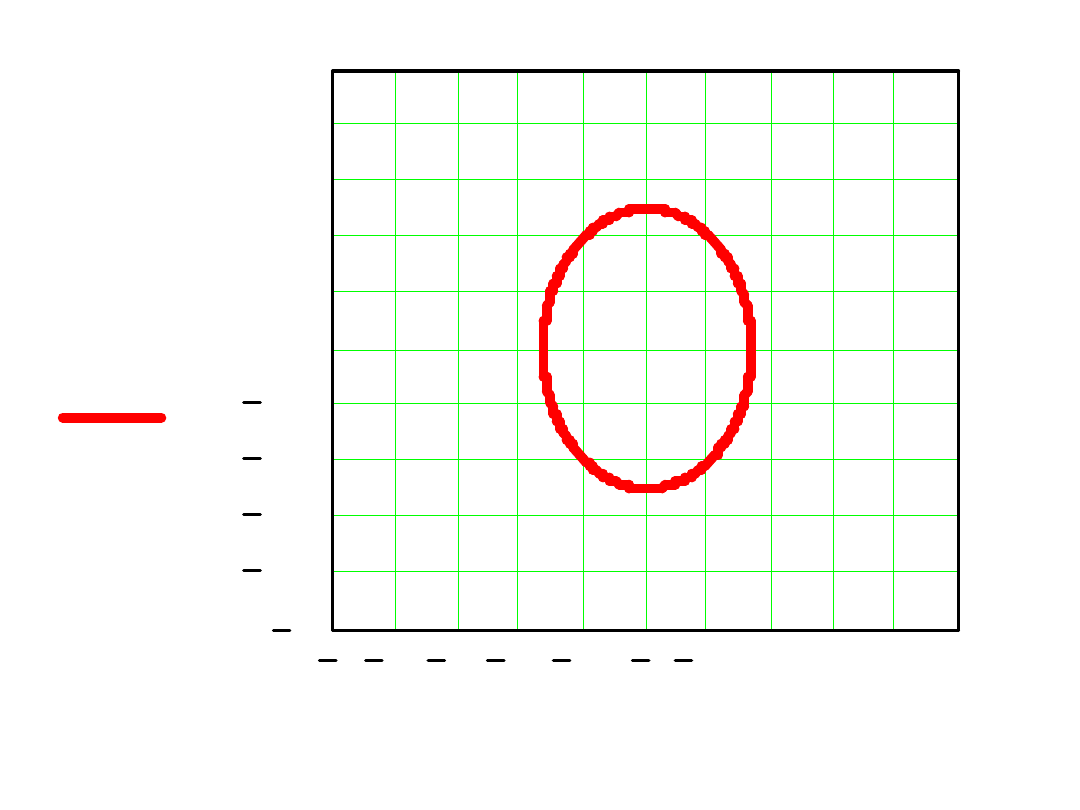
4 3.42.82.21.6 1 0.40.20.81.4 2

2

1.6

1.2

0.8

0.4

0

0.4

0.8

1.2

1.6

2

2

2



Imv 

 





2

4



Rev 

 





Oznacza to, że

niejawna metoda Eulera:





1

n

1

n

n

1

n

t

,

x

hf

x

x











jest stabilna dla dowolnej długości kroku h.

Oczywiście nie możemy zapomnieć o fizyce procesu

opisywanego równaniem czy układem równań różniczkowych

Algorytm II-go rzędu (algorytm trapezów)



 







n

n

1

n

1

n

n

1

n

t

,

x

f

t

,

x

f

2

h

x

x













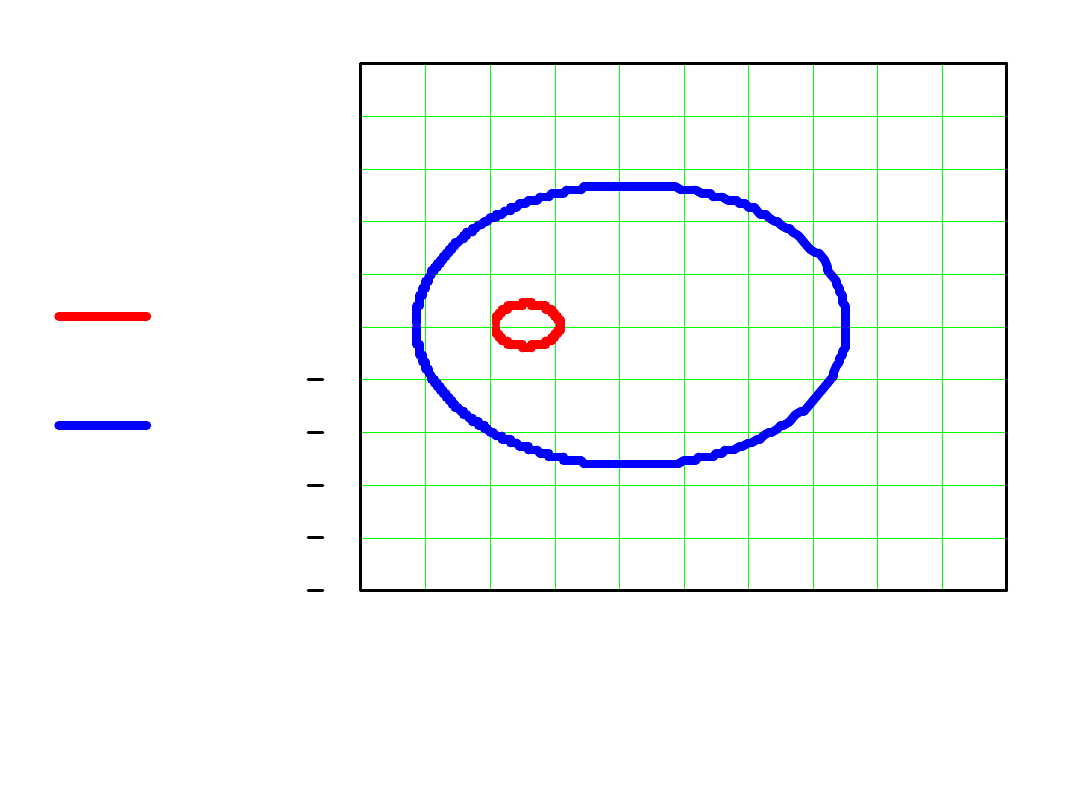
Dla odwzorowania koła jednostkowego mamy:

 





2

itg

2

1

e

2

1

e

1

i

i





















Badamy jak odwzorowuje się koło





i

re

z

czyli



















i

i

re

1

re

1

2

,

r

0 0.81.62.43.2 4 4.85.66.47.2 8

5

4

3

2

1

0

1

2

3

4

5

Imu 0.1











Imu 0.5











Reu 0.1











Reu 0.5













Wnętrze koła odwzorowuje się na prawą półpłaszczyznę

co oznacza, że jeżeli rozwiązanie równania jest stabilne,

czyli

Re()  0

, to krok całkowania h może być dowolny.

Zawsze nie możemy zapomnieć o fizyce procesu

opisywanego równaniem czy układem równań różniczkowych

i to jest główne ograniczenie wielkości kroku.

Algorytm III-go rzędu Adamsa - Moultona







































1

n

1

n

n

n

1

n

1

n

n

1

n

t

,

x

f

12

1

t

,

x

f

12

8

t

,

x

f

12

5

h

x

x





12

1

z

12

8

12

z

5

1

z

z

2













i dla koła jednostkowego





i

e

z

czyli





1

e

8

e

5

1

e

e

12

i

i

2

i

i





















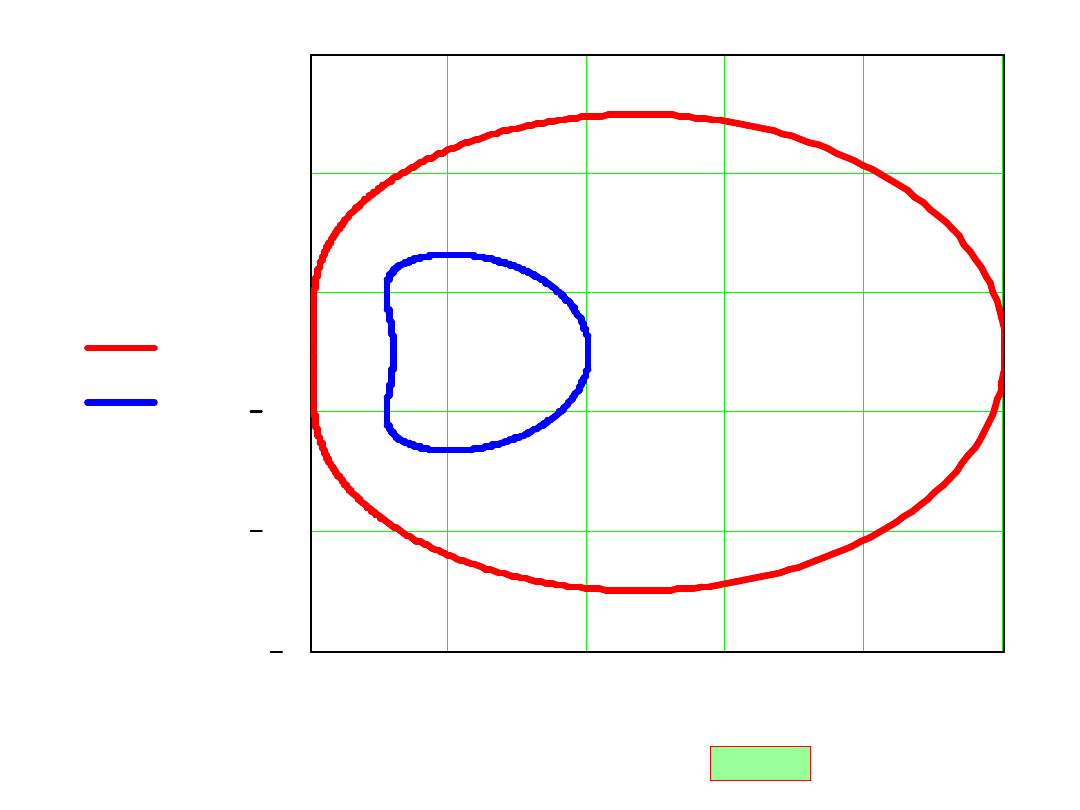
dla rzeczywistych  mamy warunek:

6

h 



0

1.2

2.4

3.6

4.8

6

4

2.4

0.8

0.8

2.4

4

Im 1 











Im 0.5











Re  1 











Re  0.5













Algorytm VI-go rzędu Adamsa - Moultona

















2

n

2

n

1

n

1

n

n

n

1

n

1

n

n

1

n

t

,

x

f

24

1

t

,

x

f

24

5

t

,

x

f

24

19

t

,

x

f

24

9

h

x

x



































24

1

z

24

5

z

24

19

24

z

9

1

z

z

2

3

2















i mamy odwzorowanie:

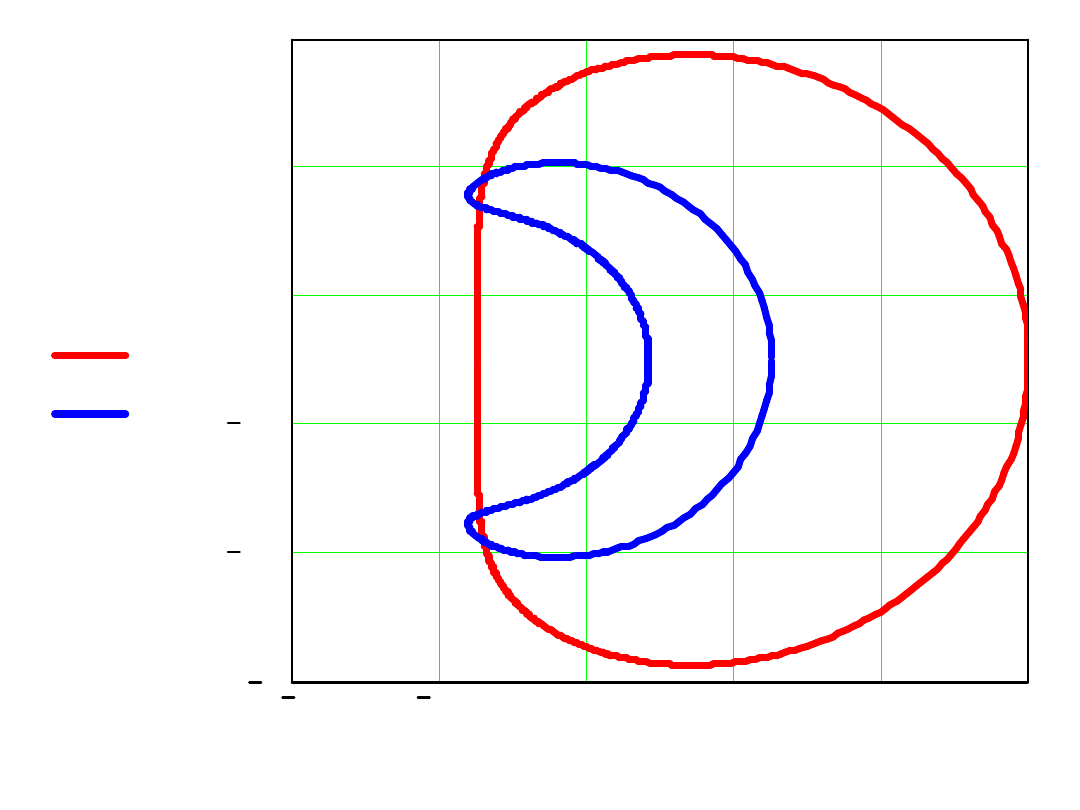
1

0.2

0.6

1.4

2.2

3

2

1.2

0.4

0.4

1.2

2

Im 1 











Im 0.5











Re  1 











Re  0.5













i

3

h



Zbierając wyniki:

Metody jawne Adamsa – Bashfortha:

5

.

0

h

1

h

2

h













i algorytm niejawny Adamsa –Moultona:

h – dowolny

h  – dowolny

h  < 6

h  < 3

Otrzymane wyniki pokazują wyższość metod niejawnych

nad metodami jawnymi.

W metodzie predyktor – korektor, gdzie metoda jawna
służy tylko i wyłącznie do otrzymania zerowego przybliżenia
rozwiązania równania metody niejawnej, o stabilności
decyduje

tylko metoda niejawna.

Jak widać również z podanych ocen z punktu widzenia
stabilności zbyt wysoki rząd metody nie jest korzystny

Równania sztywne

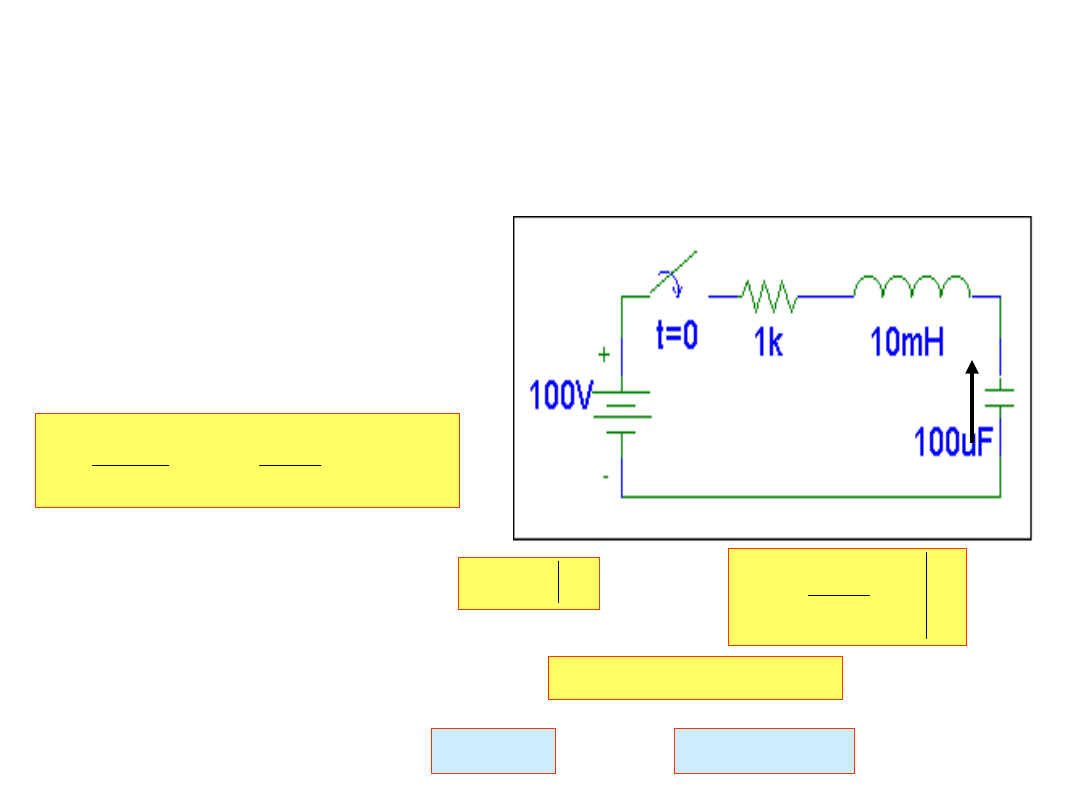
Dany jest obwód elektryczny:

u

C

Równanie różniczkowe

dla napięcia u

C

na kondensatorze jest:

E

u

dt

du

RC

dt

u

d

LC

C

C

2

C

2







Warunki początkowe są:

0

t

C

0

u





0

t

C

0

dt

du

C

i







i

Równanie charakterystyczne:

0

1

RCr

LCr

2







które ma pierwiastki:

10

r

1





10000

r

2





i

 

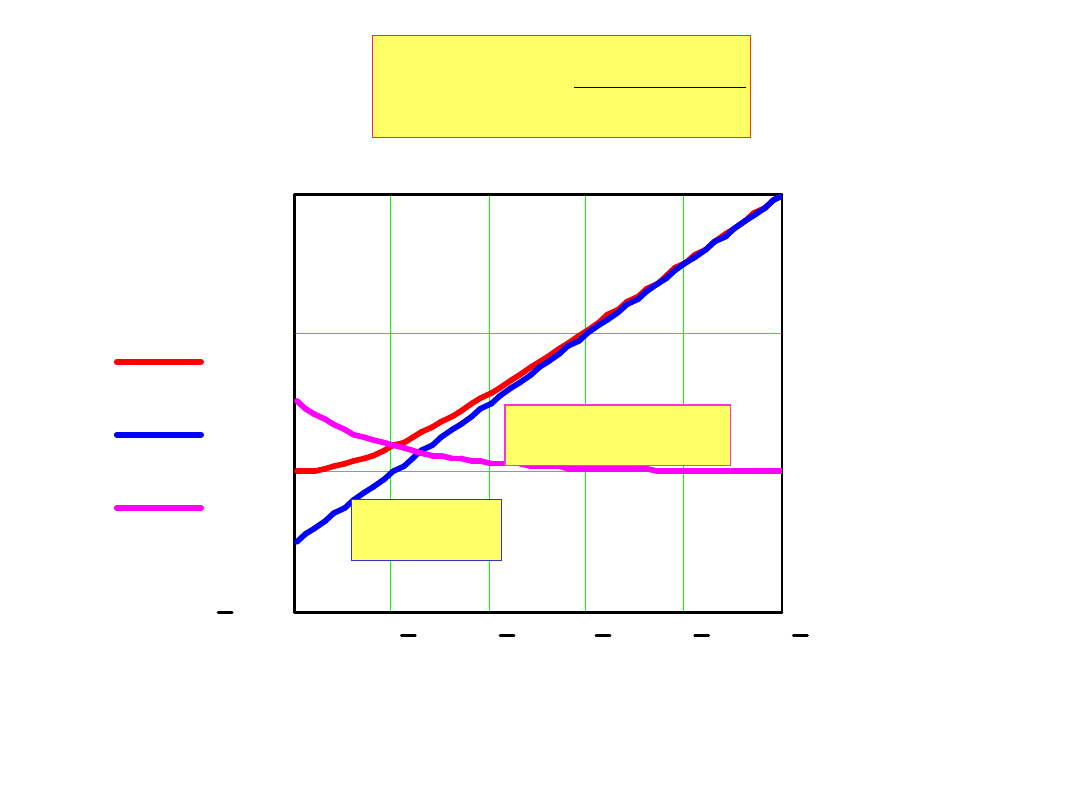
1

2

t

r

1

t

r

2

C

r

r

e

r

e

r

E

E

t

u

2

1









0 110

4

210

4

310

4

410

4

510

4

0.2

0

0.2

u t

( )

u1 t

( )

u2 t

( )

t

r

1

=-10

r

2

=-10000

Zapiszmy równanie:

E

u

dt

du

RC

dt

u

d

LC

C

C

2

C

2







w postaci normalnej:

C

i

dt

du

L

u

i

L

R

L

E

dt

di

C

C









lub podstawiając dane:

i

10

dt

du

u

10

i

10

10

dt

di

4

C

C

2

5

4









warunki początkowe:

0

u

0

i

0

C

0



 Wybierzmy metodę

jawną Eulera, krok
h=10

-5

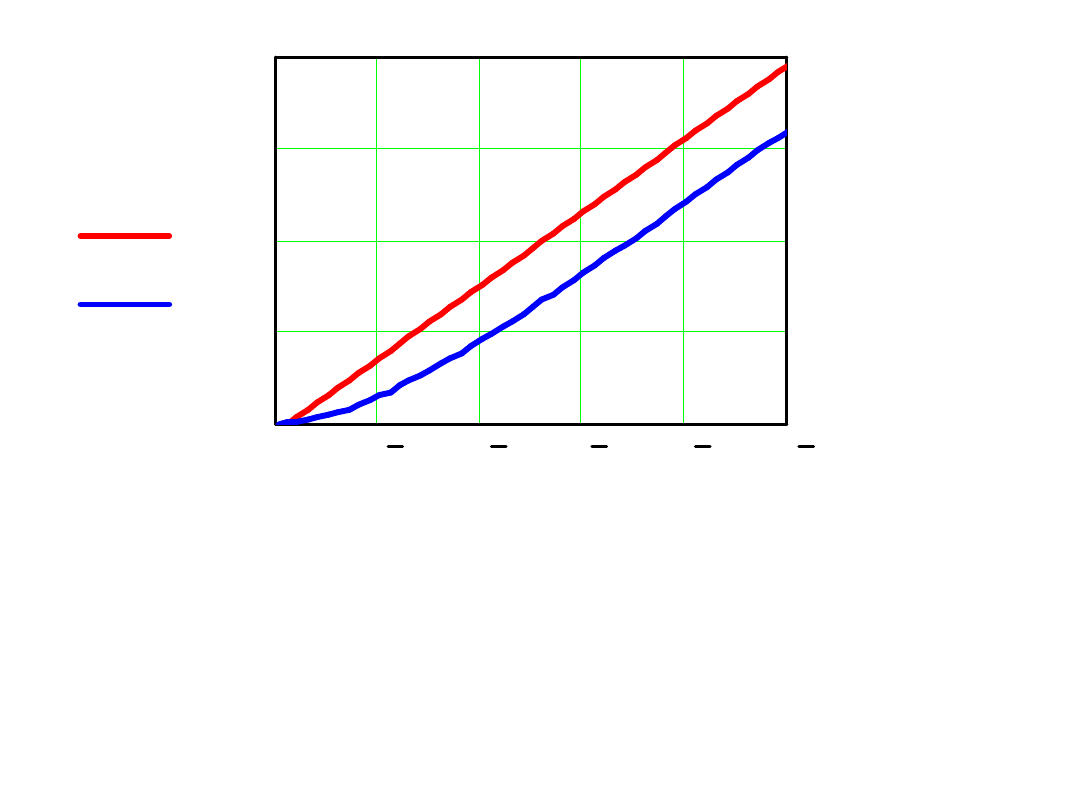
0 110

4

210

4

310

4

410

4

510

4

0

0.13

0.25

0.38

0.5

un k

( )

u k h



(

)

k h



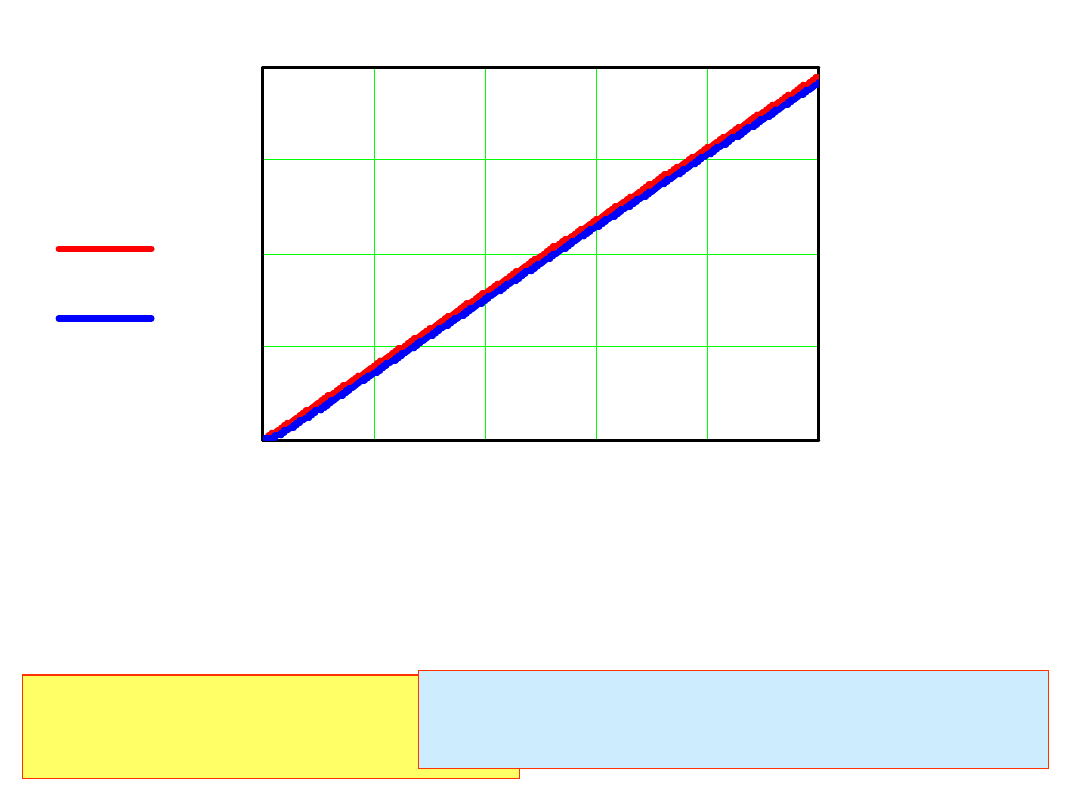
0

0.0010.0020.0030.0040.005

0

1.25

2.5

3.75

5

un k

( )

u k h



(

)

k h



Ponieważ dla czasów 0.005 zanikła składowa u

2

(t)~exp(-10000t)

weźmy dokładne wartości startowe w punkcie t=0.005

i(t=0.005)=0.09521816

u

C

(t=0.005)=4.781839

stała czasowa 0.1 więc można

przyjąć krok h=0.01

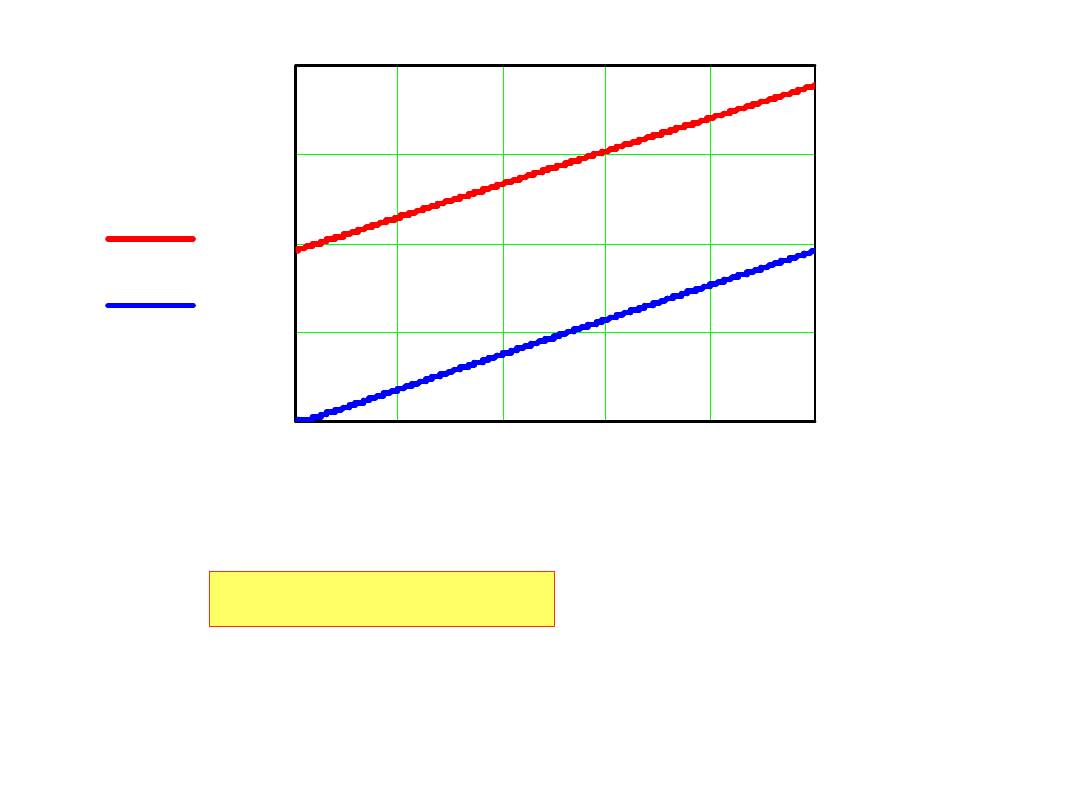
0.0050.0060.0070.0080.009 0.01

0

2.5

5

7.5

10

un k

( )

u k h



(

)

0.005k h





krok h=0.00001

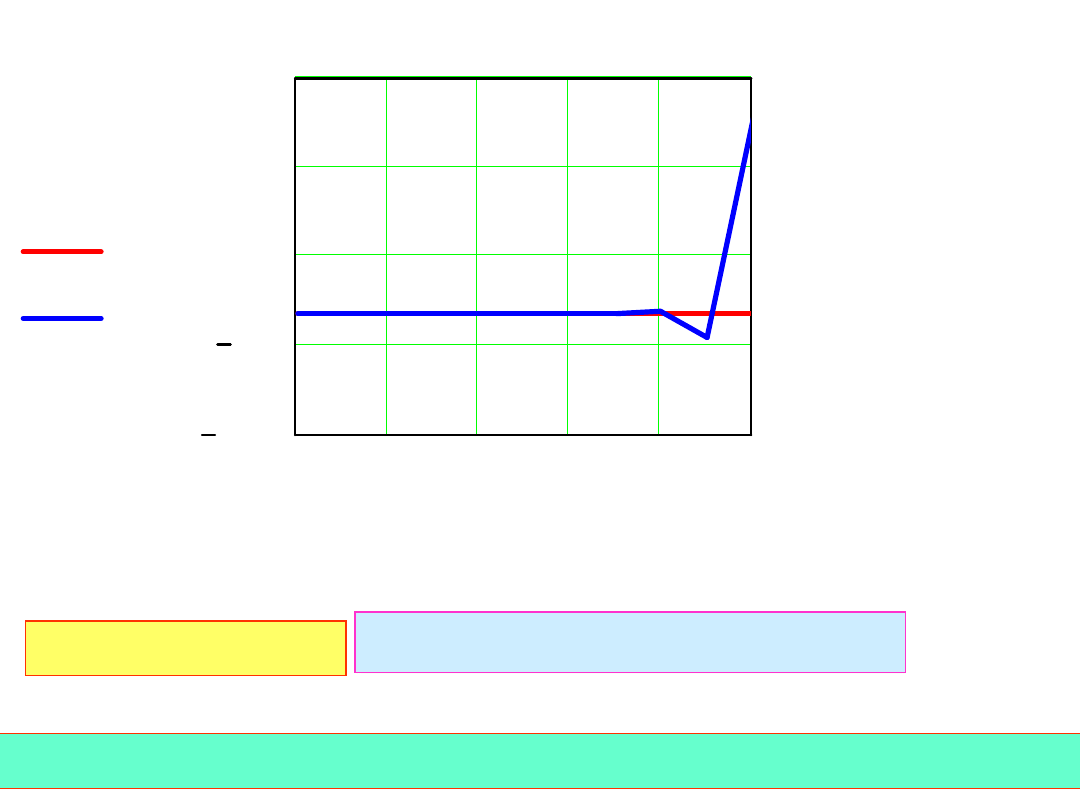
krok h=0.0001

0.0050.0052

0.0054

0.0056

0.00580.006

2000

500

1000

2500

4000

u 0.005k h





(

)

un k

( )

0.005k h





krytyczny krok h

kr

<0.0002

start w punkcie t=0.005 z dokładnych wartości początkowych

Rozważamy układ n równań różniczkowych:

i

i

i

x

x









i=1,2,...,n



i

może być liczbą zespoloną postaci:

i

i

i

i









Jedno z rozwiązań układu równań różniczkowych
będzie postaci:



  

t

sin

t

exp

C

i

i

i







gdzie C

i

jest stałą całkowania.

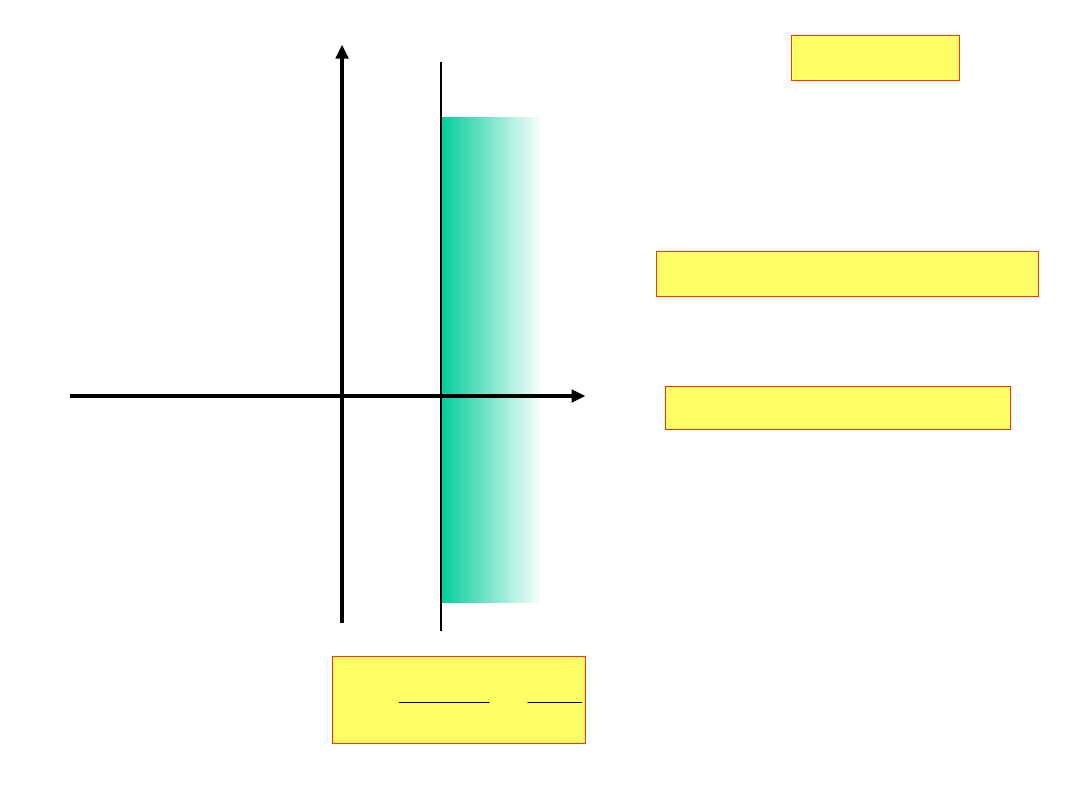
Przypadek 1.

0

i





ponieważ =h, więc

 

0

h

Re

i









czyli jest to prawa półpłaszczyzna

Im

Re



III

stabilny

0

h

i









liczba  dobrana tak,

że po jednym kroku
praktycznie:



 



0

h

sin

h

exp

C

i

i

i









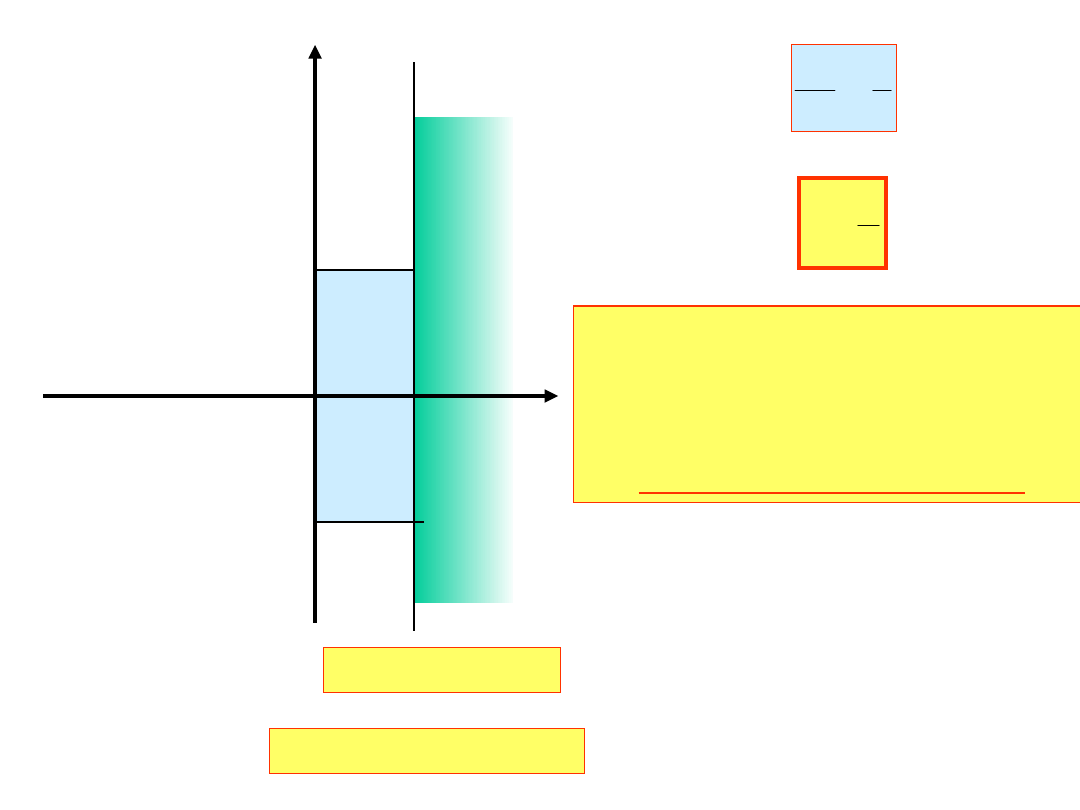
0

W obszarze:

 

 













h

Re

Re

0

rozwiązanie powinno być

i dokładne i stabilne,

bo składowa przejściowa

nie znikła i mamy oscylacje

Liczba oscylacji:

 













2

h

2

Im

N

i

Dla uzyskania dokładności
w fazie początkowej powinno
być N<1/8. Oznaczając =

i

h

Im

Re



III

stabilny

0

mamy:

8

1

2







czyli

4







-



II

W obszarze II

rozwiązanie numeryczne

musi być:

dokładne i stabilne

Przypadek 2.

 

0

h

Re

i











  

t

sin

t

exp

C

i

i

i







Rozwiązanie

jest narastające i można
liczyć tylko odpowiednio
małym krokiem

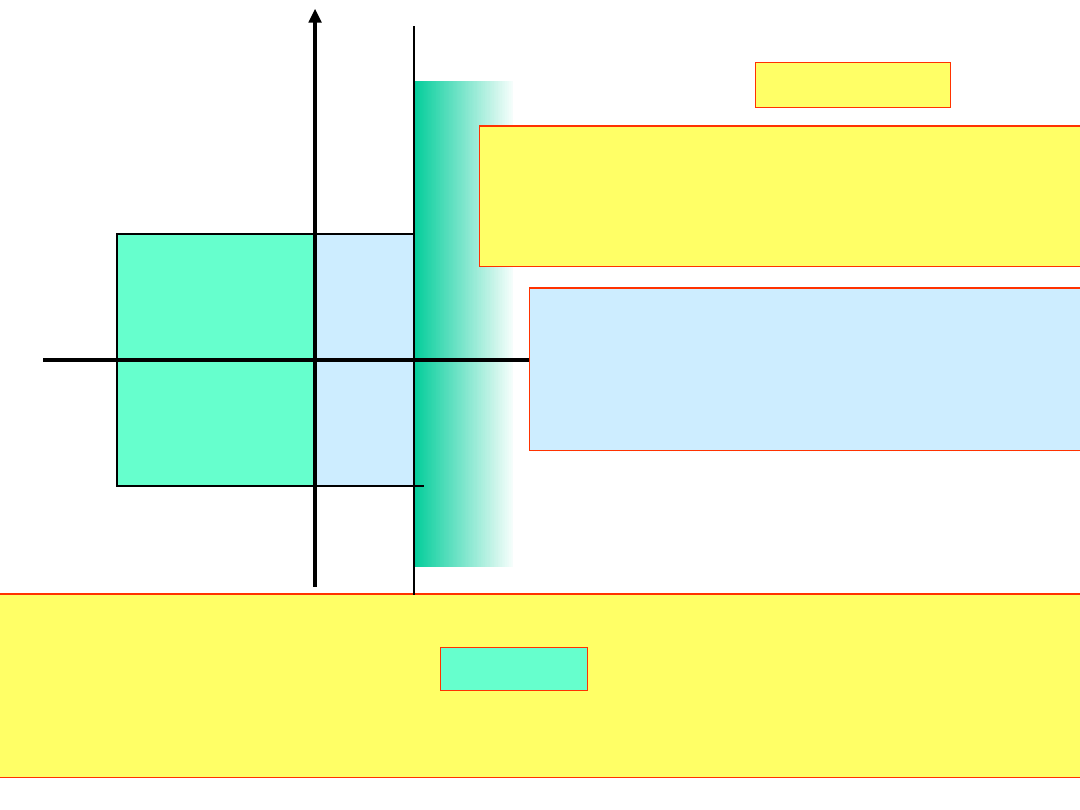
Algorytm wielokrokowy, stabilny bezwzględnie w obszarze

nie może być rzędu wyższego niż 2. Najlepszy jest algorytm
trapezów.

Im

Re



III

stabilny

0

-



II

czyli

0

h

i











algorytm powinien

być

dokładny i względnie stabilny

-

I

Twierdzenie Dahlquista:

 

0

Re





Algorytmy spełniające

warunki I, II, III nazywamy

sztywno stabilnymi

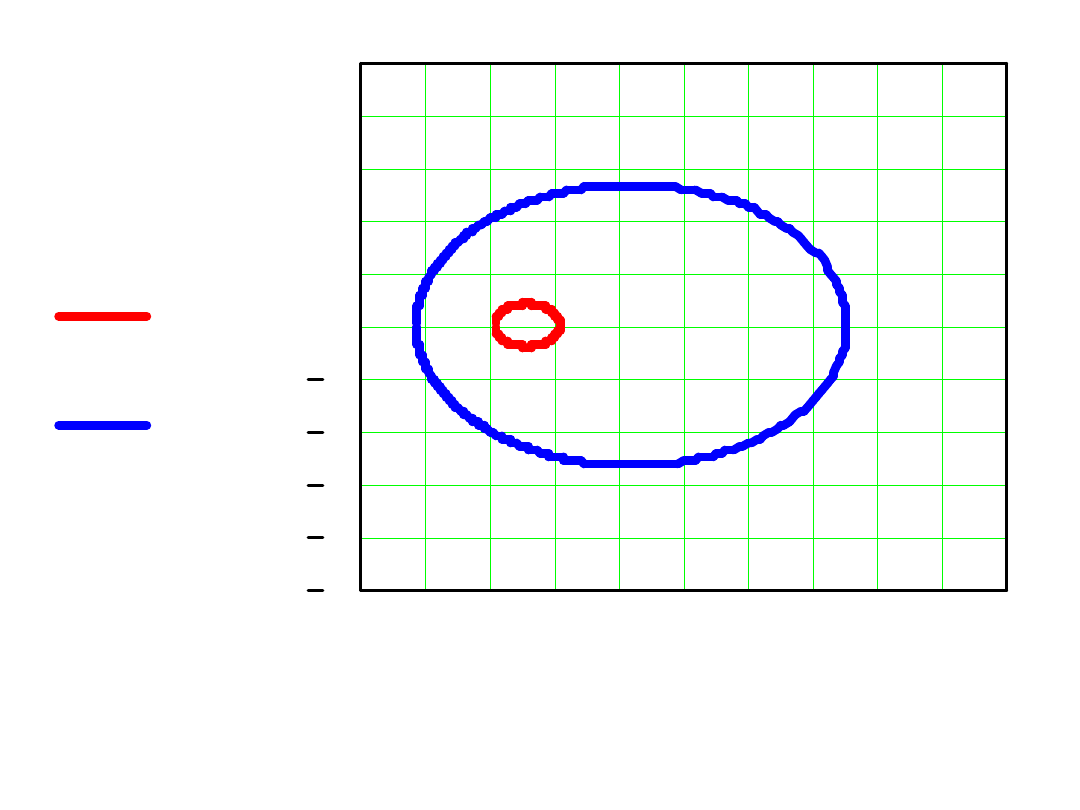
0 0.81.62.43.2 4 4.85.66.47.2 8

5

4

3

2

1

0

1

2

3

4

5

Imu 0.1











Imu 0.5











Reu 0.1











Reu 0.5













Trapezy prawa półpłaszczyzna =0

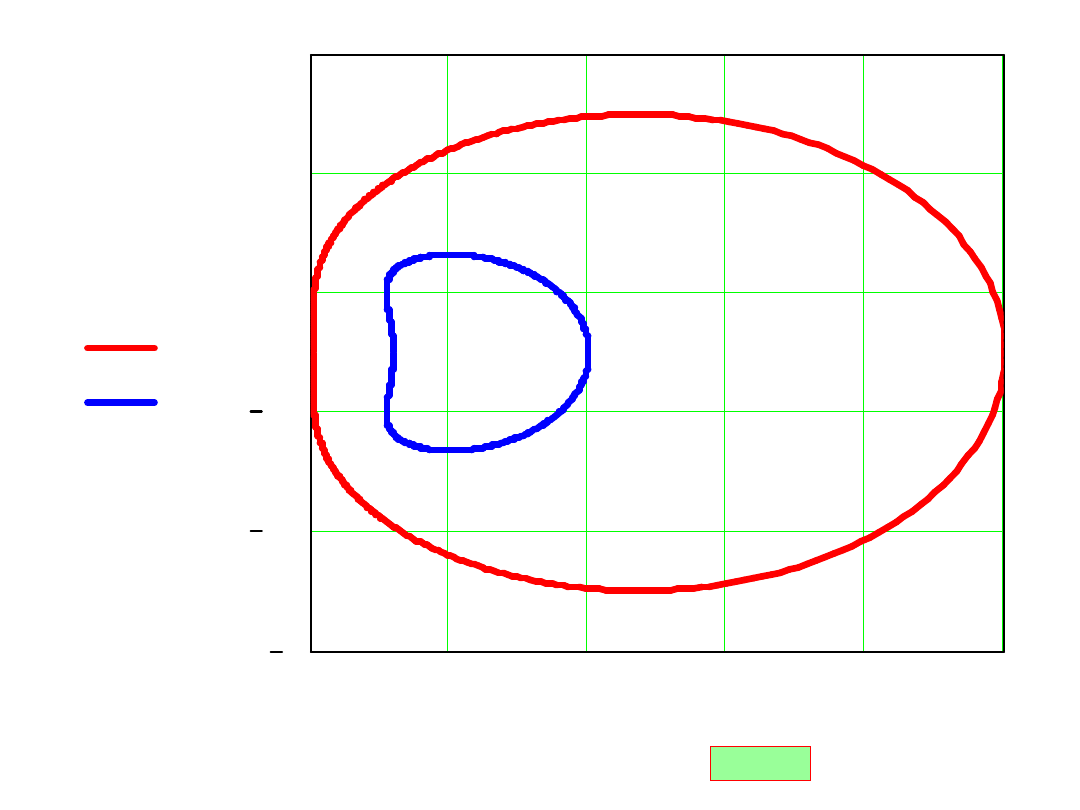
dla rzeczywistych  mamy warunek:

6

h 



0

1.2

2.4

3.6

4.8

6

4

2.4

0.8

0.8

2.4

4

Im 1 











Im 0.5











Re  1 











Re  0.5













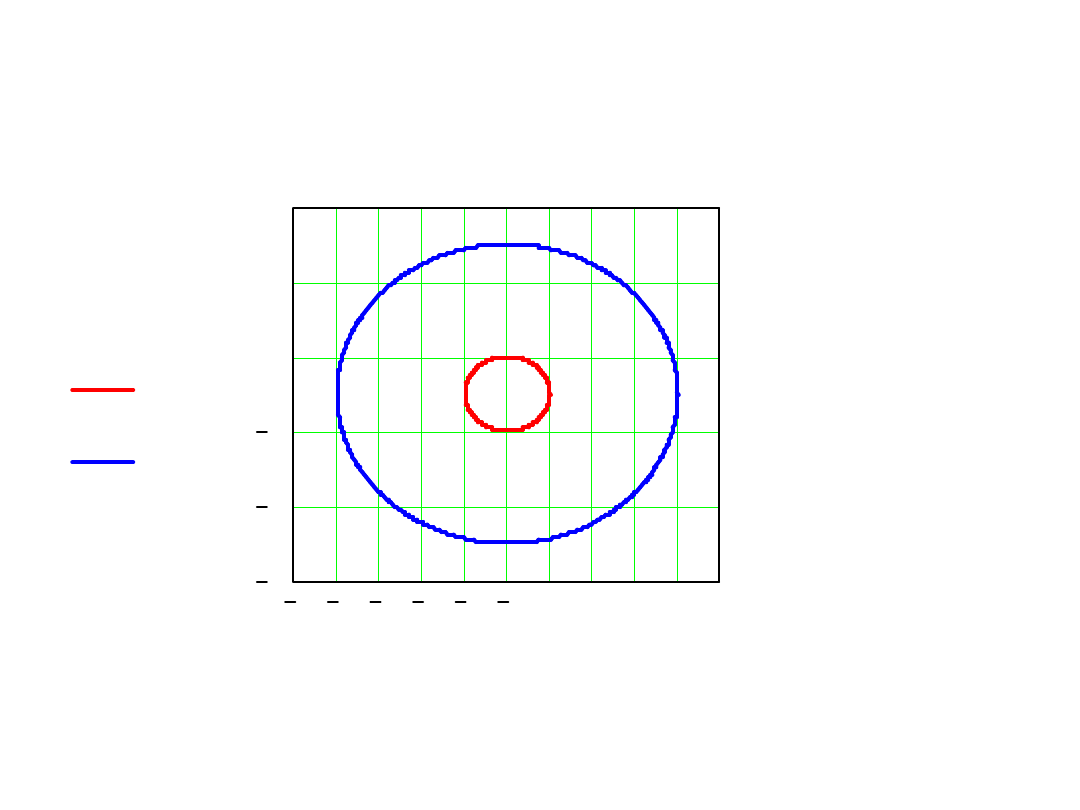
=0

trzeci rząd

1

0.2

0.6

1.4

2.2

3

2

1.2

0.4

0.4

1.2

2

Im 1 











Im 0.5











Re  1 











Re  0.5













=0

czwarty rząd

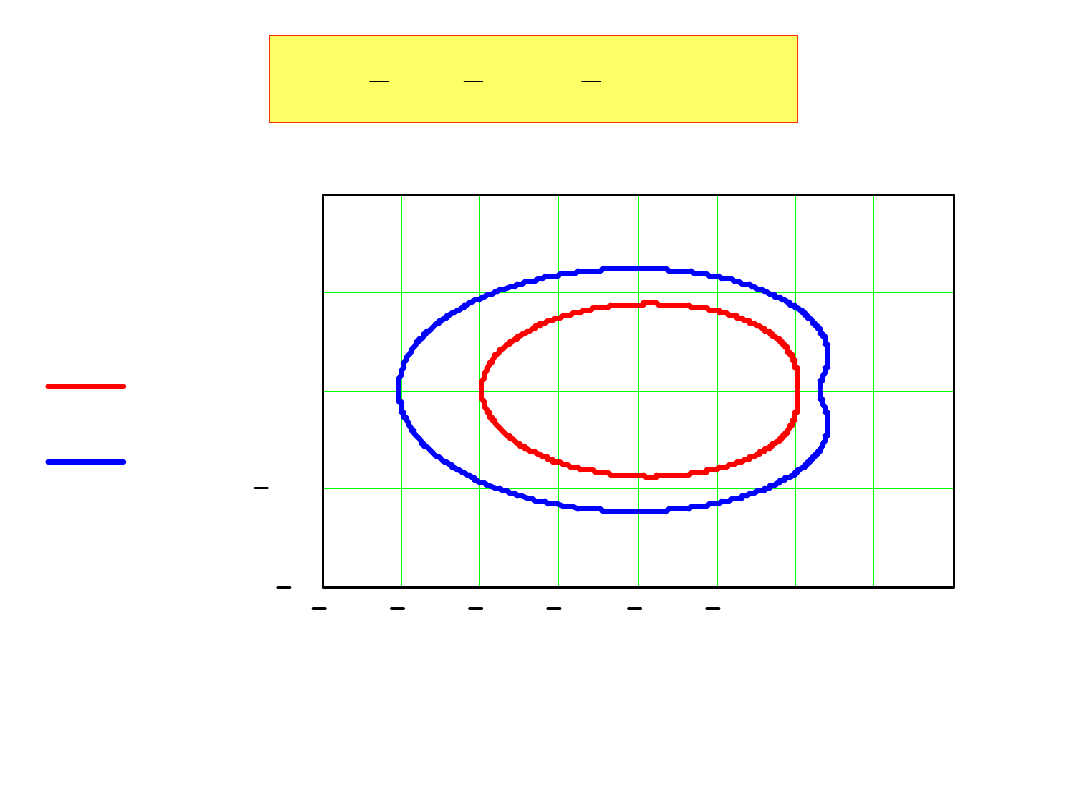
Algorytmy sztywno stabilne Geara

Pierwszego





1

n

1

n

n

1

n

t

,

x

hf

x

x











6 5 4 3 2 1 0 1 2 3 4

5

3

1

1

3

5

Imz11 



 





Imz10.25











Rez11 



 





Rez10.25













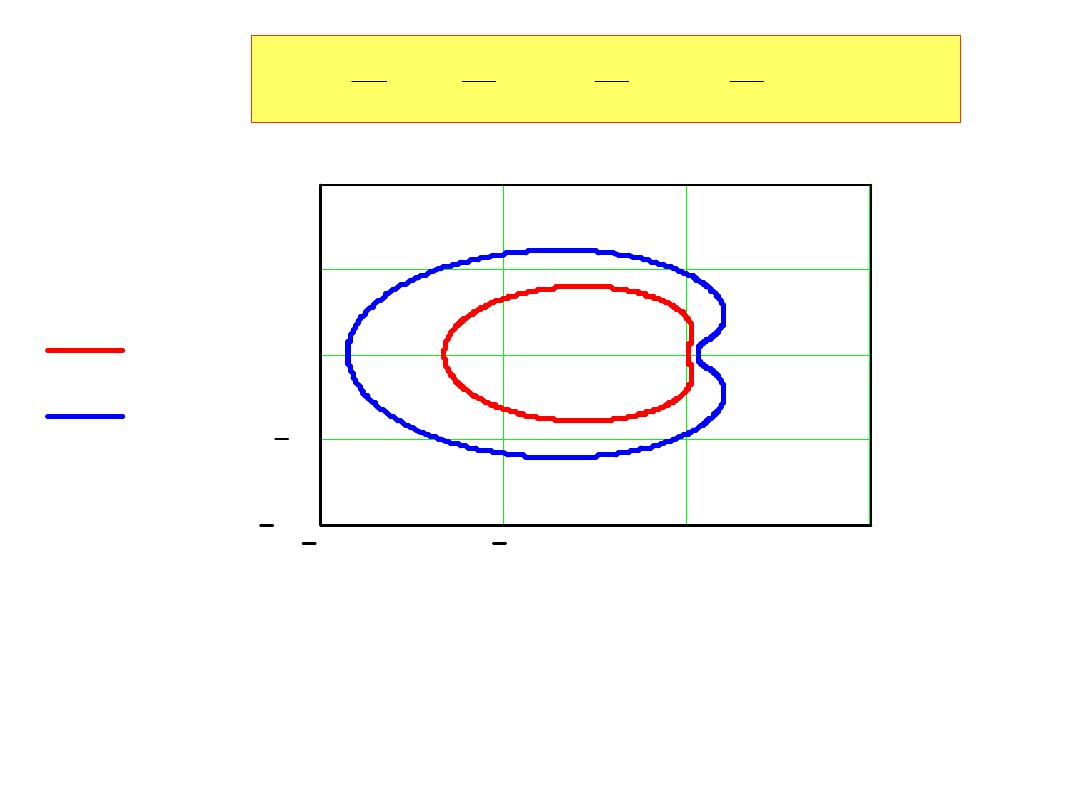
drugiego:





1

n

1

n

1

n

n

1

n

t

,

x

hf

3

2

x

3

1

x

3

4

x















6

5

4

3

2

1

0

1

2

5

2.5

0

2.5

5

Imz21 



 





Imz20.75











Rez21 



 





Rez20.75













trzeciego:





1

n

1

n

2

n

1

n

n

1

n

t

,

x

hf

11

6

x

11

2

x

11

9

x

11

18

x



















10

5

0

5

10

5

0

5

10

Imz31 



 





Imz30.75











Rez31 



 





Rez30.75













czwartego:





1

n

1

n

3

n

2

n

1

n

n

1

n

t

,

x

hf

25

12

x

25

3

x

25

16

x

25

36

x

25

48

x























20

10

0

10

20

10

0

10

20

Imz41 



 





Imz40.75











Rez41 



 





Rez40.75













Metoda Runge - Kutty

Równanie

 

t

,

x

f

x 



Rozwiązujemy stosując szereg Taylora





 

 

 

 























t

x

6

h

t

x

2

h

t

x

h

t

x

h

t

x

3

2

ale

   

t

,

x

f

t

x 



 

 

 





t

,

t

x

f

dt

d

x

dt

d

t

x









 





t

x

,

f

f

,

f

t

f

dt

dx

x

f

t

,

t

x

f

dt

d

















czyli

t

x

,

f

,

f

)

t

(

x







 

 

   

 





t

,

x

,

f

t

,

x

,

f

t

,

x

f

dt

d

x

dt

d

t

x

t

x













 





tt

xt

t

t

t

,

f

,

f

t

,

f

dt

dx

x

,

f

t

,

x

,

f

dt

d





















dt

,

df

f

,

f

dt

df

,

f

dt

d

x

x

x









dt

,

df

f

,

f

dt

df

,

f

dt

d

x

x

x





ale

t

x

,

f

f

,

f

dt

df





a

xt

xx

x

x

x

,

f

,

f

t

,

f

dt

dx

x

,

f

dt

,

df

















Podstawiając do

 

 

   

 





t

,

x

,

f

t

,

x

,

f

t

,

x

f

dt

d

x

dt

d

t

x

t

x













i porządkując mamy

tt

t

y

2

y

xt

xx

2

,

f

,

f

,

f

,

f

,

f

2

,

f

f

x















Metoda Runge -Kutty





p

2,3,...,

i

h

a

t

,

K

b

x

hf

K

t

,

x

hf

K

K

w

x

x

i

n

1

i

1

j

j

ij

n

i

n

n

i

p

1

i

i

i

n

1

n







































Sposób wyznaczania współczynników na przykładzie
metody drugiego rzędu (p=2):













h

b

t

,

t

,

x

hf

b

x

hf

w

t

,

x

hf

w

x

x

21

n

n

n

21

n

2

n

n

1

n

1

n















Drugi składnik rozwijamy w szereg Taylora
w otoczeniu punktu x

n

, t

n

















h

b

,

f

f

b

,

f

t

,

x

f

h

b

t

,

t

,

x

hf

b

x

f

21

t

21

x

n

n

21

n

n

n

21

n













Podstawiając i porządkując mamy:



 





 











n

n

t

n

n

n

n

x

2

21

2

n

n

2

1

n

1

n

t

,

x

,

f

t

,

x

f

t

,

x

,

f

h

b

w

t

,

x

hf

w

w

x

x















a porównując z szeregiem Taylora







 











n

n

t

n

n

x

n

n

2

n

n

n

1

n

t

,

x

,

f

t

,

x

,

f

t

,

x

f

2

h

t

,

x

hf

x

x











przy tych samych potęgach h otrzymujemy:

2

1

b

w

1

w

w

21

2

2

1







Przyjmując w

2

=1 mamy:

w

1

=0, b

21

=1/2

i stąd algorytm:

2

1

b

w

1

w

w

21

2

2

1















h

5

.

0

t

,

t

,

x

hf

5

.

0

x

hf

x

x

n

n

n

n

n

1

n











lub w1=w2=w i rozwiązując otrzymujemy:

w=0.5, b

21

=1 i stąd inny algorytm:

















1

n

n

n

n

n

n

n

1

n

t

,

t

,

x

hf

x

f

t

,

x

f

h

5

.

0

x

x













Przykład:
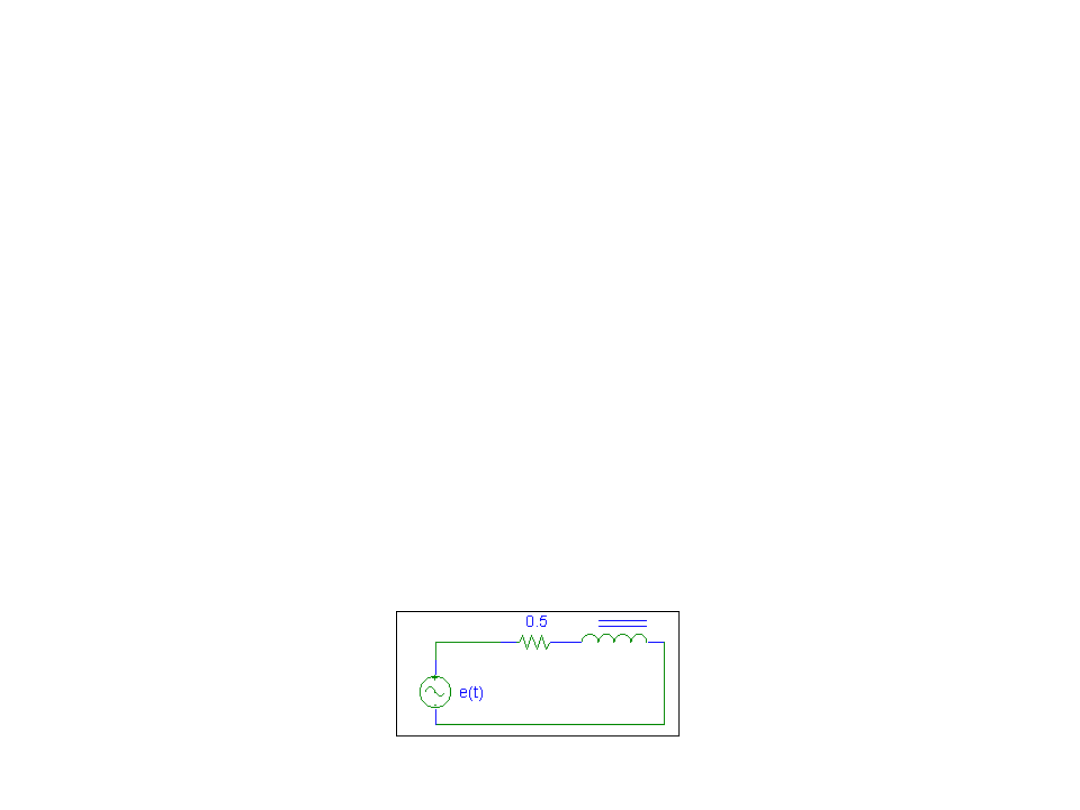
Dany jest dławik o charakterystce:

3

i

001

.

0

i

1

.

0 





Rezystancja dławika wynosi 0.5.

Obliczyć prąd płynący w obwodzie zasilanym
sem e(t)=100sin314t.

Schemat obwodu możemy przyjąć w postaci:

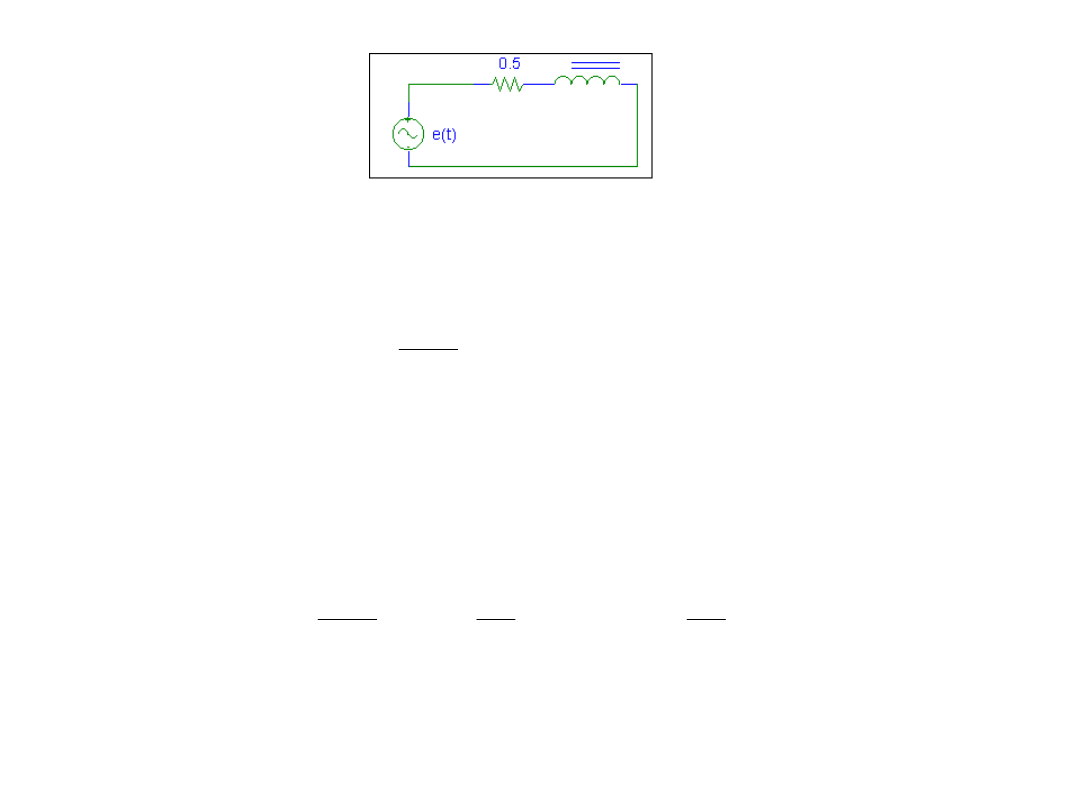
Suma spadków napięć pozwala zapisać równanie:

 

t

e

i

5

.

0

dt

d







Biorąc pod uwagę krzywą magnesowania:

dt

di

i

003

.

0

dt

di

1

.

0

dt

d

i

001

.

0

i

1

.

0

2

3













Podstawiając do równania obwodu i porządkując:

2

i

003

.

0

1

.

0

i

5

.

0

t

314

sin

100

dt

di







Warunek początkowy jest i

0

=i(t=0)=0.

Wybór kroku całkowania:

Stała czasowa liniowej części obwodu wynosi

0.1/0.5=0.2s.

Krok czasowy można przyjąć 0.2/10=20ms.

Okres wymuszenia T=20ms krok należy przyjąć
rzędu T/20=1ms. Prawdopodobnie będzie trzecia
harmoniczna więc przyjmujemy krok

h=0.2ms.

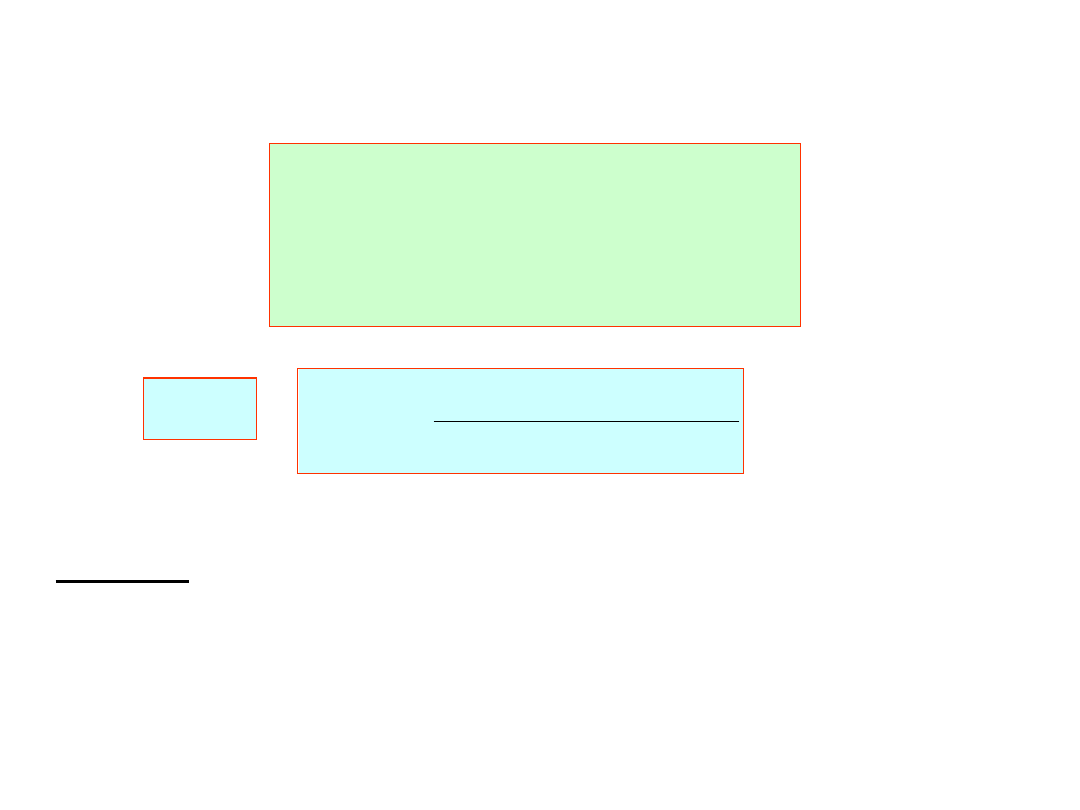
Obliczenia metodą Runge – Kutty według schematu:









2

n

1

n

1

n

2

n

n

1

K

x

x

h

5

.

0

t

,

K

5

.

0

x

hf

K

t

,

x

hf

K















 

2

i

003

.

0

1

.

0

i

5

.

0

t

314

sin

100

t

,

i

f







x=i;

Start: i(t=0)=i

0

=0

h=0.0002

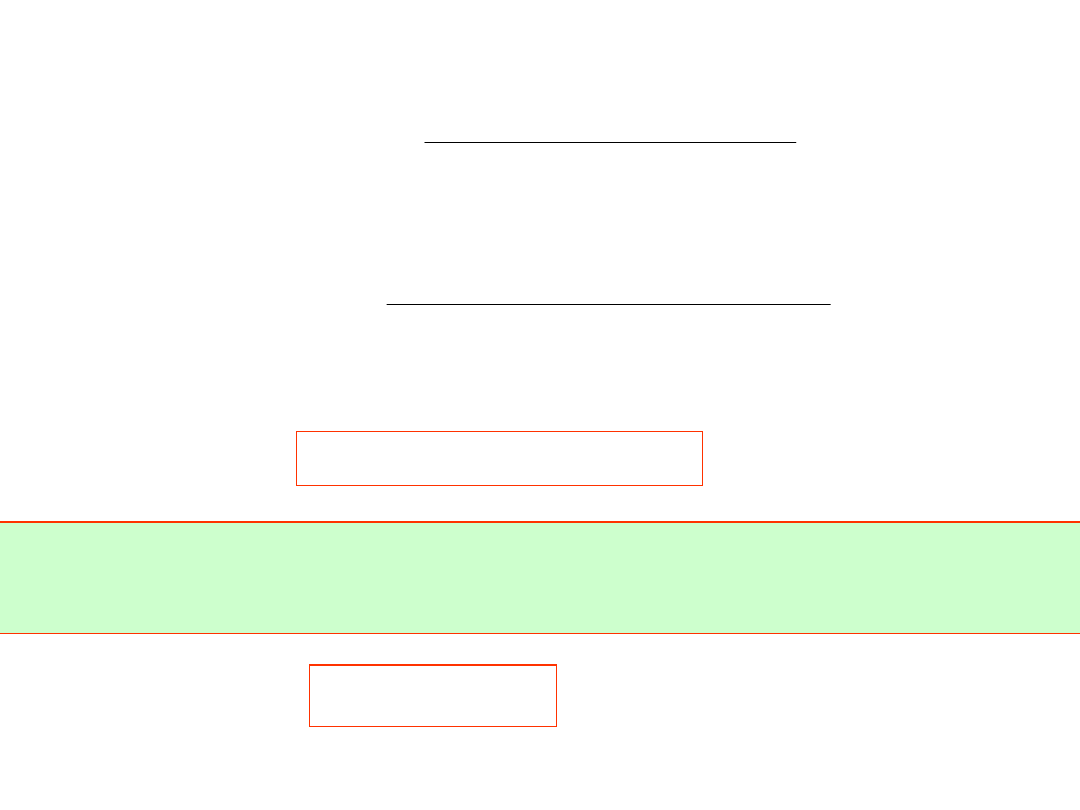
i mamy:

0

i

003

.

0

1

.

0

i

5

.

0

0

314

sin

100

0002

.

0

K

2

0

0

1



























006279

.

0

K

K

5

.

0

i

003

.

0

1

.

0

K

5

.

0

i

5

.

0

0001

.

0

0

314

sin

100

0002

.

0

K

2

2

1

0

1

0

2















006279

.

0

K

i

i

2

0

1







t=h=0.0002

Metoda Runge – Kutty pozwala zmienić krok na
każdym etapie. Zwiększamy krok dwukrotnie.

h=0.0004

2

1

006279

.

0

003

.

0

1

.

0

006279

.

0

5

.

0

0002

.

0

314

sin

100

0004

.

0

K













02509

.

0

1

K 













2

1

1

2

K

5

.

0

006279

.

0

003

.

0

1

.

0

K

5

.

0

006279

.

0

5

.

0

0002

.

0

0002

.

0

314

sin

100

0004

.

0

K

















05003

.

0

K

2



i

2

=0.006279+K

2

i

2

=0.056312

Jak ocenić czy wolno zmienić długość kroku?
Czy zmniejszyć czy zwiększyć?

Ocena błędu metodą Rungego:

Dla metody rzędu p-go mamy:









 

2

p

1

p

n

n

1

n

1

n

h

O

h

t

,

x

x

t

x





















 

2

p

2

n

n

2

1

n

n

h

O

2

h

t

,

x

x

2

h

t

x



































 









 

2

p

1

p

n

n

2

1

2

n

1

n

h

O

2

h

t

,

x

2

x

t

x































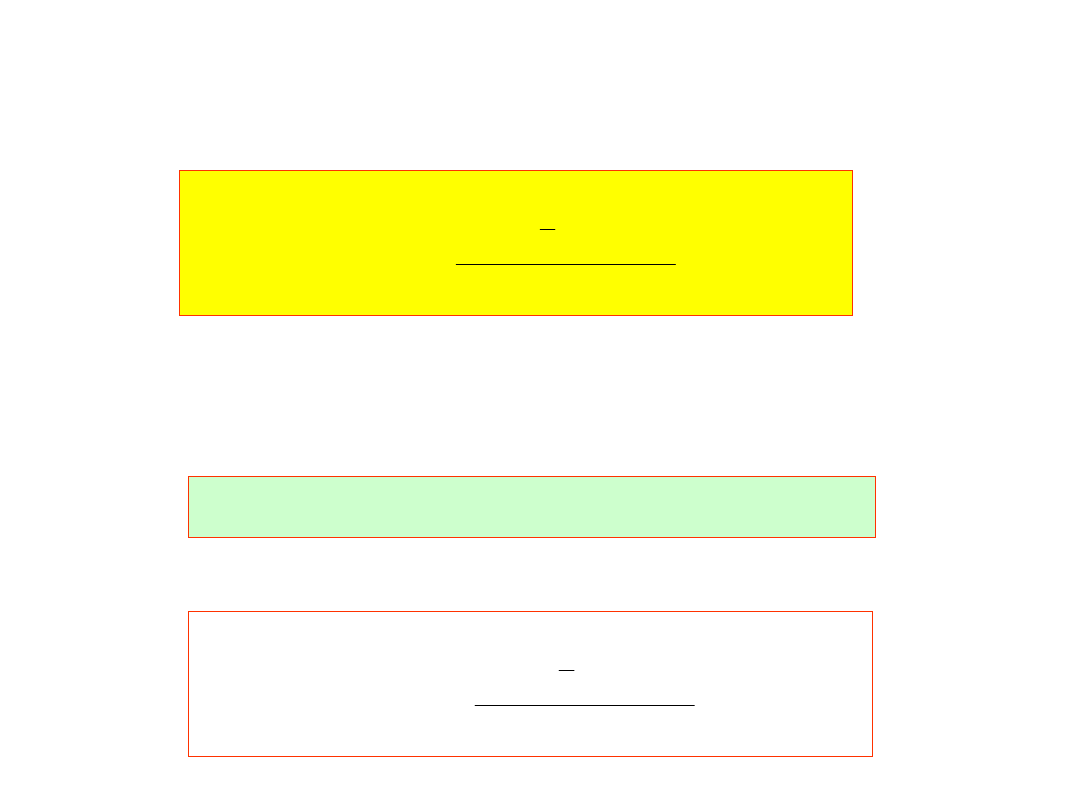
stąd ocena błędu:





 

2

p

p

1

n

2

1

2

n

1

p

n

n

h

O

2

1

x

x

h

t

,

x























Znając ocenę błędu można poprawić rozwiązanie
podstawiając do









 

2

p

1

p

n

n

1

n

1

n

h

O

h

t

,

x

x

t

x

















 

2

p

p

1

n

2

1

2

n

p

1

n

p

1

n

h

O

1

2

x

x

2

x

x























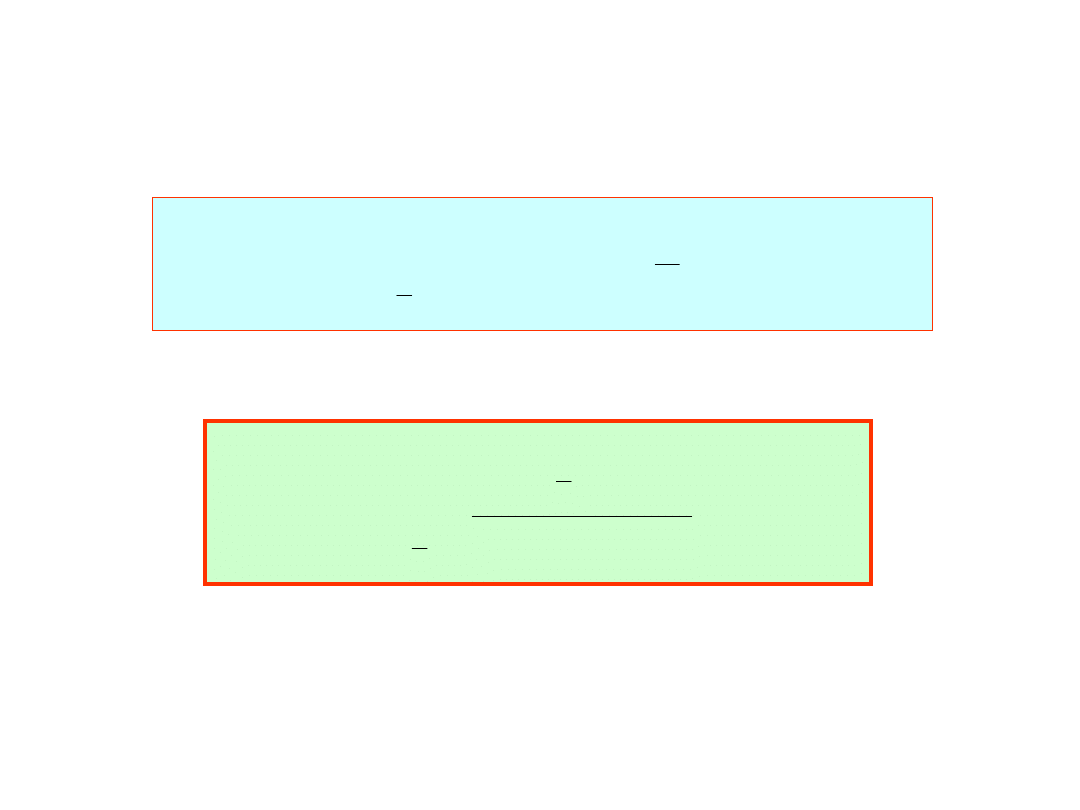
lub dokładniej z równania:









 

2

p

1

p

n

n

2

1

2

n

1

n

h

O

2

h

t

,

x

2

x

t

x































 

2

p

p

1

n

2

1

2

n

2

1

2

n

dd

1

n

h

O

1

2

x

x

x

x

























W obliczanym przypadku musimy powtórzyć
obliczenia z krokiem 0.0002 i mamy dla t=0.0004:

K

1

=0.012545

K

2

=0.0188

i

1+1/2

=0.02508

Dla t=0.0006 mamy:

K

1

=0.025029

K

2

=0.031235

i

1+2*1/2

=0.056315

i

1+2*1/2

=0.056315

Obliczone z krokiem h=0.0004 było:

i

2

=0.056312

W tym przypadku p=2 i ze wzoru:





 

2

p

p

1

n

2

1

2

n

1

p

n

n

h

O

2

1

x

x

h

t

,

x























mamy oceną błędu:





00026

.

0

t

,

i

1

1





Rozwiązanie poprawione ze wzoru:

 

2

p

p

1

n

2

1

2

n

2

1

2

n

dd

1

n

h

O

1

2

x

x

x

x

























i

2

=0.0566316

Na wykonanie jednego kroku należało policzyć
funkcję f(i

n

,t

n

)

2 – h=0.0004
1+2 – h=0.0002
razem 5 - razy

Metoda IV –go rzędu





















4

3

2

1

n

1

n

n

3

n

4

n

2

n

3

n

1

n

2

n

n

1

K

K

2

K

2

K

6

1

x

x

h

t

,

K

x

hhf

K

h

5

.

0

t

,

K

5

.

0

x

hf

K

h

5

.

0

t

,

K

5

.

0

x

hf

K

t

,

x

hf

K

































Przy ocenie dokładności obliczeń metodą Rungego
wymaga 11-krotnego obliczenia f(x,t).

Metoda Mersona





 

30

K

K

8

K

9

K

2

h

error

h

t

,

2

K

4

K

3

K

x

hf

K

2

h

t

,

8

K

3

K

x

hf

K

3

h

t

,

6

K

K

x

hf

K

3

h

t

,

3

K

x

hf

K

t

,

x

hf

K

5

4

3

1

n

4

3

1

n

5

n

3

1

n

4

n

2

1

n

3

n

1

n

2

n

n

1





























































































6

K

K

4

K

x

x

5

4

1

n

1

n











tylko 5-cio krotne obliczanie f(x,t).

Przykład

Równanie wahadła:

0

sin

2











Niech =1s

-2

Warunki początkowe:





1

.

2

0

t









około 86°





0

0

t







Sprowadzamy do układu równań I-go rzędu















sin





Warunki początkowe:

0

1

.

2

0

0











Obliczenia chcemy prowadzić z dokładnością 0.001

Startujemy z krokiem h=0.1. Krok wybrano jako
0.1 okresu wahadła liniowego.

09972

.

0

3

K

sin

h

K

003324

.

0

3

K

h

K

09972

.

0

sin

h

K

0

h

K

1

0

2

1

0

2

0

1

0

1











































































099716

.

0

6

K

K

sin

h

K

003324

.

0

6

K

K

h

K

2

1

0

3

2

1

0

3































































099224

.

0

8

K

3

K

sin

h

K

0037394

.

0

8

K

3

K

h

K

3

1

0

4

3

1

0

4































































099701

.

2

K

4

K

3

K

sin

h

K

0098734

.

0

2

K

4

K

3

K

h

K

4

3

1

0

5

4

3

1

0

5







































































Błąd:

00013043

.

0

30

K

K

8

K

9

K

2

00032914

.

0

30

K

K

8

K

9

K

2

5

4

3

1

1

5

4

3

1

1





















































Dokładność założona została osiągnięta.
W następnym kroku można zwiększyć krok.

Rozwiązanie w chwili t=0.1

099386

.

6

K

K

4

K

49186

.

1

6

K

K

4

K

5

4

1

0

1

5

4

1

0

1











































i do następnego kroku możemy wystartować z nową
wartością kroku h

Metody włożone

lub

Metody Fehelberga – Runge -Kutty

Stosujemy metodę Runge – Kutty rzędu p i rzędu p+1
i aby zmniejszyć liczbę obliczanych współczynników
wybieramy je tak, że w obu metodach jest pierwszych
p współczynników K jednakowe, czyli





n

n

1

t

,

x

hf

K 

























h

c

t

,

K

a

x

hf

K

i

n

1

i

1

j

j

ij

n

i

i=2,3,..,p+1

i mamy dla metody rzędu p-go











p

1

i

i

p

i

n

1

n

K

w

x

x

a dla metody rzędu (p+1)-go















1

p

1

i

i

1

p

i

n

1

n

K

w

x

x

Ocenę błędu można zrobić stosunkowo prosto





 

2

p

1

p

n

n

p

p

1

i

i

p

i

n

1

n

h

O

h

t

,

x

K

w

x

x

























 

3

p

2

p

n

n

1

p

1

p

1

i

i

1

p

i

n

1

n

h

O

h

t

,

x

K

w

x

x



























Po odjęciu stronami otrzymujemy:









 

2

p

1

p

1

i

i

p

i

1

p

i

n

n

p

h

O

K

w

w

t

,

x



















gdzie

0

w

p

1

p





Znając błąd możemy postępować jak w metodzie
Mersona i rozwiązanie przyjmować z dokładniejszej
metody rzędu p+1.

Najczęściej stosowana metoda RKF45 ma współczynniki



























































h

13

12

t

,

2197

K

7296

K

7200

K

1932

x

hf

K

h

8

3

t

,

32

K

9

K

3

x

hf

K

h

25

.

0

t

,

K

25

.

0

x

hf

K

t

,

x

hf

K

n

3

2

1

n

4

n

2

1

n

3

n

1

n

2

n

n

1



















































2

h

t

,

K

40

11

K

4104

1859

K

2565

3544

K

2

K

27

8

x

hf

K

h

t

,

K

4104

845

K

513

3680

K

8

K

216

439

x

hf

K

n

5

4

3

2

1

n

6

n

4

3

2

1

n

5

6

5

4

3

1

n

K

55

2

K

50

9

5

1

K

4104

2197

56430

28561

K

2565

1408

12825

6656

K

216

25

135

16













 























































Błąd

Rozwiązanie wykorzystując metodę dokładniejszą jest

6

5

3

2

1

n

1

n

K

55

2

K

50

9

K

56430

28561

K

12825

6656

K

135

16

x

x

















Metoda gwarantuje obliczenia z błędem rzędu h

4

.