
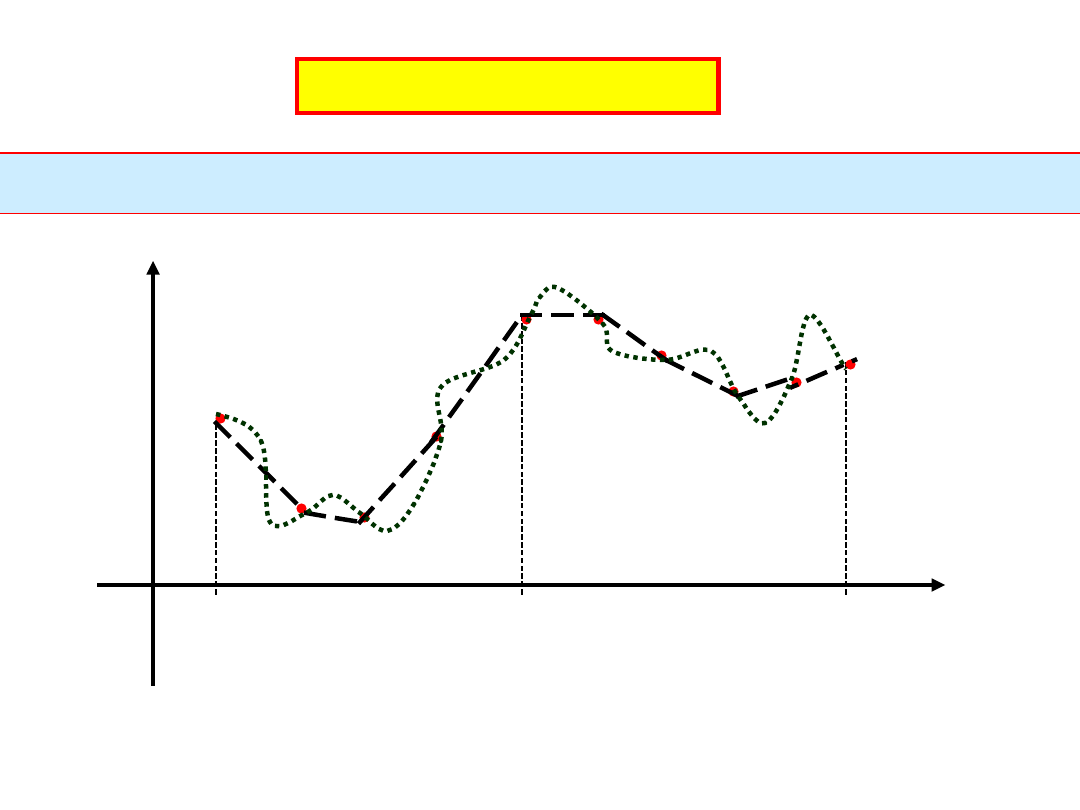
Interpolacja funkcji
Dane wartości funkcji y
n
w punktach x
n
, gdzie n=0,1,2, ....N-1.
x
y
x
0
y
0
x
n
y
n
x
N-1
y
N-1
Interpolacja wielomianowa
Twierdzenie
Istnieje dokładnie jeden wielomian stopnia co najwyżej N (N>=0),
który w punktach x
0
, x
1
,...,x
N-1
przyjmuje wartości y
0
,y
1
,...,y
N-1
.
Wzór interpolacyjny Lagrange'a:
)
x
(
y
....
)
x
(
y
)
x
(
y
)
x
(
W
1
N
1
N
1
1
0
0
n
gdzie
1
-
0,1,...N
=
k
dla
)
x
(
k
jest wielomianem stopnia co najwyżej N.
Z warunku interpolacyjnego:
1
-
N
0,1,....,
=
k
dla
y
)
x
(
W
k
k
N
powyższy układ N równań można najprościej rozwiązać
przyjmując dla wielomianów
k
(x) następujące warunki :
i
k
dla
1
i
k
dla
0
)
x
(
i
k
jako wielomian
k
(x) należy wybrać taki, który ma miejsca
zerowe we wszystkich punktach interpolacji
z wyjątkiem punktu x
k
, w którym funkcja ma wartość 1
,
1
N
1
k
1
k
1
0
x
,...,
x
,
x
,...,
x
,
x
Rozwiązaniem jest wielomian :

Rozwiązaniem jest wielomian:
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
A
)
x
(
1
N
1
k
1
k
1
0
k
z warunku:
otrzymuje się:
1
)
x
(
k
k
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
1
A
1
N
k
1
k
k
1
k
k
1
k
0
k
Wielomian Lagrange'a przyjmuje postać:
1
N
0
k
1
N
k
1
k
k
1
k
k
1
k
0
k
1
N
1
k
1
k
1
0
k
N
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
y
)
x
(
W
Ocena błędu interpolacji:
Ocena błędu interpolacji:
)
x
(
f
sup
M
)
x
x
(
)
x
(
gdzie
)
x
(
)!
1
N
(
M
)
x
(
W
)
x
(
f
)
1
N
(
]
b
,
a
[
x
1
N
N
k
0
k
k
1
N
1
N
1
n
N
Przykład 1.
Zbudować wielomian interpolacyjny dla funkcji exp(x)
w przedziale [1,2] bazując na 5 węzłach interpolacyjnych.
Wybierzmy węzły równomiernie czyli
25
.
0
4
1
2
x
mamy:
x
i
1.0
1.25
1.50
1.75
2.0
y
i
2.718
28
3.490
34
4.481
69
5.754
6
7.389
06
Wielomian Lagrange’a jest:
75
.
1
2
5
.
1
2
25
.
1
2
1
2
75
.
1
x
5
.
1
x
25
.
1
x
1
x
38906
.
7
2
75
.
1
5
.
1
75
.
1
25
.
1
75
.
1
1
75
.
1
2
x
5
.
1
x
25
.
1
x
1
x
7546
.
5
2
5
.
1
75
.
1
5
.
1
25
.
1
5
.
1
1
5
.
1
2
x
75
.
1
x
25
.
1
x
1
x
48169
.
4
2
25
.
1
75
.
1
25
.
1
5
.
1
25
.
1
1
25
.
1
2
x
75
.
1
x
5
.
1
x
1
x
49034
.
3
2
1
75
.
1
1
5
.
1
1
25
.
1
1
2
x
75
.
1
x
5
.
1
x
25
.
1
x
71828
.
2
)
x
(
W
4

lub
75
.
1
x
5
.
1
x
25
.
1
x
1
x
817
.
78
2
x
5
.
1
x
25
.
1
x
1
x
53
.
245
2
x
75
.
1
x
25
.
1
x
1
x
83
.
286
2
x
75
.
1
x
5
.
1
x
1
x
92
.
148
2
x
75
.
1
x
5
.
1
x
25
.
1
x
995
.
28
)
x
(
W
4
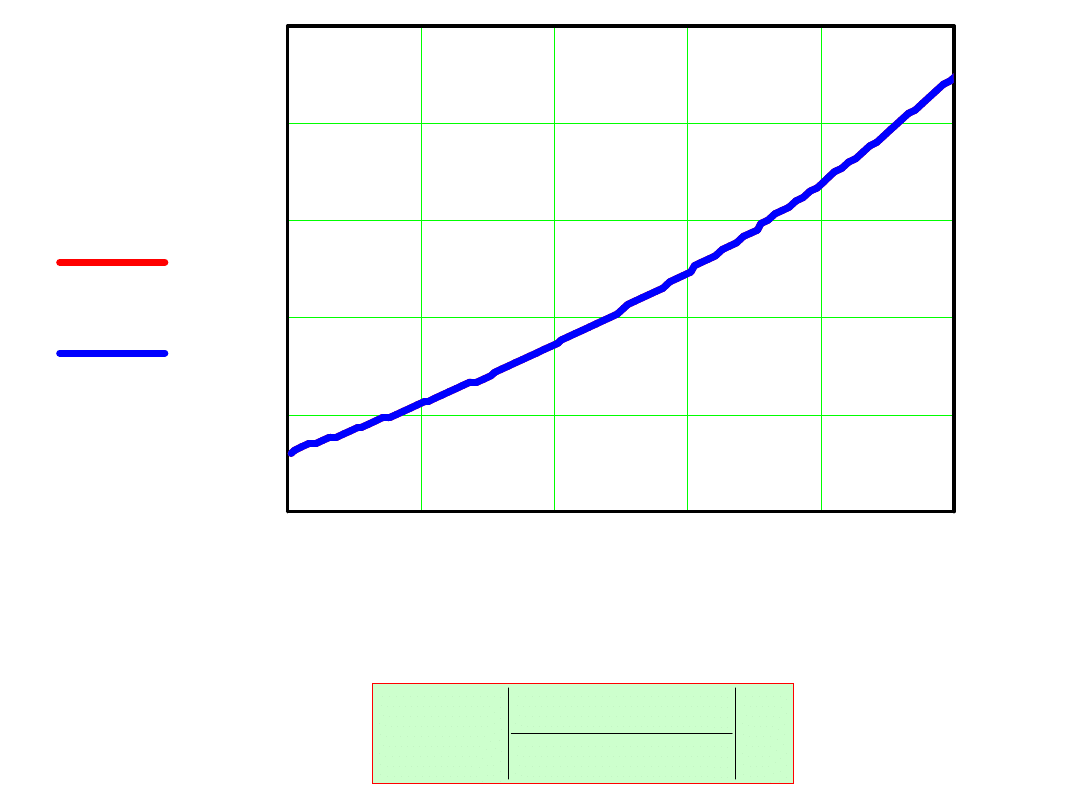
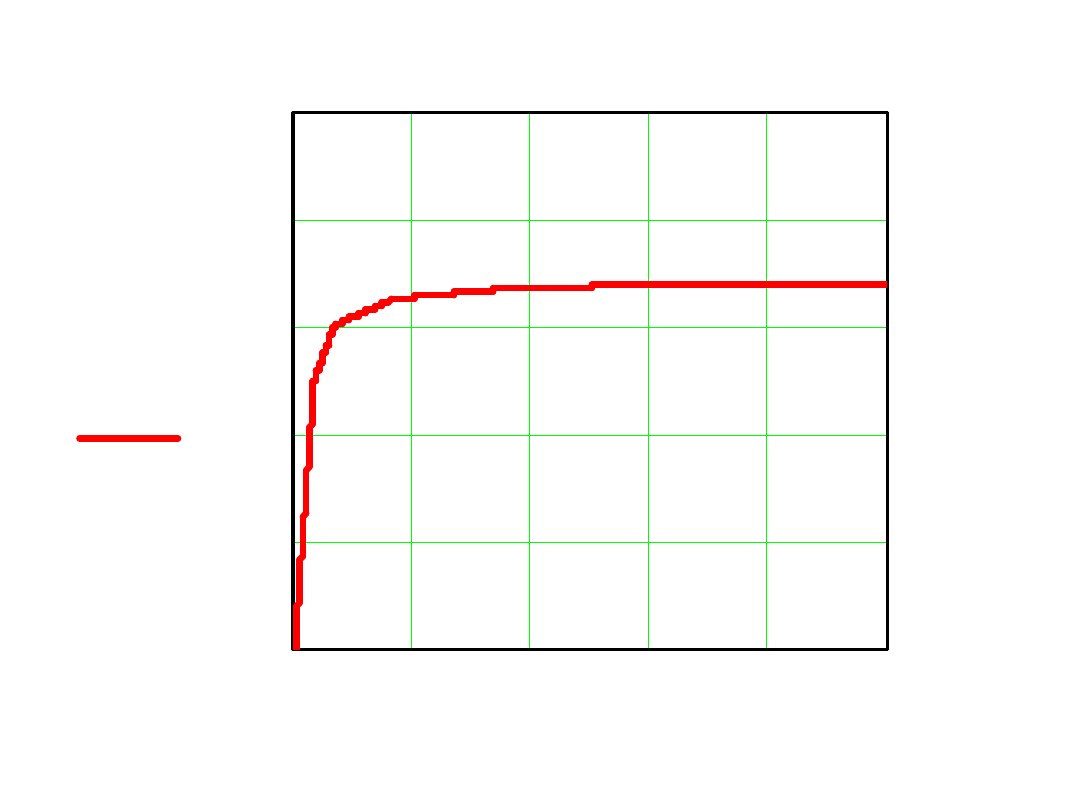
Wyniki obliczeń przedstawiono na wykresie:
1
1.2
1.4
1.6
1.8
2
2
3.2
4.4
5.6
6.8
8
w x
( )
expx
( )
x
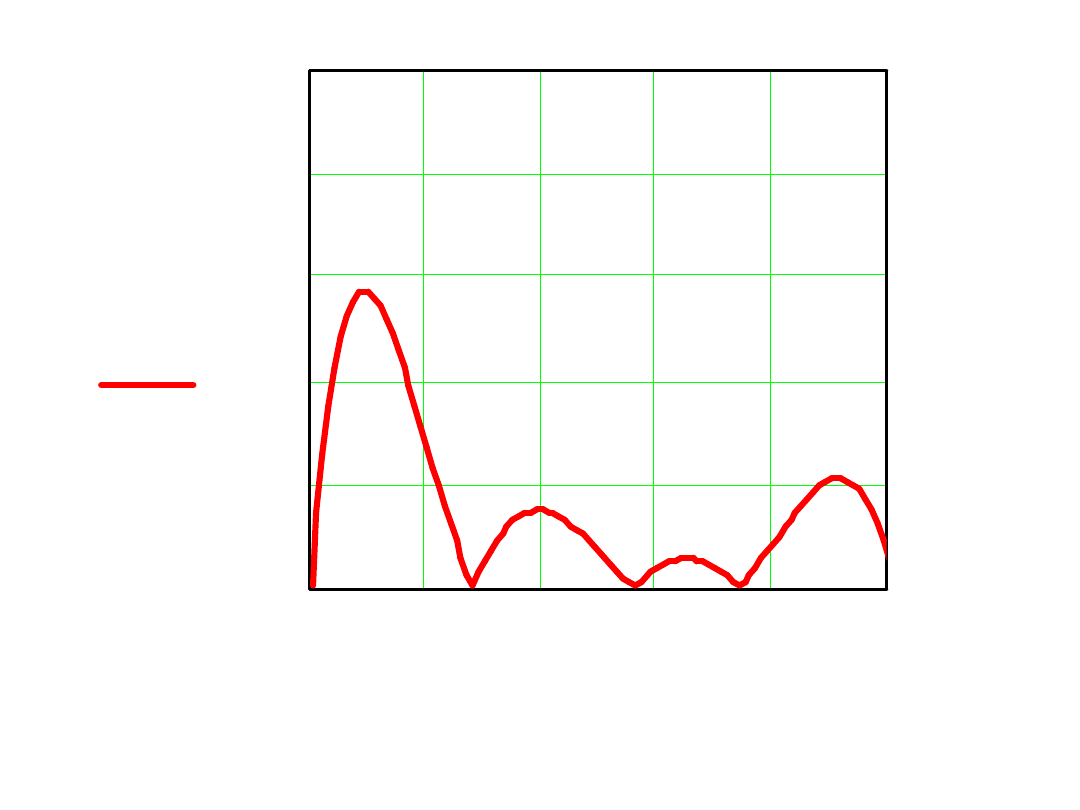
Dla lepszej oceny wykres błędu względnego:
100
)
x
exp(
)
x
exp(
)
x
(
w
)
x
(
eps
4
1
1.2
1.4 1.6
1.8
2
0
0.002
0.004
0.006
0.008
0.01
eps x
( )
x
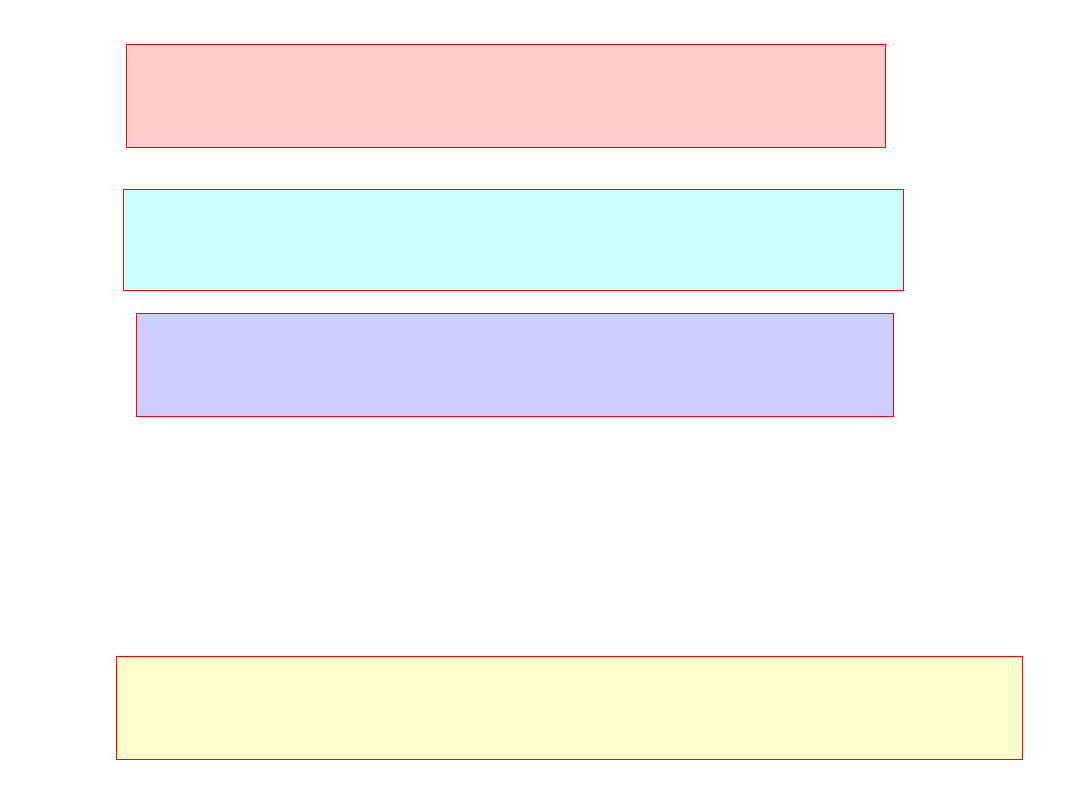
Przykład 2.
W wyniku pomiarów zdjęto pierwotną krzywą magnesowania
B=F(H). Zbudować wielomian interpolacyjny Lagrange'a
dla zakresu 0<=H <=3000A/m.
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
Kolejne wielomiany
k
(H) dla k=0,1,...8 są:
3000
0
2000
0
1500
0
1000
0
3000
H
2000
H
1500
H
1000
H
500
0
200
0
100
0
50
0
500
H
200
H
100
H
50
H
H
0
lub po obliczeniu mianownika mamy:

3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
10
2222
.
2
H
22
0
3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
H
10
4784
.
7
H
22
1
3000
H
2000
H
1500
H
1000
H
500
H
200
H
50
H
H
10
2019
.
7
H
22
2
3000
H
2000
H
1500
H
1000
H
500
H
100
H
50
H
H
10
1198
.
2
H
22
3
3000
H
2000
H
1500
H
1000
H
200
H
100
H
50
H
H
10
9753
.
1
H
23
4
3000
H
2000
H
1500
H
500
H
200
H
100
H
50
H
H
10
924
.
2
H
24
5
3000
H
2000
H
1000
H
500
H
200
H
100
H
50
H
H
10
7366
.
6
H
25
6
3000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
9965
.
9
H
26
7
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
8554
.
1
H
26
8
i wielomian aproksymacyjny jest
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
0
H
B
8
7
6
5
4
3
2
1
0
lub
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
B
8
7
6
5
4
3
2
1
0
600 1200 1800 2400 3000
4000
2800
1600
400
800
2000
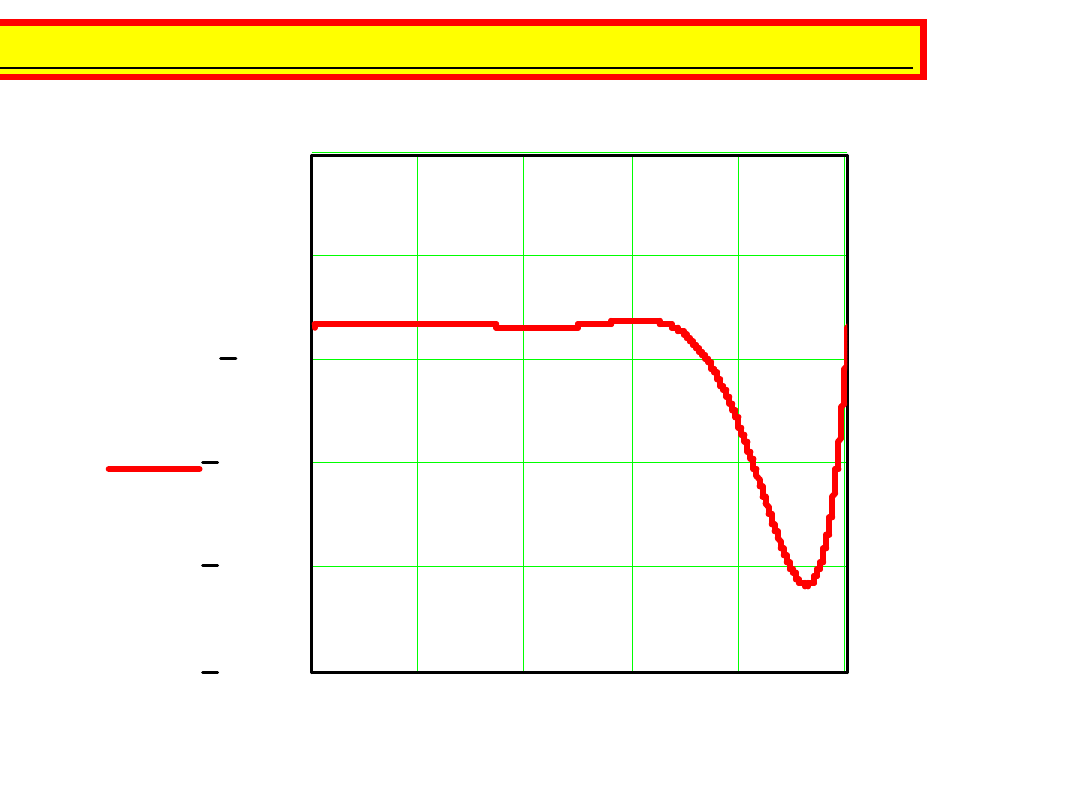
B H
( )
H
Otrzymany wynik jest niemożliwy do przyjęcia!!!
Interpolacja liniowa odcinkami:
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
0
50
0
H
75
.
0
50
0
50
H
0
H
B
1
dla
50
H
0
lub po wykonaniu działań:
H
015
.
0
H
B
1
50
H
0
dla
i podobnie:
50
H
03
.
0
100
H
015
.
0
H
B
2
dla
100
H
50
100
H
018
.
0
200
H
015
.
0
H
B
3
dla
200
H
100
200
H
0065
.
0
500
H
006
.
0
H
B
4
500
H
200
dla
500
H
004
.
0
1000
H
0039
.
0
H
B
5
dla
1000
H
500
1000
H
00404
.
0
1500
H
004
.
0
H
B
6
dla
1500
H
1000
1500
H
00406
.
0
2000
H
00404
.
0
H
B
7
dla
2000
H
1500
2000
H
002035
.
0
3000
H
00203
.
0
H
B
8
dla
3000
H
2000
0
600 1200 1800 2400 3000
0
0.6
1.2
1.8
2.4
3
BaH
( )
H
B(H)
0
100 200 300 400 500
0
0.4
0.8
1.2
1.6
2
BaH
( )
B H
( )
H
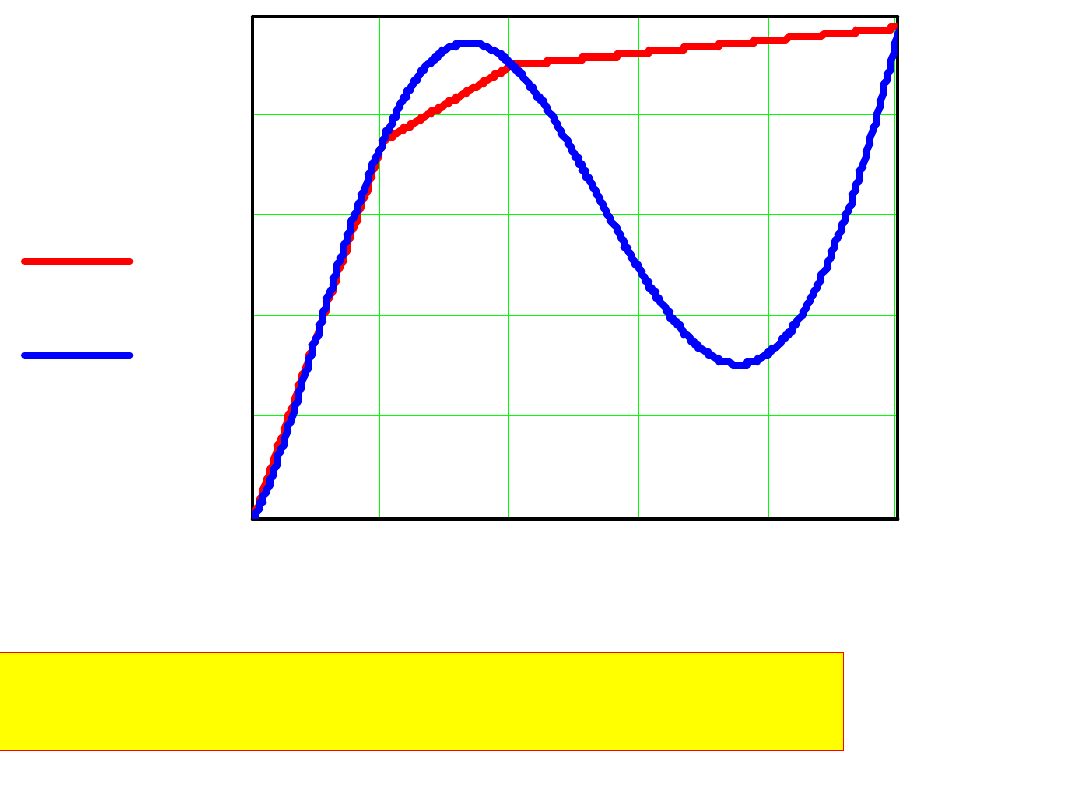
Porównanie Ba(H) – interpolacja liniowa
B(H) – wielomian 8-go stopnia
Funkcje sklejane (spline)
Dane wartości funkcji y
n
w punktach x
n
, gdzie n=0,1,2, ....N-1.
x
y
a=x
0
y
0
x
k
y
k
b=x
N
y
N
przy czym: a=x
0
<x
1
<...<x
k
<...<x
N
=b
s
m
(x)

Funkcję s
m
(x) określoną na przedziale [a,b] nazywamy
funkcją funkcją sklejaną stopnia m1, jeżeli:
1. s
m
(x) jest funkcją co najwyżej stopnia m na każdym
z podprzedziałów [x
k
,x
k+1
] gdzie k=0,1,...,N-1
2. funkcja s
m
(x) posiada ciągłą pochodną do rzędu m-1
w przedziale [a,b].
Najpowszechniej stosowane funkcje sklejane 3-go stopnia.
Z drugiego warunku wynika, że funkcja s
3
(x) musi mieć
ciągłą drugą pochodną w przedziale [a,b].
Niech:
k
k
3
M
x
s
dla k=0,1,...,N
Druga pochodna będzie ciągła, jeżeli dla przedziału [x
k
,x
k+1
]
przyjmiemy:
1
k
k
k
k
1
k
k
1
k
k
3
x
,
x
x
dla
x
x
M
x
x
M
x
s
oraz k=0,1,...,N-1
gdzie
k
1
k
k
x
x
Całkując mamy:
1
k
k
k
k
2
k
1
k
k
2
1
k
k
3
x
,
x
x
dla
A
2
x
x
M
2
x
x
M
x
s

i całkując pierwszą pochodną mamy:
1
k
k
k
k
k
k
3
k
1
k
k
3
1
k
k
3
x
,
x
x
dla
B
x
x
A
6
x
x
M
6
x
x
M
x
s
Z warunków interpolacji mamy:
N
0,1,...,
k
dla
y
x
s
k
k
3
Dla każdego z N przedziałów piszemy:
y
B
x
x
A
6
x
x
M
x
s
y
B
6
x
x
M
x
s
1
k
k
k
1
k
k
k
3
k
1
k
1
k
1
k
3
k
k
k
3
k
1
k
k
k
3
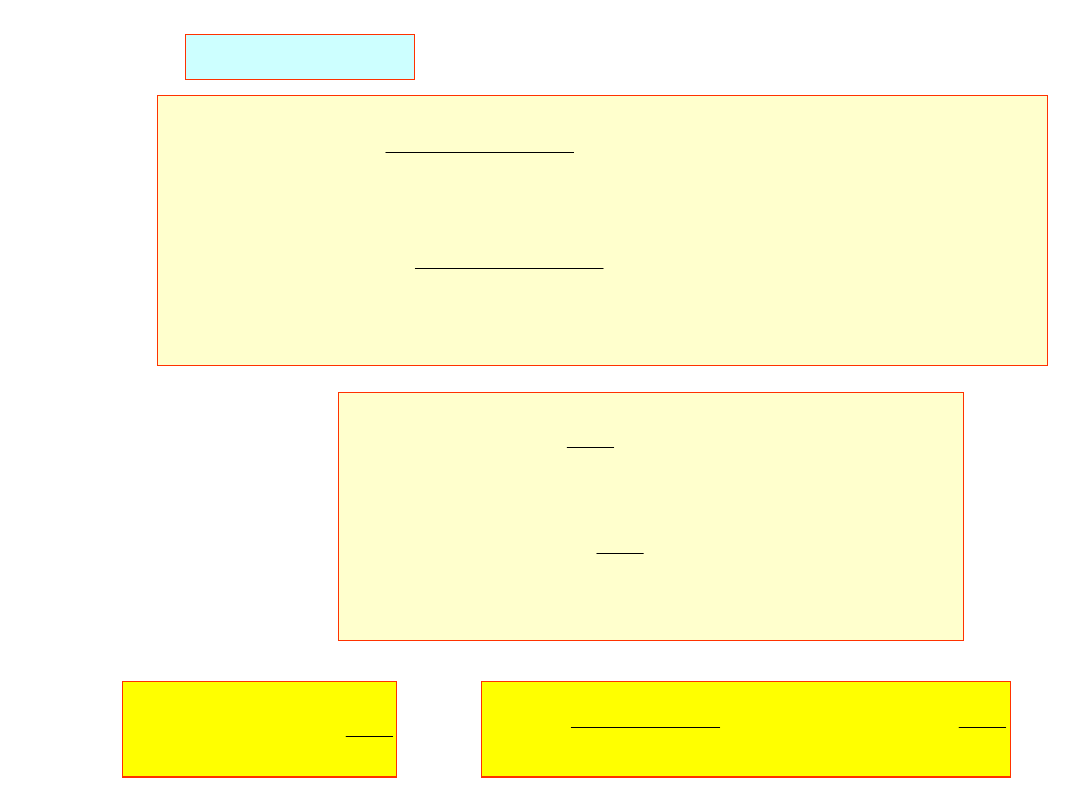
ale
k
1
k
k
x
x
czyli
y
B
x
x
A
6
x
x
M
x
s
y
B
6
x
x
M
x
s
1
k
k
k
1
k
k
k
3
k
1
k
1
k
1
k
3
k
k
k
3
k
1
k
k
k
3
możemy zapisać:
y
B
A
6
M
x
s
y
B
6
M
x
s
1
k
k
k
k
2
k
1
k
1
k
3
k
k
2
k
k
k
3
stąd mamy:
6
M
y
B
2
k
k
k
k
i
6
M
M
y
y
A
k
k
1
k
k
k
1
k
k
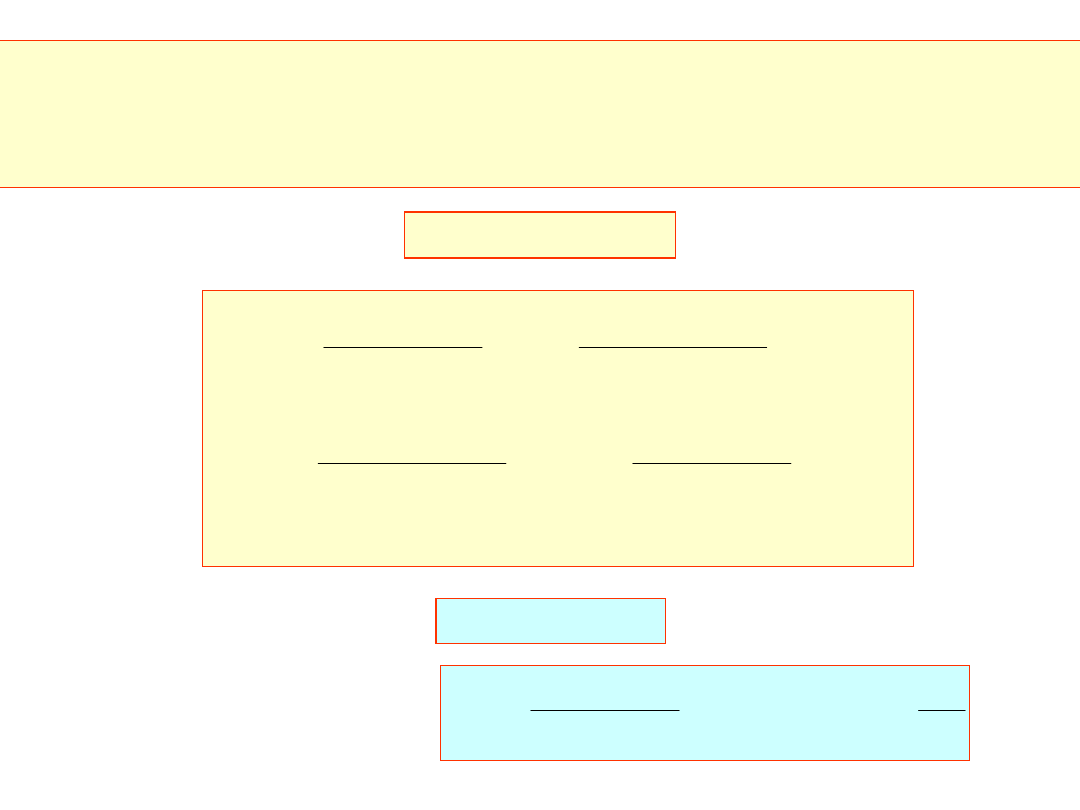
Pozostaje tylko zapewnić ciągłość pierwszej pochodnej
w węzłach interpolacji x
k
(k=1,2,...,N-1) czyli mamy N-1
równań:
k
3
k
3
x
s
x
s
stąd:
1
-
N
1,2,...,
k
dla
A
2
x
x
M
2
x
x
M
A
2
x
x
M
2
x
x
M
k
k
2
k
k
1
k
k
2
k
1
k
k
1
k
1
k
2
1
k
k
k
1
k
2
k
k
1
k
Biorąc pod uwagę, że
k
1
k
k
x
x
i
6
M
M
y
y
A
k
k
1
k
k
k
1
k
k

mamy:
1
k
1
k
k
k
k
1
k
k
k
k
1
k
k
1
k
1
k
y
y
y
y
6
M
3
M
6
M
dla k=1,2,...,N-1
mamy N-1 równań, a niewiadomych M
k
– N+1.
Potrzebne dwa dodatkowe równania, które przyjmuje się
w jednej z trzech postaci:
1. Dana jest pochodna funkcji w punkcie a i b czyli:
N
3
0
3
p
b
s
i
p
a
s

2. Dana jest druga pochodna na obu końcach przedziału, czyli:
N
3
0
3
d
b
s
i
d
a
s
3. Funkcja jest okresowa o okresie b-a i wtedy mamy:
b
s
a
s
b
s
a
s
b
s
a
s
3
3
3
3
3
3
W przypadku 1 mamy więc:
0
0
0
2
0
0
1
0
2
0
1
0
0
3
p
A
2
x
x
M
2
x
x
M
x
a
s
lub
0
0
0
1
0
1
0
p
y
y
6
M
M
2
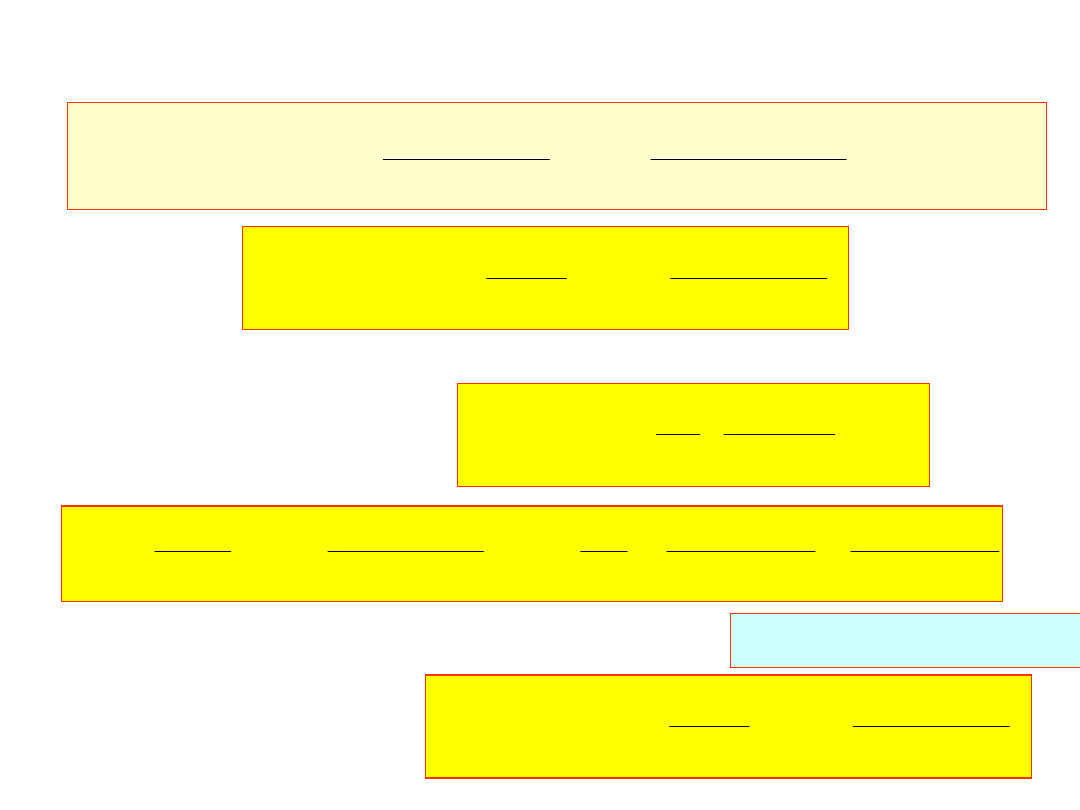
i podobnie dla drugiego końca przedziału mamy:
N
1
N
1
N
2
1
N
N
N
1
N
2
N
N
1
N
N
3
p
A
2
x
x
M
2
x
x
M
b
x
s
lub
1
N
1
N
N
N
1
N
N
1
N
y
y
p
6
M
2
M
i otrzymujemy układ N+1 równań:
0
0
0
1
0
1
0
p
y
y
6
M
M
2
1
k
1
k
k
k
k
1
k
k
k
k
1
k
k
1
k
1
k
y
y
y
y
6
M
3
M
6
M
dla k=1,2,...,N-1
1
N
1
N
N
N
1
N
N
1
N
y
y
p
6
M
2
M
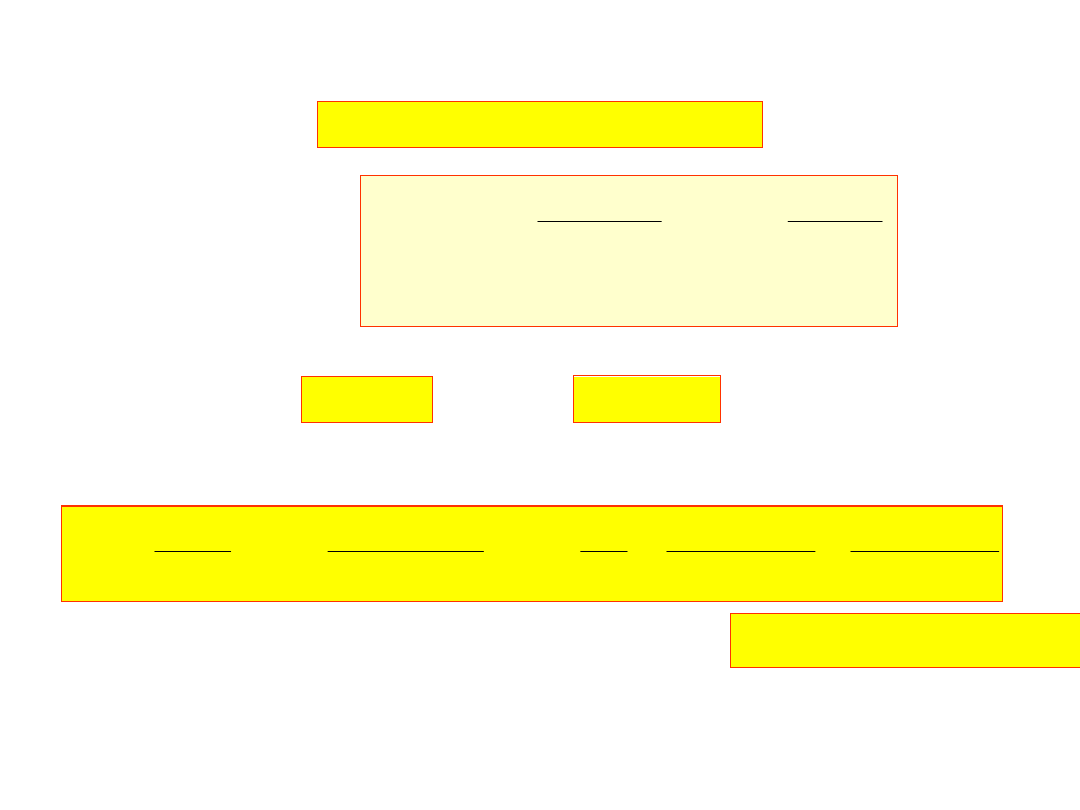
Dla drugiego typu warunków mamy:
N
3
0
3
d
b
s
i
d
a
s
czyli z definicji:
1
k
k
k
k
1
k
k
1
k
k
3
x
,
x
x
dla
x
x
M
x
x
M
x
s
wynika, że
0
0
d
M
i
N
N
d
M
i N-1 równań:
1
k
1
k
k
k
k
1
k
k
k
k
1
k
k
1
k
1
k
y
y
y
y
6
M
3
M
6
M
dla k=1,2,...,N-1
Zapiszemy otrzymane równania w postaci wygodniejszej
do obliczeń:

N
N
N
1
N
N
k
1
k
k
k
k
1
k
k
1
2
1
1
1
0
1
0
1
0
0
0
f
M
c
M
b
......
..........
..........
f
M
c
M
b
M
a
..
..........
..........
..........
f
M
c
M
b
M
a
f
M
c
M
b
Takie układy rozwiązujemy techniką „wymiatania”.
Niech
1
1
1
0
K
M
L
M
Podstawiając do drugiego równania i wyznaczając M
1
mamy:
1
1
1
1
1
1
1
1
1
2
2
1
b
L
a
K
a
f
b
L
a
M
c
M
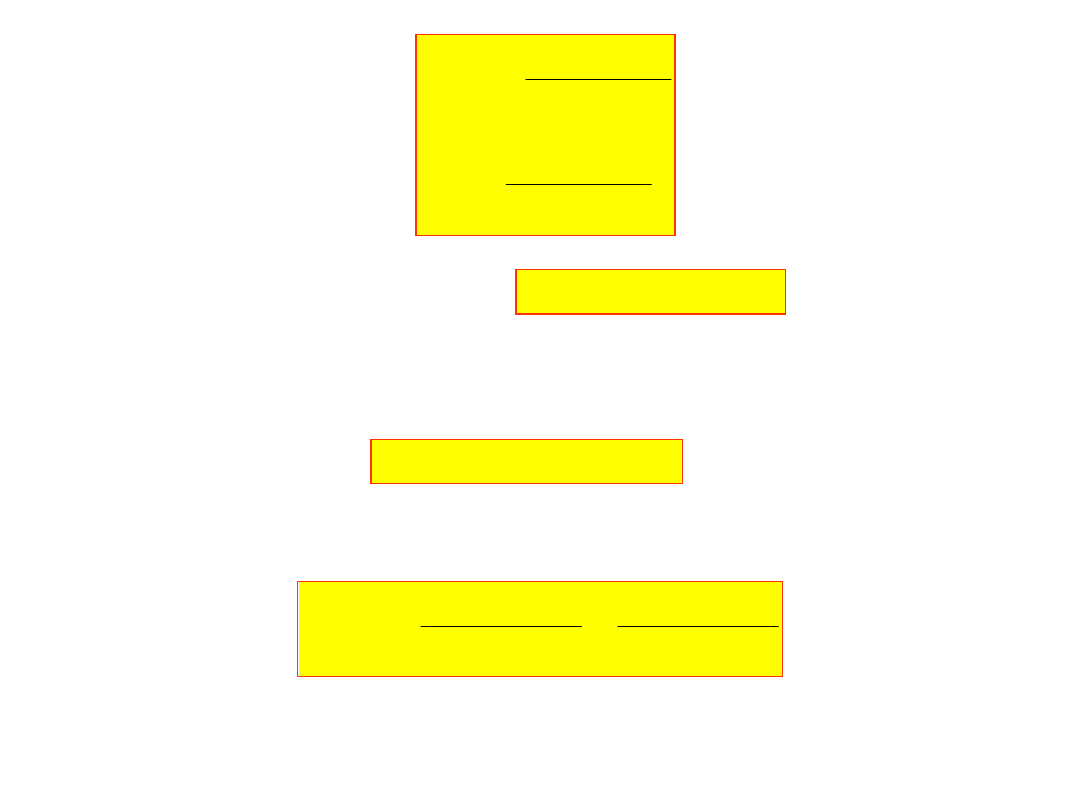
lub oznaczając:
1
1
1
1
1
1
2
1
1
1
2
2
b
L
a
K
a
f
K
b
L
a
c
L
możemy zapisać w postaci:
2
2
2
1
K
M
L
M
Wyznaczmy związek rekurencyjny spełniany przez L
k
i K
k
.
Zakładając, że
k
k
k
1
k
K
M
L
M
i podstawiając do k-go równania mamy:
k
k
k
k
k
k
k
k
k
1
k
k
k
b
L
a
K
a
f
b
L
a
M
c
M
i oznaczając:
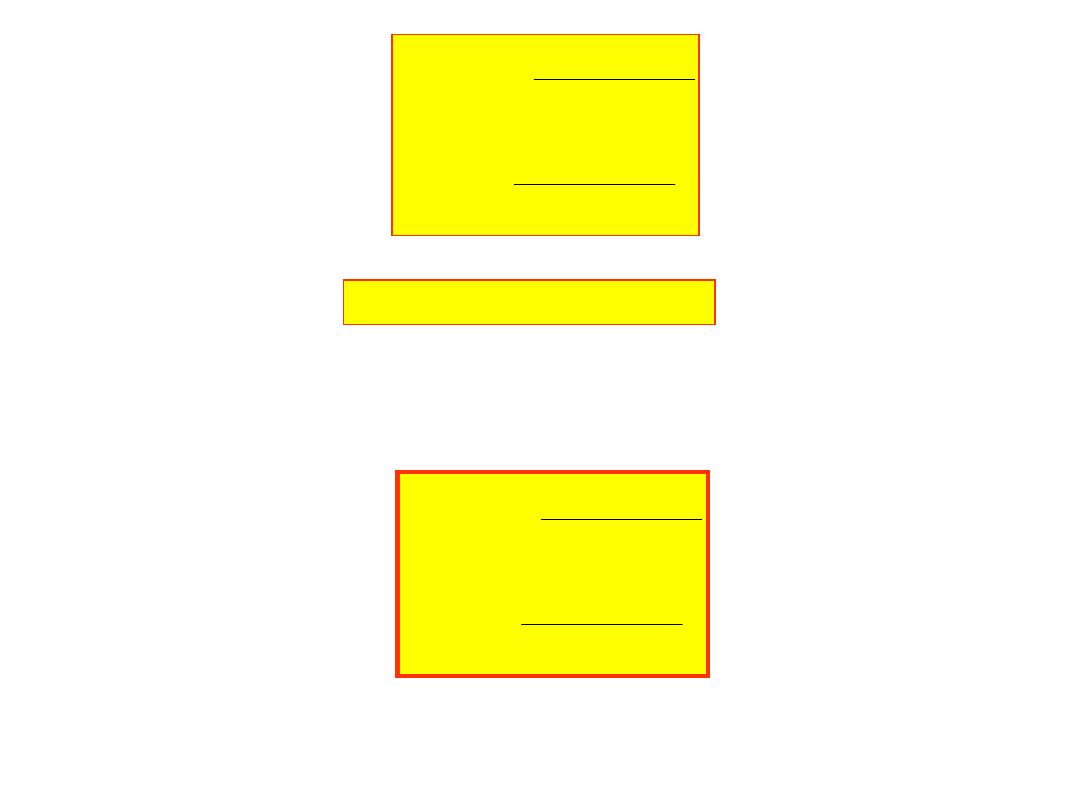
k
k
k
k
k
k
1
k
k
k
k
k
1
k
b
L
a
K
a
f
K
b
L
a
c
L
mamy:
1
k
1
k
1
k
k
K
M
L
M
a więc współczynniki L
k
,K
k
potrafimy wyznaczyć z zależności
rekurencyjnej:
k
k
k
k
k
k
1
k
k
k
k
k
1
k
b
L
a
K
a
f
K
b
L
a
c
L
jeżeli znamy wartości startowe L
1
, K
1
.
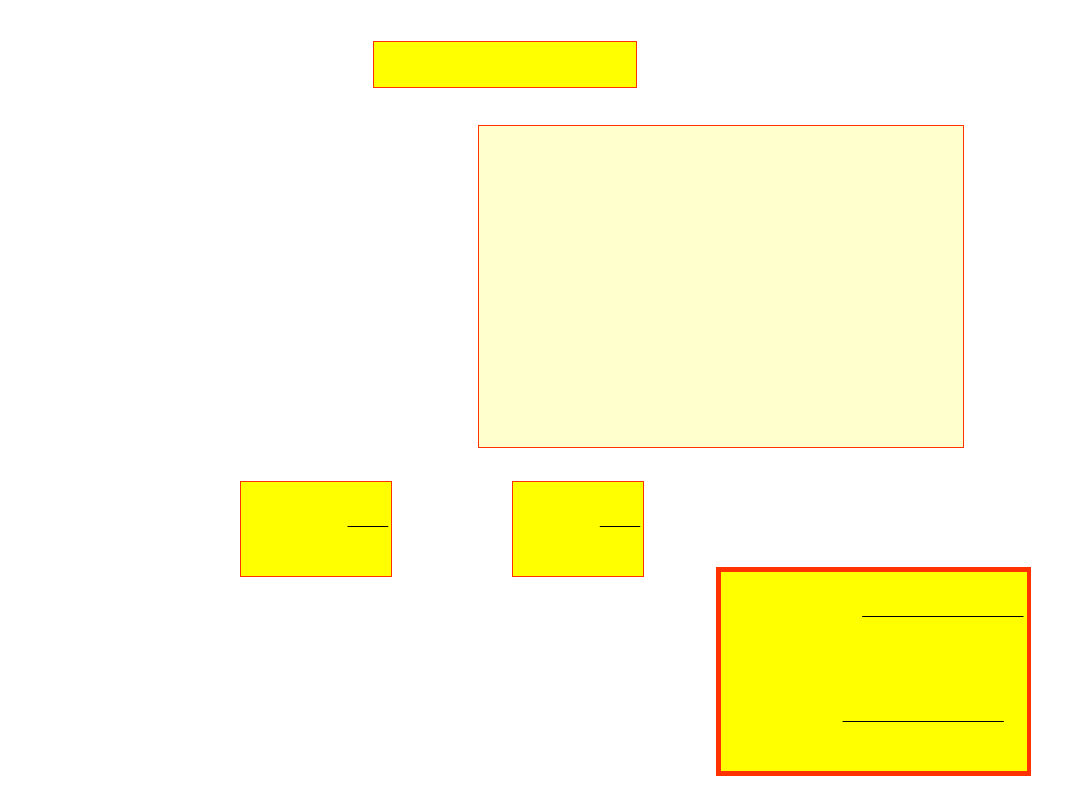
Ale porównując:
1
1
1
0
K
M
L
M
z pierwszym równaniem:
N
N
N
1
N
N
k
1
k
k
k
k
1
k
k
1
2
1
1
1
0
1
0
1
0
0
0
f
M
c
M
b
......
..........
..........
f
M
c
M
b
M
a
..
..........
..........
..........
f
M
c
M
b
M
a
f
M
c
M
b
mamy:
0
0
1
b
c
L
i
0
0
1
b
f
K
i na podstawie związku rekurencyjnego:
k
k
k
k
k
k
1
k
k
k
k
k
1
k
b
L
a
K
a
f
K
b
L
a
c
L
wyznaczmy kolejno dla k=1,2,...N-1
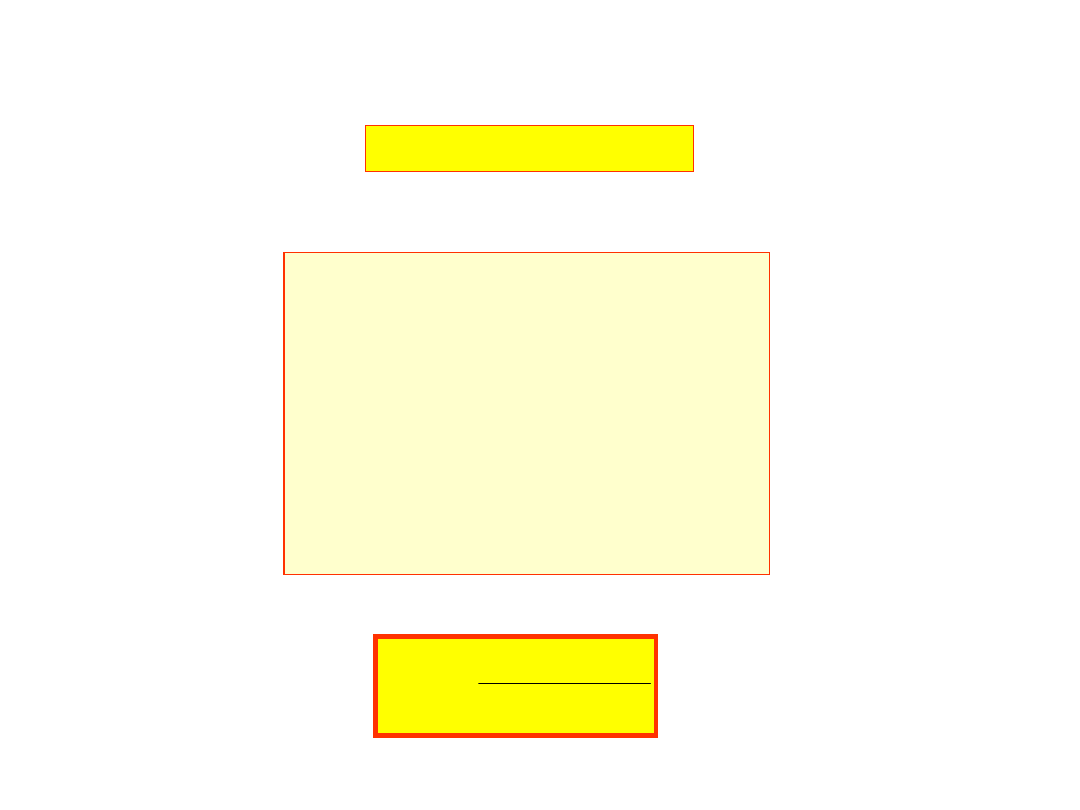
Ostatnie równanie przyjmuje postać:
N
N
N
1
N
K
M
L
M
i podstawiając do ostatniego równania:
N
N
N
1
N
N
k
1
k
k
k
k
1
k
k
1
2
1
1
1
0
1
0
1
0
0
0
f
M
c
M
b
......
..........
..........
f
M
c
M
b
M
a
..
..........
..........
..........
f
M
c
M
b
M
a
f
M
c
M
b
mamy:
N
N
N
N
N
N
N
b
L
c
b
K
f
M
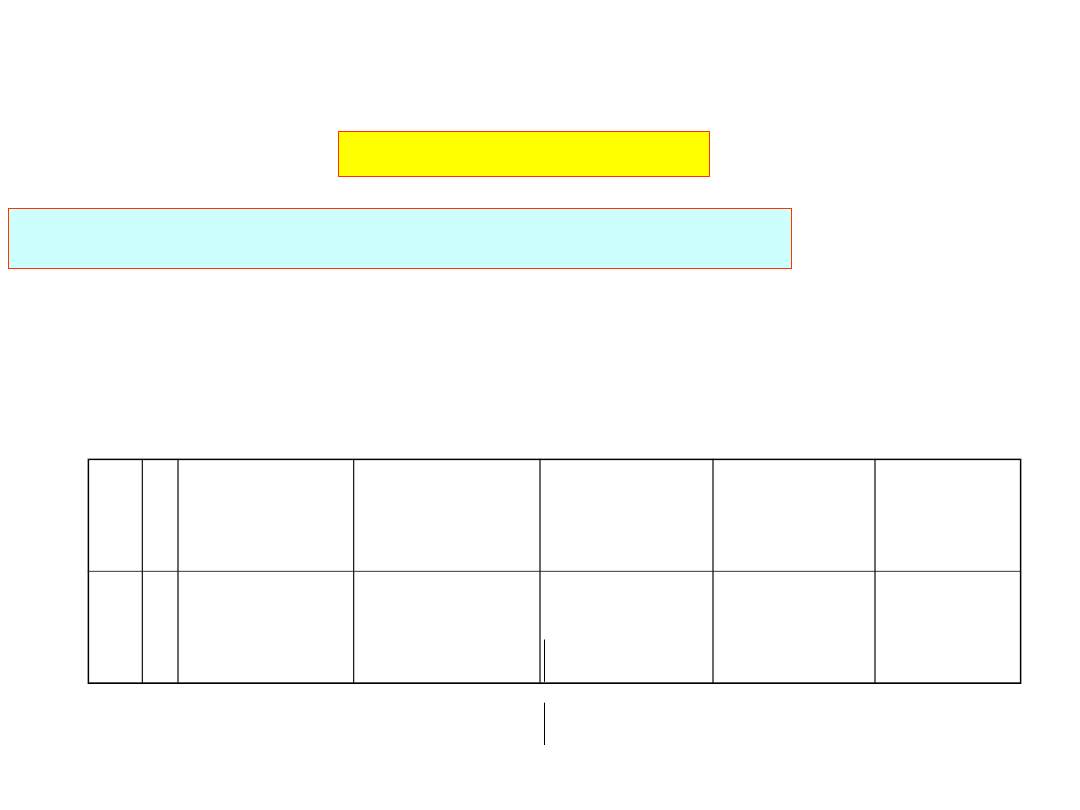
Znając M
N
wyznaczamy ze wzoru:
1
k
1
k
1
k
k
K
M
L
M
kolejne M
k
przyjmując k=N-1,N-2,...,0
Przykład:
Dane są wartości funkcji:
x 0 0.314
16
0.6283
2
0.942
48
1.256
64
1.57
08
y 0 0.309
02
0.5877
9
0.809
02
0.951
06
1
i jej pierwsze pochodne:
0
y
1
y
5708
.
1
x
0
x
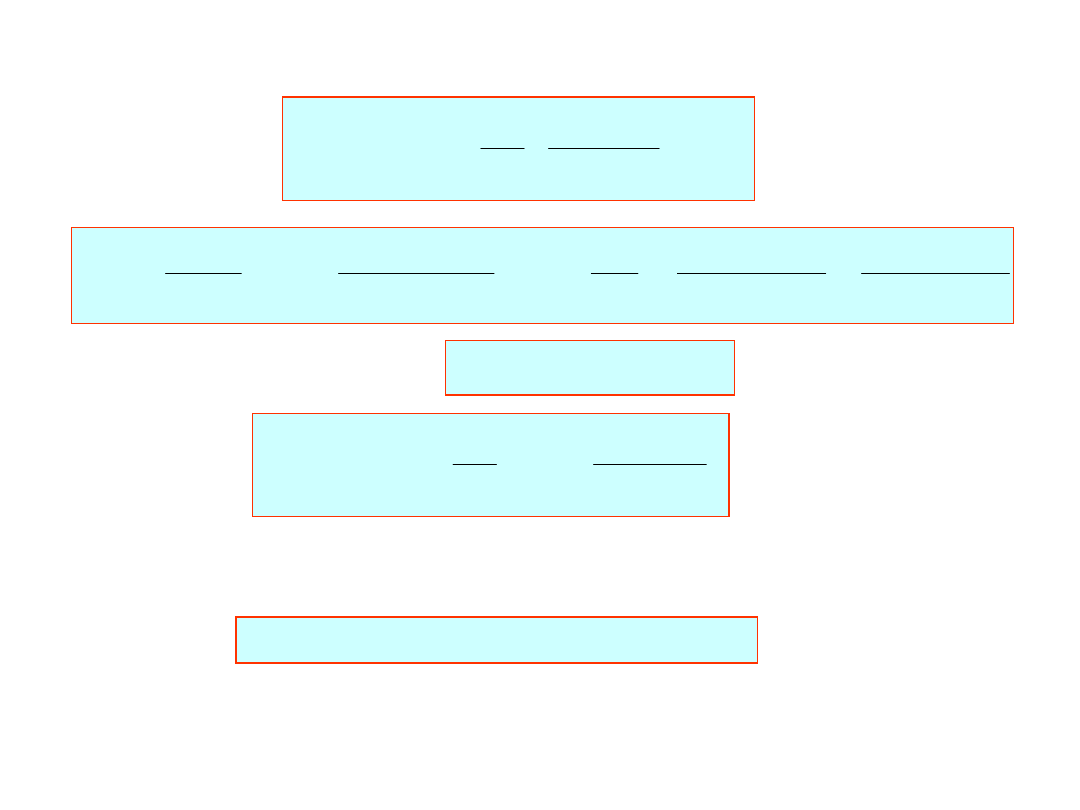
Współczynniki M
0
, M
1
, M
2
, M
3
, M
4
, M
5
wyznaczamy z układu
równań:
0
0
0
1
0
1
0
p
y
y
6
M
M
2
1
k
1
k
k
k
k
1
k
k
k
k
1
k
k
1
k
1
k
y
y
y
y
6
M
3
M
6
M
dla k=1,2,3,4
4
4
5
5
4
5
4
y
y
p
6
M
2
M
gdzie ze względu na równomierny podział mamy:
31416
.
0
4
3
2
1
0
i podstawiając dane mamy:
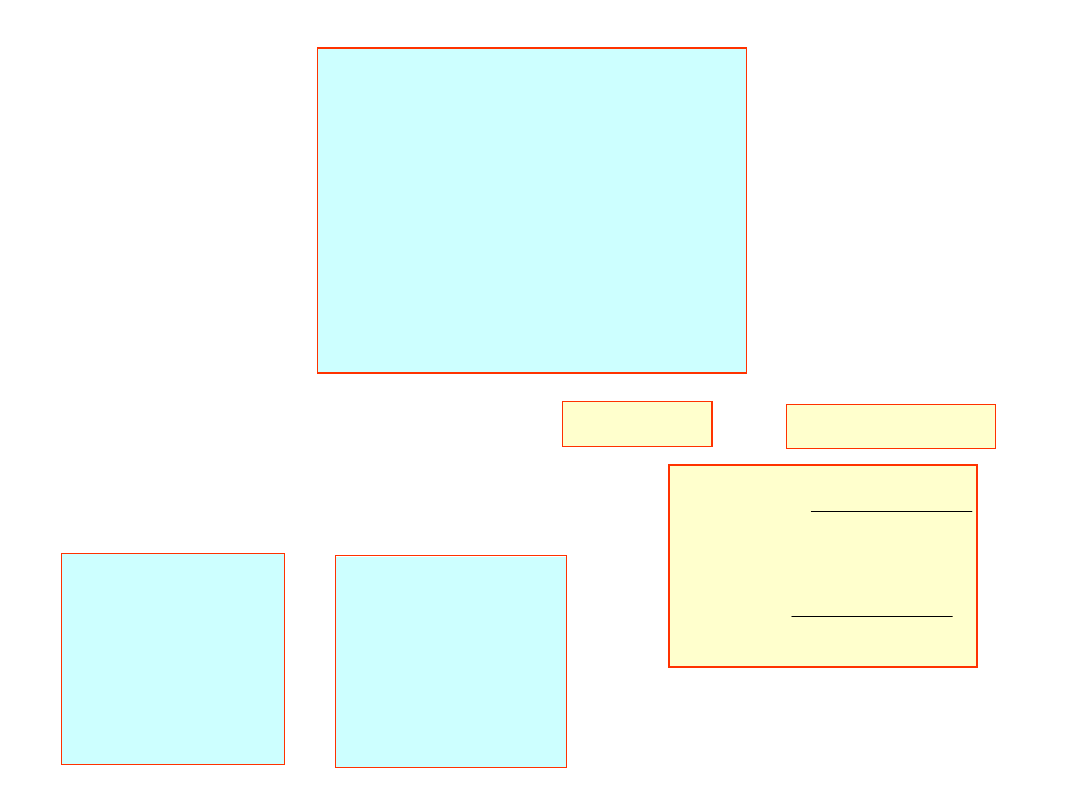
97520
.
2
M
2
M
65980
.
5
M
M
4
M
81417
.
4
M
M
4
M
49801
.
3
M
M
4
M
83898
.
1
M
M
4
M
31261
.
0
M
M
2
5
4
5
4
3
4
3
2
3
2
1
2
1
0
1
0
Z pierwszego równania mamy:
5
.
0
L
1
1563
.
0
K
1
i
i na mocy związku rekurencyjnego:
k
k
k
k
k
k
1
k
k
k
k
k
1
k
b
L
a
K
a
f
K
b
L
a
c
L
26796
.
0
L
26804
.
0
L
26923
.
0
L
28571
.
0
L
5
4
3
2
22889
.
1
K
07362
.
1
K
80875
.
0
K
48077
.
0
K
5
4
3
2
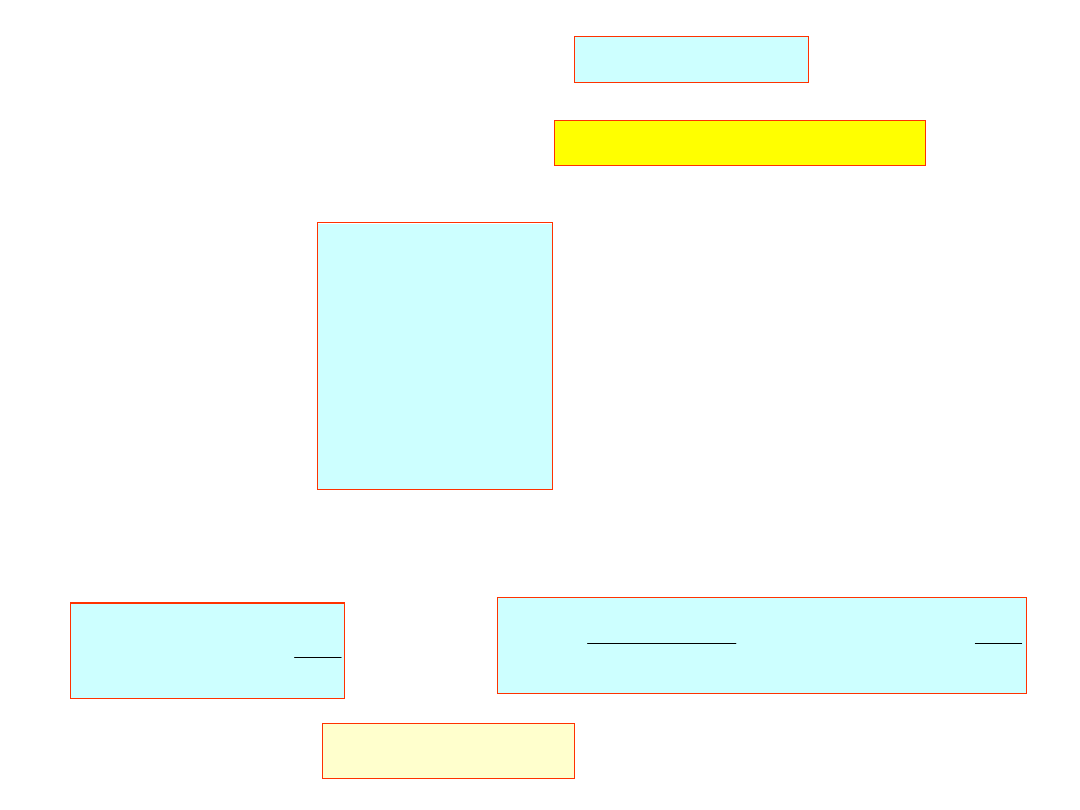
Z ostatniego równania mamy:
00828
.
1
M
5
i ze związku rekurencyjnego:
1
k
1
k
1
k
k
K
M
L
M
wyznaczamy:
00004
.
0
M
31252
.
0
M
58888
.
0
M
81665
.
0
M
95871
.
0
M
0
1
2
3
4
a następnie stałe A
k
i B
k
ze wzorów:
6
M
y
B
2
k
k
k
k
6
M
M
y
y
A
k
k
1
k
k
k
1
k
k
i
k=0,1,2,3,4
15838
.
0
A
45957
.
0
A
71612
.
0
A
93455
.
0
A
1
A
4
3
2
1
0
96683
.
0
B
82245
.
0
B
59748
.
0
B
31416
.
0
B
0
B
4
3
2
1
0
i ostatecznie mamy:
0,0.31416
x
dla
3
3
0
3
x
1658
.
0
x
31416
.
0
00002
.
0
x
x
s
62832
0.31416,0.
x
dla
3
3
1
3
31416
.
0
x
3141
.
0
x
62832
.
0
1658
.
0
31416
.
0
x
93455
.
0
31416
.
0
x
s

94248
0.62832,0.
x
dla
3
3
2
3
62832
.
0
x
43325
.
0
x
94248
.
0
31241
.
0
62832
.
0
x
71612
.
0
59748
.
0
x
s
25664
0.94248,1.
x
dla
3
3
3
3
94248
.
0
x
50861
.
0
x
25664
.
1
43325
.
0
94248
.
0
x
45957
.
0
82245
.
0
x
s
5708
1.25664,1.
x
dla
3
3
4
3
25664
.
1
x
53491
.
0
x
5708
.
1
50861
.
0
25664
.
1
x
15838
.
0
96683
.
0
x
s
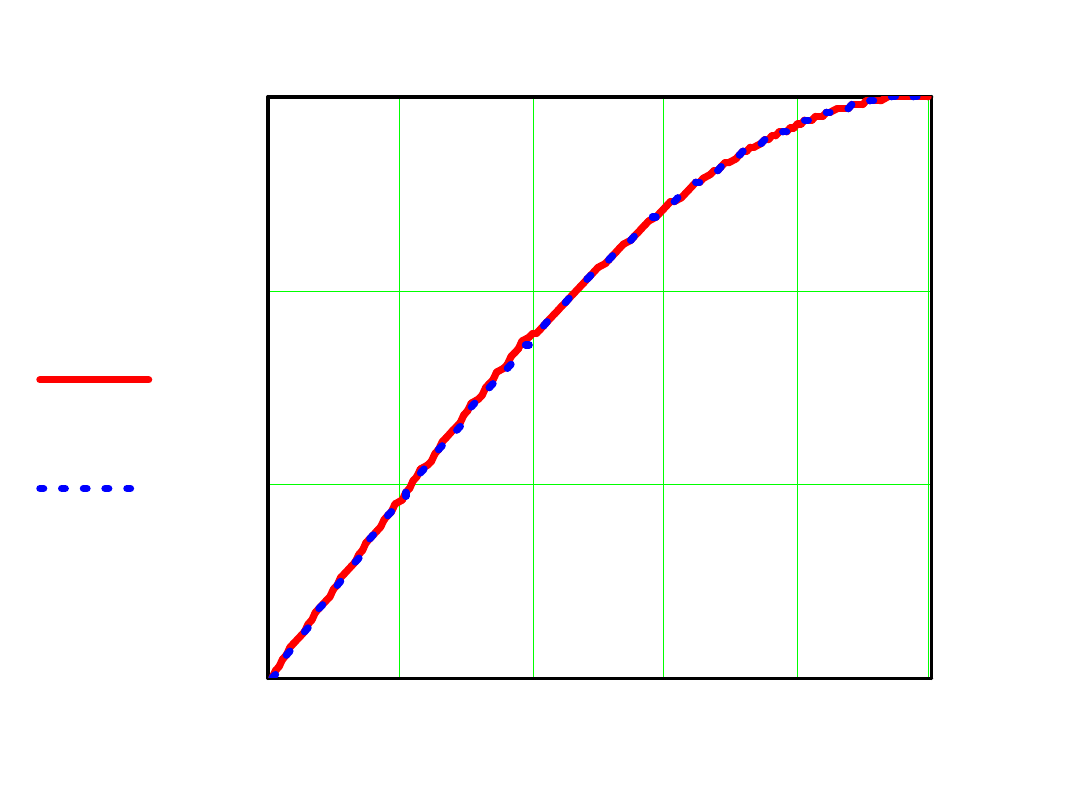
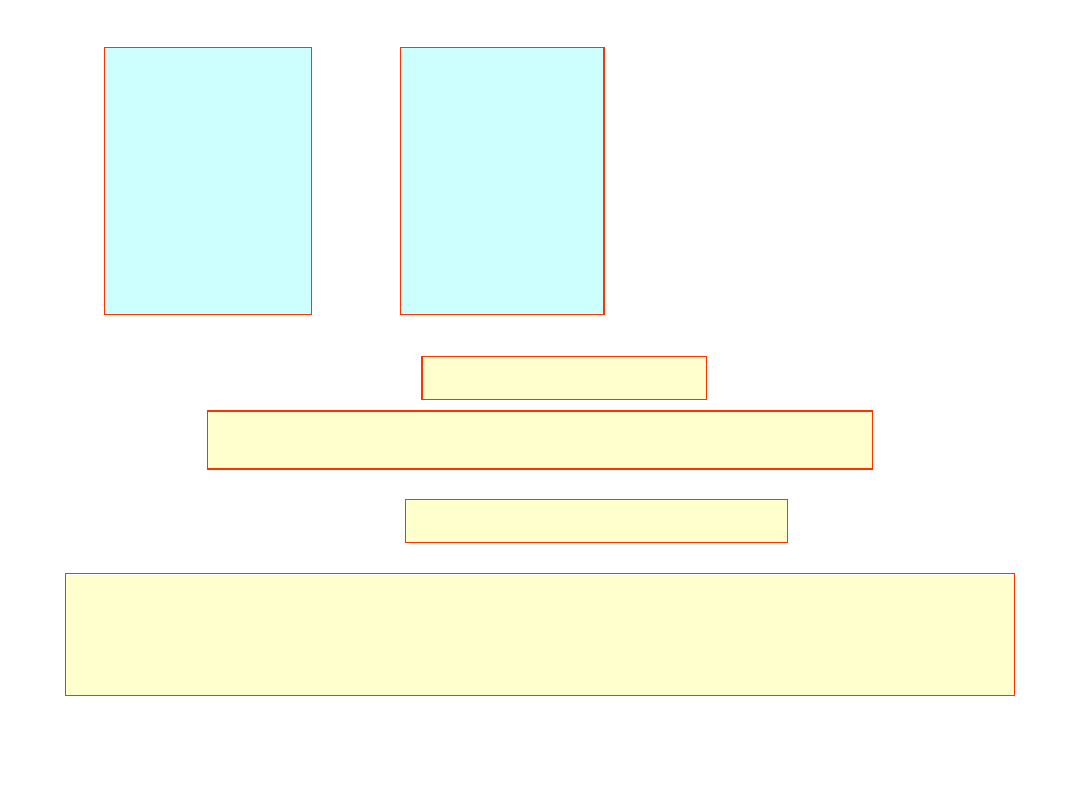
0
0.31 0.63 0.94 1.26 1.57
0
0.33
0.67
1
s x
( )
sin x
( )
x
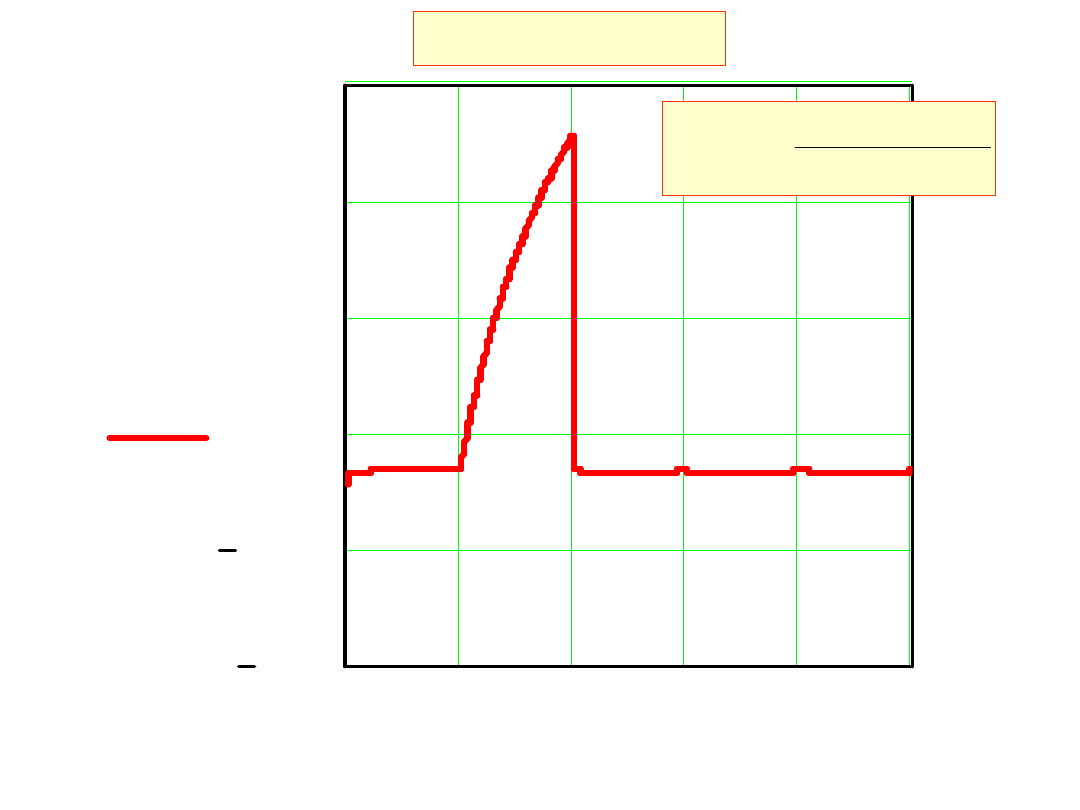
0
0.31 0.63 0.94 1.26 1.57
0.01
0.004
0.002
0.008
0.014
0.02
eps x
( )
x
Błąd względny
x
sin
x
sin
x
s
x
eps
3
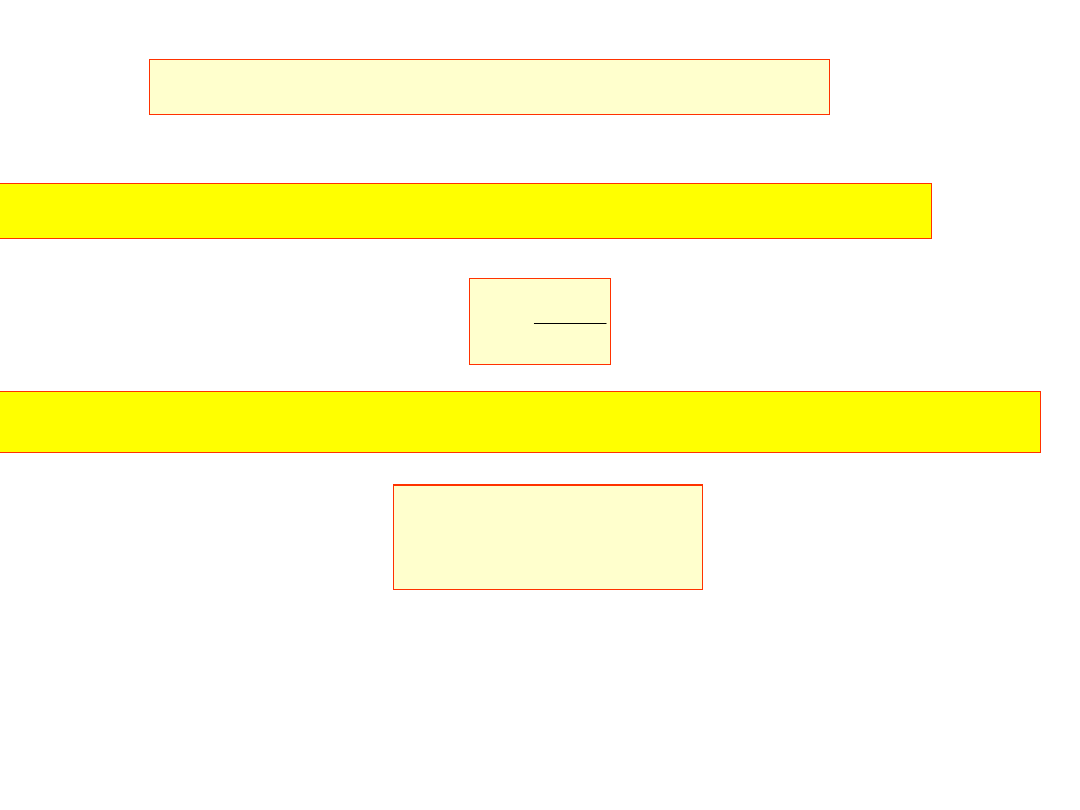
B – funkcje sklejane (B – spline)
Podział przedziału [a,b] jest równomierny, czyli
N
a
b
Funkcja sklejana s
3
(x) jest przyjmowana w postaci:
1
N
k
1
k
k
k
3
x
B
a
x
s
gdzie funkcje B
k
(x) tworzą bazę przestrzeni s
3
(x) i mają
postać:
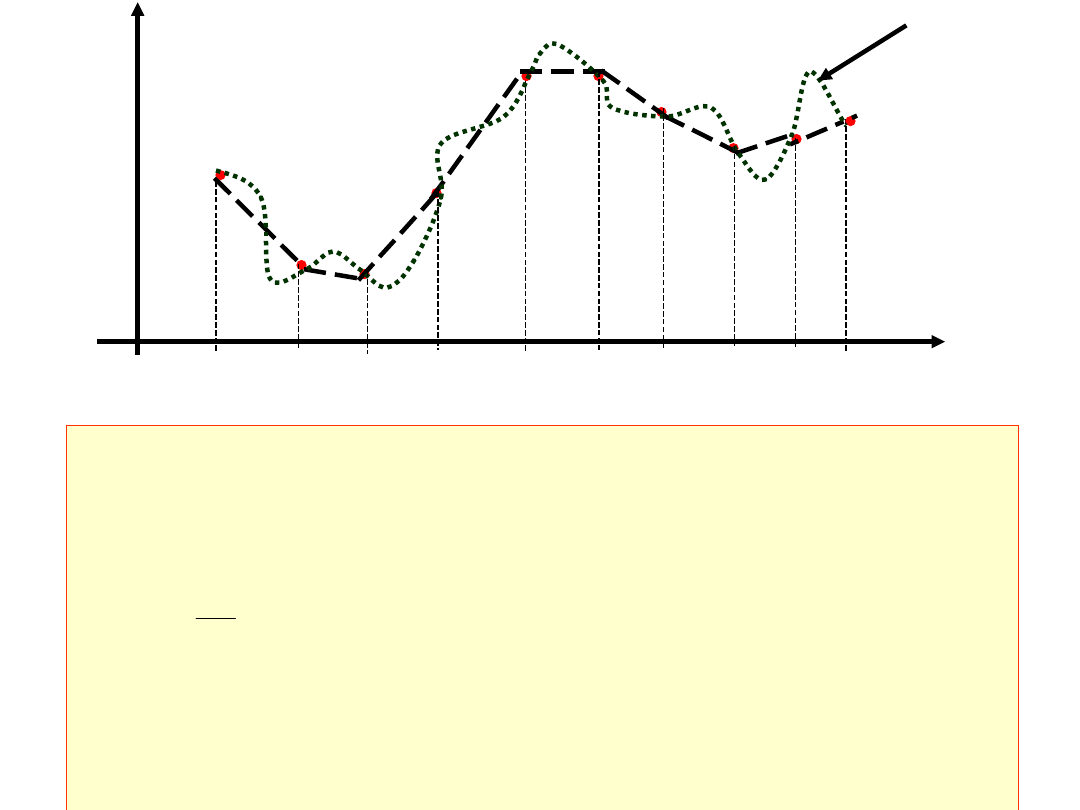
x
y
a=x
0
y
0
x
k
=k
y
k
b=N
y
N
s
m
(x)
2
k
2
-
k
2
k
1
k
3
2
k
1
k
k
3
1
k
2
1
k
1
k
2
3
k
1
-
k
3
1
k
2
1
k
1
k
2
3
1
k
2
-
k
3
2
k
3
k
x
,
x
x
dla
0
x
,
x
x
dla
x
x
x
,
x
x
dla
x
x
3
x
x
3
x
x
3
x
,
x
x
dla
x
x
3
x
x
3
x
x
3
x
,
x
x
dla
x
x
1
x
B
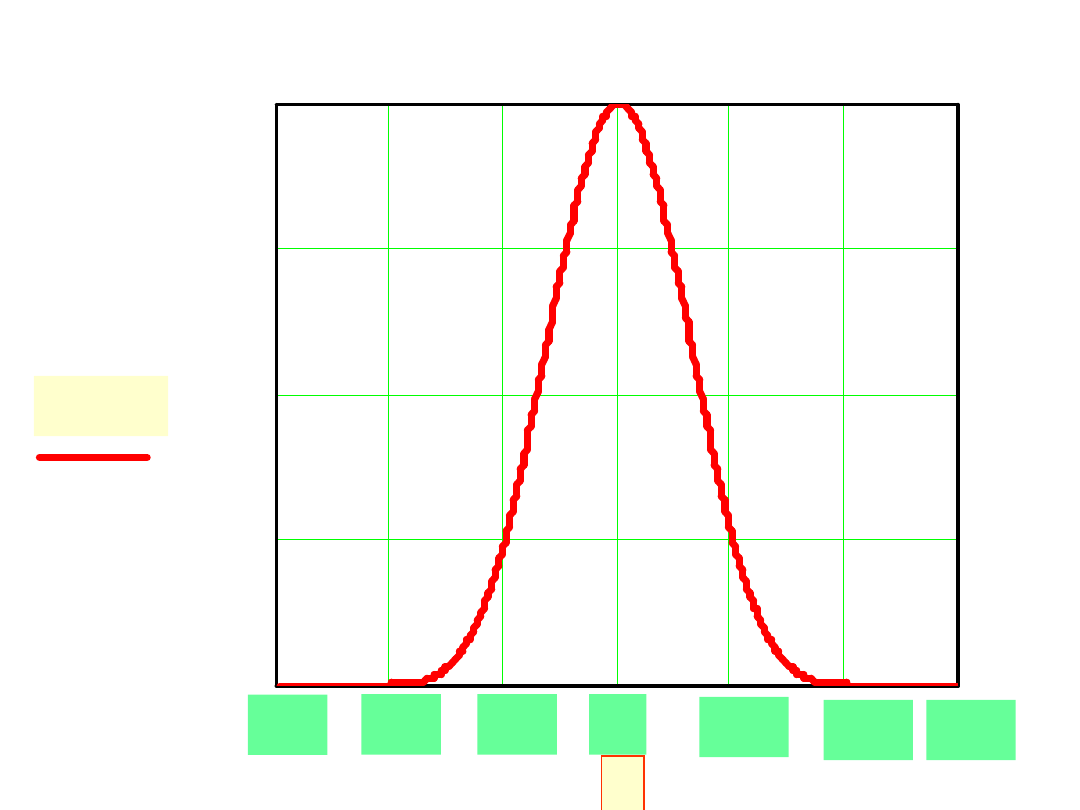
0
1
2
3
4
5
6
0
1
2
3
4
B 3 t
( )
t
x
B
k
(x)
x
k
x
k-1
x
k-2
x
k-3
x
k+1
x
k+2
x
k+3
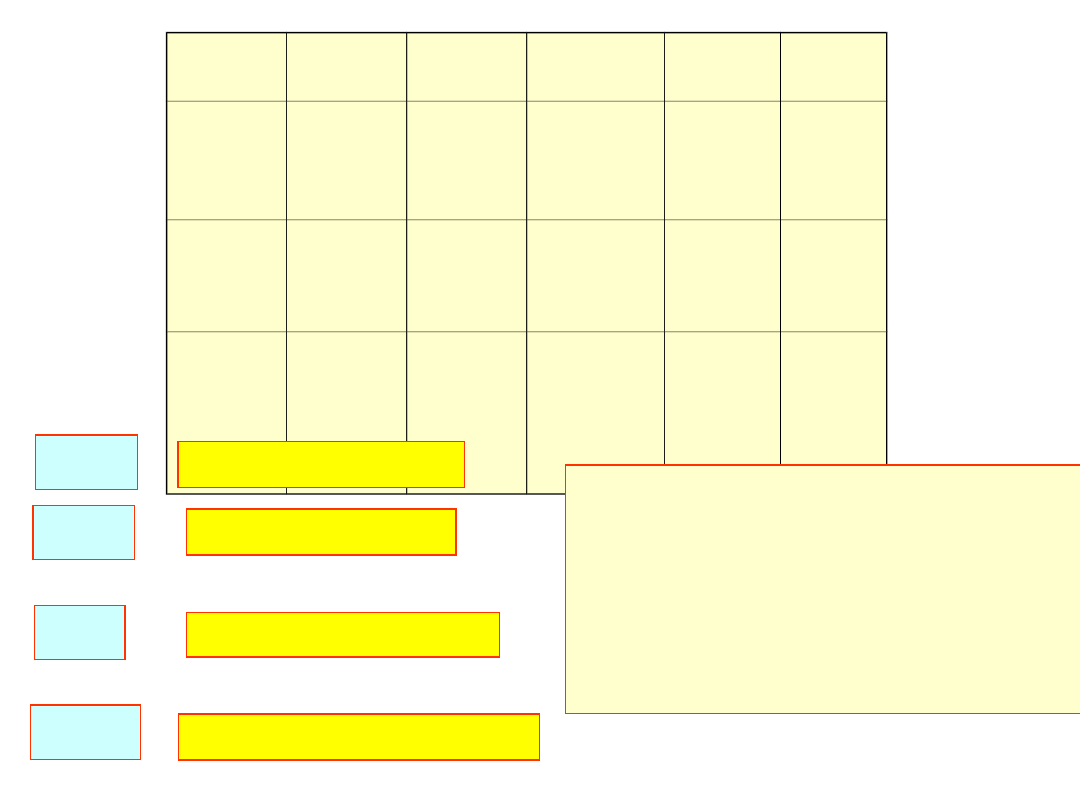
x
k-2
x
k-1
x
k
x
k+1
x
k+2
B
k
(x
)
0
1
4
1
0
0
3/
0
-
3/
0
0
6/
2
-
12/
2
6/
2
0
x
B
k
x
B
k
Na mocy tabeli w węzłach interpolacji mamy:
k=0
0
1
0
1
y
a
a
4
a
k=1
1
2
1
0
y
a
a
4
a
...............................................
k=i
i
1
i
i
1
i
y
a
a
4
a
.................................................
k=N
N
1
N
N
1
N
y
a
a
4
a
Mamy N+1 równań
i N+3 niewiadomych.
Dwa dodatkowe równania
z warunków brzegowych.
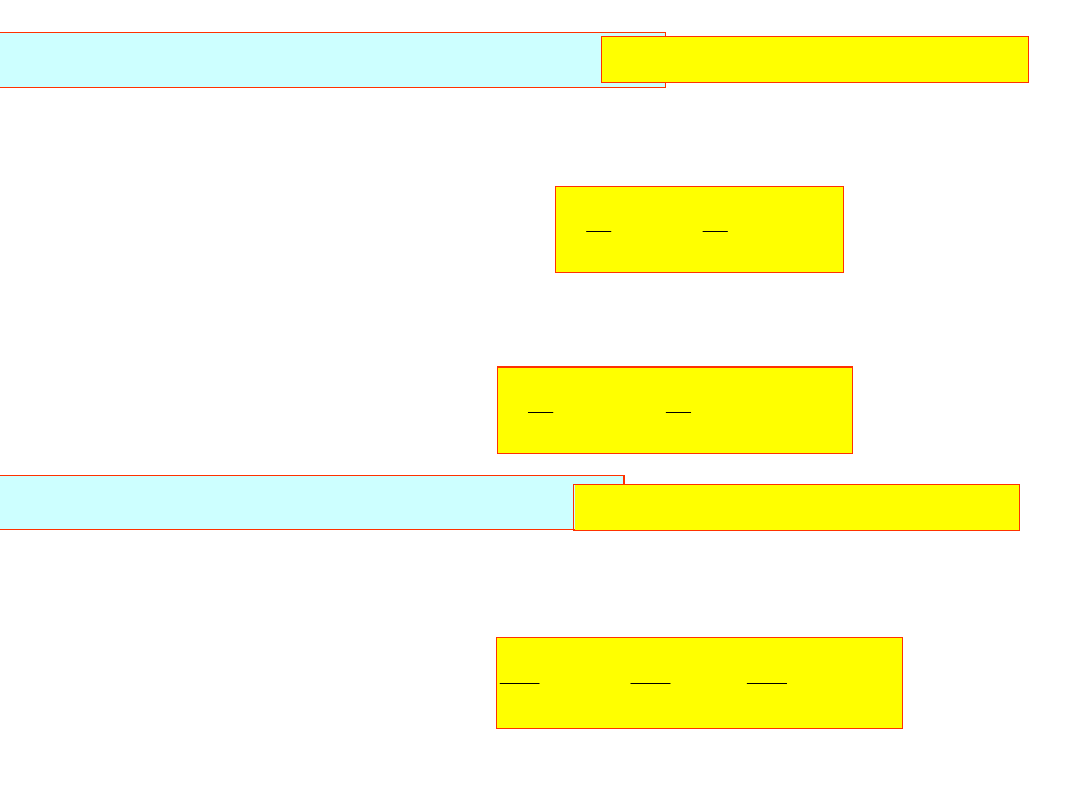
Dla warunku pierwszego rodzaju:
N
3
0
3
p
b
s
i
p
a
s
mamy na mocy tablicy – pierwsze równanie:
0
1
1
p
a
3
a
3
i ostatnie równanie:
N
1
N
1
N
p
a
3
a
3
Dla warunku drugiego rodzaju:
N
3
0
3
d
b
s
i
d
a
s
mamy na mocy tablicy – pierwsze równanie:
0
1
2
0
2
1
2
d
a
6
a
12
a
6
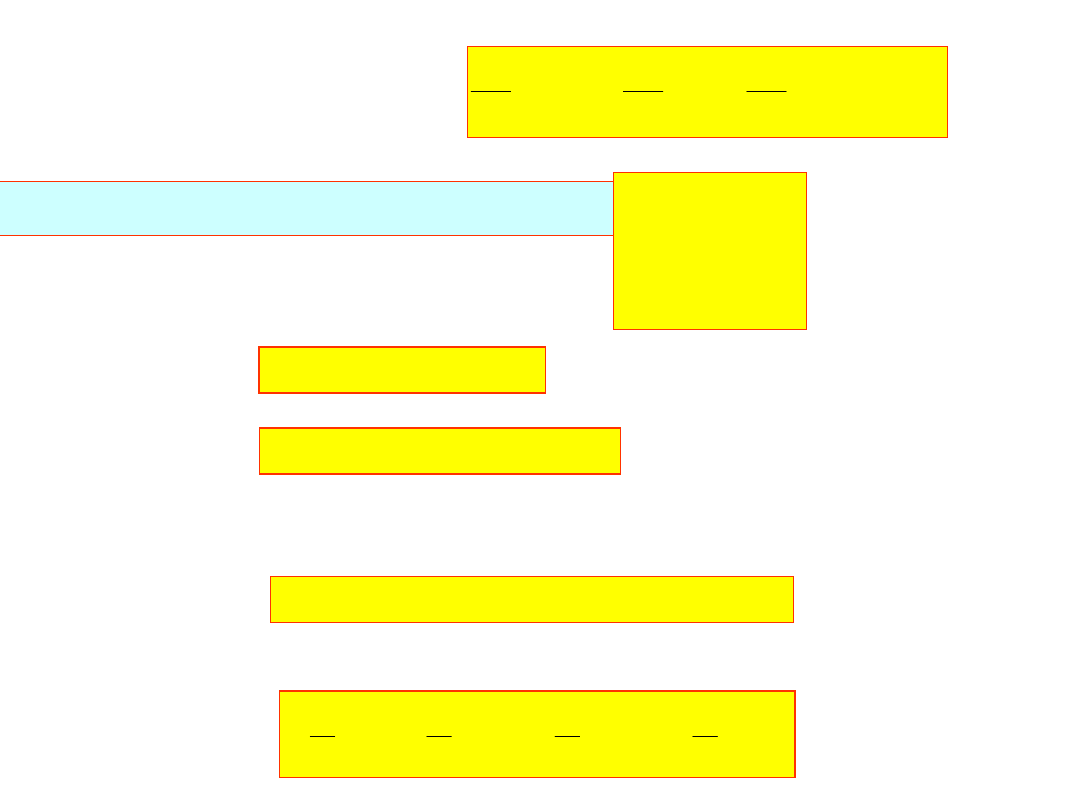
i ostatnie równanie:
N
1
N
2
N
2
1
N
2
d
a
6
a
12
a
6
Dla warunku trzeciego rodzaju:
b
s
a
s
b
s
a
s
b
s
a
s
3
3
3
3
3
3
równanie:
0
1
0
1
y
a
a
4
a
i ostatnie:
N
1
N
N
1
N
y
a
a
4
a
mają identyczne prawe strony, gdyż ze względu na okresowość
y
0
=y
N
i dlatego zamiast ostatniego równania piszemy:
1
N
N
1
N
1
0
1
a
a
4
a
a
a
4
a
i pozostałe dwa warunki dają równania:
1
N
1
N
1
1
a
3
a
3
a
3
a
3
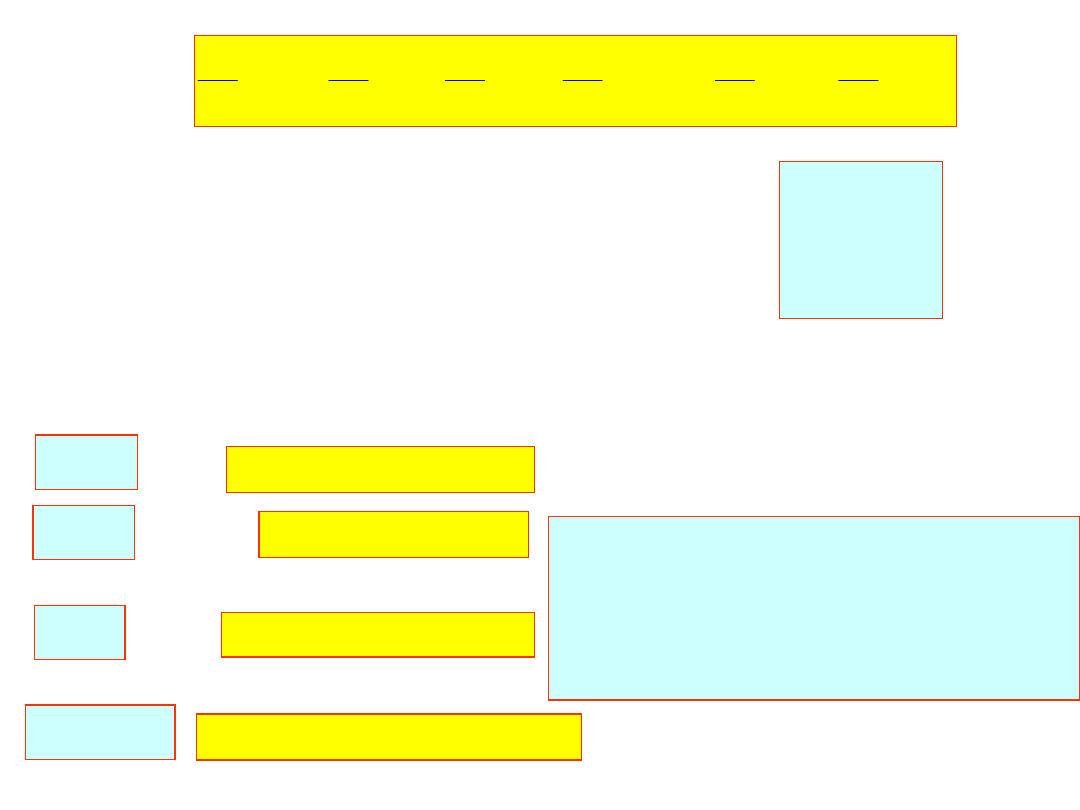
1
N
2
N
2
1
N
2
1
2
0
2
1
2
a
6
a
12
a
6
a
6
a
12
a
6
Rozwiązując powyższe trzy równania mamy:
1
N
1
N
0
1
N
1
a
a
a
a
a
a
a więc układ równań przyjmuje postać:
k=0
0
1
0
1
N
y
a
a
4
a
k=1
1
2
1
0
y
a
a
4
a
...............................................
k=i
i
1
i
i
1
i
y
a
a
4
a
.................................................
k=N-1
1
N
0
1
N
2
N
y
a
a
4
a
Jak rozwiązać otrzymany
układ równań metodą
„wymiatania” pokażemy
na przykładzie
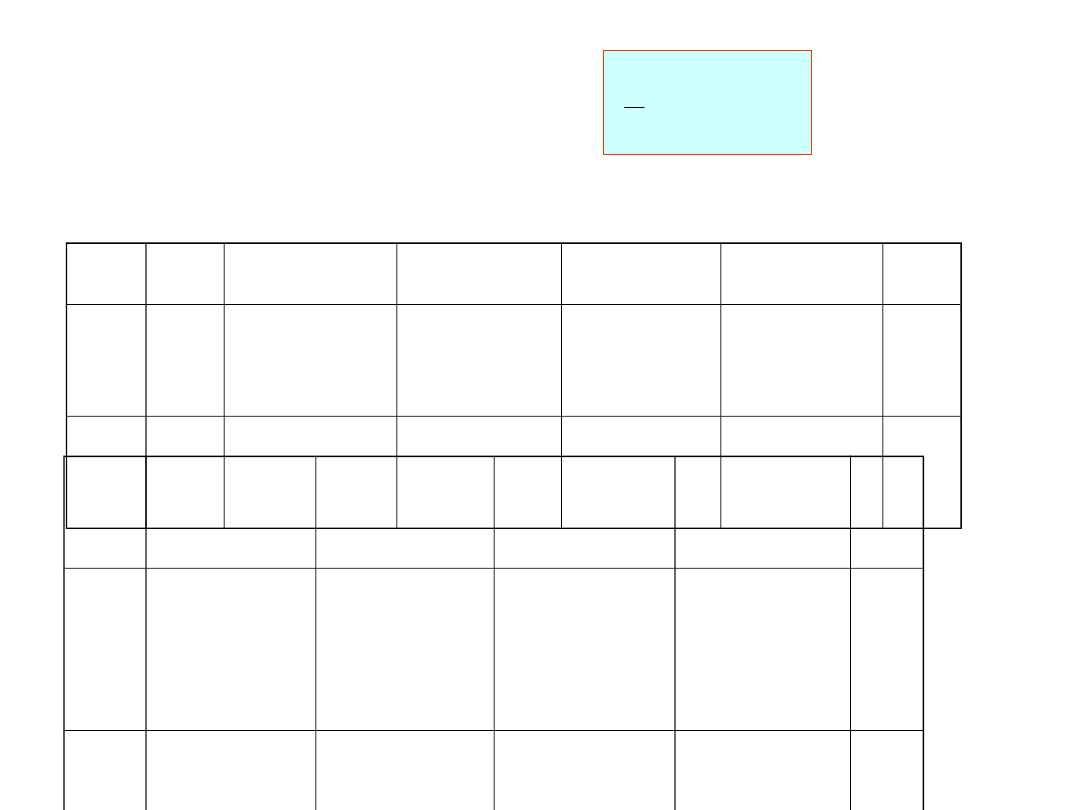
Dana jest elipsa o równaniu:
1
y
5
x
2
2
lub w postaci tablicy:
k
0
1
2
3
4
5
x
5 4.924
04
4.698
46
3.830
22
2.5
0
y
0 0.173
65
0.342
02
0.642
79
0.866
03
1
k
6
7
8
9
1
0
x
-2.5
-
3.830
22
-
4.698
46
-
4.924
04
-5
y 0.866
03
0.642
79
0.342
02
0.173
65
0
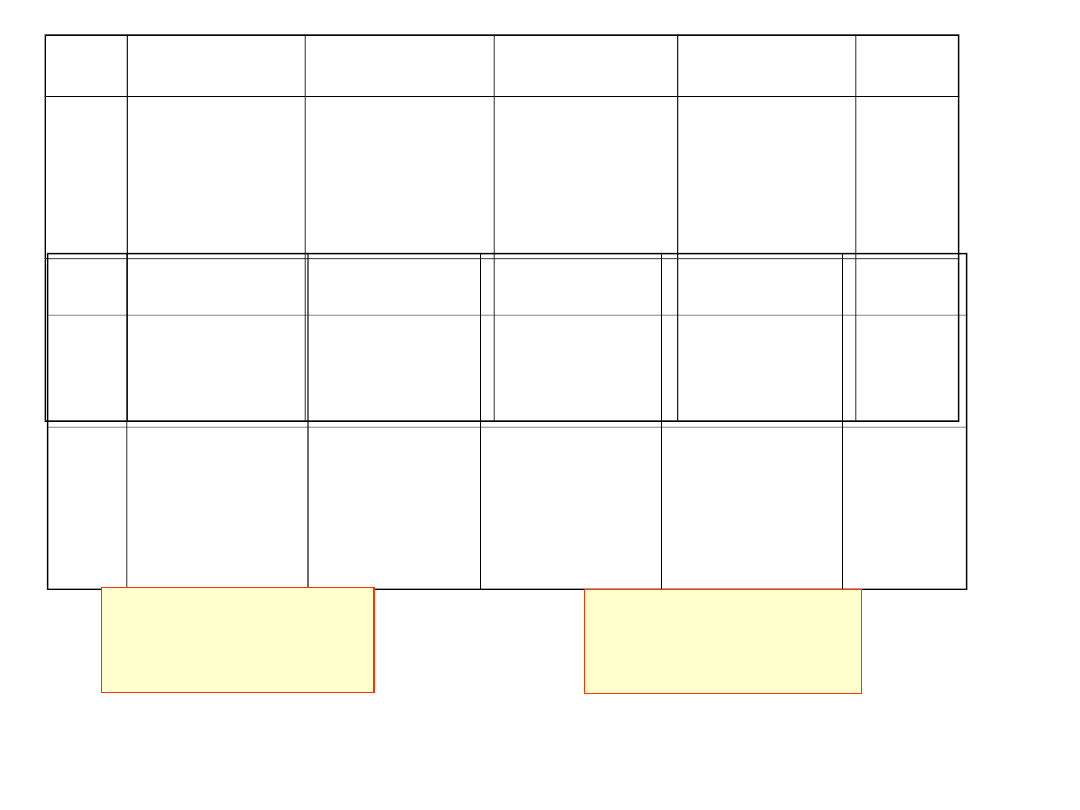
k
11
12
13
14
15
x
-
4.924
04
-
4.6984
6
-
3.8302
2
-2.5
0
y
-
0.173
65
-
0.3420
2
-
0.6427
9
-
0.866
03
1
k
16
17
18
19
20
x
2.5
3.830
22
4.698
46
4.924
04
5
y
-
0.866
03
-
0.642
79
-
0.342
02
-
0.173
65
0
Interpolację krzywej zamkniętej możemy wykonać przyjmując
przedstawienie parametryczne:
21
k
1
k
k
k
t
B
a
t
x
i
21
k
1
k
k
k
t
B
b
t
y
i mamy układ równań:

83022
.
3
a
a
4
a
69846
.
4
a
a
4
a
92404
.
4
a
a
4
a
5
a
a
4
a
92404
.
4
a
a
4
a
69846
.
4
a
a
4
a
83022
.
3
a
a
4
a
5
.
2
a
a
4
a
0
a
a
4
a
5
.
2
a
a
4
a
83022
.
3
a
a
4
a
69846
.
4
a
a
4
a
92404
.
4
a
a
4
a
5
a
a
4
a
14
13
12
13
12
11
12
11
10
11
10
9
10
9
8
9
8
7
8
7
6
7
6
5
6
5
4
5
4
3
4
3
2
3
2
1
2
1
0
1
0
19
92404
.
4
a
4
a
a
69846
.
4
a
a
4
a
83022
.
3
a
a
4
a
5
.
2
a
a
4
a
0
a
a
4
a
5
.
2
a
a
4
a
19
18
0
19
18
17
18
17
16
17
16
15
16
15
14
15
14
13
Rozwiązanie metodą „wymiatania”:
k
19
k
k
k
1
k
A
a
B
a
L
a
Podstawiając do k-go równania:
k
1
k
k
1
k
x
a
a
4
a
mamy:
k
k
k
k
19
k
k
1
k
k
L
4
A
x
L
4
a
B
L
4
a
a
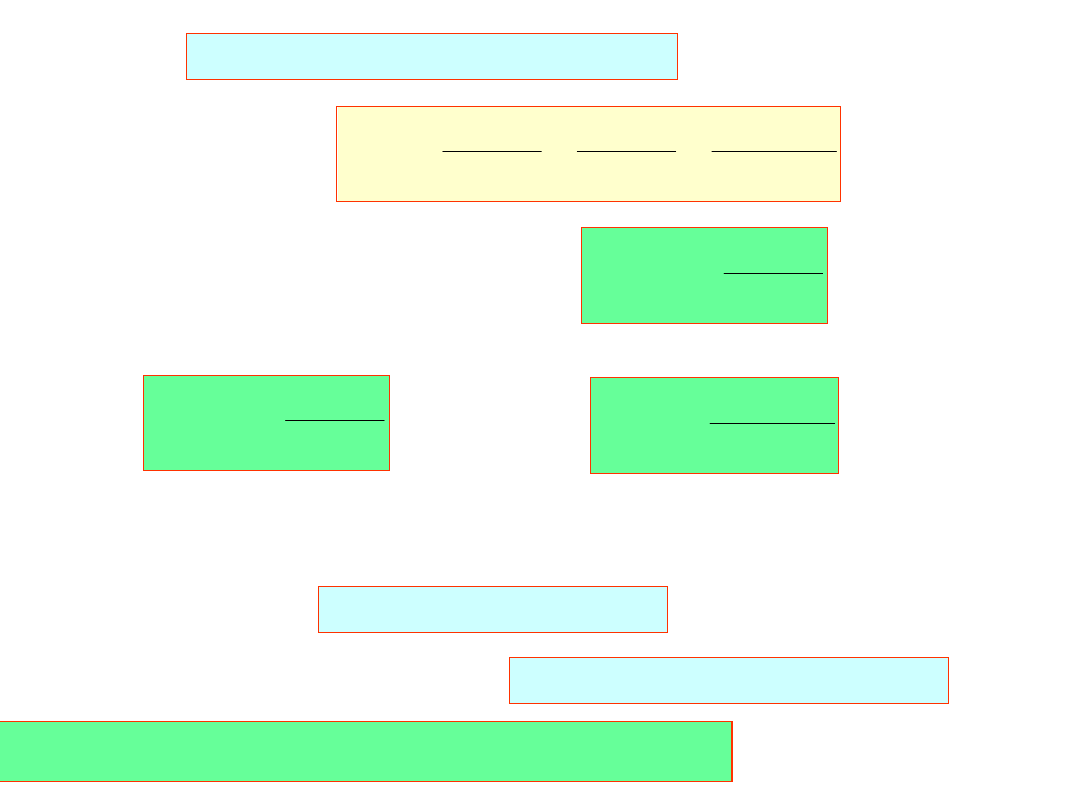
ale
1
k
19
1
k
1
k
1
k
k
A
a
B
a
L
a
i porównując z
k
k
k
k
19
k
k
1
k
k
L
4
A
x
L
4
a
B
L
4
a
a
mamy wzory rekurencyjne:
k
1
k
L
4
1
L
k
k
1
k
L
4
B
B
i
k
k
k
1
k
L
4
A
x
A
Wartości startowe L
1
, A
1
i B
1
wyznaczamy porównując wzór:
1
19
1
1
1
0
A
a
B
a
L
a
z pierwszym równaniem:
25
.
1
a
25
.
0
a
25
.
0
a
19
1
0
mamy: L
1
=-0.25, B
1
=-0.25 i A
1
=1.25

i z dokładnością do 5 cyfr mamy:
L
2
=-0.26667
L
3
=-0.26786
L
4
=-0.26794
L
5
=L
6
=...=L
19
=-0.26795
B
2
=0.066667 B
15
=-2.44585e-9
B
3
=-0.017857 B
16
=6.55364e-10
B
4
=4.78469e-3 B
17
=-1.75604e-10
B
5
=-1.28205e-3 B
18
=4.7053e-11
B
6
=3.43525e-4 B
19
=-1.26078e-11
B
7
=-9.20471e-5
B
8
=2.4664e-5
B
9
=-6.60869e-6
B
10
=1.77079e-6
B
11
=-4.74482e-7
B
12
=1.27137e-7
B
13
=-3.40663e-8
B
14
=9.128037e-9
W równaniu
92404
.
4
a
4
a
a
19
18
0
B
19
poprawia 4
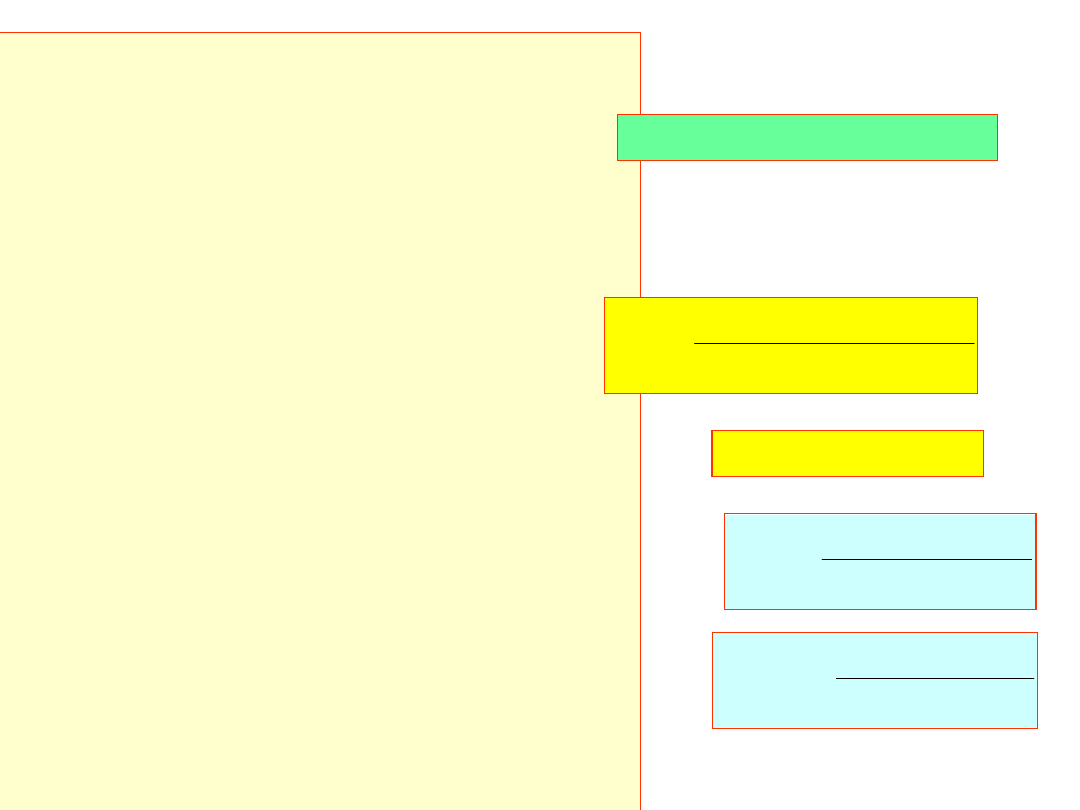
A
2
=0.97974 A
14
=-0.76330
A
3
=0.99608 A
15
=-0.46535
A
4
=0.75939 A
16
=0.12469
A
5
=0.46640 A
17
=0.63646
A
6
=-0.12497 A
18
=0.85576
A
7
=-0.63639 A
19
=1.02965
A
8
=-0.85579
A
9
=-1.02964
A
10
=-1.04350
A
11
=-1.06014
A
12
=-1.03533
A
13
=-0.98153
Podstawiając do równania:
92404
.
4
a
4
a
a
19
18
0
mamy:
19
19
0
19
19
B
L
4
a
A
92404
.
4
a
czyli
0
19
19
19
a
D
C
a
gdzie
19
19
19
19
B
L
4
A
92404
.
4
C
19
19
19
B
L
4
1
D
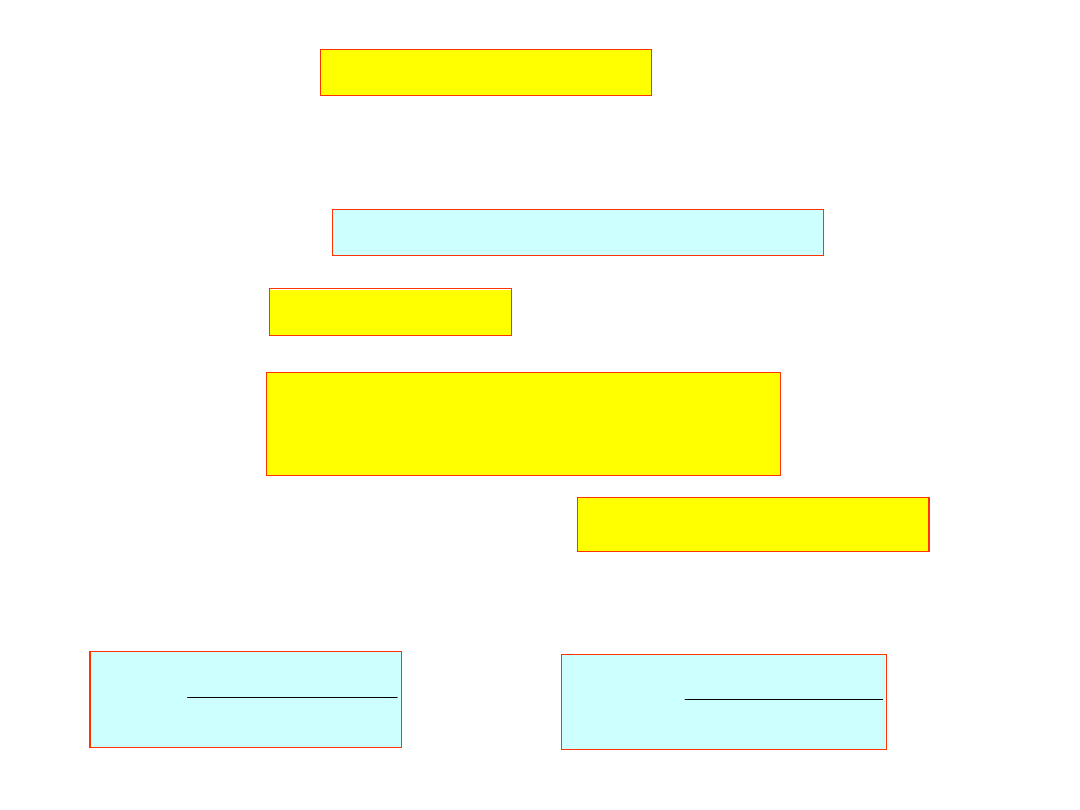
i zakładając:
0
1
k
1
k
1
k
a
D
C
a
i podstawiając do związku rekurencyjnego:
1
k
19
1
k
1
k
1
k
k
A
a
B
a
L
a
mamy:
0
k
k
k
a
D
C
a
gdzie
19
1
k
1
k
1
k
k
1
k
19
1
k
1
k
1
k
k
D
B
D
L
D
A
C
B
C
L
C
dla k=18,17,...,0
ze startowymi C
19
, D
19
z zależności:
19
19
19
19
B
L
4
A
92404
.
4
C
i
19
19
19
B
L
4
1
D
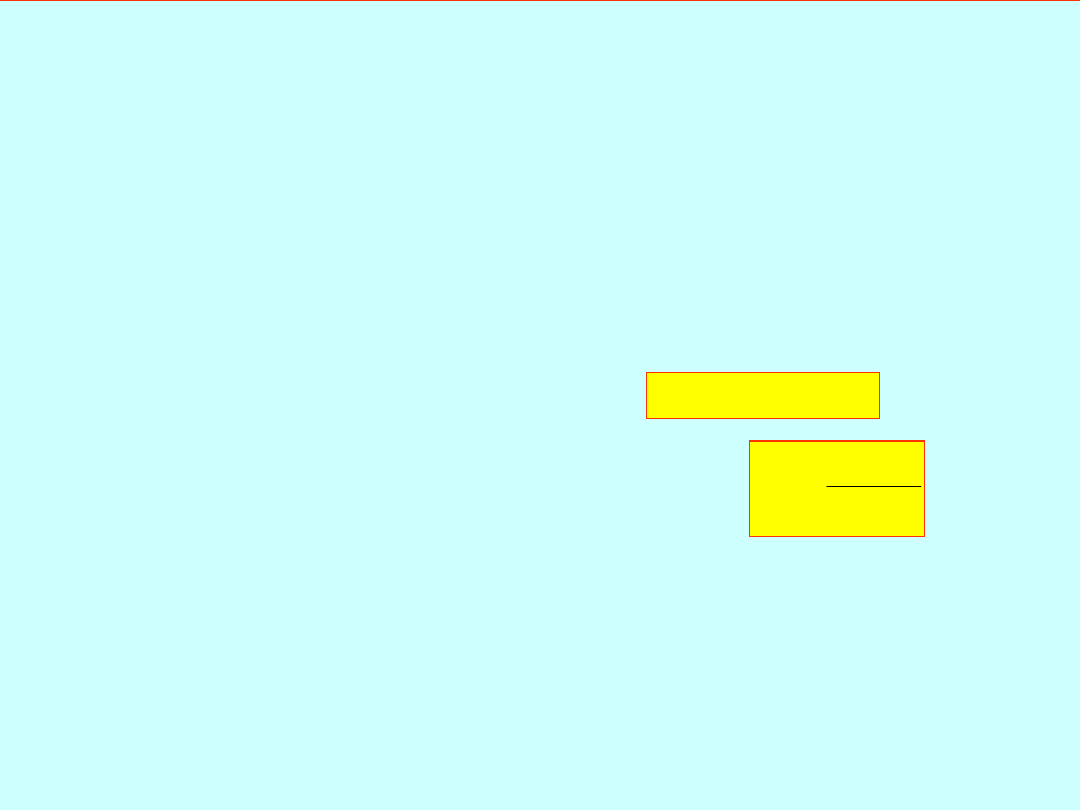
C
19
=1.04350 D
19
=-0.26795 C
4
=0.46504 D
4
=3.70097e-4
C
18
=0.75004 D
18
=0.07180 C
3
=0.63978 D
3
=-1.38122e-3
C
17
=0.65479 D
17
=-0.01924 C
2
=0.80608 D
2
=5.15478e-3
C
16
=0.46101 D
16
=5.15478e-3 C
1
=0.83436 D
1
=-0.01924
C
15
=1.16148e-3 D
15
=-1.38122e-3 C
0
=0.78054 D
0
=0.07180
C
14
=-0.46566 D
14
=3.70097e-4
C
13
=-0.63853 D
13
=-9.91696e-5 i z równania:
C
12
=-0.81044 D
12
=2.65816e-5
C
11
=-0.81817 D
11
=-7.15657e-6
C
10
=-0.84091 D
10
=2.04473e-6 mamy:
C
9
=-0.81818 D
9
=-1.02237e-6
C
8
=-0.81042 D
8
=2.04473e-6
C
7
=-0.63861 D
7
=-7.15657e-6 czyli a
0
=a
20
=0.84091
C
6
=-0.46537 D
6
=2.65816e-5
C
5
=8.33928e-5 D
5
=-9.91696e-5
0
0
0
0
a
D
C
a
0
0
0
D
1
C
a

i ze związku rekurencyjnego:
0
k
k
k
a
D
C
a
mamy:
dla k=1,2,...,19
a
1
=a
21
=0.81818 a
13
=-0.63861
a
2
=0.81042 a
14
=-0.46535
a
3
=0.63861 a
15
=0.00000
a
4
=0.46535 a
16
=0.46535
a
5
=-0.00000 a
17
=0.63861
a
6
=-0.46535 a
18
=0.81042
a
7
=-0.63861 a
-1
=a
19
=0.81818
a
8
=-0.81042
a
9
=-0.81818
a
10
=-0.84091
a
11
=-0.81818
a
12
=-0.81042
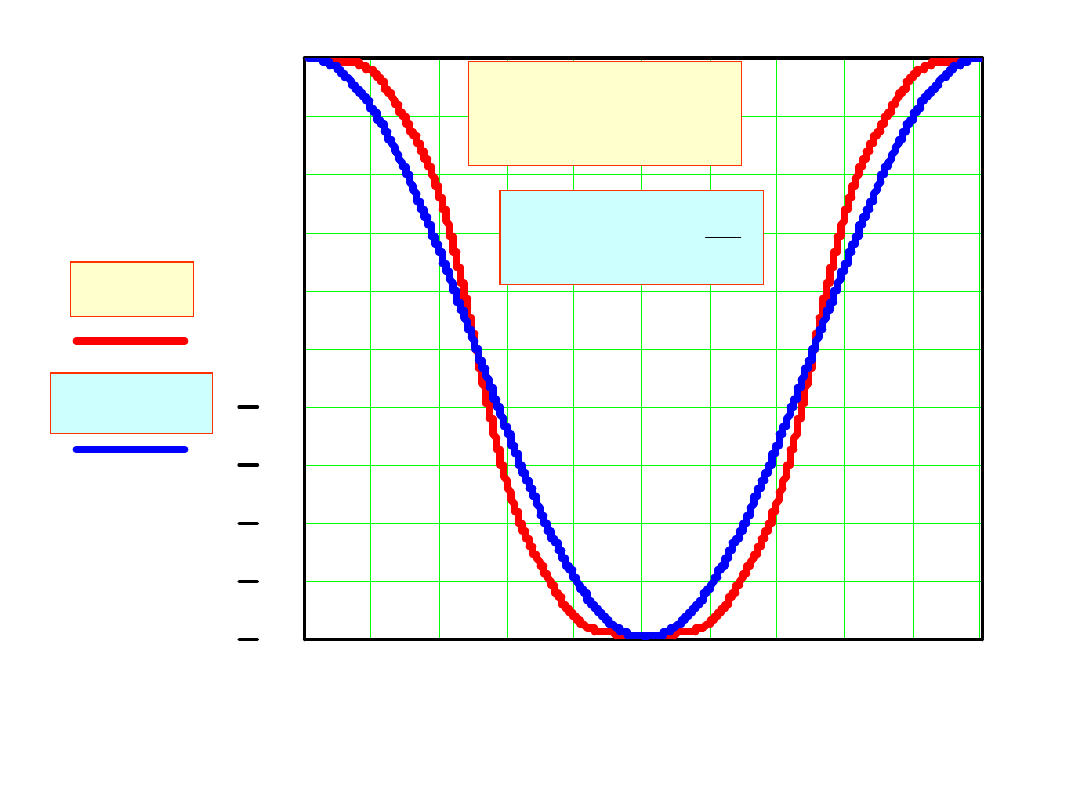
0 2 4 6 8 10 12 14 16 18 20
5
4
3
2
1
0
1
2
3
4
5
v s
( )
xd s
( )
s
x(s)
21
k
1
k
k
k
s
B
a
s
x
10
s
cos
5
s
x
d
x
d
(s)
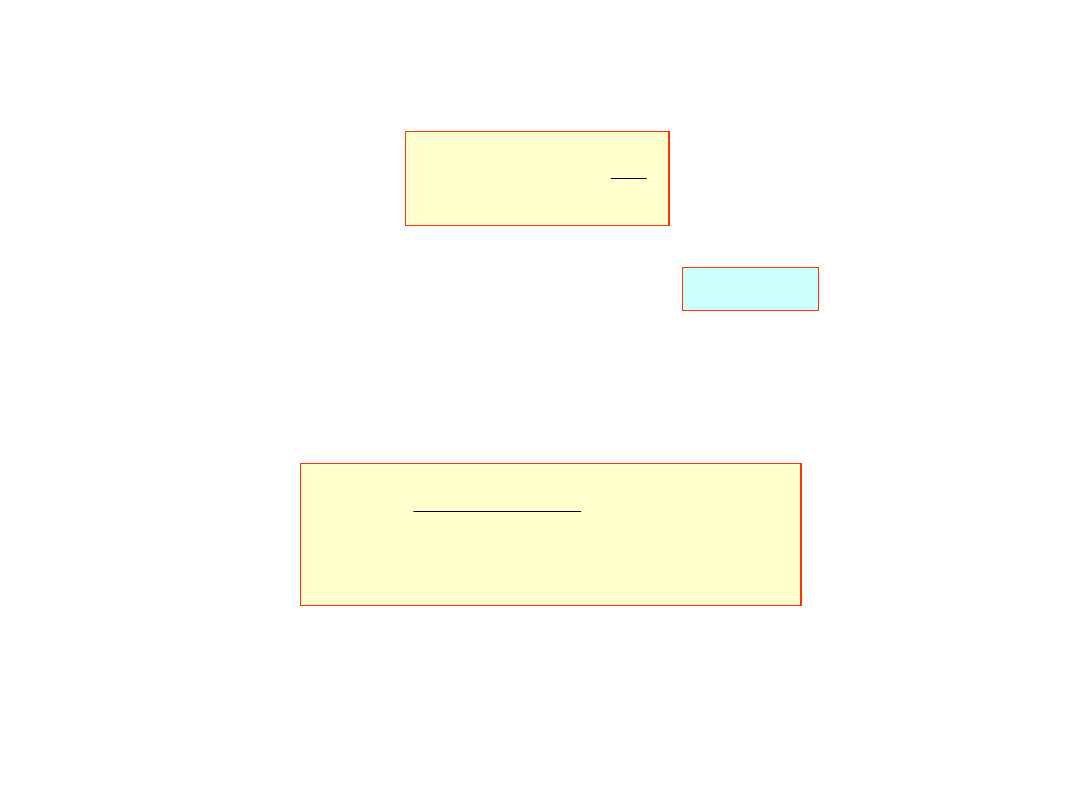
Równanie krzywej dla współrzędnej x jest:
10
s
cos
5
s
x
d
dla parametru
20
,
0
s
Błąd między wielomianem interpolacyjnym a funkcją x(s)
definiujemy:
0
s
x
if
s
x
s
x
0
s
x
if
s
x
s
x
s
x
s
d
d
d
d
d
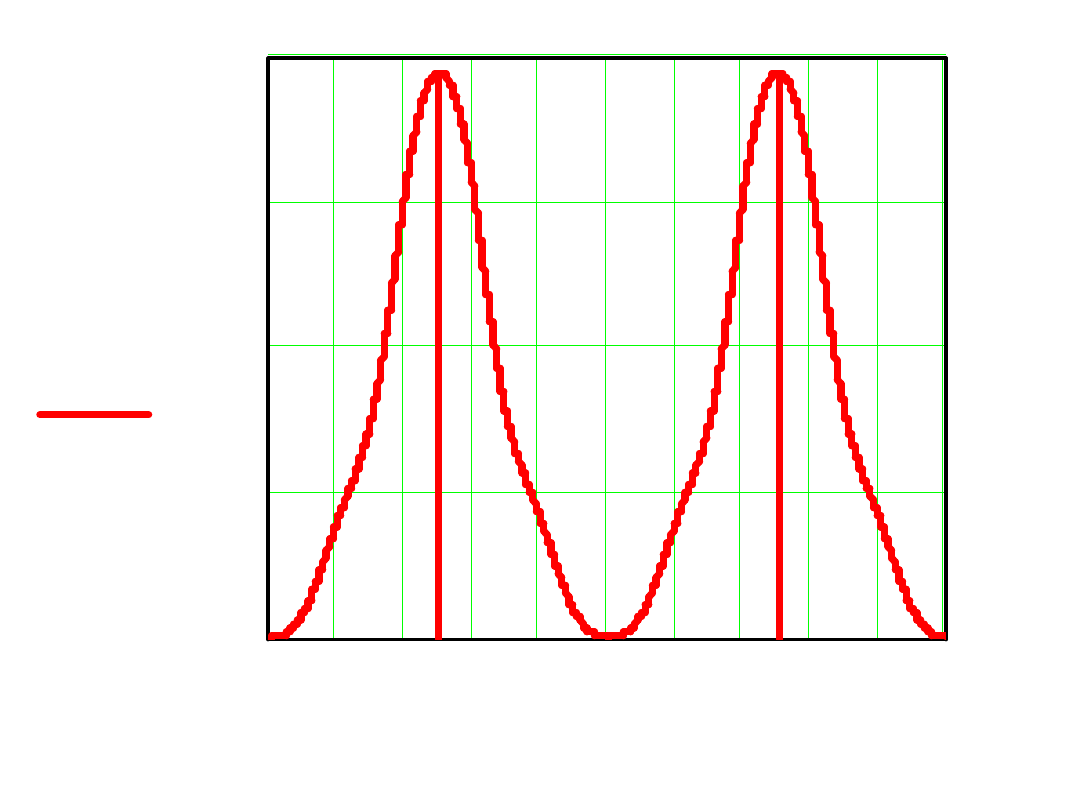
0 2 4 6 8 10 12 14 16 18 20
0
0.2
0.4
0.6
0.8
s
( )
s
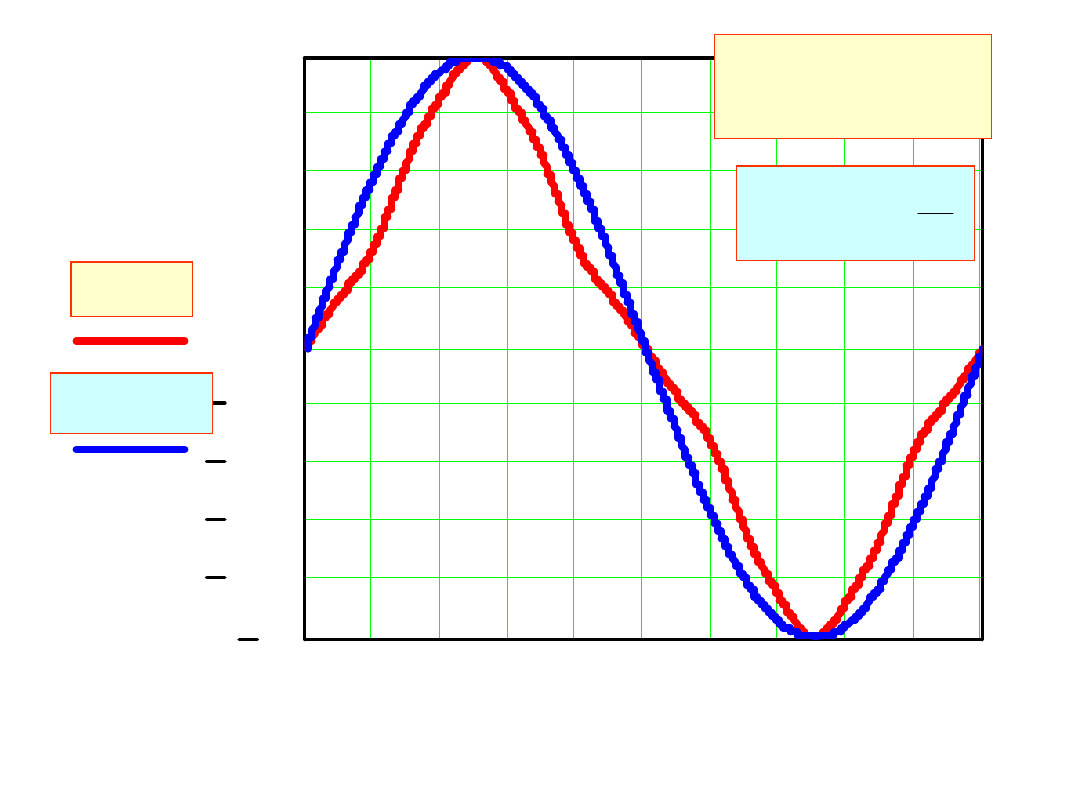
0 2 4 6 8 10 12 14 16 18 20
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
w s
( )
yd s
( )
s
21
k
1
k
k
k
s
B
b
s
y
10
s
sin
s
y
d
y(s)
y
d
(s)
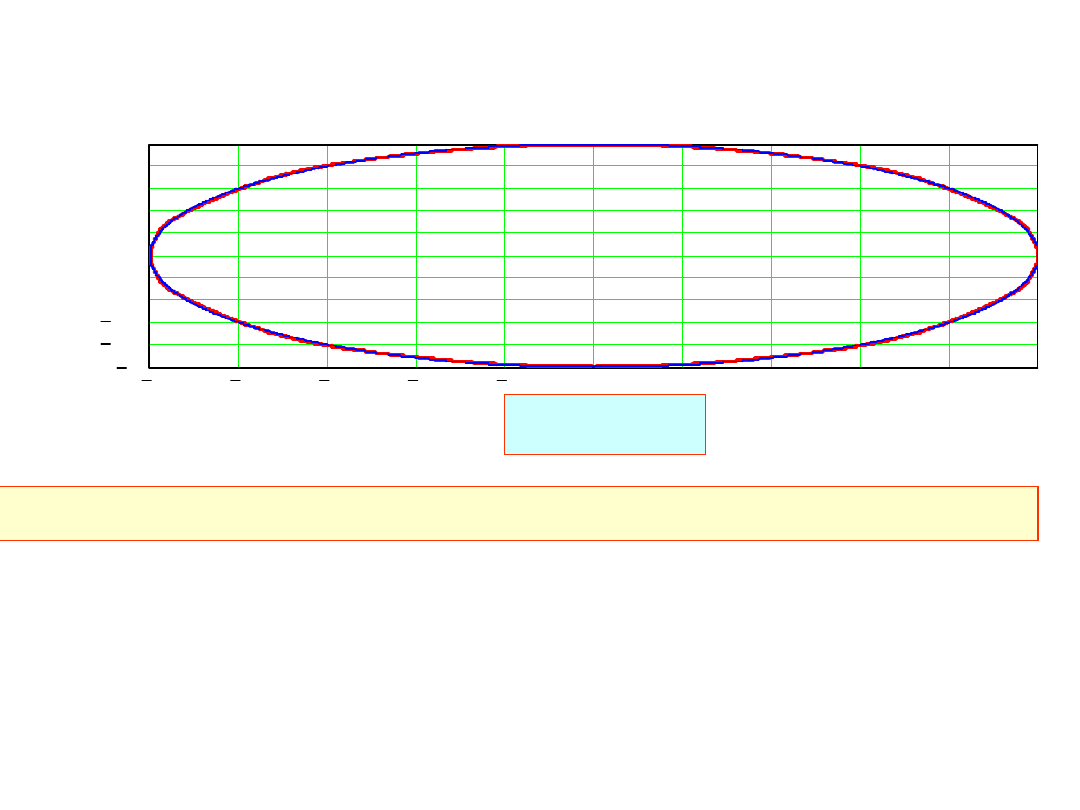
5
4
3
2
1
0
1
2
3
4
5
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
w s
( )
yd s
( )
v s
( ) xd s
( )
x(s),x
d
(s)
y(s)
y
d
(s)
elipsa otrzymana
w rezultacie
interpolacji
i
dokładna
Aproksymacja
Dążenie do minimalizacji normy.
Przykłady stosowanych norm:
b
,
a
l
i
przestrzen
w
)
)]
x
(
f
[
(
f
b
,
a
L
i
przestrzen
w
dx
)
x
(
f
)
x
(
w
f
b
,
a
L
i
przestrzen
w
dx
)
x
(
f
f
b
,
a
C
i
przestrzen
w
)
x
(
f
sup
f
N
2
N
0
i
2
1
2
i
w
2,
2
1
2
b
a
w
,
2
2
2
1
2
b
a
2
0
]
b
,
a
[
x
Zadanie aproksymacji polega na minimalizacji normy:
)
x
(
g
)
x
(
F
Niech
K
0
n
n
n
)
x
(
h
a
)
x
(
g
i dane są wartości funkcji :
i
i
F
)
x
(
F
w punktach i=0,2,...P.
Niech będzie zastosowana norma z wagą:
P
0
i
2
K
0
n
i
n
n
i
i
)
x
(
h
a
F
w
i szukamy minimum sumy ze względu na współczynniki a
n
.
Przykład:
x
0
0.2
0.5
0.6
1
y
0.1
0.2
0.4
0.45
0.4
2
2
1
0
x
a
x
a
a
)
x
(
g
Przyjmujemy wielomian aproksymujący w postaci:
przyjmując funkcję wagową równą jedności otrzymujemy:
2
2
1
0
2
2
1
0
2
2
1
0
2
2
1
0
2
0
2
1
0
a
a
a
4
.
0
36
.
0
a
6
.
0
a
a
45
.
0
25
.
0
a
5
.
0
a
a
4
.
0
04
.
0
a
2
.
0
a
a
2
.
0
)
a
1
.
0
(
)
a
,
a
,
a
(
d

Szukamy ekstremum funkcji d(a
0
,a
1
,a
2
) i przyrównując do zera
pierwsze pochodne względem a
0
, a
1
i a
2
otrzymujemy:
67
.
0
a
1937
.
1
a
349
.
1
a
65
.
1
a
d
91
.
0
a
2365
.
1
a
65
.
1
a
3
.
2
a
d
55
.
1
a
65
.
1
a
3
.
2
a
5
a
d
3
1
0
2
2
1
0
1
2
1
0
0
Rozwiązanie powyższych równań ma postać:
151
.
0
a
493
.
0
a
204
.
0
a
0
1
2
Interpolacja z wagą
2
2
1
0
2
2
1
0
2
2
1
0
2
2
1
0
2
0
2
1
0
w
a
a
a
4
.
0
5
.
0
a
36
.
0
a
6
.
0
a
45
.
0
a
25
.
0
a
5
.
0
a
4
.
0
a
04
.
0
a
2
.
0
a
2
.
0
5
.
0
a
1
.
0
25
.
0
a
,
a
,
a
d
Po obliczeniu ekstrmum mamy: a
0
=0.319
a
1
=0.158
a
2
=-0.041
Wielomian aproksymujący jest:
2
w
x
041
.
0
x
158
.
0
319
.
0
x
W
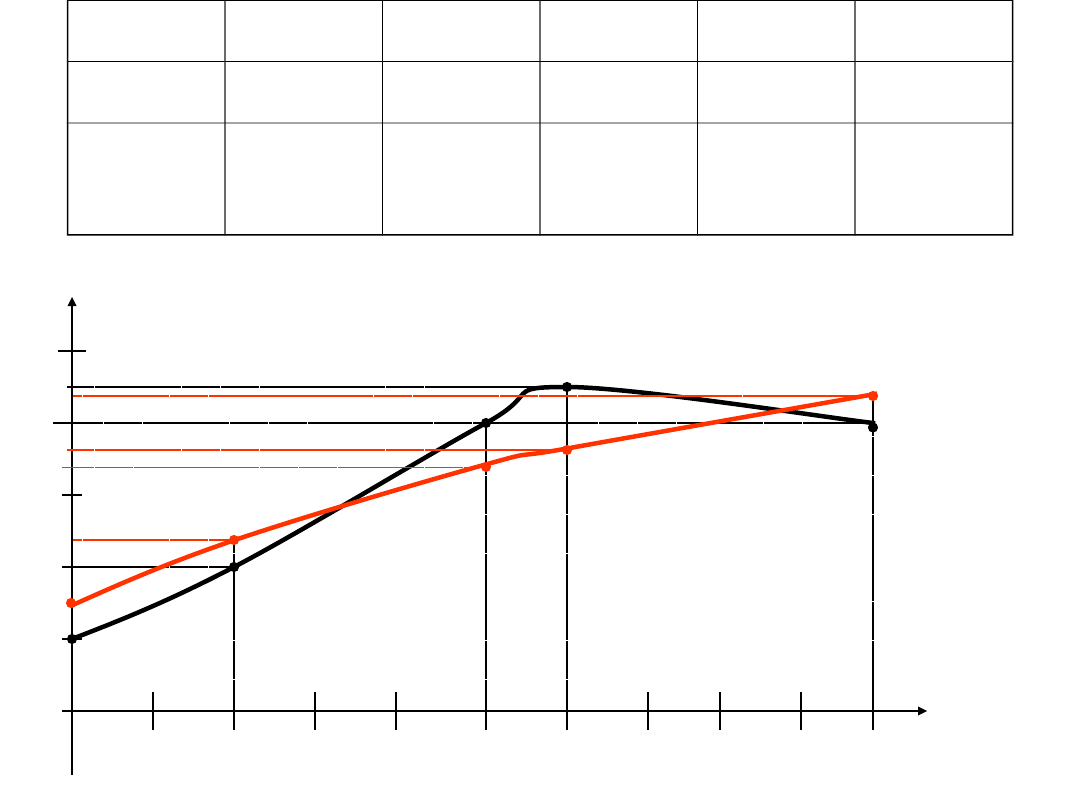
x
0
0.2
0.5
0.6
1
y
0.1
0.2
0.4
0.45
0.4
y
ap
0.151 0.241
4
0.346
5
0.373
3
0.44
1
x
0.5
0
0.2
0.1
0.2
0.4
y
y
y
ap
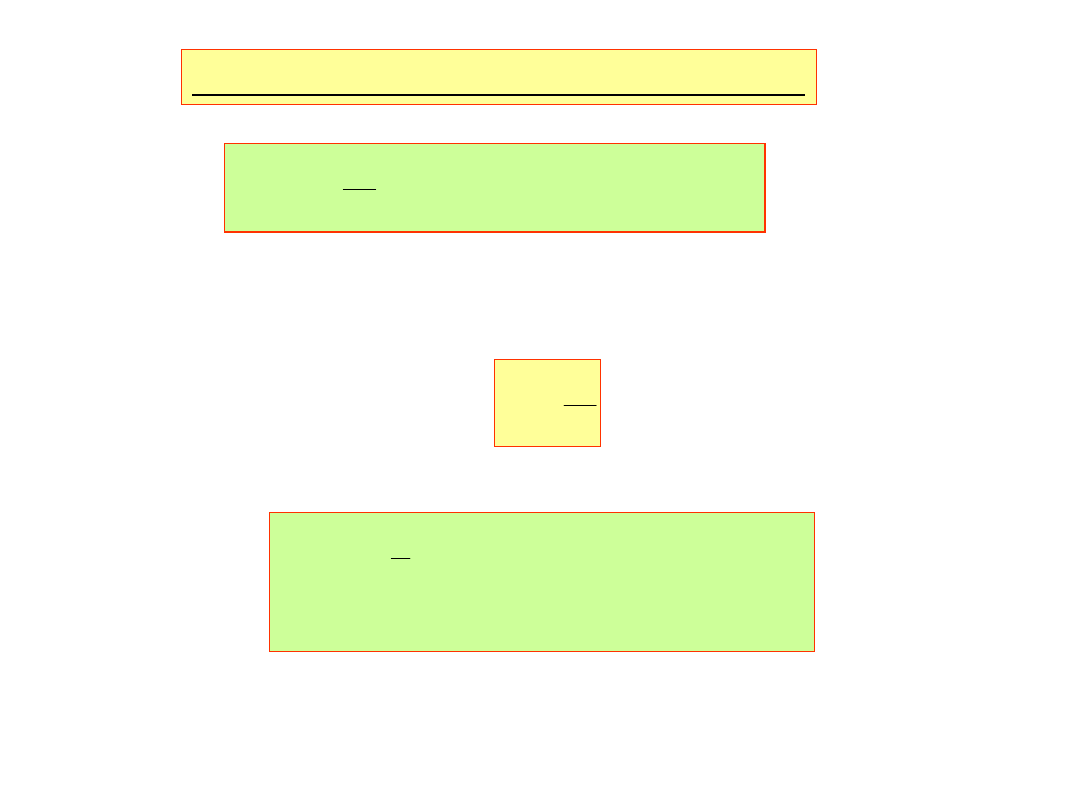
Wielomiany trygonometryczne
n
1
k
k
k
0
n
)
kx
sin
b
kx
cos
a
(
2
a
)
x
(
F
aproksymacja funkcji okresowej na dyskretnym równoodległym
zbiorze punktów:
i=0,1,2,..., 2L-1
L
i
x
i
ciągły:
L
n
)
jx
sin
b
jx
cos
a
(
a
2
1
)
x
(
y
n
1
j
i
i
0
n
a współczynniki wyznacza się z równania:
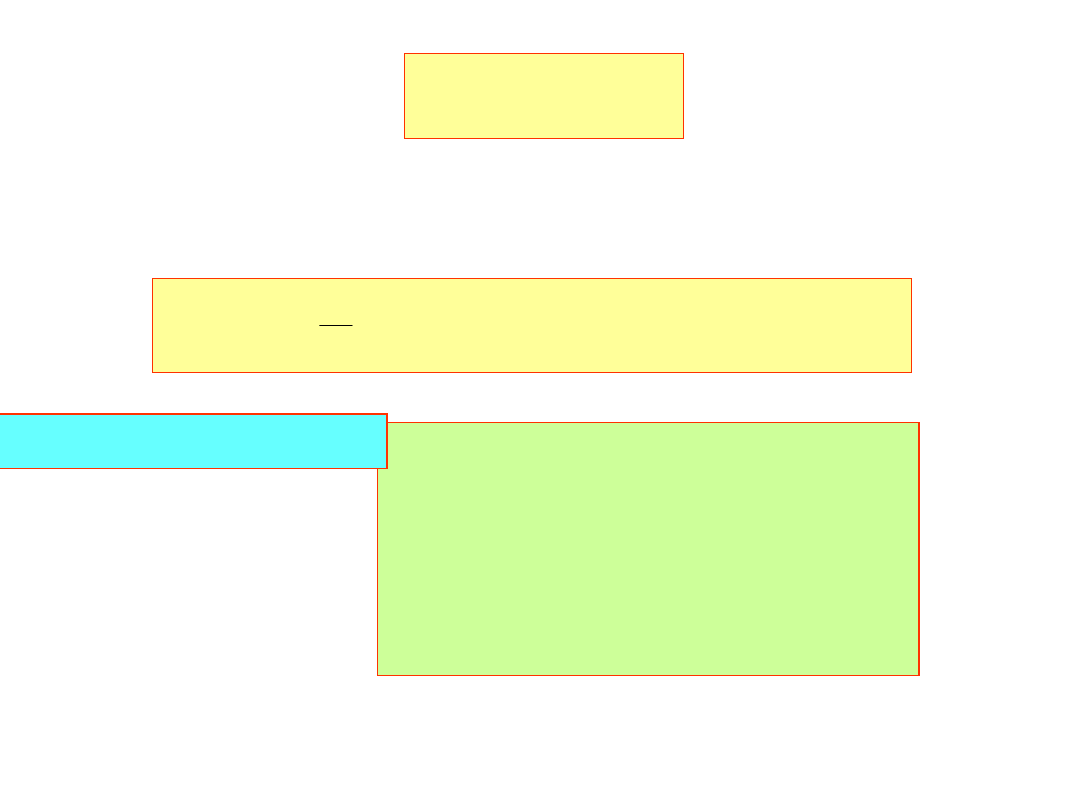
1
L
2
0
i
2
i
n
i
)
x
(
y
)
x
(
f
Różniczkując względem a
k
otrzymujemy następujące równania
dla wyznaczania współczynników:
0
kx
cos
jx
sin
b
jx
cos
a
2
a
)
x
(
f
i
1
L
2
0
i
n
1
j
i
j
i
j
0
i
0
kx
sin
jx
cos
0
=
k
=
j
dla
2L
0
k
=
j
dla
L
k
j
dla
0
kx
cos
jx
cos
1
L
2
0
l
l
l
1
L
2
0
i
i
i
Mamy tożsamości:
Na mocy powyższych tożsamości mamy:
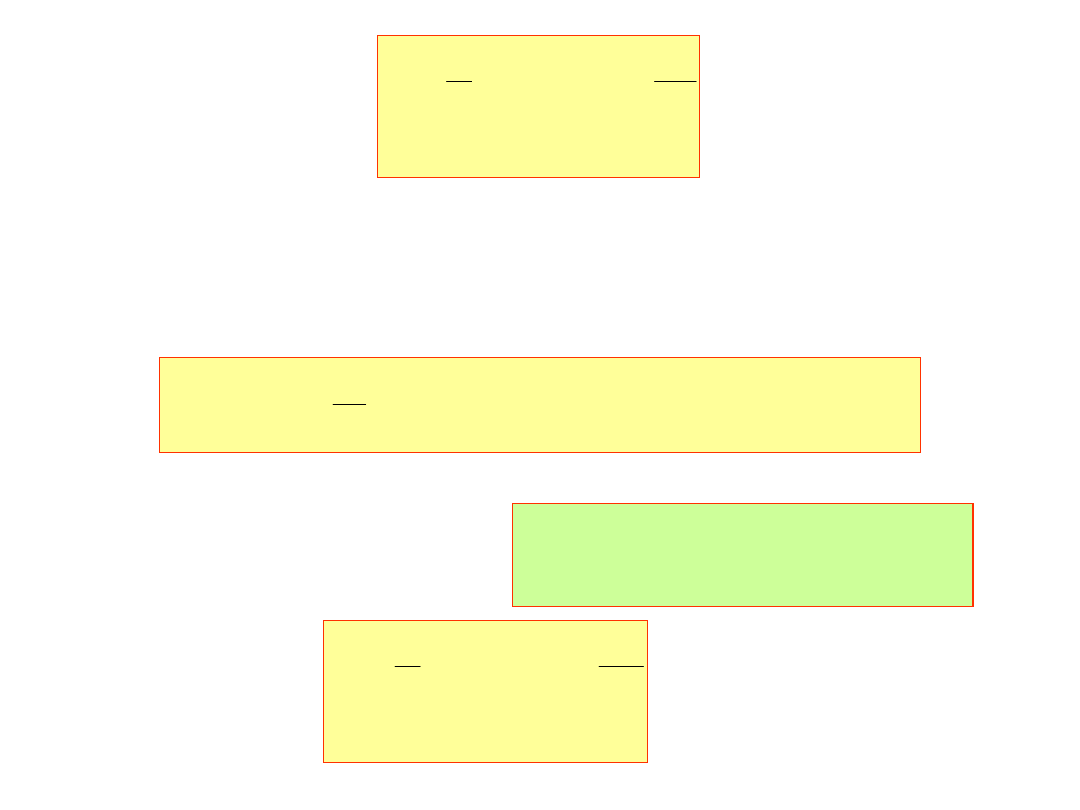
L
n
,...,
1
,
0
j
L
lj
cos
)
x
(
F
L
1
a
1
L
2
0
l
l
j
Podobnie wyznaczamy współczynniki b
j
z równania:
0
kx
sin
jx
sin
b
jx
cos
a
2
a
)
x
(
F
l
1
L
2
0
l
n
1
j
l
j
l
j
0
l
korzystając z tożsamości:
k
=
j
dla
L
k
j
dla
0
kx
sin
jx
sin
1
L
2
0
l
l
l
otrzymujemy:
L
n
,...,
1
,
0
j
L
jl
sin
)
x
(
F
L
1
b
1
L
2
0
i
l
j
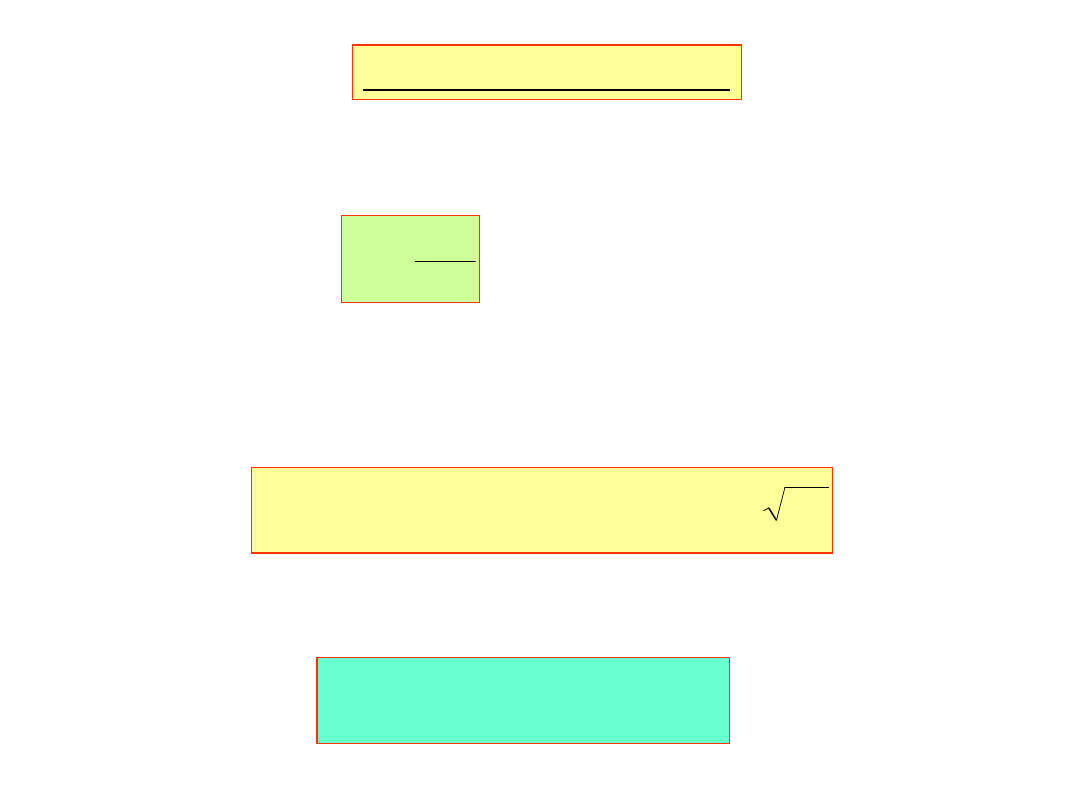
Szereg zespolony.
Dana jest funkcja określona przez podanie jej wartości f
n
w punktach:
N
n
2
x
n
gdzie n=0,1,2,...,N-1. Aproksymujemy funkcję wielomianem
trygonometrycznym postaci:
1
i
gdzie
)
ikx
exp(
c
)
x
(
w
1
N
0
k
k
Otrzymujemy N równań dla wyznaczenia współczynników c
k
:
1
N
0
k
n
k
n
n
)
ikx
exp(
c
f
)
x
(
w
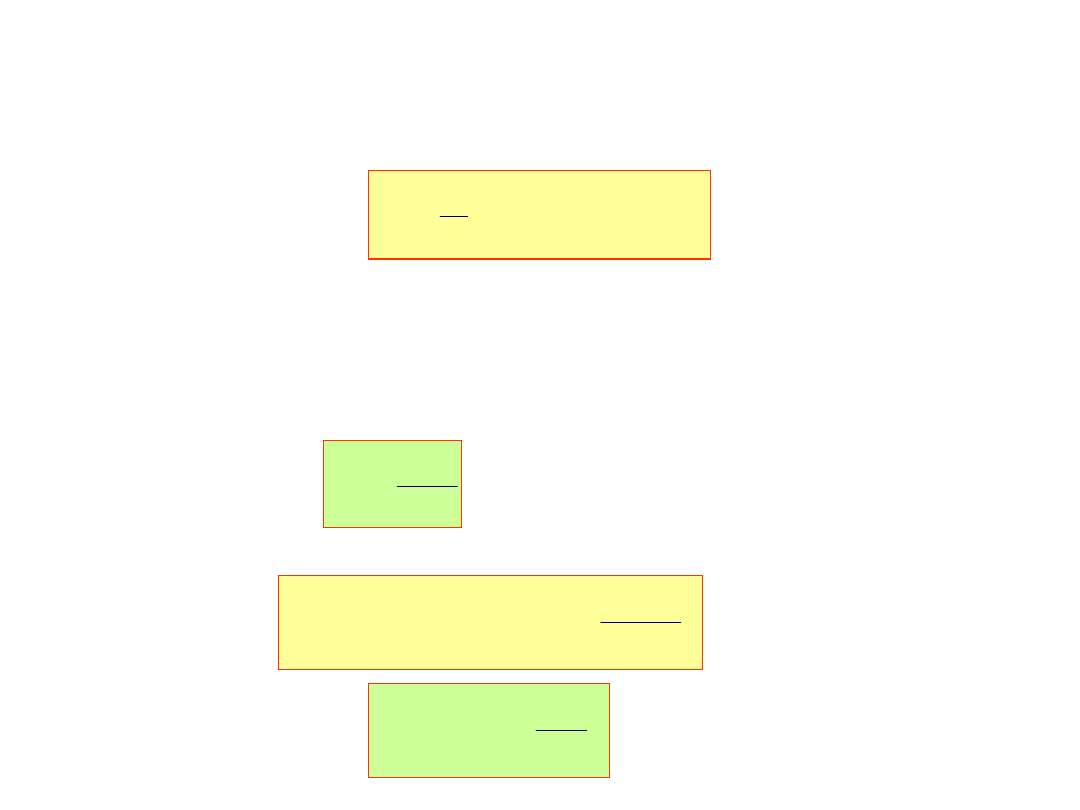
Rozwiązanie ostatniego układu równań czyli współczynniki c
k
są określane równaniami:
1
N
0
n
n
n
p
)
ipx
exp(
f
N
1
c
Idea szybkie transformaty Fouriera tzw. FFT
Fast Fourier Transform
Ponieważ
N
n
2
x
n
więc
N
pn
2
i
exp
ipx
exp
n
Oznaczmy:
N
i
2
epx
w
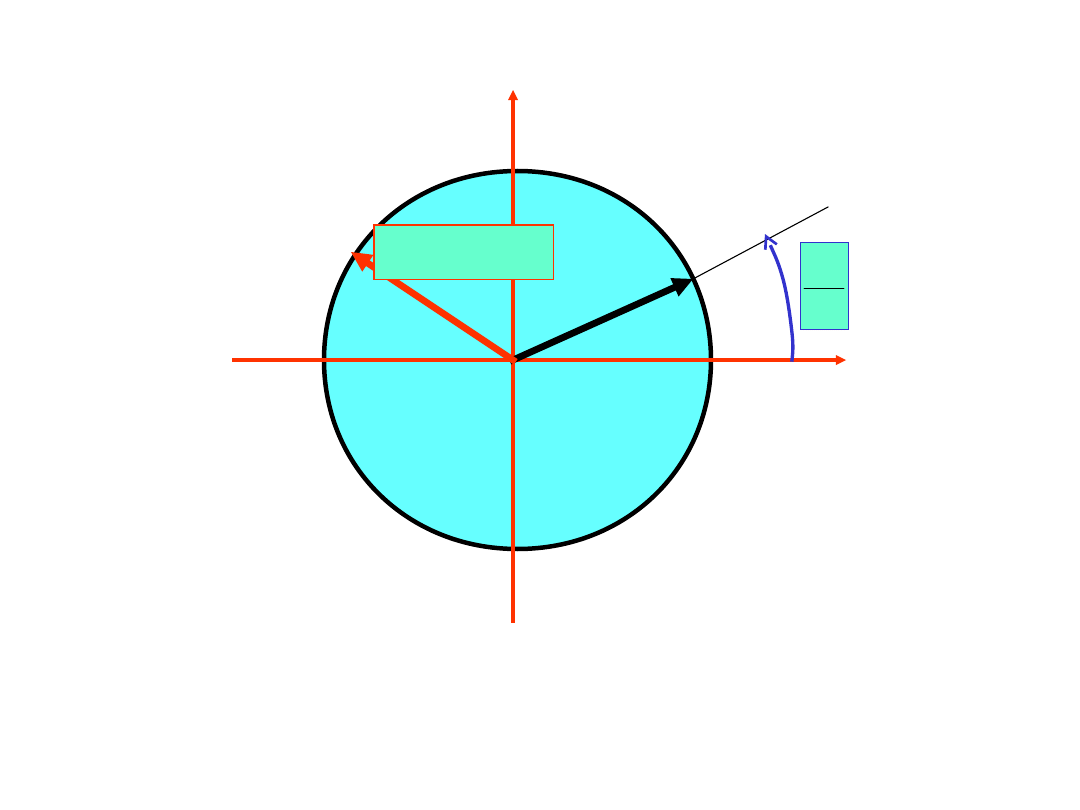
Zauważmy, że
Re
Im
w=w
N+1
N
2
w
p
=w
p+N
Każda całkowita potęga w leży na okręgu jednostkowym
i co więcej jeżeli wykładnik p potęgi w
p
jest większy od N
to punkty się nakrywają. Na tym spostrzeżeniu bazuje FFT.
Piszemy:
1
N
0
n
n
pn
p
f
w
N
1
c
Możemy zapisać w postaci macierzowej:
Oznaczając:
1
N
,...,
1
,
0
n
dla
N
f
g
n
n
n
pn
p
g
w
c
gdzie
2
1
N
1
N
0
1
N
1
0
0
0
0
pn
w
w
w
.
.
.
w
w
w
w
w
w
w
Ponieważ w
0
=1 więc nie będziemy pisać zerowej kolumny i wiersza.
Dalej mamy związki:
N
i
2
epx
w
k
k
N
w
k
N
i
2
exp
k
N
i
2
exp
N
N
i
2
exp
k
N
N
i
2
exp
w
czyli
k
k
N
w
w
a więc wiersze i kolumny: 1 i N-1
2 i N-2
..............
k i N-k
..............
N/2-1 i N/2+1 dla N parzystych
(N-1)2 i (N+1)/2 dla N nieparzystych
są sprzężone
.

W praktyce najczęściej stosowane N=2
M
.
Jeżeli liczba węzłów interpolacyjnych mniejsza od 2
M
,
to uzupełniamy zerami.
N=8
w
w
2
w
3
w
4
=-
1
(w
*
)
3
(w
*
)
2
w
*
w
2
w
4
w
6
w
8
=1 (w
*
)
6
(w
*
)
4
(w
*
)
2
w
3
w
6
w
9
w
12
=-
1
(w
*
)
9
(w
*
)
6
(w
*
)
3
w
4
w
8
w
12
w
16
=
1
(w
*
)
12
(w
*
)
8
(w
*
)
4
w
5
w
10
w
15
w
20
=-
1
(w
*
)
15
(w
*
)
10
(w
*
)
5
w
6
w
12
w
18
w
24
=
1
(w
*
)
18
(w
*
)
12
(w
*
)
6
w
7
w
14
w
21
w
28
=-
1
(w
*
)
21
(w
*
)
14
(w
*
)
7
8
i
2
epx
w
8
i
2
epx
w
*
lub inaczej
a b c
-
1
c
*
b
*
a
*
b -
1
b
*
1 b -1 b
*
c b
*
a
-
1
a
*
b c
*
-1 1 -1 1 -1 1 -1
c
*
b a
*
-
1
a b
*
c
b
*
-
1
b 1 b
*
-1 b
a
*
b
*
c
*
-
1
c b a
7
6
5
4
3
2
1
0
f
f
f
f
f
f
f
f
dla otrzymania tablicy mnożników wystarczy obliczyć połowę
pierwszego wiersza!!!
np. a=a
r
+ia
i
oraz a
*
=a
r
-ia
i
czyli np.
af
1
+a
*
f
7
=a
r
(f
1
+f
7
)+ia
i
(f
1
-f
7
)
i podobnie dla innych
operacji.
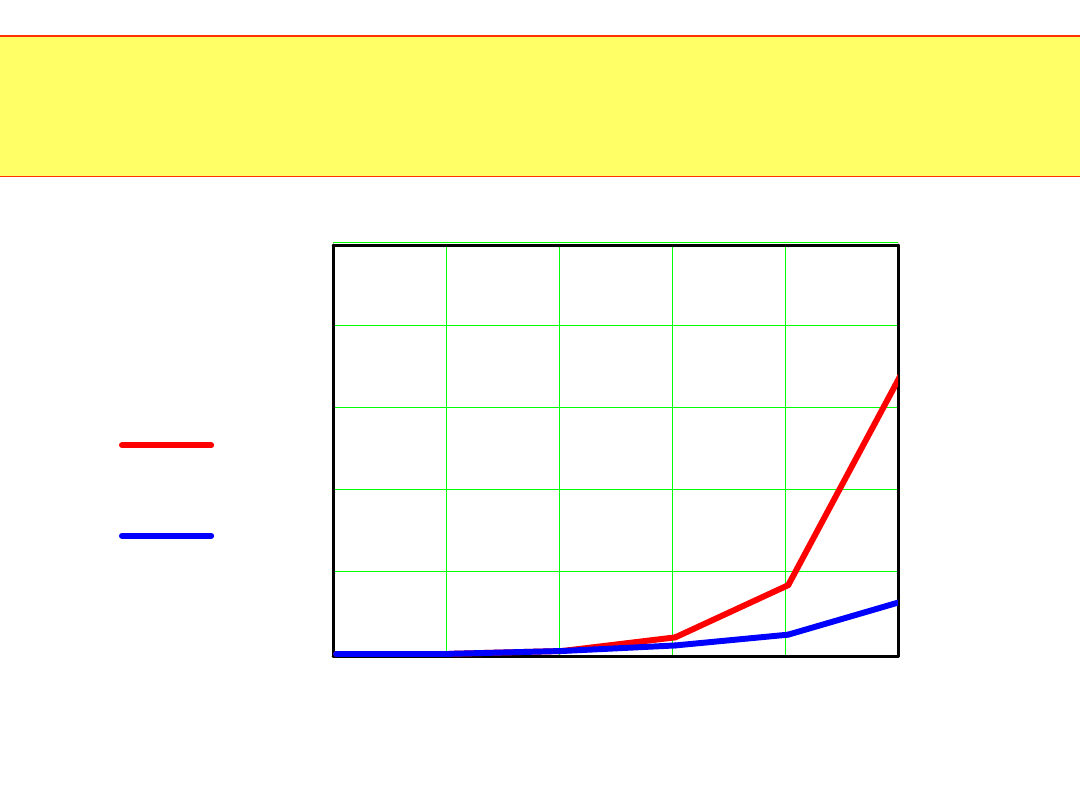
Wykorzystanie przedstawionych uproszczeń pozwala w stosunku
do zwykłego algorytmu zawierającego N
2
działań zespolonych
zmniejszyć ich liczbę dla N=2
M
do 2NM
1
2
3
4
5
6
0
1200
2400
3600
4800
6000
2
2 m
m2
m 1
m
Rozwiązywanie równań algebraicznych
f(x)=0
Metoda bisekcji
Przykład:
0
1
x
4
x
3
x
-1 0 -0.5
-0.25
-0.125
-
0.187
5
f(x
)
-4 1
-
1.12
5
-
0.0156
25
0.498
045
0.243
08
x
-
0.2187
5
-
0.2343
75
-
0.24218
75
-
0.246093
75
f(x
)
0.1145
32
0.0496
254
0.01704
45
0.000721
037
x
-
0.24804
69
-
0.246582
03
-
0.246337
9
-
0.24621
58
f(x) -
0.00744
91
-
0.001320
98
-
0.000299
93
0.00021
057
Zaleta metody: Jeżeli pierwiastek istnieje, to go znajdziemy.
Wada metody: Duża liczba obliczeń
Regula falsi.
Założenia:
a) funkcja ma w przedziale [a,b] tylko jeden pierwiastek
i zachodzi f(a)f(b)<0,
b) jest funkcja jest klasy C
2
[a,b], pierwsza i druga pochodna
nie zmieniają znaku na przedziale [a,b].
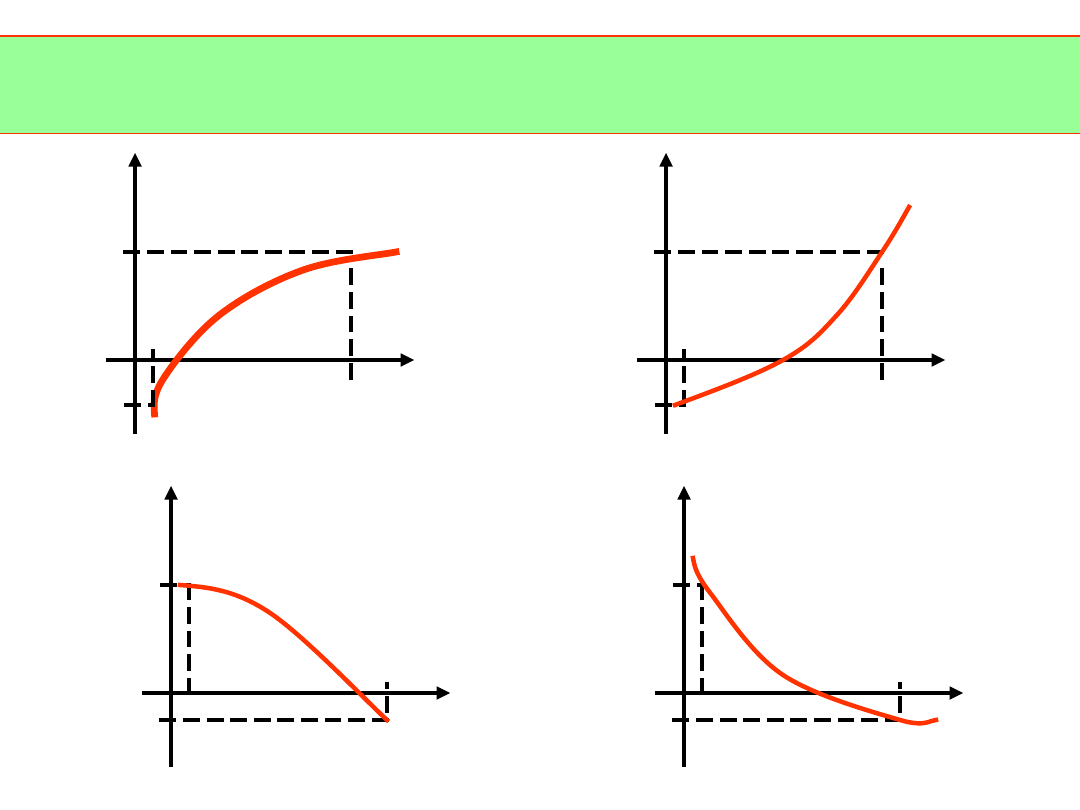
Funkcja spełniająca powyższe założenia musi mieć w otoczeniu
miejsca zerowego jeden z następujących przebiegów:
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
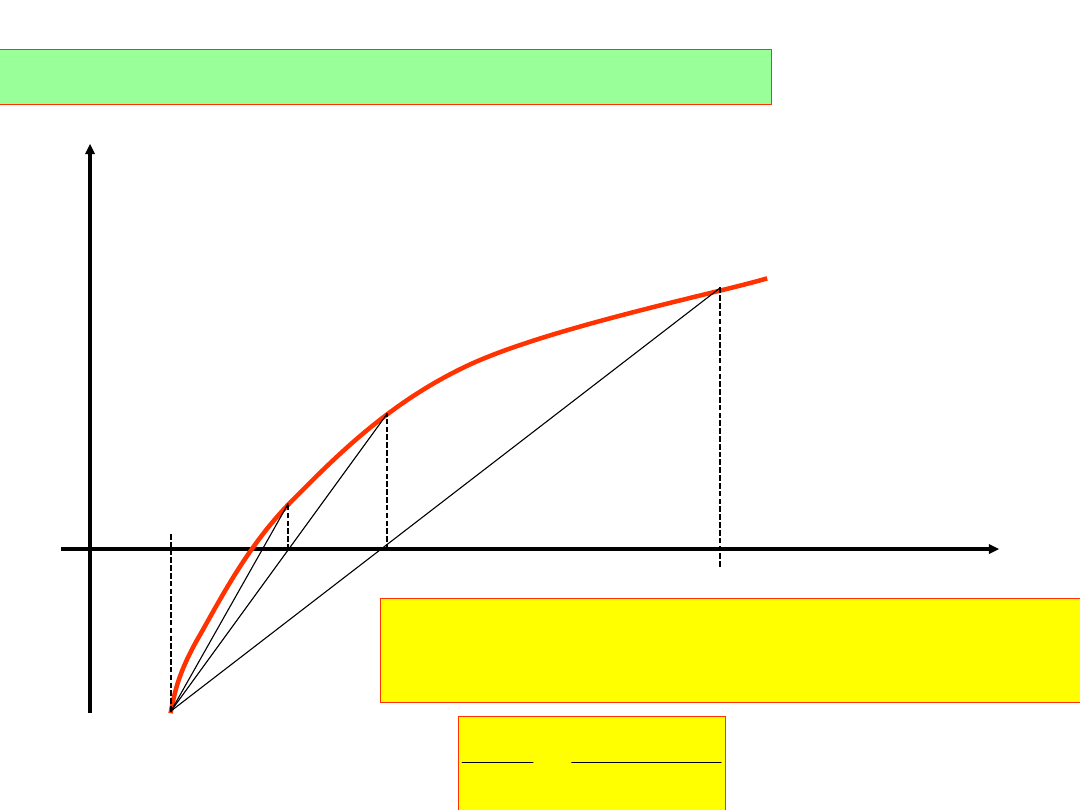
Przebieg obliczeń metodą regula falsi:
x
y
a
b
f(a)
f(b)
x
1
f(x
1
)
x
2
analitycznie: ustalamy koniec z
warunku f(x
1
)f(a)<0 lub f(x
1
)f(b)<0
Prowadzimy prostą:
a
f
b
f
a
f
x
f
a
b
a
x
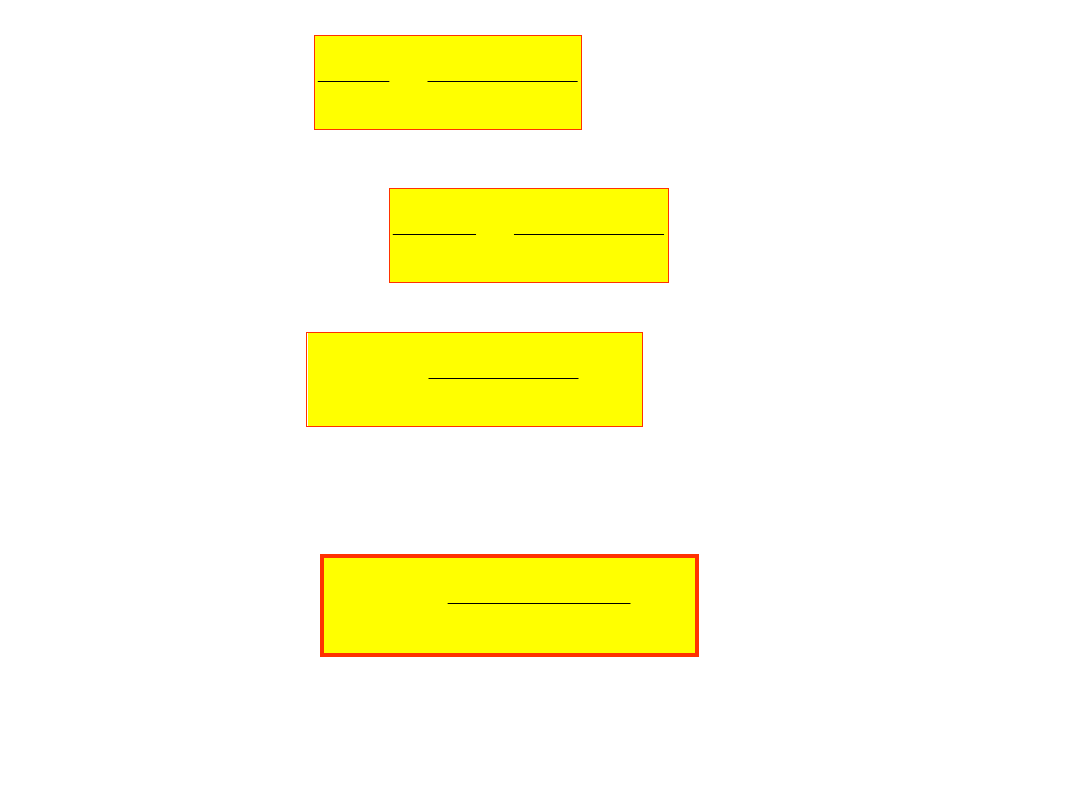
a
f
b
f
a
f
x
f
a
b
a
x
ale f(x
1
)=0 stąd
a
f
b
f
a
f
a
b
a
x
1
lub
a
f
a
f
b
f
a
b
a
x
1
Dla n-tej iteracji mamy b=x
n-1
i podstawiając mamy:
a
f
a
f
x
f
a
x
a
x
1
n
1
n
n
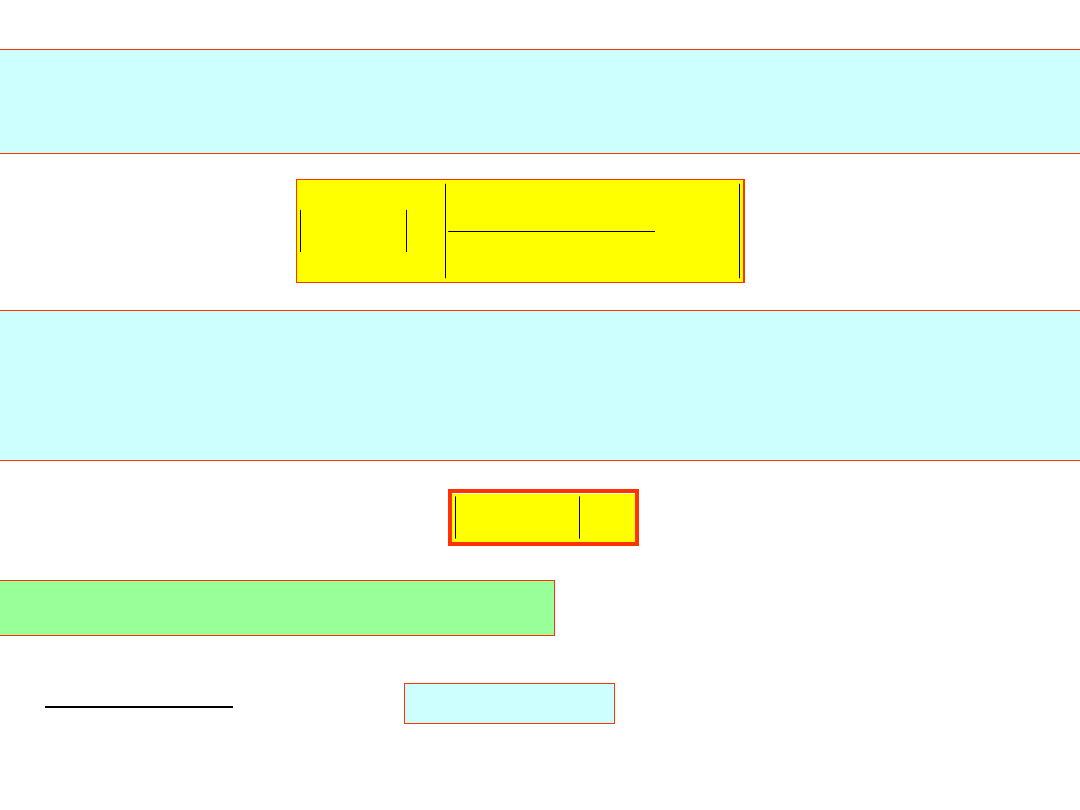
Ocena błędu dla dostatecznie małego przedziału [x
n-1
,x
n
]
można przyjąć jako:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
Metoda regula falsi jest zbieżna dowolnej funkcji ciągłej
na przedziale [a,b].
Poszukiwanie pierwiastka zostaje zakończone jeżeli:
1
n
n
x
x
Metoda jest wolno zbieżna.
Przykład:
0
1
x
4
x
3
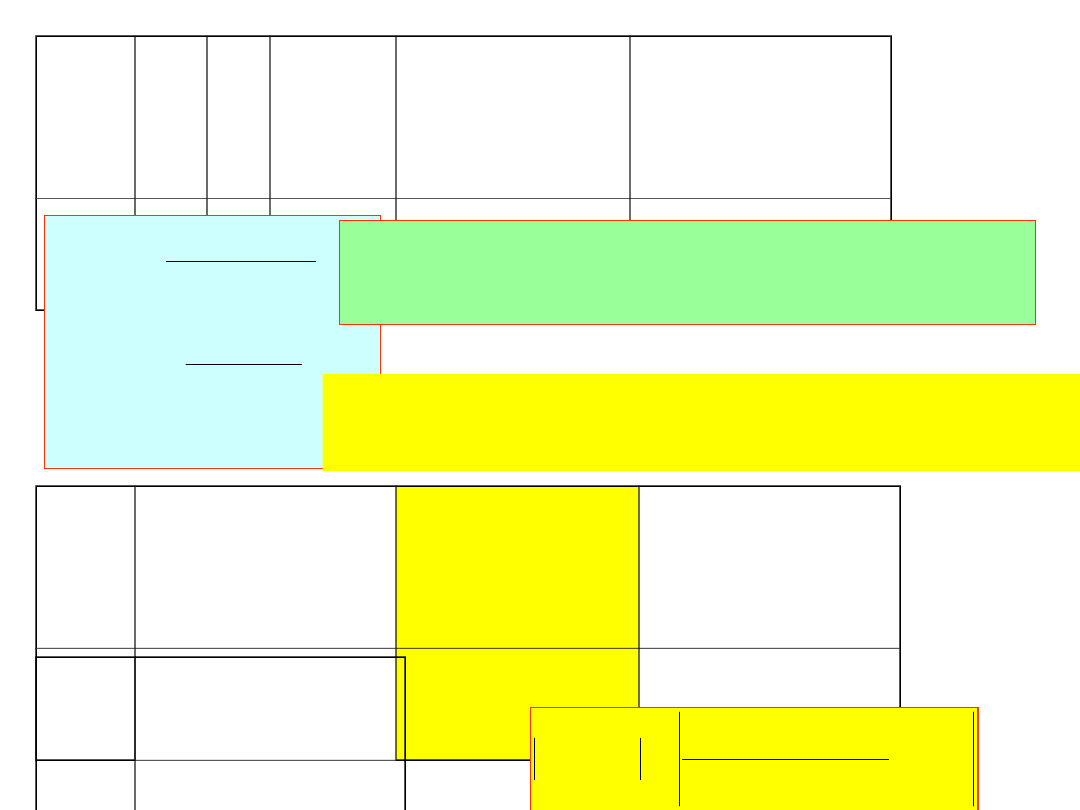
x
-1 0 -0.2
-
0.23664
12
-
0.244233
54
f(x
)
-4 1 0.19
2
0.04013
427
0.008497
292
2
.
0
x
4
4
1
1
0
1
x
a
f
a
f
b
f
a
b
a
x
1
1
1
Ponieważ f(-1)=-4, a f(x
1
)=0.192,
więc stałym punktem będzie x=-1
x
-
0.245835
632
-
0.246174
92
-
0.246246
829
f(x
)
0.001800
359
0.000381
603
0.000080
891
x
-
0.2462620
72
f(x
)
0.0000171
47
w metodzie bisekcji potrzebowaliśmy
14 kroków
ocena błędu:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
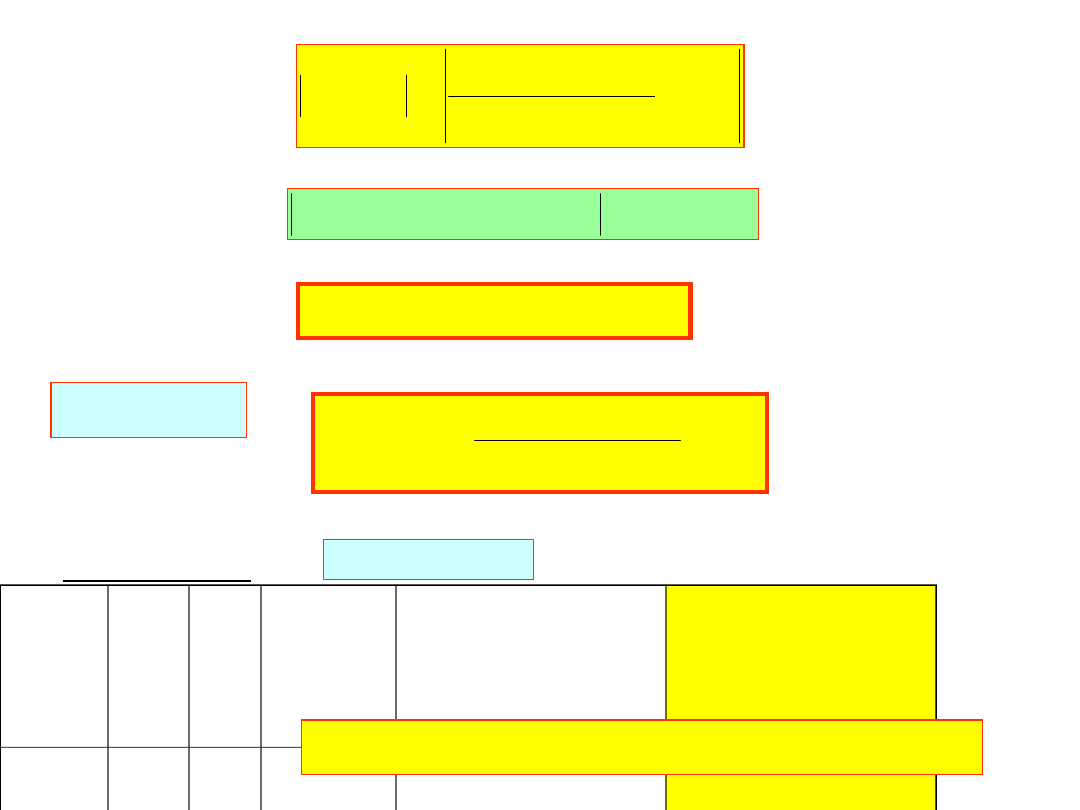
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
ocena błędu:
6
d
10
1
.
4
246262072
.
0
x
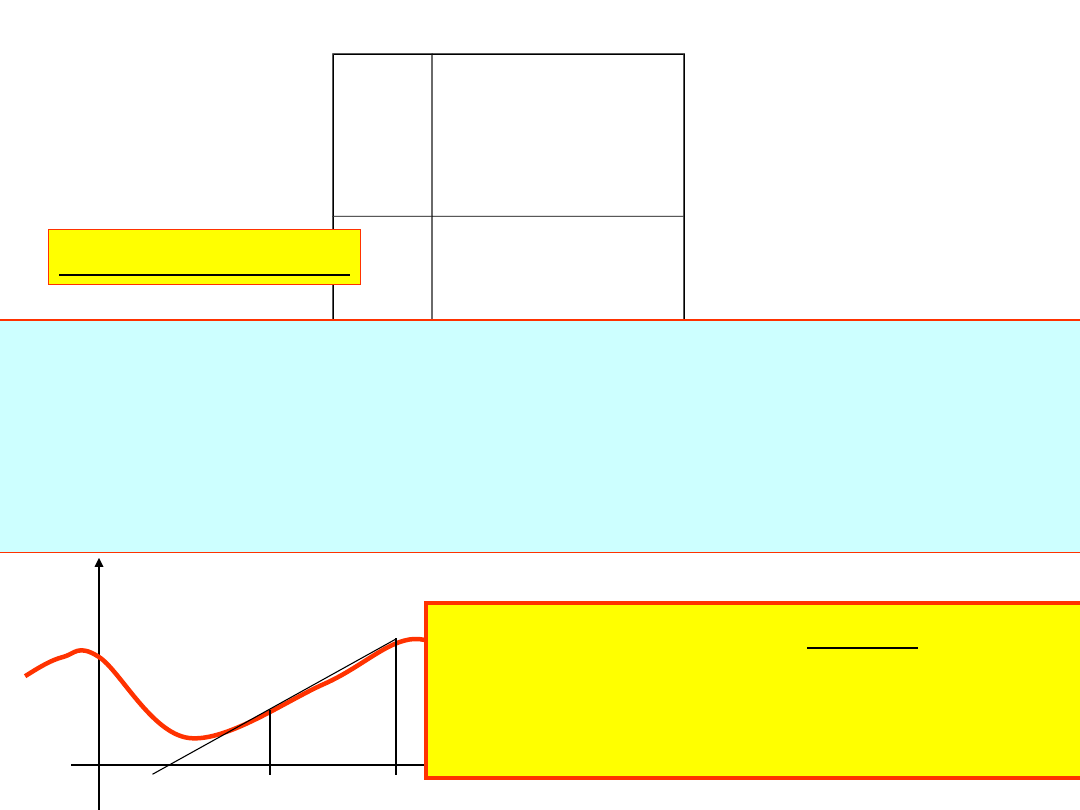
Metoda siecznych
Przepis:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
1
n
Przykład:
0
1
x
4
x
3
x
-1 0 -0.2
-
0.2475247
52
-
0.2462564
39
f(x) -4 1
0.19
2
-
0.0052644
81
0.0000407
03
w regula falsi potrzeba 8 kroków
x
-
0.246266
17
f(x
)
0.907E-8
w 6-tym kroku
Koniecznie trzeba obliczać f(x
n
) i jeżeli zaczyna narastać
należy zawęzić przedział i powtórzyć obliczenia.
Niebezpieczeństwo znalezienia fałszywego pierwiastka.
Metoda szybsza niż reguła falsi.
a
b
x
1
Pierwsza iteracja musi startować
z punktów spełniających warunek:
f(a)f(b)<0
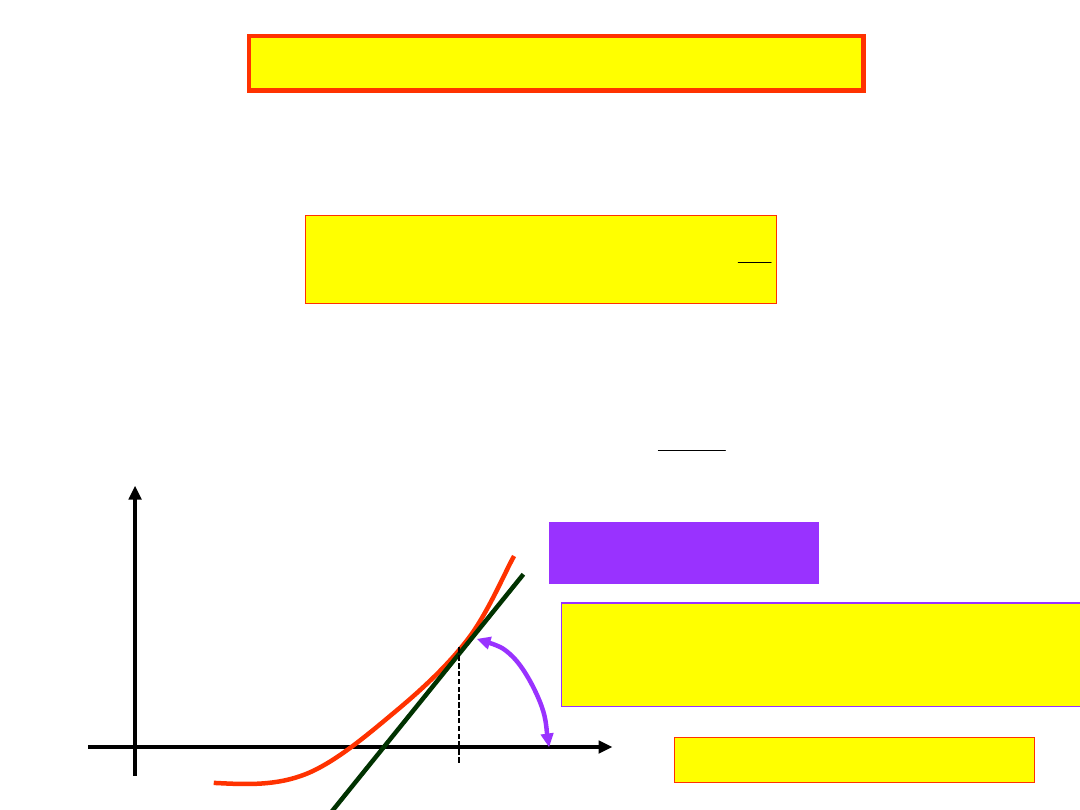
Metoda Newtona - Raphsona
Niech małe w mamy:
2
x
f
x
f
x
f
x
f
2
Pomijając małe drugiego rzędu
2
mamy, że f(x+)=0,
jeżeli
x
f
x
f
Graficznie:
x
y
x
n
n
n
n
x
f
tg
Równanie prostej stycznej
w punkcie x
n
jest:
n
n
n
x
f
x
x
x
f
y
x
n+1
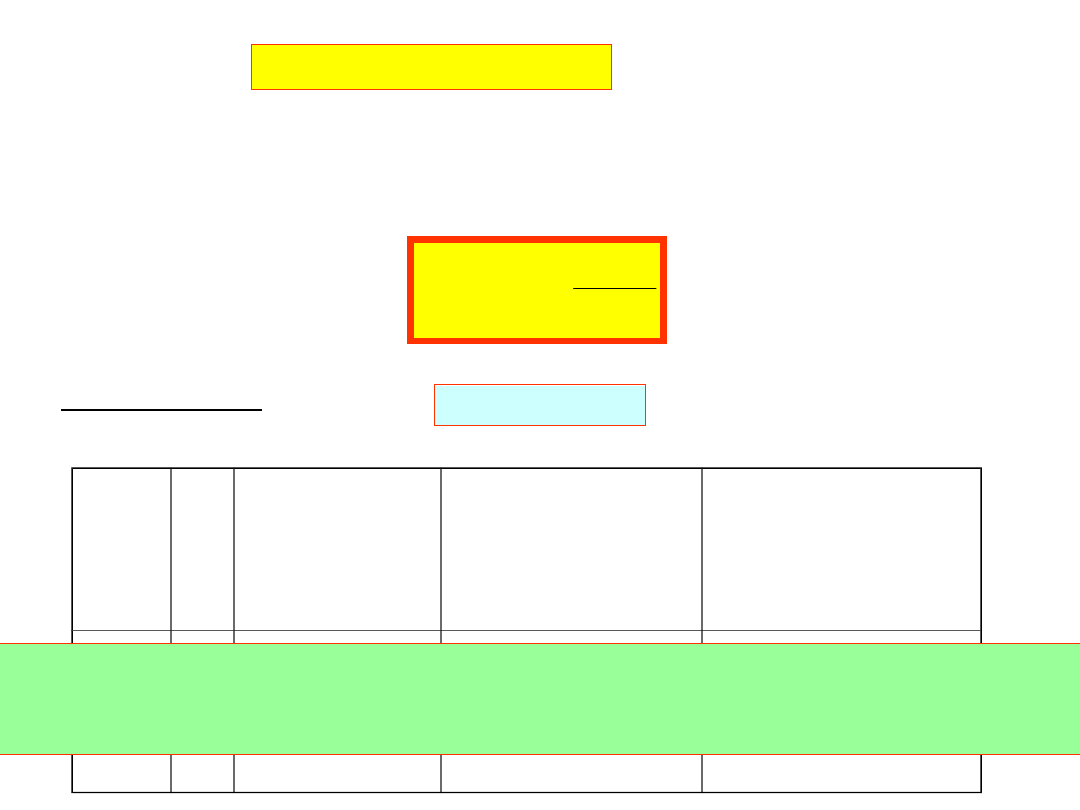
Prosta:
n
n
n
x
f
x
x
x
f
y
przechodzi przez zero, czyli y=0, w punkcie x
n+1
i mamy:
n
n
n
1
n
x
f
x
f
x
x
Przykład:
0
1
x
4
x
3
x 0
-0.25 -
0.246268
657
-
0.2462661
72
f(x
)
1 -
0.0156
25
-
0.000010
39
-0.2E-10
W 3 krokach dokładność osiągana w metodzie siecznych
w 5 krokach
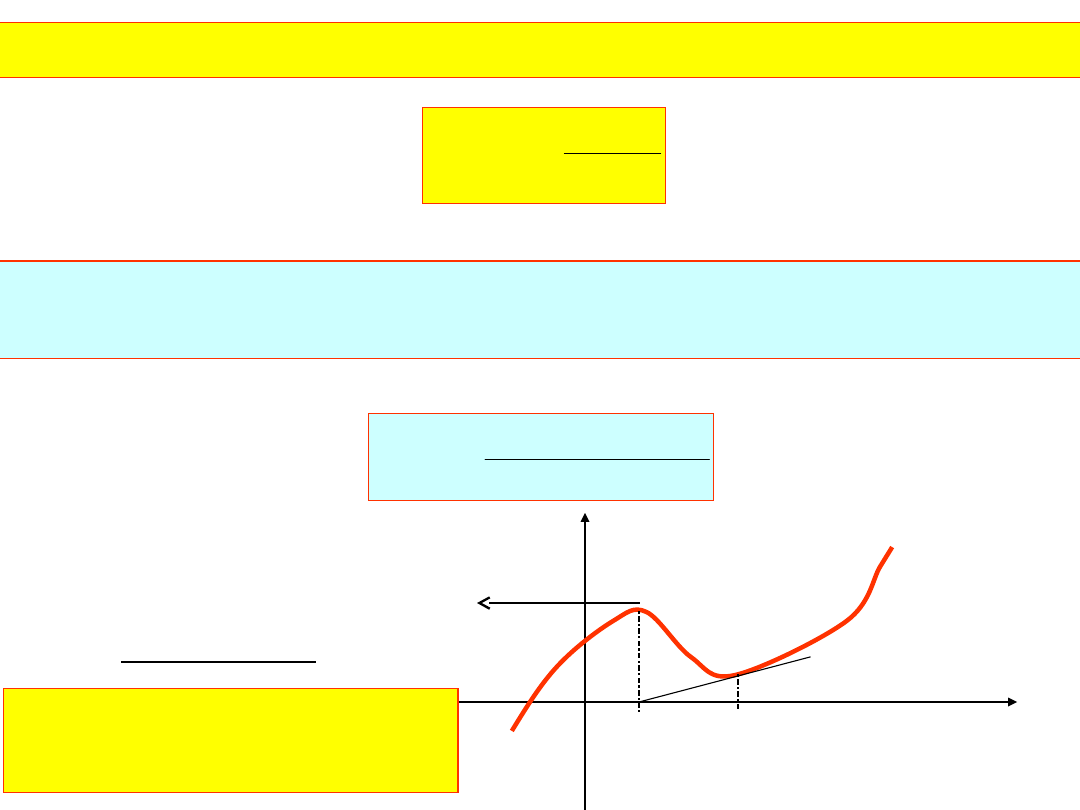
W obliczeniach numerycznych pochodną najczęściej oblicza się
numerycznie:
Metoda Newtona – Raphsona jest zbieżna kwadratowo, tzn.
i
i
2
i
1
i
x
f
2
x
f
h
x
f
h
x
f
x
f
i
i
i
„Pechowe” przypadki:
x
f(x)
x
0
x
1
x
2
rozbieżna
Zmniejszyć przedział
[x
d
,x
0
]
x
d

cykl
x
f(x)
x
1
=x
3
=...
x
2
=x
4
=...
x
d
Budując procedurę należy się zabezpieczyć przed taką możliwością.
Wystartować z punktu x
1
znajdującego się bliżej x
d
Pierwiastki wielokrotne:
0
x
f
i
0
x
f
d
d
Przy pierwiastkach wielokrotnych badać funkcję:
)
x
(
f
)
x
(
f
)
x
(
g
Pierwiastki zespolone
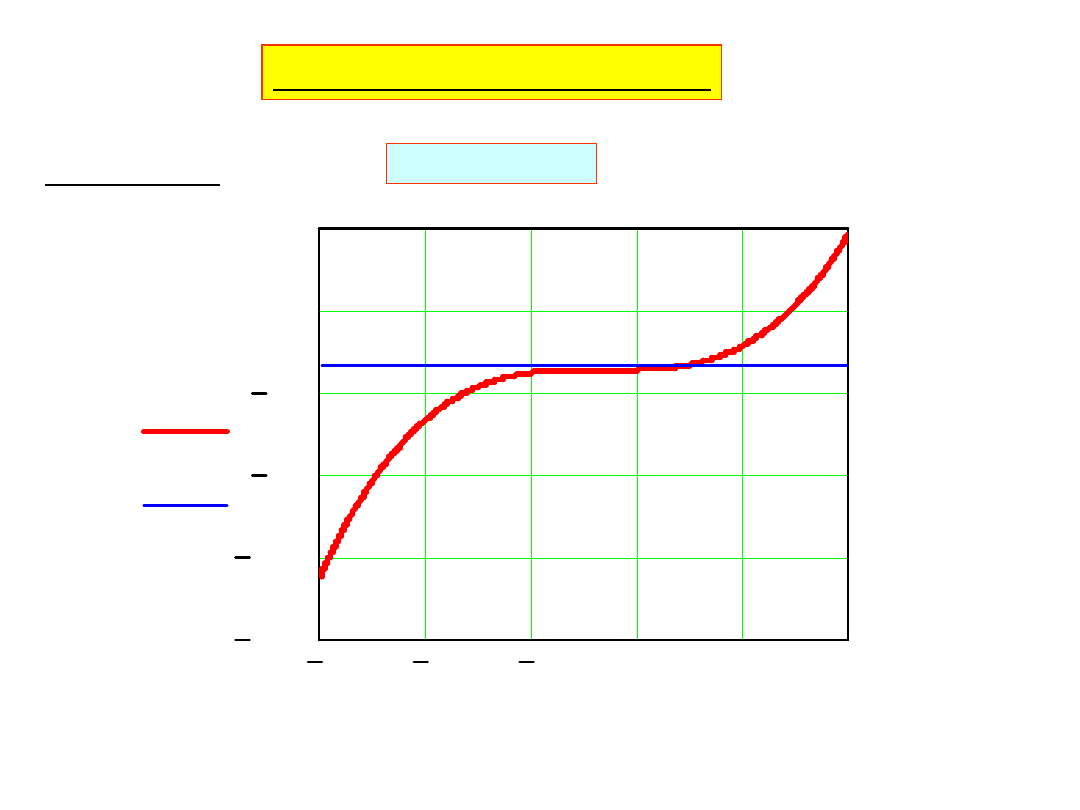
Przykład
0
4
x
x
2
3
5
3
1
1
3
5
200
140
80
20
40
100
f x
( )
0
x
Szukamy zespolonych pierwiastków metodą Newtona - Raphsona
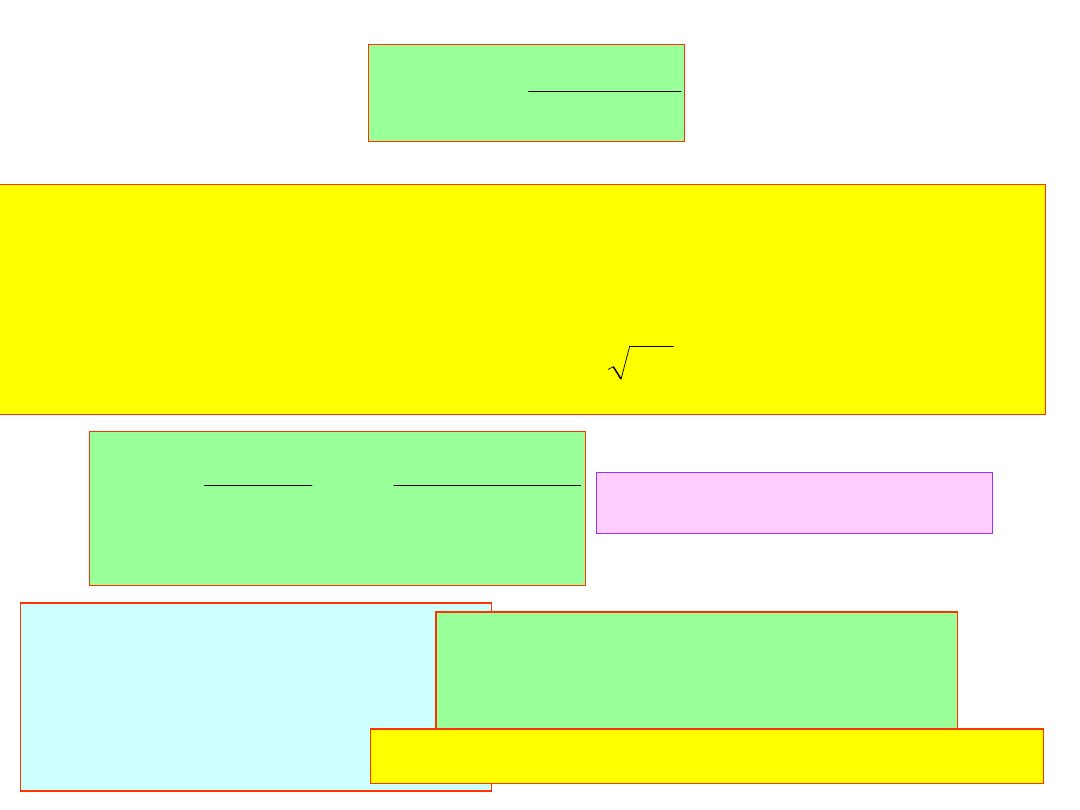
n
2
n
2
n
3
n
n
1
n
x
2
x
3
4
x
x
x
x
Jako punkt startowy musimy wybrać liczbę zespoloną:
x
0
=i
gdzie
1
i
i
2309
.
1
8462
.
0
x
e
6056
.
3
e
1623
.
3
i
i
2
3
i
3
i
x
1
69
.
213
i
43
.
198
i
1
x
2
=-0.50605+1.21289i
x
3
=-0.49471+1.32934i
x
4
=-0.50119+1.32409i
x
5
=-0.500059+1.322855i
x
6
=-0.5+1.32275i
błąd=-0.00083198+0.00043738i
x
d
=-0.5+1.322288i
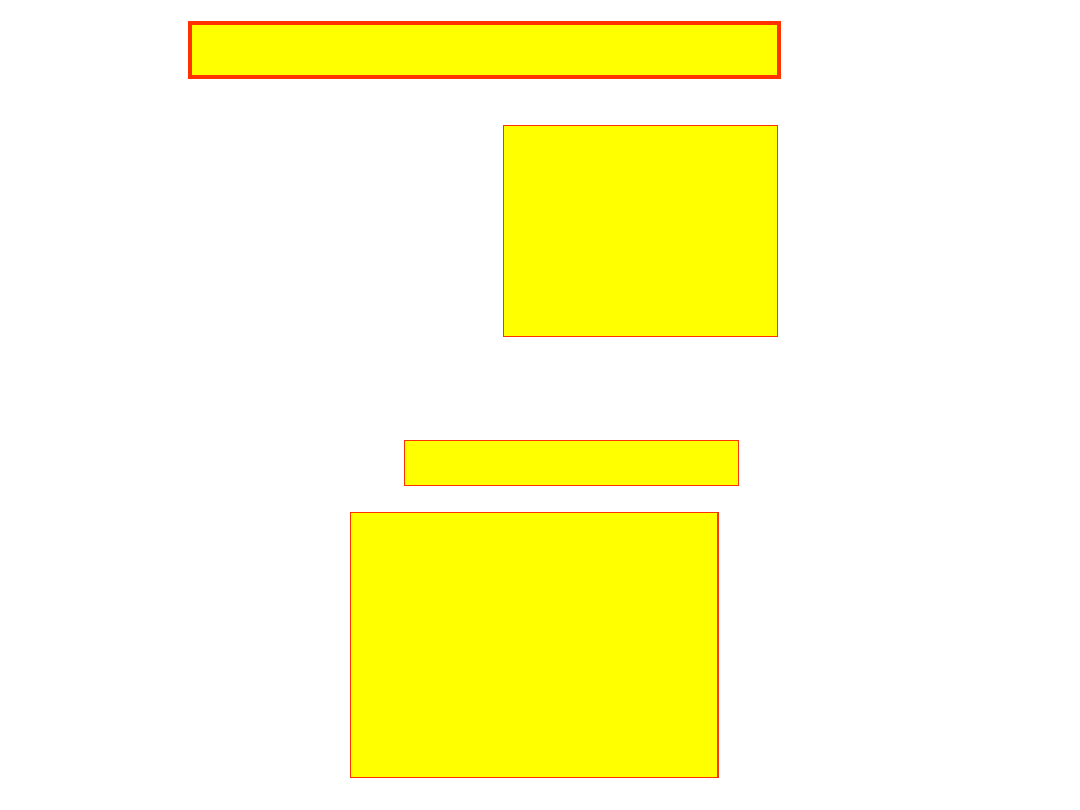
Układy równań nieliniowych
Dany jest układ równań:
0
x
,...,
x
,
x
f
..........
..........
..........
0
x
,...,
x
,
x
f
0
x
,...,
x
,
x
f
n
2
1
n
n
2
1
2
n
2
1
1
Dla skrócenia zapisu wprowadzamy oznaczenia:
X
f
x
,...,
x
,
x
f
k
n
2
1
k
oraz
)
x
,...,
x
,
x
(
f
.
.
)
x
,...,
x
,
x
(
f
)
x
,...,
x
,
x
(
f
)
X
(
F
n
2
1
n
n
2
1
2
n
2
1
1
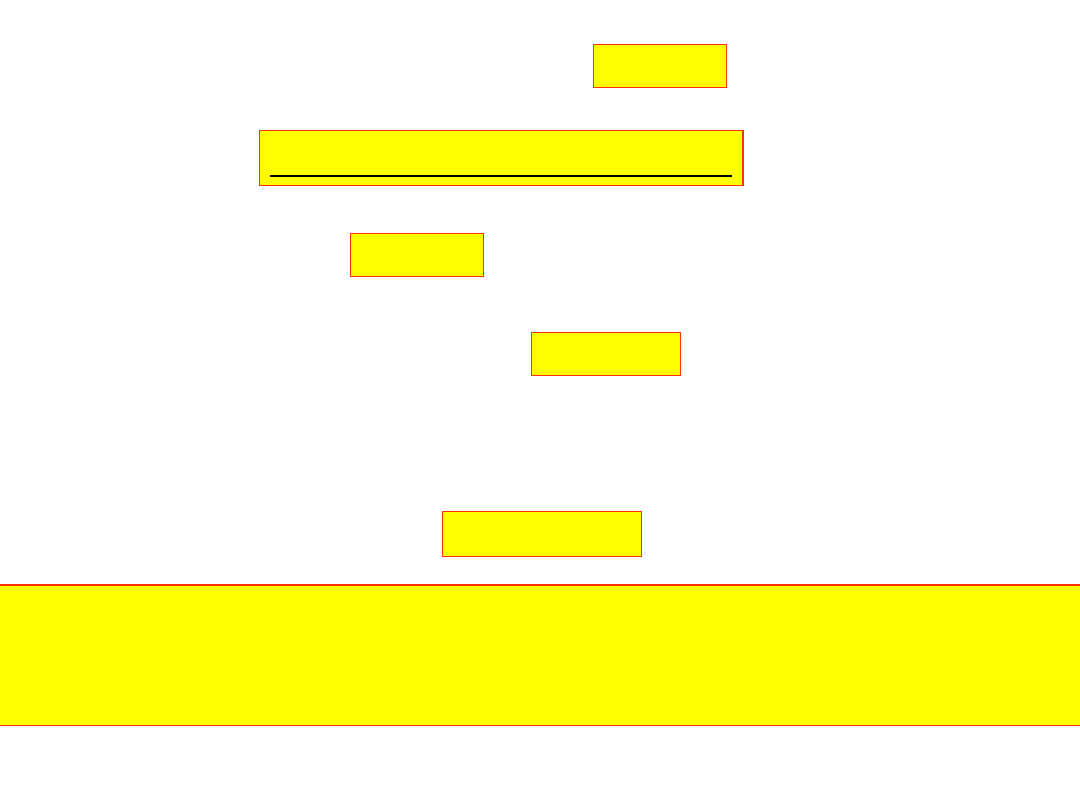
i równanie zapisujemy krótko:
0
X
F
Metoda iteracji prostej
Równanie:
0
X
F
zapisujemy w postaci:
X
G
X
i procedura iteracji prostej ma postać:
1
n
n
X
G
X
Stosowana szczególnie w przypadkach jeżeli mamy dobre
przybliżenie początkowe. Sytuacja taka występuje np. w
przypadku małej zmiany parametrów równania.
Przykład:
1
y
2
x
1
y
x
2
2
2
2
którego rozwiązaniem jest: x
1
=1; y
1
=0 oraz x
2
=-1; y
2
=0
Szukamy rozwiązania układu po małej zmianie parametrów:
1
y
01
.
2
x
95
.
0
y
x
2
2
2
2
mamy schemat iteracyjny:
01
.
2
x
1
y
y
95
.
0
x
2
1
n
n
2
1
n
n
Jako startowy punkt wybieramy: x
0
=1; y
0
=0 i mamy:
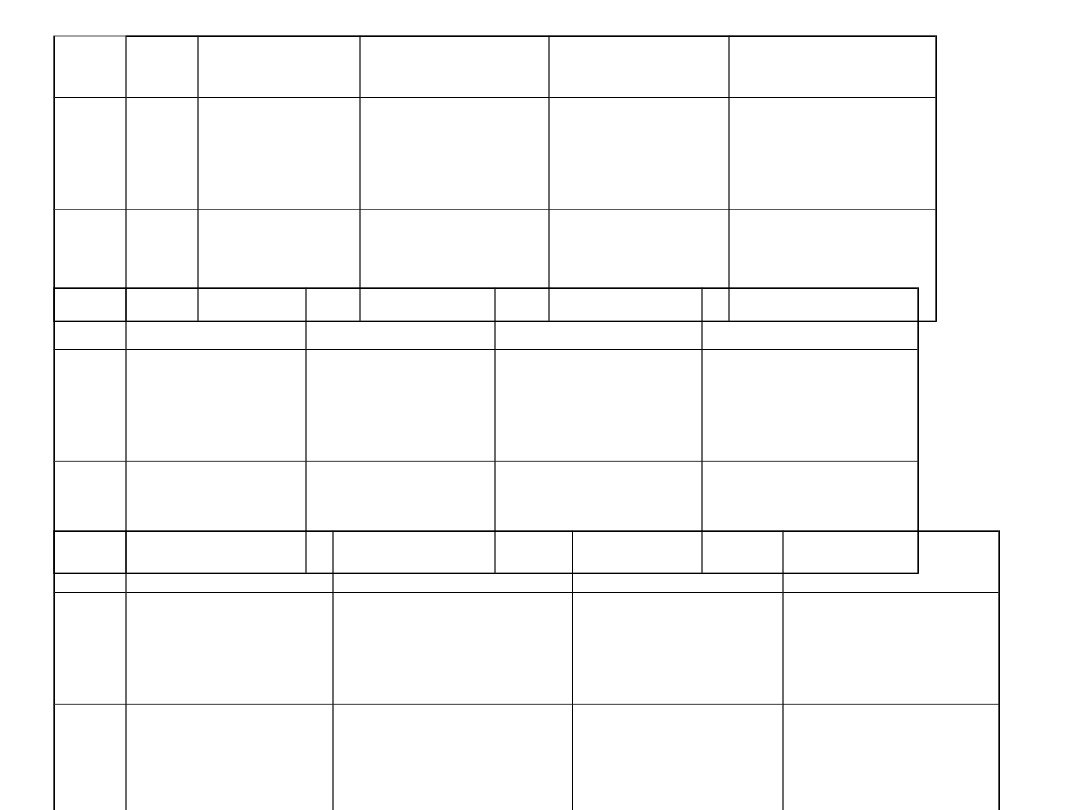
n 0
1
2
3
4
x
n
1 0.974
68
0.9746
8
0.961
834
0.9618
34
y
n
0
0
0.1577
18
0.157
718
0.1930
06
n
5
6
7
8
x
n
0.955
379
0.9553
79
0.9521
509
0.95215
1
y
n
0.193
006
0.2083
47
0.2083
47
0.21557
36
n
9
10
11
12
x
n
0.9505
409
0.95054
1
0.9497
389
0.94973
9
y
n
0.2155
734
0.21907
994
0.2190
797
0.22080
36

Z przedstawionych obliczeń widać, że metoda jest wolno
zbieżna i dlatego stosowana tylko w przypadkach, gdy
znamy bardzo dobrze zerowe przybliżenie. Zastosowanie
w równaniach różniczkowych.
Metoda Newtona - Raphsona
Rozwijamy funkcję f
k
(X) w szereg Taylora w otoczeniu
punktu X
i
:

0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
...
..........
..........
..........
..........
..........
..........
..........
..........
0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
.........
..........
..........
..........
..........
..........
..........
..........
0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
i
,
n
n
X
X
n
n
i
,
1
1
X
X
1
n
i
n
i
,
n
n
X
X
n
k
i
,
1
1
X
X
1
k
i
k
i
,
n
n
X
X
n
1
i
,
1
1
X
X
1
1
i
1
i
i
i
i
i
i
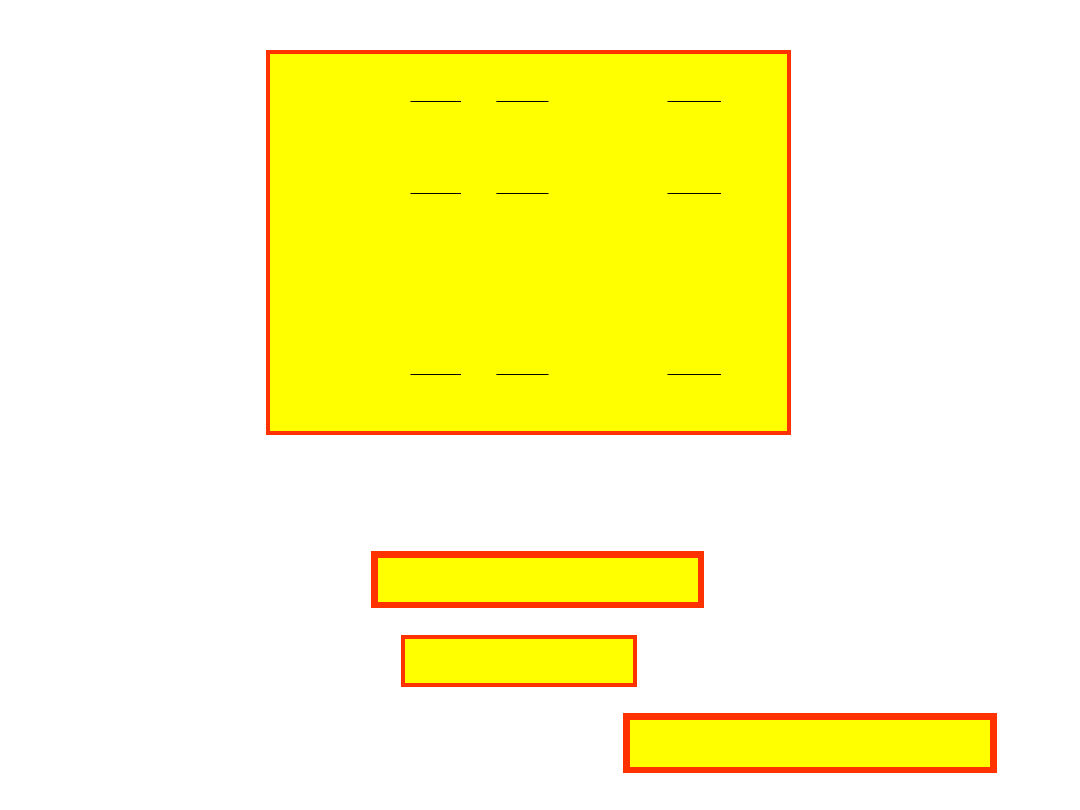
Dla uproszczenia zapisu wprowadzamy macierz Jacobiego
zdefiniowaną następująco:
i
X
X
n
n
2
n
1
n
n
2
2
2
1
2
n
1
2
1
1
1
i
x
f
.
.
x
f
x
f
.
.
.
.
.
.
.
.
.
.
x
f
.
.
x
f
x
f
x
f
.
.
x
f
x
f
)
X
(
J
i w postaci macierzowej możemy krótko zapisać układ równań:
0
X
X
J
X
F
i
i
i
gdzie oznaczono:
i
1
i
i
X
X
X
i rozwiązując symbolicznie mamy:
i
i
1
i
1
i
X
F
X
J
X
X

Przykład
B x
4
y
4
0.0221347267
1.7154013895
10
3
B x
3
y
3
0.4054281364
0.0757925914
y
3
1.6034305983
x
3
2.547524882
B x
2
y
2
2.0774058055
0.4332616428
y
2
1.2783983143
x
2
2.6115212513
B x
1
y
1
1.0181697533
0.2113862264
y
1
0.6296790316
x
1
0.8775588736
Nowa wartość startowa
x
n
y
n
x
n 1
y
n 1
J x
n 1
y
n 1
1
(
)
B x
n 1
y
n 1
n
1 10
y
0
1
x
0
1
B x y
(
)
f1 x y
(
)
f2 x y
(
)
J x y
(
)
pf1xx y
(
)
pf2xx y
(
)
pf1yx y
(
)
pf2yx y
(
)
pf2yx y
(
)
1
x y
sinx
( ) siny
( )
pf2xx y
(
)
cosx
( ) cos y
( )
1
x y
pf1yx y
(
)
expx y
(
) sin5 x
(
)
siny
( )
pf1xx y
(
)
expx y
(
) sin5 x
(
) 5 cos5 x
(
)
(
)
f2 x y
(
)
cos y
( ) sinx
( )
ln x y
f1 x y
(
)
expx y
(
) sin5 x
(
)
cos y
( )

B x
10
y
10
7.6327832943
10
16
1.0061396161
10
16
y
10
1.5326556001
x
10
2.5104053429
B x
7
y
7
7.6327832943
10
16
1.0061396161
10
16
y
7
1.5326556001
x
7
2.5104053429
B x
6
y
6
1.429500962
10
11
2.5677376891
10
13
y
6
1.5326556001
x
6
2.5104053429
B x
5
y
5
6.4971110534
10
6
3.05616917610
6
y
5
1.5326533005
x
5
2.5104046859
B x
4
y
4
0.0221347267
1.7154013895
10
3
y
4
1.5304688912
x
4
2.5085770863
B x
3
y
3
0.4054281364
0.0757925914
y
3
1.6034305983
x
3
2.547524882
B x
2
y
2
2.0774058055
0.4332616428
y
2
1.2783983143
x
2
2.6115212513
B x
1
y
1
1.0181697533
0.2113862264
y
1
0.6296790316
x
1
0.8775588736

B v
6
w
6
2.8284190988
10
4
4.0146896267
10
6
w
6
1.0538411892
v
6
0.0359317811
B v
5
w
5
3.082730668
10
3
6.399377386710
6
w
5
1.0541200235
v
5
0.0361162013
B v
4
w
4
0.0321949207
9.5125042042
10
4
w
4
1.0561052291
v
4
0.038130869
B v
3
w
3
0.2812551155
0.0206871382
w
3
1.097928869
v
3
0.0523869108
B v
2
w
2
1.4623634971
0.0241516982
w
2
0.8706086893
v
2
0.0653226558
B v
1
w
1
1.251877214
0.5666309304
w
1
0.9185509088
v
1
0.2566102428
v
n
w
n
v
n 1
w
n 1
PJ v
n 1
w
n 1
h
1
(
)
B v
n 1
w
n 1
w
0
0.1
v
0
0.1
h
0.1
PJ x y
h
(
)
f1 x h
y
(
) f1 x y
(
)
h
f2 x h
y
(
) f2 x y
(
)
h
f1 x y h
(
) f1 x y
(
)
h
f2 x y h
(
) f2 x y
(
)
h
Obliczenia przy numerycznie liczonej pochodnej
h=0.1

B v
10
w
10
2.0727367989
10
8
1.9211454649
10
10
w
10
1.0538173605
v
10
0.0359127014
B v
7
w
7
2.6276351633
10
5
1.6937433446
10
7
w
7
1.053819747
v
7
0.0359144545
B v
6
w
6
2.8284190988
10
4
4.0146896267
10
6
w
6
1.0538411892
v
6
0.0359317811
B v
5
w
5
3.082730668
10
3
6.3993773867
10
6
w
5
1.0541200235
v
5
0.0361162013
B v
4
w
4
0.0321949207
9.5125042042
10
4
w
4
1.0561052291
v
4
0.038130869
B v
3
w
3
0.2812551155
0.0206871382
w
3
1.097928869
v
3
0.0523869108
B v
2
w
2
1.4623634971
0.0241516982
w
2
0.8706086893
v
2
0.0653226558
B v
1
w
1
1.251877214
0.5666309304
w
1
0.9185509088
v
1
0.2566102428
v
n
w
n
v
n 1
w
n 1
PJ v
n 1
w
n 1
h
1
(
)
B v
n 1
w
n 1
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
- Slide 82
- Slide 83
- Slide 84
- Slide 85
- Slide 86
- Slide 87
- Slide 88
- Slide 89
- Slide 90
- Slide 91
- Slide 92
- Slide 93
- Slide 94
- Slide 95
- Slide 96
- Slide 97
- Slide 98
- Slide 99
- Slide 100
- Slide 101
- Slide 102
- Slide 103
- Slide 104
- Slide 105
Wyszukiwarka
Podobne podstrony:
Wyklad mn 2
Wyklad mn 9
Wyklad mn no 8 piątek
Wyklad mn 16
Wyklad mn 9
Wyklad mn 3
Wyklad mn no 7 piątek
Wyklad mn 6
Wyklad mn no 4 piątek
Wyklad mn 12
Wyklad mn 10
Wyklad mn 6
Wyklad mn 15
Wyklad mn no 5 piątek
Wyklad mn 8
Wyklad mn no 6 piątek
Wyklad mn 5
Wyklad mn 8
Wyklad mn no 3 piątek
więcej podobnych podstron