
B – funkcje sklejane (B – spline)
Podział przedziału [a,b] jest równomierny, czyli
N
a
b
Funkcja sklejana s
3
(x) jest przyjmowana w postaci:
1
N
k
1
k
k
k
3
x
B
a
x
s
gdzie funkcje B
k
(x) tworzą bazę przestrzeni s
3
(x) i mają
postać:
x
y
a=x
0
y
0
x
k
=k
y
k
b=N
y
N
s
m
(x)
2
k
2
-
k
2
k
1
k
3
2
k
1
k
k
3
1
k
2
1
k
1
k
2
3
k
1
-
k
3
1
k
2
1
k
1
k
2
3
1
k
2
-
k
3
2
k
3
k
x
,
x
x
dla
0
x
,
x
x
dla
x
x
x
,
x
x
dla
x
x
3
x
x
3
x
x
3
x
,
x
x
dla
x
x
3
x
x
3
x
x
3
x
,
x
x
dla
x
x
1
x
B
0
1
2
3
4
5
6
0
1
2
3
4
B 3 t
( )
t
x
B
k
(x)
x
k
x
k-1
x
k-2
x
k-3
x
k+1
x
k+2
x
k+3
x
k-2
x
k-1
x
k
x
k+1
x
k+2
B
k
(x
)
0
1
4
1
0
0
3/
0
-
3/
0
0
6/
2
-
12/
2
6/
2
0
x
B
k
x
B
k
Na mocy tabeli w węzłach interpolacji mamy:
k=0
0
1
0
1
y
a
a
4
a
k=1
1
2
1
0
y
a
a
4
a
...............................................
k=i
i
1
i
i
1
i
y
a
a
4
a
.................................................
k=N
N
1
N
N
1
N
y
a
a
4
a
Mamy N+1 równań
i N+3 niewiadomych.
Dwa dodatkowe równania
z warunków brzegowych.
Dla warunku pierwszego rodzaju:
N
3
0
3
p
b
s
i
p
a
s
mamy na mocy tablicy – pierwsze równanie:
0
1
1
p
a
3
a
3
i ostatnie równanie:
N
1
N
1
N
p
a
3
a
3
Dla warunku drugiego rodzaju:
N
3
0
3
d
b
s
i
d
a
s
mamy na mocy tablicy – pierwsze równanie:
0
1
2
0
2
1
2
d
a
6
a
12
a
6
i ostatnie równanie:
N
1
N
2
N
2
1
N
2
d
a
6
a
12
a
6
Dla warunku trzeciego rodzaju:
b
s
a
s
b
s
a
s
b
s
a
s
3
3
3
3
3
3
równanie:
0
1
0
1
y
a
a
4
a
i ostatnie:
N
1
N
N
1
N
y
a
a
4
a
mają identyczne prawe strony, gdyż ze względu na okresowość
y
0
=y
N
i dlatego zamiast ostatniego równania piszemy:
1
N
N
1
N
1
0
1
a
a
4
a
a
a
4
a
i pozostałe dwa warunki dają równania:
1
N
1
N
1
1
a
3
a
3
a
3
a
3
1
N
2
N
2
1
N
2
1
2
0
2
1
2
a
6
a
12
a
6
a
6
a
12
a
6
Rozwiązując powyższe trzy równania mamy:
1
N
1
N
0
1
N
1
a
a
a
a
a
a
a więc układ równań przyjmuje postać:
k=0
0
1
0
1
N
y
a
a
4
a
k=1
1
2
1
0
y
a
a
4
a
...............................................
k=i
i
1
i
i
1
i
y
a
a
4
a
.................................................
k=N-1
1
N
0
1
N
2
N
y
a
a
4
a
Jak rozwiązać otrzymany
układ równań metodą
„wymiatania” pokażemy
na przykładzie
Dana jest elipsa o równaniu:
1
y
5
x
2
2
lub w postaci tablicy:
k
0
1
2
3
4
5
x
5 4.924
04
4.698
46
3.830
22
2.5
0
y
0 0.173
65
0.342
02
0.642
79
0.866
03
1
k
6
7
8
9
1
0
x
-2.5
-
3.830
22
-
4.698
46
-
4.924
04
-5
y 0.866
03
0.642
79
0.342
02
0.173
65
0

k
11
12
13
14
15
x
-
4.924
04
-
4.6984
6
-
3.8302
2
-2.5
0
y
-
0.173
65
-
0.3420
2
-
0.6427
9
-
0.866
03
1
k
16
17
18
19
20
x
2.5
3.830
22
4.698
46
4.924
04
5
y
-
0.866
03
-
0.642
79
-
0.342
02
-
0.173
65
0
Interpolację krzywej zamkniętej możemy wykonać przyjmując
przedstawienie parametryczne:
21
k
1
k
k
k
t
B
a
t
x
i
21
k
1
k
k
k
t
B
b
t
y
i mamy układ równań:

83022
.
3
a
a
4
a
69846
.
4
a
a
4
a
92404
.
4
a
a
4
a
5
a
a
4
a
92404
.
4
a
a
4
a
69846
.
4
a
a
4
a
83022
.
3
a
a
4
a
5
.
2
a
a
4
a
0
a
a
4
a
5
.
2
a
a
4
a
83022
.
3
a
a
4
a
69846
.
4
a
a
4
a
92404
.
4
a
a
4
a
5
a
a
4
a
14
13
12
13
12
11
12
11
10
11
10
9
10
9
8
9
8
7
8
7
6
7
6
5
6
5
4
5
4
3
4
3
2
3
2
1
2
1
0
1
0
19
92404
.
4
a
4
a
a
69846
.
4
a
a
4
a
83022
.
3
a
a
4
a
5
.
2
a
a
4
a
0
a
a
4
a
5
.
2
a
a
4
a
19
18
0
19
18
17
18
17
16
17
16
15
16
15
14
15
14
13
Rozwiązanie metodą „wymiatania”:
k
19
k
k
k
1
k
A
a
B
a
L
a
Podstawiając do k-go równania:
k
1
k
k
1
k
x
a
a
4
a
mamy:
k
k
k
k
19
k
k
1
k
k
L
4
A
x
L
4
a
B
L
4
a
a
ale
1
k
19
1
k
1
k
1
k
k
A
a
B
a
L
a
i porównując z
k
k
k
k
19
k
k
1
k
k
L
4
A
x
L
4
a
B
L
4
a
a
mamy wzory rekurencyjne:
k
1
k
L
4
1
L
k
k
1
k
L
4
B
B
i
k
k
k
1
k
L
4
A
x
A
Wartości startowe L
1
, A
1
i B
1
wyznaczamy porównując wzór:
1
19
1
1
1
0
A
a
B
a
L
a
z pierwszym równaniem:
25
.
1
a
25
.
0
a
25
.
0
a
19
1
0
mamy: L
1
=-0.25, B
1
=-0.25 i A
1
=1.25

i z dokładnością do 5 cyfr mamy:
L
2
=-0.26667
L
3
=-0.26786
L
4
=-0.26794
L
5
=L
6
=...=L
19
=-0.26795
B
2
=0.066667 B
15
=-2.44585e-9
B
3
=-0.017857 B
16
=6.55364e-10
B
4
=4.78469e-3 B
17
=-1.75604e-10
B
5
=-1.28205e-3 B
18
=4.7053e-11
B
6
=3.43525e-4 B
19
=-1.26078e-11
B
7
=-9.20471e-5
B
8
=2.4664e-5
B
9
=-6.60869e-6
B
10
=1.77079e-6
B
11
=-4.74482e-7
B
12
=1.27137e-7
B
13
=-3.40663e-8
B
14
=9.128037e-9
W równaniu
92404
.
4
a
4
a
a
19
18
0
B
19
poprawia 4
A
2
=0.97974 A
14
=-0.76330
A
3
=0.99608 A
15
=-0.46535
A
4
=0.75939 A
16
=0.12469
A
5
=0.46640 A
17
=0.63646
A
6
=-0.12497 A
18
=0.85576
A
7
=-0.63639 A
19
=1.02965
A
8
=-0.85579
A
9
=-1.02964
A
10
=-1.04350
A
11
=-1.06014
A
12
=-1.03533
A
13
=-0.98153
Podstawiając do równania:
92404
.
4
a
4
a
a
19
18
0
mamy:
19
19
0
19
19
B
L
4
a
A
92404
.
4
a
czyli
0
19
19
19
a
D
C
a
gdzie
19
19
19
19
B
L
4
A
92404
.
4
C
19
19
19
B
L
4
1
D
i zakładając:
0
1
k
1
k
1
k
a
D
C
a
i podstawiając do związku rekurencyjnego:
1
k
19
1
k
1
k
1
k
k
A
a
B
a
L
a
mamy:
0
k
k
k
a
D
C
a
gdzie
19
1
k
1
k
1
k
k
1
k
19
1
k
1
k
1
k
k
D
B
D
L
D
A
C
B
C
L
C
dla k=18,17,...,0
ze startowymi C
19
, D
19
z zależności:
19
19
19
19
B
L
4
A
92404
.
4
C
i
19
19
19
B
L
4
1
D
C
19
=1.04350 D
19
=-0.26795 C
4
=0.46504 D
4
=3.70097e-4
C
18
=0.75004 D
18
=0.07180 C
3
=0.63978 D
3
=-1.38122e-3
C
17
=0.65479 D
17
=-0.01924 C
2
=0.80608 D
2
=5.15478e-3
C
16
=0.46101 D
16
=5.15478e-3 C
1
=0.83436 D
1
=-0.01924
C
15
=1.16148e-3 D
15
=-1.38122e-3 C
0
=0.78054 D
0
=0.07180
C
14
=-0.46566 D
14
=3.70097e-4
C
13
=-0.63853 D
13
=-9.91696e-5 i z równania:
C
12
=-0.81044 D
12
=2.65816e-5
C
11
=-0.81817 D
11
=-7.15657e-6
C
10
=-0.84091 D
10
=2.04473e-6 mamy:
C
9
=-0.81818 D
9
=-1.02237e-6
C
8
=-0.81042 D
8
=2.04473e-6
C
7
=-0.63861 D
7
=-7.15657e-6 czyli a
0
=a
20
=0.84091
C
6
=-0.46537 D
6
=2.65816e-5
C
5
=8.33928e-5 D
5
=-9.91696e-5
0
0
0
0
a
D
C
a
0
0
0
D
1
C
a

i ze związku rekurencyjnego:
0
k
k
k
a
D
C
a
mamy:
dla k=1,2,...,19
a
1
=a
21
=0.81818 a
13
=-0.63861
a
2
=0.81042 a
14
=-0.46535
a
3
=0.63861 a
15
=0.00000
a
4
=0.46535 a
16
=0.46535
a
5
=-0.00000 a
17
=0.63861
a
6
=-0.46535 a
18
=0.81042
a
7
=-0.63861 a
-1
=a
19
=0.81818
a
8
=-0.81042
a
9
=-0.81818
a
10
=-0.84091
a
11
=-0.81818
a
12
=-0.81042
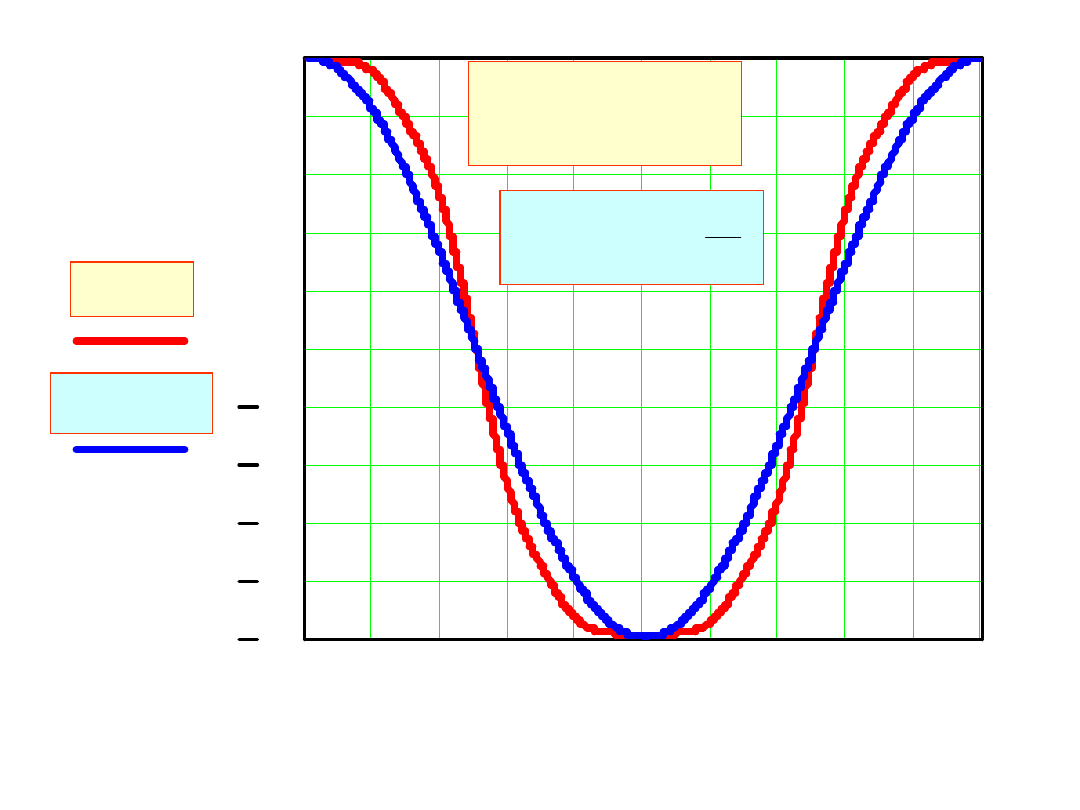
0 2 4 6 8 10 12 14 16 18 20
5
4
3
2
1
0
1
2
3
4
5
v s
( )
xd s
( )
s
x(s)
21
k
1
k
k
k
s
B
a
s
x
10
s
cos
5
s
x
d
x
d
(s)

Równanie krzywej dla współrzędnej x jest:
10
s
cos
5
s
x
d
dla parametru
20
,
0
s
Błąd między wielomianem interpolacyjnym a funkcją x(s)
definiujemy:
0
s
x
if
s
x
s
x
0
s
x
if
s
x
s
x
s
x
s
d
d
d
d
d
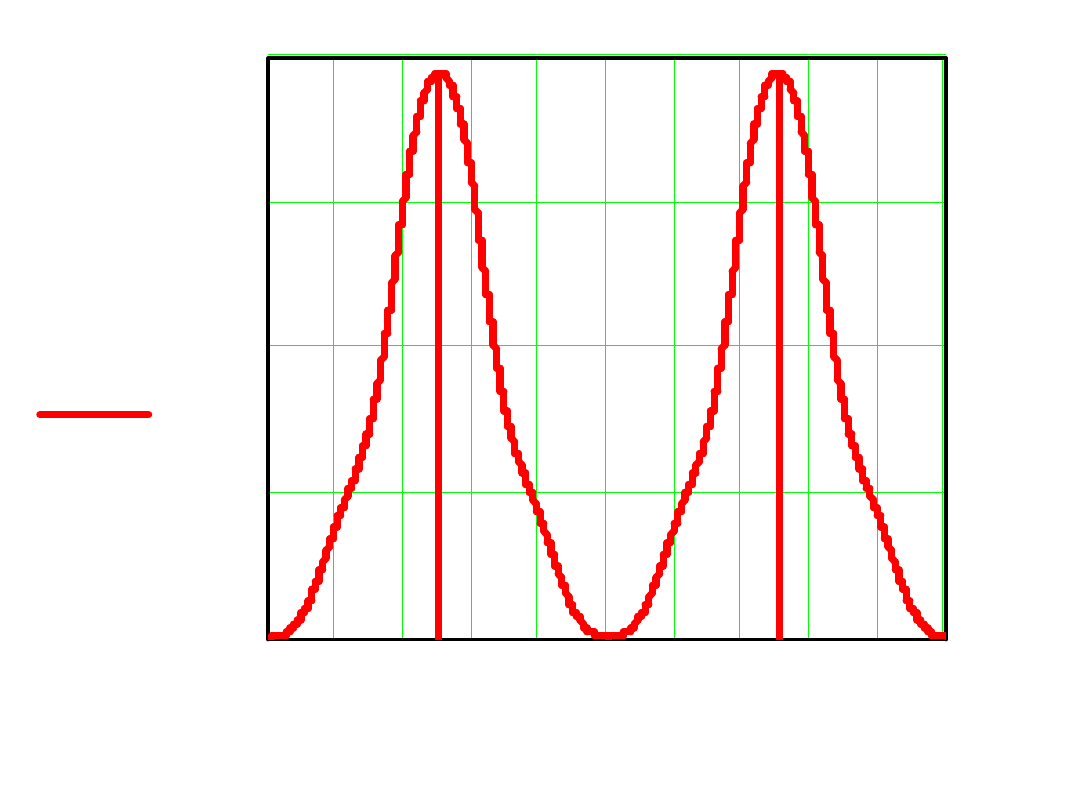
0 2 4 6 8 10 12 14 16 18 20
0
0.2
0.4
0.6
0.8
s
( )
s
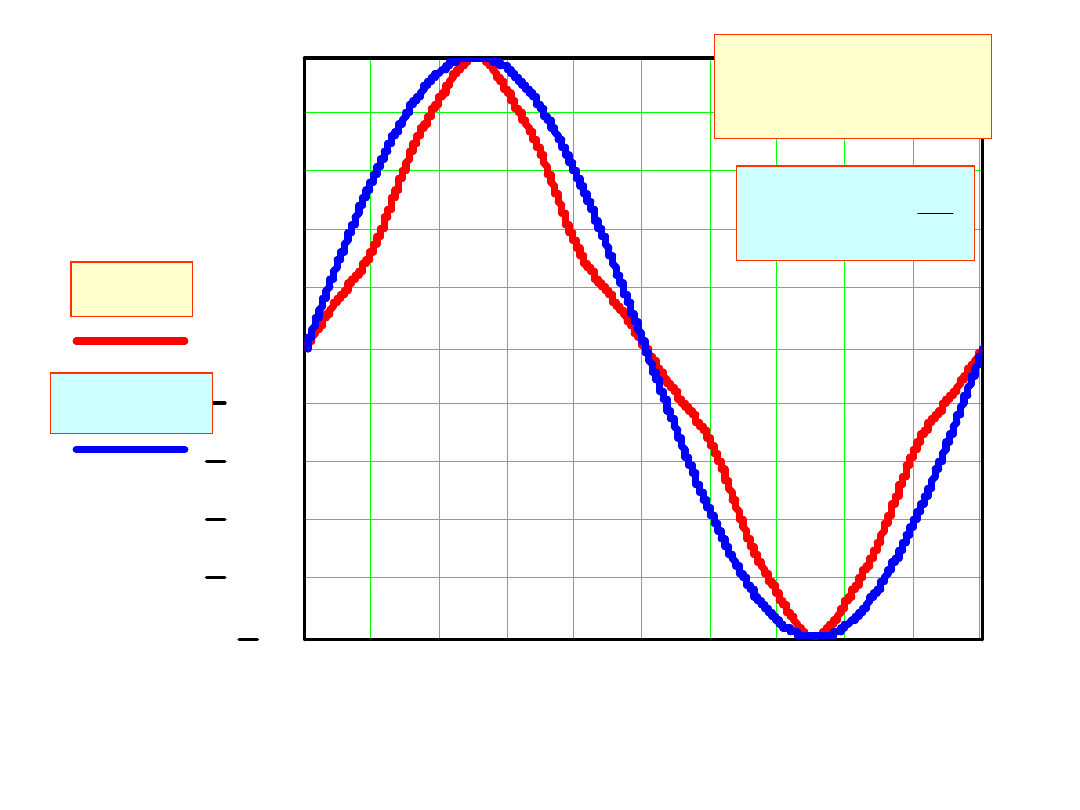
0 2 4 6 8 10 12 14 16 18 20
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
w s
( )
yd s
( )
s
21
k
1
k
k
k
s
B
b
s
y
10
s
sin
s
y
d
y(s)
y
d
(s)

5
4
3
2
1
0
1
2
3
4
5
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
w s
( )
yd s
( )
v s
( ) xd s
( )
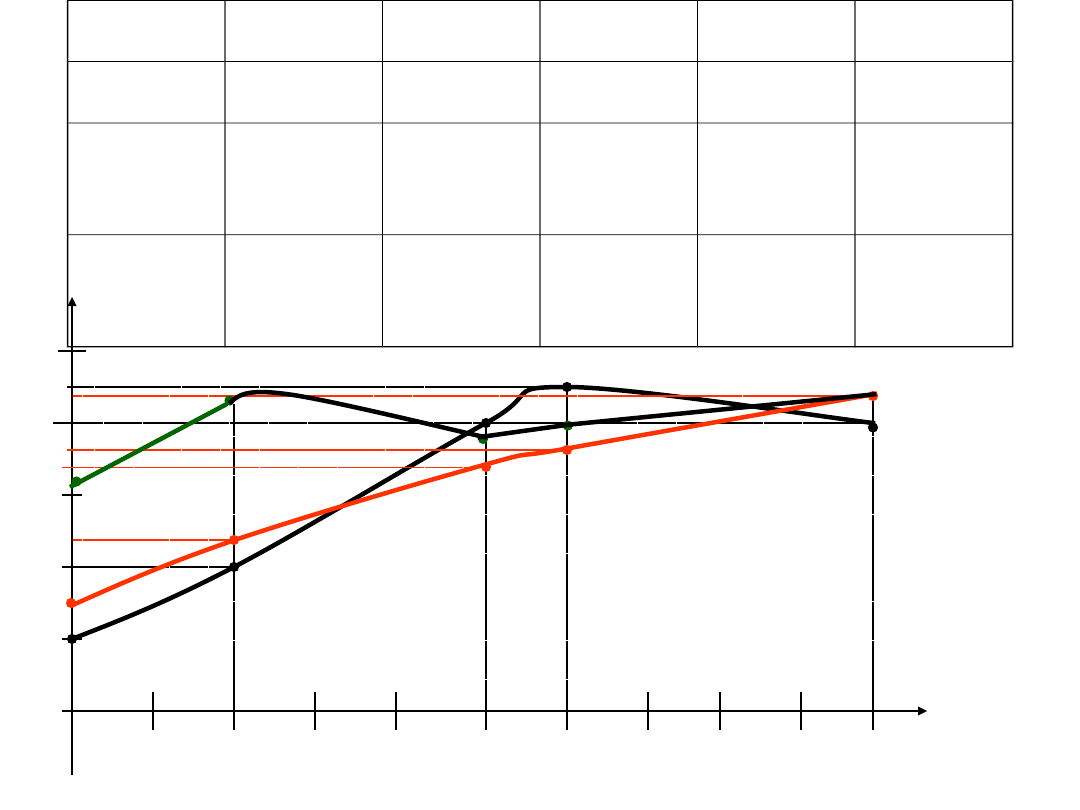
x(s),x
d
(s)
y(s)
y
d
(s)
elipsa otrzymana
w rezultacie
interpolacji
i
dokładna
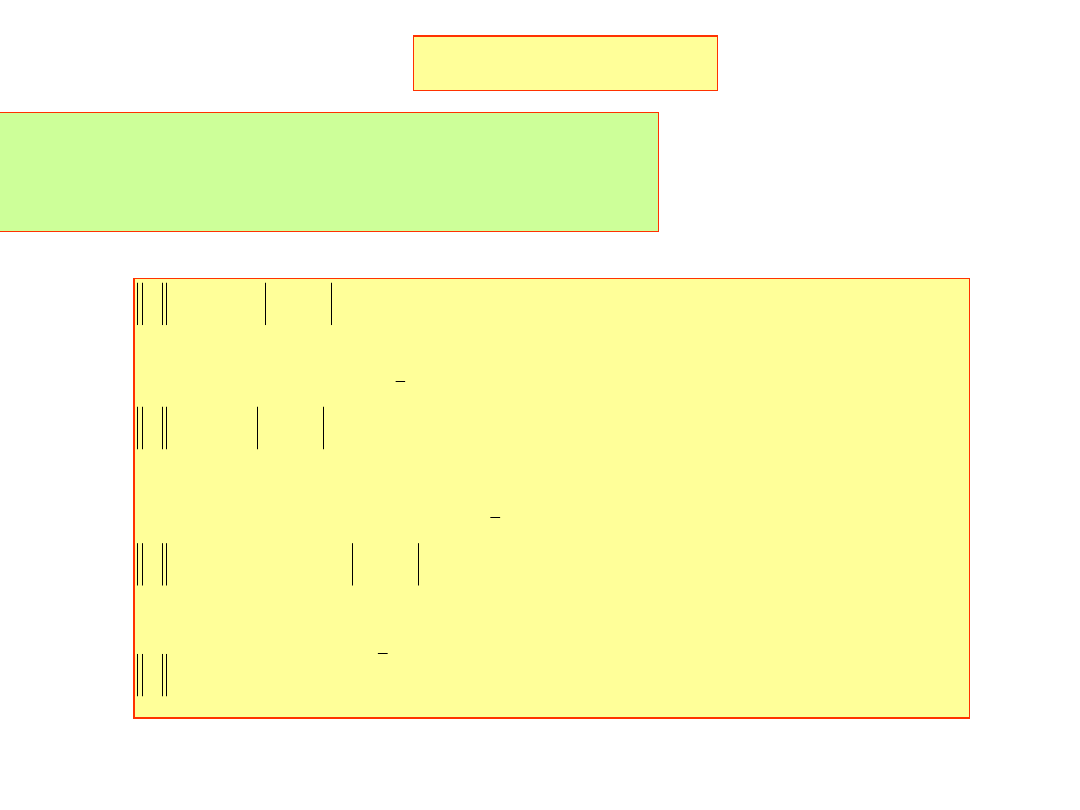
Aproksymacja
Dążenie do minimalizacji normy.
Przykłady stosowanych norm:
b
,
a
l
i
przestrzen
w
)
)]
x
(
f
[
(
f
b
,
a
L
i
przestrzen
w
dx
)
x
(
f
)
x
(
w
f
b
,
a
L
i
przestrzen
w
dx
)
x
(
f
f
b
,
a
C
i
przestrzen
w
)
x
(
f
sup
f
N
2
N
0
i
2
1
2
i
w
2,
2
1
2
b
a
w
,
2
2
2
1
2
b
a
2
0
]
b
,
a
[
x
Zadanie aproksymacji polega na minimalizacji normy:
)
x
(
g
)
x
(
F
Niech
K
0
n
n
n
)
x
(
h
a
)
x
(
g
i dane są wartości funkcji :
i
i
F
)
x
(
F
w punktach i=0,2,...P.
Niech będzie zastosowana norma z wagą:
P
0
i
2
K
0
n
i
n
n
i
i
)
x
(
h
a
F
w
i szukamy minimum sumy ze względu na współczynniki a
n
.

Przykład:
x
0
0.2
0.5
0.6
1
y
0.1
0.2
0.4
0.45
0.4
2
2
1
0
x
a
x
a
a
)
x
(
g
Przyjmujemy wielomian aproksymujący w postaci:
przyjmując funkcję wagową równą jedności otrzymujemy:
2
2
1
0
2
2
1
0
2
2
1
0
2
2
1
0
2
0
2
1
0
a
a
a
4
.
0
36
.
0
a
6
.
0
a
a
45
.
0
25
.
0
a
5
.
0
a
a
4
.
0
04
.
0
a
2
.
0
a
a
2
.
0
)
a
1
.
0
(
)
a
,
a
,
a
(
d

Szukamy ekstremum funkcji d(a
0
,a
1
,a
2
) i przyrównując do zera
pierwsze pochodne względem a
0
, a
1
i a
2
otrzymujemy:
67
.
0
a
1937
.
1
a
349
.
1
a
65
.
1
a
d
91
.
0
a
2365
.
1
a
65
.
1
a
3
.
2
a
d
55
.
1
a
65
.
1
a
3
.
2
a
5
a
d
3
1
0
2
2
1
0
1
2
1
0
0
Rozwiązanie powyższych równań ma postać:
151
.
0
a
493
.
0
a
204
.
0
a
0
1
2
Interpolacja z wagą
2
2
1
0
2
2
1
0
2
2
1
0
2
2
1
0
2
0
2
1
0
w
a
a
a
4
.
0
5
.
0
a
36
.
0
a
6
.
0
a
45
.
0
a
25
.
0
a
5
.
0
a
4
.
0
a
04
.
0
a
2
.
0
a
2
.
0
5
.
0
a
1
.
0
25
.
0
a
,
a
,
a
d
Po obliczeniu ekstrmum mamy: a
0
=0.319
a
1
=0.158
a
2
=-0.041
Wielomian aproksymujący jest:
2
w
x
041
.
0
x
158
.
0
319
.
0
x
W
x
0
0.2
0.5
0.6
1
y
0.1
0.2
0.4
0.45
0.4
y
ap
0.151 0.241
4
0.346
5
0.373
3
0.44
y
apw
0.319 0.42 0.387
8
0.399 0.436
1
x
0.5
0
0.2
y
y
y
ap
y
apw
Wielomiany trygonometryczne
n
1
k
k
k
0
n
)
kx
sin
b
kx
cos
a
(
2
a
)
x
(
F
aproksymacja funkcji okresowej na dyskretnym równoodległym
zbiorze punktów:
i=0,1,2,..., 2L-1
L
i
x
i
ciągły:
L
n
)
jx
sin
b
jx
cos
a
(
a
2
1
)
x
(
y
n
1
j
i
i
0
n
a współczynniki wyznacza się z równania:
1
L
2
0
i
2
i
n
i
)
x
(
y
)
x
(
f
Różniczkując względem a
k
otrzymujemy następujące równania
dla wyznaczania współczynników:
0
kx
cos
jx
sin
b
jx
cos
a
2
a
)
x
(
f
i
1
L
2
0
i
n
1
j
i
j
i
j
0
i
0
kx
sin
jx
cos
0
=
k
=
j
dla
2L
0
k
=
j
dla
L
k
j
dla
0
kx
cos
jx
cos
1
L
2
0
l
l
l
1
L
2
0
i
i
i
Mamy tożsamości:
Na mocy powyższych tożsamości mamy:
L
n
,...,
1
,
0
j
L
lj
cos
)
x
(
F
L
1
a
1
L
2
0
l
l
j
Podobnie wyznaczamy współczynniki b
j
z równania:
0
kx
sin
jx
sin
b
jx
cos
a
2
a
)
x
(
F
l
1
L
2
0
l
n
1
j
l
j
l
j
0
l
korzystając z tożsamości:
k
=
j
dla
L
k
j
dla
0
kx
sin
jx
sin
1
L
2
0
l
l
l
otrzymujemy:
L
n
,...,
1
,
0
j
L
jl
sin
)
x
(
F
L
1
b
1
L
2
0
i
l
j

Szereg zespolony.
Dana jest funkcja określona przez podanie jej wartości f
n
w punktach:
N
n
2
x
n
gdzie n=0,1,2,...,N-1. Aproksymujemy funkcję wielomianem
trygonometrycznym postaci:
1
i
gdzie
)
ikx
exp(
c
)
x
(
w
1
N
0
k
k
Otrzymujemy N równań dla wyznaczenia współczynników c
k
:
1
N
0
k
n
k
n
n
)
ikx
exp(
c
f
)
x
(
w
Rozwiązanie ostatniego układu równań czyli współczynniki c
k
są określane równaniami:
1
N
0
n
n
n
p
)
ipx
exp(
f
N
1
c
Idea szybkie transformaty Fouriera tzw. FFT
Fast Fourier Transform
Ponieważ
N
n
2
x
n
więc
N
pn
2
i
exp
ipx
exp
n
Oznaczmy:
N
i
2
epx
w
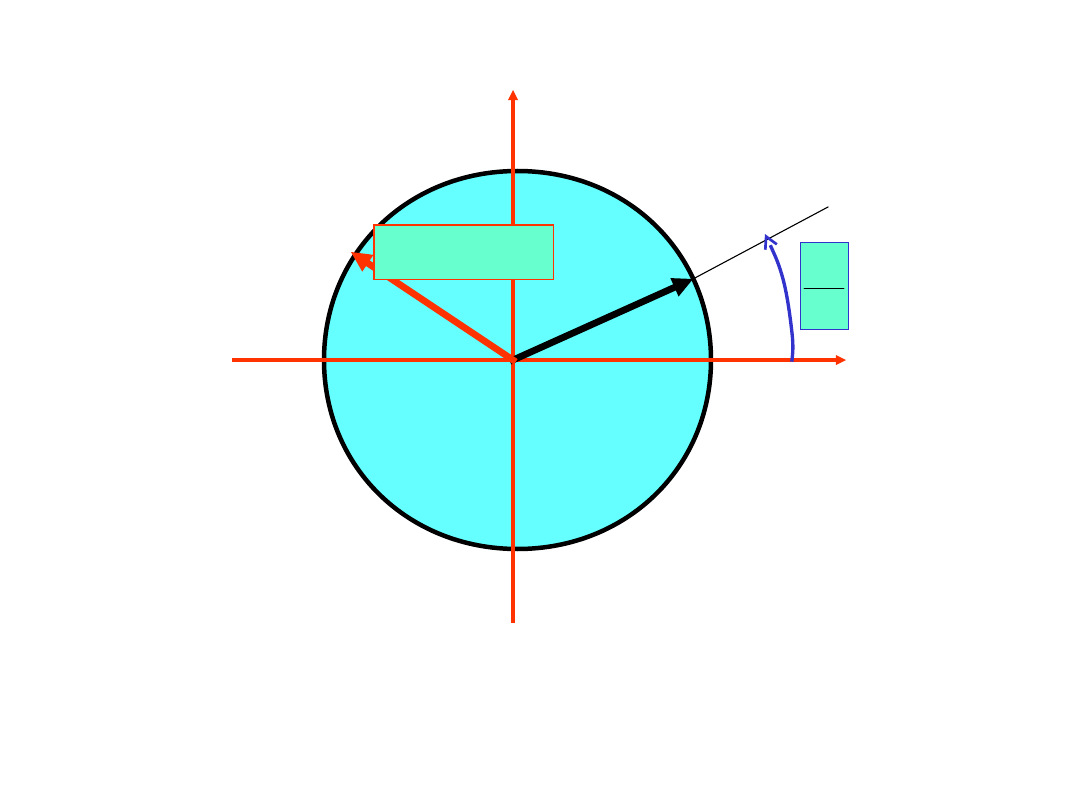
Zauważmy, że
Re
Im
w=w
N+1
N
2
w
p
=w
p+N
Każda całkowita potęga w leży na okręgu jednostkowym
i co więcej jeżeli wykładnik p potęgi w
p
jest większy od N
to punkty się nakrywają. Na tym spostrzeżeniu bazuje FFT.
Piszemy:
1
N
0
n
n
pn
p
f
w
N
1
c
Możemy zapisać w postaci macierzowej:
Oznaczając:
1
N
,...,
1
,
0
n
dla
N
f
g
n
n
n
pn
p
g
w
c
gdzie
2
1
N
1
N
0
1
N
1
0
0
0
0
pn
w
w
w
.
.
.
w
w
w
w
w
w
w
Ponieważ w
0
=1 więc nie będziemy pisać zerowej kolumny i wiersza.
Dalej mamy związki:
N
i
2
epx
w
k
k
N
w
k
N
i
2
exp
k
N
i
2
exp
N
N
i
2
exp
k
N
N
i
2
exp
w
czyli
k
k
N
w
w
a więc wiersze i kolumny: 1 i N-1
2 i N-2
..............
k i N-k
..............
N/2-1 i N/2+1 dla N parzystych
(N-1)2 i (N+1)/2 dla N nieparzystych
są sprzężone
.

W praktyce najczęściej stosowane N=2
M
.
Jeżeli liczba węzłów interpolacyjnych mniejsza od 2
M
,
to uzupełniamy zerami.
N=8
w
w
2
w
3
w
4
=-
1
(w
*
)
3
(w
*
)
2
w
*
w
2
w
4
w
6
w
8
=1 (w
*
)
6
(w
*
)
4
(w
*
)
2
w
3
w
6
w
9
w
12
=-
1
(w
*
)
9
(w
*
)
6
(w
*
)
3
w
4
w
8
w
12
w
16
=
1
(w
*
)
12
(w
*
)
8
(w
*
)
4
w
5
w
10
w
15
w
20
=-
1
(w
*
)
15
(w
*
)
10
(w
*
)
5
w
6
w
12
w
18
w
24
=
1
(w
*
)
18
(w
*
)
12
(w
*
)
6
w
7
w
14
w
21
w
28
=-
1
(w
*
)
21
(w
*
)
14
(w
*
)
7
8
i
2
epx
w
8
i
2
epx
w
*
lub inaczej
a b c
-
1
c
*
b
*
a
*
b -
1
b
*
1 b -1 b
*
c b
*
a
-
1
a
*
b c
*
-1 1 -1 1 -1 1 -1
c
*
b a
*
-
1
a b
*
c
b
*
-
1
b 1 b
*
-1 b
a
*
b
*
c
*
-
1
c b a
7
6
5
4
3
2
1
0
f
f
f
f
f
f
f
f
dla otrzymania tablicy mnożników wystarczy obliczyć połowę
pierwszego wiersza!!!
np. a=a
r
+ia
i
oraz a
*
=a
r
-ia
i
czyli np.
af
1
+a
*
f
7
=a
r
(f
1
+f
7
)+ia
i
(f
1
-f
7
)
i podobnie dla innych
operacji.
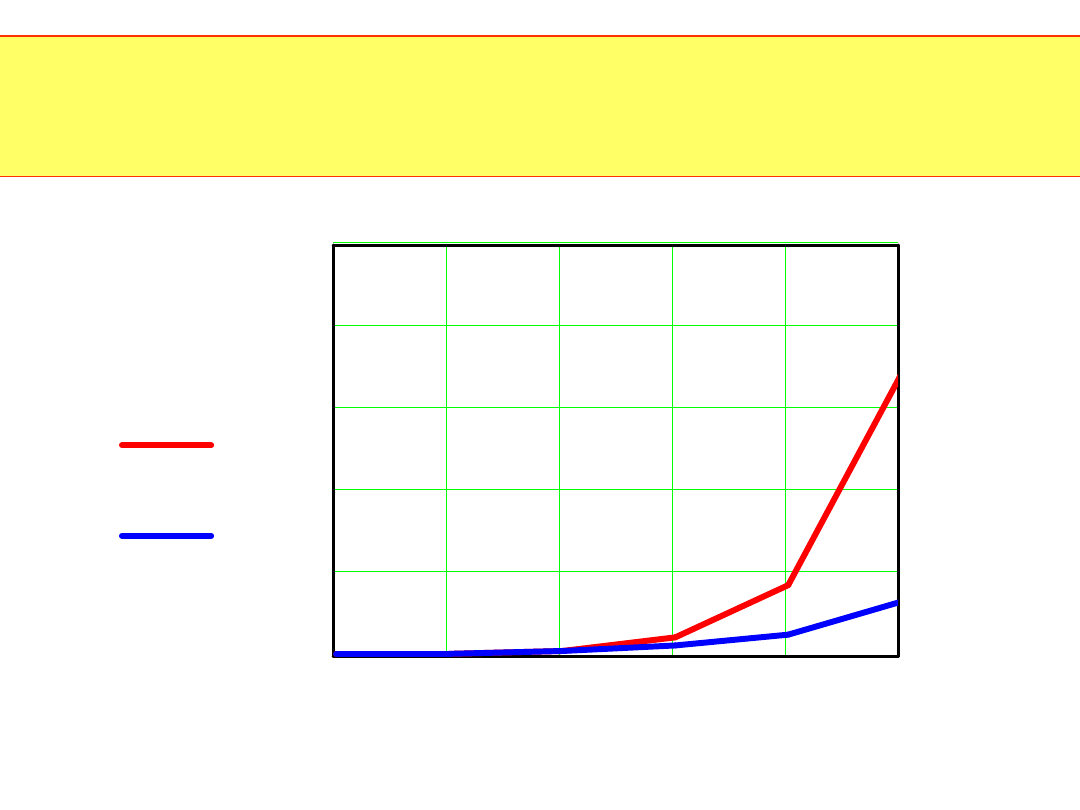
Wykorzystanie przedstawionych uproszczeń pozwala w stosunku
do zwykłego algorytmu zawierającego N
2
działań zespolonych
zmniejszyć ich liczbę dla N=2
M
do 2NM
1
2
3
4
5
6
0
1200
2400
3600
4800
6000
2
2 m
m2
m 1
m
Rozwiązywanie równań algebraicznych
f(x)=0
Metoda bisekcji
Przykład:
0
1
x
4
x
3
x
-1 0 -0.5
-0.25
-0.125
-
0.187
5
f(x
)
-4 1
-
1.12
5
-
0.0156
25
0.498
045
0.243
08
x
-
0.2187
5
-
0.2343
75
-
0.24218
75
-
0.246093
75
f(x
)
0.1145
32
0.0496
254
0.01704
45
0.000721
037
x
-
0.24804
69
-
0.246582
03
-
0.246337
9
-
0.24621
58
f(x) -
0.00744
91
-
0.001320
98
-
0.000299
93
0.00021
057
Zaleta metody: Jeżeli pierwiastek istnieje, to go znajdziemy.
Wada metody: Duża liczba obliczeń
Regula falsi.
Założenia:
a) funkcja ma w przedziale [a,b] tylko jeden pierwiastek
i zachodzi f(a)f(b)<0,
b) jest funkcja jest klasy C
2
[a,b], pierwsza i druga pochodna
nie zmieniają znaku na przedziale [a,b].
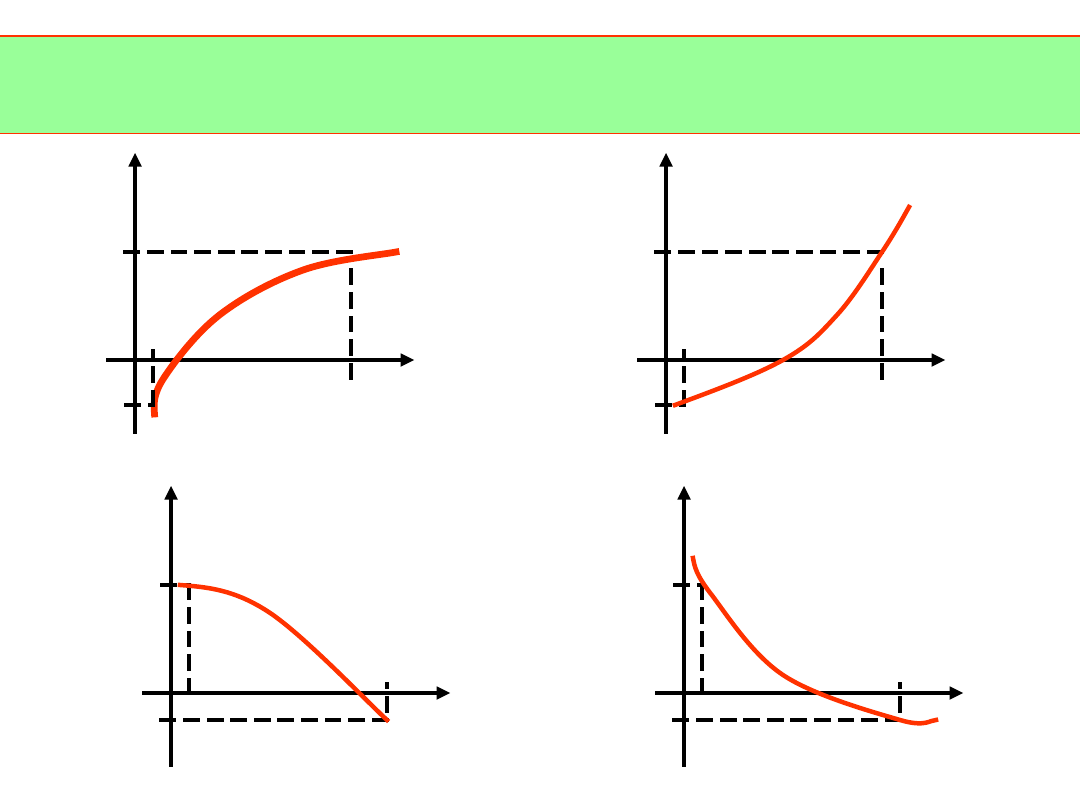
Funkcja spełniająca powyższe założenia musi mieć w otoczeniu
miejsca zerowego jeden z następujących przebiegów:
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
f(a)
a
b
f(b)
x
y
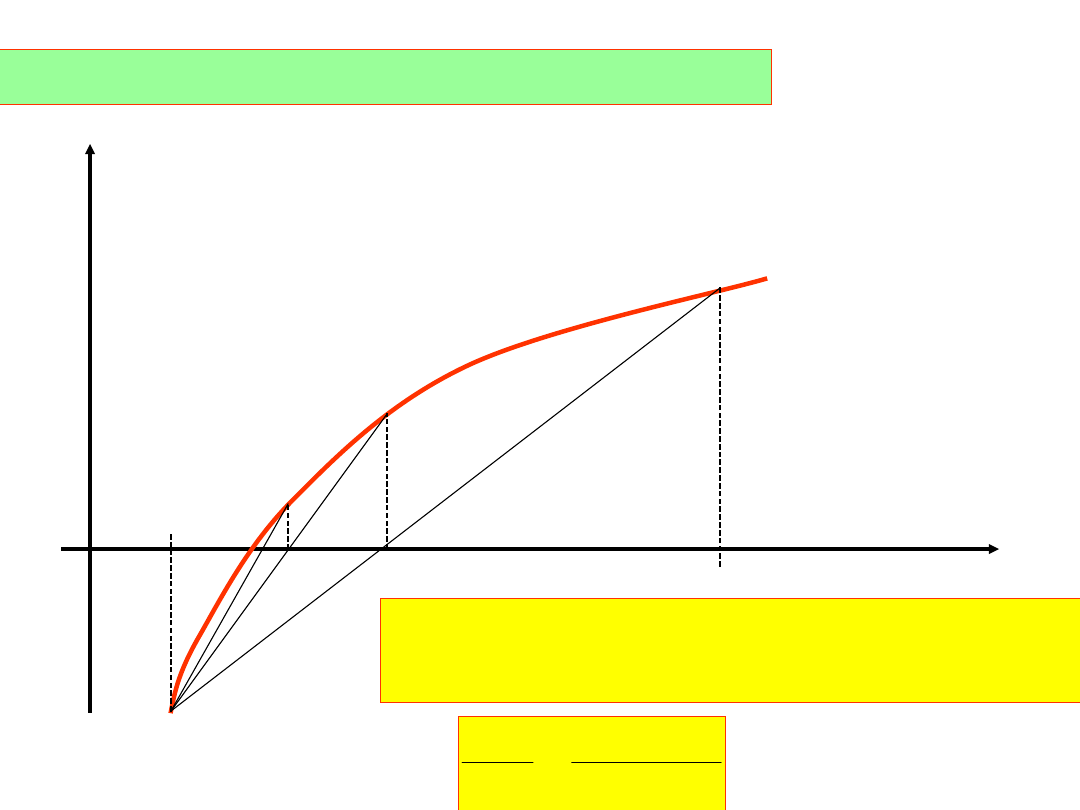
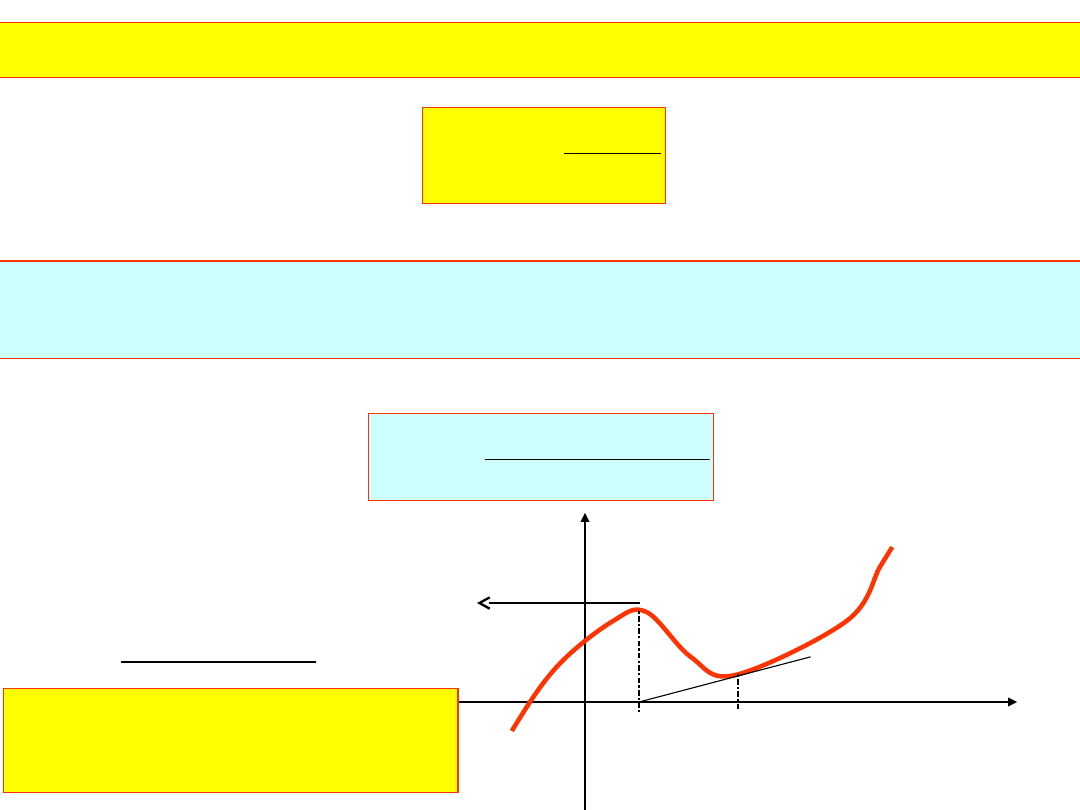
Przebieg obliczeń metodą regula falsi:
x
y
a
b
f(a)
f(b)
x
1
f(x
1
)
x
2
analitycznie: ustalamy koniec z
warunku f(x
1
)f(a)<0 lub f(x
1
)f(b)<0
Prowadzimy prostą:
a
f
b
f
a
f
x
f
a
b
a
x
a
f
b
f
a
f
x
f
a
b
a
x
ale f(x
1
)=0 stąd
a
f
b
f
a
f
a
b
a
x
1
lub
a
f
a
f
b
f
a
b
a
x
1
Dla n-tej iteracji mamy b=x
n-1
i podstawiając mamy:
a
f
a
f
x
f
a
x
a
x
1
n
1
n
n

Ocena błędu dla dostatecznie małego przedziału [x
n-1
,x
n
]
można przyjąć jako:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
Metoda regula falsi jest zbieżna dowolnej funkcji ciągłej
na przedziale [a,b].
Poszukiwanie pierwiastka zostaje zakończone jeżeli:
1
n
n
x
x
Metoda jest wolno zbieżna.
Przykład:
0
1
x
4
x
3
x
-1 0 -0.2
-
0.23664
12
-
0.244233
54
f(x
)
-4 1 0.19
2
0.04013
427
0.008497
292
2
.
0
x
4
4
1
1
0
1
x
a
f
a
f
b
f
a
b
a
x
1
1
1
Ponieważ f(-1)=-4, a f(x
1
)=0.192,
więc stałym punktem będzie x=-1
x
-
0.245835
632
-
0.246174
92
-
0.246246
829
f(x
)
0.001800
359
0.000381
603
0.000080
891
x
-
0.2462620
72
f(x
)
0.0000171
47
w metodzie bisekcji potrzebowaliśmy
14 kroków
ocena błędu:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
d
ocena błędu:
6
d
10
1
.
4
246262072
.
0
x
Metoda siecznych
Przepis:
)
x
(
f
)
x
(
f
)
x
(
f
x
x
x
x
n
1
n
n
1
n
n
n
1
n
Przykład:
0
1
x
4
x
3
x
-1 0 -0.2
-
0.2475247
52
-
0.2462564
39
f(x) -4 1
0.19
2
-
0.0052644
81
0.0000407
03
w regula falsi potrzeba 8 kroków
x
-
0.246266
17
f(x
)
0.907E-8
w 6-tym kroku
Koniecznie trzeba obliczać f(x
n
) i jeżeli zaczyna narastać
należy zawęzić przedział i powtórzyć obliczenia.
Niebezpieczeństwo znalezienia fałszywego pierwiastka.
Metoda szybsza niż reguła falsi.
a
b
x
1
Pierwsza iteracja musi startować
z punktów spełniających warunek:
f(a)f(b)<0
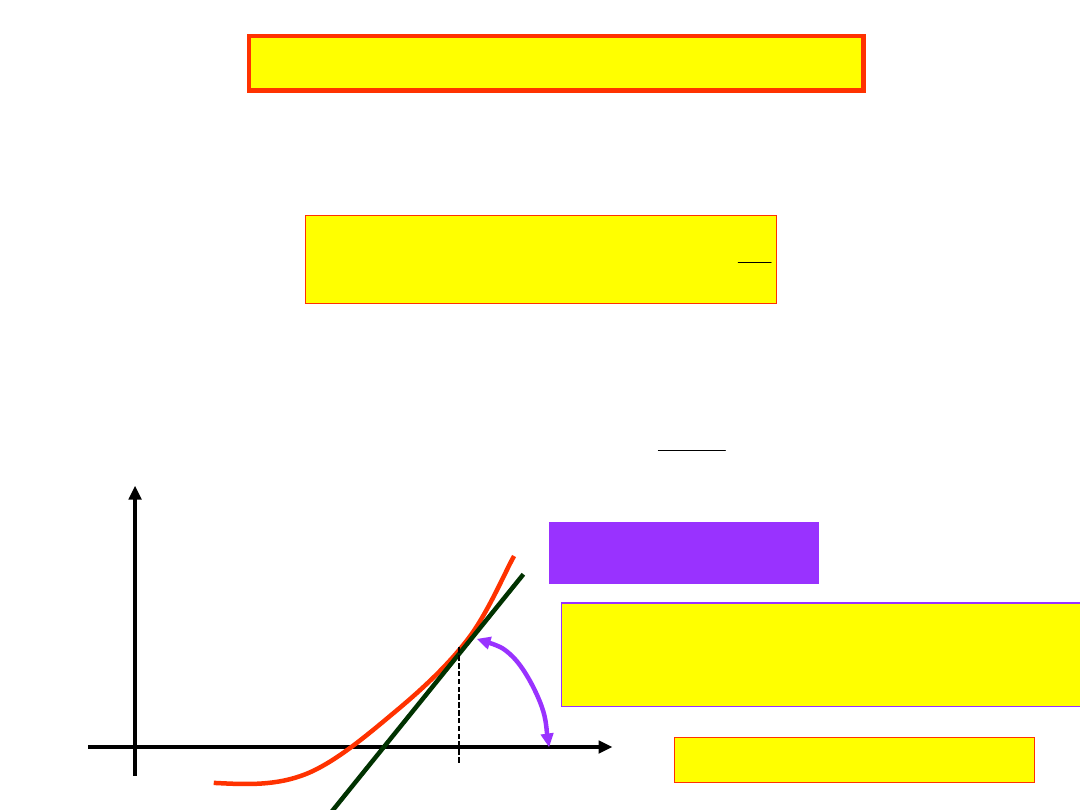
Metoda Newtona - Raphsona
Niech małe w mamy:
2
x
f
x
f
x
f
x
f
2
Pomijając małe drugiego rzędu
2
mamy, że f(x+)=0,
jeżeli
x
f
x
f
Graficznie:
x
y
x
n
n
n
n
x
f
tg
Równanie prostej stycznej
w punkcie x
n
jest:
n
n
n
x
f
x
x
x
f
y
x
n+1
Prosta:
n
n
n
x
f
x
x
x
f
y
przechodzi przez zero, czyli y=0, w punkcie x
n+1
i mamy:
n
n
n
1
n
x
f
x
f
x
x
Przykład:
0
1
x
4
x
3
x 0
-0.25 -
0.246268
657
-
0.2462661
72
f(x
)
1 -
0.0156
25
-
0.000010
39
-0.2E-10
W 3 krokach dokładność osiągana w metodzie siecznych
w 5 krokach
W obliczeniach numerycznych pochodną najczęściej oblicza się
numerycznie:
Metoda Newtona – Raphsona jest zbieżna kwadratowo, tzn.
i
i
2
i
1
i
x
f
2
x
f
h
x
f
h
x
f
x
f
i
i
i
„Pechowe” przypadki:
x
f(x)
x
0
x
1
x
2
rozbieżna
Zmniejszyć przedział
[x
d
,x
0
]
x
d

cykl
x
f(x)
x
1
=x
3
=...
x
2
=x
4
=...
x
d
Budując procedurę należy się zabezpieczyć przed taką możliwością.
Wystartować z punktu x
1
znajdującego się bliżej x
d
Pierwiastki wielokrotne:
0
x
f
i
0
x
f
d
d
Przy pierwiastkach wielokrotnych badać funkcję:
)
x
(
f
)
x
(
f
)
x
(
g
Pierwiastki zespolone
Przykład
0
4
x
x
2
3
5
3
1
1
3
5
200
140
80
20
40
100
f x
( )
0
x
Szukamy zespolonych pierwiastków metodą Newtona - Raphsona
n
2
n
2
n
3
n
n
1
n
x
2
x
3
4
x
x
x
x
Jako punkt startowy musimy wybrać liczbę zespoloną:
x
0
=i
gdzie
1
i
i
2309
.
1
8462
.
0
x
e
6056
.
3
e
1623
.
3
i
i
2
3
i
3
i
x
1
69
.
213
i
43
.
198
i
1
x
2
=-0.50605+1.21289i
x
3
=-0.49471+1.32934i
x
4
=-0.50119+1.32409i
x
5
=-0.500059+1.322855i
x
6
=-0.5+1.32275i
błąd=-0.00083198+0.00043738i
x
d
=-0.5+1.322288i

Układy równań nieliniowych
Dany jest układ równań:
0
x
,...,
x
,
x
f
..........
..........
..........
0
x
,...,
x
,
x
f
0
x
,...,
x
,
x
f
n
2
1
n
n
2
1
2
n
2
1
1
Dla skrócenia zapisu wprowadzamy oznaczenia:
X
f
x
,...,
x
,
x
f
k
n
2
1
k
oraz
)
x
,...,
x
,
x
(
f
.
.
)
x
,...,
x
,
x
(
f
)
x
,...,
x
,
x
(
f
)
X
(
F
n
2
1
n
n
2
1
2
n
2
1
1
i równanie zapisujemy krótko:
0
X
F
Metoda iteracji prostej
Równanie:
0
X
F
zapisujemy w postaci:
X
G
X
i procedura iteracji prostej ma postać:
1
n
n
X
G
X
Stosowana szczególnie w przypadkach jeżeli mamy dobre
przybliżenie początkowe. Sytuacja taka występuje np. w
przypadku małej zmiany parametrów równania.

Przykład:
1
y
2
x
1
y
x
2
2
2
2
którego rozwiązaniem jest: x
1
=1; y
1
=0 oraz x
2
=-1; y
2
=0
Szukamy rozwiązania układu po małej zmianie parametrów:
1
y
01
.
2
x
95
.
0
y
x
2
2
2
2
mamy schemat iteracyjny:
01
.
2
x
1
y
y
95
.
0
x
2
1
n
n
2
1
n
n
Jako startowy punkt wybieramy: x
0
=1; y
0
=0 i mamy:
n 0
1
2
3
4
x
n
1 0.974
68
0.9746
8
0.961
834
0.9618
34
y
n
0
0
0.1577
18
0.157
718
0.1930
06
n
5
6
7
8
x
n
0.955
379
0.9553
79
0.9521
509
0.95215
1
y
n
0.193
006
0.2083
47
0.2083
47
0.21557
36
n
9
10
11
12
x
n
0.9505
409
0.95054
1
0.9497
389
0.94973
9
y
n
0.2155
734
0.21907
994
0.2190
797
0.22080
36

Z przedstawionych obliczeń widać, że metoda jest wolno
zbieżna i dlatego stosowana tylko w przypadkach, gdy
znamy bardzo dobrze zerowe przybliżenie. Zastosowanie
w równaniach różniczkowych.
Metoda Newtona - Raphsona
Rozwijamy funkcję f
k
(X) w szereg Taylora w otoczeniu
punktu X
i
:

0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
...
..........
..........
..........
..........
..........
..........
..........
..........
0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
.........
..........
..........
..........
..........
..........
..........
..........
0
)
x
x
(
x
f
...
)
x
x
(
x
f
)
X
(
f
i
,
n
n
X
X
n
n
i
,
1
1
X
X
1
n
i
n
i
,
n
n
X
X
n
k
i
,
1
1
X
X
1
k
i
k
i
,
n
n
X
X
n
1
i
,
1
1
X
X
1
1
i
1
i
i
i
i
i
i
Dla uproszczenia zapisu wprowadzamy macierz Jacobiego
zdefiniowaną następująco:

i
X
X
n
n
2
n
1
n
n
2
2
2
1
2
n
1
2
1
1
1
i
x
f
.
.
x
f
x
f
.
.
.
.
.
.
.
.
.
.
x
f
.
.
x
f
x
f
x
f
.
.
x
f
x
f
)
X
(
J
i w postaci macierzowej możemy krótko zapisać układ równań:
0
X
X
J
X
F
i
i
i
gdzie oznaczono:
i
1
i
i
X
X
X
i rozwiązując symbolicznie mamy:
i
i
1
i
1
i
X
F
X
J
X
X

Przykład
F x y
f1 x y
f2 x y
i równanie: F(x,y)=0
f1 x y
expx y
sin5 x
cosy
f2 x y
cosy
sinx
ln x y
Obliczamy pochodne:
p1xx y
expx y
sin5 x
5 expx y
cos5 x
p1yx y
expx y
sin5 x
cosy
p2xx y
cosx
cosy
1
x y
J x y
p1xx y
p2xx y
p1yx y
p2yx y
Jakobian układu równań jest:
p2yx y
sinx
siny
1
x y
x
0
0.1
Przyjmujemy zerowe przybliżenie:
y
0
0
i liczymy z równania:
x
n 1
y
n 1
x
n
y
n
J x
n
y
n
1
F x
n
y
n
dla n=0,1,...,N

x
0
0
1
2
3
4
5
6
7
8
9
10
11
0.1
-0.141899943936
-0.029185837303
-0.044892694856
-0.036465491584
-0.035920867262
-0.035912407482
-0.035912710982
-0.035912699597
-0.035912700025
-0.035912700009
-0.035912700009
y
0
0
1
2
3
4
5
6
7
8
9
10
11
0
0.486244256751
0.743862659111
1.019360058647
1.053479318574
1.053828713899
1.053816932667
1.053817374634
1.053817358052
1.053817358674
1.053817358651
1.053817358652
Błąd:
n
F x
n
y
n
1
0.03514978332
1.191145539803
n
F x
n
y
n
n
F x
n
y
n
10
8.754941216438
10
12
0
n
F x
n
y
n
5
1.226398353761
10
4
5.476867793418
10
7
Obliczenia pierwiastka z pochodną liczoną numerycznie
p1xx y
h
f1 x h
y
f1 x y
h
p1yx y
h
f1 x y h
f1 x y
h
p2xx y
h
f2 x h
y
f2 x y
h
p2yx y
h
f2 x y h
f2 x y
h
Przybliżona macierz Jacobiego:

J x y
h
p1xx y
h
p2xx y
h
p1yx y
h
p2yx y
h
Przyjmując dla kroku h:h
0.01
mamy wyniki:

x
0
0
1
2
3
4
5
6
7
8
9
10
11
0.1
-0.245620510404
0.129212408651
-0.139883972512
-0.026332867153
-0.035690080158
-0.035909711413
-0.03591266157
-0.035912699505
-0.035912700003
-0.035912700009
-0.035912700009

y
0
0
1
2
3
4
5
6
7
8
9
10
11
0
0.612829446354
0.575992105371
1.206911594234
1.055296091227
1.053366833955
1.053814123293
1.053817303719
1.053817357993
1.053817358643
1.053817358651
1.053817358652

Błąd:
1
0.541728756272
1.200733537706
n
F x
n
y
n
1
0.03514978332
1.191145539803
Jakobian dokładnie
Jakobian numerycznie
n
F x
n
y
n
5
1.226398353761
10
4
5.476867793418
10
7
5
3.53469633664
10
3
1.279336142867
10
4
n
F x
n
y
n
10
8.754941216438
10
12
0
10
1.281363903871
10
12
1.06512021425
10
14

h
0.0001
Zmiana kroku różniczkowania
x
0
0
1
2
3
4
5
6
7
8
9
10
11
0.1
-0.243293030521
0.133173725428
-0.147314343999
-0.019012944127
-0.035661321744
-0.035912657661
-0.035912700004
-0.035912700009
-0.035912700009
-0.035912700009
-0.035912700009

y
0
0
1
2
3
4
5
6
7
8
9
10
11
0
0.597853320049
0.554664046616
1.208957700299
1.048065432775
1.05347013074
1.053817373468
1.053817358641
1.053817358652
1.053817358652
1.053817358652
1.053817358652
h=0.01
h=0.0001
1
0.510450698944
1.235991747404
1
0.541728756272
1.200733537706
5
3.771637969603
10
3
1.923653534576
10
5
5
3.53469633664
10
3
1.279336142867
10
4
10
0
0
10
1.281363903871
10
12
1.06512021425
10
14
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
Wyszukiwarka
Podobne podstrony:
Wyklad mn 2
Wyklad mn 9
Wyklad mn no 8 piątek
Wyklad mn 16
Wyklad mn 9
Wyklad mn 3
Wyklad mn no 7 piątek
Wyklad mn 6
Wyklad mn no 4 piątek
Wyklad mn 12
Wyklad mn 10
Wyklad mn 6
Wyklad mn 15
Wyklad mn no 5 piątek
Wyklad mn 8
Wyklad mn no 6 piątek
Wyklad mn 8
Wyklad mn no 3 piątek
Wyklad mn 4
więcej podobnych podstron