

Rozkład LU. Metoda Croute’a.
Rozkład na macierze trójkątne
Dana jest macierz A i przedstawiamy ją w postaci:
A=LU
gdzie macierz L jest macierzą dolną trójkątną:
55
54
53
52
51
44
43
42
41
33
32
31
22
21
11
l
l
l
l
l
0
l
l
l
l
0
0
l
l
l
0
0
0
l
l
0
0
0
0
l
L
lub ogólnie:
i
j
dla
obliczane
i
j
dla
0
u
u
ij
ij
U
Macierz U górna trójkątna:
55
45
44
35
34
33
25
24
23
22
15
14
13
12
11
u
0
0
0
0
u
u
0
0
0
u
u
u
0
0
u
u
u
u
0
u
u
u
u
u
U
lub ogólnie:
j
i
dla
obliczane
j
i
dla
1
j
i
dla
0
l
l
ij
ij
L
Jeżeli
A=LU
, to dla układu równań
AX=b
mamy:
b
LY
Y
UX
b
LUX
Rozwiązanie układu LY=b z dolną macierzą trójkątną jest łatwe:
1
i
1
j
j
ij
i
ii
i
11
1
1
y
l
b
l
1
y
l
b
y
i=2,3,...,N
i rozwiązanie równania UX=Y z górną macierzą trójkątną
jest łatwe:
N
1
i
j
j
ij
i
ii
i
NN
N
N
x
u
y
u
1
x
u
y
x
i=N-1,N-2,...,1
Duża zaleta:
Znając rozkład LU możemy go wykorzystać wielokrotnie dla
różnych prawych stron.
Obliczanie wyrazów macierzy L i U
NN
kN
kk
N
2
k
2
22
N
1
k
1
12
11
1
N
,
N
Nj
1
N
1
k
,
k
1
k
21
u
0
0
0
0
0
.
.
.
.
.
.
u
.
u
.
0
0
.
.
.
.
.
.
u
.
u
.
u
0
u
.
u
.
u
u
1
l
.
l
.
l
.
.
.
.
.
.
0
.
1
l
.
l
.
.
.
.
.
.
0
0
0
0
1
l
0
0
0
0
0
1
w wyniku mnożenia obu macierzy mamy macierz B=[b
ij
]
Zaczynamy kolejno:
pierwszy wiersz macierzy L razy k-ta kolumna macierzy U:
k
1
k
1
u
b
k-ty wiersz macierzy L razy pierwszy wiersz macierzy U:
1
k
11
1
k
b
u
l
NN
kN
kk
N
2
k
2
22
N
1
k
1
12
11
1
N
,
N
Nj
1
N
1
k
,
k
1
k
21
u
0
0
0
0
0
.
.
.
.
.
.
u
.
u
.
0
0
.
.
.
.
.
.
u
.
u
.
u
0
u
.
u
.
u
u
1
l
.
l
.
l
.
.
.
.
.
.
0
.
1
l
.
l
.
.
.
.
.
.
0
0
0
0
1
l
0
0
0
0
0
1
k-ty wiersz macierzy L razy j-ta (jk) kolumna macierzy U:
kj
kj
1
k
i
1
i
ij
ki
b
u
u
l
j-ty wiersz (j>k) macierzy L razy k-ta kolumna macierzy U:
jk
k
i
1
i
ik
ji
b
u
l
ponieważ musi zachodzić B=A, czyli b
ij
=a
ij
dla (i,j=1,2,...,N)
stąd otrzymujemy kolejno:
Pierwszy wiersz macierzy U:
k
1
k
1
a
u
pierwsza kolumna macierzy L:
11
1
k
1
k
u
a
l
k-ty wiersz macierzy U:
1
k
i
1
i
ij
ki
kj
kj
u
l
a
u
dla j=k,k+1,...,N
k-ta kolumna macierz L:
1
k
i
1
i
ik
ji
jk
kk
jk
u
l
a
u
1
l
dla j=k+1,k+2,...,N
Przykład:
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
Zgodnie z:
k
1
k
1
a
u pierwszy wiersz macierzy U:
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
.
.
.
.
0
0
0
2
1
4
U
Pierwsza kolumna macierzy L zgodnie z
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
11
1
k
1
k
u
a
l
gdzie u
11
=4
1
.
.
.
0
0
1
.
.
0
0
0
1
.
0
0
0
0
1
5
.
0
0
0
0
0
1
L

10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
drugi wiersz macierzy U zgodnie ze wzorem:
1
i
1
i
ij
i
2
j
2
j
2
u
l
a
u
j=2,3,4,5
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
.
0
0
1
.
.
0
0
0
1
.
0
0
0
0
1
5
.
0
0
0
0
0
1
L
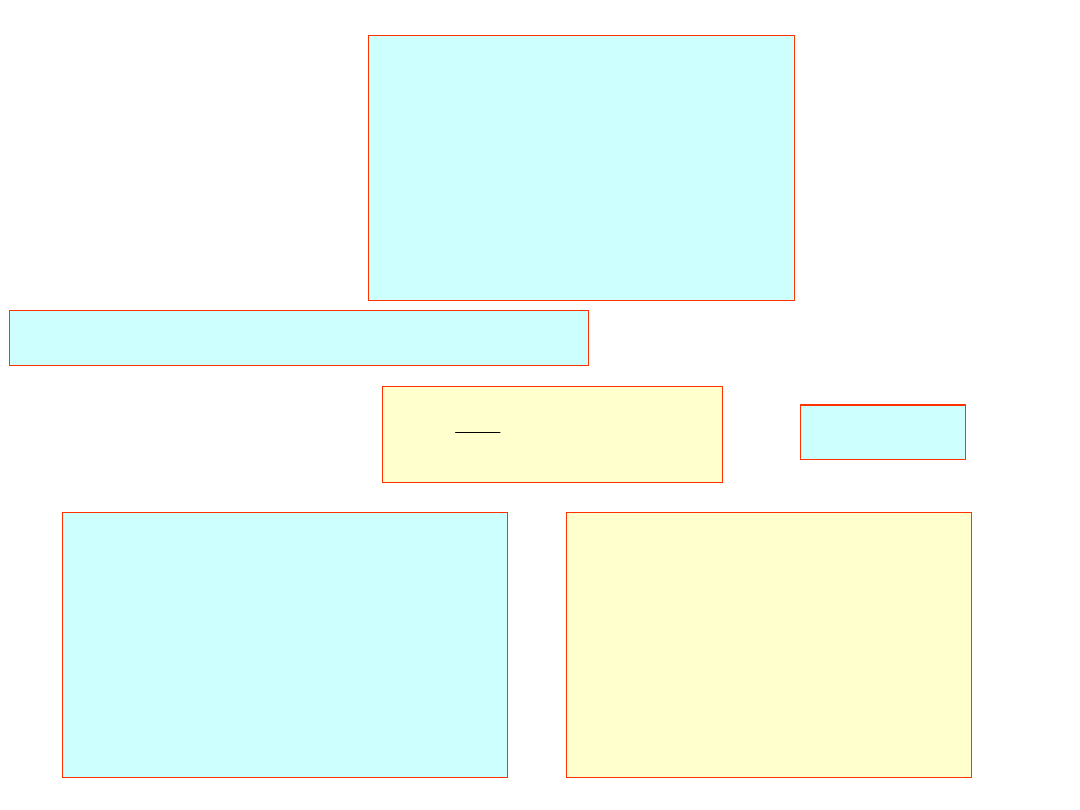
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
j=3,4,5
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
0
0
0
1
.
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
1
i
1
i
2
i
ji
2
j
22
2
j
u
l
a
u
1
l
Druga kolumna macierzy L:
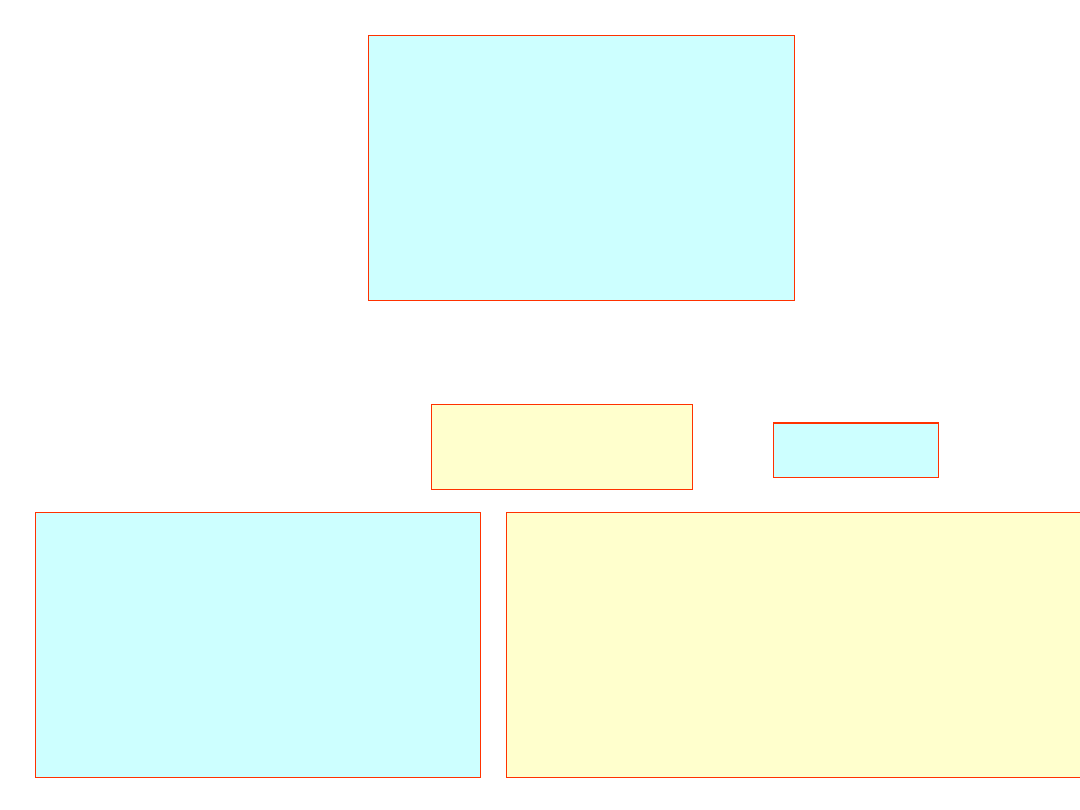
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
trzeci wiersz macierzy U zgodnie ze wzorem:
2
i
1
i
ij
i
3
j
3
j
3
u
l
a
u
j=3,4,5
.
0
0
0
0
.
.
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
0
0
0
1
.
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
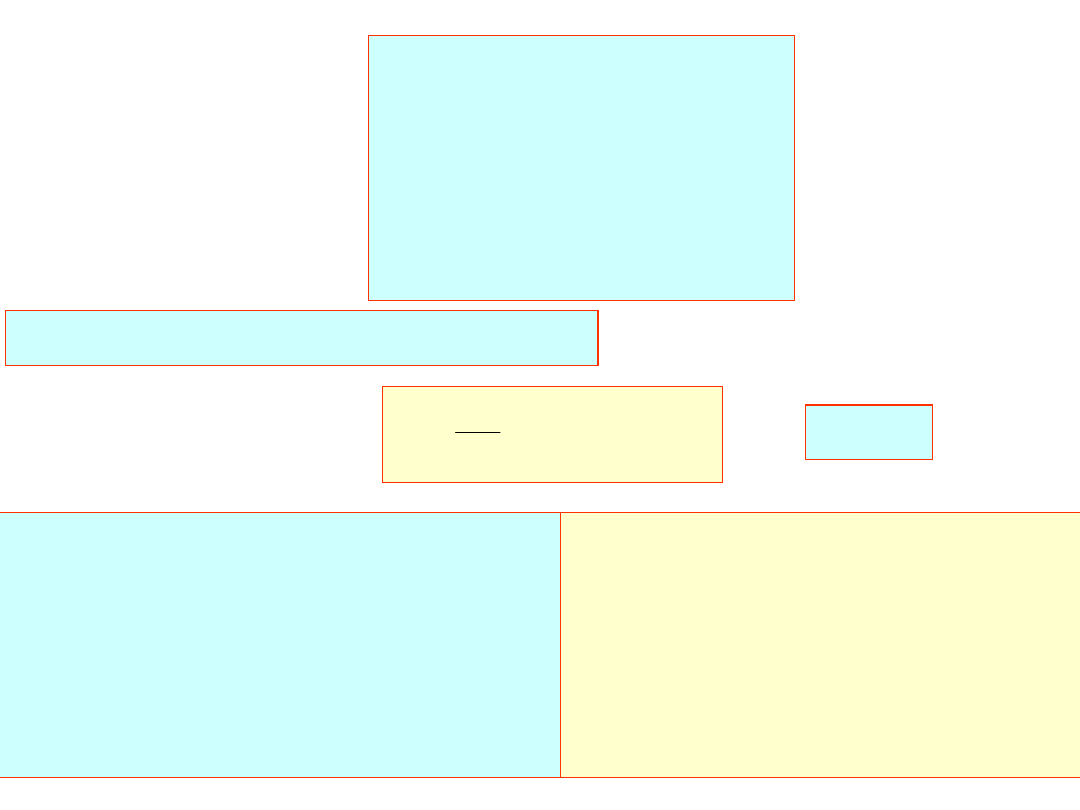
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
.
0
0
0
0
.
.
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
j=4,5
2
i
1
i
3
i
ji
3
j
33
3
j
u
l
a
u
1
l
trzecia kolumna macierzy L:
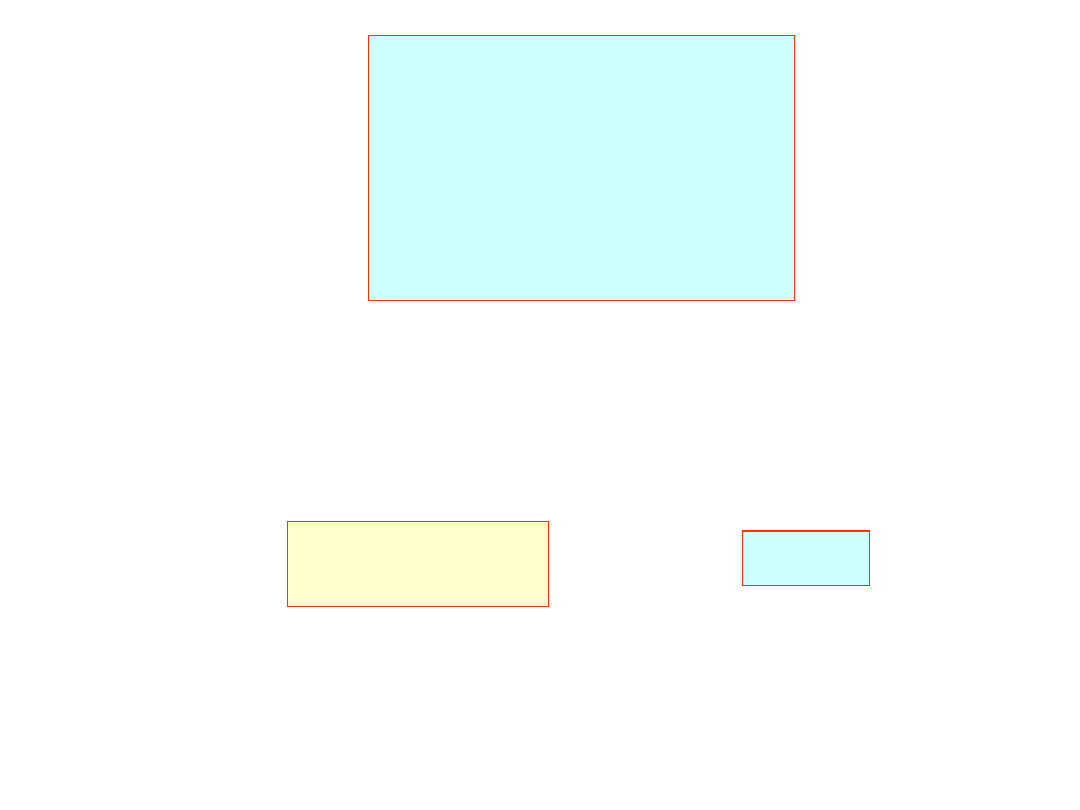
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
czwarty wiersz macierzy U zgodnie ze wzorem:
3
i
1
i
ij
i
4
j
4
j
4
u
l
a
u
j=4,5
1
.
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
.
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
j=5
3
i
1
i
4
i
ji
4
j
44
4
j
u
l
a
u
1
l
czwarta kolumna macierzy L:

1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
.
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
i ostatecznie u
55
z zależności:
4
i
1
i
5
i
i
5
55
55
u
l
a
u

1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U

Dla sprawdzenia czy nie popełniliśmy błędu obliczamy: B=LU
1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
B
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
B
Mając macierz A=LU możemy rozwiązać równanie LUX=b
dla dowolnego wektora prawej strony.
Znając rozkład LU macierzy łatwo obliczyć wyznacznik
główny |A| macierzy A=LU. Mamy:
U
L
LU
A
ale
1
L
a
N
1
i
ii
u
U
i ostatecznie:
N
i
1
i
ii
u
A
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
3480
A

Obliczanie macierzy odwrotnej
Dana macierz:
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
Macierz odwrotna : AA
-1
=1
i A
-1
A=1
Oznaczając: X=A
-1
mamy N układów N równań liniowych:
AX=1
Metoda Gaussa - Jordana

Dla określenia macierzy odwrotnej X mamy równanie:
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
55
54
53
52
51
45
44
43
42
41
35
34
33
32
31
25
24
23
22
21
15
14
13
12
11
Zapisujemy w postaci tablicy uzupełnionej:
1
0
0
0
0
10
1
0
0
0
0
1
0
0
0
4
8
4
0
0
0
0
1
0
0
1
8
2
1
0
0
0
0
1
0
0
3
1
5
2
0
0
0
0
1
0
0
2
1
4
i procedura eliminacji Gaussa – Jordana:
1
0
0
0
0
10
1
0
0
0
0
1
0
0
0
4
8
4
0
0
0
0
1
0
0
1
8
2
1
0
0
0
0
1
5
.
0
0
3
2
5
.
5
0
0
0
0
0
25
.
0
0
0
5
.
0
25
.
0
1
1
0
0
0
0
10
1
0
0
0
0
1
0
0
0
4
8
4
0
0
0
0
1
0
0
1
8
2
1
0
0
0
0
1
5
.
0
0
3
2
5
.
5
0
0
0
0
0
25
.
0
0
0
5
.
0
25
.
0
1
1
0
0
0
0
10
1
0
0
0
0
1
0
0
0
4
8
4
0
0
0
0
1
18182
.
0
090909
.
0
1
5454
.
8
3636
.
2
0
0
0
0
0
18182
.
0
090909
.
0
0
54545
.
0
36364
.
0
1
0
0
0
0
045455
.
0
22727
.
0
0
13636
.
0
40909
.
0
0
1
Ponieważ pierwsze dwie kolumny już nie ulegną zmianie
dlatego ze względu na oszczędność miejsca zostaną usunięte

1
0
0
0
0
10
1
0
0
1
0
0
0
4
8
4
0
0
1
18182
.
0
090909
.
0
1
5454
.
8
3636
.
2
0
0
0
18182
.
0
090909
.
0
0
54545
.
0
36364
.
0
0
0
0
045455
.
0
22727
.
0
0
13636
.
0
40909
.
0
1
0
0
0
0
10
1
0
0
1
6923
.
1
3077
.
0
15385
.
0
3077
.
2
4616
.
6
0
0
0
42308
.
0
076925
.
0
038462
.
0
42308
.
0
6154
.
3
1
0
0
15385
.
0
15385
.
0
076923
.
0
15385
.
0
76925
.
0
0
0
0
17308
.
0
076924
.
0
21154
.
0
17308
.
0
6154
.
1
0
Pomijamy pierwszą kolumnę

1
15476
.
0
2619
.
0
04762
.
0
02381
.
0
357
.
10
0
0
15476
.
0
2619
.
0
04762
.
0
02381
.
0
35714
.
0
1
0
55952
.
0
52379
.
0
09524
.
0
047621
.
0
7143
.
1
0
0
11905
.
0
47617
.
0
19048
.
0
095239
.
0
42858
.
0
0
0
25
.
0
24999
.
0
000001348
.
0
25
.
0
75
.
0
0
Pomijamy pierwszą kolumnę:
1
0
0
0
0
10
1
0
1
6923
.
1
3077
.
0
15385
.
0
3077
.
2
4616
.
6
0
0
42308
.
0
076925
.
0
038462
.
0
42308
.
0
6154
.
3
0
0
15385
.
0
15385
.
0
076923
.
0
15385
.
0
76925
.
0
0
0
17308
.
0
076924
.
0
21154
.
0
17308
.
0
6154
.
1

096553
.
0
014943
.
0
025287
.
0
0045979
.
0
0022989
.
0
1
034483
.
0
14942
.
0
25287
.
0
045978
.
0
022989
.
0
0
16552
.
0
5339
.
0
48044
.
0
087358
.
0
04368
.
0
0
041381
.
0
11265
.
0
036779
.
0
18851
.
0
094254
.
0
0
072415
.
0
23879
.
0
23102
.
0
0034471
.
0
24828
.
0
0
i otrzymujemy macierz odwrotną:
1
15476
.
0
2619
.
0
04762
.
0
02381
.
0
357
.
10
0
15476
.
0
2619
.
0
04762
.
0
02381
.
0
35714
.
0
0
55952
.
0
52379
.
0
09524
.
0
047621
.
0
7143
.
1
0
11905
.
0
47617
.
0
19048
.
0
095239
.
0
42858
.
0
0
25
.
0
24999
.
0
000001348
.
0
25
.
0
75
.
0

Sprawdzamy poprawność obliczonej macierzy odwrotnej
obliczając AA
-1
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
096553
.
0
014943
.
0
025287
.
0
0045979
.
0
0022989
.
0
034483
.
0
14942
.
0
25287
.
0
045978
.
0
022989
.
0
16552
.
0
5339
.
0
48044
.
0
087358
.
0
04368
.
0
041381
.
0
11265
.
0
036779
.
0
18851
.
0
094254
.
0
072415
.
0
23879
.
0
23102
.
0
0034471
.
0
24828
.
0

1
AX
3
.
1
1
0
1
.
0
0
4
.
0
2
.
1
2
.
5
04
.
0
36
.
0
4
.
0
3
.
3
4
.
1
01
.
0
09
.
0
4
.
0
3
5
.
2
02
.
2
3
.
0
1
.
0
1
1
.
2
56
.
0
4
.
1
10
5
Macierz odwrotną można również obliczyć korzystając z
rozkładu LU
Niech A=LU
mamy rozwiązać N układów N równań algebraicznych:
LUX=1
oznaczając:
Y=UX
mamy:
LY=1
Postępowanie jest proste:
Krok pierwszy – rozwiązujemy N - krotnie układ N równań
z dolną macierzą trójkątną L wyznaczając Y:
LY=1
Krok drugi – rozwiązujemy N – krotnie układ N równań
z górną macierzą trójkątną U wyznaczając macierz odwrotną
A
-1
=X:
UX=Y

Dana macierz:
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
i
1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U

LY=1
Równanie
jest
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
55
54
53
52
51
45
44
43
42
41
35
34
33
32
31
25
24
23
22
21
15
14
13
12
11

Macierz odwrotna do dolnej trójkątnej też jest macierzą dolną
trójkątną i w przypadku macierzy L główna przekątna
to 1 czyli
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
1
y
y
y
y
0
1
y
y
y
0
0
1
y
y
0
0
0
1
y
0
0
0
0
1
1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
54
53
52
51
43
42
41
32
31
21

Pozostałe wyrazy macierzy Y wyznaczamy rozpoczynając
od pierwszej kolumny i kolejno następne:
1
15476
.
0
2619
.
0
047619
.
0
023809
.
0
0
1
6923
.
1
3077
.
0
15385
.
0
0
0
1
18182
.
0
09091
.
0
0
0
0
1
5
.
0
0
0
0
0
1
1
L
Y
Pozostaje do rozwiązania równanie:
UX=Y
55
54
53
52
51
45
44
43
42
41
35
34
33
32
31
25
24
23
22
21
15
14
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
1
15476
.
0
2619
.
0
047619
.
0
023809
.
0
0
1
6923
.
1
3077
.
0
15385
.
0
0
0
1
18182
.
0
09091
.
0
0
0
0
1
5
.
0
0
0
0
0
1
Startujemy kolejno od pierwszej kolumny kolejno do piątej,
a niewiadome w kolumnach wyznaczamy od ostatniej tj. x
Nk
096552
.
0
014942
.
0
025287
.
0
0045977
.
0
0022988
.
0
034483
.
0
14942
.
0
25287
.
0
045978
.
022989
.
0
16552
.
0
53389
.
0
48045
.
0
087359
.
0
043679
.
0
04138
.
0
11264
.
0
03678
.
0
18851
.
0
094253
.
0
072415
.
0
23878
.
0
23103
.
0
003448
.
0
24828
.
0
1
X
A
Dla porównania macierz odwrotna obliczona
metodą Gaussa - Jordana
096553
.
0
014943
.
0
025287
.
0
0045979
.
0
0022989
.
0
034483
.
0
14942
.
0
25287
.
0
045978
.
0
022989
.
0
16552
.
0
5339
.
0
48044
.
0
087358
.
0
04368
.
0
041381
.
0
11265
.
0
036779
.
0
18851
.
0
094254
.
0
072415
.
0
23879
.
0
23102
.
0
0034471
.
0
24828
.
0

Metody iteracyjne
Metoda iteracji prostej:
b
Ax
Macierz A przedstawiamy w postaci:
G
L
D
A
gdzie jeżeli
NN
Nk
2
N
1
N
kN
kk
2
k
1
k
N
2
k
2
22
21
N
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
to

0
.
a
.
a
a
.
.
.
.
.
.
0
.
0
.
a
a
.
.
.
.
.
.
0
.
0
.
0
a
0
.
0
.
0
0
D
Nk
2
N
1
N
2
k
1
k
21
NN
kk
22
11
a
.
0
.
0
0
.
.
.
.
.
.
0
.
a
.
0
0
.
.
.
.
.
.
0
.
0
.
a
0
0
.
0
.
0
a
L
0
.
0
.
0
0
.
.
.
.
.
.
a
.
0
.
0
0
.
.
.
.
.
.
a
.
a
.
0
0
a
.
a
.
a
0
G
kN
N
2
k
2
N
1
k
1
12
i równanie:
b
Ax
piszemy:
ponieważ
G
L
D
A
b
Gx
Lx
Dx
Ax
lub
x
G
D
b
Lx
i mamy:
x
G
D
L
b
L
x
1
1
Otrzymujemy algorytm:
n
1
1
1
n
x
G
D
L
b
L
x
Warunek zbieżności
1
G
D
L
1
Przykład:
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1
0
1
2
0
0
0
0
2
.
0
0
0
0
1
0
0
0
0
D
4
0
0
0
0
10
0
0
0
0
5
0
0
0
0
4
L
0
0
0
0
1
0
0
0
2
0
0
0
0
2
.
0
1
0
G
25
.
0
0
0
0
0
1
.
0
0
0
0
0
2
.
0
0
0
0
0
25
.
0
L
1

podstawiając
n
1
1
1
n
x
G
D
L
b
L
x
25
.
1
1
0
5
.
7
b
L
1
0
1
2
0
1
0
0
2
.
0
2
0
0
1
0
2
.
0
1
0
25
.
0
0
0
0
0
1
.
0
0
0
0
0
2
.
0
0
0
0
0
25
.
0
G
D
L
1
0
25
.
0
5
.
0
0
1
.
0
0
0
02
.
0
4
.
0
0
0
2
.
0
0
05
.
0
25
.
0
0
G
D
L
1
Niech zerowe przybliżenie
0
0
0
0
x
0
dla pierwszego mamy:
25
.
1
1
0
5
.
7
x
1
Podstawiamy do równania:
n
1
1
1
n
x
G
D
L
b
L
x
i znajdujemy
1
725
.
2
45
.
7
x
2
Badamy normę:
475
.
2
25
.
0
175
.
0
2
05
.
0
x
x
1
1
2
024
.
2
x
x
2
1
2
2
x
x
1
2
Po 9-ciu krokach mamy:
x
9
8.112
2.565
0.602
2.383
x
10
8.111
2.576
0.599
2.382
=
X
d
8.1147767
2.5788529
0.5987301
2.3897439
Rozwiązanie dokładne:
Normy:
016
.
0
001
.
0
003
.
0
011
.
0
001
.
0
x
x
1
9
10
01149
.
0
x
x
2
9
10
011
.
0
x
x
9
10
x
19
8.114772
2.578831
0.598735
2.389734
=
X
d
8.1147767
2.5788529
0.5987301
2.3897439
x
20
8.114771
2.578848
0.598731
2.389732
000024
.
0
x
x
1
19
20
00001761
.
0
x
x
2
19
20
000017
.
0
x
x
19
20
Metoda Gaussa - Seidela
Rozkładamy macierz:
G
L
D
A
jak w metodzie iteracji prostej i mamy:
b
Gx
Lx
Dx
Ax
x
G
D
b
Lx
ale „receptę” dla algorytmu piszemy:
n
1
1
n
1
1
1
n
Gx
L
Dx
L
b
L
x
Powtórzmy nasz przykład
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1
Rozkład na macierze:
0
1
2
0
0
0
0
2
.
0
0
0
0
1
0
0
0
0
D
dolna
4
0
0
0
0
10
0
0
0
0
5
0
0
0
0
4
L
diagonalna
0
0
0
0
1
0
0
0
2
0
0
0
0
2
.
0
1
0
G
górna
i mamy:
25
.
0
0
0
0
0
1
.
0
0
0
0
0
2
.
0
0
0
0
0
25
.
0
L
1
i algorytm Gaussa – Seidla będzie:

25
.
1
1
0
5
.
7
b
L
1
0
25
.
0
5
.
0
0
0
0
0
02
.
0
0
0
0
2
.
0
0
0
0
0
D
L
1
0
0
0
0
1
.
0
0
0
0
4
.
0
0
0
0
0
05
.
0
25
.
0
0
G
L
1
i
n
4
n
3
n
2
n
1
1
n
4
1
n
3
1
n
2
1
n
1
1
n
4
1
n
3
1
n
2
1
n
1
X
X
X
X
0
0
0
0
1
.
0
0
0
0
4
.
0
0
0
0
0
05
.
0
25
.
0
0
X
X
X
X
0
25
.
0
5
.
0
0
0
0
0
02
.
0
0
0
0
2
.
0
0
0
0
0
25
.
1
1
0
5
.
7
X
X
X
X
startujemy z zerowego przybliżenia
0
0
0
0
x
0
i z pierwszego równania:
0
3
0
2
1
1
x
05
.
0
x
25
.
0
5
.
7
x
mamy:
5
.
7
x
1
1
i drugie równanie jest:
0
4
1
1
1
2
x
4
.
0
x
2
.
0
x
więc:
5
.
1
x
1
2
Trzecie równanie:
0
4
1
1
1
3
x
1
.
0
x
02
.
0
1
x
i stąd:
85
.
0
x
1
3
czwarte:
1
3
1
2
1
4
x
25
.
0
x
5
.
0
25
.
1
x
czyli:
2875
.
0
x
1
4
w iteracji prostej było:
25
.
1
1
0
5
.
7
x
1

Drugie przybliżenie:
x
2
7.8325
2.2815
0.6646
2.2246
iteracje proste:
1
725
.
2
45
.
7
x
2
dokładne:
=
X
d
8.1147767
2.5788529
0.5987301
2.3897439

Po 10-ciu krokach w metodzie Gaussa – Seidla mamy:
x
10
8.114768
2.578843
0.598732
2.389739
iteracja prosta:
x
10
8.111
2.576
0.599
2.382
dokładne:
=
X
d
8.1147767
2.5788529
0.5987301
2.3897439

Po 20-tu Gauss – Seidel:
iteracja prosta:
x
20
8.114771
2.578848
0.598731
2.389732
=
X
d
8.1147767
2.5788529
0.5987301
2.3897439
dokładne:
x
20
8.11477673
2.57885292
0.59873007
2.38974394
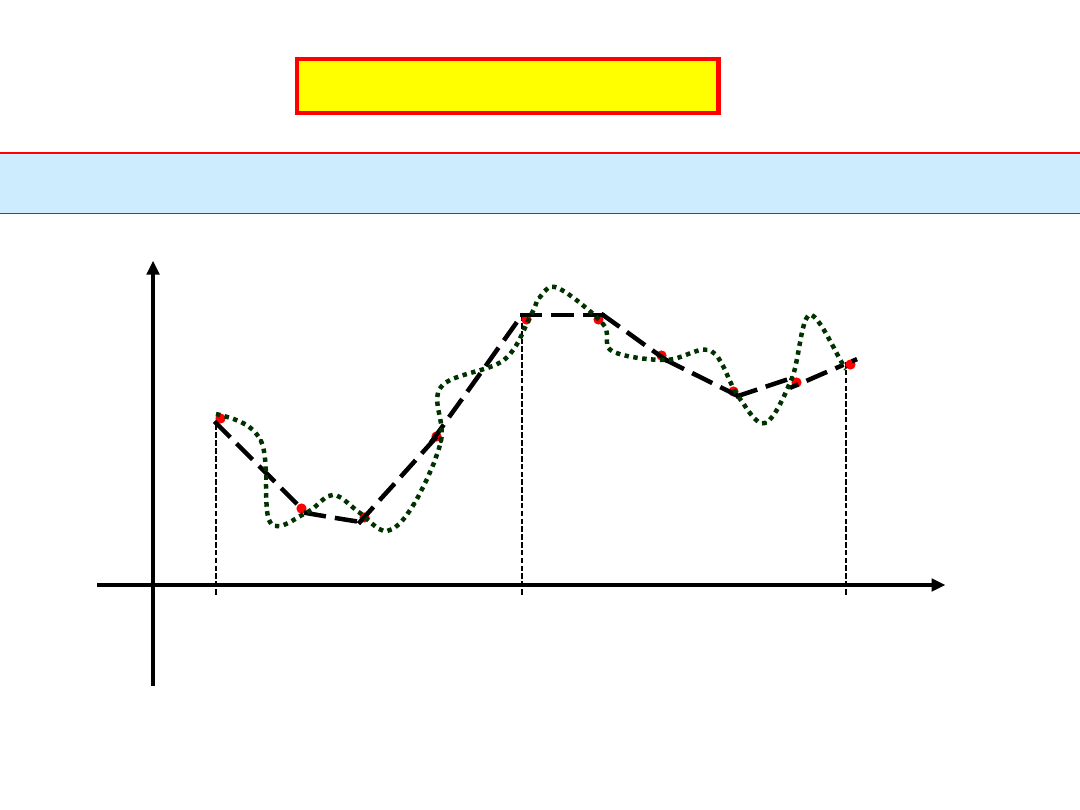
Interpolacja funkcji
Dane wartości funkcji y
n
w punktach x
n
, gdzie n=0,1,2, ....N-1.
x
y
x
0
y
0
x
n
y
n
x
N-1
y
N-1
Interpolacja wielomianowa
Twierdzenie
Istnieje dokładnie jeden wielomian stopnia co najwyżej N (N>=0),
który w punktach x
0
, x
1
,...,x
N-1
przyjmuje wartości y
0
,y
1
,...,y
N-1
.
Wzór interpolacyjny Lagrange'a:
)
x
(
y
....
)
x
(
y
)
x
(
y
)
x
(
W
1
N
1
N
1
1
0
0
n
gdzie
1
-
0,1,...N
=
k
dla
)
x
(
k
jest wielomianem stopnia co najwyżej N.
Z warunku interpolacyjnego:
1
-
N
0,1,....,
=
k
dla
y
)
x
(
W
k
k
N
powyższy układ N równań można najprościej rozwiązać
przyjmując dla wielomianów
k
(x) następujące warunki :
i
k
dla
1
i
k
dla
0
)
x
(
i
k
jako wielomian
k
(x) należy wybrać taki, który ma miejsca
zerowe we wszystkich punktach interpolacji
z wyjątkiem punktu x
k
, w którym funkcja ma wartość 1
,
1
N
1
k
1
k
1
0
x
,...,
x
,
x
,...,
x
,
x
Rozwiązaniem jest wielomian :

Rozwiązaniem jest wielomian:
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
A
)
x
(
1
N
1
k
1
k
1
0
k
z warunku:
otrzymuje się:
1
)
x
(
k
k
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
1
A
1
N
k
k
1
k
k
1
k
1
k
0
k
Wielomian Lagrange'a przyjmuje postać:
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
)
x
x
)...(
x
x
)(
x
x
)...(
x
x
)(
x
x
(
y
)
x
(
W
1
N
k
1
k
k
1
k
k
1
k
0
k
1
N
1
k
1
k
1
0
k
N
Ocena błędu interpolacji:
Ocena błędu interpolacji:
)
x
(
f
sup
M
)
x
x
(
)
x
(
gdzie
)
x
(
)!
1
N
(
M
)
x
(
W
)
x
(
f
)
1
N
(
]
b
,
a
[
x
1
N
N
k
0
k
k
1
N
1
N
1
n
N
Przykład 1.
Zbudować wielomian interpolacyjny dla funkcji exp(x)
w przedziale [1,2] bazując na 5 węzłach interpolacyjnych.
Wybierzmy węzły równomiernie czyli
25
.
0
4
1
2
x
mamy:
x
i
1.0
1.25
1.50
1.75
2.0
y
i
2.718
28
3.490
34
4.481
69
5.754
6
7.389
06
Wielomian Lagrange’a jest:
75
.
1
2
5
.
1
2
25
.
1
2
1
2
75
.
1
x
5
.
1
x
25
.
1
x
1
x
38906
.
7
2
75
.
1
5
.
1
75
.
1
25
.
1
75
.
1
1
75
.
1
2
x
5
.
1
x
25
.
1
x
1
x
7546
.
5
2
5
.
1
75
.
1
5
.
1
25
.
1
5
.
1
1
5
.
1
2
x
75
.
1
x
25
.
1
x
1
x
48169
.
4
2
25
.
1
75
.
1
25
.
1
5
.
1
25
.
1
1
25
.
1
2
x
75
.
1
x
5
.
1
x
1
x
49034
.
3
2
1
75
.
1
1
5
.
1
1
25
.
1
1
2
x
75
.
1
x
5
.
1
x
25
.
1
x
71828
.
2
)
x
(
W
4

lub
75
.
1
x
5
.
1
x
25
.
1
x
1
x
817
.
78
2
x
5
.
1
x
25
.
1
x
1
x
53
.
245
2
x
75
.
1
x
25
.
1
x
1
x
83
.
286
2
x
75
.
1
x
5
.
1
x
1
x
92
.
148
2
x
75
.
1
x
5
.
1
x
25
.
1
x
995
.
28
)
x
(
W
4
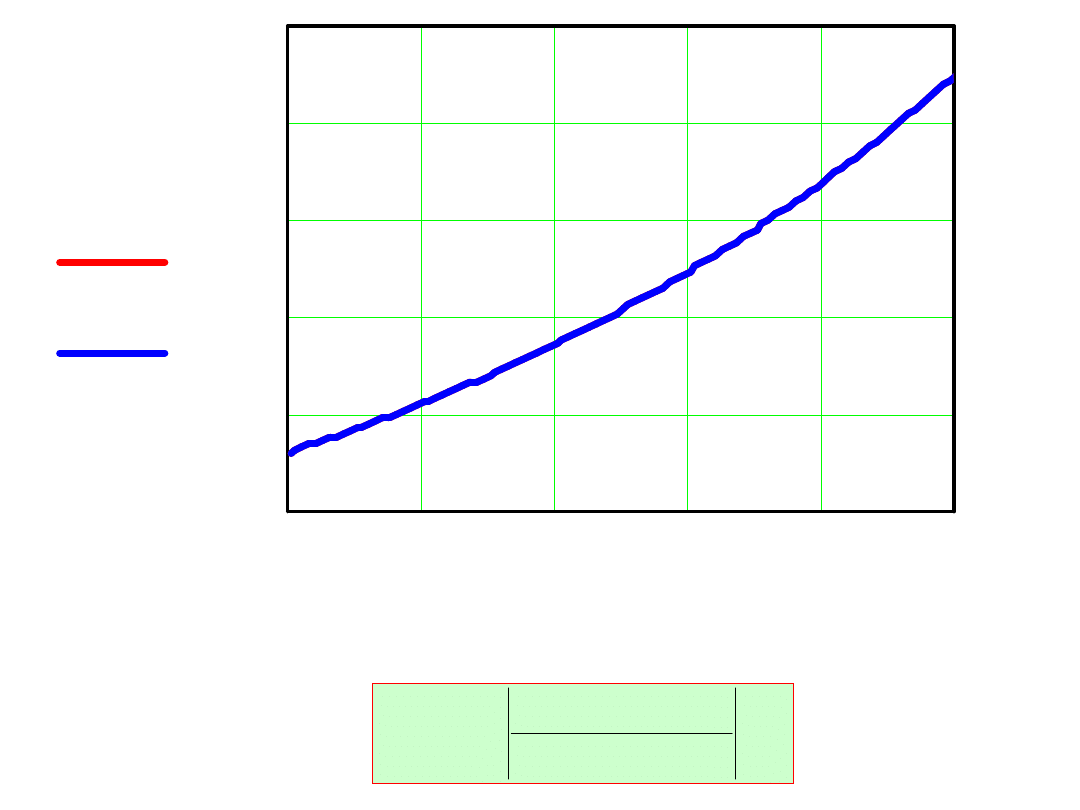
Wyniki obliczeń przedstawiono na wykresie:
1
1.2
1.4
1.6
1.8
2
2
3.2
4.4
5.6
6.8
8
w x
( )
expx
( )
x
Dla lepszej oceny wykres błędu względnego:
100
)
x
exp(
)
x
exp(
)
x
(
w
)
x
(
eps
4
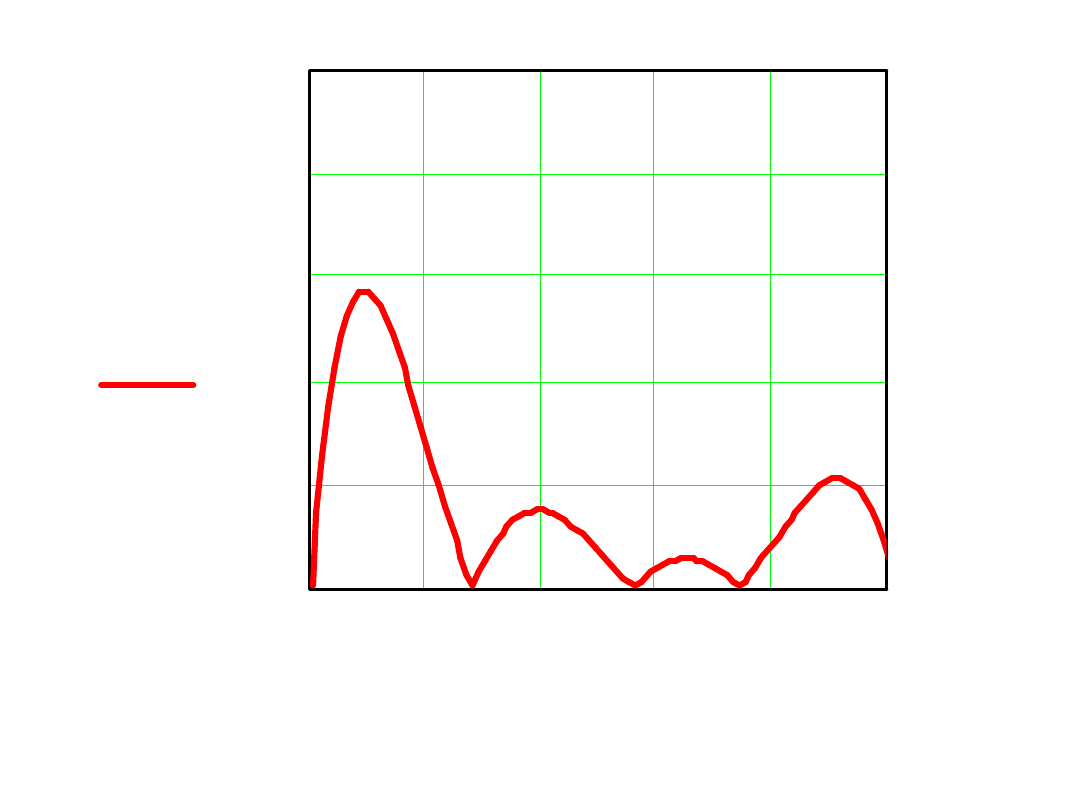
1
1.2
1.4 1.6
1.8
2
0
0.002
0.004
0.006
0.008
0.01
eps x
( )
x
Przykład 2.
W wyniku pomiarów zdjęto pierwotną krzywą magnesowania
B=F(H). Zbudować wielomian interpolacyjny Lagrange'a
dla zakresu 0<=H <=3000A/m.
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
Kolejne wielomiany
k
(H) dla k=0,1,...8 są:
3000
0
2000
0
1500
0
1000
0
3000
H
2000
H
1500
H
1000
H
500
0
200
0
100
0
50
0
500
H
200
H
100
H
50
H
H
0
lub po obliczeniu mianownika mamy:

3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
10
2222
.
2
H
22
0
3000
H
2000
H
1500
H
1000
H
500
H
200
H
100
H
H
10
4784
.
7
H
22
1
3000
H
2000
H
1500
H
1000
H
500
H
200
H
50
H
H
10
2019
.
7
H
22
2
3000
H
2000
H
1500
H
1000
H
500
H
100
H
50
H
H
10
1198
.
2
H
22
3
3000
H
2000
H
1500
H
1000
H
200
H
100
H
50
H
H
10
9753
.
1
H
23
4
3000
H
2000
H
1500
H
500
H
200
H
100
H
50
H
H
10
924
.
2
H
24
5
3000
H
2000
H
1000
H
500
H
200
H
100
H
50
H
H
10
7366
.
6
H
25
6
3000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
9965
.
9
H
26
7
2000
H
1500
H
1000
H
500
H
200
H
100
H
50
H
H
10
8554
.
1
H
26
8
i wielomian aproksymacyjny jest
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
0
H
B
8
7
6
5
4
3
2
1
0
lub
H
035
.
2
H
03
.
2
H
02
.
2
H
2
H
95
.
1
H
8
.
1
H
5
.
1
H
75
.
0
H
B
8
7
6
5
4
3
2
1
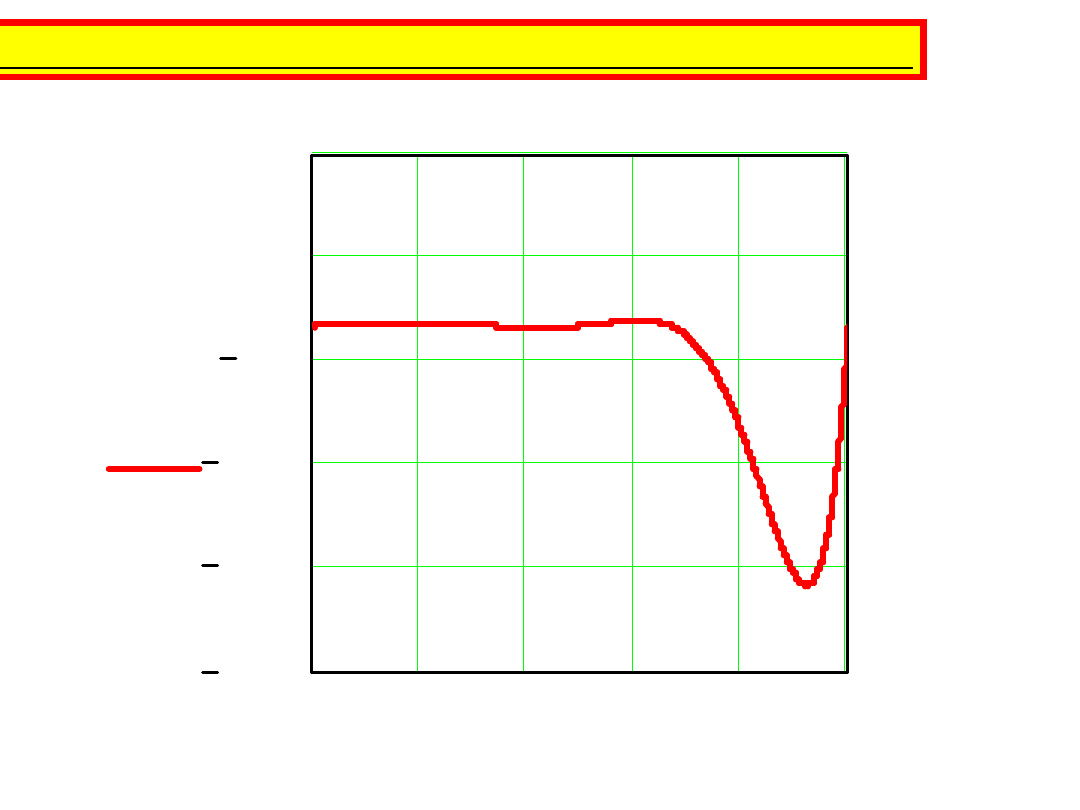
0
600 1200 1800 2400 3000
4000
2800
1600
400
800
2000
B H
( )
H
Otrzymany wynik jest niemożliwy do przyjęcia!!!
Aproksymacja liniowa odcinkami:
H[A/m
]
0
50
10
0
20
0
50
0
100
0
150
0
200
0
3000
B[T]
0 0.7
5
1.5 1.8 1.9
5
2.0 2.0
2
2.0
3
2.03
5
0
50
0
H
75
.
0
50
0
50
H
0
H
B
1
dla
50
H
0
lub po wykonaniu działań:
H
015
.
0
H
B
1
50
H
0
dla
i podobnie:
50
H
03
.
0
100
H
015
.
0
H
B
2
dla
100
H
50
100
H
018
.
0
200
H
015
.
0
H
B
3
dla
200
H
100
200
H
0065
.
0
500
H
006
.
0
H
B
4
500
H
200
dla
500
H
004
.
0
1000
H
0039
.
0
H
B
5
dla
1000
H
500
1000
H
00404
.
0
1500
H
004
.
0
H
B
6
dla
1500
H
1000
1500
H
00406
.
0
2000
H
00404
.
0
H
B
7
dla
2000
H
1500
2000
H
002035
.
0
3000
H
00203
.
0
H
B
8
dla
3000
H
2000
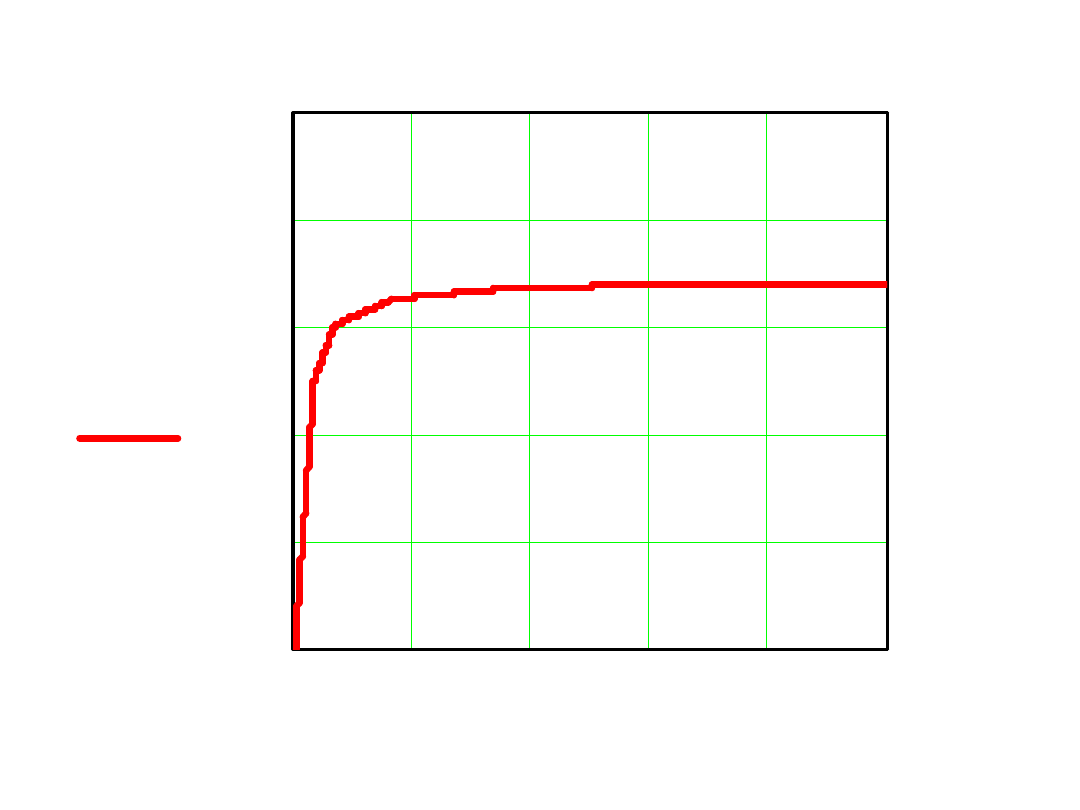
0
600 1200 1800 2400 3000
0
0.6
1.2
1.8
2.4
3
BaH
( )
H
B(H)
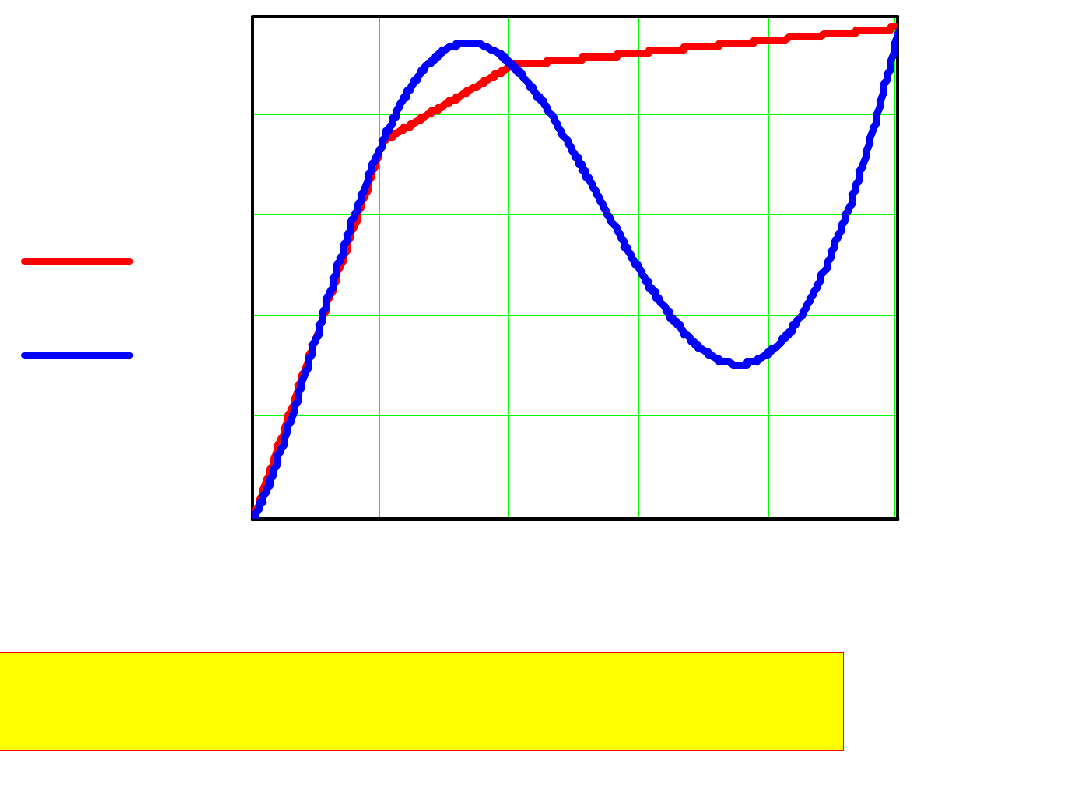
0
100 200 300 400 500
0
0.4
0.8
1.2
1.6
2
BaH
( )
B H
( )
H
Porównanie Ba(H) – interpolacja liniowa
B(H) – wielomian 8-go stopnia
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
Wyszukiwarka
Podobne podstrony:
Wyklad mn 2
Wyklad mn 9
Wyklad mn no 8 piątek
Wyklad mn 16
Wyklad mn 9
Wyklad mn no 7 piątek
Wyklad mn 6
Wyklad mn no 4 piątek
Wyklad mn 12
Wyklad mn 10
Wyklad mn 6
Wyklad mn 15
Wyklad mn no 5 piątek
Wyklad mn 8
Wyklad mn no 6 piątek
Wyklad mn 5
Wyklad mn 8
Wyklad mn no 3 piątek
Wyklad mn 4
więcej podobnych podstron