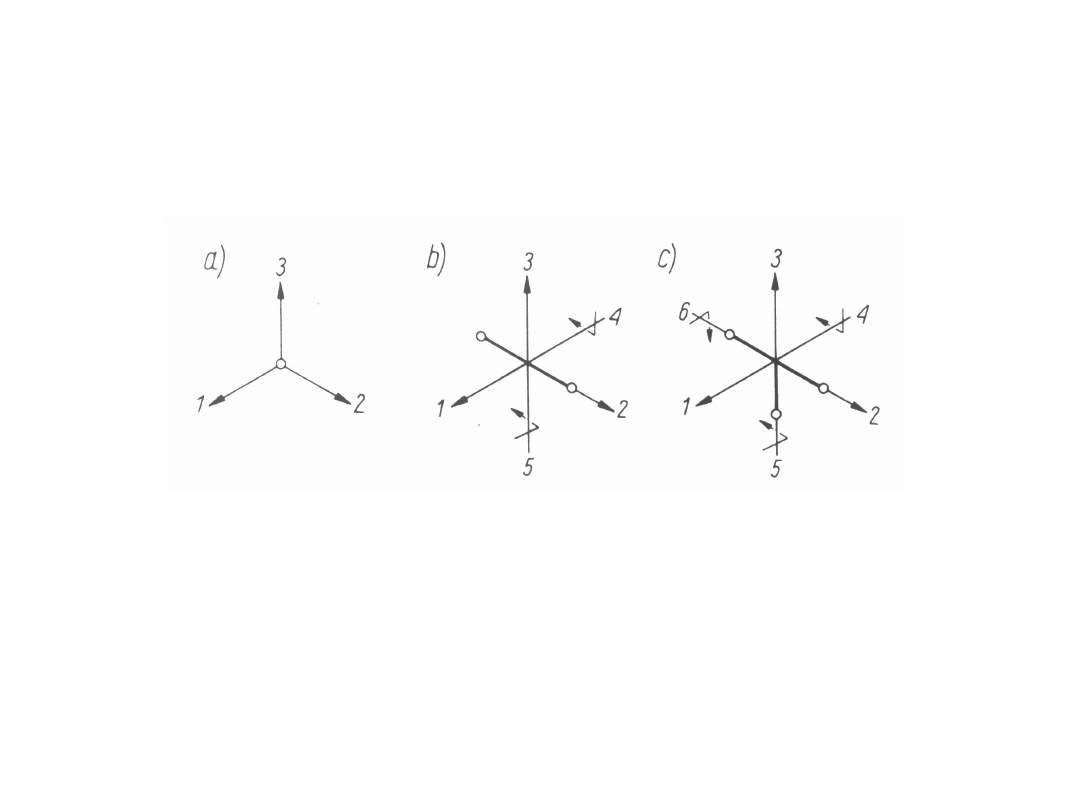
WŁAŚCIWOŚCI GAZÓW
DOSKONAŁYCH

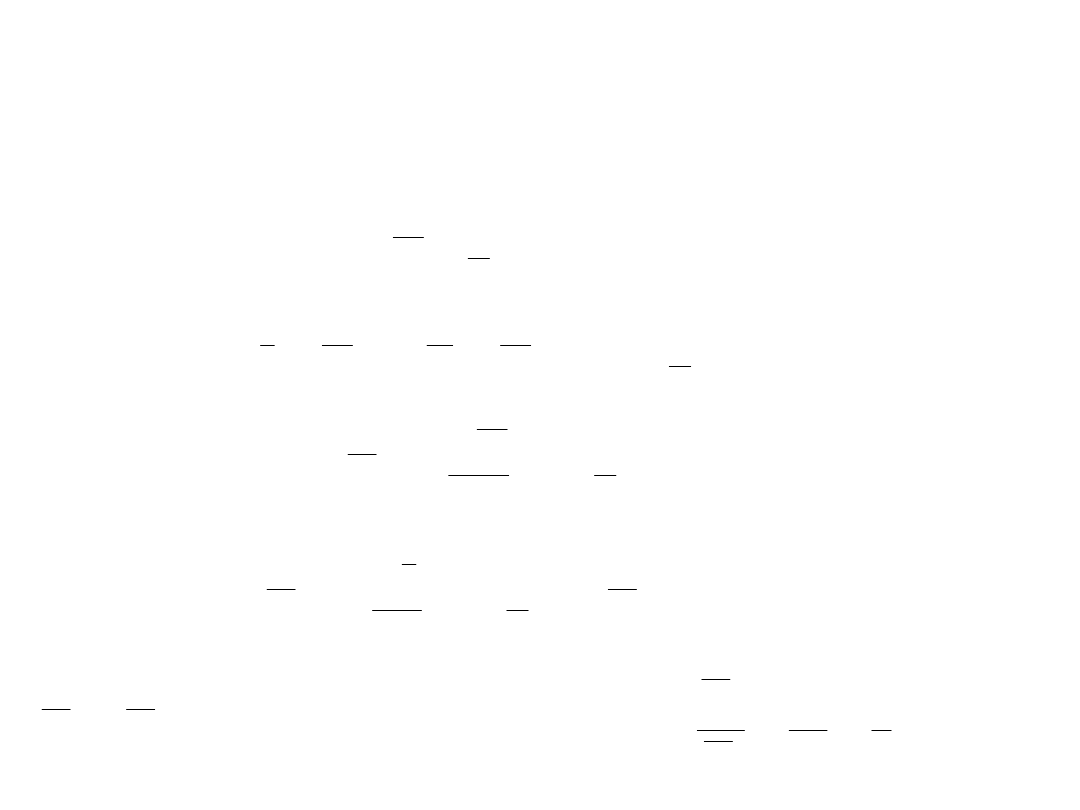
JEDNOATOMOWE GAZY DOSKONAŁE

BT

U

2

3



BT

BT

U

V

p

U

I

2

5











B

T

U

C

V

v

2

3





















B

C

B

T

I

C

v

p

p

























2

5

...

666

,

1

3

5

















v

p

v

p

v

p

v

p

c

c

C

C

R

c

c

B

C

C



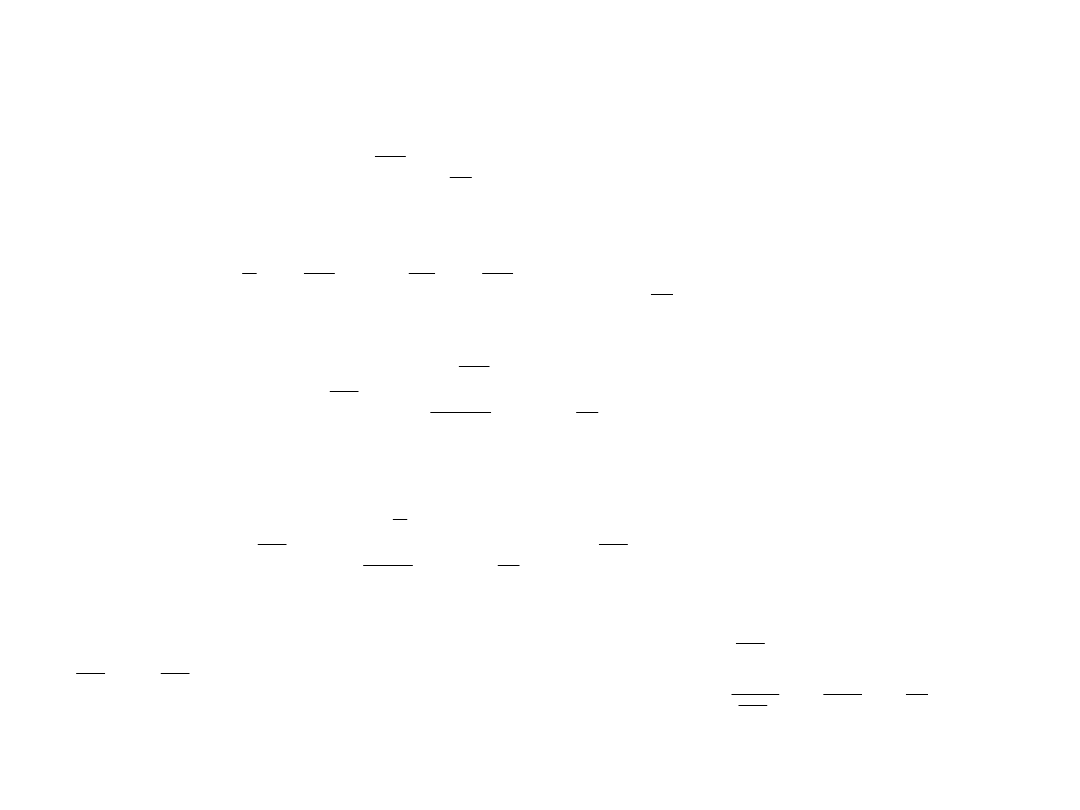
DWUATOMOWE GAZY DOSKONAŁE

BT

U

2

5



BT

BT

U

V

p

U

I

2

7











B

T

U

C

V

v

2

5





















B

C

B

T

I

C

v

p

p

























2

7

4

,

1

5

7

















v

p

v

p

v

p

v

p

c

c

C

C

R

c

c

B

C

C



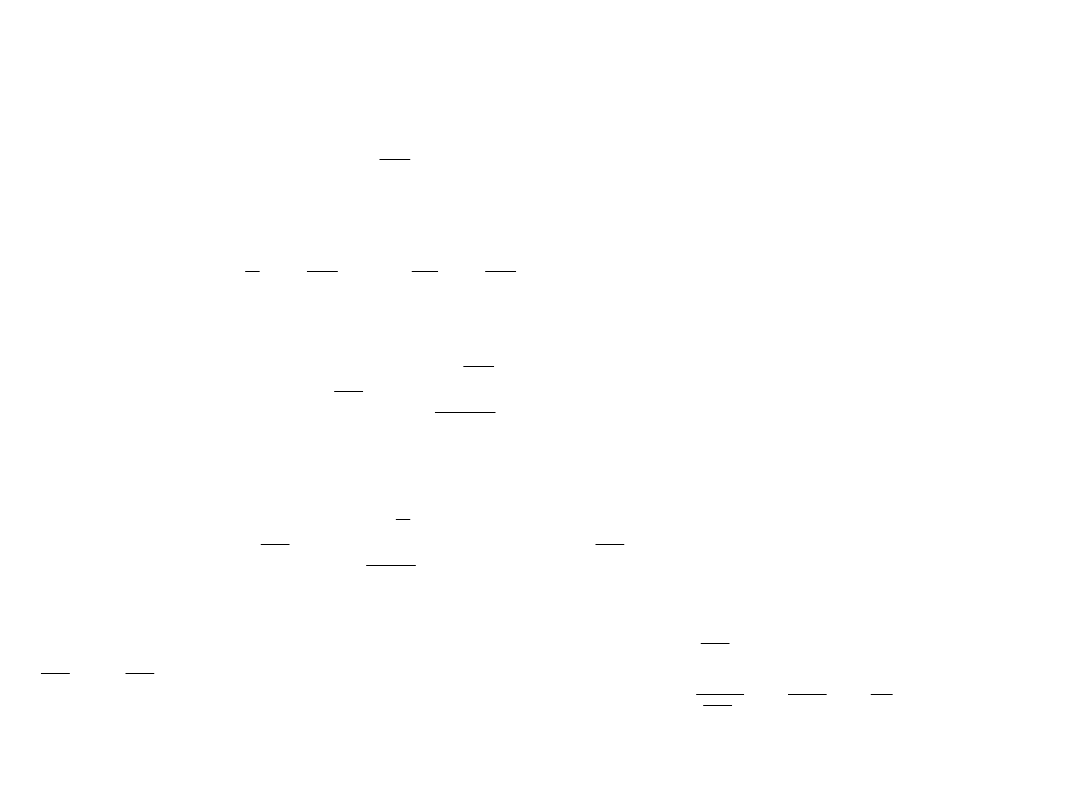
BT

U 3



BT

BT

U

V

p

U

I

4











B

T

U

C

V

v

3





















B

C

B

T

I

C

v

p

p

























4

...

333

,

1

3

4

















v

p

v

p

v

p

v

p

c

c

C

C

R

c

c

B

C

C



WIELOATOMOWE GAZY DOSKONAŁE

GAZY PÓŁDOSKONAŁE

PRZEMIANY GAZÓW DOSKONAŁYCH

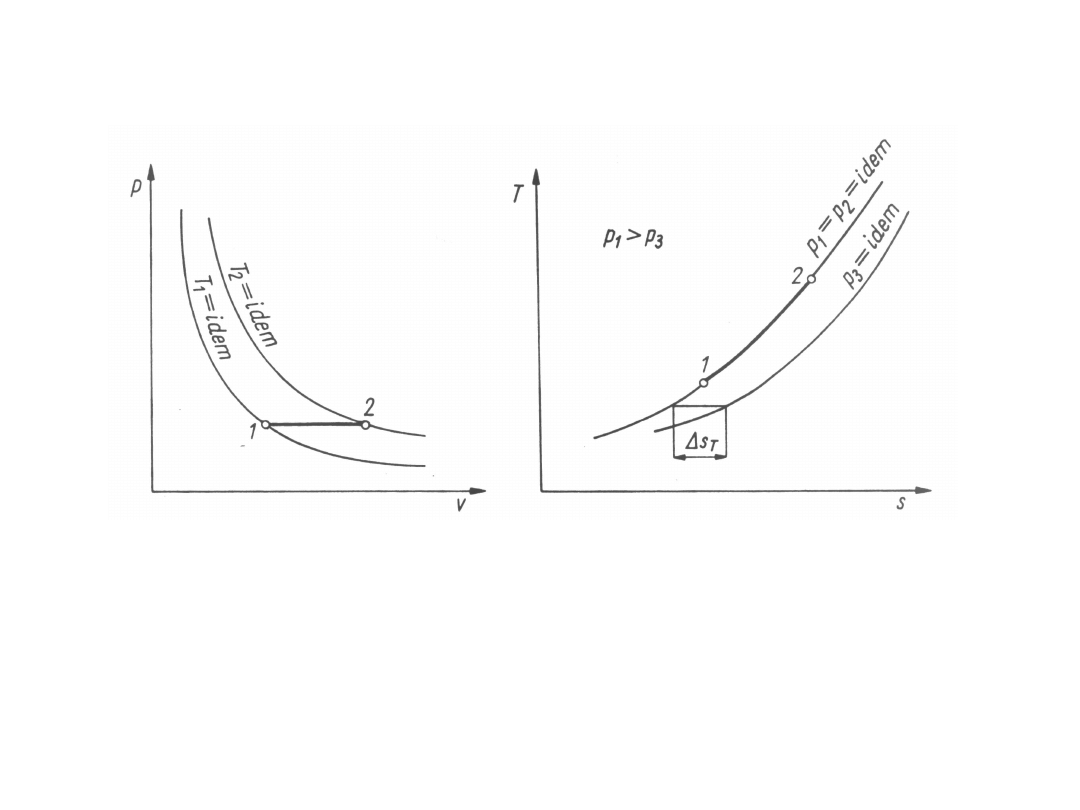
Przemiany izotermiczne

 Przemiany izotermiczne są przemianami przy stałej
temperaturze (indeks T), tj. dT = 0, T

1

= T

2

= T =

idem.

Z równania stanu gazów doskonałych dla przemian
izotermicznych wynika, że

p

1

v

1

= p

2

v

2

= pv = RT

przy

stałej

temperaturze

iloczyn

ciśnienia

bezwzględnego przez objętość właściwą jest dla gazów
doskonałych wielkością stałą (prawo Boyle’a i
Mariotte’a).

 Energia wewnętrzna właściwa i entalpia właściwa
gazów doskonałych są funkcjami tylko temperatury.

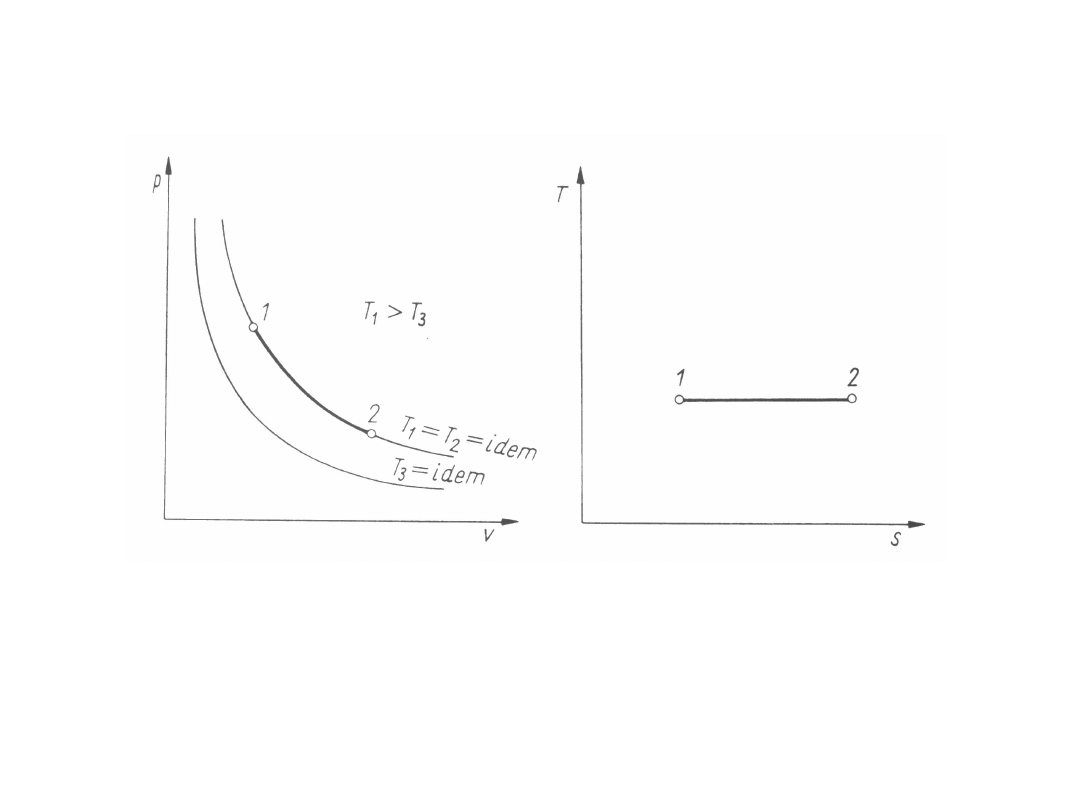
Przemiany izotermiczne gazów doskonałych są
zarazem przemianami izoenergetycznymi (u = idem)
oraz

izentalpowymi

(i = idem). Zatem z równań wyrażających pierwszą
zasadę termodynamiki wynika, że ciepło przemiany
izotermicznej gazów doskonałych jest równe pracy
zmiany objętości i pracy technicznej przemiany

2

,

1

2

,

1

2

,

1

tT

T

T

l

l

q





1

2

1

1

1

2

2

2

2

1

2

2

2

1

1

1

2

1

1

2

2

,

1

ln

ln

ln

ln

ln

ln

)

(

2

1

2

1

v

v

v

p

v

v

v

p

p

p

v

p

p

p

v

p

p

p

RT

v

v

RT

v

dv

RT

dv

v

p

l

v

v

v

v

T

T























Ciepło przemiany izotermicznej między stanami 1 i 2,
odniesione do 1 kg, można również prosto obliczyć z
przyrostu entropii właściwej:

)

(

1

2

2

,

1

2

1

s

s

T

Tds

q

s

s

T









Ponieważ znak ciepła przemiany izotermicznej jest
zgodny ze znakiem pracy zmiany objętości
przemiany i ze znakiem pracy technicznej, w
przypadku ekspansji (v

2

> v

1

) oraz rozprężania (p

2

<

p

1

) ciepło przemiany izotermicznej jest dodatnie, a

w przypadku kompresji (v

2

< v

1

) oraz sprężania (p

2

> p

1

) – ujemne.

Przyrost

entropii

właściwej

dla

przemiany

izotermicznej między stanami 1 i 2 można obliczyć
ze wzoru:

2

1

1

2

2

,

1

1

2

ln

ln

)

(

p

p

R

v

v

R

T

q

s

s

T

T









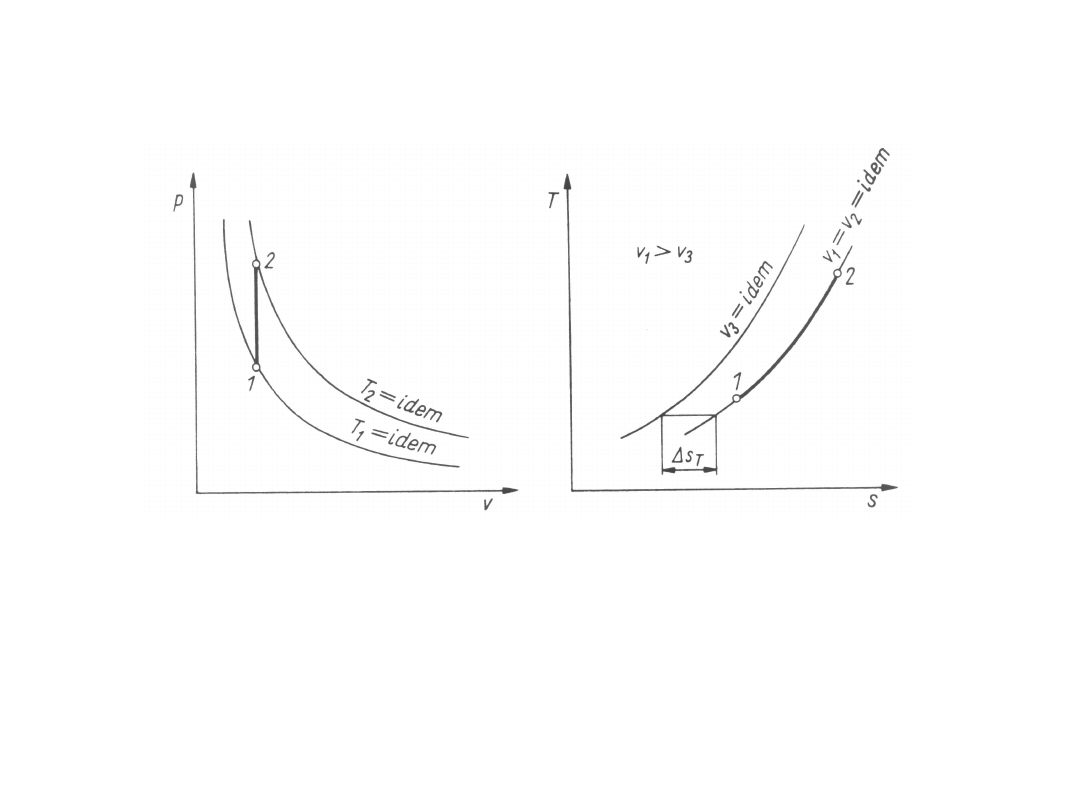
Przemiany izochoryczne

 Przemiany izochoryczne są przemianami przy stałej
objętości (indeks V), a przy rozważaniu stałej ilości
jednorodnej substancji są także przemianami przy
stałej

objętości

właściwej

(indeks

v),

tj. dv = 0, v

1

= v

2

= v = idem. Obrazem

geometrycznym

przemiany

izochorycznej

jest

izochora.

Po podzieleniu stronami równań stanu gazów
doskonałych dla stanów 1 i 2 o jednakowych
objętościach właściwych otrzymuje się

1

2

1

2

T

T

p

p



Przy stałej objętości właściwej ciśnienie bezwzględne
gazu doskonałego jest wprost proporcjonalne do
temperatury bezwzględnej (prawo Charlesa).

Praca zmiany objętości dla przemiany izochorycznej
(dv = 0) jest równa zeru







2

1

0

2

,

1

v

v

v

pdv

l

Wobec tego z równania wyrażającego pierwszą zasadę
termodynamiki

wynika,

że

ciepło

przemiany

izochorycznej jest zużywane w całości na przyrost
energii wewnętrznej.

Ciepło przemiany izochorycznej między stanami 1 i 2,
odniesione do 1 kg, wynosi

1

0

2

0

1

2

2

,

1

1

2

T

c

T

c

u

u

q

T

v

T

v

v









a dla gazów doskonałych o stałym cieple właściwym

)

(

1

)

(

1

)

(

1

2

1

2

1

2

2

,

1

p

p

v

T

T

R

T

T

c

q

v

v





















Na skutek izochorycznego ogrzewania wzrastają
temperatura i ciśnienie gazu doskonałego.

Praca

techniczna

przemiany

izochorycznej,

odniesiona do 1 kg, wynosi:

Przyrost

entropii

właściwej

dla

przemiany

izochorycznej między stanami 1 i 2 jest równy

a dla gazów doskonałych o stałym cieple właściwym

2

,

1

2

1

2

1

2

,

1

)

1

(

)

(

)

(

2

1

v

p

p

tv

q

T

T

R

p

p

v

vdp

l























1

2

1

2

1

2

ln

)

(

)

(

]

)

(

[

)

(

)

(

2

1

2

1

T

T

R

T

s

T

s

T

dT

R

T

c

T

dT

T

c

s

s

p

p

T

T

p

T

T

v

v



















1

2

1

2

1

2

ln

ln

)

(

p

p

c

T

T

c

s

s

v

v

v







Na wykresie o współrzędnych T-s izochora gazu
doskonałego
o stałym cieple właściwym jest krzywą logarytmiczną.
Izochora
o większej objętości właściwej v

1

= idem przebiega na

wykresie
o współrzędnych T-s przy większych wartościach
entropii niż izochora o mniejszej objętości właściwej
v

3

= idem. Pozioma odległość między izochorami jest

stała i wynosi

3

1

1

3

ln

)

(

v

v

R

s

s

s

T

T









Przemiany izobaryczne

 Przemiany izobaryczne są przemianami przy stałym
ciśnieniu (indeks p), tj. dp = 0, p

1

= p

2

= p = idem.

Obrazem geometrycznym przemiany izobarycznej
jest izobara.

Po podzieleniu stronami równań stanu gazów
doskonałych dla stanów 1 i 2 o jednakowych
ciśnieniach otrzymuje się

 Przy stałym ciśnieniu objętość właściwa gazu
doskonałego

jest

wprost

proporcjonalna

do

temperatury bezwzględnej (prawo Gay-Lussaca).

Praca techniczna przemiany izobarycznej (dp = 0)
jest równa zeru 

1

2

1

2

T

T

v

v

p























2

1

0

2

,

1

p

p

tp

vdp

l

Z

równania

wyrażającego

pierwszą

zasadę

termodynamiki

wynika,

że

ciepło

przemiany

izobarycznej jest zużywane w całości na przyrost
entalpii.

Ciepło przemiany izobarycznej między stanami 1 i 2,
odniesione do 1 kg, wynosi

  

a dla gazów doskonałych o stałym cieple właściwym

 

Praca zmiany objętości przemiany izobarycznej między
stanami 1 i 2, odniesiona do 1 kg, wynosi

1

0

2

0

1

2

2

,

1

1

2

T

c

T

c

i

i

q

T

p

T

p

p









)

(

1

)

(

1

)

(

1

2

1

2

1

2

2

,

1

v

v

p

T

T

R

T

T

c

q

p

p

























2

,

1

1

2

1

2

2

,

1

1

)

(

)

(

2

1

p

v

v

p

q

T

T

R

v

v

p

pdv

l





















Przyrost entropii właściwej dla przemiany izobarycznej
między stanami 1 i 2 dla gazów o stałym cieple
właściwym jest równy

 

Na wykresie o współrzędnych T-s izobara gazu
doskonałego o stałym cieple właściwym jest krzywą
logarytmiczną przebiegającą łagodniej niż izochora,
ponieważ podstyczne są równe ciepłu właściwemu
a c

p

> c

v

. Izobara o wyższym ciśnieniu p

1

= idem.

Pozioma odległość między tymi izobarami jest stała i
wynosi 

1

2

1

2

1

2

ln

ln

)

(

v

v

c

T

T

c

s

s

p

p

p







1

3

2

3

ln

)

(

p

p

R

s

s

s

T

T









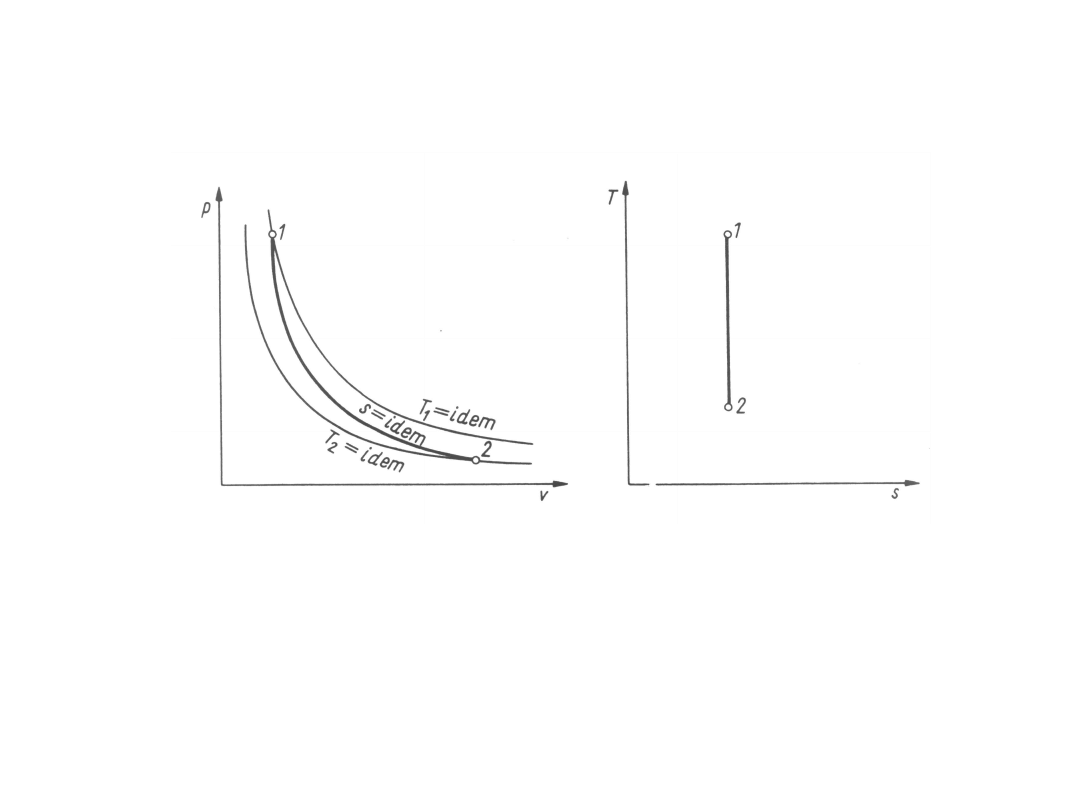
Przemiany adiabatyczne

 Przemiany adiabatyczne są przemianami bez
wymiany

ciepła

z otoczeniem (dq

z

= 0). Odwracalne (dq

w

= 0)

przemiany

adiabatyczne

są

przemianami

izentropowymi:

0

,

0











ds

Tds

dq

dq

dq

w

z

Dla gazów doskonałych o stałym cieple właściwym  

lub w postaci zależności między parametrami
dowolnego stanu przemiany izentropowej































;

1

2

1

1

2

2

1

1

2





p

p

v

v

v

v

p

p

idem





pv

Dla gazów doskonałych o stałym cieple właściwym
stosunek ciepła właściwego przy stałym ciśnieniu do
ciepła właściwego przy stałej objętości



nazywany

jest wykładnikiem izentropy.

 Ponieważ

 

na wykresie o współrzędnych p- izentropa przebiega

bardziej stromo niż izoterma.

T

s

v

p

v

p

v

p

v

p













































Jeżeli podzieli się stronami równania stanu gazów
doskonałych dla stanów 1 i 2

1

2

1

1

2

2

T

T

v

p

v

p



to po uwzględnieniu równań * otrzymuje się

1

1

2

1

1

2

1

2

1

1

2

;





































T

T

v

v

v

v

T

T

1

1

2

1

2

1

1

2

1

2

;









































T

T

p

p

p

p

T

T

lub w postaci zależności między parametrami
dowolnego stanu przemiany izentropowej

 

 

Ciepło przemiany izentropowej (ds = 0) między
stanami 1 i 2 jest równe zeru

 

idem

idem;

1

1















Tp

Tv







2

1

0

2

,

1

s

s

s

Tds

q

Z równania wyrażającego pierwszą zasadę
termodynamiki wynika więc, że praca przemiany
izentropowej jest wykonywana kosztem spadku
energii wewnętrznej i w odniesieniu do 1 kg
substancji dla gazów doskonałych o stałym cieple
właściwym wynosi

Praca techniczna przemiany izentropowej jest
wykonywana kosztem spadku entalpii i dla gazów
doskonałych o stałym cieple właściwym w
odniesieniu do 1 kg wynosi





































































































1

1

2

1

1

2

1

1

1

2

2

1

1

2

1

2

1

2

,

1

1

1

1

1

1

)

(

1

)

(

p

p

RT

v

v

v

p

v

p

v

p

T

T

R

T

T

c

l

v

s

2

,

1

2

1

2

,

1

)

(

s

p

ts

l

T

T

c

l









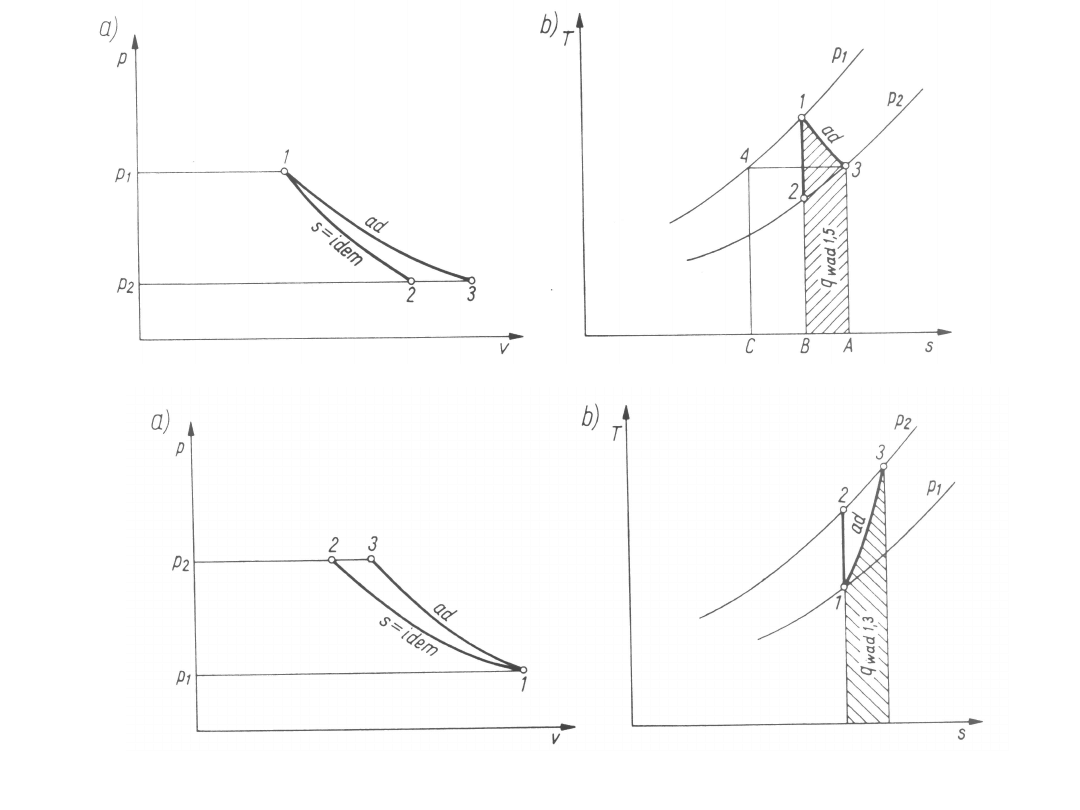
Zewnętrzne ciepło przemiany adiabatycznej jest
równe

zeru

(q

zad1,3

=

0).

Całkowite

ciepło

przemiany

adiabatycznej jest równe ciepłu rozpraszania pracy.  

Zewnętrzna

praca

techniczna

przemiany

adiabatycznej jest wykonywana kosztem spadku
entalpii i dla gazów doskonałych (przy stałym cieple
właściwym) jest równa

 

Zewnętrzną

pracę

techniczną

przemiany

adiabatycznej można łatwo odczytać z wykresu o
współrzędnych i-s jako odpowiedni spadek entalpii
właściwej.

)

(

1

)

(

3

1

3

1

3

1

3

,

1

T

T

R

T

T

c

i

i

l

p

ztad



















Sprawność izentropowa (adiabatyczna) rozprężania
jest zdefiniowana jako stosunek nieodwracalnego
adiabatycznego spadku entalpii do izentropowego
spadku

entalpii

od

tego

samego

stanu

początkowego

do

takiego

samego

ciśnienia

końcowego.

 

Sprawność izentropowa (adiabatyczna) sprężania
jest zdefiniowana jako stosunek izentropowego
wzrostu

entalpii

do

nieodwracalnego

adiabatycznego wzrostu entalpii od tego samego
stanu początkowego do takiego samego ciśnienia
końcowego.

 

Przemiany politropowe

Rodzina przemian politropowych (indeks n)
zdefiniowana jest przez równanie

gdzie wykładnik politropy n = idem jest wielkością
stałą dla danej przemiany, a dla różnych przemian
może przybierać dowolne wartości rzeczywiste

Obrazem geometrycznym przemiany politropowej jest
politropa

idem



n

pv











n

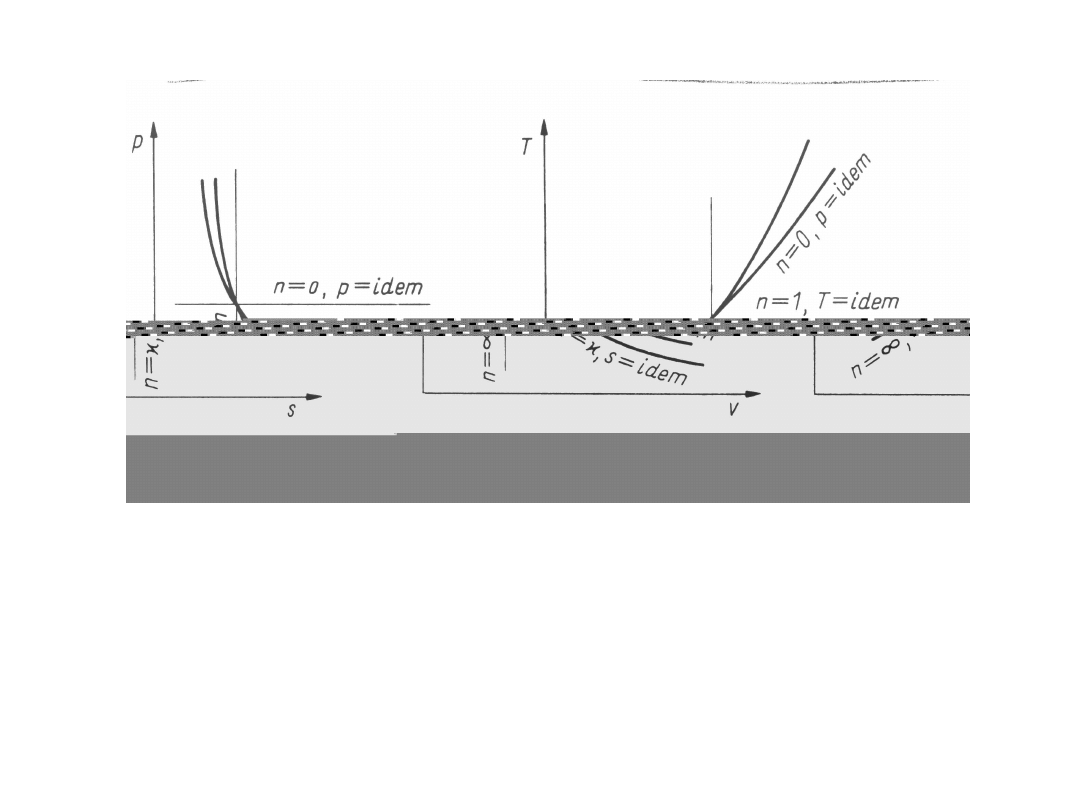
Dla szczególnych wartości wykładnika politropy
otrzymuje się:

  - przemiany izobaryczne substancji dowolnych: n = 0,
p = idem;

-    

-

przemiany izotermiczne gazów doskonałych: n = 1,

pv = idem,
T = idem

-     

- przemiany izentropowe gazów doskonałych o

stałym cieple
właściwym;

n = , pv



= idem;

-     

- przemiany izochoryczne substancji dowolnych: n =

,

v = idem.

 

Należy zauważyć, że przemiany izentropowe gazów
doskonałych
o cieple właściwym zależnym od temperatury nie są
przemianami politropowymi.

idem

1





v

p

1

1

2

1

1

2

1

2

1

1

2

;

































n

n

T

T

v

v

v

v

T

T

1

1

2

1

2

1

1

2

1

2

;

































n

n

n

n

T

T

p

p

p

p

T

T

n

n

p

p

v

v

v

v

p

p

1

2

1

1

2

2

1

1

2

;





























Praca przemiany politropowej





















































































































































n

n

n

n

n

n

n

p

p

n

v

p

v

v

n

v

p

p

p

n

RT

v

v

n

RT

T

T

n

R

l

1

1

2

1

1

1

2

1

1

1

1

1

2

1

1

2

1

1

2

1

2

,

1

1

1

1

1

1

1

1

1

)

(

1

Praca techniczna przemiany politropowej

2

,

1

1

1

2

2

2

,

1

2

,

1

)

(

n

n

tn

nl

v

p

v

p

l

l









Ciepło właściwe przemiany politropowej wynosi

R

n

n

R

n

n

T

n

T

c

n

R

T

c

T

c

v

v

n























































1

1

1

1

1

1

1

)

(

)

(

1

)

(

)

(









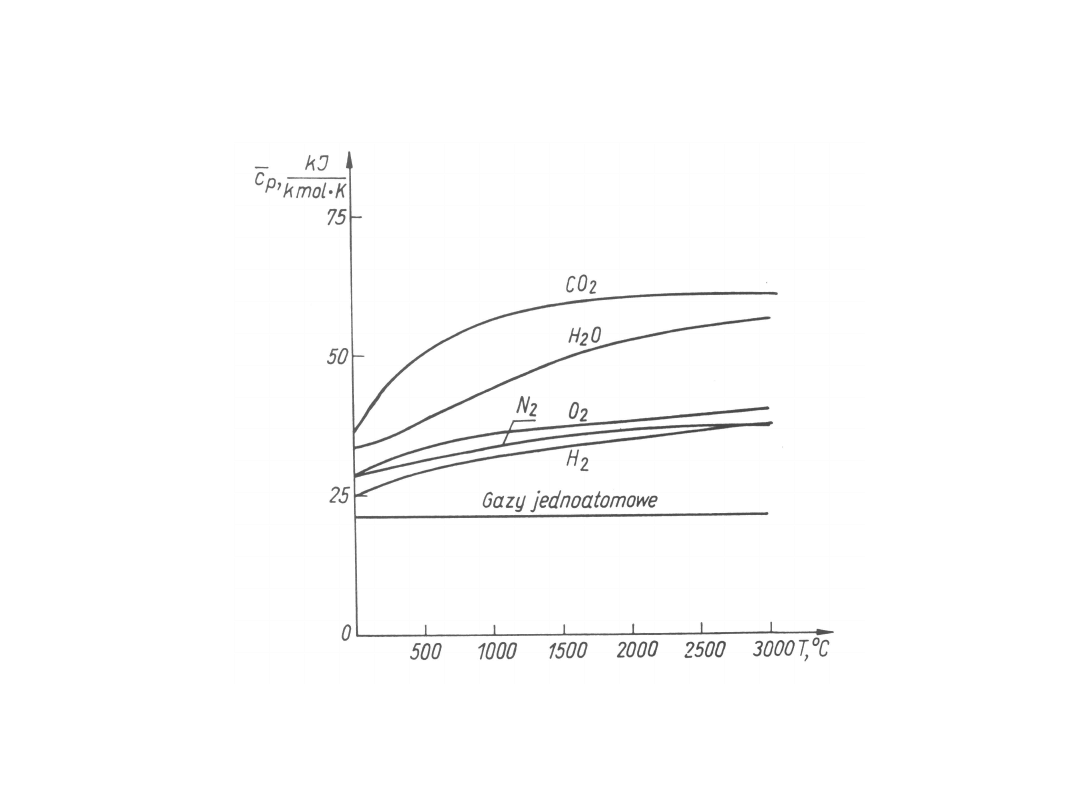
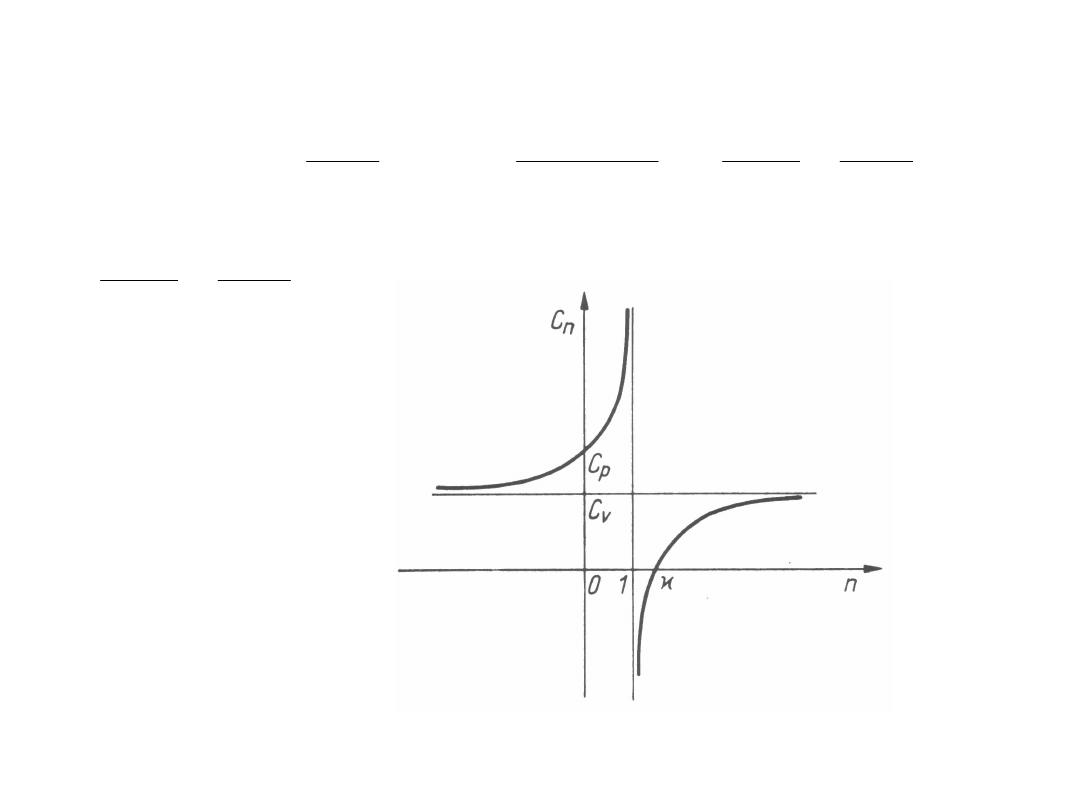
Na rysunku podano zależność ciepła właściwego
przemian politropowych od wykładniki politropy dla
gazów

doskonałych

o

stałym

cieple

właściwym.

Dla

przemian

izobarycznych, gdy n = 0, jest c

n

= c



= c

p

. Dla

przemian izotermicznych, gdy n = 1, jest
c

n

= c

T

= . Dla przemian izentropowych, gdy n = ,

jest c

n

= c

T

= . Dla przemian izentropowych, gdy n

=

,

jest

c

n

=

c

s

=

0.

Dla przemian izochorycznych, gdy n = , jest c

n

= c



.

 

 Dla przemian izentropowych jest c

n

= 0, czyli n = .

Ciepło przemiany politorpowej między stanami 1 i 2,
odniesione do 1 kg, dla gazów doskonałych o stałym
cieple właściwym wynosi

v

n

p

n

v

n

c

c

c

c

n

n

n

c

c













1



)

(

1

)

(

1

)

(

1

2

1

2

1

2

2

,

1

u

u

n

n

T

T

n

n

c

T

T

c

q

v

n

n

























Iloczyny parametrów p, v, T przeciwległych punktów
przecięć politrop (tj. iloczyny parametrów punktów
parzystych
i nieparzystych) w obiegu składającym się z dwóch
politrop
o jednakowych wykładnikach przeciętych dwoma
politropami
o jednakowych wykładnikach są sobie równe.

p

1

p

3

= p

2

p

4

v

1

v

3

= v

2

v

4

T

1

T

3

= T

2

T

4