Geometria obliczeniowa –

przecinanie się odcinków

• Łukasz Gos
• Kamil Kasprzyk
• Grupa 312A

Jak liczyć przecinanie się odcinków

• Jeżeli mamy punkty: A=(x1,y1), B=(x2,y2), C=(x3,y3) i D=(x4,y4)
• Gdy chcemy sprawdzić czy odcinki |AB| i |CD| przecinają się

musimy sprawdzić czy oba końce danego odcinka leżą po
przeciwnych stronach danego odcinka

• W tym celu musi zachodzić pewna nierówność:

sign[det(A,B,C)] <> sign[det(A,B,D)]
Która oznacza, że punkty C i D leżą po przeciwnych stronach
odcinka |AB|

• Dla pewniejszego wyniku należy sprawdzić 2 nierówności:

sign[det(A,B,C)] <> sign[det(A,B,D)]
sign[det(C, D, A)] <> sign[det(C, D, B)]

Geometryczne podejście do nakładania się:

• mamy daną sieć złożoną z odcinków tworzącą zbiory
• dla dwóch zbiorów obliczyć wszystkie przecięcia pomiędzy

odcinkami z jednego zbioru i odcinkami drugiego zbioru

• odcinki zdefiniowane są jako domknięte, czyli koniec jednego

docinka, leżący na drugim odcinku, liczy się jako przecięcie

• odcinki z obydwu zbiorów umieszczamy w jednym i wyznaczamy

ich przecięcia

Sposoby obliczania przecięć:

• algorytm siłowy
• algorytm zamiatania

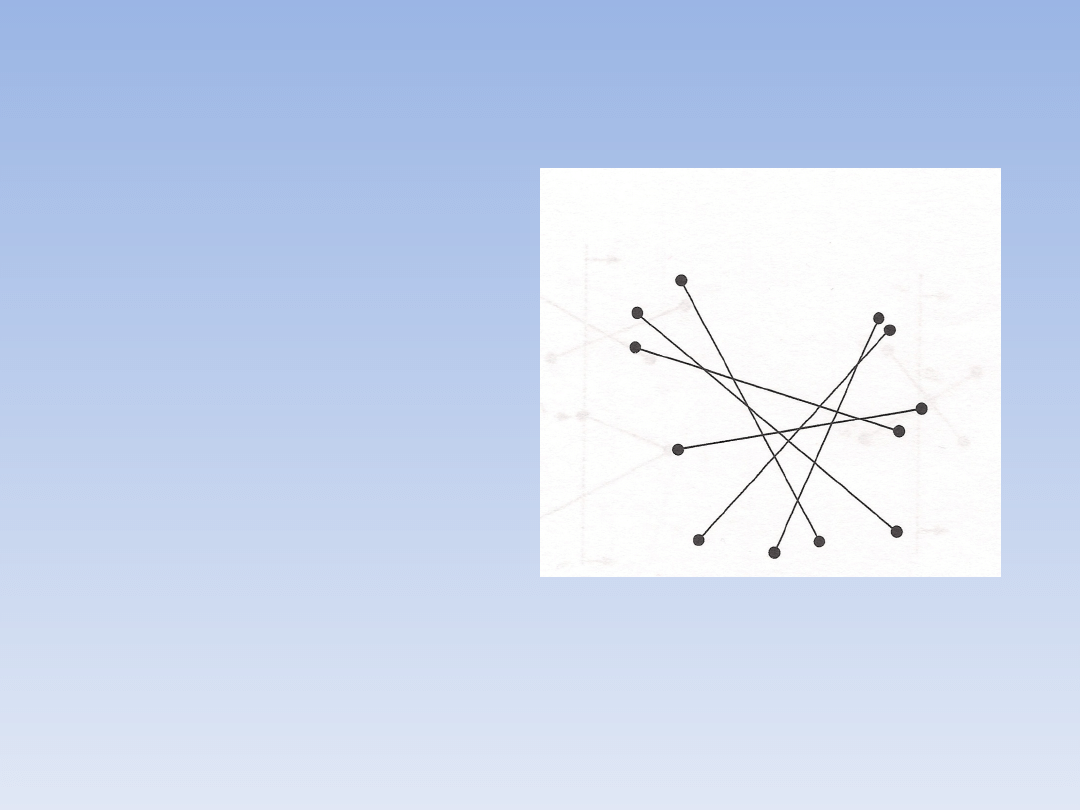
Algorytm siłowy:

• dla każdej pary odcinków ze
zbioru obliczamy możliwość
przecięcia

Wady tej metody to:
• wolny czas wykonywania
O(n

2

)

• gdy każda para odcinków
przecina się algorytm wymaga
czasu Ω(n

2

)

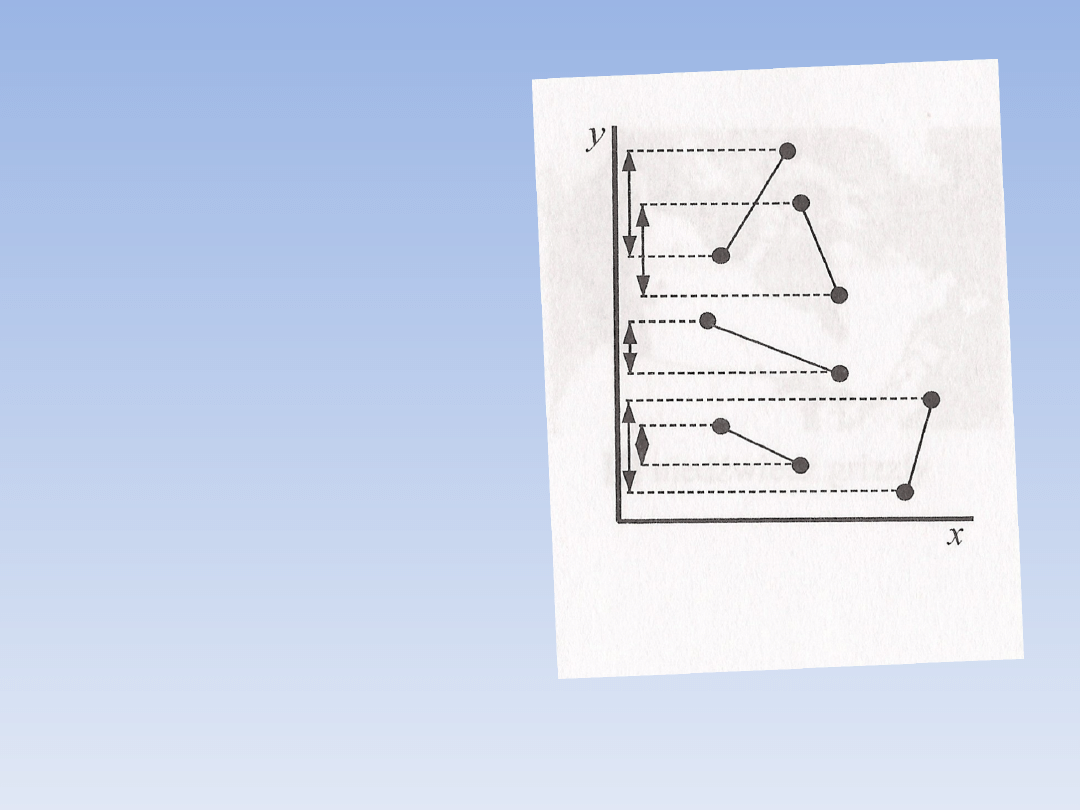
Algorytm zamiatania:

• Stosowany by
zoptymalizować czas szukania
przecinanych odcinków

Zasada działania:

• Mamy dany zbiór odcinków
S:={s

1

, s

2

,…, s

n

}

Krok 1:
Próba wyeliminowania par
odcinków leżących daleko od
siebie:

• przedział odcinka definiujemy
jako rzut prostopadły na oś y

• gdy przedziały par odcinków
nie zachodzą na siebie
traktujemy je jako oddalone
daleko od siebie bez możliwości
przecinania

• sprawdzamy więc tylko pary
odcinków których przedziały
zachodzą na siebie

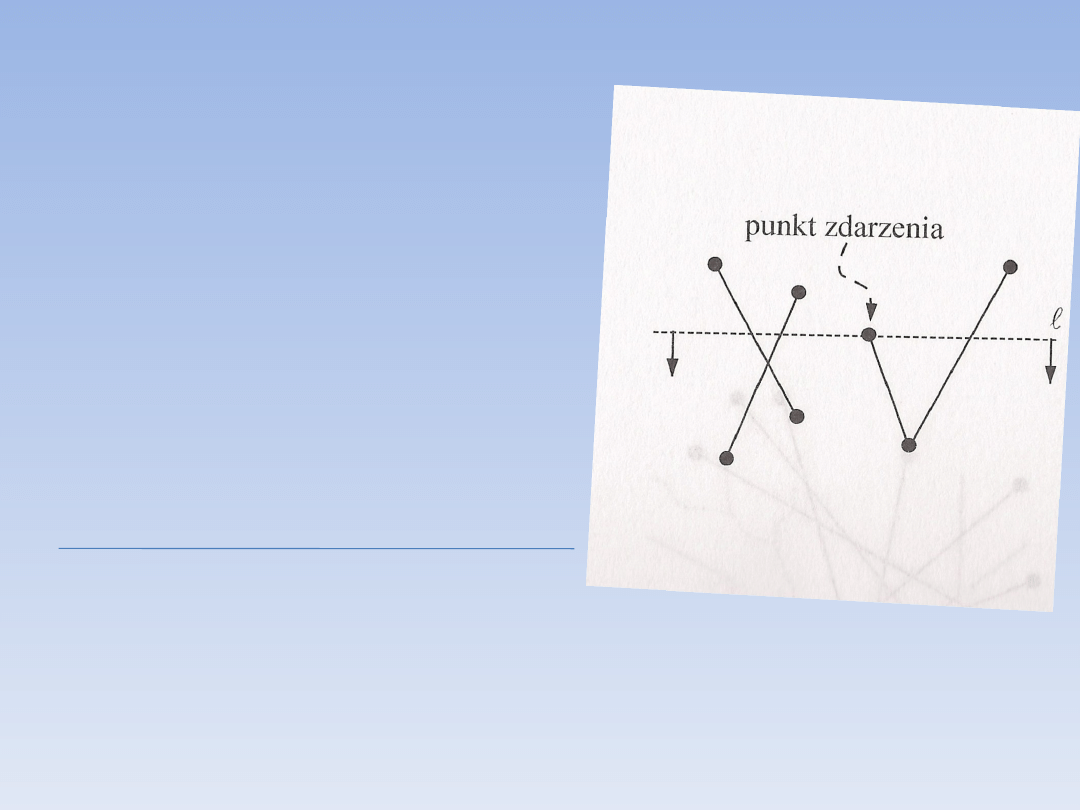
Krok 2:

• używamy tzw. miotły (prostej
poziomej) która przesuwa się w dół

• stanem miotły jest zbiór odcinków
przecinających ją

• aktualizacja stanu zmienia się
jedynie w pewnych sytuacjach
nazywanych punktami zdarzeń (są
nimi końce odcinków)

• tylko w punktach zdarzeń algorytm
aktualizuje stan miotły i wykonuje
testy przecięć

• odcinki usuwane ze stanu gdy
punkt zdarzeń jest dolnym punktem
końcowym odcinka

W dalszym ciągu jednak możliwe są
układy dla których sprawdzamy
kwadratową liczbę par podczas gdy
jest niewielka liczba punktów
przecięcia np. wszystkie docinki
przecinają oś x.

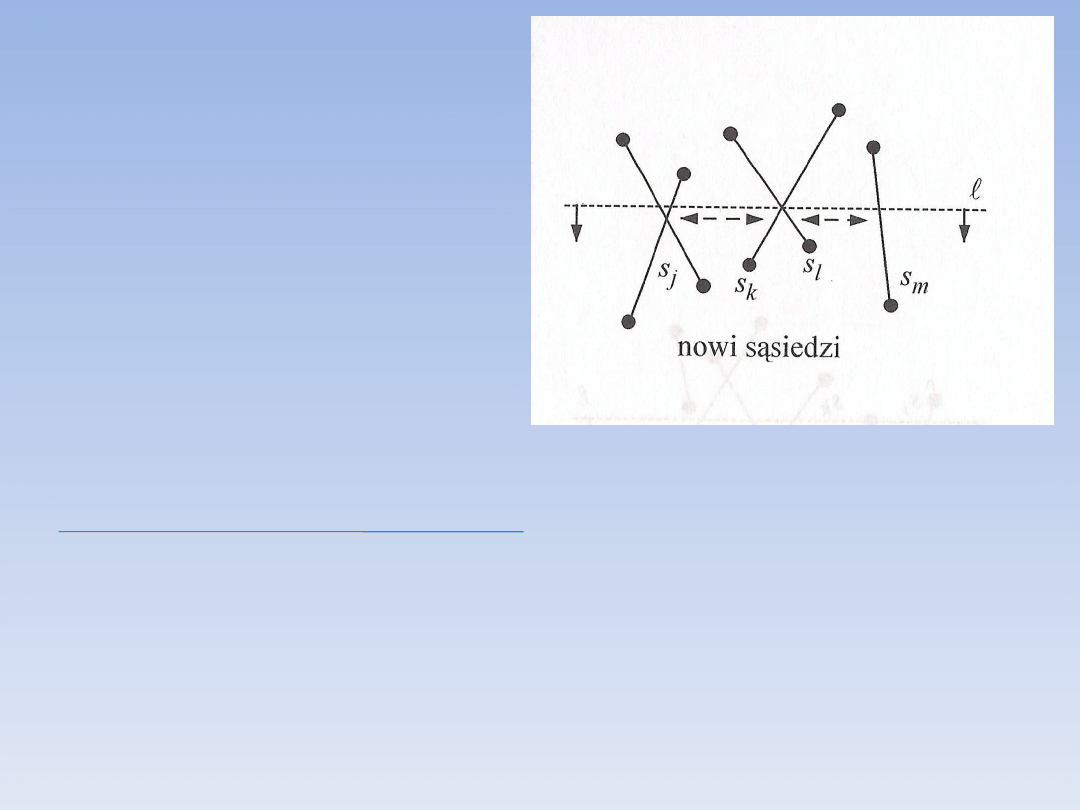
Krok 3:

• Porządkujemy odcinki od lewej
do prawej

• sprawdzamy tylko 2 odcinki
bezpośrednio po lewej i po prawej
od punktu zdarzeń

• w chwili przecięcia zmienia się
porządek odcinków, przez co
należy sprawdzić nowe pary
docinków

• stan miotły zmienia się w
punktach zdarzeń jak również w
punktach przecięcia

Założenie jest poprawne jeśli przyjmiemy że:

• nie bierzemy pod uwagę odcinków poziomych

• żadne trzy docinki nie krzyżują się w jednym punkcie

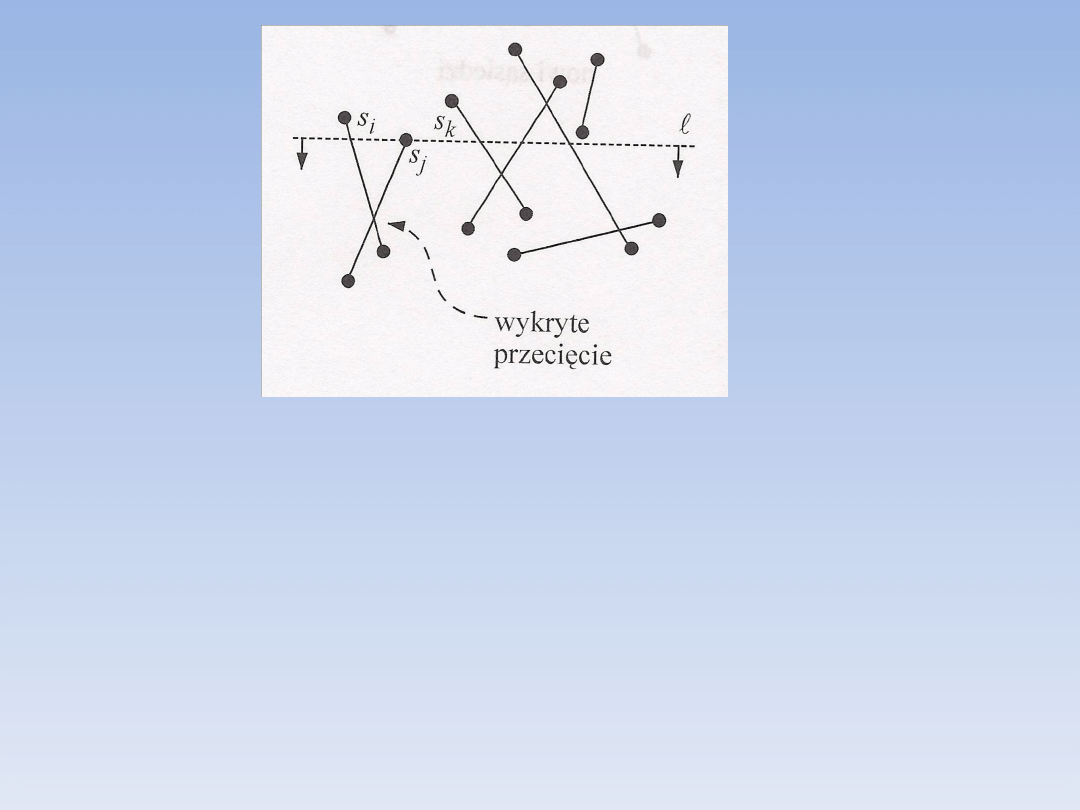
Przykład zmiany sprawdzania stanu spowodowanej wykryciem
nowego odcinka przecinającego:

• s

i

i s

k

sąsiadują ze sobą na miotle

• między nimi pojawia się nowy odcinek s

j

• należy sprawdzić w związku z tym przecięcia s

j

z s

i

i s

k

Struktury danych wykorzystywane przez

algorytm zamiatania:

• kolejka zdarzeń (przechowuje zdarzenia)

Do obsługi kolejki zdarzeń wykorzystywany jest algorytm który
dodaje i usuwa zdarzenia z niej. Jeśli 2 odcinki maja jednakową
współrzędną y to zwrócony z kolejki zdarzeń będzie zwracany ten
z mniejsza współrzędną x

• zrównoważone drzewo wyszukiwań binarnych

Przechowuje informacje o odcinkach które w danej chwili
przecinają miotłę

Algorytm FindIntersections

• Jest to algorytm wykorzystujący struktury:

- kolejki zdarzeń
- zrównoważone drzewo wyszukiwań binarnych

• Jego zadaniem jest wykrycie przecinających się odcinków
• Algorytm ten poprawnie oblicza wszystkie punkty przecięcia i

odcinki które je zawierają

• Czas działania algorytmu dla zbioru S, zawierającego n odcinków

na płaszczyźnie wynosi O(n log n + I log n), gdzie I jest liczbą
punktów przecięcia odcinków z S