Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Krawędź przecięcia się dwóch płaszczyzn opisanych śladami
Każde dwie płaszczyzny
i
nierównoległe względem siebie przecinają się
wzdłuż krawędzi k. Jest to prosta, należąca jednocześnie do obu płaszczyzn. Do jej
wyznaczenia potrzeba zatem określić alternatywnie:
Dwa punkty należące jednocześnie do obu płaszczyzn,
Jeden punkt wspólny dla obu płaszczyzn oraz prostą równoległą do obu
płaszczyzn.
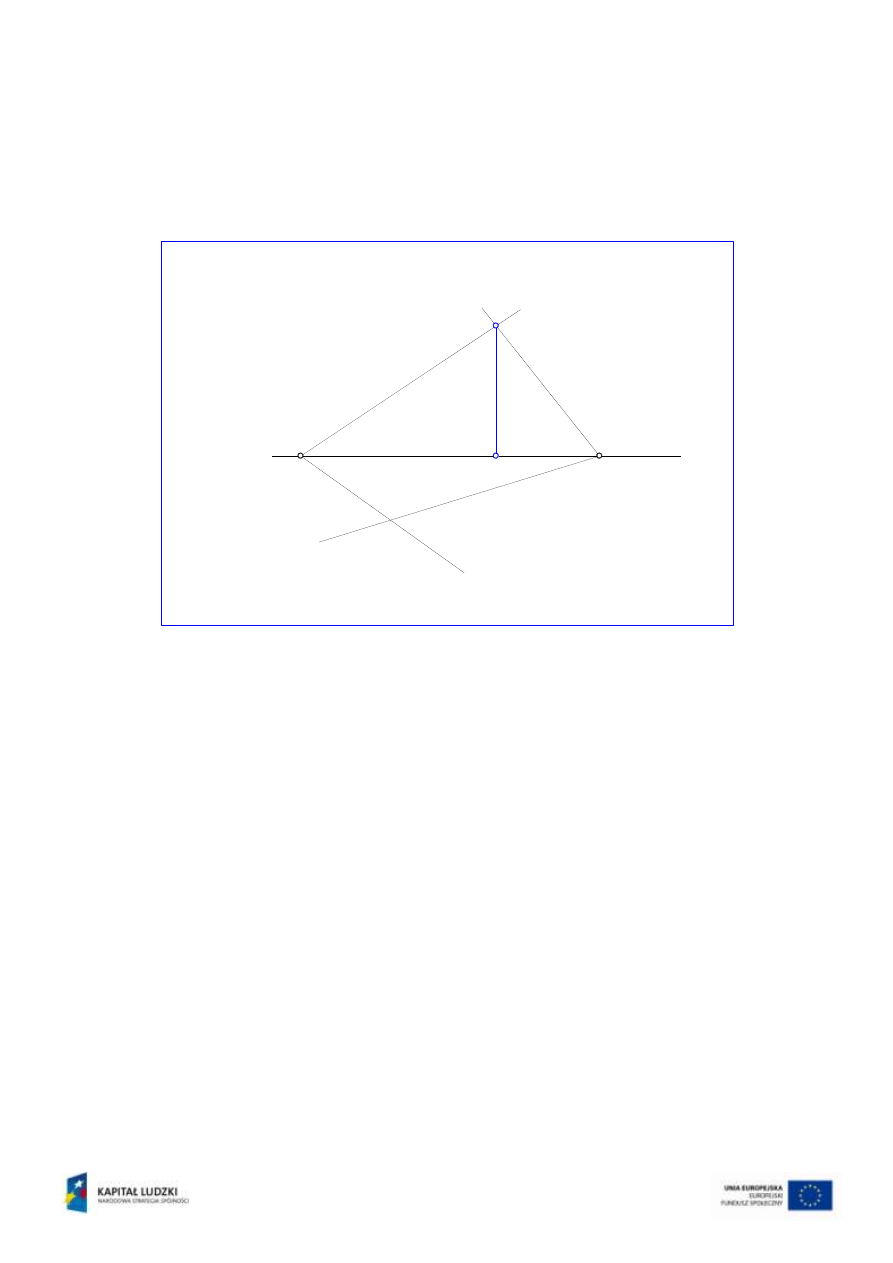
Zadanie 1
Należy wyznaczyć krawędź przecięcia płaszczyzn
i
, które opisane są śladami
(rys.1).
x
v
h
h
v
X
X
Rys.1
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
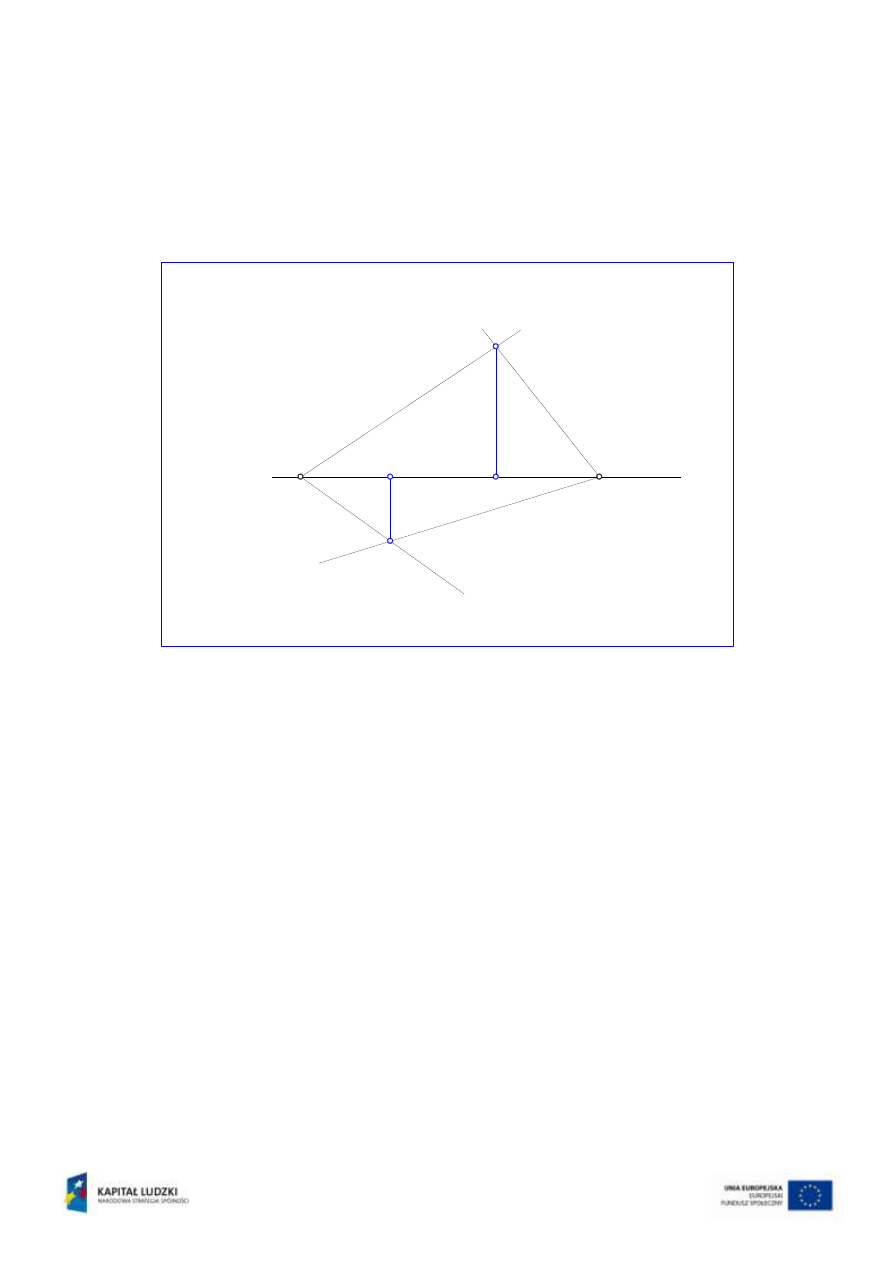
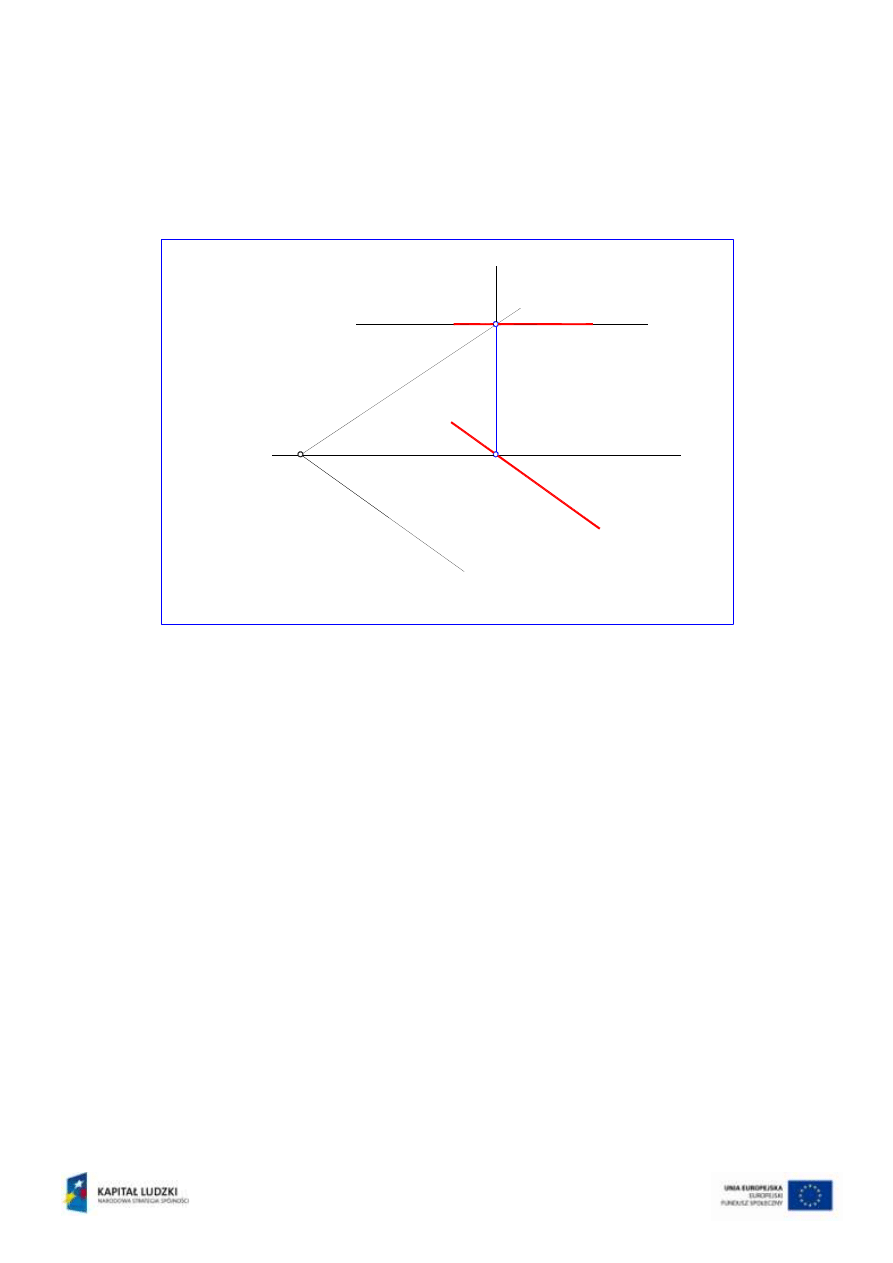
Ślady pionowe płaszczyzn v
i v
to proste leżące na rzutni pionowej
2
i
przecinające się w punkcie V
k
. Punkt ten zatem jest pierwszym punktem
wspólnym, leżącym na rzutni pionowej, reprezentowanym przez dwa swoje
rzuty: pionowy V
k
=V’’
k
oraz poziomy V’
k
(rys.2).
x
v
h
h
v
X
X
V
k
=V''
k
V'
k
Rys.2
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
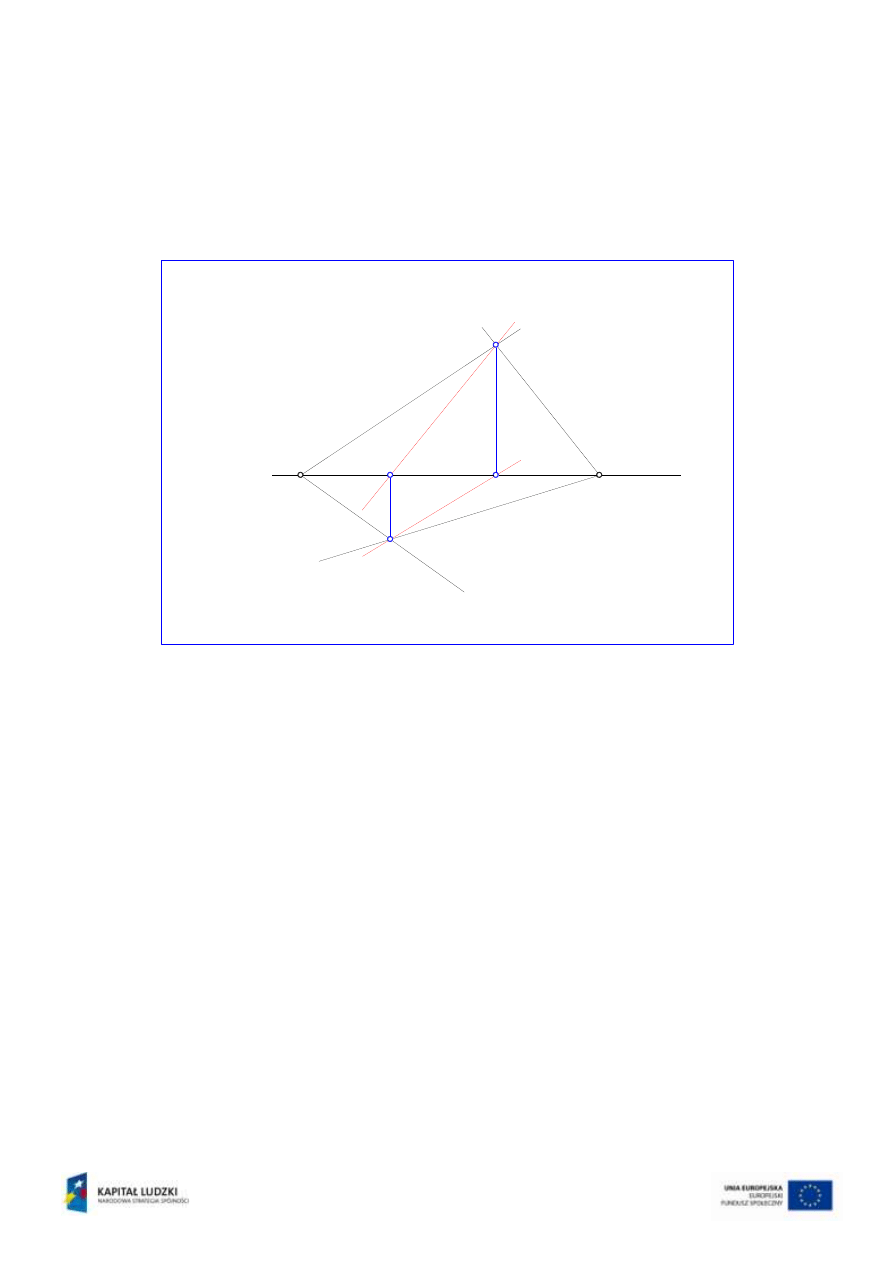
Ślady poziome h
i h
płaszczyzn
i
, to proste leżące na rzutni poziomej
1
.
Przecinają się one w punkcie H
k
, dając drugi wspólny punkt obu płaszczyzn. Leży on
na rzutni poziomej i jest reprezentowany przez dwa swoje rzuty: : poziomy H
k
=H’
k
oraz pionowy H’’
k
(rys.3).
x
v
h
h
v
X
X
V
k
=V''
k
V'
k
H
k
=H'
k
H''
k
Rys.3
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
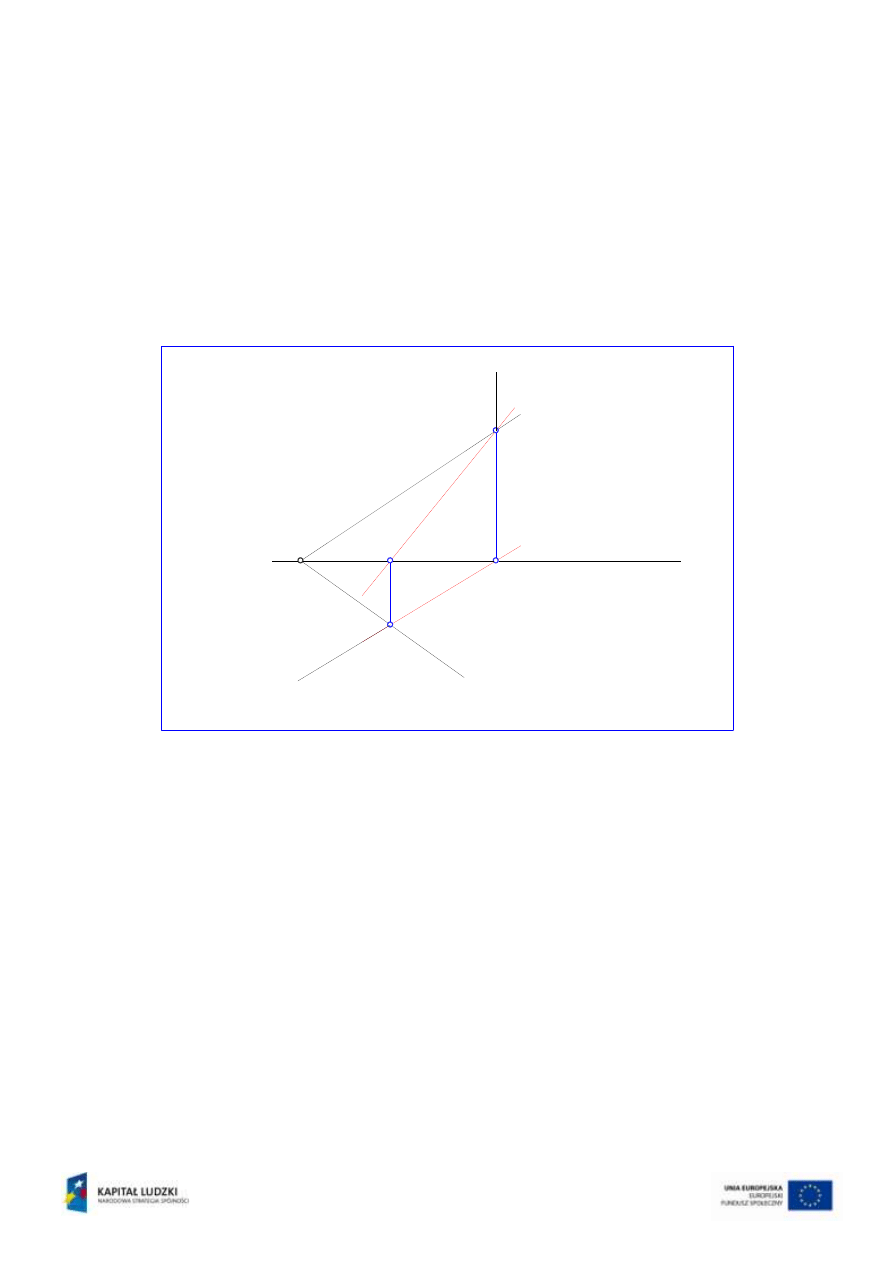
Przez tak znalezione dwa punkty należące jednocześnie do obu płaszczyzn można
poprowadzić prostą k, która stanowi krawędź przecięcia płaszczyzn. Rzut poziomy k’
krawędzi k uzyska się łącząc rzuty poziome punktów: H
k
=H’
k
oraz V’
k
, zaś rzut
pionowy k’’ krawędzi k uzyska się łącząc rzuty pionowe punktów: H’’
k
oraz V
k
=V’’
k
(rys.4).
x
v
h
h
v
X
X
V
k
=V''
k
V'
k
H
k
=H'
k
H''
k
k'
k''
Rys.4
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Podana wyżej reguła może być zastosowana z powodzeniem dla przypadków, w
których jedna lub obie płaszczyzny są rzutujące.
Zadanie 2
Wyznaczyć krawędź przecięcia płaszczyzn
i
, które opisane są śladami (rys.5).
Płaszczyzna
jest dowolna, zaś płaszczyzna
to płaszczyzna poziomo-rzutująca.
x
v
h
h
v
X
X
V
k
=V''
k
V'
k
H
k
=H'
k
H''
k
k'
k''
Rys.5
Realizując konstrukcję, jak w poprzednim przypadku, wyznacza się punkty
przecięcia śladów poziomych i pionowych płaszczyzn, otrzymując kolejno punkty H
k
oraz V
k
i ich rzu
ty. Prowadząc rzut poziomy krawędzi k’ przez rzuty poziome obu
punktów uzyskuje się jednoczenie k’ oraz śladu h
płaszczyzny
.
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Zadanie 3
Na rys.6 przedstawiono krawędź przecięcia dwóch płaszczyzn rzutujących
-
poziomo-
rzutującej oraz
- pionowo-rzu
tującej. Zastosowano analogiczny jakw
poprzednich przypadkach tok postępowania
x
v
h
h
v
X
X
V
k
=V''
k
V'
k
H
k
=H'
k
H''
k
k'
k''
Rys. 6
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
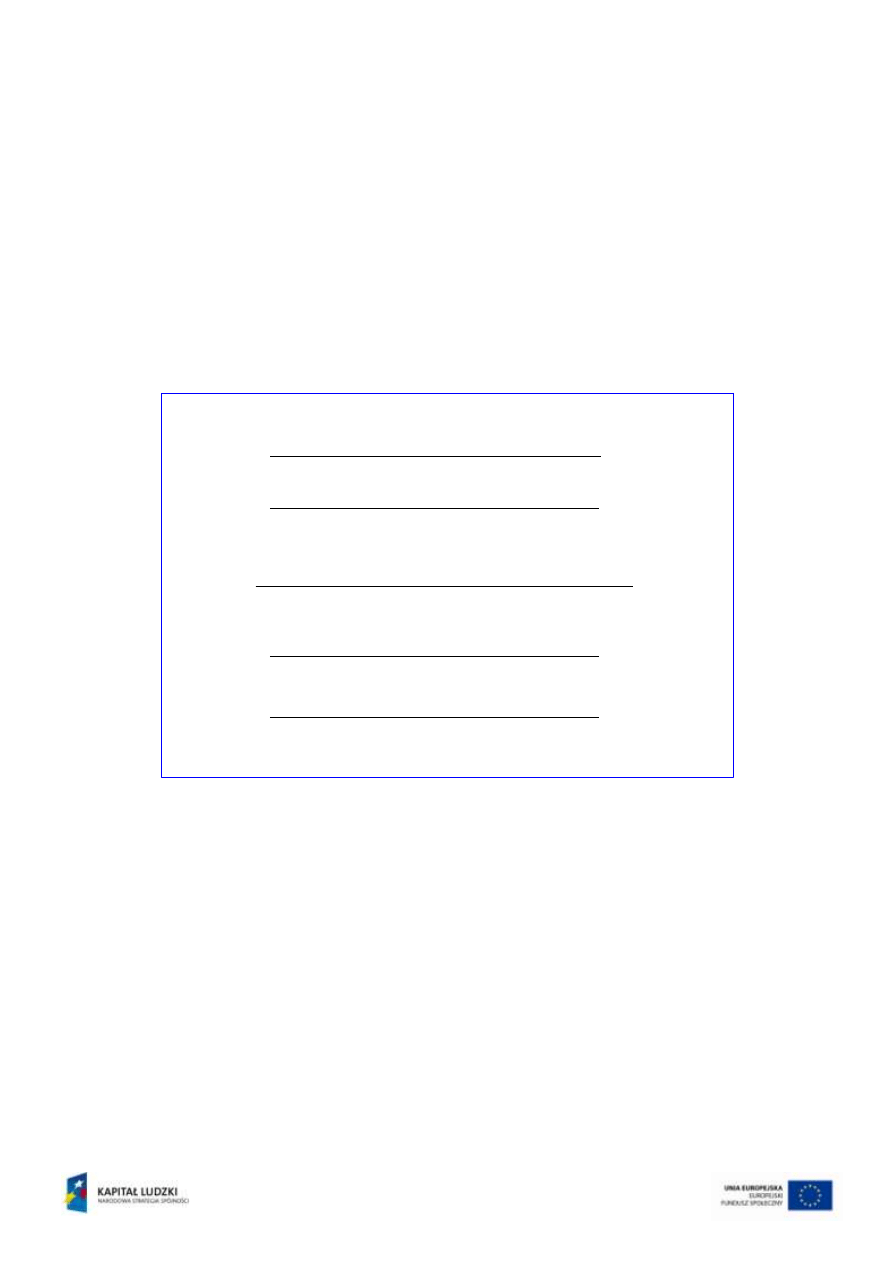
Warto przypatrzyć się konstrukcji krawędzi przecięcia płaszczyzn, z których jedna
jest płaszczyzną poziomą (rys.7).
Zadanie 4
x
v
h
v
''
X
V
k
=V''
k
V'
k
k'
k''
Rys.7
Płaszczyzna pozioma
reprezentowana jest przez swój rzut pionowy
’’
jednoczący się ze swoim śladem v
, brak jest śladu poziomego h
. Otrzymuje się
zatem tylko jeden wspólny punkt V
k
obu płaszczyzn. Krawędź musi przechodzić
przez ten punkt, a ponieważ należy także do płaszczyzny poziomej, więc sama jest
także prostą poziomą. Prosta pozioma (krawędź) z racji przynależności także do
płaszczyzny dowolnej musi spełniać odpowiednie warunki:
Rzut pionowy k’’ krawędzi przecięcia
z dowolną płaszczyzną
musi jednoczyć się
zatem z
’’, zaś rzut poziomy przechodzi przez V’
k
i jest równoległy do h
.
Analogiczne postępowanie dotyczy poszukiwania krawędzi przecięcia
płaszczyzny dowolnej i czołowej.
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Krawędź przecięcia się dwóch płaszczyzn opisanych śladami
zastosowanie konstrukcji krawędzi pomocniczych
Dla niektórych położeń płaszczyzn, dla określenia ich krawędzi przecięcia,
wymagane jest wprowadzenie konstrukcji płaszczyzn pomocniczych.
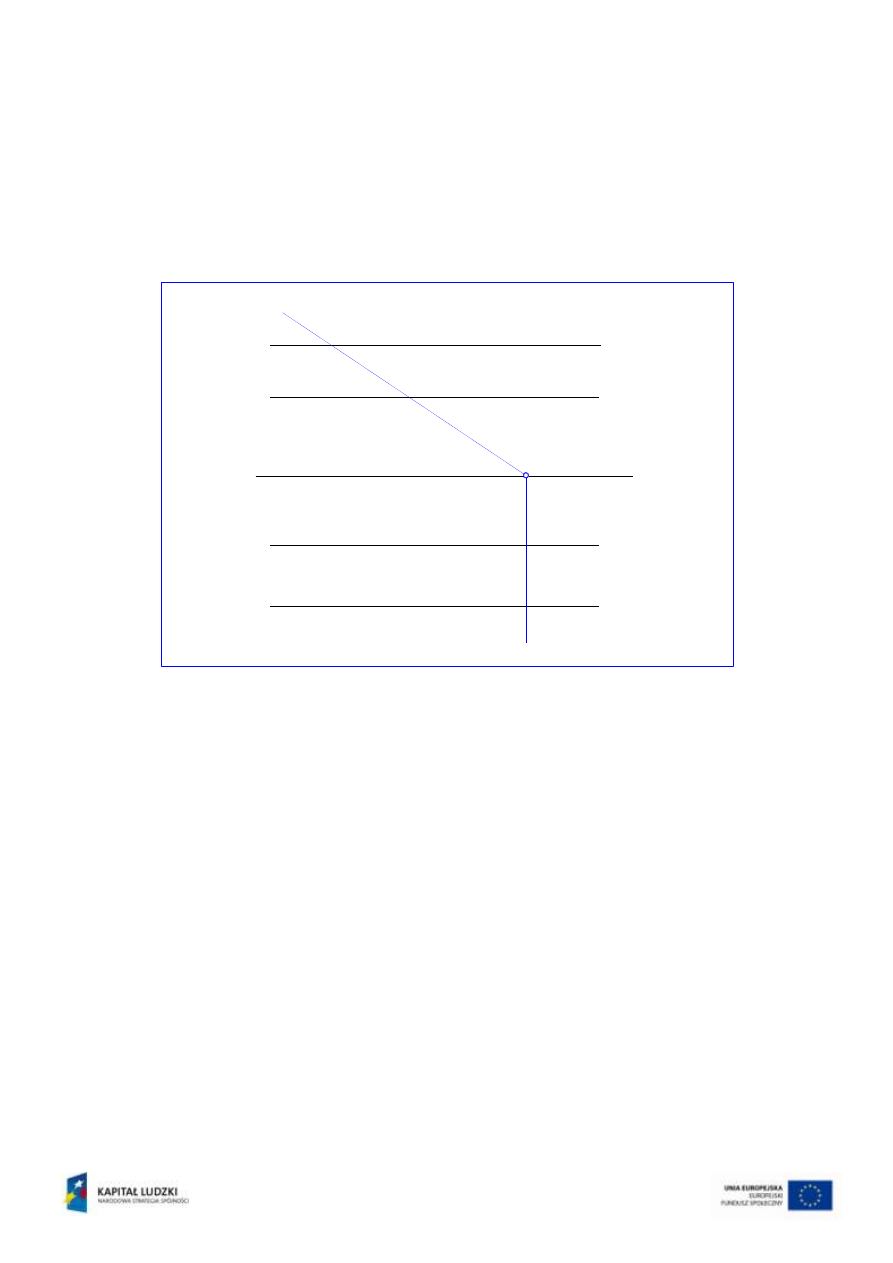
Zadanie 5
Na rys.8 przedstawiono dwie
płaszczyzny
i
równoległe do osi rzutów x. Należy
wyznaczyć krawędź przecięcia tych płaszczyzn.
x
v
h
v
h
Rys.8
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
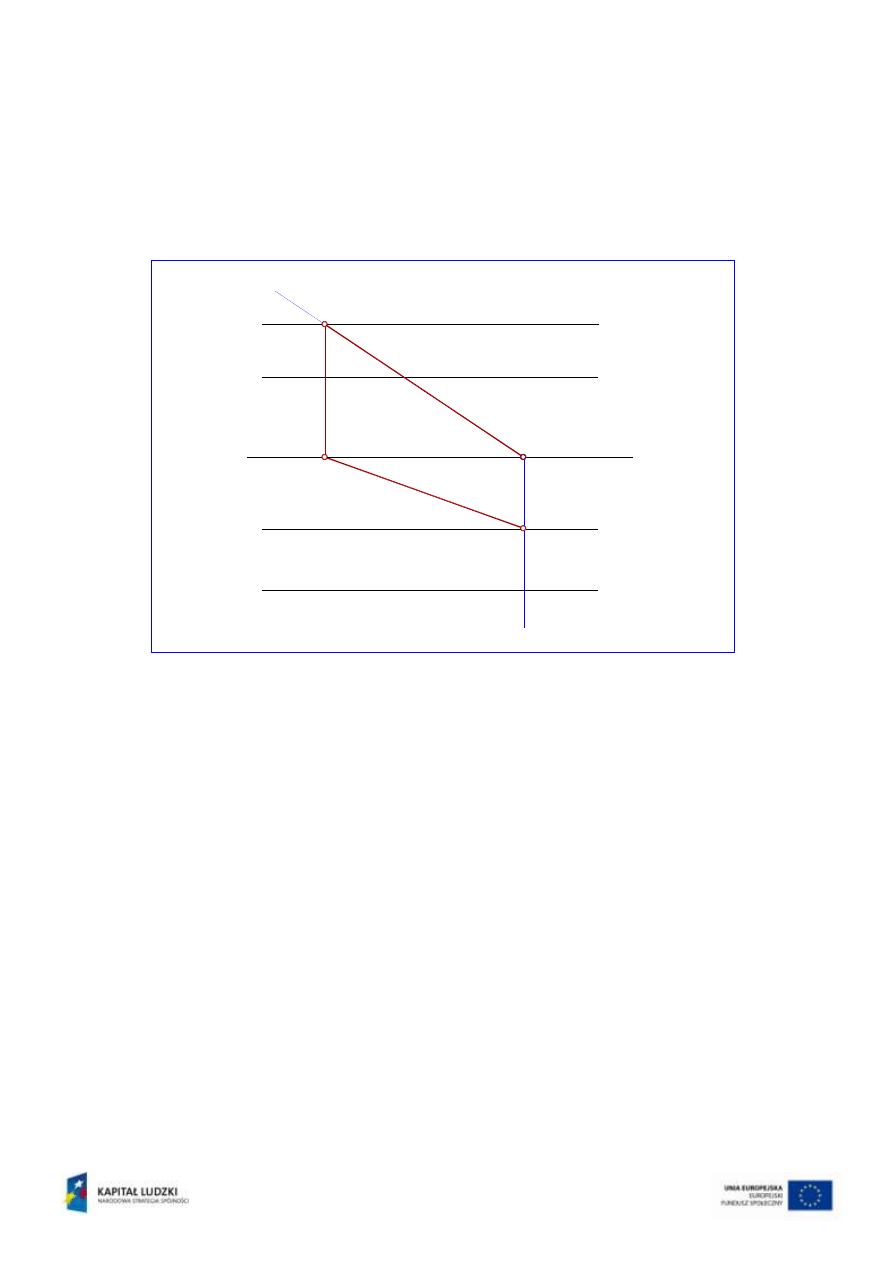
Ślady płaszczyzn nie przecinają się, zatem nie można zastosować dotychczas
poznanego sposobu postępowania. Przyjąć należy jedynie, że krawędź przecięcia k
będzie mieć oba rzuty k’ i k’’ równoległe do osi x. Należy jednak wyznaczyć jeden
wspólny punkt, przez który krawędź ta (oba rzuty) będzie przechodzić. Do tego celu
wprowadzona zostanie pomocnicza płaszczyzna pionowo-rzutująca
(rys.9).
x
v
h
v
h
h
v
X
Rys.9
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
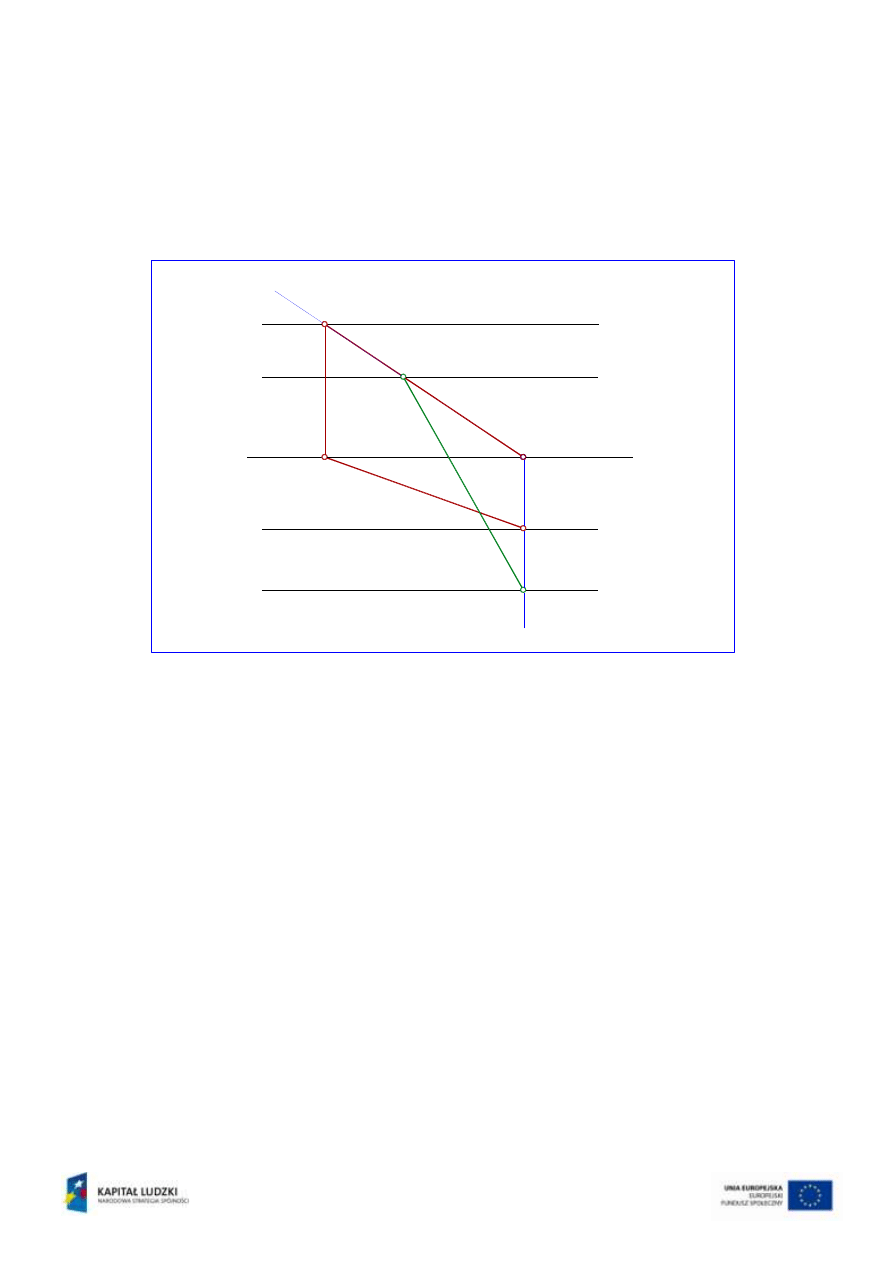
Płaszczyzna pomocnicza
pozwala na wyznaczenie krawędzi przecięcia k
1
z
płaszczyzną
. W tym celu wyznacza się dwa punkty wspólne płaszczyzn
oraz
.
Są to: punkt V
k1
przecięcia śladów pionowych v
i v
tych płaszczyzn oraz H
k1
–
punkt przecięcia śladów poziomych h
i h
tych płaszczyzn (rys.10).
x
v
h
v
h
h
v
X
V
k1
=V''
k1
H
k1
=H'
k1
V'
k1
k1'
k1''
Rys.10
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
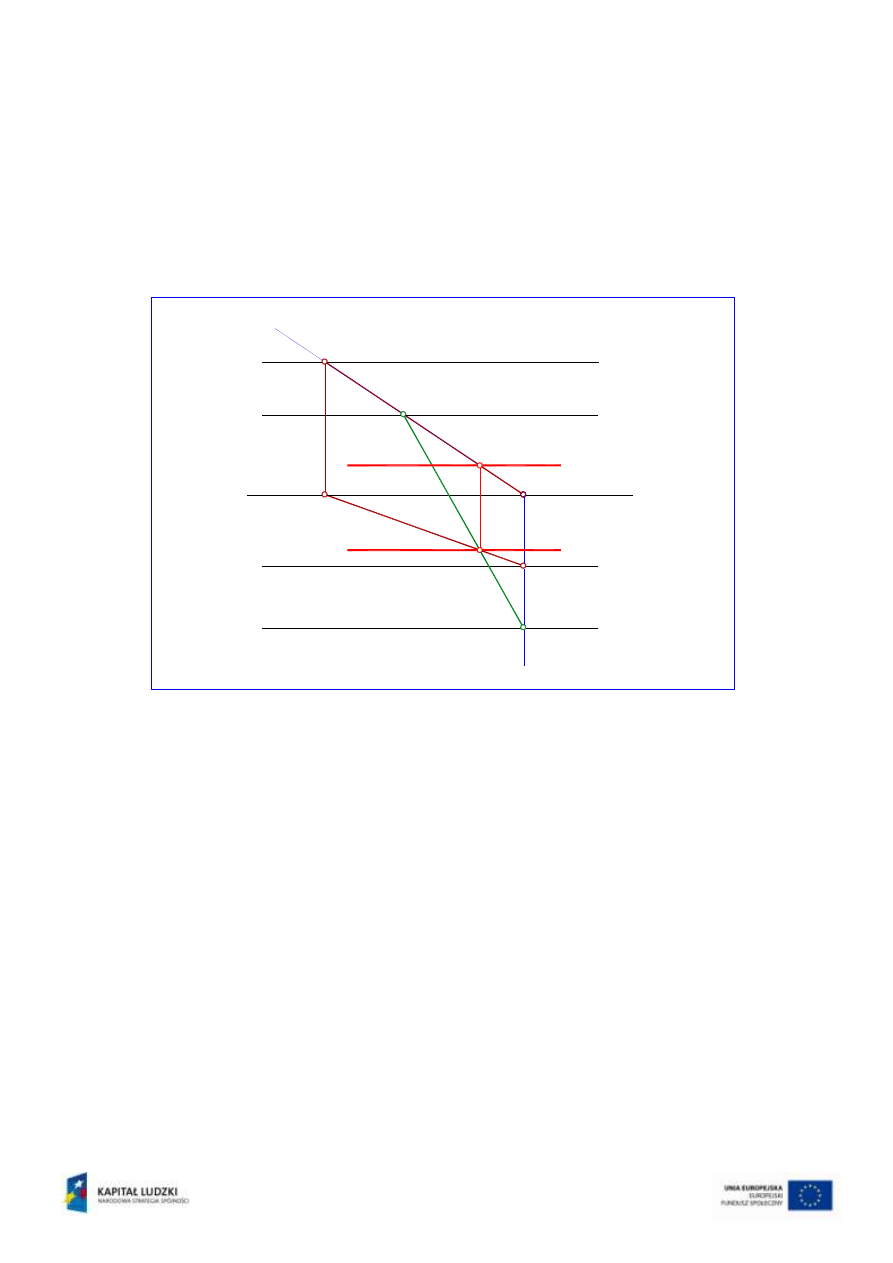
Płaszczyzna pomocnicza
pozwala również na wyznaczenie krawędzi przecięcia k
2
z płaszczyzną
. W tym
celu wyznacza się dwa punkty wspólne płaszczyzn
oraz
.
Są to: punkt V
k2
przecięcia śladów pionowych v
i v
tych płaszczyzn oraz H
k2
– punkt
przecięcia śladów poziomych h
i h
tych płaszczyzn (rys.11).
x
v
h
v
h
h
v
X
V
k1
=V''
k1
H
k1
=H'
k1
V'
k1
k
1
'
k
1
''
V
k2
=V''
k2
H
k2
=H'
k2
k
2
'
=k
2
''
Rys.11
Projekt Podbeskidzka Strefa Edukacji: Rozwój potencjału dydaktycznego i doskonalenie procesu
kształcenia w Bielskiej Wyższej Szkole im. J. Tyszkiewicza
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego.
Wyz
naczone krawędzie k1 i k2 przecinają się w punkcie P, którego dokładne
położenie widoczne jest w rzucie poziomym jako P’. Drugi rzut tego punktu znajduje
się na prostej odnoszącej w miejscu przecięcia z rzutami pionowymi k1’’ oraz k2’’.
Punkt P jest jedyny
m wspólnym punktem wszystkich rozpatrywanych płaszczyzn, a
więc płaszczyzny
,
i pomocniczej
. Prze punkt ten zatem przechodzi krawędź k
w dwóch swoich rzutach: k’ oraz k’’. (rys.12).
x
v
h
v
h
h
v
X
V
k1
=V''
k1
H
k1
=H'
k1
V'
k1
k
1
'
k
1
''
V
k2
=V''
k2
H
k2
=H'
k2
k
2
'
=k
2
''
P'
P''
k'
k''
Rys.12