1

Badanie
współzależności
zjawisk

KORELACJA I REGRESJA
LINIOWA

2

Wstęp



Prezentowane dotychczas metody statystyczne dotyczyły
analizy struktury zbiorowości i opierały się na
obserwacjach jednej zmiennej (cechy). Tymczasem
jednostki tworzące zbiorowość charakteryzowane są
zazwyczaj za pomocą więcej niż jednej cechy. Cechy te nie
są od siebie odizolowane, ale wzajemnie się warunkują.
Zachodzi zatem potrzeba ich łącznego badania. Celem
tego rodzaju analizy jest stwierdzenie, czy między
badanymi zmiennymi zachodzą jakieś zależności, jaka jest
ich siła, kształt i kierunek. Dział statystyki zajmujący się
badaniem związków między kilkoma zmiennymi nosi
nazwę teorii współzależności.

3

Rodzaje zależności



Zależność funkcyjna (deterministyczna) – występuje,

gdy ściśle określonej wartości jednej zmiennej (tzw.

zmiennej niezależnej) odpowiada ściśle określona i

zawsze ta sama wartość drugiej zmiennej (tzw.

zmiennej zależnej).



Zależność korelacyjna – występuje, gdy ściśle

określonej wartości zmiennej niezależnej odpowiada

przybliżona wartość zmiennej zależnej.
Zależność korelacyjna jest szczególnym przypadkiem

zależności stochastycznej tj. takiej, że z każdą

wartością zmiennej niezależnej związana jest

populacja wartości zmiennej zależnej o określonym

rozkładzie prawdopodobieństwa.

4

Rodzaje zależności
korelacyjnych



Ze względu na liczbę zmiennych:

- proste - jedna zmienna zależna i jedna zmienna

niezależna,

-

złożone – jedna (wiele) zmiennych zależnych i

wiele (jedna) zmienna niezależna.



Ze względu na postać zależności:

-

zależność liniowa,

-

zależność krzywoliniowa.

W dalszej części wykładu ograniczymy się do

interpretacji prostej zależności liniowej.

5

Metody oceny istnienia
zależności

1.

Ocena kształtu rozkładu punktowego wykresu
korelacyjnego.

2.

Ocena wartości współczynnika korelacji.

3.

Wyliczenie równania prostej regresji i ocena
współczynnika kierunkowego prostej.

4.

Analiza wariancji w regresji.

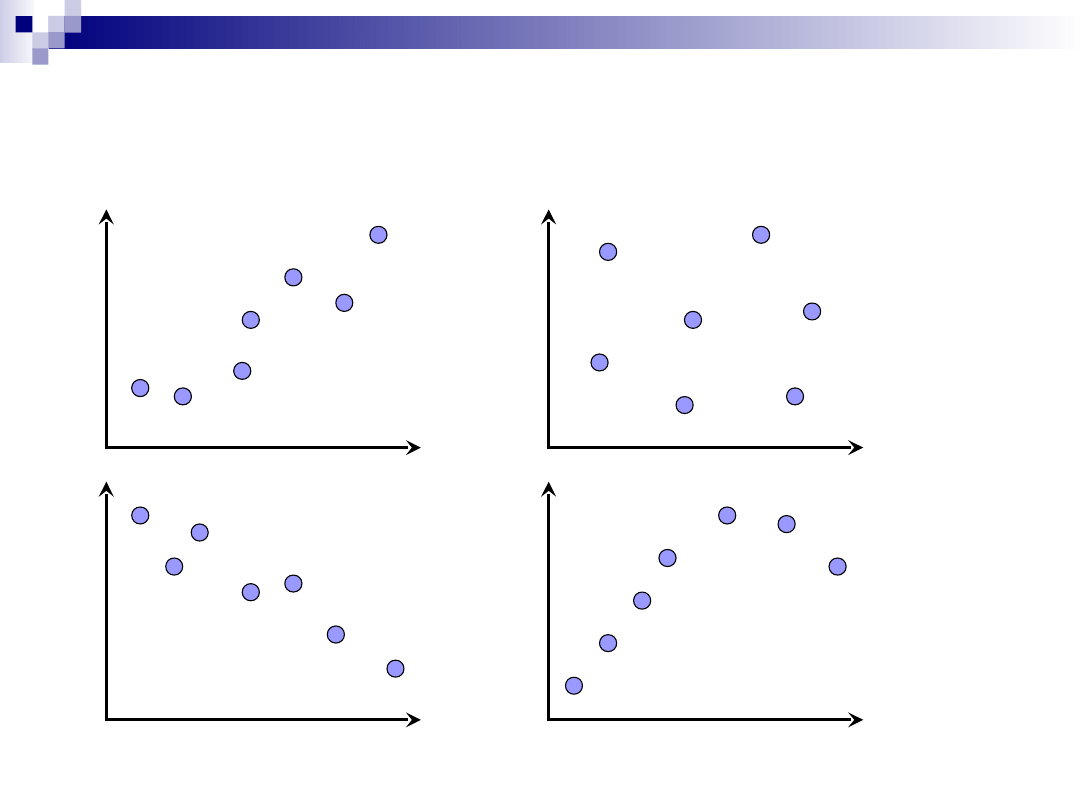
6

Punktowy wykres
korelacyjny

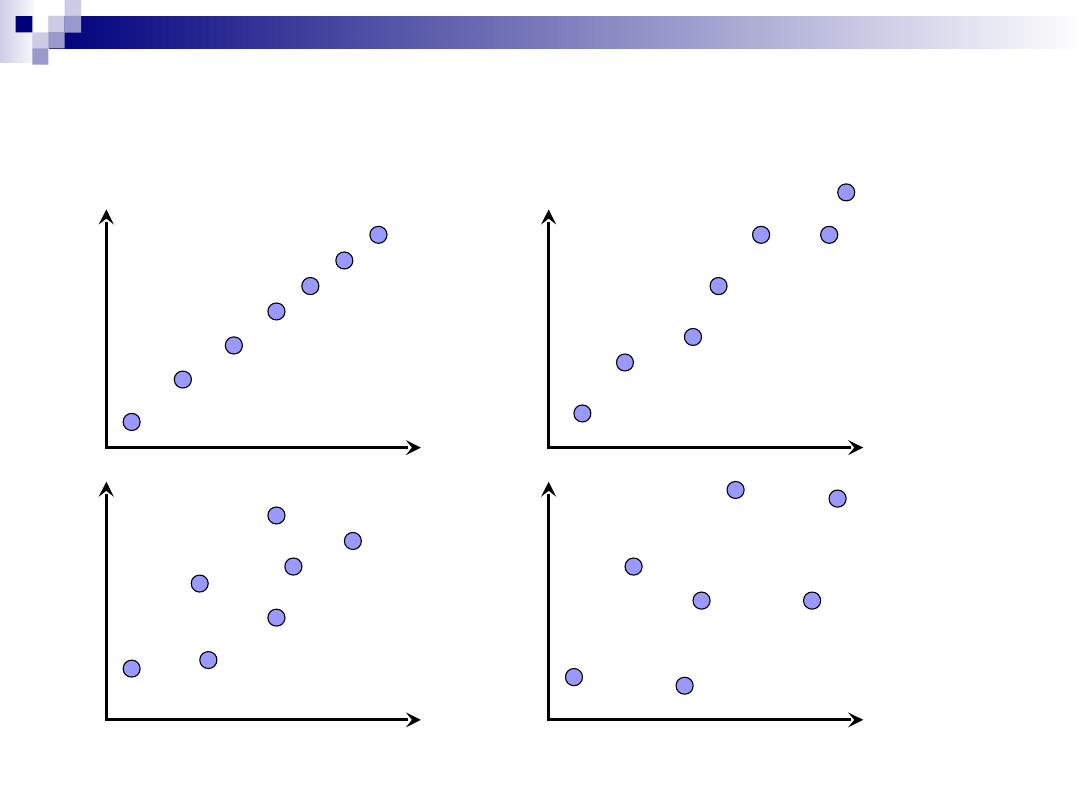
7

Ocena siły zależności na
wykresie

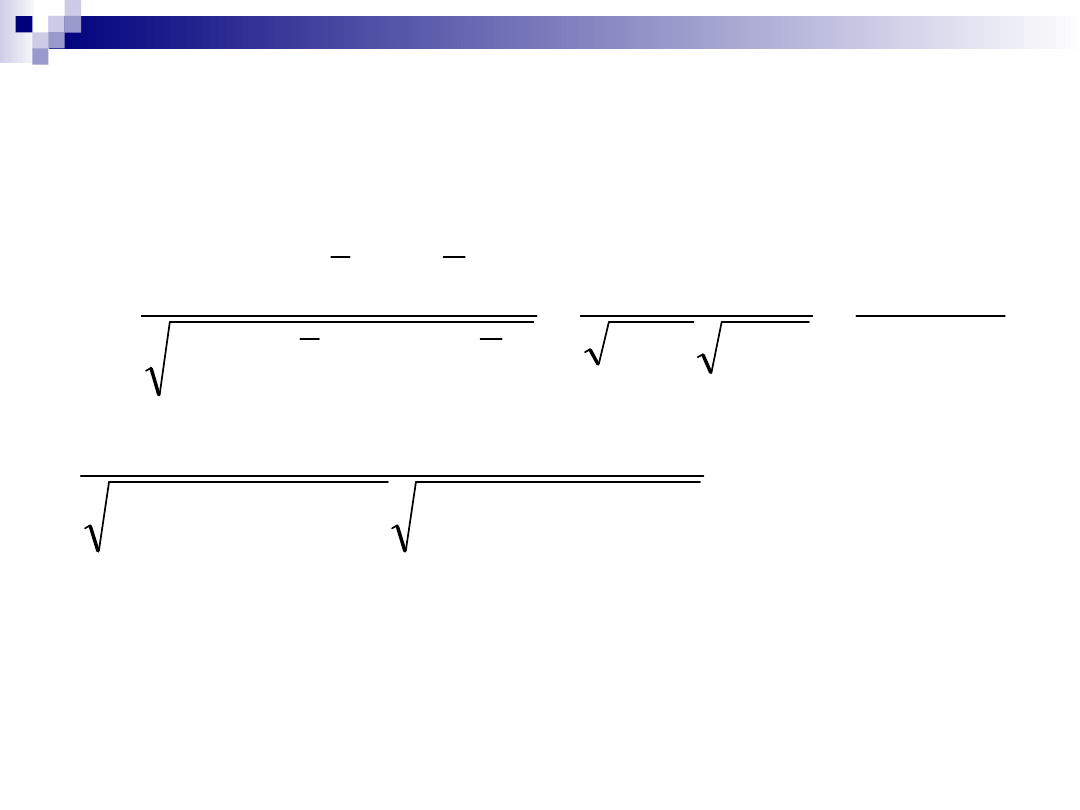
8

Współczynnik korelacji
liniowej









 



 

 









 

zmiennych

tych

e

standardow

odchylenia

-

y,

i

x

zmiennych

a

kowariancj

-

,

cov

:

,

cov

var

var

,

cov

2

2

2

2

2

2

,

y

x

i

i

i

i

i

i

i

i

y

x

i

i

i

i

y

x

s

s

y

x

gdzie

y

y

n

x

x

n

y

x

y

x

n

s

s

y

x

y

x

y

x

y

y

x

x

y

y

x

x

r













































9

Współczynnik korelacji -
interpretacja

Dla oceny korelacji linowej posługujemy się

współczynnikiem korelacji Pearsona „r”. Jego

wartość waha się w zakresie <-1;1> Wartość „0”

wskazuje na brak istnienia zależności. W miarę

wzrostu wartości bezwzględnej zależność wzrasta.

Znak przed współczynnikiem określa kierunek

zależności. W przypadku „-” oznacza to, że wraz ze

wzrostem wartości zmiennej niezależnej – wartość

zmiennej zależnej maleje. W przypadku „+” – wraz

ze wzrostem wartości zmiennej niezależnej,

wartość zmiennej zależnej także wzrasta.

10

Ocena siły współczynnika
korelacji

Przy ocenie siły związku zwykle stosuje się

następującą skalę:

-

r = 0 – brak korelacji,

-

0 < r < 0,1 – korelacja nikła,

-

0,1 < r < 0,3 – korelacja słaba,

-

0,3 < r < 0,5 – korelacja przeciętna,

-

0,5 < r < 0,7 – korelacja wysoka,

-

0,7 < r < 0,9 – korelacja bardzo wysoka,

-

0,9 < r < 1 – korelacja prawie pełna

11

Ocena istotności
współczynnika korelacji



Do oceny istotności współczynnika korelacji można

posłużyć się tablicami istotności. Po wyliczeniu

wartości współczynnika korelacji (na podstawie

pobranej próby), który określimy jako empiryczny

(r

emp

) jego wartość porównujemy z wartością

krytyczną odczytaną z tablic dla określonego przez

nas poziomu istotności  liczby zmiennych

porównywanych k (dla korelacji prostej k=2) i liczby

stopni swobody  = n - k. W przypadku, gdy wartość

empiryczna jest większa od krytycznej dla 0,05

– korelacja jest istotna (a dla  = 0,01 – wysoce

istotna)

12

Współczynnik determinacji



Współczynnik determinacji „d” określa w jakim
stopniu zmiany zmiennej zależnej spowodowane
są zmianami zmiennej niezależnej, a w jakim
innymi zmiennymi, których nie badaliśmy.
Wyrażany jest w przedziale od <0;1> lub po
przemnożeniu przez 100 w „%”

d = r

2

13

Równanie regresji liniowej i
ocena jego współczynników



Ogólna postać prostej regresji dana jest wzorem:

ŷ = a + bx

gdzie:
ŷ – szacowana wartość zmiennej zależnej,
a – wyraz wolny równania, decydujący na wykresie

o miejscu przecięcia prostej z osią OY,

b – współczynnik kierunkowy prostej, który w

interpretacji na wykresie określa kąt pomiędzy

osią OX, a prostą regresji

14

Wyliczenie i interpretacja
współczynnika regresji b



Współczynnik ten określa, o ile zmieni się
wartość zmiennej zależnej, jeśli wartość zmiennej
niezależnej zmieni się o jednostkę

 

x

xy

b

var

cov



15

Odchylenie standardowe regresji

(błąd standardowy estymacji) s

y/x



Mówi o przeciętnym odchyleniu punktów

od prostej regresji

)

2

(

var

)

(cov

var

2

)

(

2

2

^

/















n

n

x

xy

y

n

y

y

s

i

i

x

y

16

Błąd standardowy

współczynnika regresji s

b

x

s

n

s

x

y

b

var

2

/





jest miarą błędu oszacowania współczynnika b

17

Wyliczenie równania prostej
regresji

Mając wyliczony współczynnik kierunkowy prostej b,
łatwo jest określić pełne równanie prostej regresji:

Po wyliczeniu wartości współrzędnych dwóch punktów
można wykreślić prostą regresji.

 

x

x

b

y

y







ˆ

18

Ocena istotności
współczynników równania
regresji liniowej



Stosując test t-Studenta można ocenić niezależnie
istotność współczynnika kierunkowego prostej i wyrazu
wolnego równania wg wzorów,

(gdzie s

b

i s

a

– błędy standardowe odpowiednich współczynników)

porównując te wartości z wartościami z tablic dla danego
poziomu istotności i liczby stopni swobody n-2.

a

emp

b

emp

s

a

t

s

b

t





;

19

Ocena istotności
współczynników równania
regresji - interpretacja

Hipoteza zerowa zakłada, że dany współczynnik równa

się zero, hipoteza alternatywna – że jest różny od
zera.

H

0

: b = 0

H

0

: a = 0

H

1

: b ≠ 0

H

1

: a ≠ 0

W sytuacji, gdy współczynnik regresji nie różni się

istotnie od zera oznacza to, że brak jest istotnej
zależności między zmiennymi. Ocena istotności
wyrazu wolnego ma jedynie znaczenie pomocnicze.

20

Analiza wariancji w regresji



Analiza wariancji w regresji jest jedną z metod

oceny istotności zależności między zmiennymi.

Dzieli ona wariancję próby na dwa rodzaje:

-

wynikającą z istnienia zależności, która powoduje

że wartości zmiennej zależnej odchylają się od

wartości średniej,

-

wynikającą z istnienia zmienności błędu, do

którego zaliczamy wszystkie czynniki, których nie

jesteśmy w stanie skontrolować, a które to

odchylają wyniki od ich wartości teoretycznej

wyliczonej na podstawie równania.

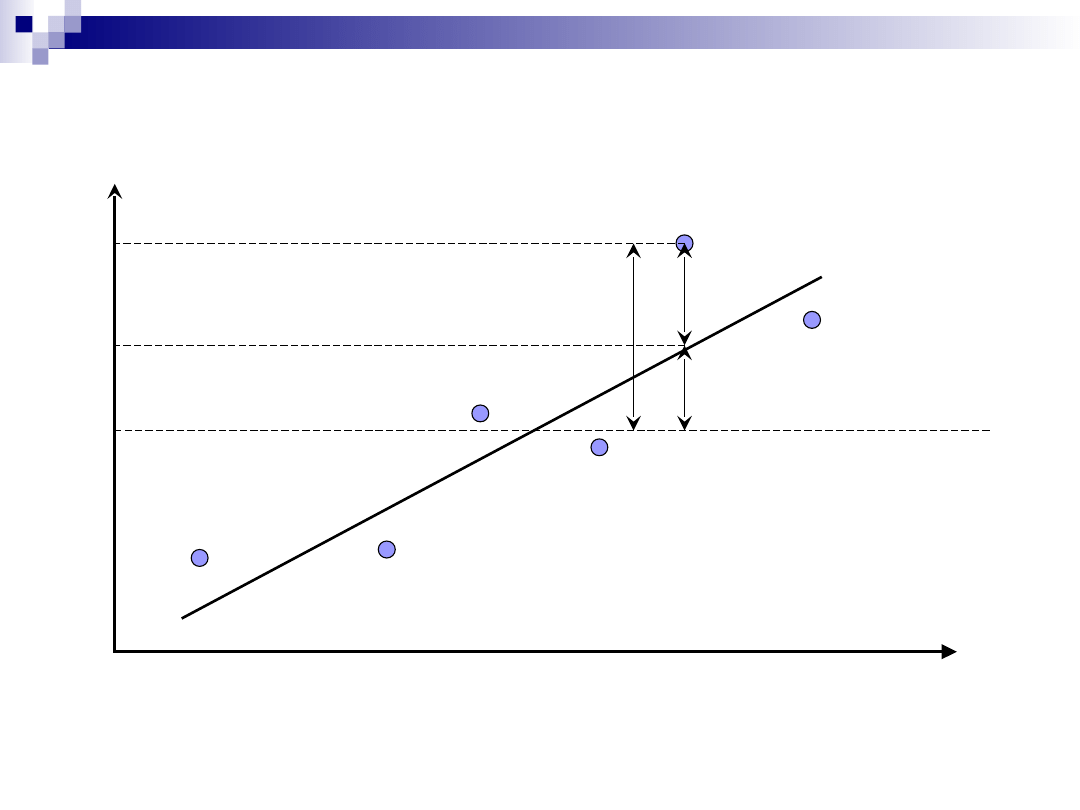
21

Analiza wariancji w regresji – ilustracja
zasady na wykresie

zmienność
ogólna

zmienność
wyjaśniona regresją

zmienno
ść
losowa
(błąd)

S

2

= S

2

E

+S

2

R



y

^

y

i

y

X

i

22

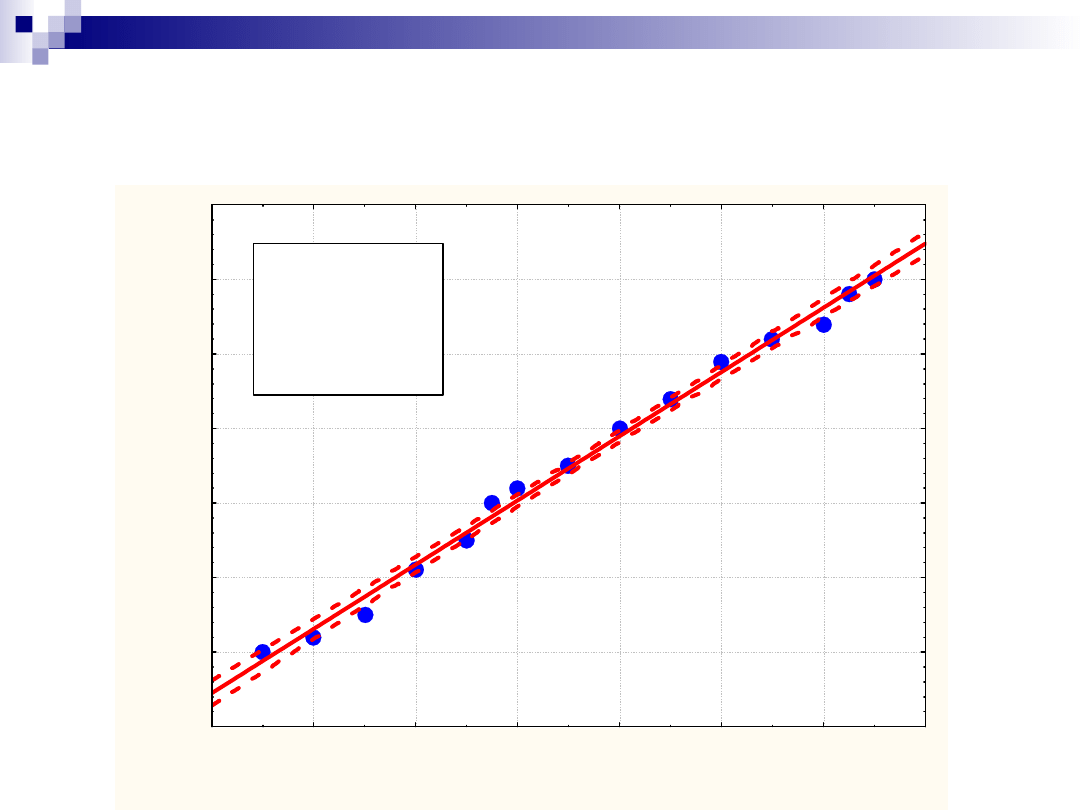
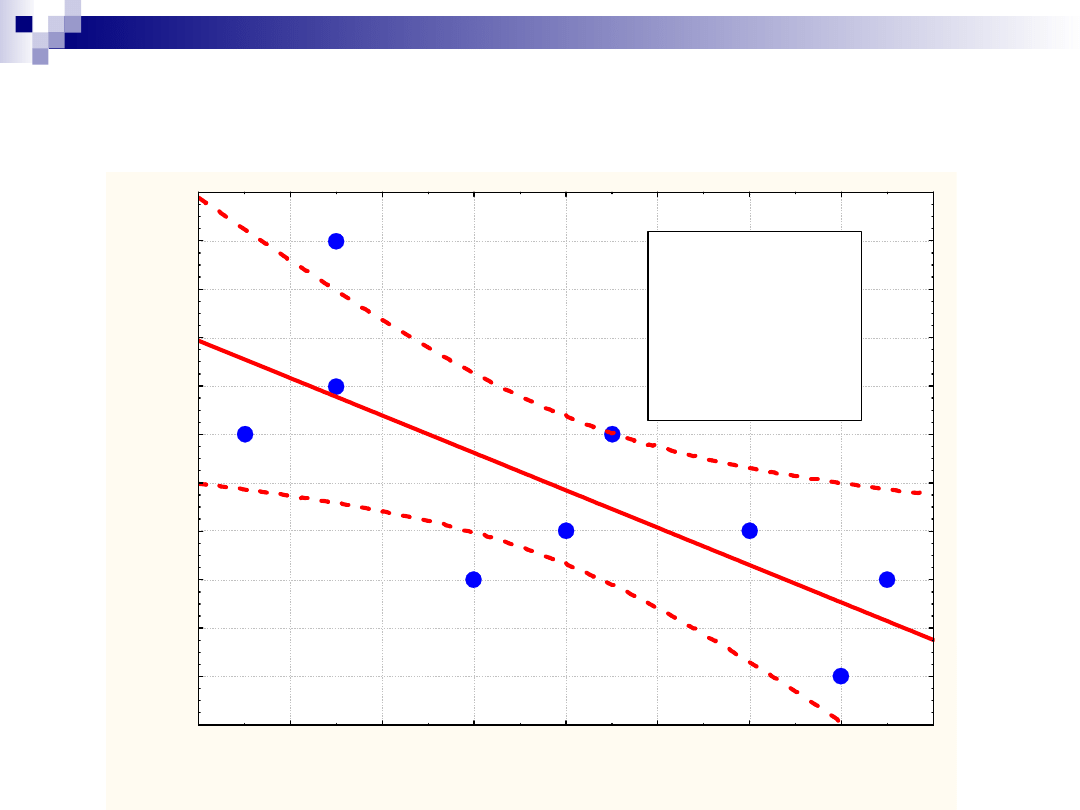
Obszar ufności i krzywe
ufności

6

8

1 0

1 2

1 4

1 6

1 8

2 0

W ie k - x

1 1 0

1 2 0

1 3 0

1 4 0

1 5 0

1 6 0

1 7 0

1 8 0

W

zro

st

- y

y = 8 8 ,7 + 4 ,3 0 x

n = 1 5 ;
r = 0 , 9 9 7 ;
p = 0 , 0 0 0 0 ;

23

Przykła
d

W celu określenia zależności

między zawartością tłuszczu (%) w
mleku a mlecznością [l/dobę] badano
obie cechy
u dziewięciu krów (n = 9) i uzyskano
następujące wyniki:

24



x

Mleczność

[l/doba]

x

Tłuszcz

(%)

y

x

2

y

2

xy

27

3,8

729

14,44

102,6

20

3,9

400

15,21

78

15

4,2

225

17,64

63

15

4,5

225

20,25

67,5

21

4,1

441

16,81

86,1

24

3,9

576

15,21

93,6

18

3,8

324

14,44

68,4

26

3,6

676

12,96

93,6

13

4,1

169

16,81

53,3

179

35,9

3765

143,77

706,1

19,9

3,99

25

1 2

1 4

1 6

1 8

2 0

2 2

2 4

2 6

2 8

M le c z n o ś ć [l/ d o b a ]

3 , 5

3 , 6

3 , 7

3 , 8

3 , 9

4 , 0

4 , 1

4 , 2

4 , 3

4 , 4

4 , 5

4 , 6

Z

aw

ar

to

ść

tłu

sz

cz

u [

%

]

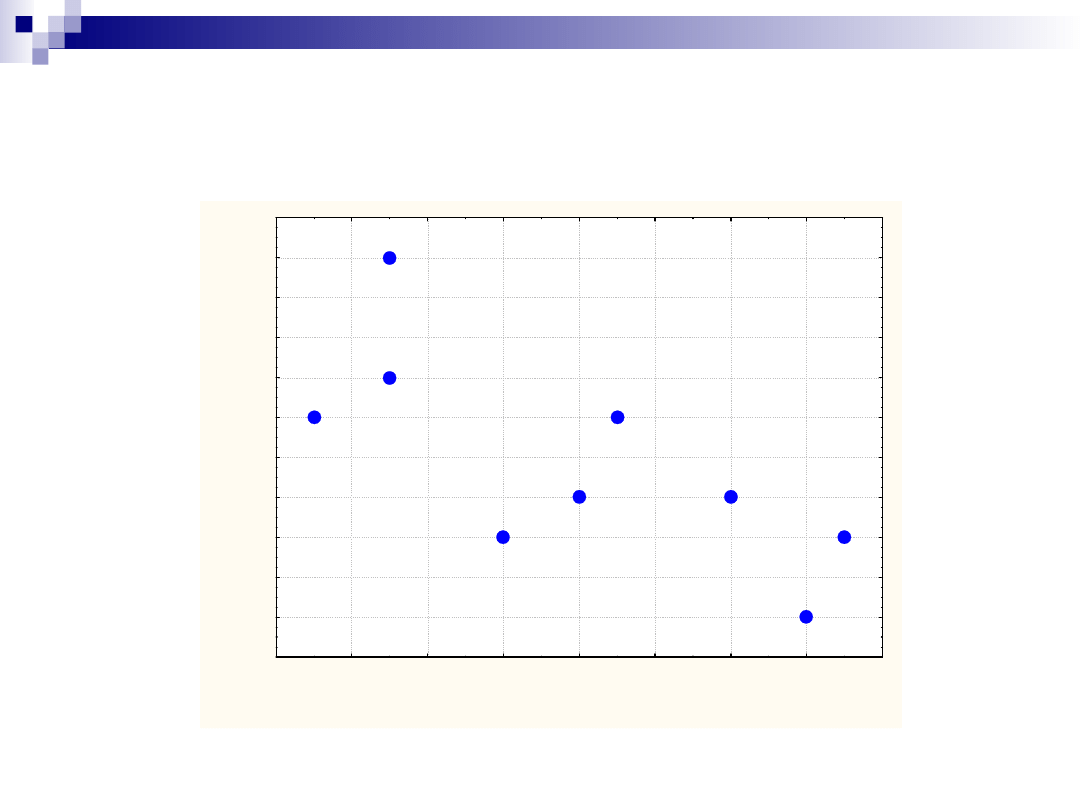
PUNKTOWY WYKRES KORELACYJNY

26

 

 

05

,

0

7

2

9

;

05

,

0

;

05

,

0

2

2

2

2

2

2

666

,

0

734

,

0

83

,

5

1844

2

,

71

9

,

35

77

,

143

9

179

3765

9

9

,

35

179

1

,

706

9

r

r

r

r

y

y

n

x

x

n

y

x

xy

n

r

emp

k

n

emp







































































 

 

%

0386

,

0

1844

2

,

71

179

3765

9

9

,

35

179

1

,

706

9

var

cov

2

2

2

/







































x

x

n

y

x

xy

n

x

xy

b

x

y

Współczynnik korelacji

Współczynnik regresji

194

,

0

)

2

9

(

9

1844

)

2

,

71

(

83

,

5

)

2

(

var

)

(cov

var

2

2

/

















n

n

x

xy

y

x

y

S

Odchylenie standardowe regresji

27

 

x

y

x

y

x

y

x

x

b

y

y

0386

,

0

76

,

4

ˆ

768

,

0

0386

,

0

99

,

3

ˆ

)

9

,

19

)(

0386

,

0

(

99

,

3

ˆ

ˆ

























Równanie regresji

0135

,

0

1844

194

,

0

9

var

2

2

/











x

s

n

x

y

Sb

Błąd standardowy s

b

28

Przedstawienie
graficzne

1 2

1 4

1 6

1 8

2 0

2 2

2 4

2 6

2 8

M le c z n o ś ć - x [l/ d o b a ]

3 , 5

3 , 6

3 , 7

3 , 8

3 , 9

4 , 0

4 , 1

4 , 2

4 , 3

4 , 4

4 , 5

4 , 6

Z

aw

ar

to

ść

tłu

sz

cz

u -

y

[%

]

y = 4 ,7 6 - 0 ,0 3 8 6 x

r = - 0 , 7 3 4 ;
r

2

= 0 , 5 3 7

p = 0 , 0 2 4 ;