1

1

Klasyczny model

Klasyczny model

regresji liniowej –

regresji liniowej –

przypadek wielu

przypadek wielu

zmiennych

zmiennych

objaśniających

objaśniających

2

2

Model ekonometryczny

Model ekonometryczny

jest równaniem (lub układem

jest równaniem (lub układem

równań), które przedstawia

równań), które przedstawia

zasadnicze powiązanie ilościowe

zasadnicze powiązanie ilościowe

między rozpatrywanymi

między rozpatrywanymi

zjawiskami ekonomicznymi

zjawiskami ekonomicznymi

3

3

Ze względu na rolę zjawisk

Ze względu na rolę zjawisk

ekonomicznych w modelu

ekonomicznych w modelu

ekonometrycznym można

ekonometrycznym można

wyróżnić

wyróżnić

•

zjawisko ekonomiczne wyjaśniane

zjawisko ekonomiczne wyjaśniane

przez model (czyli zmienną

przez model (czyli zmienną

objaśnianą)

objaśnianą)

•

zjawiska, które oddziałują na

zjawiska, które oddziałują na

zmienną objaśnianą (czyli zmienne

zmienną objaśnianą (czyli zmienne

objaśniające)

objaśniające)

4

4

Dane dotyczące sprzedaży

Dane dotyczące sprzedaży

wody mineralnej

wody mineralnej

Tygodni

e

Ilość sprzedanej wody

Mineralnej (tyś. litrów)

Cena

jednego

litra (zl.)

Wydatki

na

rekłamu

(zl.)

Y

X

1

X

2

1

10

1,3

9

2

6

2

7

3

5

1,7

5

4

12

1,5

14

5

10

1,6

15

6

15

1,2

12

7

5

1,6

6

8

12

1,4

10

9

17

1

15

10

20

1,1

21

5

5

Modele ekonometryczne można

Modele ekonometryczne można

sklasyfikować według różnych

sklasyfikować według różnych

kryteriów:

kryteriów:

1. Liczby równań w modelu

1. Liczby równań w modelu



model jednorównaniowy

model jednorównaniowy



model wielorównaniowy

model wielorównaniowy

2. Liczby zmiennych objaśniających

2. Liczby zmiennych objaśniających



modele z jedną zmienną objaśniającą

modele z jedną zmienną objaśniającą



modele z wieloma zmiennymi

modele z wieloma zmiennymi

objaśniającymi

objaśniającymi

3. Postaci analitycznej

3. Postaci analitycznej



modele liniowe

modele liniowe



modele nieliniowe

modele nieliniowe

4. Roli czynnika czasu w równaniach modelu

4. Roli czynnika czasu w równaniach modelu



modele statyczne

modele statyczne



modele dynamiczne

modele dynamiczne

6

6

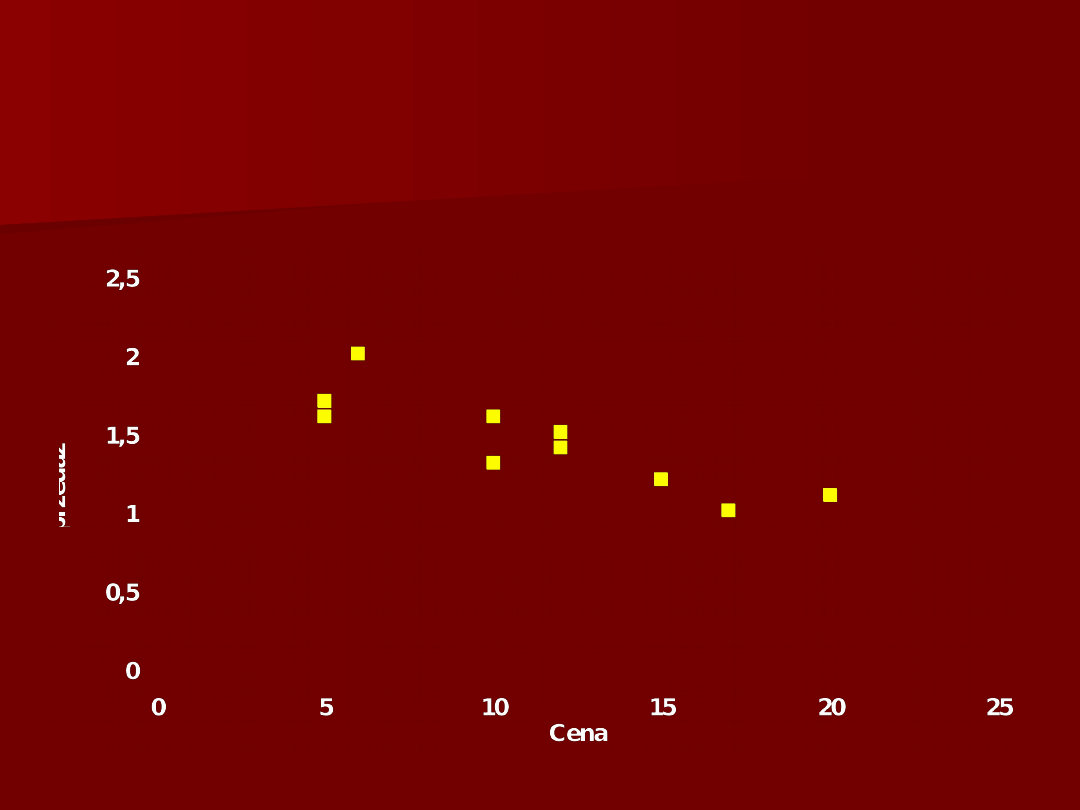
Wykres rozrzutu zmiennych X

Wykres rozrzutu zmiennych X

1

1

i Y

i Y

(cena i ilość sprzedaży)

(cena i ilość sprzedaży)

7

7

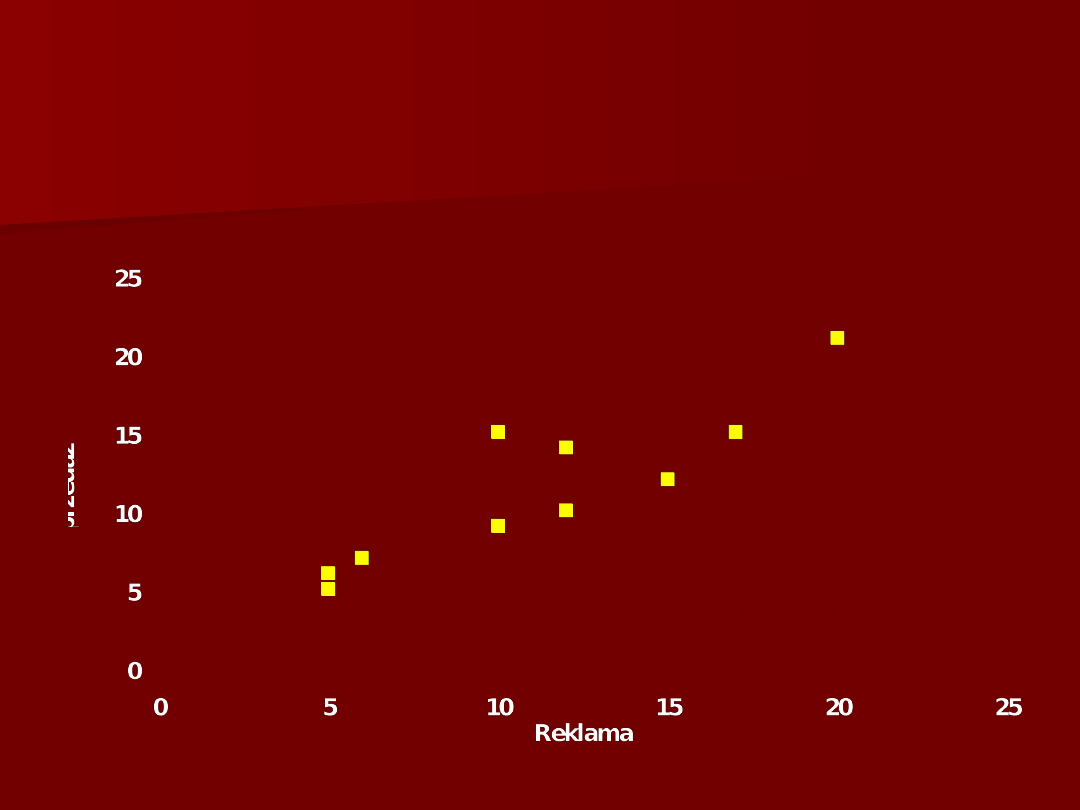
Wykres rozrzutu zmiennych X

Wykres rozrzutu zmiennych X

2

2

i Y

i Y

(cena i reklama)

(cena i reklama)

8

8

Obser-

Obser-

wacje

wacje

Zmienna

Zmienna

objaśniana

objaśniana

(zależna)

(zależna)

Zmienne objaśniające

Zmienne objaśniające

(niezależne)

(niezależne)

Y

Y

X

X

1

1

X

X

2

2

X

X

k

k

1

1

Y

Y

1

1

X

X

11

11

X

X

12

12

X

X

1k

1k

2

2

Y

Y

2

2

X

X

21

21

X

X

22

22

X

X

2k

2k

3

3

Y

Y

3

3

X

X

31

31

X

X

32

32

X

X

3k

3k

…

…

…

…

…

…

…

…

…

…

n

n

Y

Y

n

n

X

X

n1

n1

X

X

n2

n2

X

X

nk

nk

9

9

Obliczenie

Obliczenie

współczynników korelacji

współczynników korelacji



 





 

























2

2

2

2

Y

Y

n

X

X

n

Y

X

XY

n

r

86

,

0

7

,

138

8

,

119

112

488

,

1

10

4

,

14

56

,

21

10

112

4

,

14

3

,

149

10

2

2

1





























yx

r

10

10

Macierz współczynników

Macierz współczynników

korelacji

korelacji

 

Y

X

1

X

2

Y

1

 

 

X

1

-

0,

8
6

1

 

X

2

0,89

-

0,

6
5

1

11

11

Y

X

1

X

2

1

2

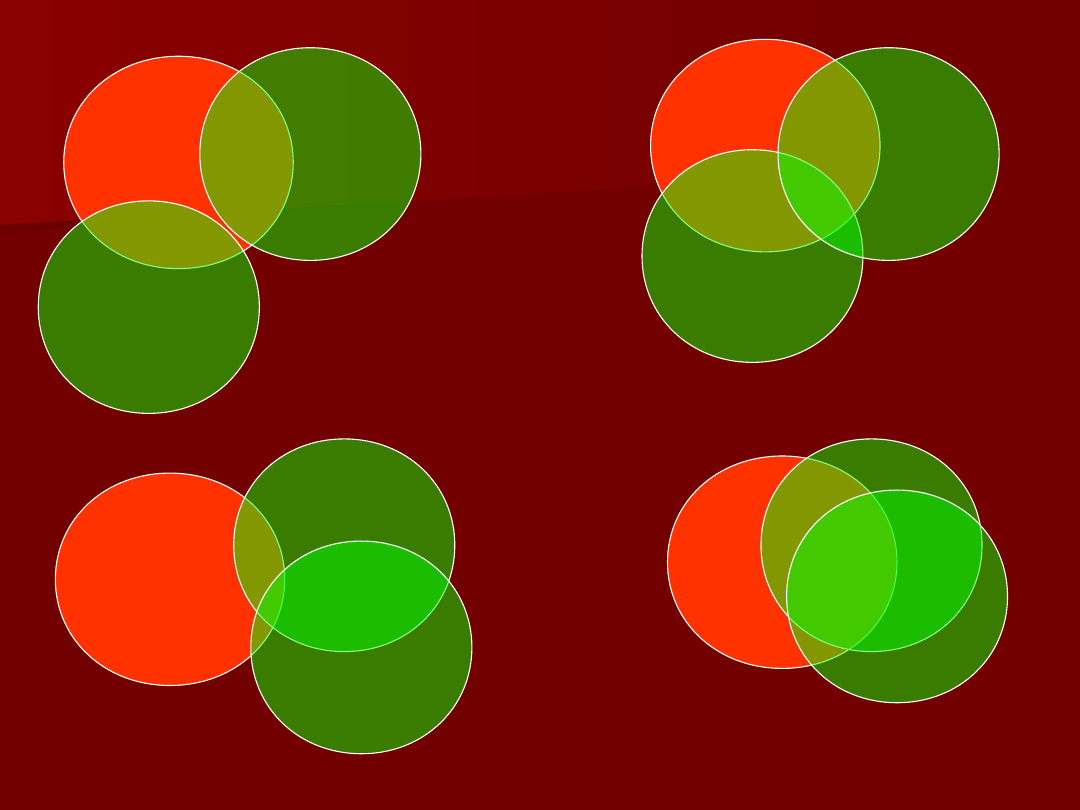
Okrąg Y reprezentuje

wariancje zmiennej

zależnej

Okręgi X

1

i X

2

reprezentują wariancje

zmiennych niezależnych

Obszar 1 odpowiada

tej części wariancji

Y, która poprzez

model wyjaśnia

zmienność X

1

Obszar 2

odpowiada tej

części wariancji Y,

która poprzez

model wyjaśnia

zmienność X

2

12

12

Y

X

1

X

2

1

2

Sytuacja, gdy nie ma

korelacji między

zmiennymi X

1

i X

2

13

13

Y

X

1

X

2

Sytuacja, gdy

zmienne niezależne

X

1

i X

2

również

skorelowane

(obszar 3)

3

Powoduje to, iż część

wariancji Y może zostać

przypisana jednocześnie

zmienności X

1

lub X

2

14

14

Y

X

1

X

2

Zwykłe wymaga się dodatkowo,

aby współczynnik korelacji

pomiędzy zmiennymi

niezależnymi był mniejszy od

współczynnika korelacji

pomiędzy Y a X

15

15

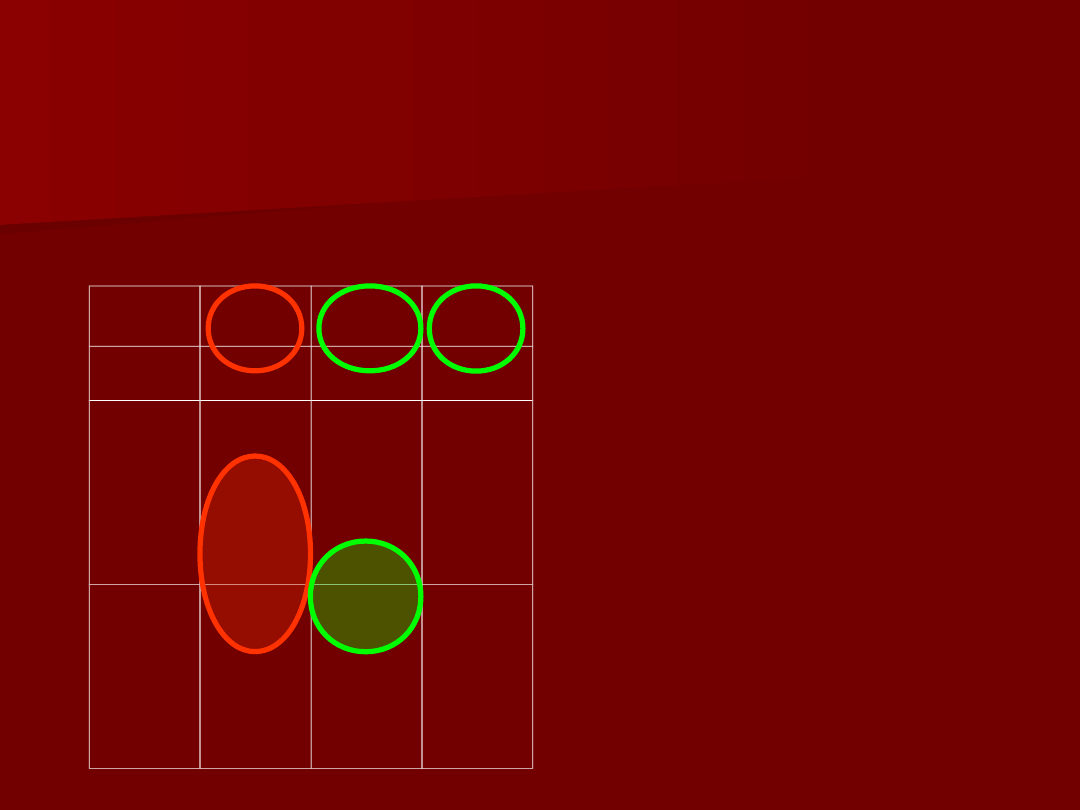
Y

Y

Y

Y

X

1

X

1

X

1

X

1

X

2

X

2

X

2

X

2

b

a

c

d

16

16

Macierz współczynników

Macierz współczynników

korelacji

korelacji

 

Y

X

1

X

2

Y

1

 

 

X

1

-

0,

8
6

1

 

X

2

0,89

-

0,

6
5

1

17

17

Liniowy model regresji

Liniowy model regresji

wielu zmiennych

wielu zmiennych

Y

Y

– zmienna objaśniana

– zmienna objaśniana

X

X

k

k

– zmienne objaśniające

– zmienne objaśniające

β

β

0

0

β

β

1

1

…

…

β

β

k

k

–

–

nieznane parametry strukturalne

nieznane parametry strukturalne

modelu

modelu

ε

ε

-

-

składnik losowy

składnik losowy

k

k

– numeruje kolejne zmienne objaśniające

– numeruje kolejne zmienne objaśniające





















k

k

X

X

X

Y

...

2

2

1

1

0

18

18

Metoda najmniejszych

Metoda najmniejszych

kwadratów

kwadratów

opiera się na koncepcji poszukiwania takich

opiera się na koncepcji poszukiwania takich

warto

warto

ś

ś

ci

ci

b

b

0

0

b

b

1

1

… b

… b

k

k

parametrów

parametrów

strukturalnych

strukturalnych

β

β

0

0

,

,

β

β

1

1

…

…

β

β

k

k

przy których

przy których

suma kwadratów reszt osiąga minimum

suma kwadratów reszt osiąga minimum

















n

i

i

i

n

i

i

Y

Y

e

SSE

1

2

1

2

)

ˆ

(













n

i

i

i

i

X

b

X

b

b

Y

1

2

2

2

1

1

0

)

(

min







n

i

i

e

1

2

19

19

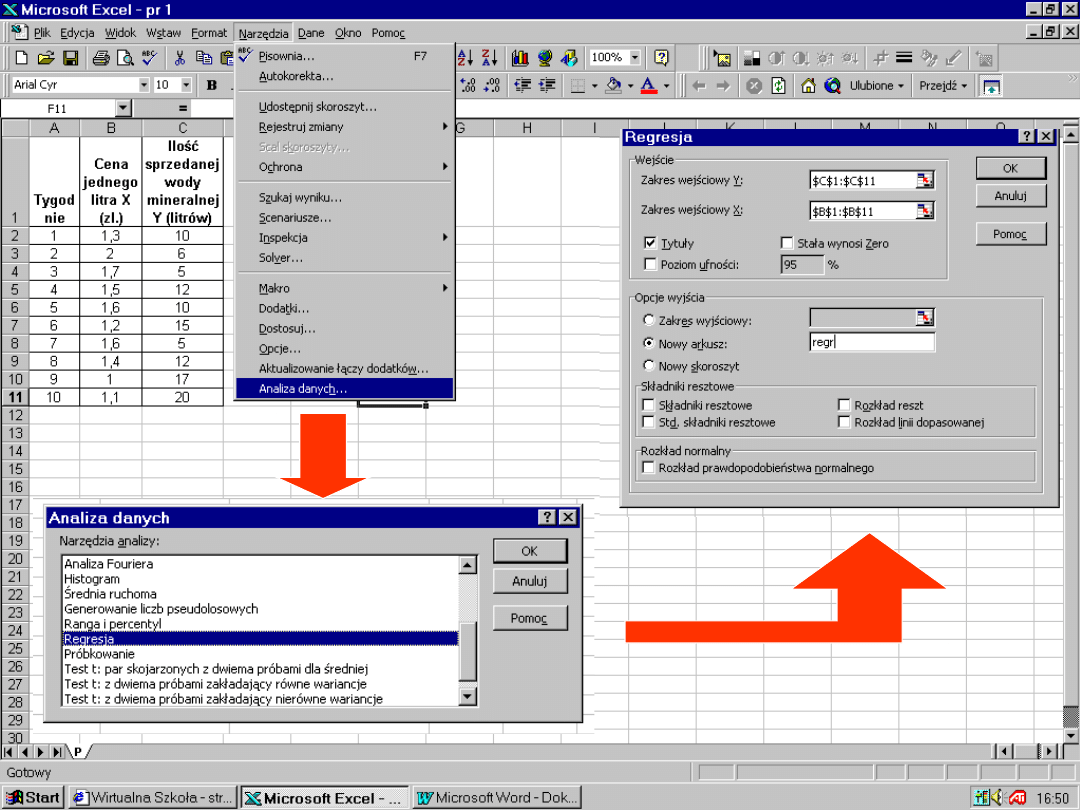
b

b

1

1

= -8,248

= -8,248

b

b

0

0

= 16,406

= 16,406

Ŷ

Ŷ

= 16,406 – 8,248

= 16,406 – 8,248

X

X

1

1

+ 0,585

+ 0,585

X

X

2

2

2

2

1

1

0

ˆ

i

i

i

X

b

X

b

b

Y







b

b

2

2

= 0,585

= 0,585

20

20

21

21

Weryfikacja modelu

Weryfikacja modelu

ekonometrycznego

ekonometrycznego

1. Badanie dopasowania modelu do danych

1. Badanie dopasowania modelu do danych

obserwowanych

obserwowanych



współczynnik determinacji i współczynnik

współczynnik determinacji i współczynnik

zbieżności

zbieżności



współczynnik zmienności losowej

współczynnik zmienności losowej

2. Badanie istotności parametrów

2. Badanie istotności parametrów

strukturalnych

strukturalnych

β

β

i

i



test

test

t-Studenta

t-Studenta



test F

test F

3. Badanie własności odchyleń losowych

3. Badanie własności odchyleń losowych



losowość składnika losowego

losowość składnika losowego



normalność rozkładu składnika losowego

normalność rozkładu składnika losowego



jednorodność wariancji składnika losowego

jednorodność wariancji składnika losowego



autokorelacja składnika losowego

autokorelacja składnika losowego

22

22

1. Badanie dopasowania

1. Badanie dopasowania

modelu do danych

modelu do danych

obserwowanych

obserwowanych

23

23

Dokładność dopasowania

Dokładność dopasowania

prostej metodą najmniejszych

prostej metodą najmniejszych

kwadratów

kwadratów

Punktem wyjścia przy dokonywaniu

Punktem wyjścia przy dokonywaniu

pomiaru dokładności dopasowania

pomiaru dokładności dopasowania

prostej regresji do danych empirycznych

prostej regresji do danych empirycznych

jest następujący podział odchylenia

jest następujący podział odchylenia

obserwowanej wartości Y

obserwowanej wartości Y

i

i

od średniej Y

od średniej Y

̅

̅

)

ˆ

(

)

ˆ

(

i

i

i

i

Y

Y

Y

Y

Y

Y











24

24

Pierwszy z tych składników (

Pierwszy z tych składników (

Ŷ

Ŷ

i

i

–

– Ῡ

)

)

można traktować jako tę część

można traktować jako tę część

całkowitego odchylenia Y

całkowitego odchylenia Y

i

i

od

od Ῡ

, która

, która

jest wyjaśniona regresją Y względem X.

jest wyjaśniona regresją Y względem X.

Drugi składnik

Drugi składnik

(Y

(Y

i

i

-

-

Ŷ

Ŷ

i

i

) jest resztą e

) jest resztą e

i

i

dla

dla

x=x

x=x

i

i

, a zatem jest to ta część

, a zatem jest to ta część

całkowitego odchylenia Y

całkowitego odchylenia Y

i

i

od Y, która

od Y, która

nie została wyjaśniona regresją Y

nie została wyjaśniona regresją Y

względem X

względem X

)

ˆ

(

)

ˆ

(

i

i

i

i

Y

Y

Y

Y

Y

Y











25

25

Analogiczna równość zachodzi

Analogiczna równość zachodzi

także dla sum kwadratów

także dla sum kwadratów

odpowiednich odchyleń

odpowiednich odchyleń























n

i

n

i

i

i

i

n

i

i

Y

Y

Y

Y

Y

Y

1

1

2

2

1

2

)

ˆ

(

)

ˆ

(

)

(

26

26























n

i

n

i

i

i

i

n

i

i

Y

Y

Y

Y

Y

Y

1

1

2

2

1

2

)

ˆ

(

)

ˆ

(

)

(









n

i

i

Y

Y

SST

1

2

)

(









n

i

i

Y

Y

SSE

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

SST = SSR + SSE

odchylenie

odchylenie

odchylenie

całkowite

wyjaśnione regresją

niewyjaśnione

regresją

27

27









n

i

i

Y

Y

SST

1

2

)

(









n

i

i

Y

Y

SSE

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

SST = SSR + SSE

odchylenie

odchylenie

odchylenie

całkowite

wyjaśnione regresją

niewyjaśnione

regresją

SS – Sum of Squares

SS – Sum of Squares

T – Total

T – Total

R – Regression

R – Regression

E – Error

E – Error

28

28

Postępując analogicznie jak przy

Postępując analogicznie jak przy

konstrukcji współczynnika korelacji,

konstrukcji współczynnika korelacji,

tzn. dzieląc sumę kwadratów odchyleń

tzn. dzieląc sumę kwadratów odchyleń

wyjaśnioną regresją przez całkowitą sumę

wyjaśnioną regresją przez całkowitą sumę

kwadratów odchyleń,

kwadratów odchyleń,

otrzymamy miarę dokładności dopasowania

otrzymamy miarę dokładności dopasowania

prostej

prostej

współczynnik determinacji

współczynnik determinacji

(r

(r

2

2

)

)

SST

SSE

Y

Y

Y

Y

SST

SSR

Y

Y

Y

Y

r

n

i

i

n

i

i

i

n

i

i

n

i

i





































1

)

(

)

ˆ

(

1

)

(

)

ˆ

(

1

2

1

2

1

2

1

2

2

29

29

Współczynnik determinacji

Współczynnik determinacji

(r

(r

2

2

)

)

informuje, jaka część całkowitej zmienności

informuje, jaka część całkowitej zmienności

zmiennej objaśnianej (Y) stanowi

zmiennej objaśnianej (Y) stanowi

zmienność wyjaśniona przez model

zmienność wyjaśniona przez model

calkowite

odchylenie

regresja

wyjasnione

odchylenie

Y

Y

Y

Y

r

n

i

i

n

i

i

_

_

_

)

(

)

ˆ

(

1

2

1

2

2

















calkowite

odchylenie

regresja

one

niewyjasni

odchylenie

Y

Y

Y

Y

r

n

i

i

n

i

i

i

_

_

_

1

)

(

)

ˆ

(

1

1

2

1

2

2





















30

30

Y

X1

X2

Ŷ

(Y-Ŷ)

(Y-Ŷ)^2

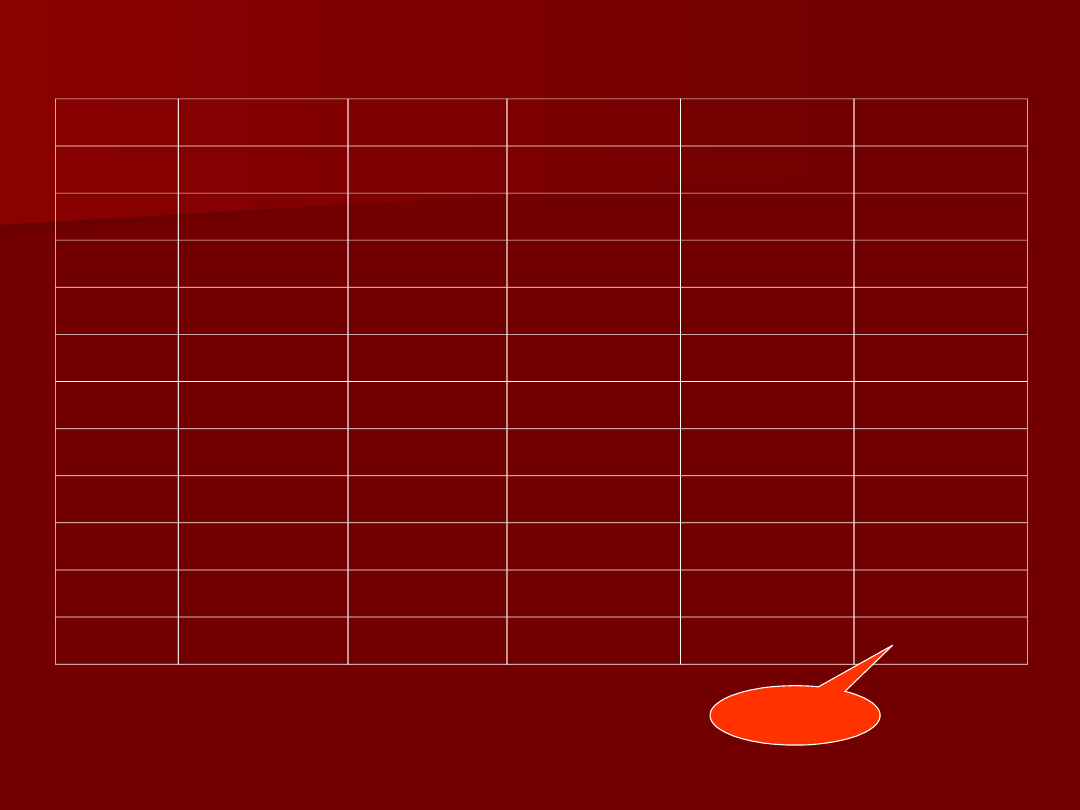
10

1,3

9

10,95

-0,95

0,90

6

2

7

4,01

2,00

3,98

5

1,7

5

5,31

-0,31

0,10

12

1,5

14

12,22

-0,22

0,05

10

1,6

15

11,98

-1,98

3,94

15

1,2

12

13,53

1,47

2,17

5

1,6

6

6,72

-1,72

2,96

12

1,4

10

10,71

1,29

1,67

17

1

15

16,93

0,07

0,00

20

1,1

21

19,62

0,38

0,15

Suma

0,02

15,90

Dane dotyczące sprzedaży wody

Dane dotyczące sprzedaży wody

mineralnej

mineralnej

SSE

31

31



SST = 233,6

SST = 233,6



SSE = 19,9

SSE = 19,9

SSR = SST – SSE =

SSR = SST – SSE =

= 233,6 – 19,9 = 117,7

= 233,6 – 19,9 = 117,7

93

,

0

6

,

233

7

,

217

2







SST

SSR

r

Dane dotyczące sprzedaży wody mineralnej

Dane dotyczące sprzedaży wody mineralnej

32

32

Sum of

Sum of

Squares

Squares

SSE

SST

SSR

33

33

SST

r

2

SSR

34

34

r

r

2

2

r

r

35

35

(współczynnik korelacji)

(współczynnik korelacji)

2

2

= współczynnik

= współczynnik

determinacji

determinacji

(r)

(r)

2

2

= r

= r

2

2

(0,965)

(0,965)

2

2

= 0,932

= 0,932

36

36

Y

X1

X2

Ŷ

(Y-Ŷ)

(Y-Ŷ)^2

10

1,3

9

10,95

-0,95

0,90

6

2

7

4,01

2,00

3,98

5

1,7

5

5,31

-0,31

0,10

12

1,5

14

12,22

-0,22

0,05

10

1,6

15

11,98

-1,98

3,94

15

1,2

12

13,53

1,47

2,17

5

1,6

6

6,72

-1,72

2,96

12

1,4

10

10,71

1,29

1,67

17

1

15

16,93

0,07

0,00

20

1,1

21

19,62

0,38

0,15

Dane dotyczące sprzedaży wody

Dane dotyczące sprzedaży wody

mineralnej

mineralnej

37

37

r

2

bliskie 1

r

2

bliskie 0

r

2

bliskie 0

38

38

Stopnie swobody

Stopnie swobody



Przez

Przez

stopnie swobody

stopnie swobody

rozumie się

rozumie się

liczbę niezależnych wyników obserwacji

liczbę niezależnych wyników obserwacji

pomniejszoną o liczbę związków, które

pomniejszoną o liczbę związków, które

łączą wyniki obserwacji ze sobą

łączą wyniki obserwacji ze sobą

10 + 5 = 15

10 + 5 = 15



Liczba stopni swobody

Liczba stopni swobody

wskazuje, jak

wskazuje, jak

wiele niezależnych informacji

wiele niezależnych informacji

zawartych w

zawartych w

n

n

niezależnych

niezależnych

wartościach y

wartościach y

1

1

, y

, y

2

2

, … , y

, … , y

n

n

jest

jest

potrzebnych do zestawienia danej

potrzebnych do zestawienia danej

sumy kwadratów

sumy kwadratów

1

2

3

???

n-1 stopni

swobody

3-1=2

39

39

Stopnie swobody

Stopnie swobody









n

i

i

Y

Y

SST

1

2

)

(



ma n-1 stopni swobody,

ma n-1 stopni swobody,

ponieważ mamy n

ponieważ mamy n

obserwacji oraz jeden

obserwacji oraz jeden

łączący je związek,

łączący je związek,

mianowicie

mianowicie



ma k stopni swobody.

ma k stopni swobody.

potrzeba k informacji

potrzeba k informacji

uzyskanych na podstawie

uzyskanych na podstawie

Y

Y

1

1

, Y

, Y

2

2

, … , Y

, … , Y

n

n

, mianowicie:

, mianowicie:

b

b

1

1

, b

, b

2

2

, … , b

, … , b

k

k



ma n-k-1 stopni swobody,

ma n-k-1 stopni swobody,

gdyż jest n obserwacji oraz

gdyż jest n obserwacji oraz

k+1 związków określonych

k+1 związków określonych

przez układ równań

przez układ równań

normalnych

normalnych















n

i

i

n

i

i

e

Y

Y

SSE

1

2

1

2

)

ˆ

(









n

i

i

Y

n

Y

1









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

40

40

Stopnie swobody

Stopnie swobody









n

i

i

Y

Y

SST

1

2

)

(















n

i

i

n

i

i

e

Y

Y

SSE

1

2

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(



df (SST) = n-1

df (SST) = n-1



df (SSR) = k

df (SSR) = k



df (SSE) = n-k-1

df (SSE) = n-k-1

degree of freedom

liczba stopni

swobody

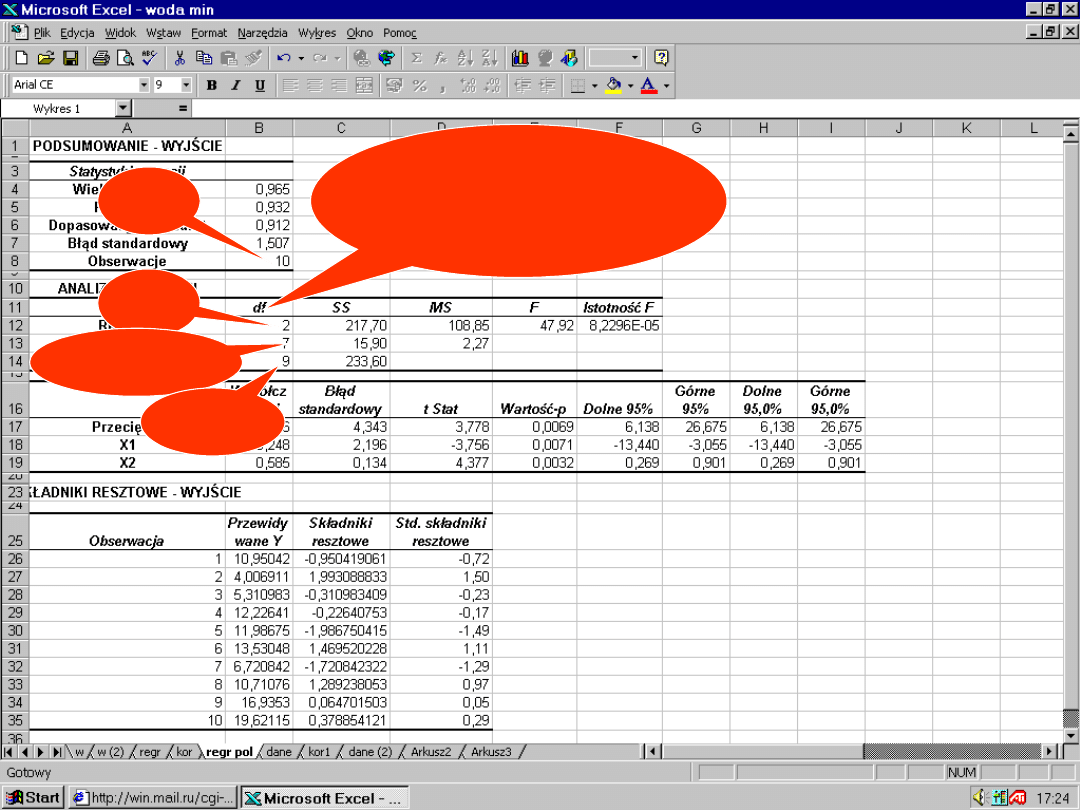
41

41

degree of

freedom

liczba stopni

swobody

2

2

10-2-

10-2-

1

1

10-

10-

1

1

n

n

42

42

)

1

/(

)

1

/(

1

)

1

/(

)

(

)

1

/(

)

ˆ

(

1

2

1

1

2

2

























































n

SST

k

n

SSE

n

Y

Y

k

n

Y

Y

r

n

i

i

n

i

i

i

dop

r

2

= 0,93

r

2

dop

= 0,91

r

2

– r

2

dop

<

5%

43

43

Wartość średnia kwadratów

Wartość średnia kwadratów

reszt

reszt



Wartość średnia kwadratów reszt

Wartość średnia kwadratów reszt

(wariancja składnika losowego) MSE

(wariancja składnika losowego) MSE

mówi o

mówi o

zgodności z danymi obserwowanymi w modelu.

zgodności z danymi obserwowanymi w modelu.

(informuje o zmienności składnika losowego)

(informuje o zmienności składnika losowego)

1

1

1

)

ˆ

(

1

2

1

2





























k

n

SSE

k

n

e

k

n

Y

Y

MSE

n

i

i

n

i

i

44

44

Wartość średnia kwadratów

Wartość średnia kwadratów

reszt

reszt

Suma

Suma

kwadrató

kwadrató

w

w

Stopnie
swobod

y

Wartość średnia

Wartość średnia

kwadratów

kwadratów

Regresja

Regresja

SSR

SSR

k

k

MSR = SSR / k

MSR = SSR / k

Resztkow

Resztkow

y

y

SSE

SSE

n-k-1

n-k-1

MSE = SSE /

MSE = SSE /

(n-k-1)

(n-k-1)

Razem

Razem

SST

SST

n-1

n-1

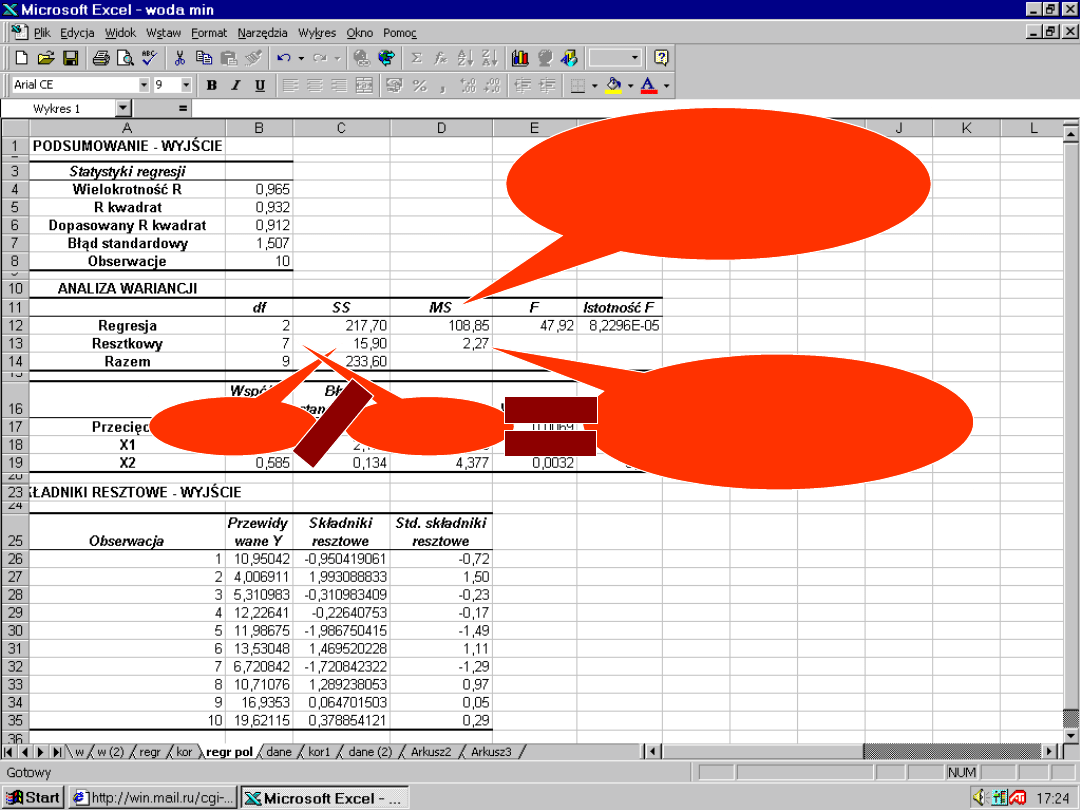
45

45

Wartość

średnia

kwadratów

reszt

Mean of Squares

Wartość średnia

kwadratów

SSE

n-k-1

46

46

Odchylenie standardowe

Odchylenie standardowe

reszt

reszt



Odchylenie standardowe reszt

Odchylenie standardowe reszt

(standardowy błąd estymacji)

(standardowy błąd estymacji)

informuje

informuje

o ile średnio wartości obserwowane Y

o ile średnio wartości obserwowane Y

odchylają się od wartości prognozowanych

odchylają się od wartości prognozowanych

Ŷ

Ŷ

modelu

modelu

1

1

2













k

n

e

MSE

S

n

i

i

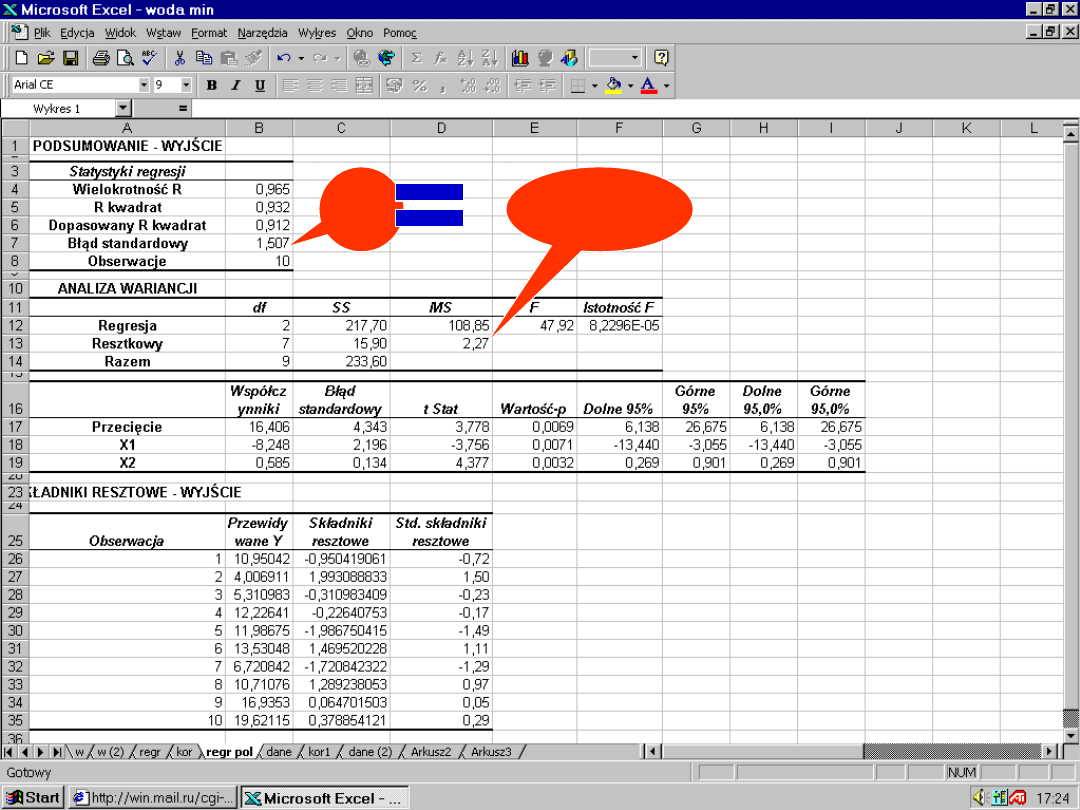
47

47

S

MSE

√

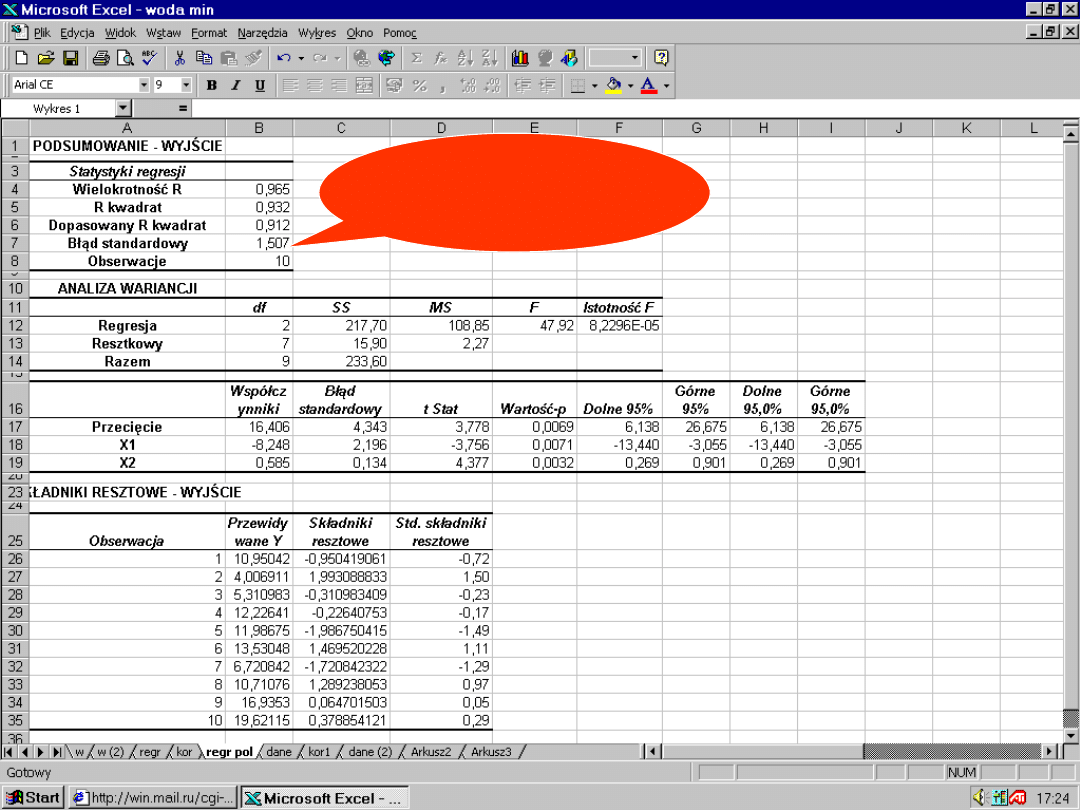
48

48

1,51 ???

?

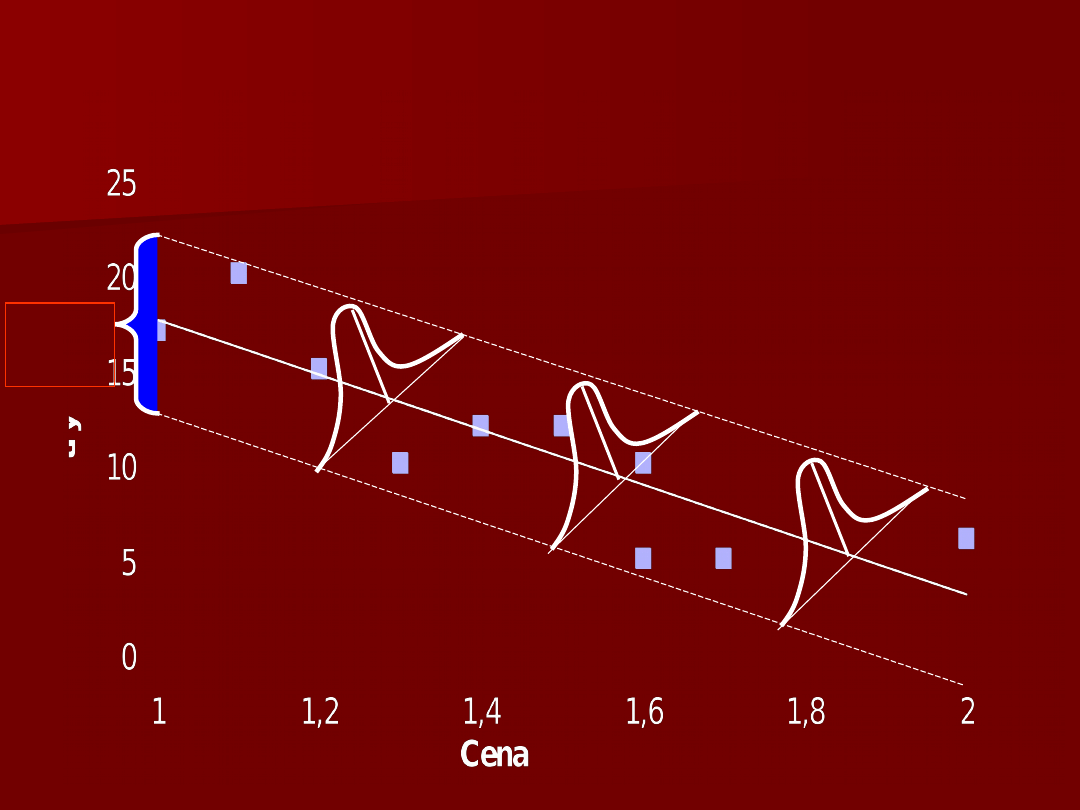
49

49

Y [5;20] S = 2,7

Y [5;20] S = 2,7

2,7x
2

Y i
X

1

S = 1,5

S = 1,5

Y i X

1

,

X

2

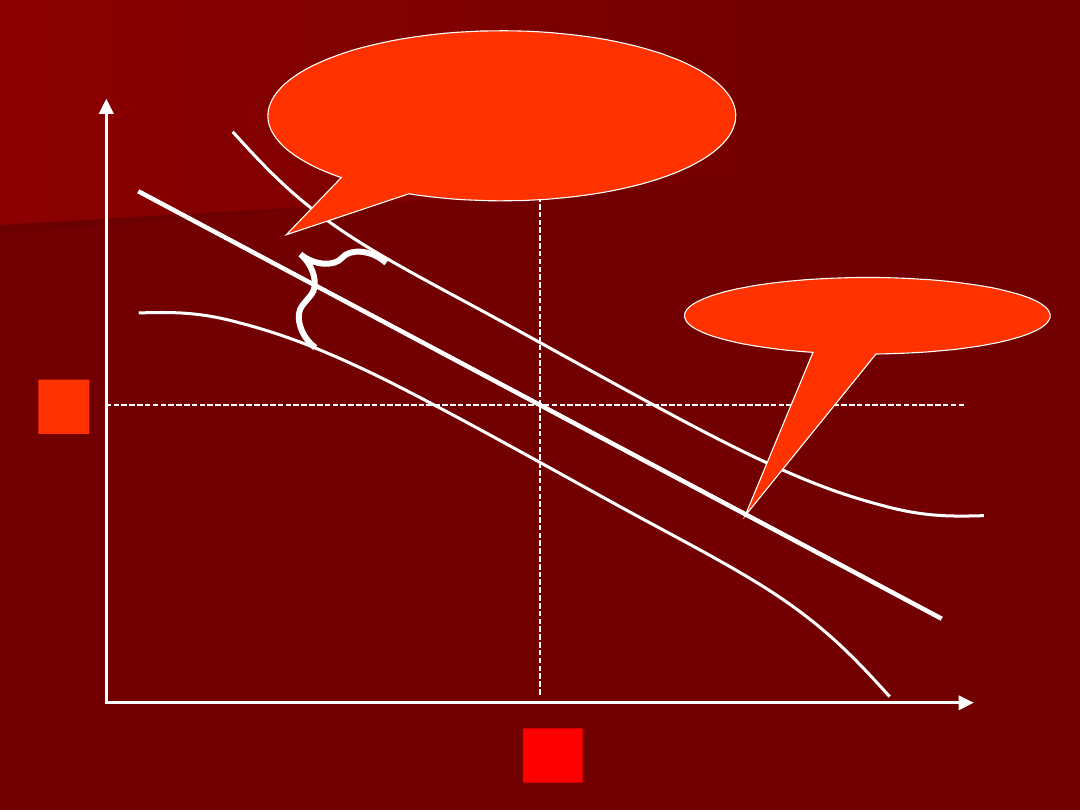
50

50

X̅

Ῡ

Przedział
ufności dla
linii regresji

linia

regresji

51

51

2. Badanie istotności

2. Badanie istotności

parametrów

parametrów

strukturalnych

strukturalnych

β

β

i

i

52

52



Pierwszym krokiem weryfikacji oszacowanego

Pierwszym krokiem weryfikacji oszacowanego

modelu jest badanie istotności parametrów

modelu jest badanie istotności parametrów

strukturalnych w celu sprawdzenia, które ze

strukturalnych w celu sprawdzenia, które ze

zmiennych objaśniających istotnie wpływają na

zmiennych objaśniających istotnie wpływają na

opisywany proces

opisywany proces



Wymaganie jest, aby wszystkie zmienne objaśniające

Wymaganie jest, aby wszystkie zmienne objaśniające

modelu były istotnie

modelu były istotnie



Zazwyczaj nie bada się istotność wyrazu wolnego

Zazwyczaj nie bada się istotność wyrazu wolnego

β

β

0

0

,

,

ponieważ bez względu na to jaki ma on wpływ na

ponieważ bez względu na to jaki ma on wpływ na

zmienną objaśnianą nie usuwa się go z modelu

zmienną objaśnianą nie usuwa się go z modelu

ik

k

i

i

i

X

X

X

Y









...

2

2

1

1

0









Istotność parametrów strukturalnych

Istotność parametrów strukturalnych

β

β

i

i

53

53

2.1. Test

2.1. Test

t-Studenta

t-Studenta



Badanie istotności parametrów strukturalnych

Badanie istotności parametrów strukturalnych

modelu polega na weryfikacji hipotez postaci

modelu polega na weryfikacji hipotez postaci

H

H

0

0

:

:

β

β

j

j

= 0

= 0

H

H

A

A

:

:

β

β

j

j

≠ 0

≠ 0



parametr

parametr

β

β

j

j

nieistotnie różni się od

nieistotnie różni się od

zera

zera



zmienna objaśniająca X

zmienna objaśniająca X

j

j

nieistotnie

nieistotnie

wpływa na zmienną objaśnianą Y

wpływa na zmienną objaśnianą Y



parametr

parametr

β

β

j

j

istotnie różni się od zera

istotnie różni się od zera



zmienna objaśniająca X

zmienna objaśniająca X

j

j

istotnie

istotnie

wpływa na zmienną objaśnianą Y

wpływa na zmienną objaśnianą Y

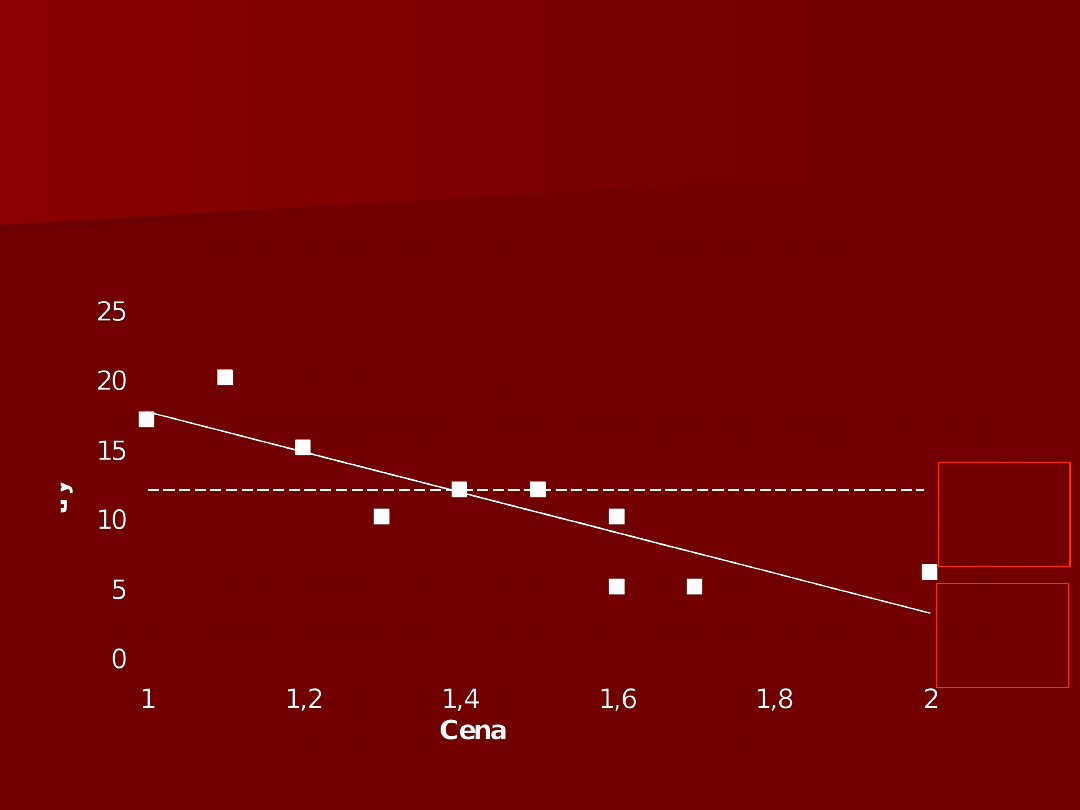
54

54

β

β

1

1

≠

≠

0

0

β

β

1

1

=

=

0

0

55

55

1

1

1

b

b

S

b

t 









n

i

i

b

X

X

S

S

1

2

)

(

1

Średni błąd
resztowy
parametru b

1

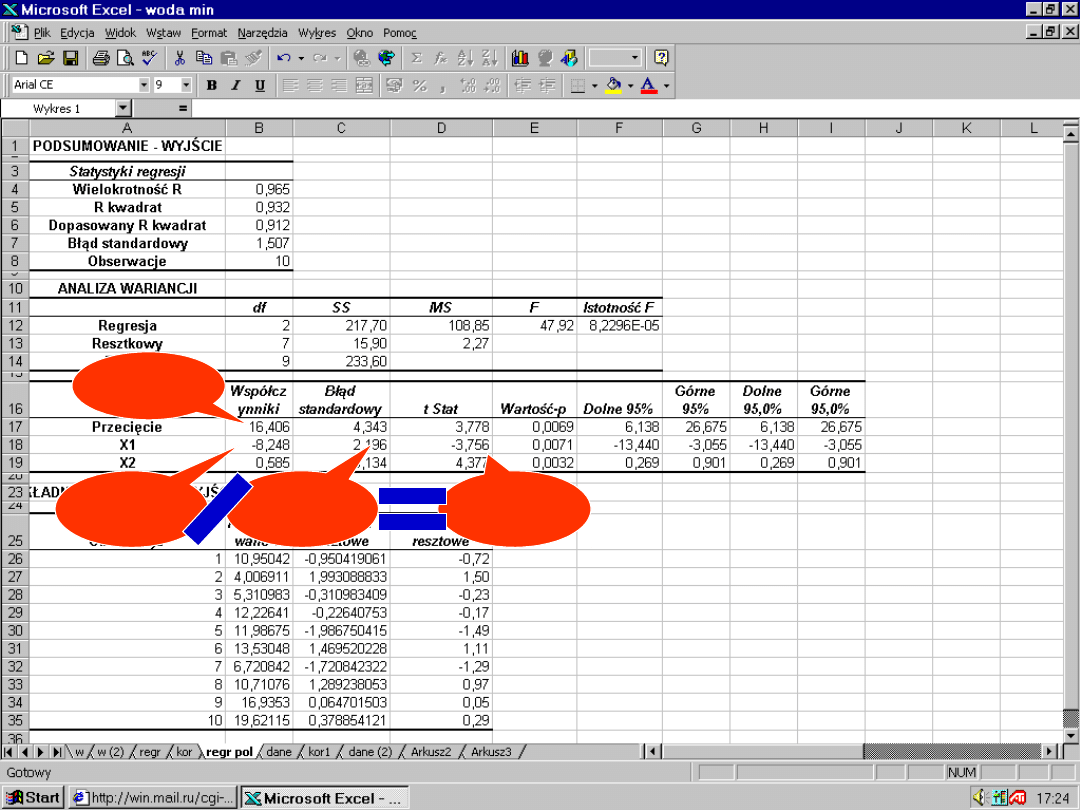
56

56

b

0

b

1

S

b1

t

b1

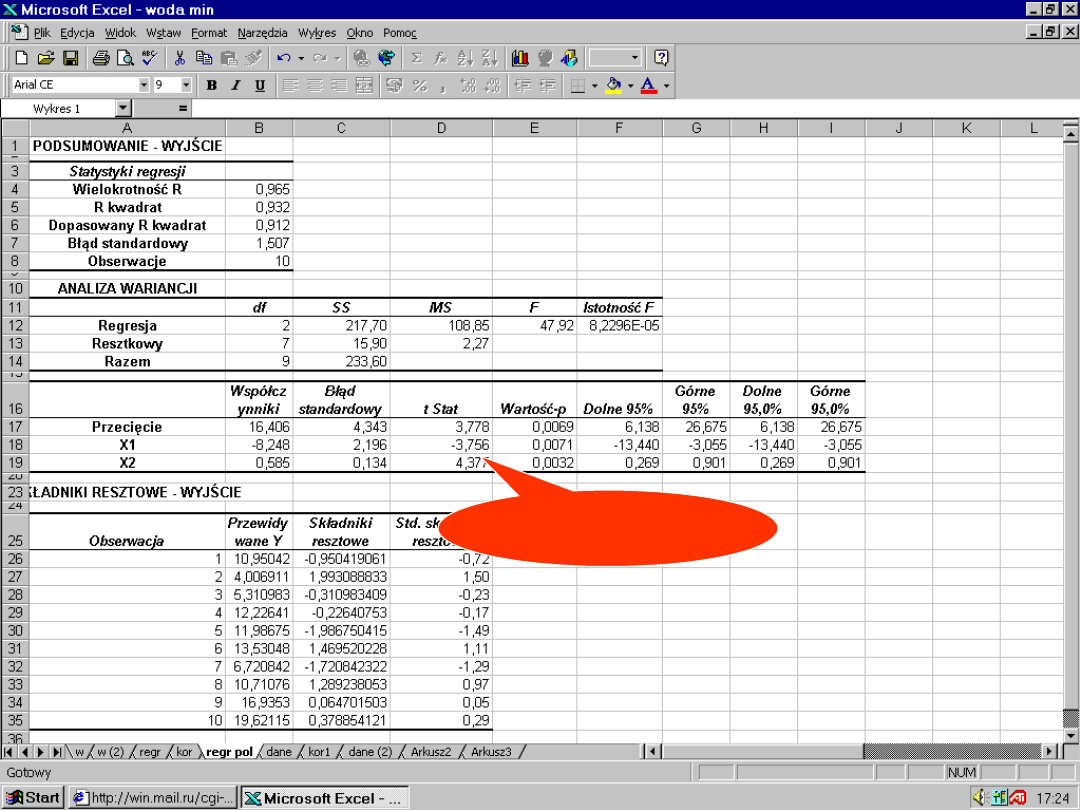
57

57

-3,76 ???

58

58

Wartość

Wartość

p

p



Wartość

Wartość

p

p

jest krytycznym poziomem

jest krytycznym poziomem

istotności dla testu

istotności dla testu

t-Studenta

t-Studenta



Wartość

Wartość

p

p

jest poziomem

jest poziomem

prawdopodobieństwa przy którym nie

prawdopodobieństwa przy którym nie

ma podstaw do odrzucenia hipotezy

ma podstaw do odrzucenia hipotezy

zerowej H

zerowej H

0

0



Przyjmując, że poziom istotności

Przyjmując, że poziom istotności

ustala się zwykle jako 5% (0,05) ,

ustala się zwykle jako 5% (0,05) ,

hipoteza zerową jest odrzucona, gdy

hipoteza zerową jest odrzucona, gdy

wartość p

wartość p

≤ 0,05

≤ 0,05

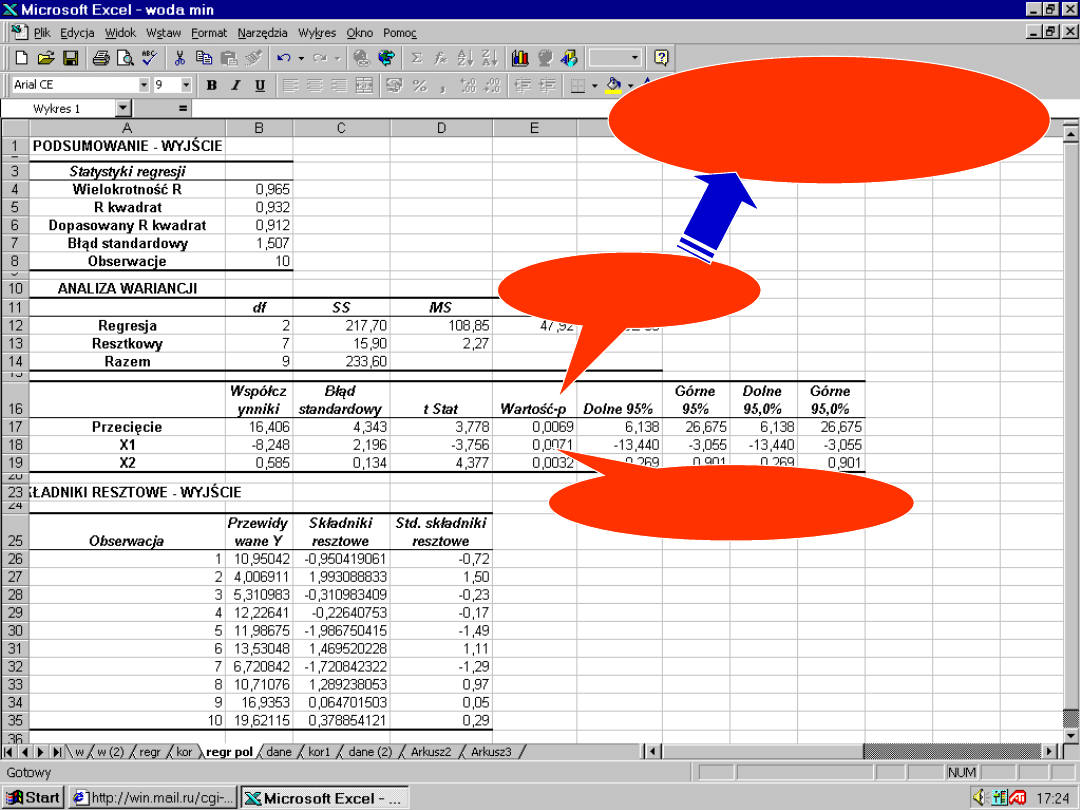
59

59

0,007 ≤

0,007 ≤

0,05

0,05

p ≤

p ≤

0,05

0,05

Hipotezę H

o

odrzucamy

60

60

Wartość p jest mniejsza

Wartość p jest mniejsza

od 0,05 , wobec tego

od 0,05 , wobec tego

parametr b

parametr b

1

1

jest istotny

jest istotny

na poziomie istotności

na poziomie istotności

5%

5%

p ≤

p ≤

0,05

0,05

61

61

2.2. Test F

2.2. Test F



Badanie istotności parametrów strukturalnych

Badanie istotności parametrów strukturalnych

testem F polega na badaniu istotności wszystkich

testem F polega na badaniu istotności wszystkich

parametrów strukturalnych łącznie

parametrów strukturalnych łącznie

H

H

0

0

:

:

β

β

1

1

=

=

β

β

2

2

= … =

= … =

β

β

k

k

= 0

= 0



parametr

parametr

β

β

1

1

nieistotnie różni się od

nieistotnie różni się od

β

β

2,

2,

β

β

k,

k,

zera

zera



zmienna objaśniająca X nieistotnie wpływa na

zmienna objaśniająca X nieistotnie wpływa na

zmienną objaśnianą Y

zmienną objaśnianą Y

H

H

A

A

:

:

β

β

j

j

≠ 0

≠ 0



parametr

parametr

β

β

j

j

istotnie różni się od zera

istotnie różni się od zera



zmienna objaśniająca X istotnie wpływa na

zmienna objaśniająca X istotnie wpływa na

zmienną objaśnianą Y

zmienną objaśnianą Y

62

62

MSE

MSR

F 

Wartość średnia
kwadratów
regresji

Wartość średnia
kwadratów reszt

63

63

MSR

MSR

Test F

Test F

MSE

MSE

F

F

64

64

47,9 ??

?

65

65

8,23*10

8,23*10

-5

-5

≤ 0,05

≤ 0,05

Istotność F ≤

Istotność F ≤

0,05

0,05

Hipotezę H

o

odrzucamy

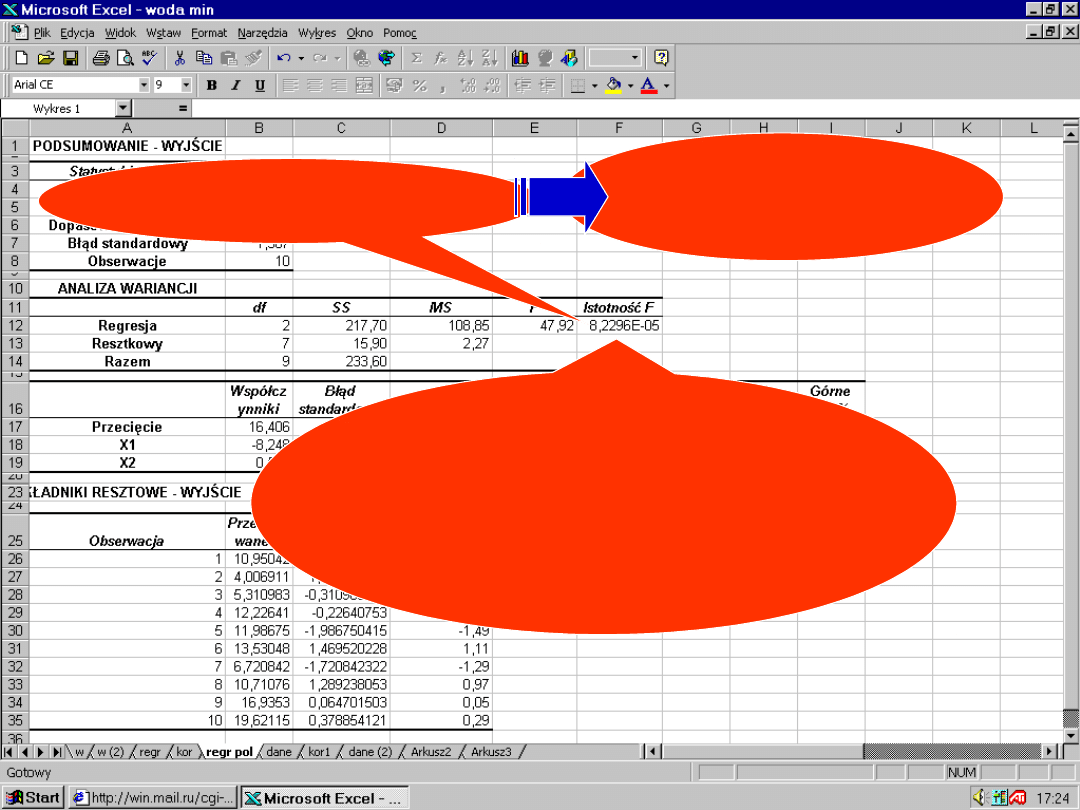
66

66

Istotność F

Istotność F

jest

jest

mniejsza od 0,05 ,

mniejsza od 0,05 ,

wobec tego parametr

wobec tego parametr

b1 jest istotny na

b1 jest istotny na

poziomie istotności 5%

poziomie istotności 5%

Istotność F ≤

Istotność F ≤

0,05

0,05

Hipotezę H

o

odrzucamy

67

67

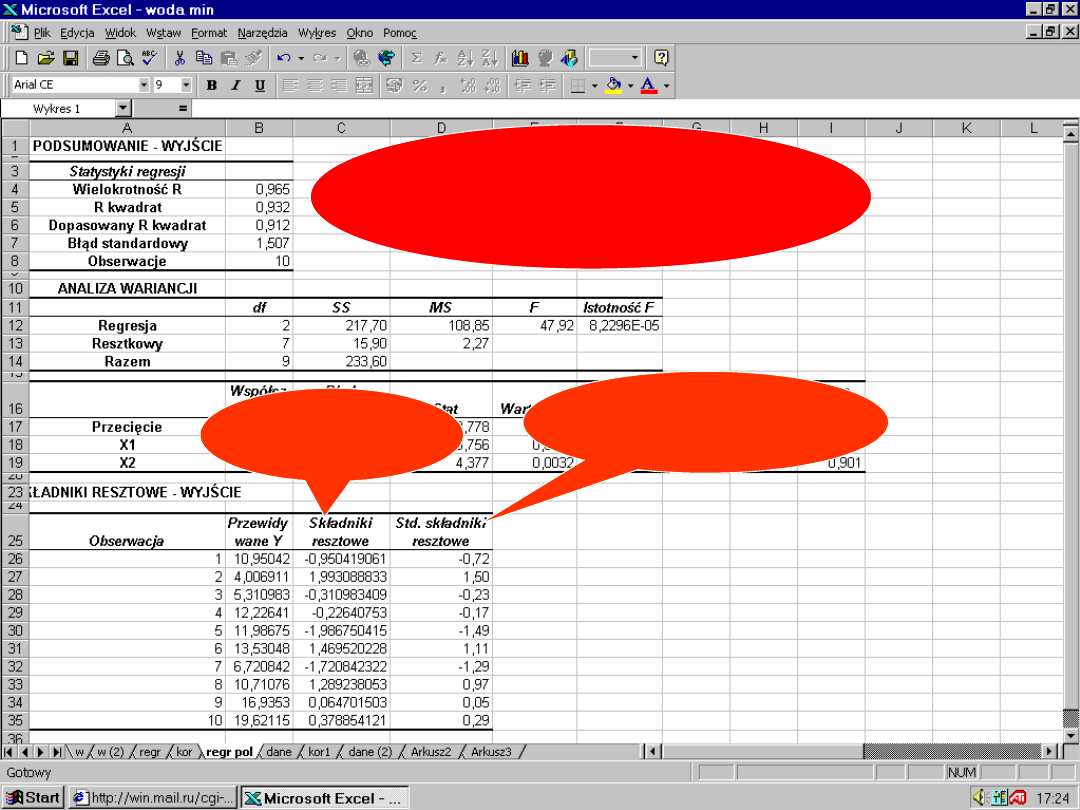
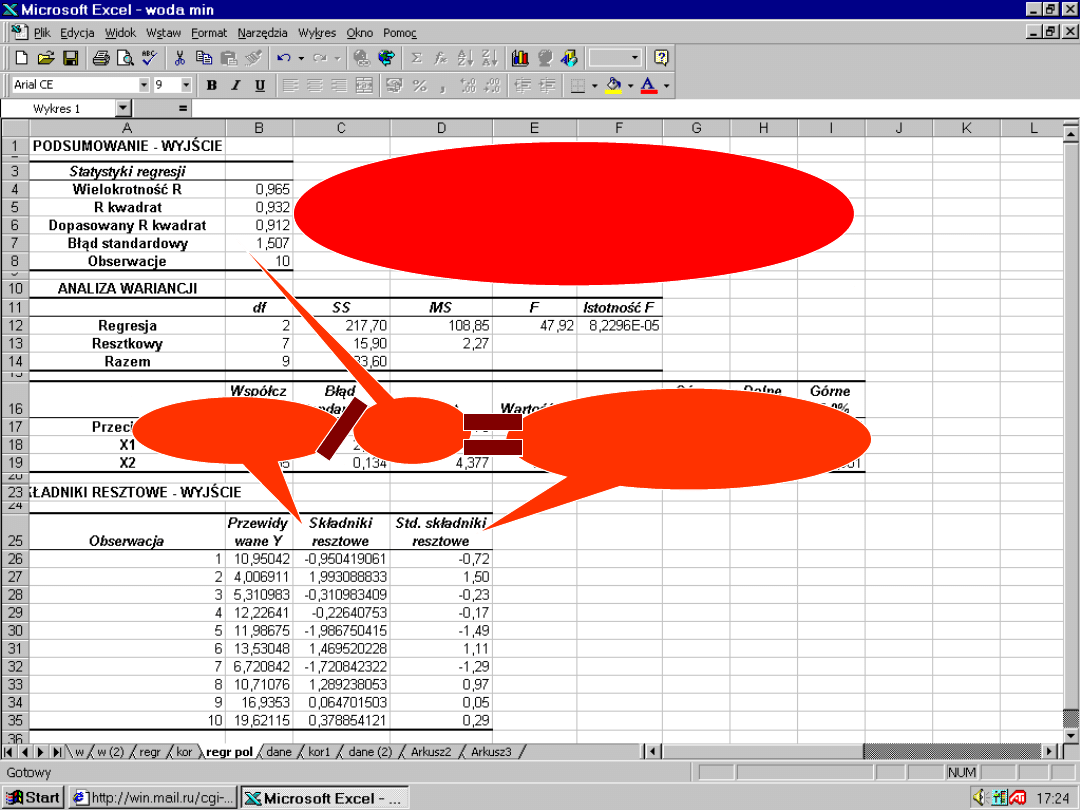
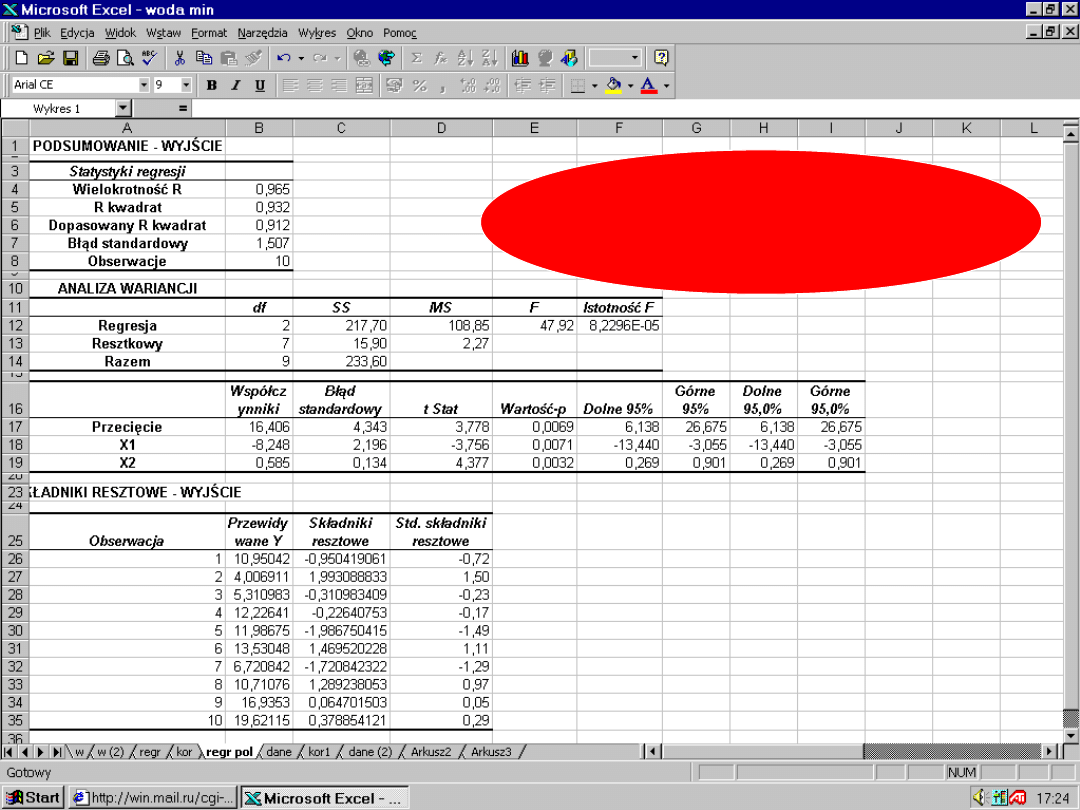
Interpretacja oznaczeń

Interpretacja oznaczeń

wyników analizy regresji w

wyników analizy regresji w

Excel

Excel



Wielokrotność R

Wielokrotność R

–

–

współczynnik korelacji

współczynnik korelacji



R kwadrat –

R kwadrat –

współczynnik

współczynnik

determinacji r

determinacji r

2

2



Błąd standardowy

Błąd standardowy

–

–

standardowy błąd

standardowy błąd

reszt S

reszt S

e

e



Obserwacje

Obserwacje

– liczba

– liczba

obserwacji w badaniu

obserwacji w badaniu

2

r

r 

SST

SSE

SST

SSR

r







1

2

1

1

2













k

n

e

MSE

S

n

i

i

n

68

68

Interpretacja oznaczeń

Interpretacja oznaczeń

wyników analizy regresji w

wyników analizy regresji w

Excel

Excel



df

df

–

–

degree of freedom

degree of freedom

(

(

liczba stopni swobody)

liczba stopni swobody)



SS –

SS –

Sum of Squares

Sum of Squares

(suma kwadratów reszt)

(suma kwadratów reszt)

(

(

suma kwadratów regresji

suma kwadratów regresji

)

)



MS

MS

–

–

Mean of Squares

Mean of Squares

(

(

wartość średnia

wartość średnia

kwadratów reszt)

kwadratów reszt)

(

(

wartość średnia

wartość średnia

kwadratów regresji)

kwadratów regresji)









n

i

i

Y

Y

SSE

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

1







k

n

SSE

MSE

1

SSR

MSR

69

69

Interpretacja oznaczeń

Interpretacja oznaczeń

wyników analizy regresji w

wyników analizy regresji w

Excel

Excel



F

F

– wartość statystyki F

– wartość statystyki F

służącej do weryfikacji

służącej do weryfikacji

hipotezy o łącznej istotności

hipotezy o łącznej istotności

zmiennych objaśniających

zmiennych objaśniających



Współczynniki –

Współczynniki –

ocena

ocena

parametrów strukturalnych

parametrów strukturalnych



Błędy standardowe

Błędy standardowe

– średni

– średni

błędy ocen parametrów

błędy ocen parametrów

strukturalnych

strukturalnych

MSE

MSR

F 

b

0

b

1

b

2

b

k

S

b0

S

b1

S

b2

S

bk

70

70

Interpretacja oznaczeń

Interpretacja oznaczeń

wyników analizy regresji w

wyników analizy regresji w

Excel

Excel



t Stat

t Stat

– wartość testu t-

– wartość testu t-

Studenta, służące do badania

Studenta, służące do badania

istotności parametrów

istotności parametrów

strukturalnych

strukturalnych



Wartość-p –

Wartość-p –

wartość

wartość

„prawdopodobieństwa

„prawdopodobieństwa

empirycznego”

empirycznego”

(prawdopodobieństwo

(prawdopodobieństwo

zdarzenia, że statystyka t

zdarzenia, że statystyka t

b

b

znajdzie się w przedziale

znajdzie się w przedziale

ufności

ufności

prawdziwość hipotezy zerowej

prawdziwość hipotezy zerowej

H

H

0

0

)

)

j

j

b

j

b

S

b

t 

71

71

3. Badanie własności

3. Badanie własności

odchyleń losowych

odchyleń losowych

72

72



Badanie własności składników losowych ma

Badanie własności składników losowych ma

na celu weryfikację założeń metody

na celu weryfikację założeń metody

najmniejszych kwadratów.

najmniejszych kwadratów.



Weryfikacja jest prowadzona na podstawie

Weryfikacja jest prowadzona na podstawie

reszt będących oszacowanymi składników

reszt będących oszacowanymi składników

losowych w modelu ekonometrycznym.

losowych w modelu ekonometrycznym.



Jeśli okaże się, że jakiś warunek nie jest

Jeśli okaże się, że jakiś warunek nie jest

spełniony, to estymatory tracą niektóre

spełniony, to estymatory tracą niektóre

własności. Wówczas należy ponownie

własności. Wówczas należy ponownie

oszacować parametry, stosując inną

oszacować parametry, stosując inną

metodę estymacji, albo zmienić model.

metodę estymacji, albo zmienić model.

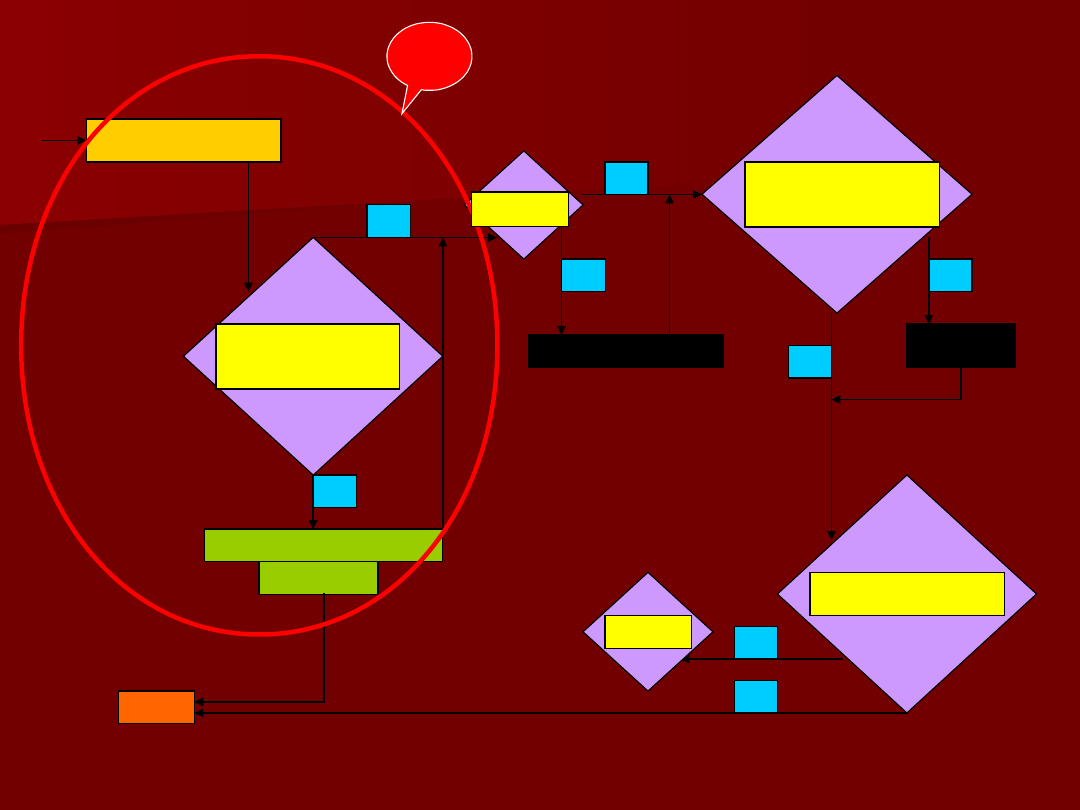
73

73

Studentyzacja

reszt

Czy są

obserwacje

odstające? |

stde|>3

T

Jeśli <10% to

eliminacja

Jeśli
>10%

Dan

e

N

N

T

Test

normalności

Czy są

homoskedastyc

zne?

N

T

Box-

Cox

Czy są

niezależne?

T

N

STOP

1

n>=15

*k

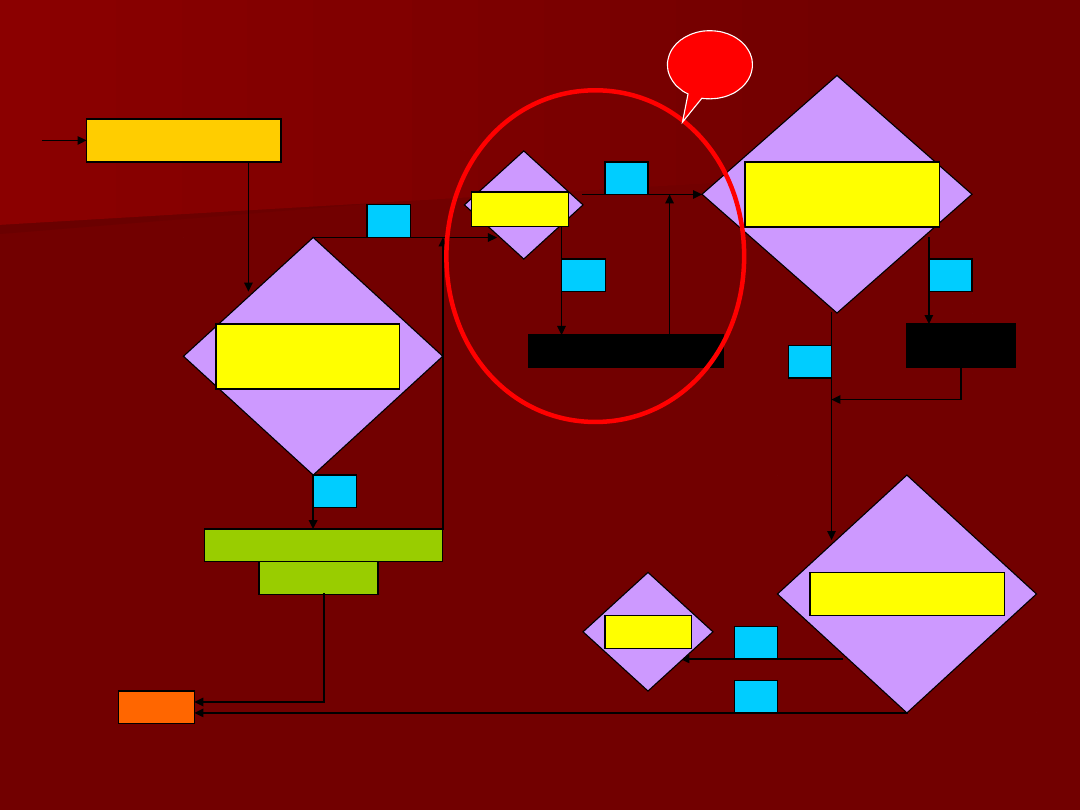
74

74

Studentyzacja

reszt

Czy są

obserwacje

odstające? |

stde|>3

T

Jeśli <10% to

eliminacja

Jeśli
>10%

Dan

e

N

N

T

Test

normalności

Czy są

homoskedastyc

zne?

N

T

Box-

Cox

Czy są

niezależne?

T

N

STOP

2

n>=15

*k

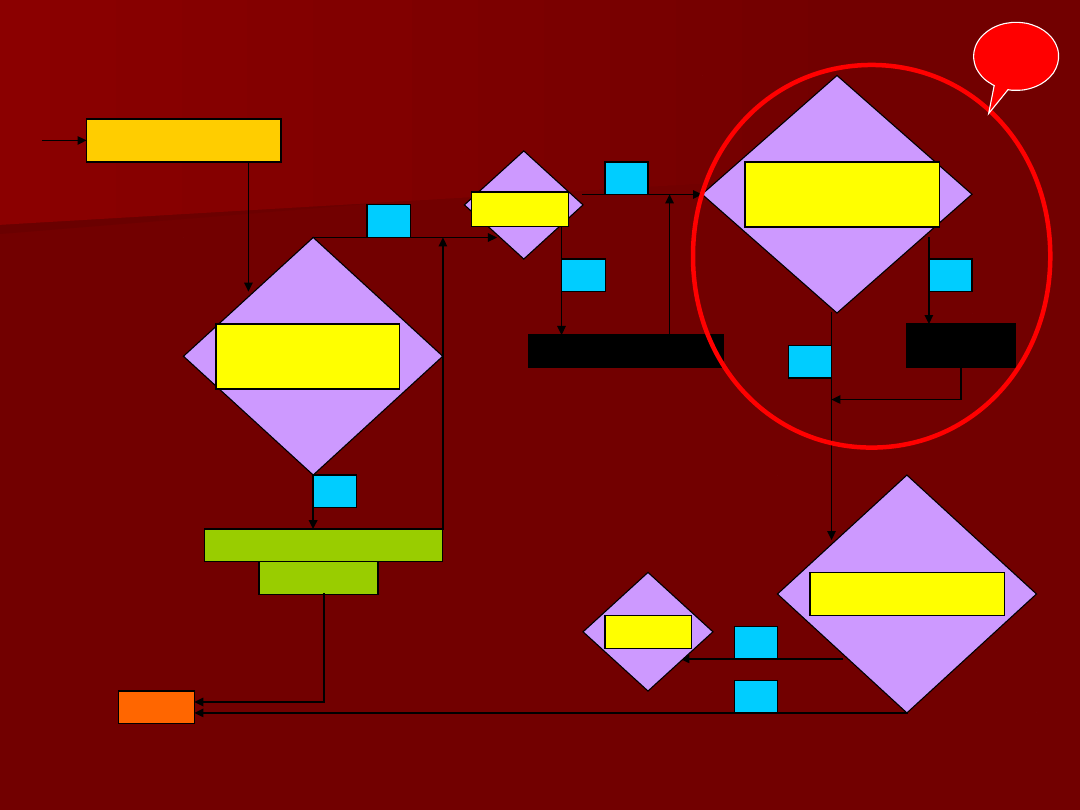
75

75

Studentyzacja

reszt

Czy są

obserwacje

odstające? |

stde|>3

T

Jeśli <10% to

eliminacja

Jeśli
>10%

Dan

e

N

N

T

Test

normalności

Czy są

homoskedastyc

zne?

N

T

Box-

Cox

Czy są

niezależne?

T

N

STOP

3

n>=15

*k

76

76

Studentyzacja

reszt

Czy są

obserwacje

odstające? |

stde|>3

T

Jeśli <10% to

eliminacja

Jeśli
>10%

Dan

e

N

N

T

Test

normalności

Czy są

homoskedastyc

zne?

N

T

Box-

Cox

Czy są

niezależne?

T

N

STOP

4

n>=15

*k

77

77

78

78

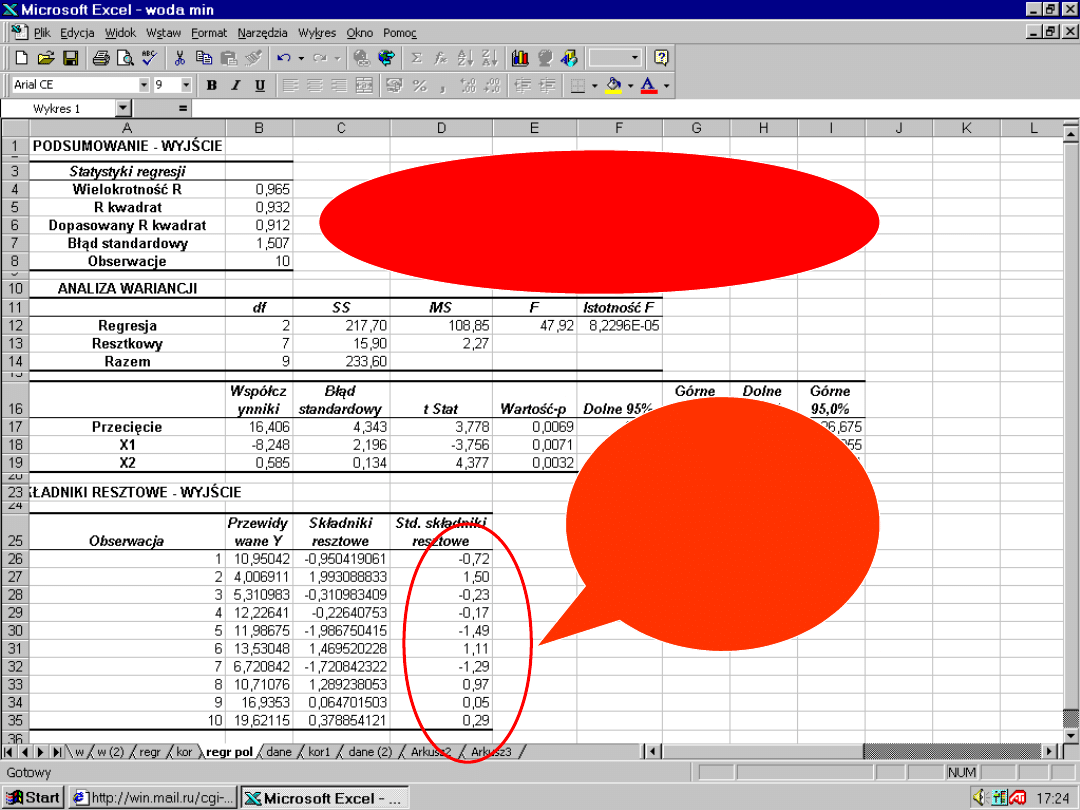
Studentezow

ane reszty

reszty

e

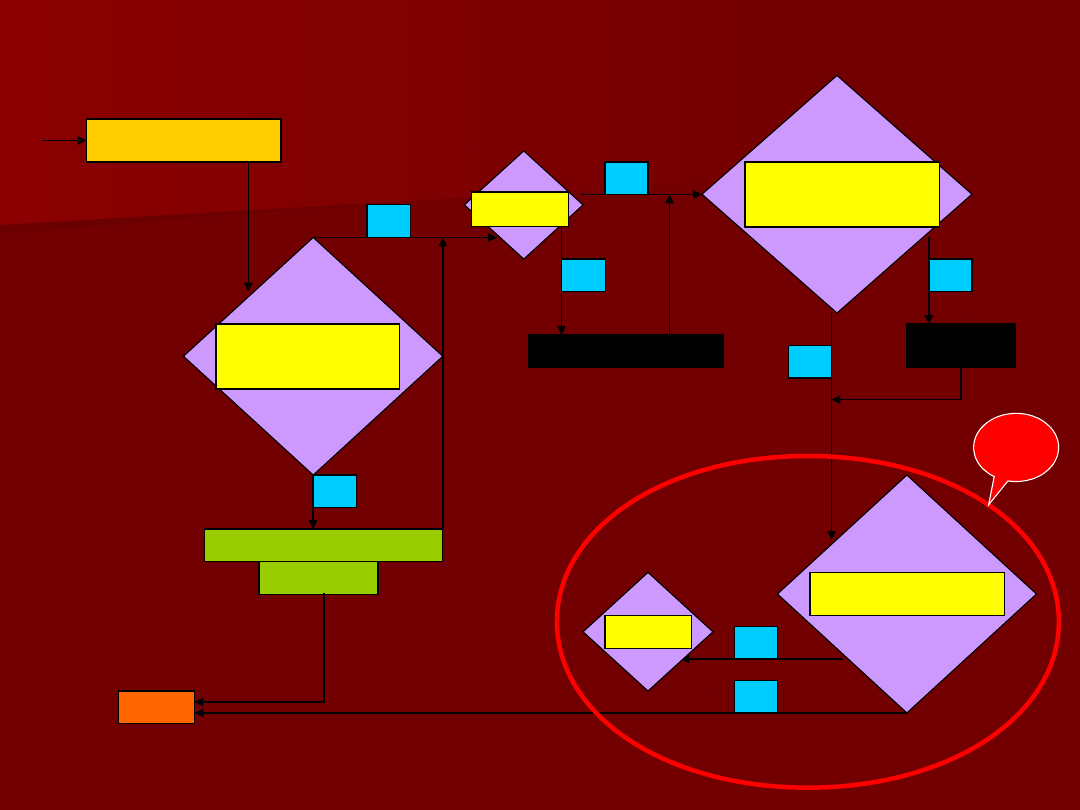
1. Studentyzacja
reszt

79

79

Studentezow

ane reszty

e = Y –

Ŷ

S

1. Studentyzacja
reszt

80

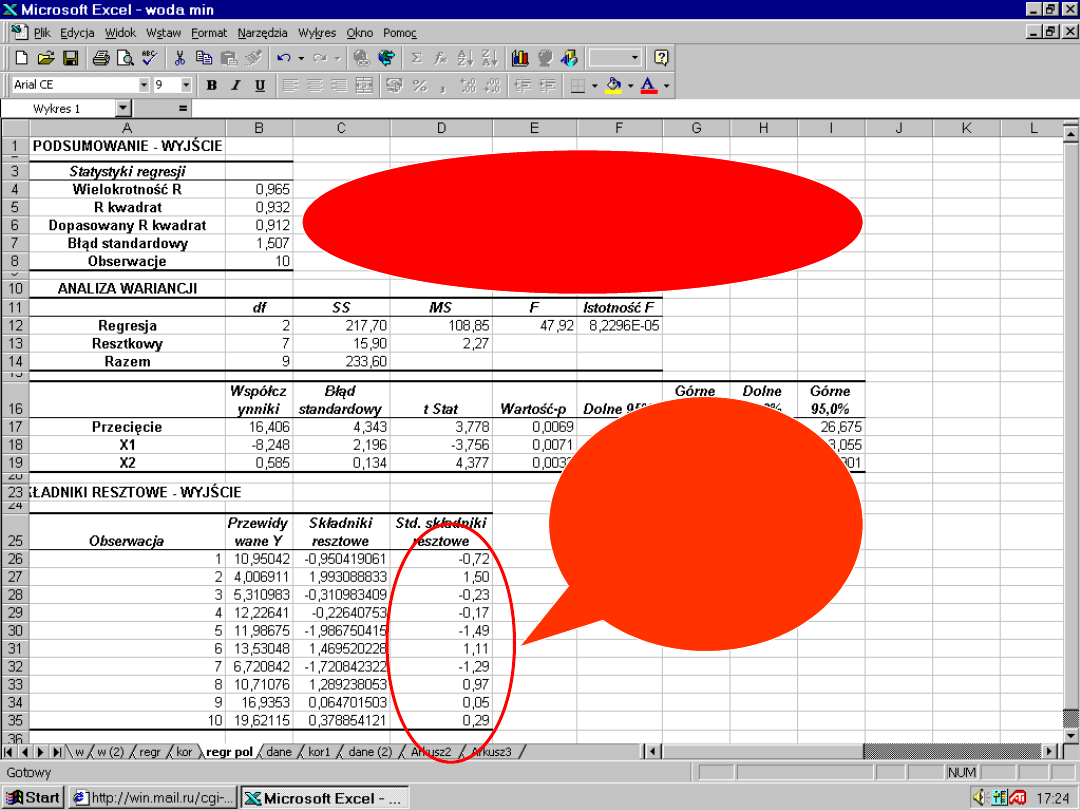
80

Czy są

obserwacji

odstające??

?

< -3

> 3

1. Studentyzacja
reszt

81

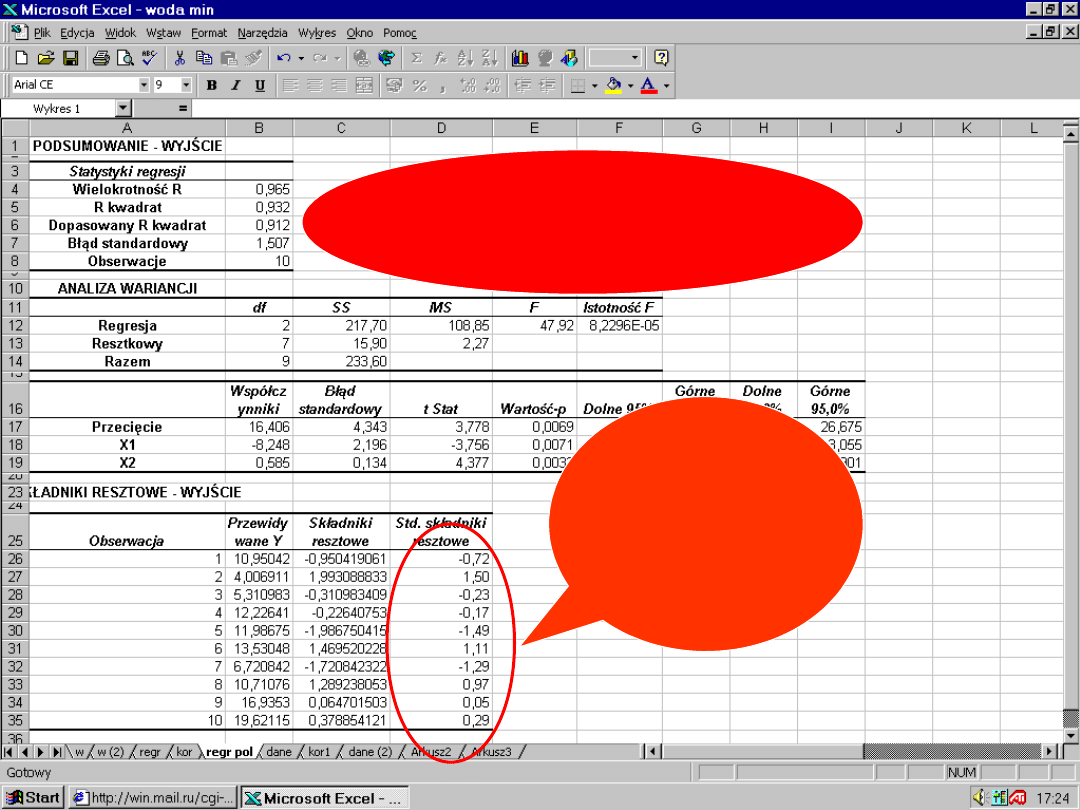
81

jeśli

<

10%

wyeliminow

ać

i jeszcze

raz obliczyć

1. Studentyzacja
reszt

82

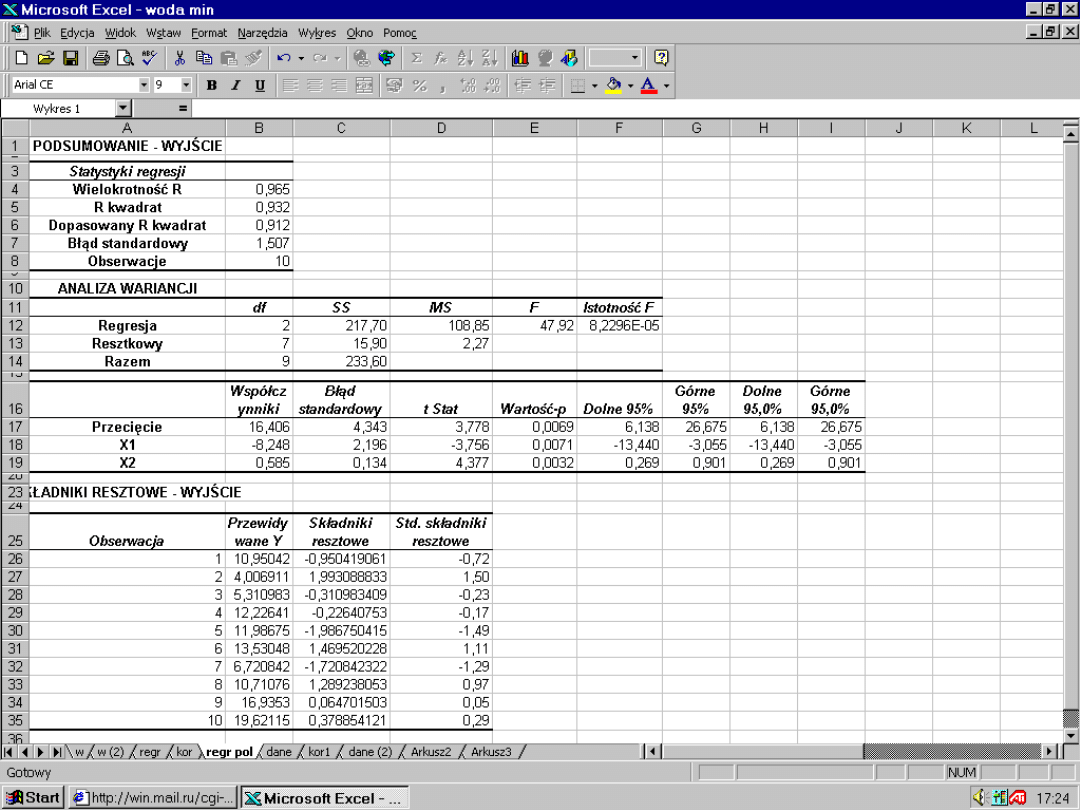
82

jeśli

<

10%

wyeliminow

ać

i jeszcze

raz obliczyć

1. Studentyzacja
reszt

83

83

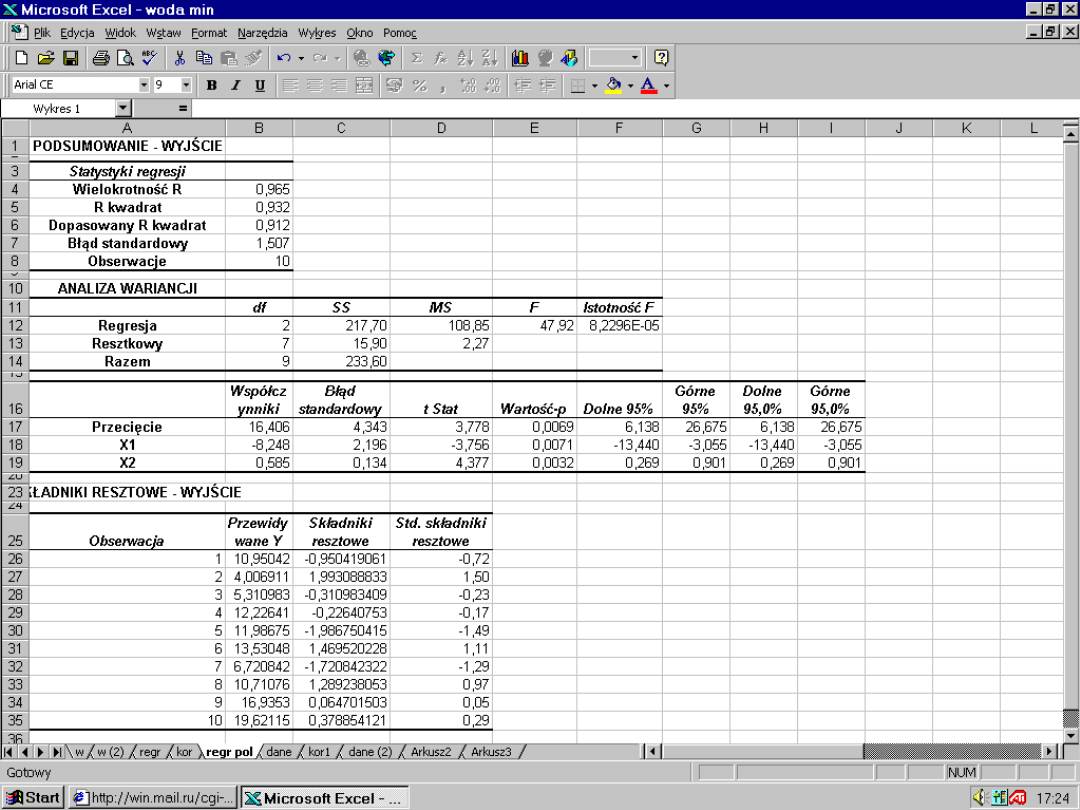
84

84

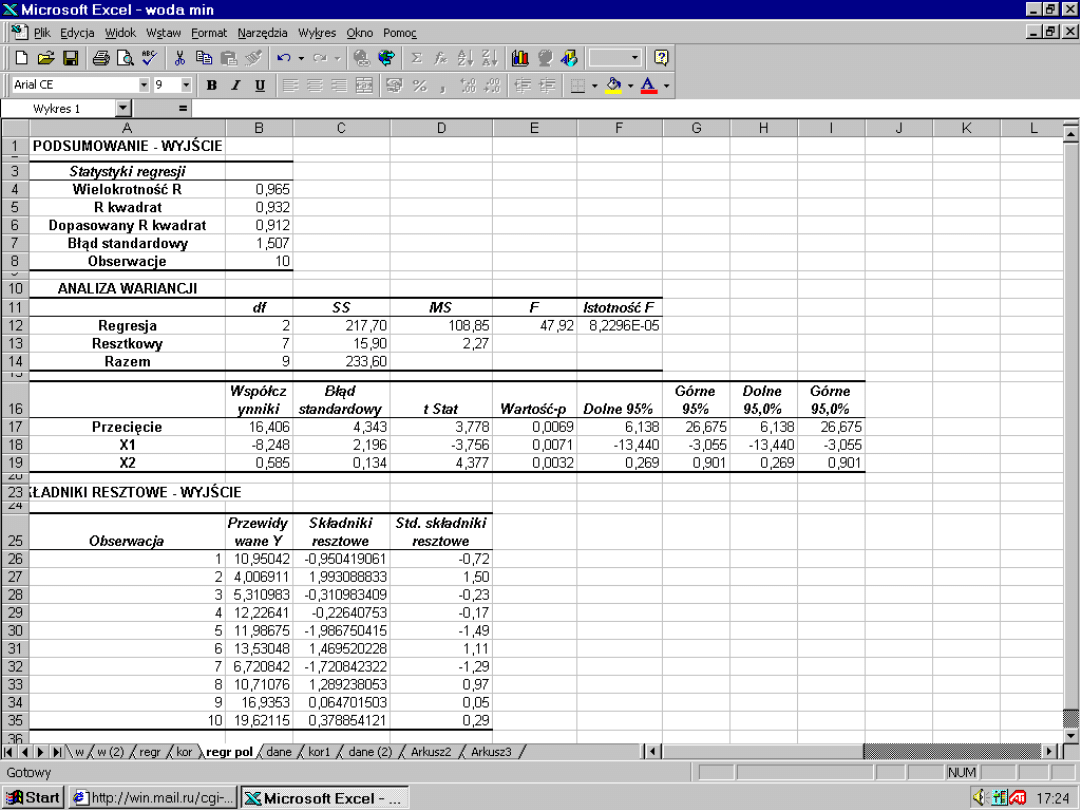
85

85

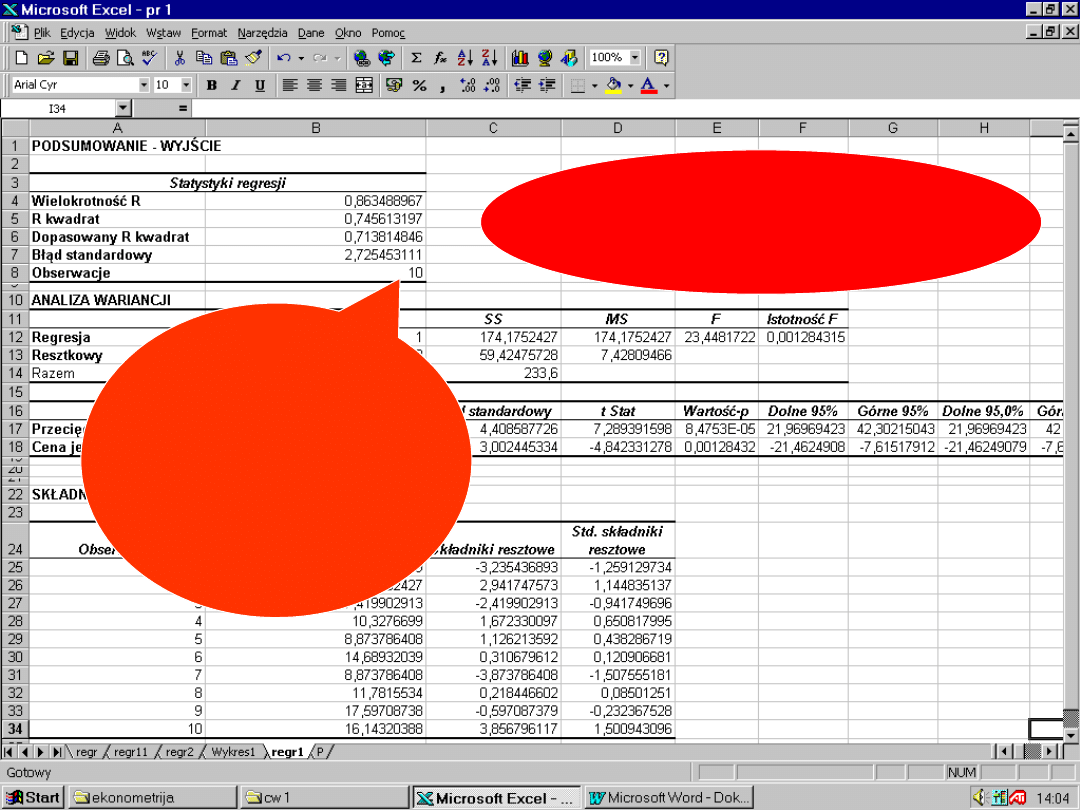
86

86

Jeśli ≤

30

obserwacji,

sprawdzamy,

czy rozkład

reszt jest

rozkładem

normalnym

2. Badanie
normalności

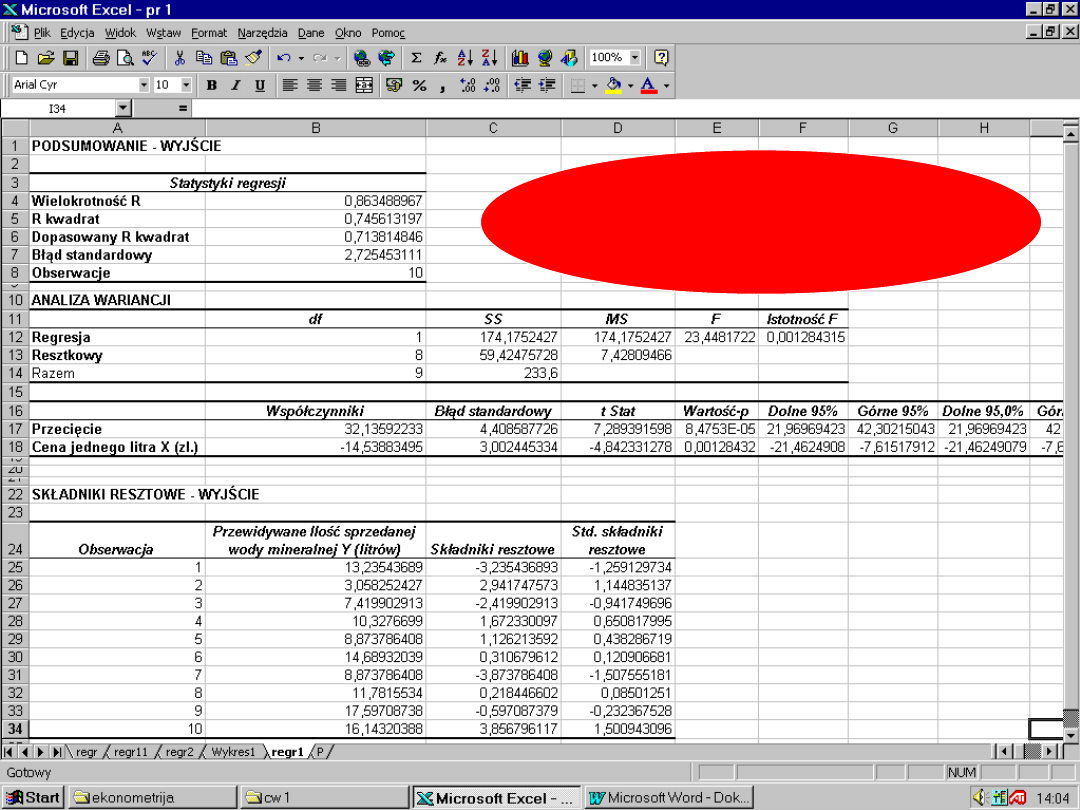
87

87

2. Badanie
normalności

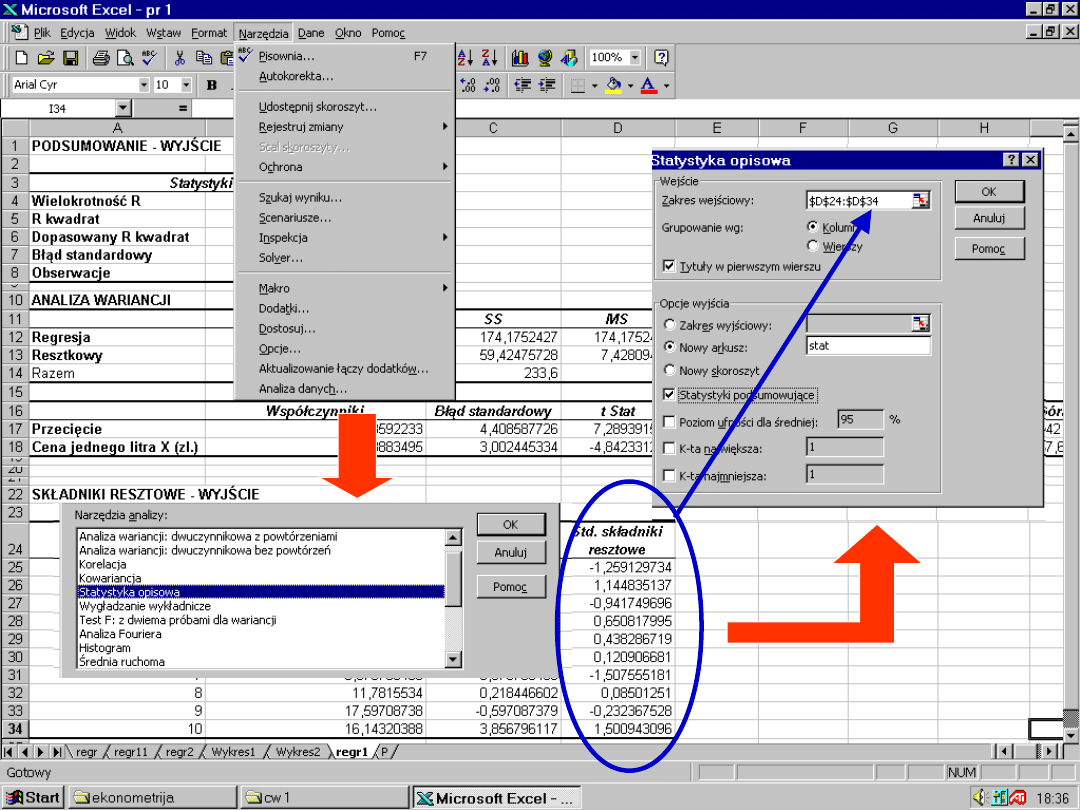
88

88

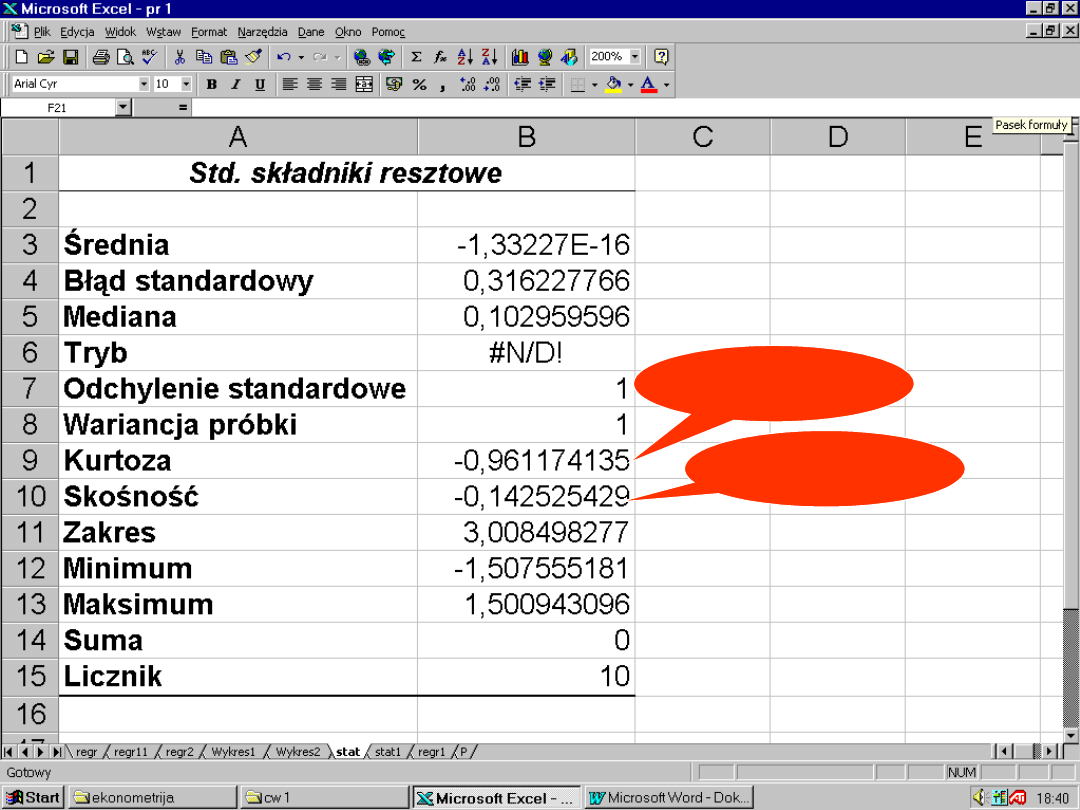
89

89

[-1;1]

[-1;1]

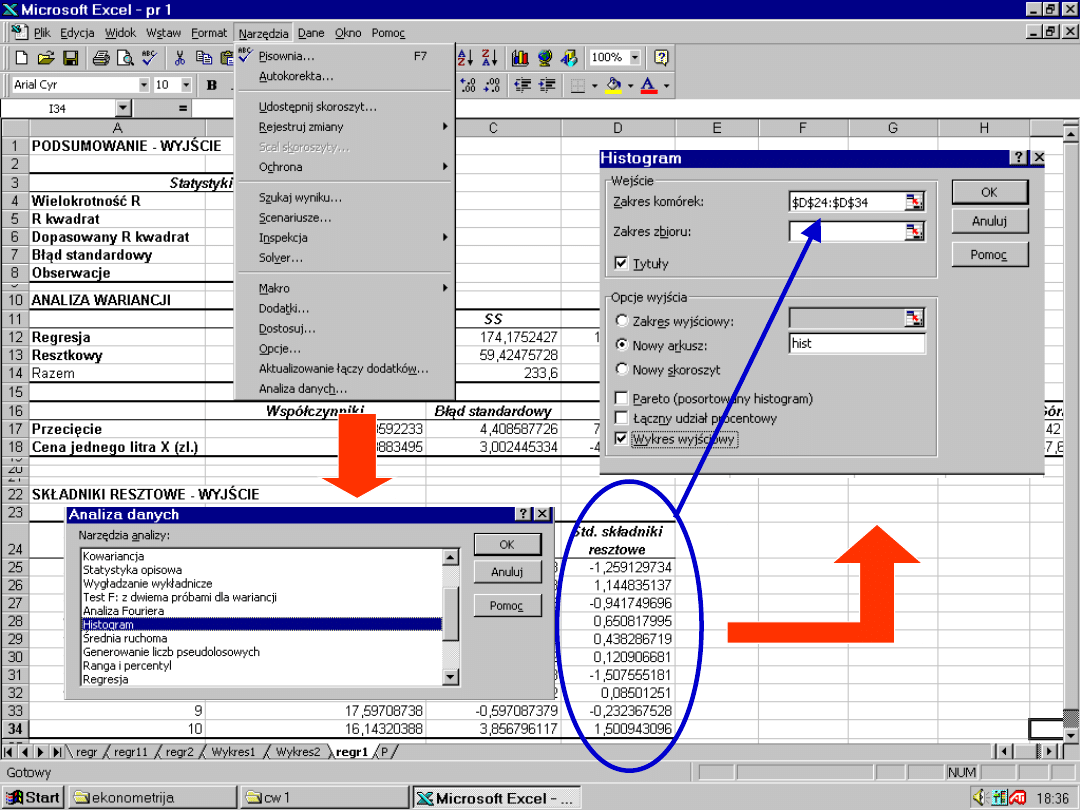
90

90

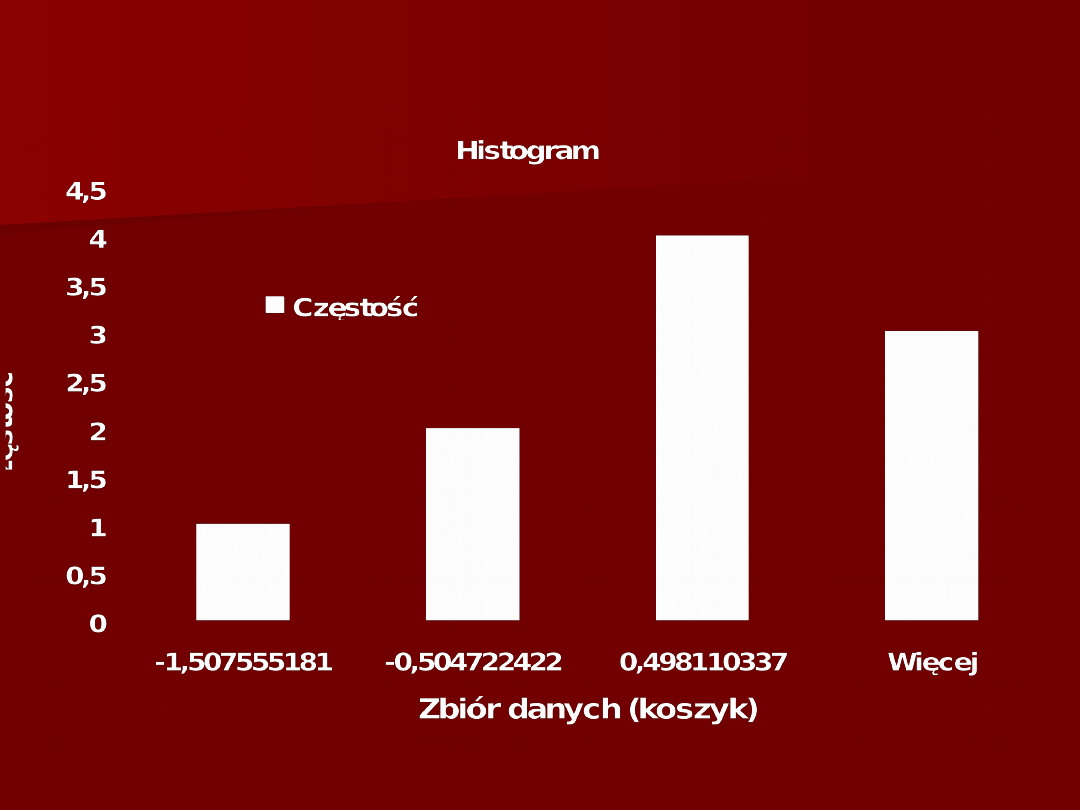
91

91

92

92

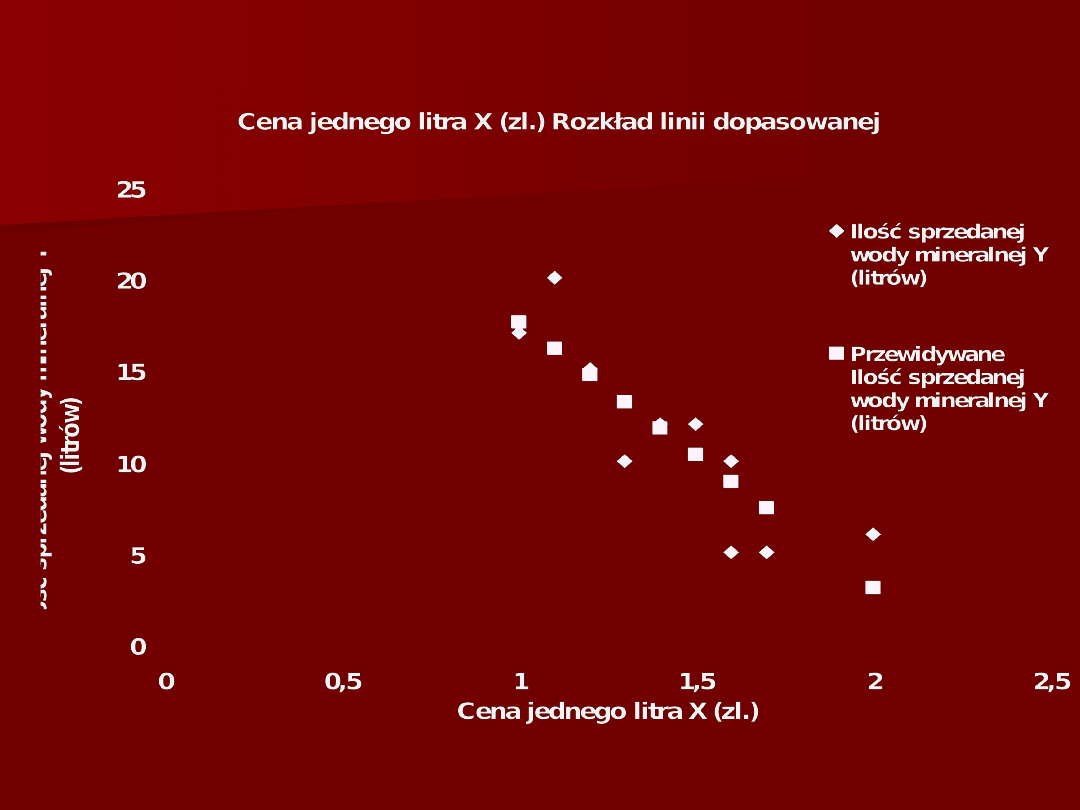
3. Badanie

homoskedastycznoś

ci

93

93

94

94

95

95

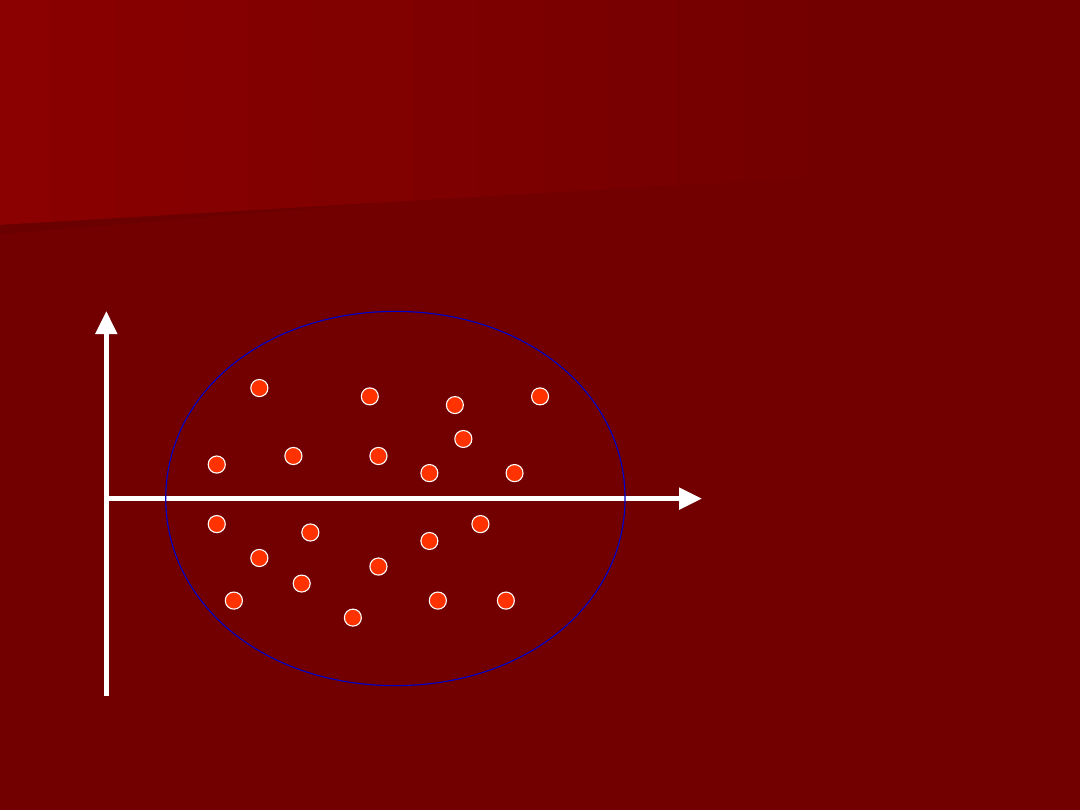
Homoskedastyczność

Homoskedastyczność



stałość

stałość

wariancji

wariancji

reszt

reszt

X

96

96

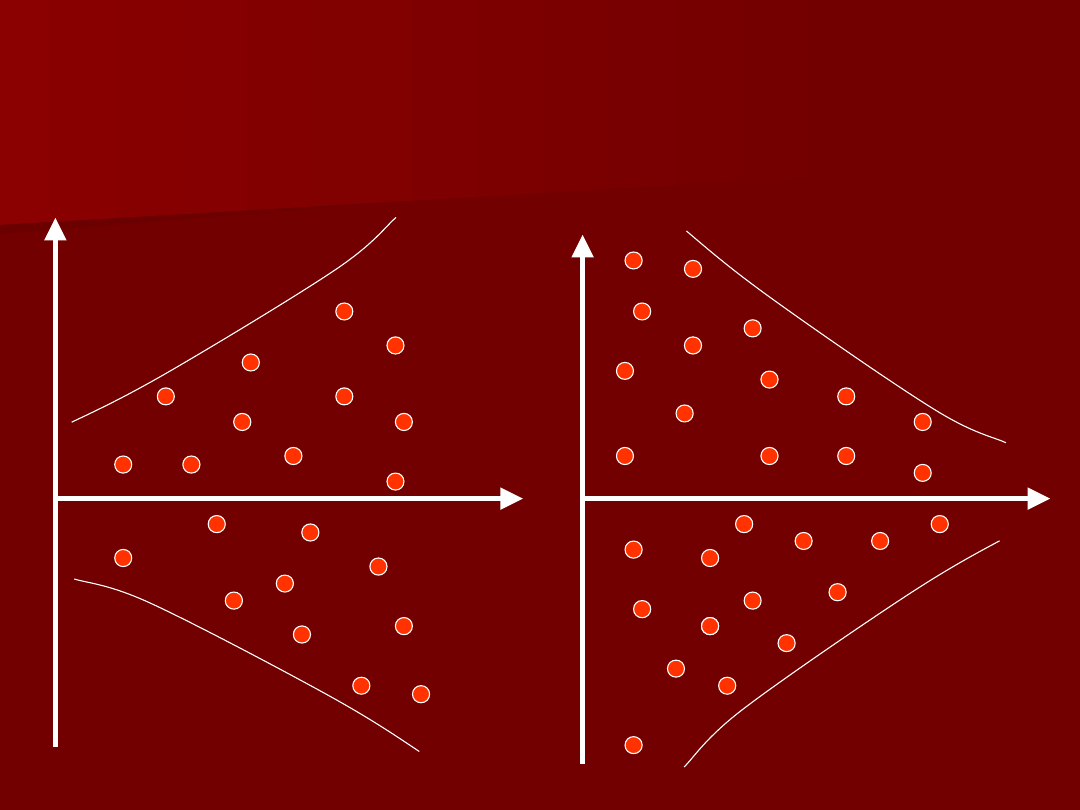
Heteroskedastyczność

Heteroskedastyczność

X

X

97

97

98

98

99

99

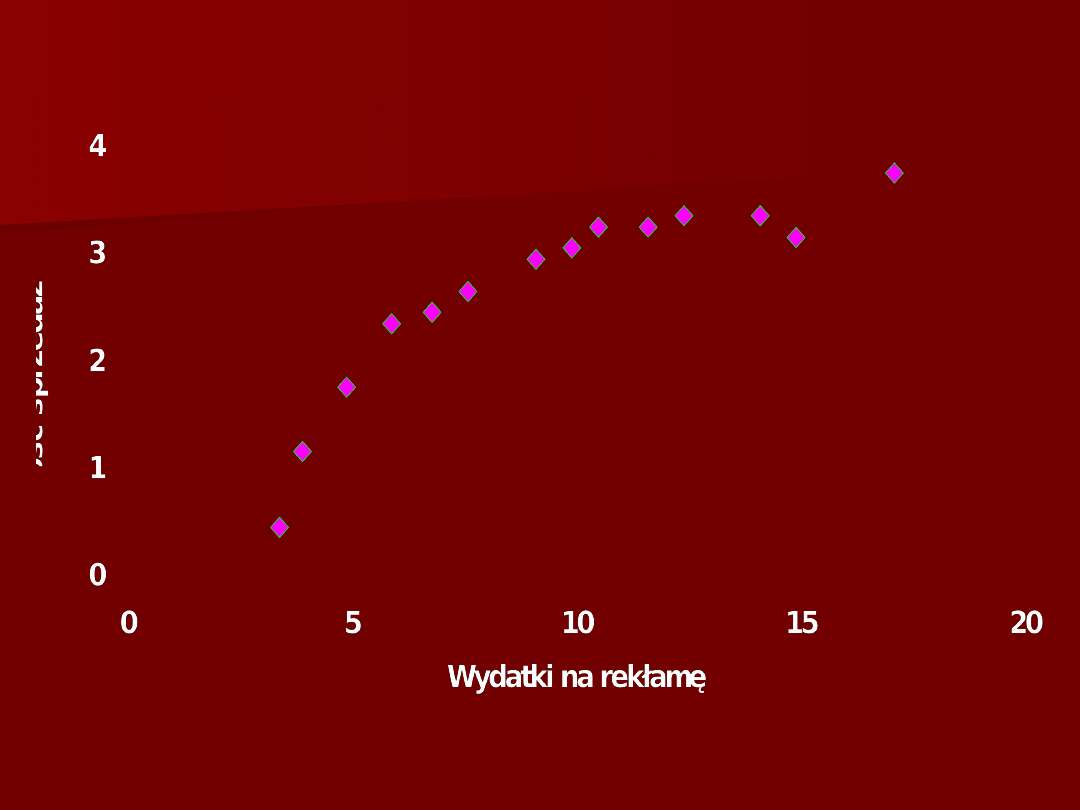
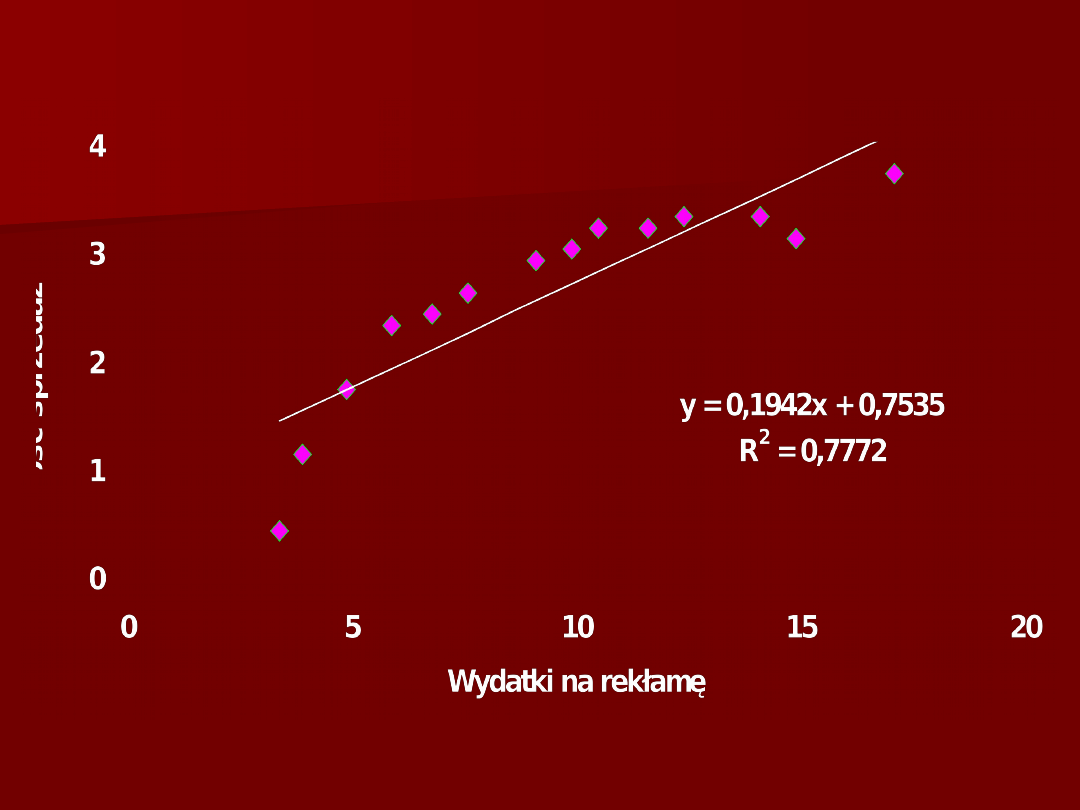
100

100

Wydatki na

reklamę (X)

Ilość

sprzedaż

(Y)

ln (X)

SQR

(X)

X*X

1/X

3,9

1,1

1,36

1,97

15,21

0,26

4,9

1,7

1,59

2,21

24,01

0,20

7,6

2,6

2,03

2,76

57,76

0,13

6,8

2,4

1,92

2,61

46,24

0,15

5,9

2,3

1,77

2,43

34,81

0,17

9,1

2,9

2,21

3,02

82,81

0,11

3,4

0,4

1,22

1,84

11,56

0,29

11,6

3,2

2,45

3,41

134,56

0,09

14,1

3,3

2,65

3,75

198,81

0,07

14,9

3,1

2,70

3,86

222,01

0,07

10,5

3,2

2,35

3,24

110,25

0,10

9,9

3

2,29

3,15

98,01

0,10

17,1

3,7

2,84

4,14

292,41

0,06

12,4

3,3

2,52

3,52

153,76

0,08

101

101

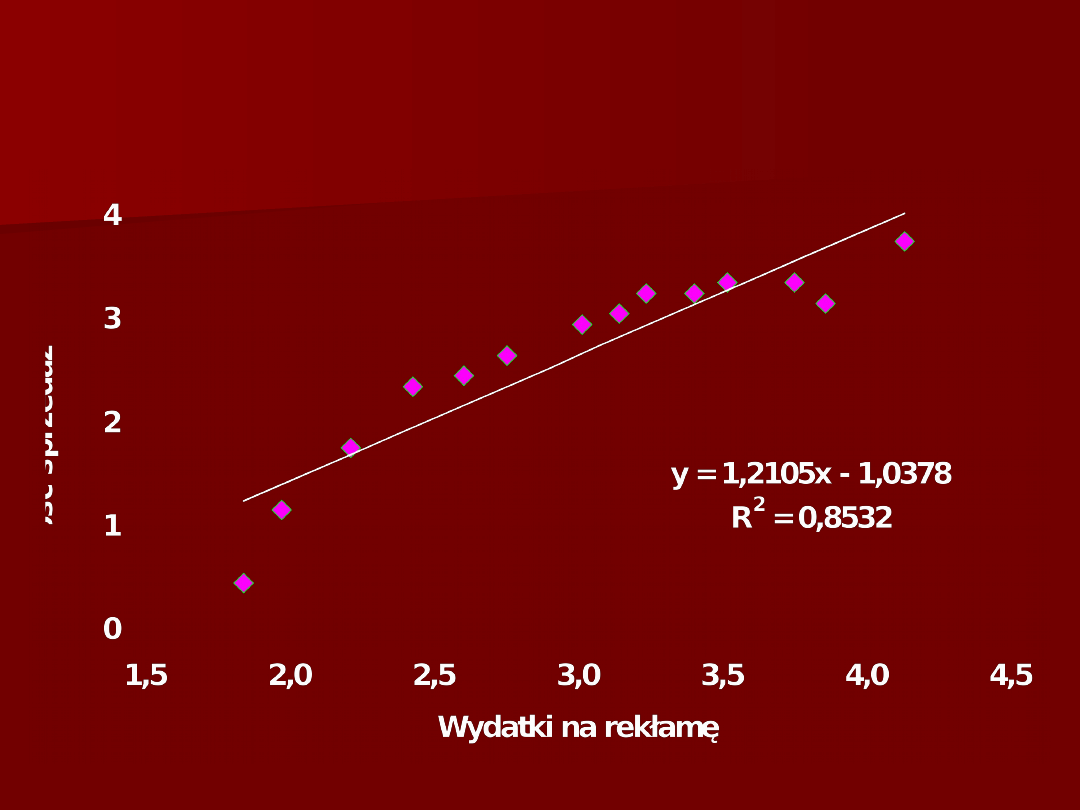
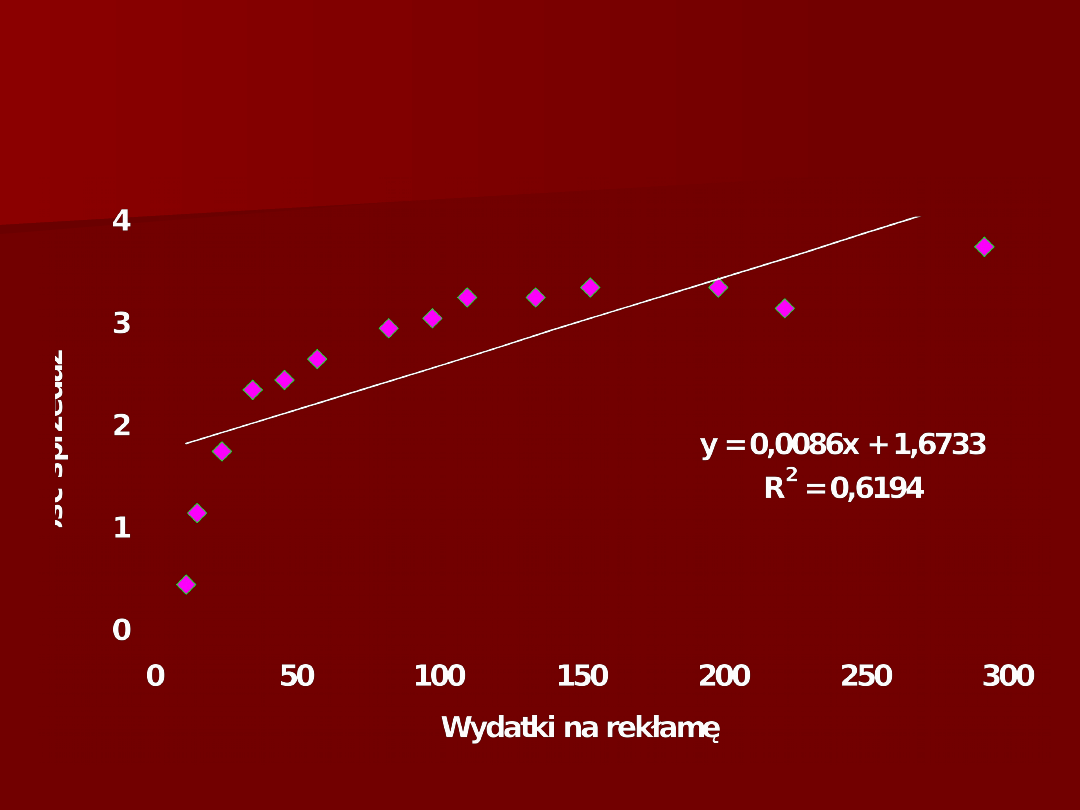
Przekształcenie potęgowe Z

Przekształcenie potęgowe Z

t

t

=X

=X

t

t

1/2

1/2

102

102

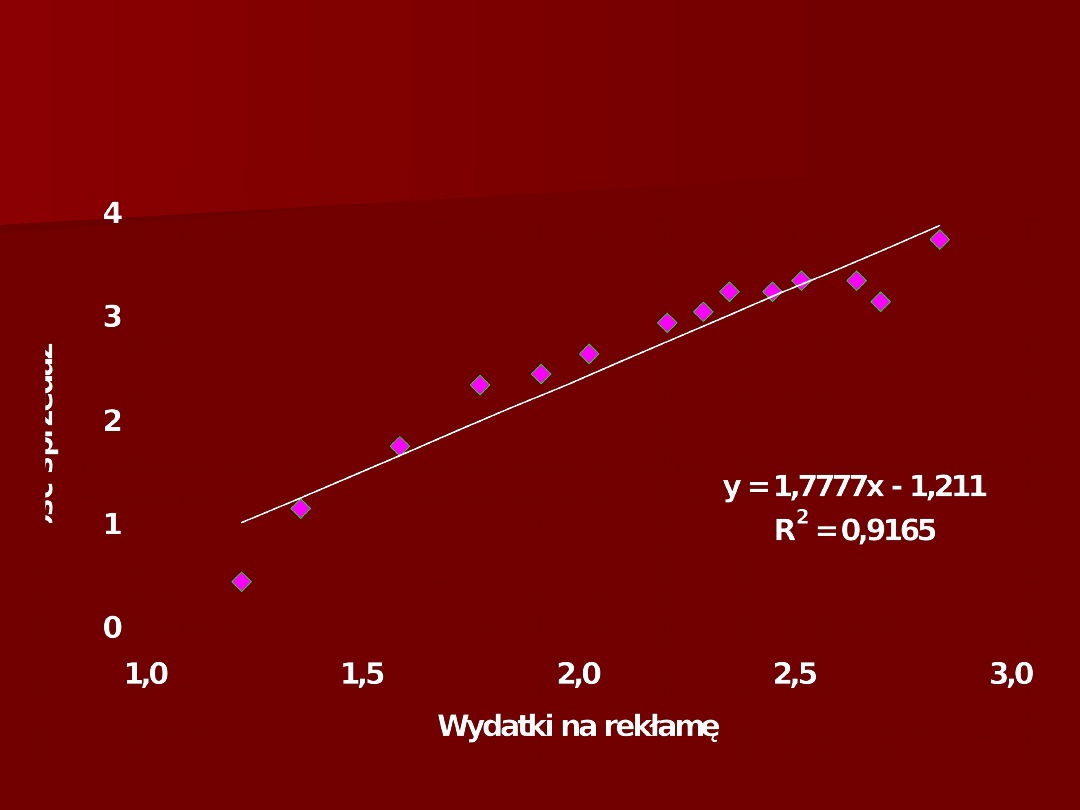
Przekształcenie potęgowe

Przekształcenie potęgowe

Z

Z

t

t

=X

=X

t

t

2

2

103

103

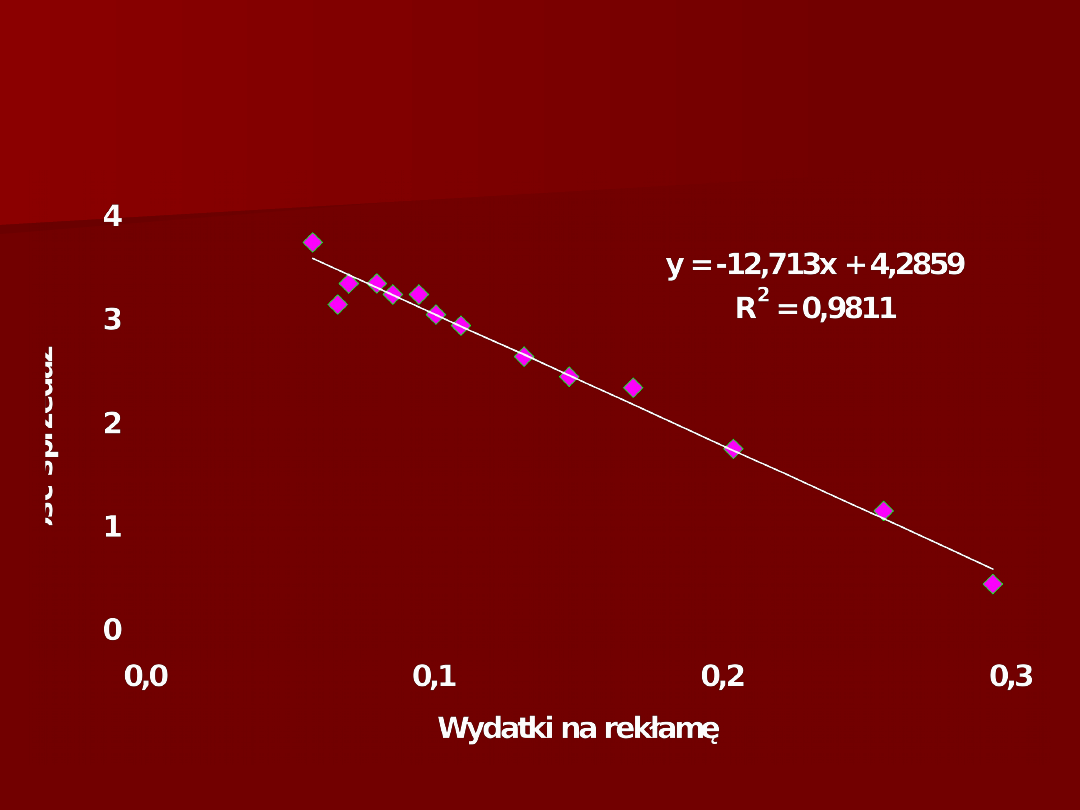
Przekształcenie logarytmiczne Z

Przekształcenie logarytmiczne Z

t

t

= ln(X

= ln(X

t

t

)

)

104

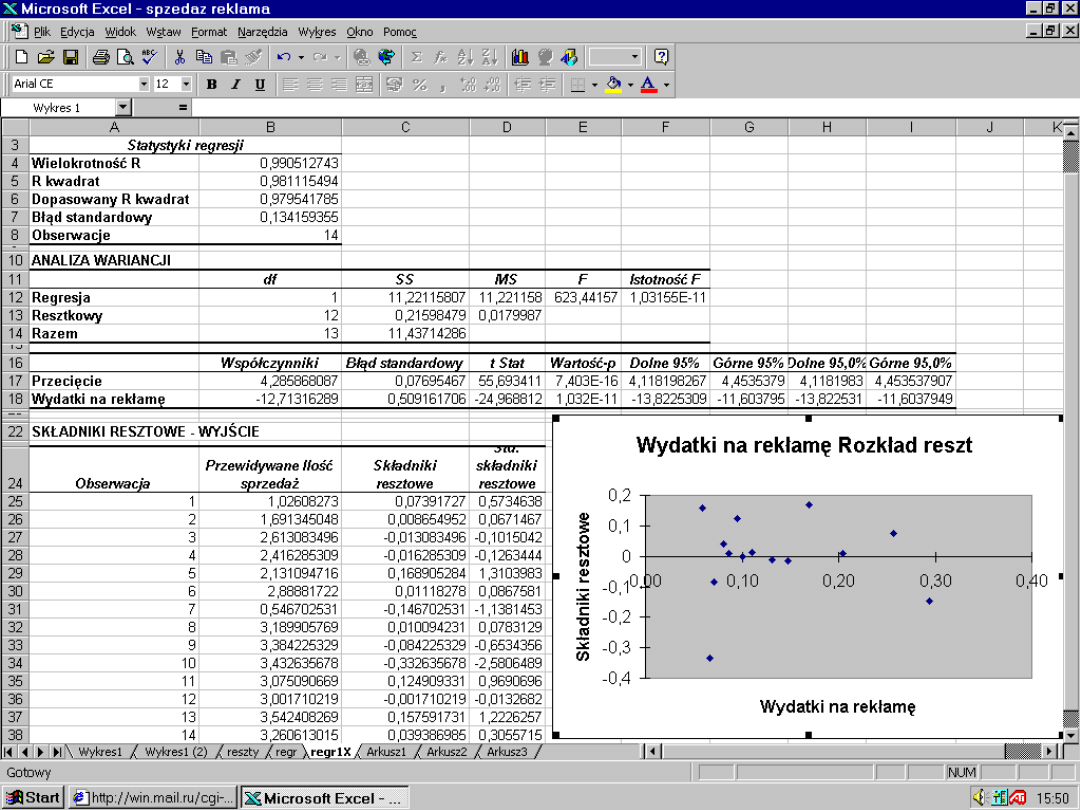
104

Przekształcenie Z

Przekształcenie Z

t

t

= 1 / X

= 1 / X

t

t

=

=

X

X

t

t

-1

-1

105

105

106

106

Przekształcenie potęgowe Z

Przekształcenie potęgowe Z

t

t

= Y

= Y

t

t

p

p



Jeśli p

Jeśli p

<

<

0, to przekształcona zmienna

0, to przekształcona zmienna

Z

Z

t

t

= Y

= Y

t

t

p

p

ma odwrotny trend do wyjściowej

ma odwrotny trend do wyjściowej



Jeśli 0

Jeśli 0

<

<

p

p

<

<

1, to przekształcona zmienna

1, to przekształcona zmienna

Z

Z

t

t

=

=

Y

Y

t

t

p

p

ma mniejsze zmiany amplitud niż wyjściowa

ma mniejsze zmiany amplitud niż wyjściowa



Jeśli

Jeśli

p

p

>

>

1, to przekształcona zmienna

1, to przekształcona zmienna

Z

Z

t

t

= Y

= Y

t

t

p

p

będzie miała większe zmiany amplitud niż

będzie miała większe zmiany amplitud niż

wyjściowa

wyjściowa

Przekształcenie logarytmiczne Z

Przekształcenie logarytmiczne Z

t

t

= ln(Y

= ln(Y

t

t

)

)



Cel przekształcenia logarytmicznego jest

Cel przekształcenia logarytmicznego jest

podobny jak przekształcenia potęgowego Z

podobny jak przekształcenia potęgowego Z

t

t

=

=

Y

Y

t

t

p

p

dla 0

dla 0

<

<

p

p

<

<

1

1

Chodzi o spowolnienie zmian wartości i amplitud

Chodzi o spowolnienie zmian wartości i amplitud

wyjściowych danych

wyjściowych danych

107

107

4. Niezależność
reszt

108

108



Badanie losowości rozkładu składnika

Badanie losowości rozkładu składnika

losowego ma na celu zweryfikowanie

losowego ma na celu zweryfikowanie

hipotezy o trafności doboru postaci

hipotezy o trafności doboru postaci

analitycznej modelu.

analitycznej modelu.



Czy model liniowy poprawnie opisuje

Czy model liniowy poprawnie opisuje

zależność pomiędzy zmienną

zależność pomiędzy zmienną

objaśnianą a zmienną objaśniającej.

objaśnianą a zmienną objaśniającej.

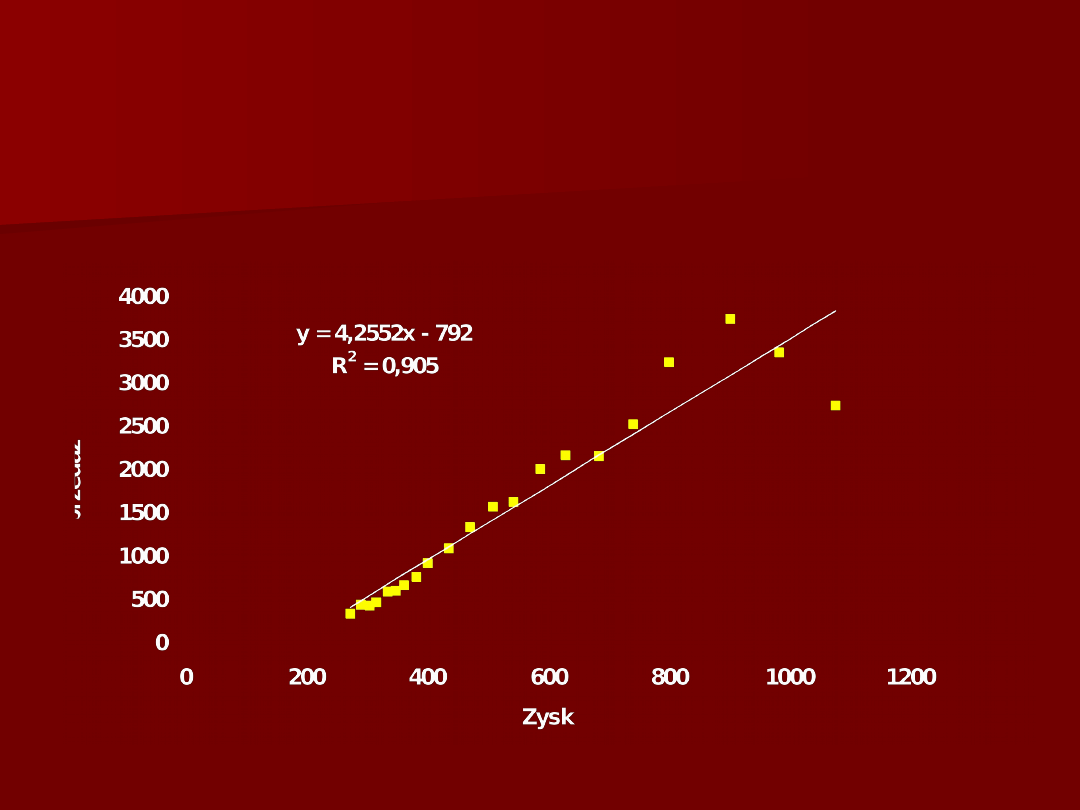
109

109

Wielkość sprzedaż kompanii

Wielkość sprzedaż kompanii

Reynolds Metals

Reynolds Metals

110

110

Test Durbina - Watsona

Test Durbina - Watsona



















n

i

i

n

i

i

i

e

e

e

DW

1

2

2

2

1

1

1

1

ˆ

ˆ















t

t

i

t

t

i

Y

Y

e

Y

Y

e

111

111



H

H

0

0

:

:

ρ

ρ

= 0

= 0



H

H

A

A

:

:

ρ

ρ

> 0

> 0



Jeśli DW > U , przyjmujemy

Jeśli DW > U , przyjmujemy

H

H

0

0

:

:

ρ

ρ

= 0

= 0



Jeśli DW < L , przyjmujemy H

Jeśli DW < L , przyjmujemy H

A

A

:

:

ρ

ρ

> 0

> 0



Jeśli L ≤ DW ≤ U , brak decyzji

Jeśli L ≤ DW ≤ U , brak decyzji

112

112

Rok

Sprzeda

ży

Zysk

 

Reszt

y

 

 

 

 

Y

X

Ŷ

E

t

E

t

-E

t-1

(E

t

-E

t-

1

)^2

E

t

^2

197

6

295

273,

4

371,

4

-76,4

 

 

5831,0

197

7

400

291,

3

447,

5

-47,5

28,8

831,3

2258,9

197

8

390

306,

9

513,

9

-

12

3,9 -76,4

5834,0

15353,4

197

9

425

317,

1

557,

3

-

13

2,3

-8,4

70,6

17506,3

198

0

547

336,

1

638,

2

-91,2

41,2

1693,5

8310,1

…

…

…

…

…

…

…

…

199

4

3702

903,

1

3050

,8 651,2

69,8

4875,4

424010,

2

199

5

3316

983,

6

3393

,4

-77,4

-

72

8,5

530771,

9

5987,7

199

6

2702

1076

,7

3789

,5

-

10

87,

5

-

10

10,

2

102041

5,2

1182735

,2

 

 

 

 

 

Suma

192603

2

2210646





87

,

0

2210646

1926032

1

2

2

2

1



















n

i

i

n

i

i

i

e

e

e

DW

113

113

DW = 0,87

DW = 0,87

DW < L

DW < L

0,87 < 1,22

0,87 < 1,22



α

α

= 0,05

= 0,05



k = 1

k = 1



n = 21

n = 21



L = 1,22

L = 1,22



U = 1,42

U = 1,42

114

114