Przykład 1

Problem badawczy

(na podstawie danych, plik budżet-produkcja.xls)

Zbadaj wpływ wysokości produkcji sprzedanej na dochody budżetów gmin wykorzystując model regresji liniowej prostej. Dokonaj jego pełnej charakterystyki.

Równanie prognozy ma postać:

Estymatory parametrów:

Miara dopasowania modelu

Zmienność zmiennej zależnej
została wyjaśniona przez model w 94%, tzn. model jest bardzo dobrze dopasowany do danych.

Istotność modelu

Współczynnik determinacji
jest istotny dla modelu, gdyż w teście istotności próbkowy poziom istotności F-value=3,716*10^-31, tj. 0,00%, jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

Istotność parametrów modelu

• istotność
  

Parametr istotny, gdyż w teście istotności próbkowy poziom istotności p-value=7,724*10^-9, tj. 0,00%, jest jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

• istotność
  

Parametr istotny, gdyż w teście istotności próbkowy poziom istotności p-value=3,716*10^-31, tj. 0,00%, jest jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

Współczynnik korelacji

Współczynnik korelacji
wskazuje na bardzo silny dodatni zwiazek między analizowanymi zmiennymi.

Wyznaczanie prognozy dla wartości typowych

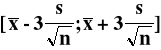
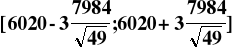
Do równania prognozy w miejsce zmiennej niezależnej można podstawiać jednynie wartości z powyższego przedziału.

Przyrost krańcowy (marginalny)

Wyznaczenie przyrostu krańcowego to obliczenie pochodnej równania prognozy względem zmiennej X.

Jeśli zmienna niezależna X (produkcja sprzedana przemysłu) wzrośnie o 1 jednostkę (o 1 mln zł) to zmienna zależna (dochody budżetu gmin) Y wzrośnie o 0,074 jednostki (o 0,074 mln zł)

Elastyczność

Za zmienne X i Y zostały podstawione mediany, gdyż rozkład X i rozkład Y nie jest normalny.

Jeśli zmienna niezależna X (produkcja sprzedana przemysłu) wzrośnie o 1% to zmienna zależna Y (dochody budżetu gmin) wzrośnie o 0,64%.

Autokorelacja składnika resztowego

Wartość statystyki z próby:

Przy
oraz
wartości z tablic rozkładu Durbina-Watsona wynoszą
oraz

Wartość statystyki testowej z próby należy do obszaru przyjęć. Wobec tego stwierdzamy, iż nie występuje autokorelacja składników losowych. Jest to sytuacja pożądana w modelu.

Przykład 2

Problem badawczy

(na podstawie danych, plik samochody-spalanie.xls)

Zbadaj w jakim stopniu moc samochodu (ilość koni mechanicznych) wpływa na zużycie benzyny (ilość mil na 1 galonie) wykorzystując model regresji liniowej prostej. Dokonaj jego pełnej charakterystyki.

Równanie prognozy ma postać:

Estymatory parametrów:

Miara dopasowania modelu

Zmienność zmiennej zależnej
została wyjaśniona przez model w 70%, tzn. model jest dobrze dopasowany do danych.

Istotność modelu

Współczynnik determinacji
jest istotny dla modelu, gdyż w teście próbkowy poziom istotności F-value= 2,127*10^-22, tj. 0,00%, jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

Istotność parametrów modelu

• istotność
  

Parametr istotny, gdyż w teście istotności próbkowy poziom istotności p-value=1,177*10^-48, tj. 0,00%, jest jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

• istotność
  

Parametr istotny, gdyż w teście istotności próbkowy poziom istotności p-value=2,127*10^-22, tj. 0,00%, jest jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

Współczynnik korelacji

Współczynnik korelacji
wskazuje na silny dodatni zwiazek między analizowanymi zmiennymi.

Wyznaczanie prognozy dla wartości typowych

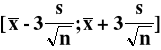
Do równania prognozy w miejsce zmiennej niezależnej można podstawiać jednynie wartości z powyższego przedziału.

Przyrost krańcowy (marginalny)

Wyznaczenie przyrostu krańcowego to obliczenie pochodnej równania prognozy względem zmiennej X.

Jeśli zmienna niezależna X (ilość koni mechanicznych) wzrośnie o 1 jednostkę (o 1 KM) to zmienna zależna Y (ilość mil na 1 galonie) zmaleje o 0,68 jednostki (o 0,68 mili).

Elastyczność

Za zmienne X i Y zostały podstawione mediany, gdyż rozkład X i rozkład Y nie jest normalny.

Jeśli zmienna niezależna X (ilość koni mechanicznych) wzrośnie o 1% to zmienna zależna Y (ilość mil na 1 galonie) zmaleje o 0,25%.

Autokorelacja składnika resztowego

Wartość statystyki z próby:

Przy
oraz
wartości z tablic rozkładu Durbina-Watsona wynoszą
oraz

Wartość statystyki testowej z próby należy do obszaru odrzuceń. Wobec tego stwierdzamy, iż występuje autokorelacja składników losowych. Jest to sytuacja niepożądana w modelu.

Przykład 3

Problem badawczy

(na podstawie danych, plik bezrobocie-przestępczość.xls)

Wykorzystując model regresji liniowej prostej zbadaj wpływ stopy bezrobocia wśród mężczyzn na poziom przestępczości. Dokonaj pełnej charakterystyki modelu.

Równanie prognozy ma postać:

Estymatory parametrów:

Miara dopasowania modelu

Zmienność zmiennej zależnej
została wyjaśniona przez model w 0,00%, tzn. model nie jest dopasowany do danych.

Istotność modelu

Współczynnik determinacji
nie jest istotny dla modelu, gdyż w teście istotności próbkowy poziom istotności F-value=0,736, tj, 73,6% jest większy od 5%, a więc hipoteza zerowa nie została odrzucona. Oznacza to nie przyjęcie tego modelu, gdyż model ten nie jest istotny.

Dalsza część przykładu jest objaśniona jedynie w celach ćwiczeniowych, gdyż odrzucenie modelu nie pozwala na przyjęcie poniższych wniosków za wiarygodne.

Istotność parametrów modelu

• istotność
  

Parametr istotny, gdyż w teście istotności próbkowy poziom istotności p-value=0,002, tj. 0,2% jest jest mniejszy od 5%, a więc hipoteza zerowa została odrzucona.

• istotność
  

Parametr nie istotny, gdyż w teście istotności próbkowy poziom istotności p-value=0,736, tj. 73,6% jest jest większy od 5%, a więc hipoteza zerowa nie została odrzucona.

Współczynnik korelacji

Współczynnik korelacji
wskazuje na bardzo słaby ujemny zwiazek między analizowanymi zmiennymi.

Wyznaczanie prognozy dla wartości typowych

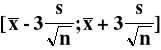
Do równania prognozy w miejsce zmiennej niezależnej można podstawiać jednynie wartości z powyższego przedziału.

Przyrost krańcowy (marginalny)

Wyznaczenie przyrostu krańcowego to obliczenie pochodnej równania prognozy względem zmiennej X.

Jeśli zmienna niezależna X (stopa bezrobocia) wzrośnie o 1 jednostkę (o 1 osobę bezrobotną na 1000) to zmienna zależna Y (stopa przestępczości) zmaleje o 0,11 jednostki (o 0,11 przestępstwa na 1 mln mieszkańców).

Elastyczność

Za zmienną X została podstawiona średnia, gdyż jej rozkład jest normalny, natomiast za Y została podstawiona mediana, gdyż jej rozkład nie jest normalny.

Jeśli zmienna niezależna X (stopa bezrobocia) wzrośnie o 1% to zmienna zależna Y (stopa przestępczości) zmaleje o 0,13%.

Autokorelacja składnika resztowego

Wartość statystyki z próby:

Przy
oraz
wartości z tablic rozkładu Durbina-Watsona wynoszą
oraz

Wartość statystyki testowej z próby należy do obszaru, gdzie nie można podjąć żadnej decyzji, co do występowania bądź też nie autokorelacji składników losowych. Jest to sytuacja patowa, niekorzystna dla modelu regresji.

---