Model prostej regresji liniowej

Model regresji w populacji generalnej:

ε

α

α

+

+

=

X

Y

1

0

Y – zmienna objaśniana, zależna
X – zmienna objaśniająca, predyktor

ε

- zakłócenie, błąd losowy, o którym zakładamy, że

2

2

)

(

;

0

)

(

σ

ε

ε

=

=

D

E

oraz najczęściej,

ż

e podlega rozkładowi normalnemu

0

α

- wyraz wolny

1

α

- współczynnik kierunkowy, miara nachylenia linii

X

Y

1

0

α

α

+

=

względem osi odciętych

Przyjmujemy, że X jest wielkością nielosową – wartości jakie przyjmuje są ustalone.

Model średniej warunkowej:

X

X

Y

E

1

0

)

|

(

α

α

+

=

Metoda najmniejszych kwadratów (MNK):

Metoda uzyskiwania ocen parametrów

0

α

i

1

α

gwarantujących minimalizację sumy

kwadratów odchyleń między wartościami empirycznymi i dopasowanymi zmiennej
objaśnianej modelu. Aby móc znaleźć takie oceny musimy dysponować n-elementową próbą
statystyczną wartości zmiennych X oraz Y – parami wartości (x

i

, y

i

) i=1,...,n.

n

i

x

y

i

i

i

,...,

1

1

0

=

+

+

=

ε

α

α

Oznaczenia:

a

0

, a

1

– oceny parametrów modelu

i

ε

- zaburzenie losowe odpowiadające i-tej obserwacji na zmiennej objaśnianej (związane z i-

tym obiektem w próbie lub z i-tym okresem próby)

i

i

x

a

a

y

1

0

ˆ

+

=

- wartości dopasowane (teoretyczne)zmiennej objaśnianej (leżące na

dopasowanej prostej regresji) odpowiadające i-tej obserwacji na zmiennej
objaśniającej x

i

.

i

i

i

y

y

e

ˆ

−

=

- reszta, odchylenie między wartością empiryczną a dopasowaną odpowiadające

i-tej obserwacji na zmiennej objaśniającej x

i

Kryterium MNK:

SSE =

(

)

(

)

min

ˆ

1

2

1

0

1

1

2

2

→

−

−

=

−

=

∑

∑

∑

=

=

=

n

i

i

i

n

i

n

i

i

i

i

x

a

a

y

y

y

e

SSE – suma kwadratów reszt regresji (residual sum of squares)

Licząc pochodne cząstkowe funkcji SSE względem a

0

i a

1

oraz przyrównując je do zera

(warunek konieczny dla ekstremum) otrzymujemy układ dwóch równań zwany układem
równań normalnych, z rozwiązania którego uzyskujemy formuły pozwalające obliczyć a

0

i a

1

.

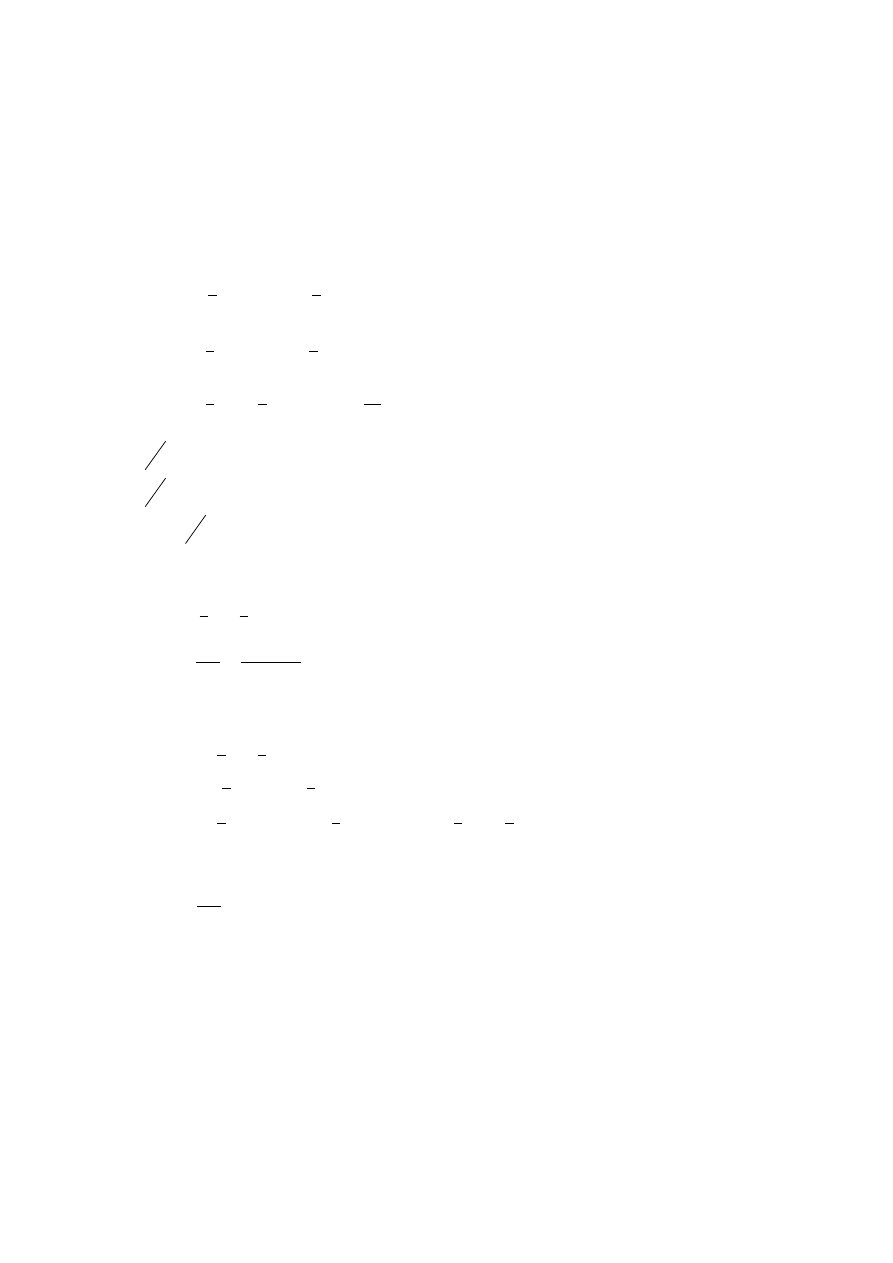
Układ równań normalnych:

∑

∑

∑

∑

∑

=

=

=

=

=

=

+

=

+

n

i

n

i

i

i

n

i

i

i

n

i

n

i

i

i

y

x

x

a

x

a

y

x

a

na

1

1

1

2

1

0

1

1

1

0

Oznaczenia:

(

)

(

)

(

)(

)

Y

X

S

n

Y

X

C

Y

S

n

S

X

S

n

S

y

x

n

y

x

y

y

x

x

S

x

n

x

x

x

S

y

n

y

y

y

S

xy

yy

y

xx

x

n

i

i

i

i

n

i

i

xy

n

i

i

n

i

i

xx

n

i

i

n

i

i

yy

i

zmiennych

próbkowa

a

kowariancj

-

1

)

,

(

zmiennej

próby

z

wariancja

-

1

zmiennej

próby

z

wariancja

-

1

2

2

1

1

1

2

2

2

1

2

1

2

2

1

=

=

=

−

=

−

−

=

−

=

−

=

−

=

−

=

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

Przy przyjętych oznaczeniach oceny MNK parametrów modelu prostej regresji można
wyrazić następująco:

2

1

1

0

)

,

(

x

xx

xy

S

Y

X

C

S

S

a

x

a

y

a

=

=

−

=

Sumę kwadratów reszt regresji można przedstawić następująco:

(

)

(

)

[

]

(

)

(

)

(

)(

)

SSR

SSTO

S

a

S

S

S

S

S

a

S

a

S

x

x

y

y

a

x

x

a

y

y

x

x

a

y

y

x

a

x

a

y

y

x

a

a

y

SSE

xy

yy

xx

xy

yy

xy

xx

yy

i

i

i

i

i

i

i

i

i

i

−

=

=

−

=

=

−

=

=

−

+

=

=

−

−

−

−

+

−

=

=

−

−

−

=

=

−

+

−

=

=

−

−

=

∑

∑

∑

∑

∑

∑

1

2

1

2

1

1

2

2

1

2

2

1

2

1

1

2

1

0

2

2

)

(

)

(

gdzie
SSTO=S

yy

- całkowita suma kwadratów (total sum of squares)

SSR=a

1

S

xy

- objaśniona suma kwadratów (regression sum of squares)

Współczynnik korelacji w populacji generalnej:

y

x

xy

Y

X

σ

σ

ρ

)

,

cov(

=

,

gdzie
cov(X,Y) – kowariancja zmiennych X i Y w populacji generalnej

y

x

σ

σ

,

- odchylenia standardowe zmiennych

X i Y w populacji generalnej

Współczynnik korelacji z próby:

yy

xx

xy

y

x

xy

S

S

S

S

S

Y

X

C

r

=

=

=

)

,

(

Współczynnik determinacji:

Udział SSR w SSTO i zarazem udział wariancji objaśnionej za pomocą prostej regresji

w wariancji całkowitej zmiennej Y z próby można mierzyć jako kwadrat współczynnika
korelacji r

xy

. Miara ta przyjmująca wartości z przedziału [0,1] nosi nazwę współczynnika

determinacji.

yy

xy

yy

xx

xy

xy

S

S

a

S

S

S

SSTO

SSE

SSTO

SSE

SSTO

SSTO

SSR

r

R

1

2

2

2

1

=

=

=

−

=

−

=

=

≡

Wnioskowanie statystyczne w modelu prostej regresji

Przy poczynionych założeniach odnośnie parametrów rozkładu składnika losowego modelu
prostej regresji, estymatory MNK parametrów modelu są nieobciążone, zgodne i posiadają
najmniejsze wariancje w klasie liniowych nieobciążonych estymatorów. Przyjęte założenia
należy rozszerzyć w sytuacji rozpatrywania regresji w warunkach gdy dysponujemy już n-
elementową losową próbą na zmiennych modelu:
1.

0

)

(

=

i

E

ε

, dla każdego i=1,...,n

2.

2

2

)

(

σ

ε

=

i

D

, dla każdego i=1,...,n

3.

i

ε

i

j

ε

są niezależnymi zmiennymi losowymi dla

j

i

≠

4.

j

x

są wielkościami nielosowymi

Dla celów wnioskowania statystycznego – konstrukcji przedziałów ufności dla parametrów
modelu, weryfikacji hipotez – zakładamy dodatkowo, że wszystkie zakłócenia

i

ε

podlegają

normalnemu rozkładowi prawdopodobieństwa.

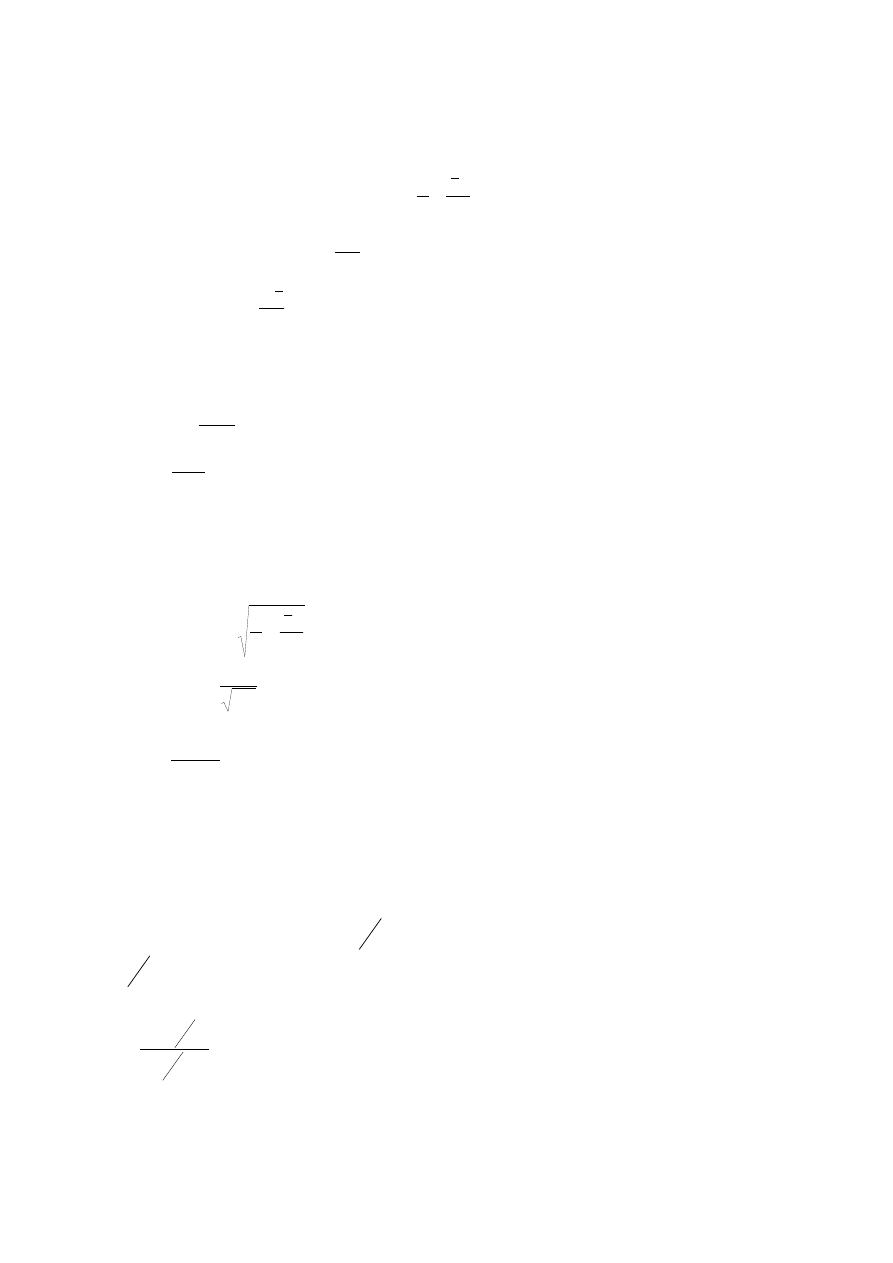
Najważniejsze wyniki:

1. Oceny a

0

i a

1

podlegają łącznemu, dwuwymiarowemu rozkładowi normalnemu o

następujących parametrach:

0

)

(

α

=

o

a

E













+

=

xx

S

x

n

a

D

2

2

0

2

1

)

(

σ

1

1

)

(

α

=

a

E

xx

S

a

D

2

1

2

)

(

σ

=













−

=

xx

S

x

a

a

2

1

0

)

,

cov(

σ

Powyższe wyniki mogą być wykorzystane w praktyce pod warunkiem znanej wariancji

2

σ

.

Nieobciążonym estymatorem tego parametru w przypadku prostej regresji jest funkcja:

2

2

−

=

n

SSE

S

e

(tzw. wariancja resztowa)

Ponadto

2

σ

SSE

ma rozkład

2

χ

o n-2 stopniach swobody i jest on niezależny od rozkładów

estymatorów a

i

i=0,1. Wynik ten można wykorzystać przy konstrukcji przedziału ufności dla

2

σ

oraz weryfikacji hipotez o

2

σ

.

Standardowe błędy szacunku parametrów prostej regresji za pomocą MNK można wyrazić
wzorami:

xx

e

xx

e

S

S

a

S

S

x

n

S

a

S

=

+

=

)

(

1

)

(

1

2

0

Ponadto zachodzi:

Funkcja

)

(

i

i

i

a

S

a

α

−

ma rozkład t-Studenta o n-2 stopniach swobody. Wynik ten może być

wykorzystany do konstrukcji przedziałów ufności dla parametrów prostej regresji oraz
weryfikacji hipotez.
Pierwiastek kwadratowy z wariancji resztowej S

e

nazywany jest średnim błędem szacunku.

Analiza wariancji (ANOVA):

Przy poczynionych założeniach

2

σ

SSE

ma rozkład

2

χ

o n-2 stopniach swobody oraz

2

σ

SSR

ma rozkład

2

χ

o 1 stopniu swobody wówczas, gdy parametr

1

α

=0. Co więcej te dwa

rozkłady są niezależne. Zatem gdy

1

α

=0, to statystyka

2

1

−

=

n

SSE

SSR

F

ma rozkład Fishera ze stopniami swobody 1 i n-2. Wynik ten może być

wykorzystany w teście dla hipotezy

1

α

=0.

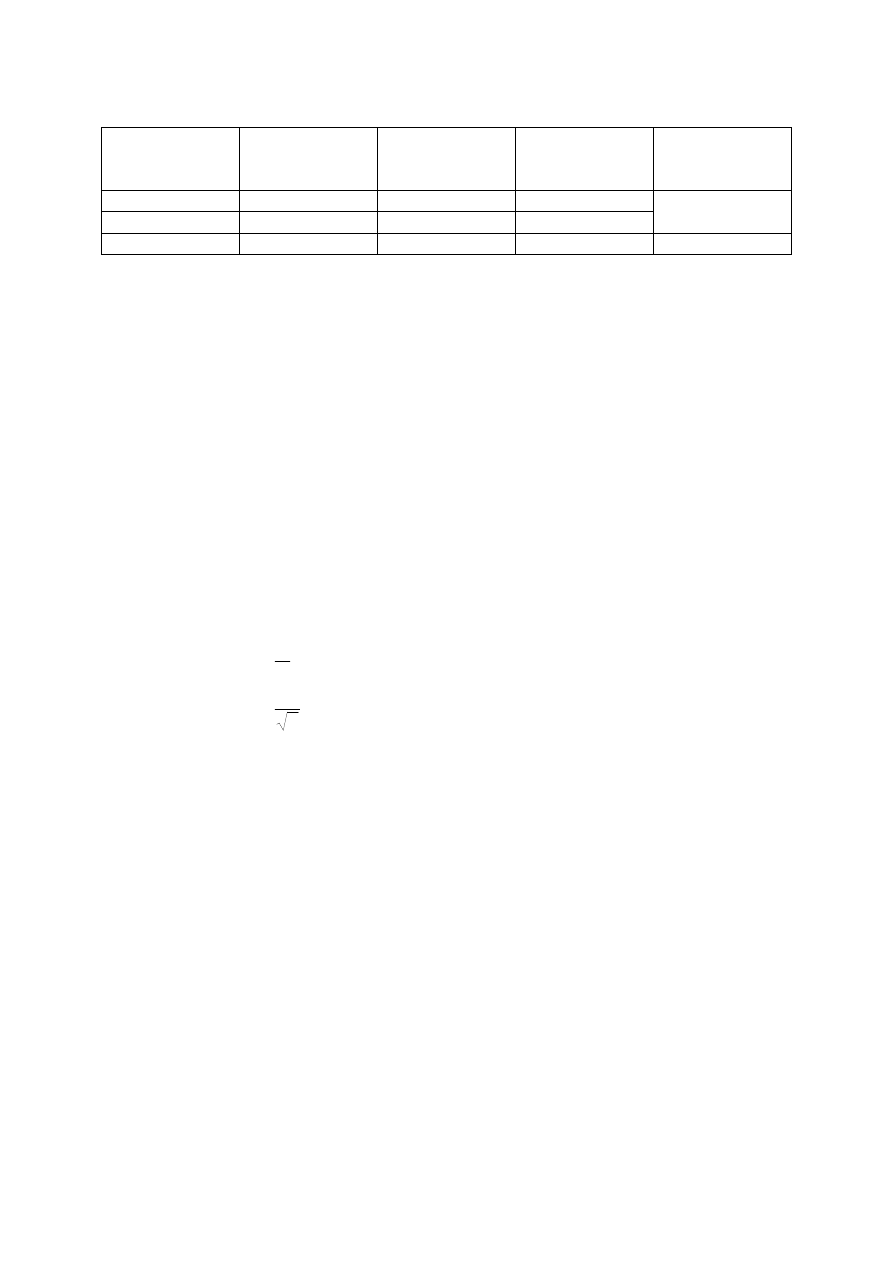
Tablica ANOVA
Ź

ródło

zmienności

Suma kwadratów
odchyleń

Liczba stopni
swobody

Ś

rednie

odchylenie
kwadratowe

Iloraz F

Regresja

SSR

1

SSR/1

Reszty

SSE

n-2

SSE/(n-2)

SSR(n-2)/SSE

Suma

SSTO=S

yy

n-1

Analiza reszt

1. Sprawdzanie stałości wariancji składnika losowego – np. wykres reszt względem x lub

yˆ ; reszty nie powinny wzrastać lub maleć ze wzrostem x lub yˆ .

2. Sprawdzanie czy nie pominięto ważnych zmiennych objaśniających – powinno się

włączyć do modelu zmienną, względem której reszty wykazują tendencję do
regularnych zmian

3. Wykrywanie związków krzywoliniowych między X i Y – wykresy
4. Wykrywanie niezgodności z założeniem rozkładu normalnego – normal probability

plot

5. Występowanie obserwacji nietypowych – wykresy
6. Alternatywne postaci funkcyjne dla regresji, łatwo transformowalne do postaci

liniowej względem zmiennych:

x

Y

x

Y

Ax

Y

Ae

Y

x

Y

x

β

α

β

α

β

α

β

β

+

=

+

=

=

=

+

=

log