
Lecture 3
LIMITS OF FUNCTIONS
CONTINUITY

INTERVALS
INTERVALS
If a and b are real numbers and a ≤ b, then we shall use the
standard interval notation
[a,b] = {x R: a ≤ x ≤ b}
[a,b) = {x R: a ≤ x < b}
(a,b] = {x R: a < x ≤ b}
(a,b) = {x R: a < x < b}.
As you may know, an interval of the form [a,b] is called a
closed interval and an interval of the form (a,b) is called an
open interval. We can also define intervals of infinite length:
If a is any real number, then we define
[a,∞) = {x R: a ≤ x}
(a,∞) = {x R: a < x}
(-∞,a] = {x R: x ≤ a}
(-∞,a) = {x R: x < a},
and, finally, the symbol (-∞,∞) is the set R of all real
numbers.
Note that if a is any real number then the interval (a,a) is the
empty set

Definition
A neighbourhood of point a is an open interval of the form
Definition
A punctured neighbourhood of point a is a set of the form
)
a
,
a
(
)
a
,
a
(
)
a
,
a
(
)
x
(
D
0
for some
0
for some
0
)
,
(
)
(
D
)
,
(
)
(
D
The neighbourhoods of infinity

LIMITS OF FUNCTIONS

Definition (by Heine)
Suppose Let f be a function defined on
a punctured neighbourhood D(x
0
) of a point x
0
.
We say that is the limit of f at x
0
if
for every sequence (x
n
) of elements of the punctured
neighbourhood S(x
0
), tending to x
0
, L is the limit of a
sequence (f (x
n
)) i.e.
L
)
x
(
f
x
x
n
0
n
.
This is denoted by
For the limit is called finite. For
we say that the limit is infinite.
].
,
[
x
0
]
,
[
L
L
)
x
(
f
or
L
)
x
(
f
lim
0
0
x
x
x
x
)
,
(
L
L
,
L

THEOREM
If a function has a limit at a point, then that
limit is unique.
L
)
a
(
f
x
a
n
0
n
M
)
b
(
f
x
b
n
0
n
M
L
If there exist two diferent sequences (a
n
) and (b
n
) both of elements of
the domain of f tending to x
0
, for which
and
with
then the limit of f at x
0
does not exist.

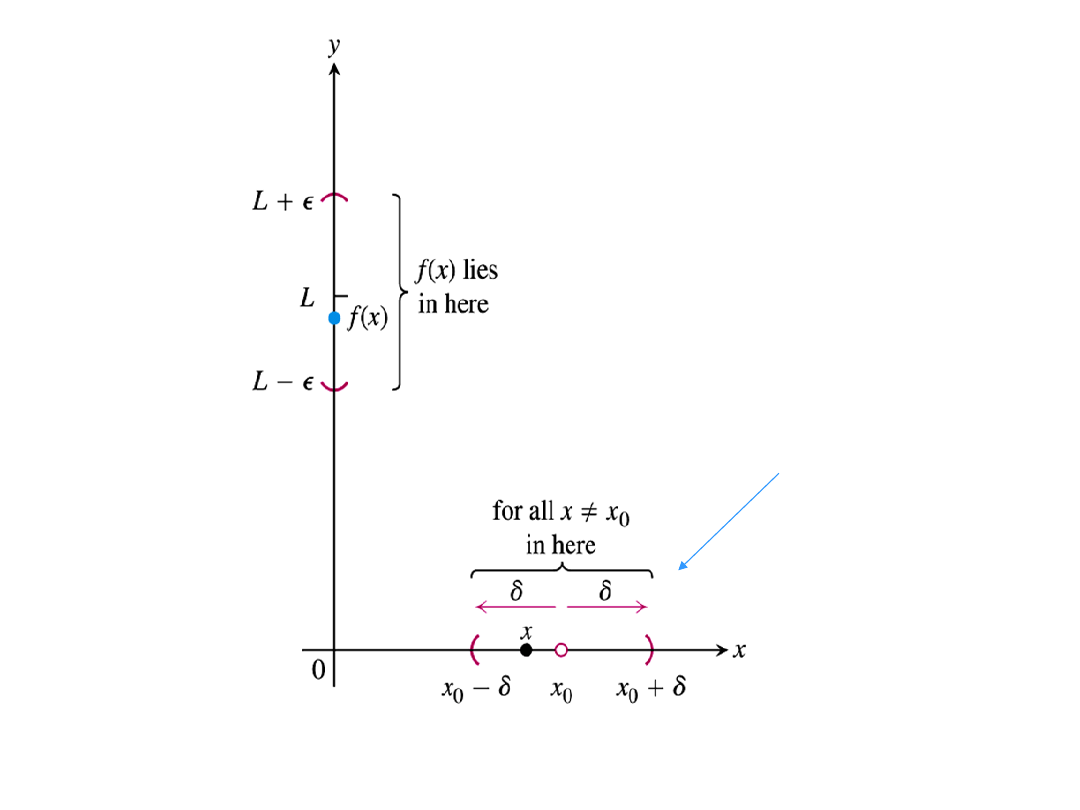
Epsilon-delta definition
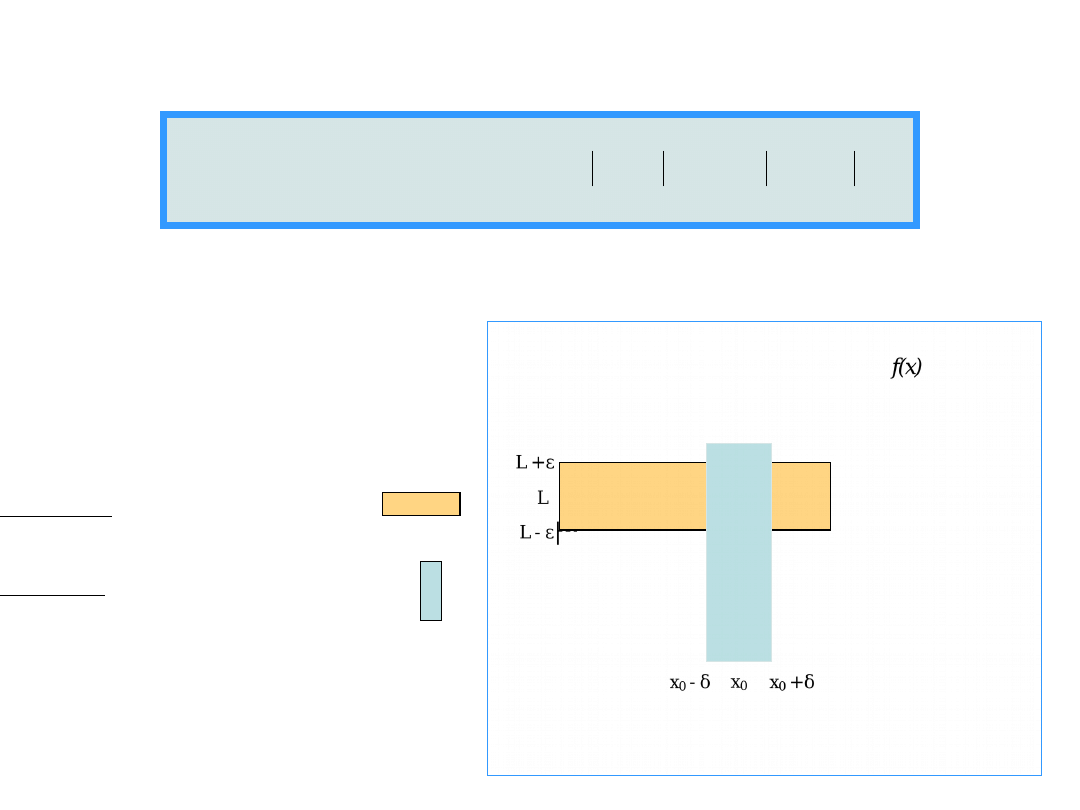
Challange: be as close as ε to L,
Response: keep closer than δ to x
0
.
L
)
x
(
f
x
x
,
0
,
0
L
)
x
(
f
lim
0
x
x
0
find such δ
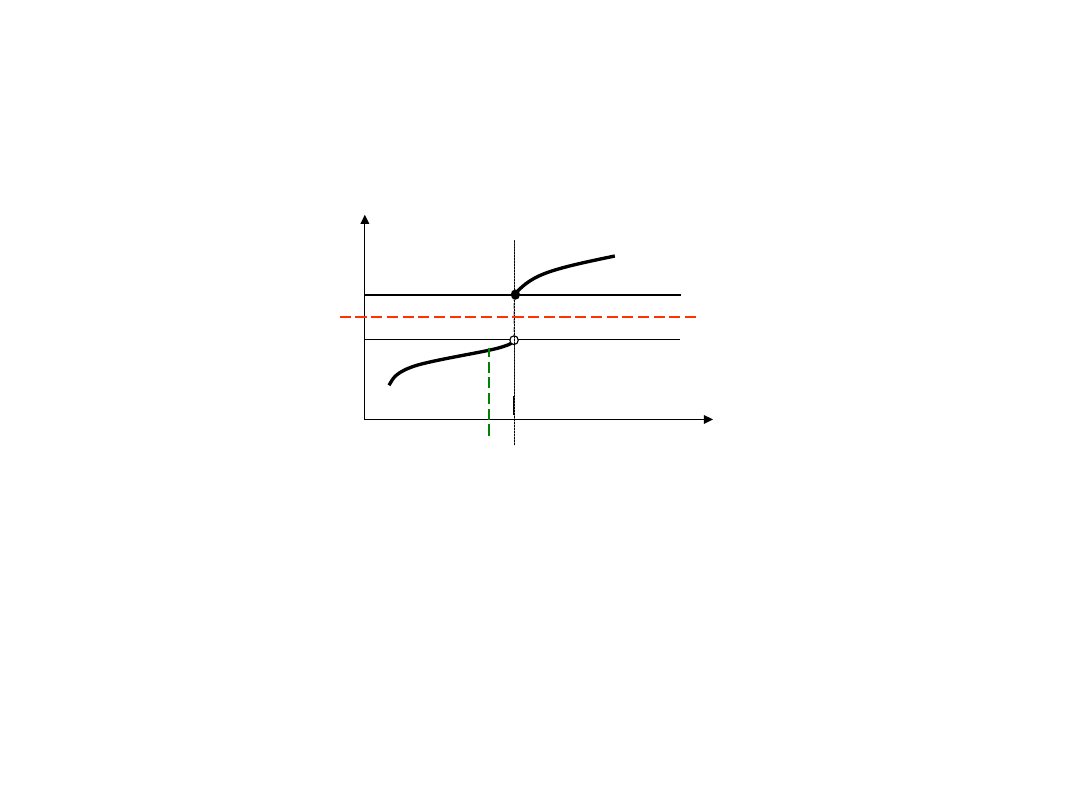
There is no way to be closer then ε (e.g. at point L-ε) to L
(here we have a one side limit).
L
L - ε

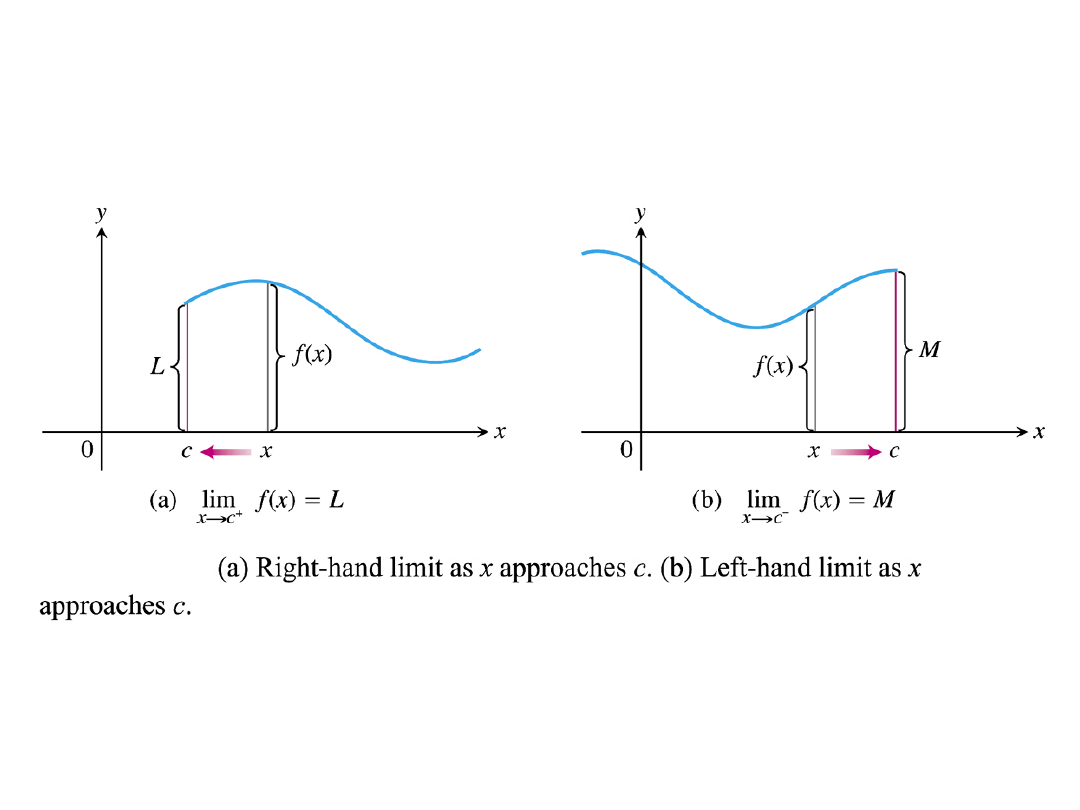
One sided limits and limits to infinity


Theorem
PROPERTIES – THE COMBINATION RULES
0
n
provided
x
f
lim
))
x
(
f
(
lim
n
x
x
n
x
x
0
0
)
x
g
(lim
)
x
f
(lim
x
g
x
f
lim
0
0
0
x
x
x
x
x
x
0
x
g
lim
and
0
x
g
if
x
g
lim
x
f
lim
x
g
x
f
lim
0
0
o
0
x
x
x
x
x
x
x
x
x
g
lim
x
f
lim
x
g
x
f
lim
0
0
0
x
x
x
x
x
x
defined
is
)
x
(
f
provided
x
f
lim
)
x
(
f
lim
n
n
x
x
n
x
x
0
0
1
.
2.
3
.
4.
5.
)
,
(
L
],
,
[
x
0

LIMIT RULES
n
n
0
1
n
n
0
1
n
n
x
b
a
b
x
b
x
b
a
x
a
x
a
lim
0
b
x
b
x
b
a
x
a
x
a
lim
0
1
m
m
0
1
n
n
x
m
n
0
1
m
m
0
1
n
n
x
b
a
sgn
b
x
b
x
b
a
x
a
x
a
lim
Theorem
n < m
n > m
n = m
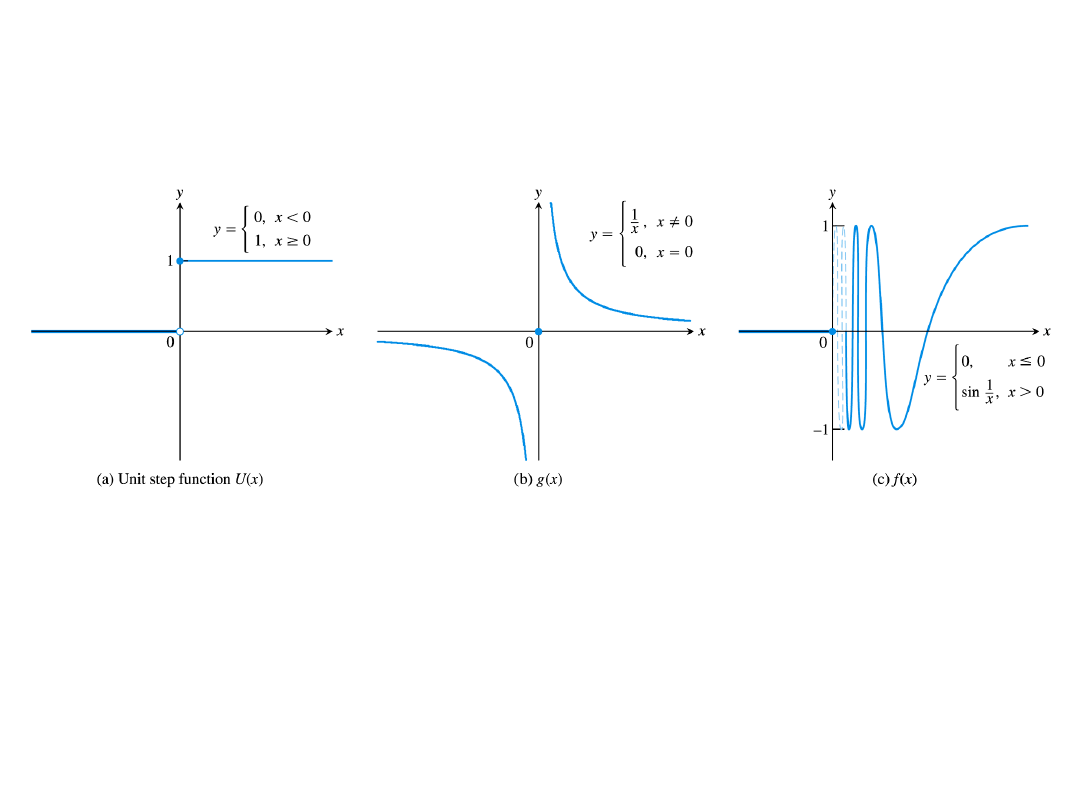
None of these functions has a limit as x tends to 0.

5
2
1
5
x
13
x
1
4
1
x
3
5
lim
x
13
x
x
4
1
x
3
5
lim
x
13
x
x
4
1
x
3
5
lim
13
x
x
4
x
3
x
5
lim
2
x
2
2
x
2
x
2
x
-|x|, x is negative
x
1
sin
)
x
(
f
,
R
)
,
0
(
:
f
)
6
,
001
.
0
(
x
1
2
3
4
5
6
-1
-0.5
0.5
1
)
1
,
001
.
0
(
x
0.2
0.4
0.6
0.8
1
-1
-0.5
0.5
1
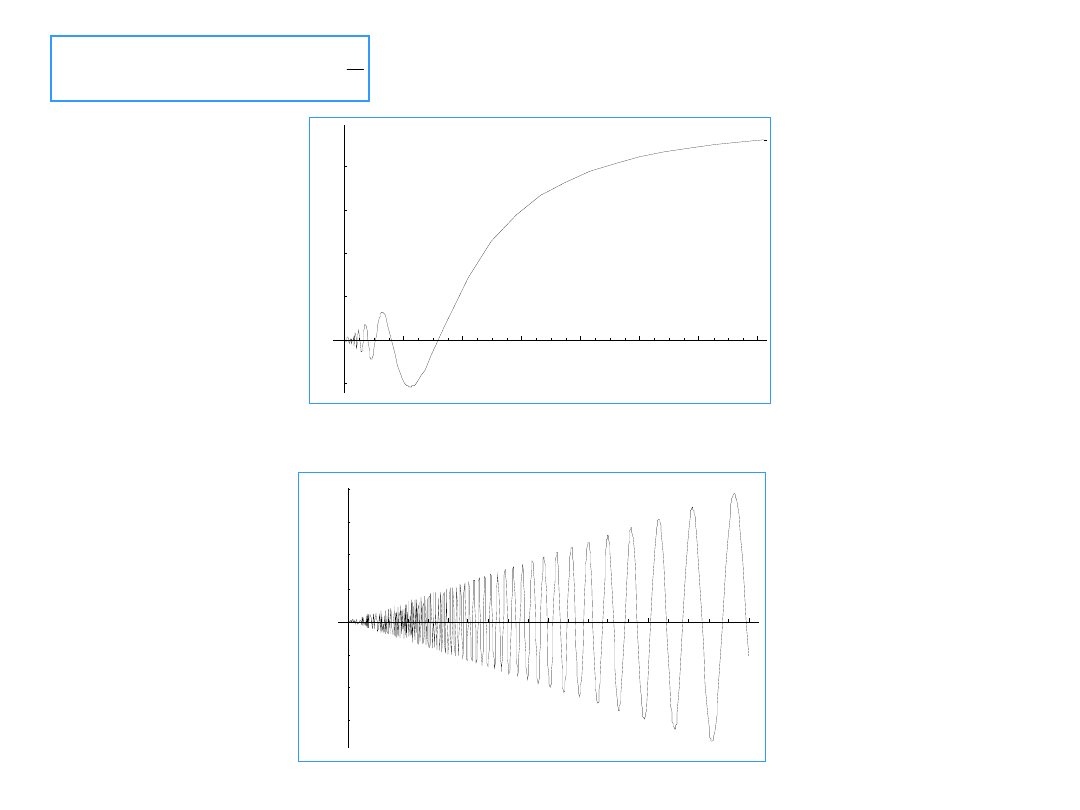
A function for which the limit does not exist
zoom in:
)
01
.
0
,
001
.
0
(
x
0.002
0.004
0.006
0.008
0.01
-1
-0.5
0.5
1
x
1
sin
)
x
(
f
,
R
)
,
0
(
:
f
Computing the limit by substitution
)
y
(
f
lim
y
y
x
x
)
x
(
g
y
))
x
(
g
(
f
lim
0
0
y
y
0
0
x
x

THE SQUEEZE PRINCIPLE
Let I be an interval containing the point a. Let f, g, and
h be functions defined on I, except possibly at a itself.
Suppose that for every
we have:
and also suppose that:
Then
.
a
x
x
,
I
g (x) < f (x) < h (x)
L
)
(
lim
)
(
lim
x
h
x
g
a
x
a
x
L
)
(
lim
x
f
a
x
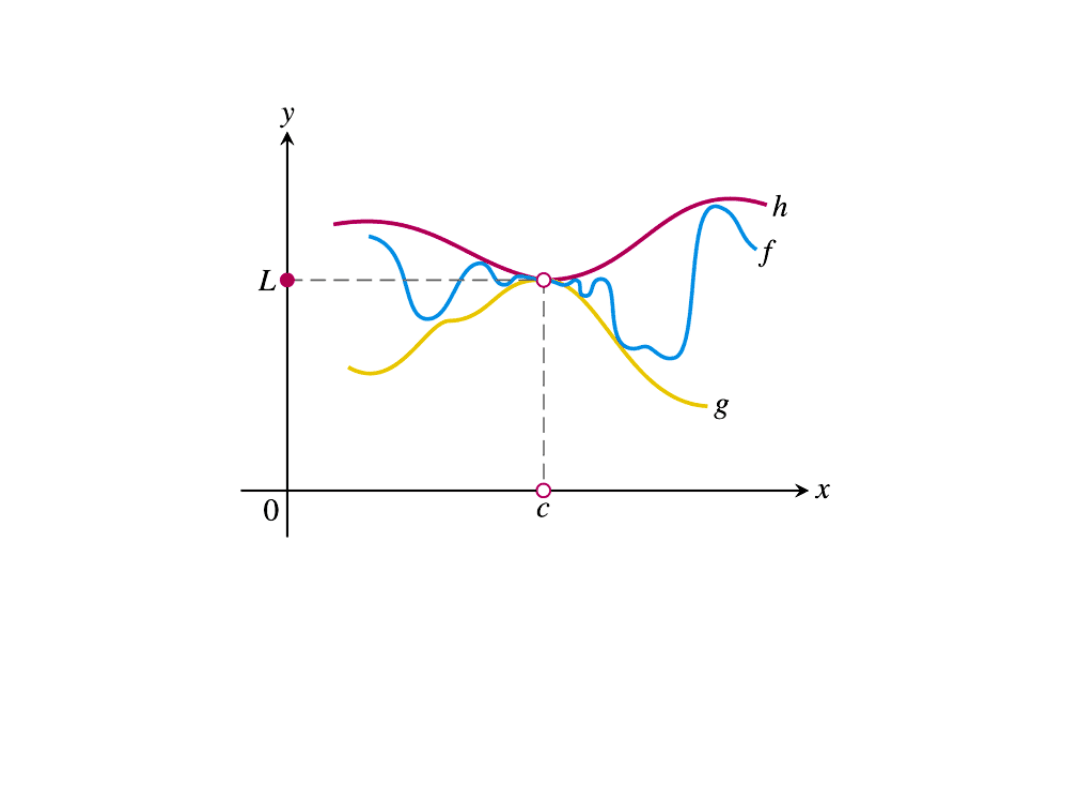
The graph of f is squeezed between g and h.
?
)
x
2
x
sin
x
(
lim
x
x
x
2
x
x
2
x
sin
x
x
lim
x
)
x
2
x
sin
x
(
lim
x
Find
?
)
x
2
x
sin
x
(
lim
x
x
2
x
sin
x
x
2
x
x
)
x
x
sin
x
2
(
lim
x
Find
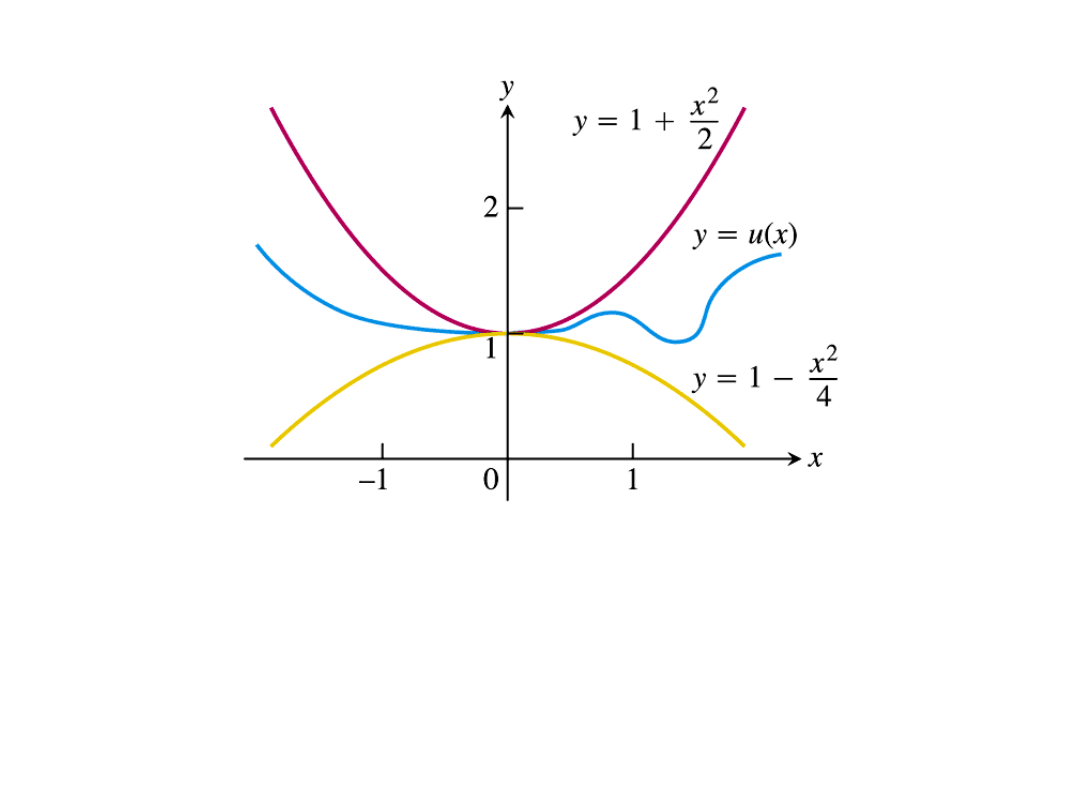
Any function whose graph is squeezed
between
1+ x
2
/2 and 1- x
2
/4 has a limit 1 as x-
> 0.
Theorem
If a function g(x) is bounded in a neighborhood O(a)
of a point a and
bounded
0
)
(
)
(
lim
then
,
0
)
(
lim
x
g
x
f
x
f
a
x
a
x
A consequence of the Squeeze Theorem:
0.2
0.4
0.6
0.8
1
1.2
1.4
-0.2
0.2
0.4
0.6
0.8
x
1
sin
x
)
x
(
f
,
R
)
,
0
(
:
f
0.005
0.01
0.015
0.02
-0.015
-0.01
-0.005
0.005
0.01
0.015
0.02
)
2
,
0
(
x
)
02
.
0
,
0
(
x
1
x
x
sin
lim
x
x
sin
)
x
(
f
,
R
)
,
(
:
f
0
x
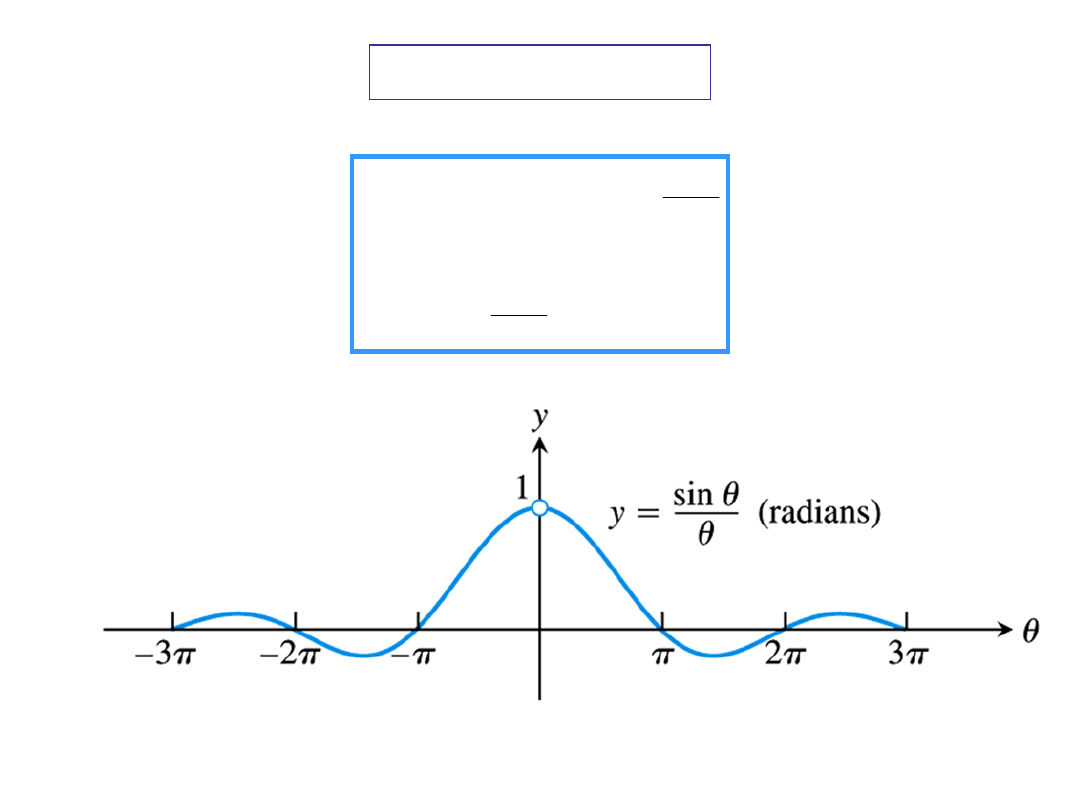
USEFULL LIMIT
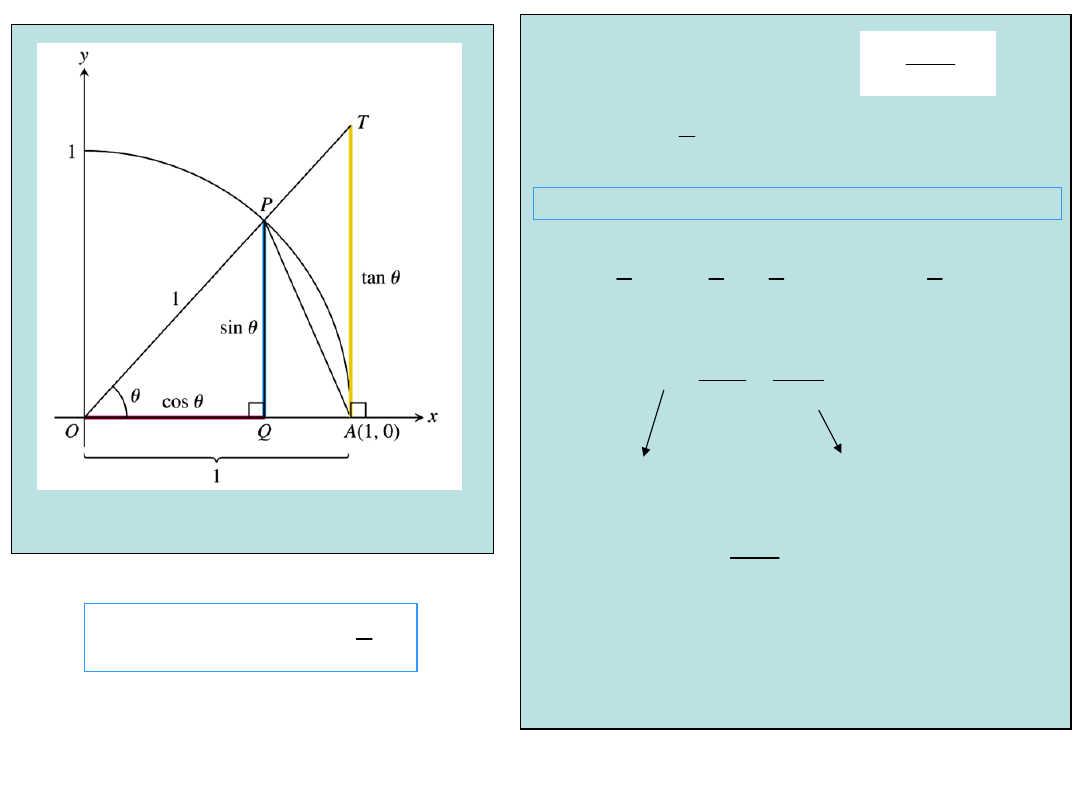
Sketch of the
proof of
1
sin
lim
0
tan
so
,
1
but
,
tan
TA
OA
TA/OA
limit
hand
right
2
0
.
1
OAT
OAP
OAP
Δ
Area
tor
sec
circular
Area
Area
2
r
2
1
tor
sec
circular
of
Area
cos
1
sin
1
sin
2
1
tan
2
1
2
1
sin
2
1
Sinθ is even, so the left-hand limit exists and
has the same value as the right-hand limit.
1
1
1
sin
lim
0
1
x
x
sin
lim
..
4
0
x
e
x
1
1
lim
.
3
x
x
e
y
y
y
1
0
1
lim
a
n
x
e
x
a
1
lim
0
x
tan
c
arc
lim
,
x
tan
c
arc
lim
,
2
x
arctan
lim
,
2
x
arctan
lim
.
5
x
x
x
x
x
ln
lim
,
x
ln
lim
.
6
x
0
x
1
a
0
for
1
a
for
0
a
lim
1
a
0
for
0
1
a
for
a
lim
.
2
x
x
x
x
0
a
for
0
x
1
lim
x
lim
0
a
for
,
x
lim
.
1
a
x
a
x
a
x
IMPOTRANT
LIMITS

ASYMPTOTES
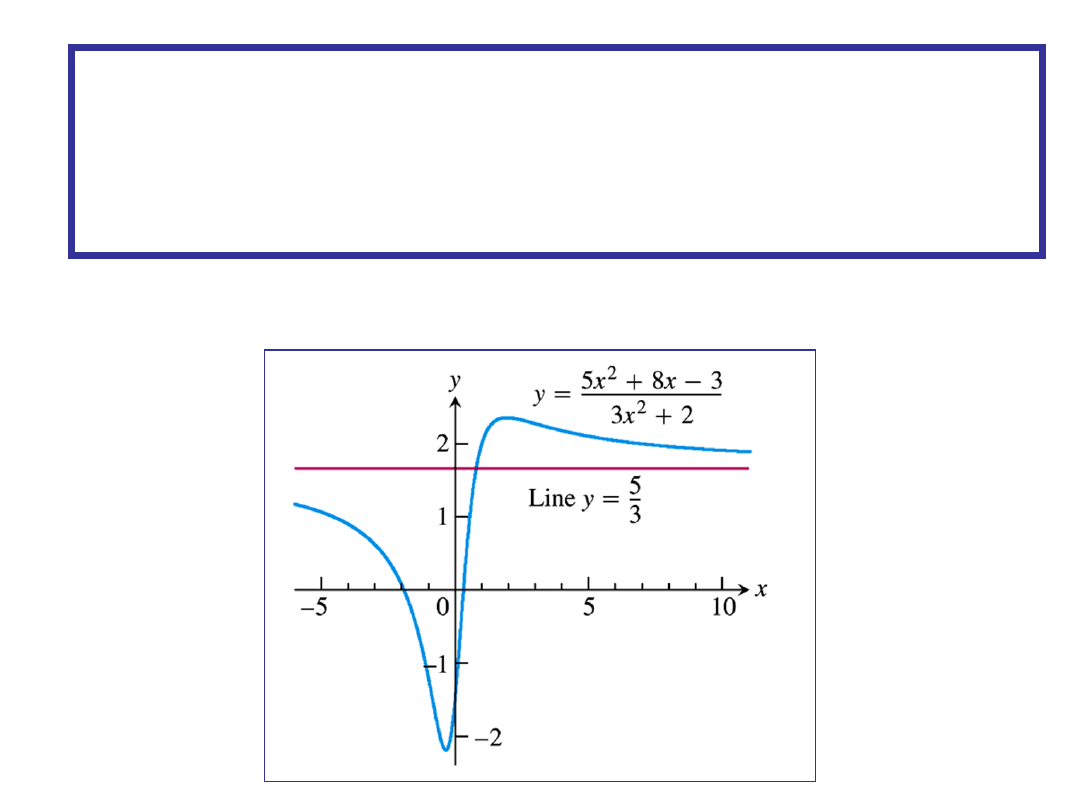
The line y = a is a HORIZONTAL ASYMPTOTE for f if
a
x
f
)
(
lim
x
a
x
f
)
(
lim
x
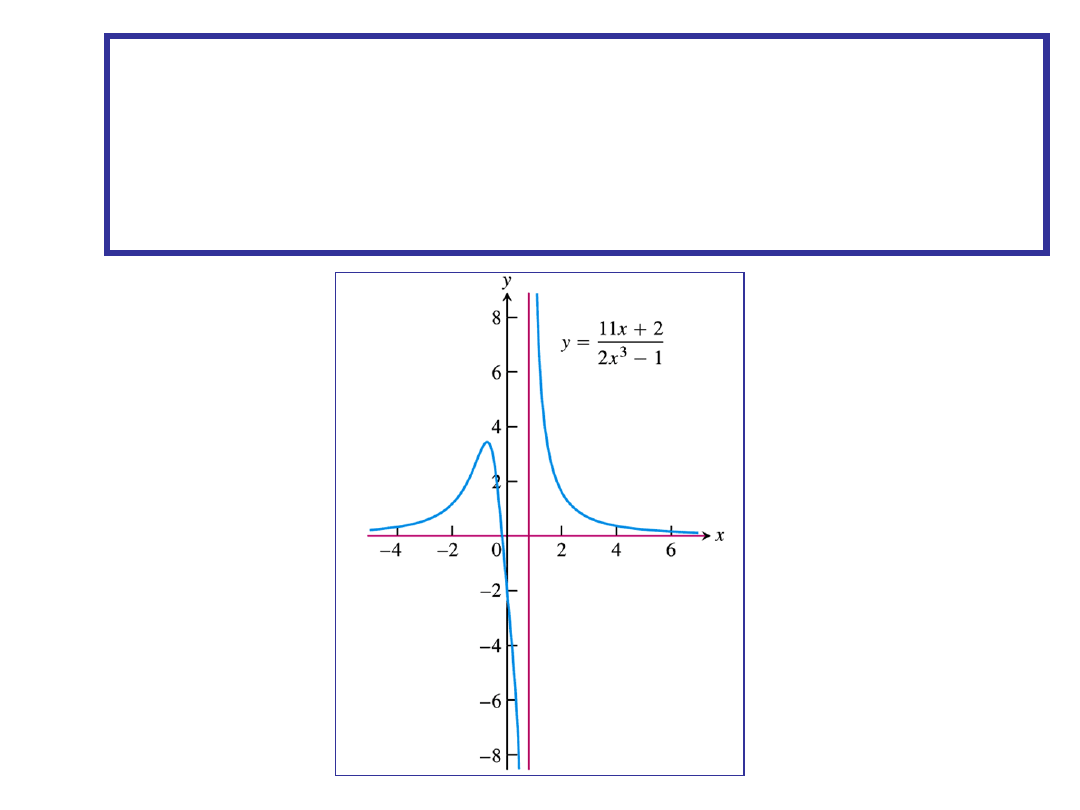
The line x = a is a VERTICAL ASYMPTOTE of a
function f if either of the following conditions is true:
)
x
(
lim
a
x
f
)
x
(
lim
a
x
f
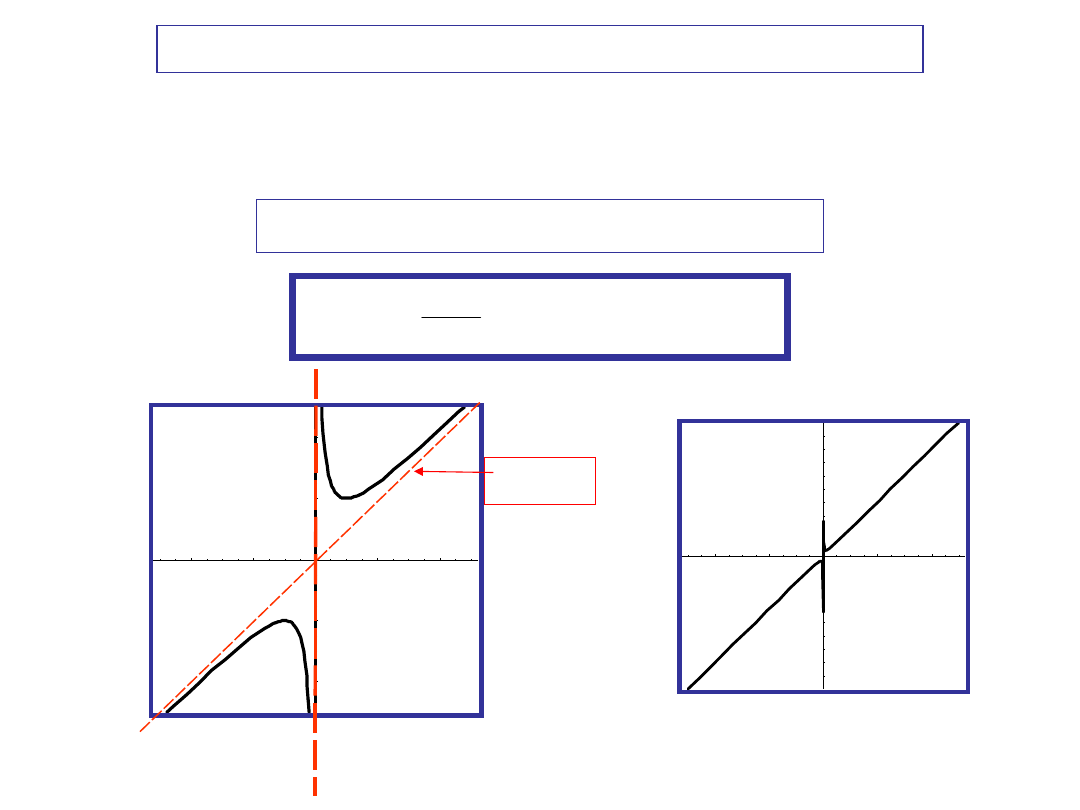
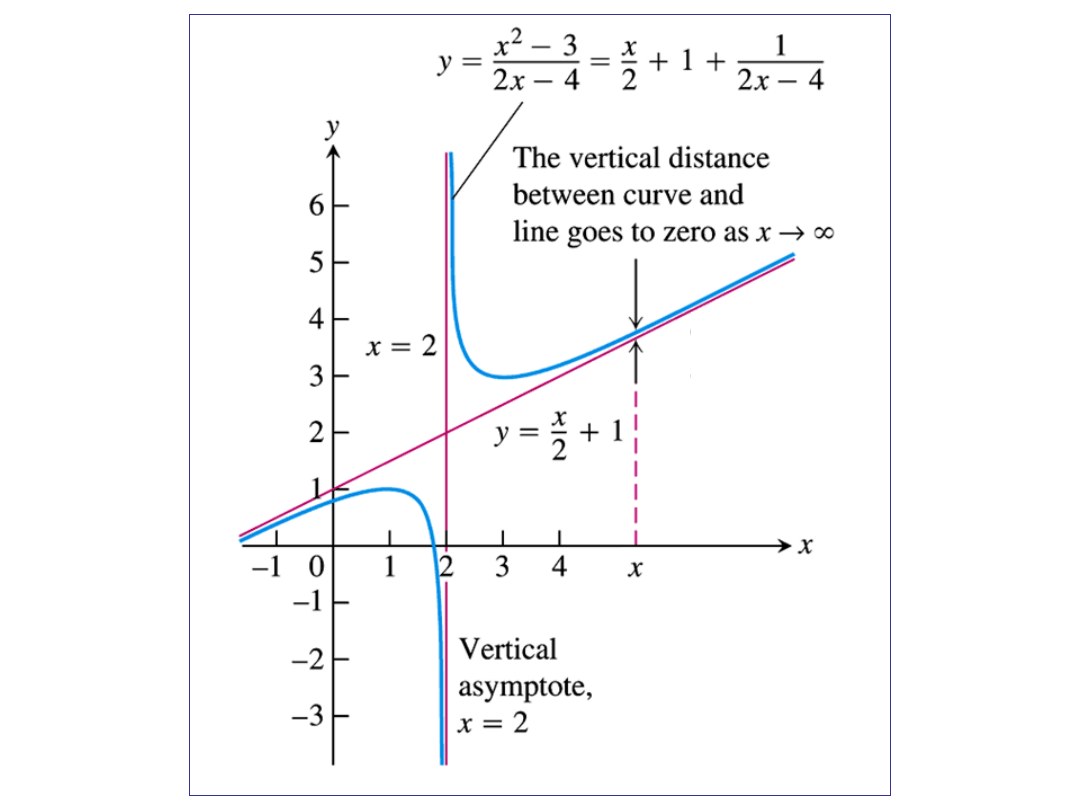
SLANT = OBLIQUE = TILTED ASYMPTOTE:
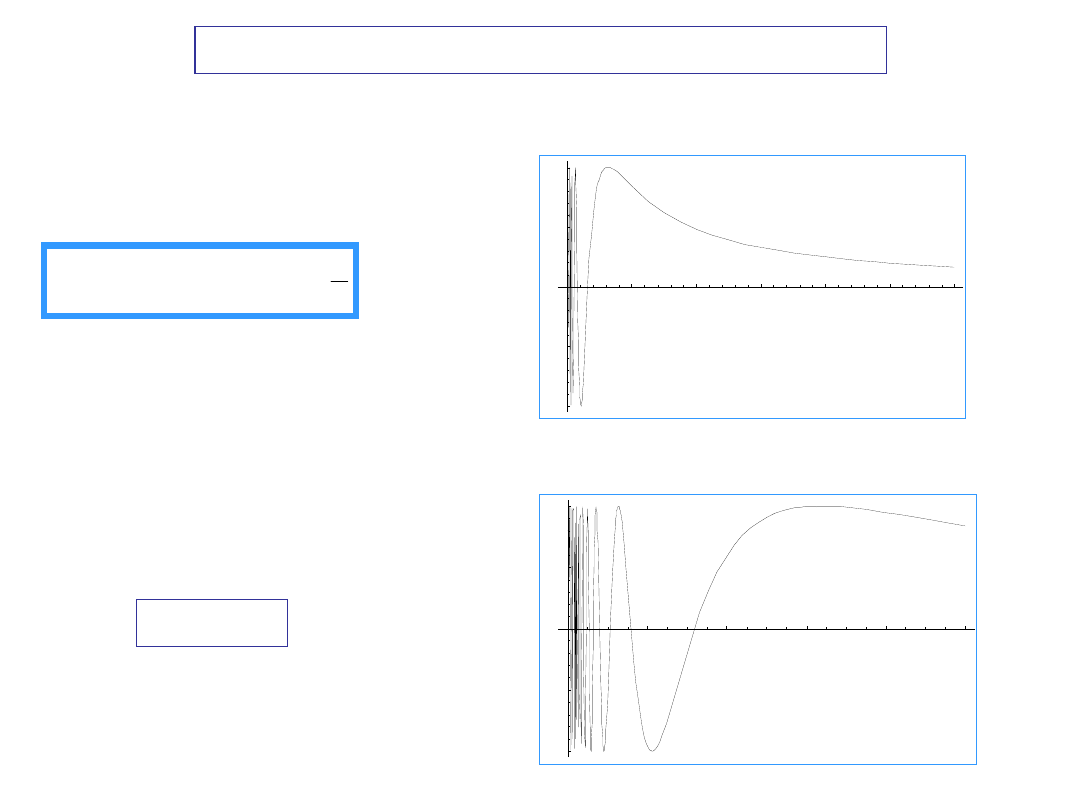
If y = m x + b, is any non-vertical line, then the function f (x) is asymptotic to it if
]
)
(
[
lim
)
(
lim
x
x
mx
x
f
b
x
x
f
m
0
)
(
lim
0
)
(
lim
x
x
b
mx
x
f
b
mx
x
f
-4
-2
2
4
-4
-2
2
4
-40
-20
20
40
-40
-20
20
40
mx+b
Slant
asypto
te

Two Slant Asymptotes
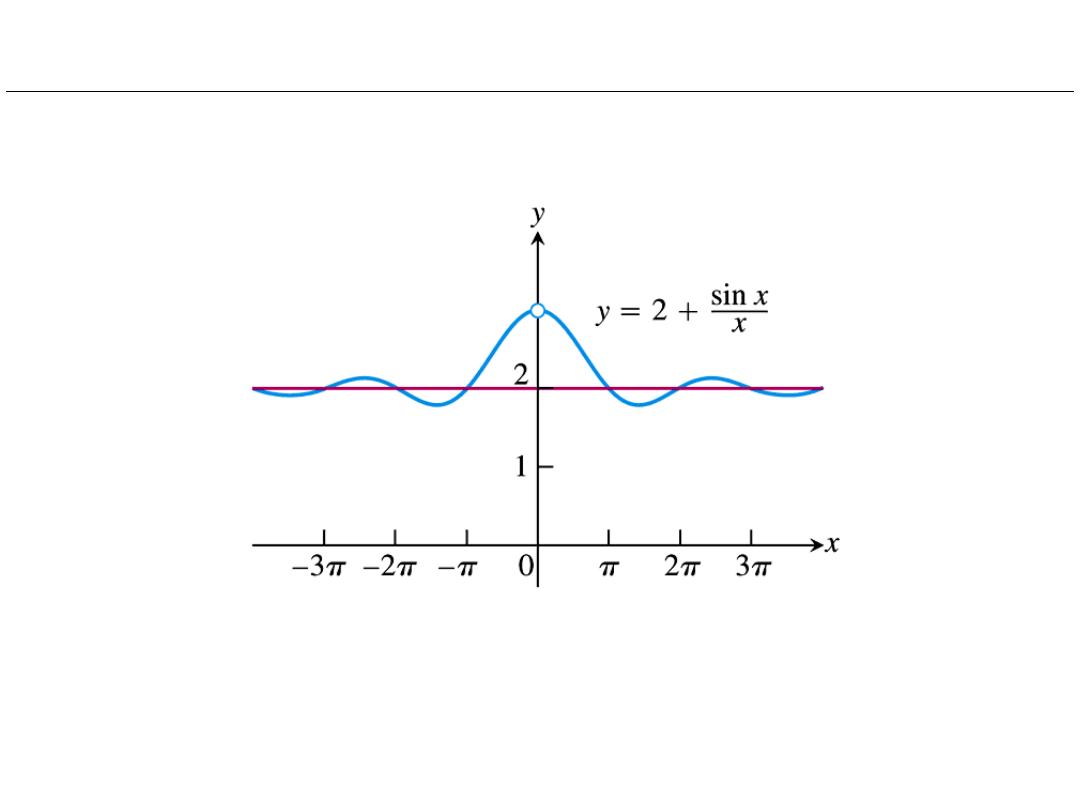
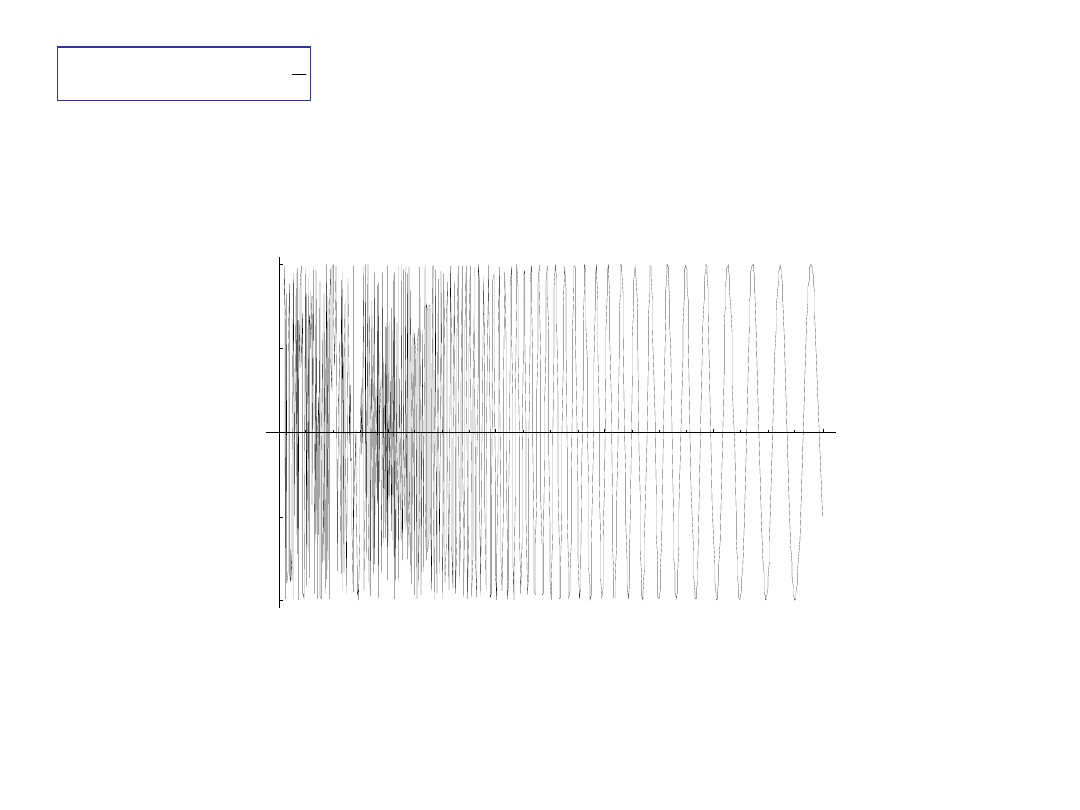
A curve can intersect its asymptote, even infinitely many times.

CONTINUITY
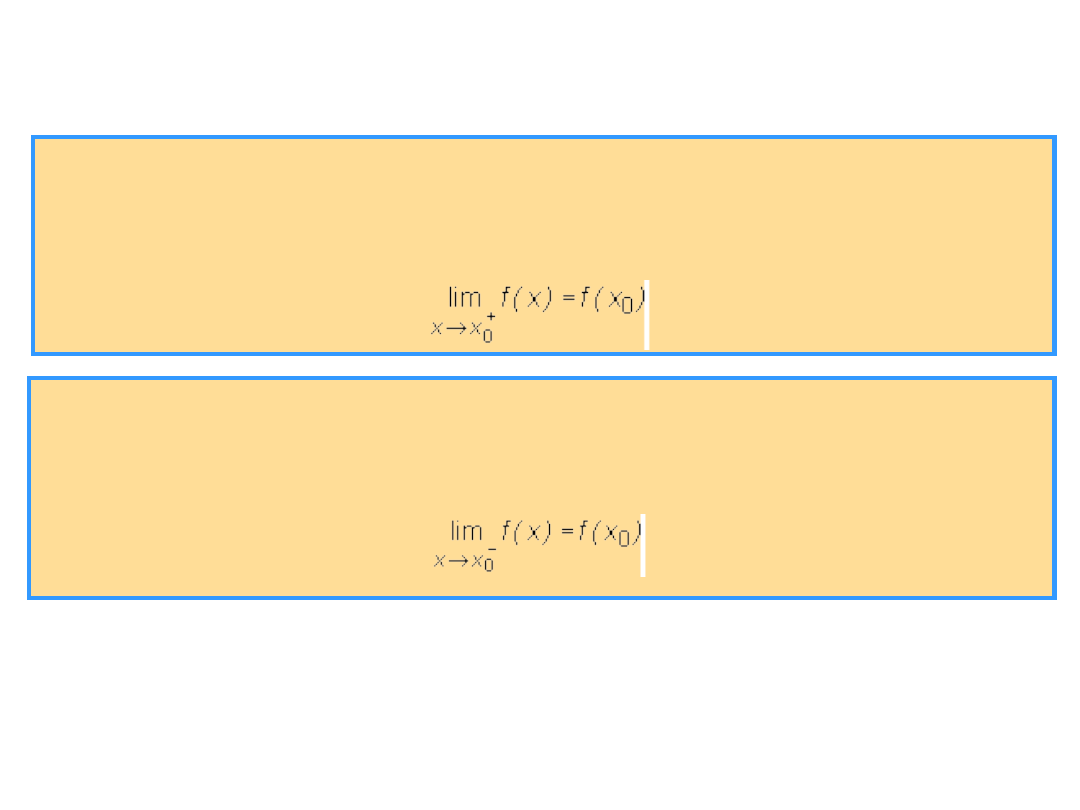
)
x
(
O
0
)
x
(
O
0
Continuous from the right at a point x
0
, if there exists a right-hand neighborhood
of the point x
0
which is contained in the domain D
f
and
.
Continuous from the left at a point x
0
, if there exists a left-hand neighborhood
of the point x
0
which is contained in the domain D
f
and
Definition
A function f is said to be:

Definition
A function f is said to be:
Continuous at a point x
0
, if there exists a neighborhood
O(x
0
) of the point x
0
which is contained in the domain D
f
and
.
Theorem
A function f is continuous at point x
0
if BOTH one-sided limits at x
0
exist
and
)
x
(
f
)
x
(
f
lim
0
x
x
0
)
x
(
f
)
x
(
f
lim
)
x
(
f
lim
0
x
x
x
x
0
0
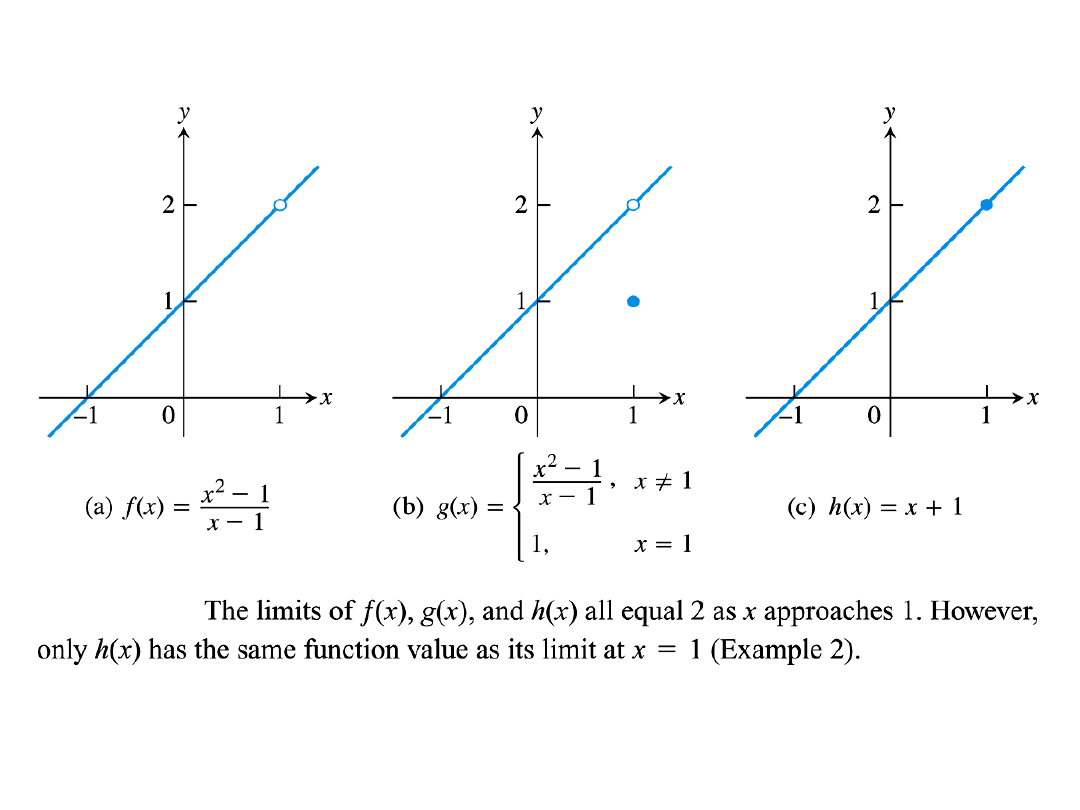


Theorem
If the functions f and g are continuous at a point x
0
, then the functions:
1. f + g, f - g
2. f g
3. a f and a f + bg, where
4. f / g (provided g (x
0
) ≠ 0)
are continuous at x
0
as well.
R
b
,
a

Definition
Let be an interval.
If P = (a, b) (is open), then we say that a function f is
continuous on P if f is continuous at each point of P.
If P = [a, b] then we say that a function f is continuous
on P if f is continuous from the right at a, continuous
on the left at b and continuous at each point of an open
interval Int P = (a, b).
If P = [a, b) then we say that a function f is continuous
on P if f is continuous from the right at a, and
continuous at each point of an open interval Int P = (a,
b). Likewise is defined the continuity of a function f on
(a,b].
f
D
P
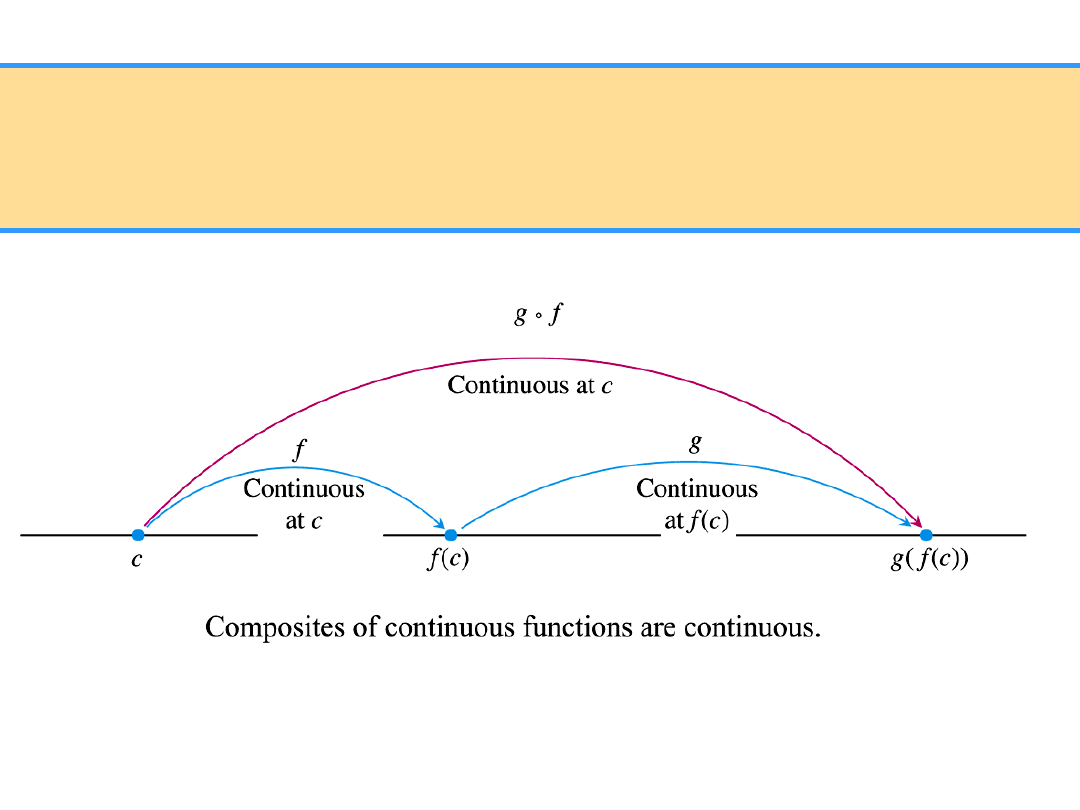
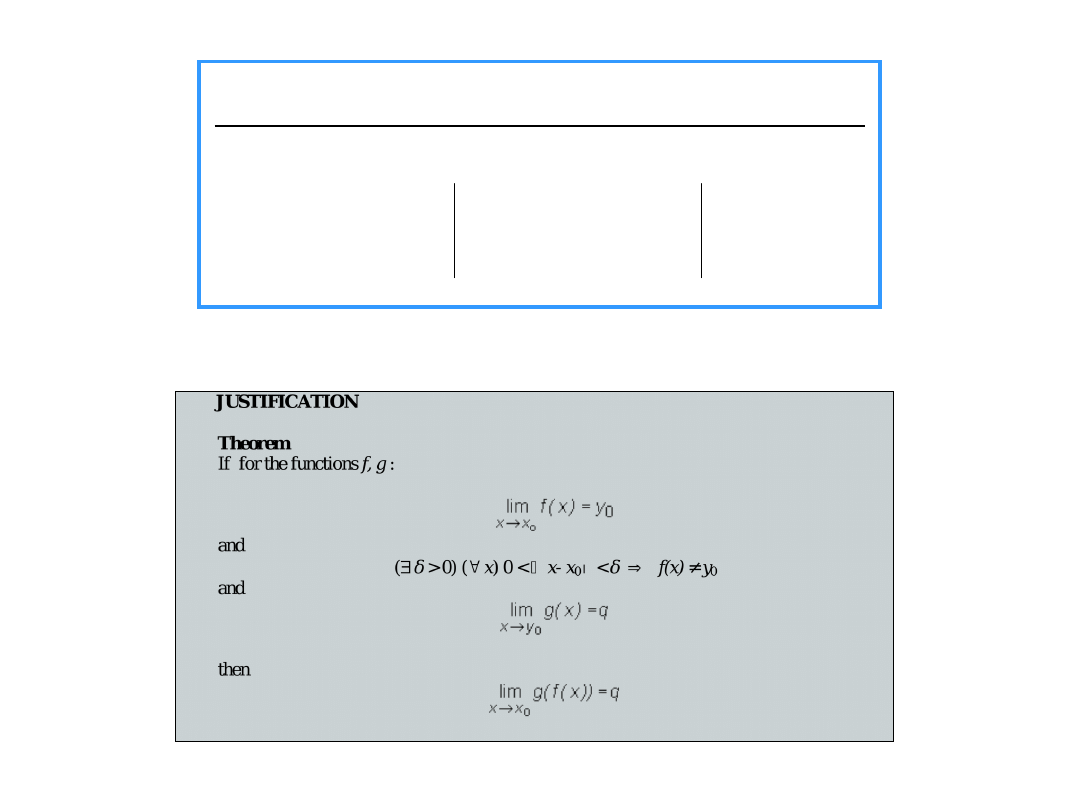
Theorem (on continuity of a composition)
If functions f and g are continuous at points x
0
and f (x
0
), respectively,
then a compound function g (f (x)) is continuous at x
0
.

Theorem (on the continuity of inverse functions)
If the domain D
f
of a function f is an interval and f is
either strictly decreasing or increasing and continuous,
then
(a) the range f (D
f
) of f is an interval
(b) the inverse function f
-1
exists and is continuous in its
domain f(D
f
).

CONTINUITY OF ELEMENTARY FUNCTIONS!!!
Definition
The basic elementary functions are: constant, power (incl.
root), exponential, logarithmic, trigonometric and inverse
trigonometric functions.
The elementary functions are basic elementary functions
and all functions built up of a finite combination of basic
elementary functions, arithmetic operations using the four
elementary operations (+ – × ÷). and compositions of
functions.

•Every polynomial w(x) = a
n
x
n
+ a
n-1
x
n-1
+...+a
1
x+a
0
is the elementary function
•Every rational function, i.e. the ratio of two polynomials, is an elementary function
•The equality
implies that g(x) = x
tgx
is an elementary function.
•The equality implies that h(x) = | x | is an elementary function.
)
x
ln(tan
x
)
x
(
g
,
e
)
x
(
f
where
),
x
)(
g
f
(
x
x
x
tan
x
x
2 2

Theorem
Elementary functions are continuous in every interval
contained in their domain.

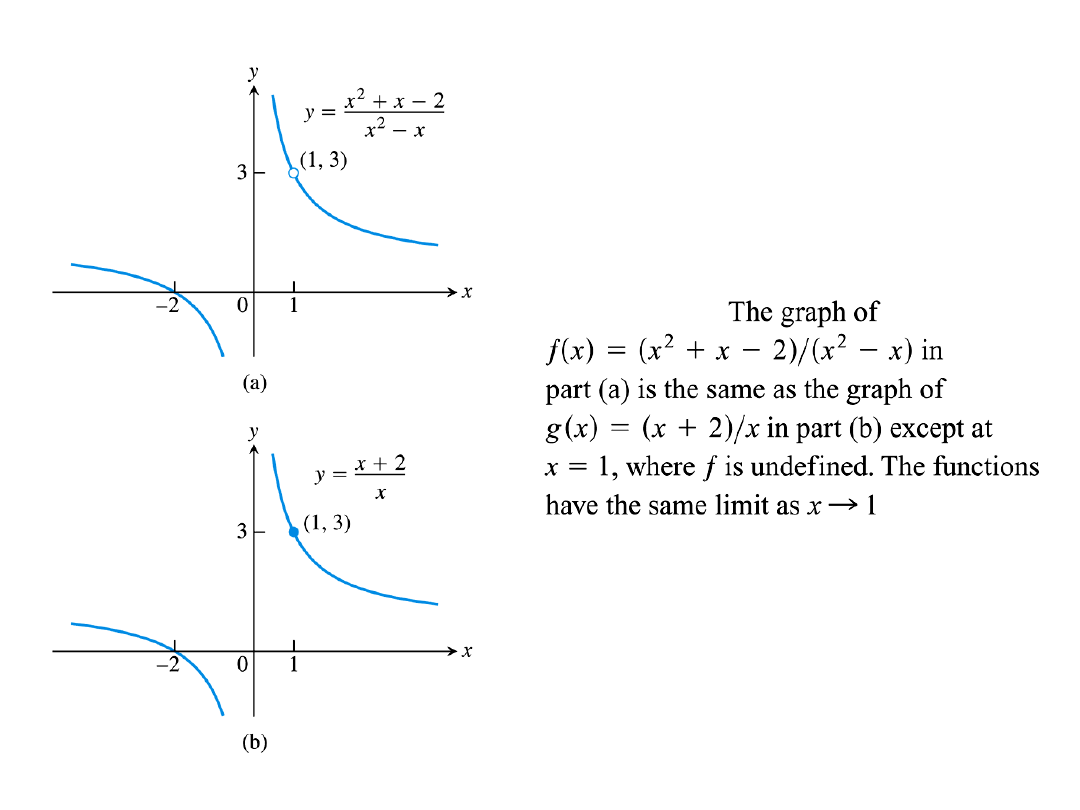

THEOREMS
Theorem (the intermediate value theorem)
If y = f(x) is continuous on [a,b], f (a) ≠ f (b), and u is a
number between f(a) and f(b), then there is at least one c ,
between a < c < b such that
f(c) = u.
x
y
a
c
b
f(a)
f(b)
u
f(x)


Corollary
If a function f is continuous in a closed interval [a, b] and
f (a) f (b) < 0, then there exists a point such
that f (c) = 0.
This corollary is frequently used to demonstrate the
existence of a root of an equation in a given interval.
]
b
,
a
[
c
The theorem represents the idea that the graph of a
continuous function on a closed interval can be drawn without
lifting your pencil from the paper.
c
2
b
y = f(x)
a
=
c
1
max
min
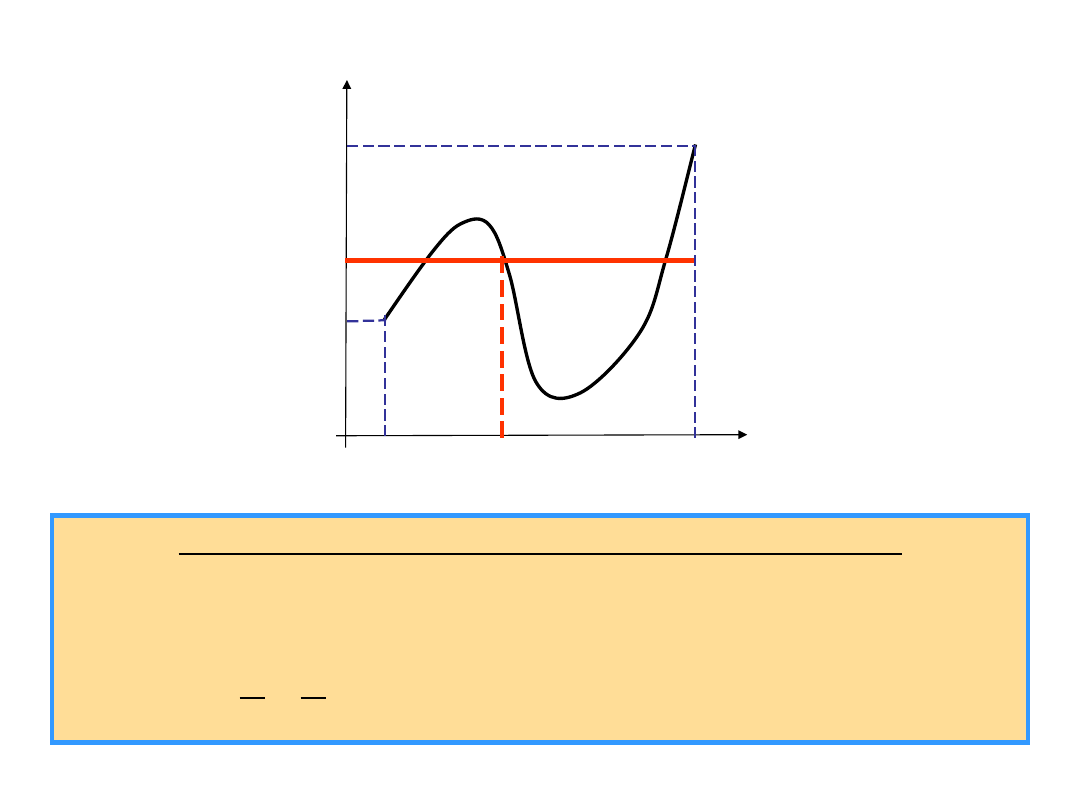
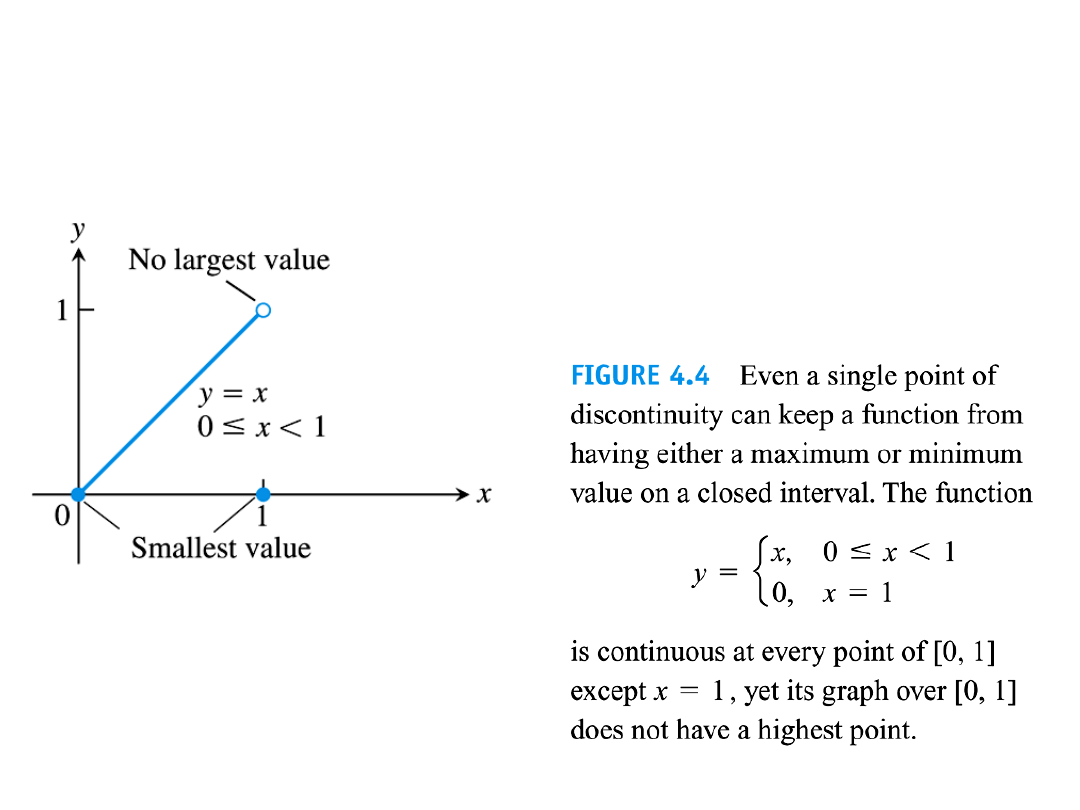
Theorem (Extreme Value Theorem - Weierstrass)
If a function f is continuous on a closed interval [a, b],
then there exists two points c
1
, c
2
in [a,b] such that
f(c
1
) is the global minimum of f on [a,b] i.e. f (c
1
) ≤ f (x)
and such that f( c
2
) is the global maximum of f on
[a,b] i.e. f (x) ≤ f (c
2
)
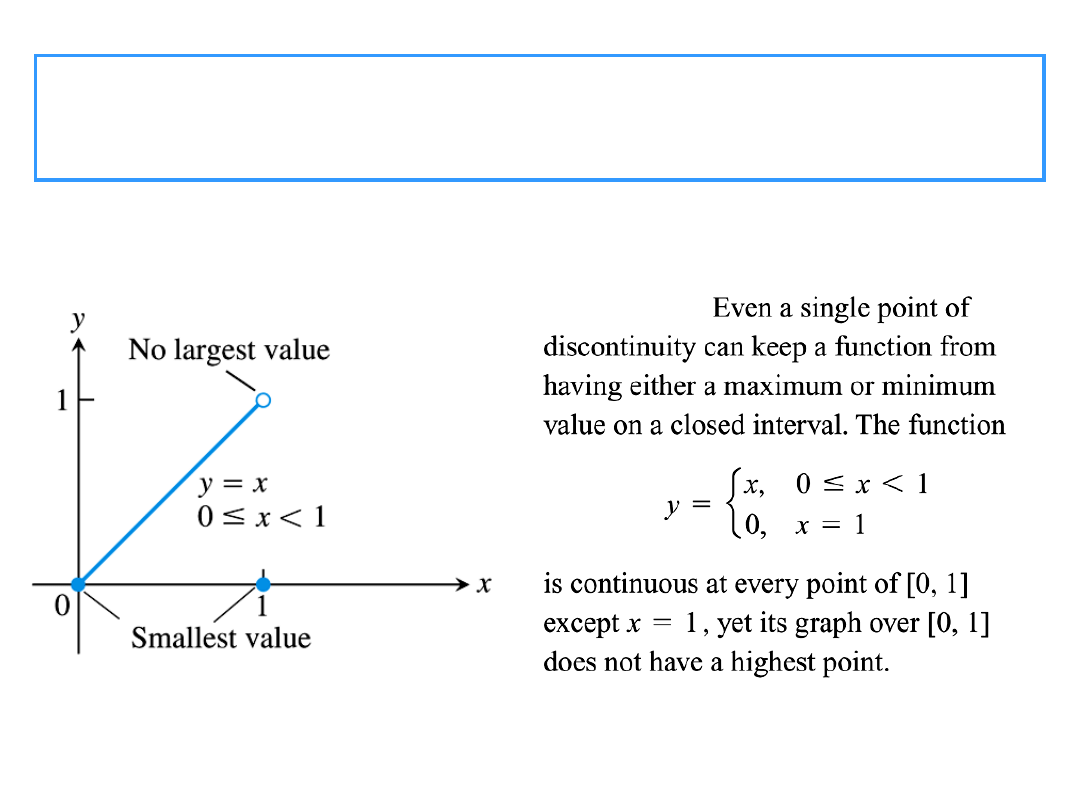
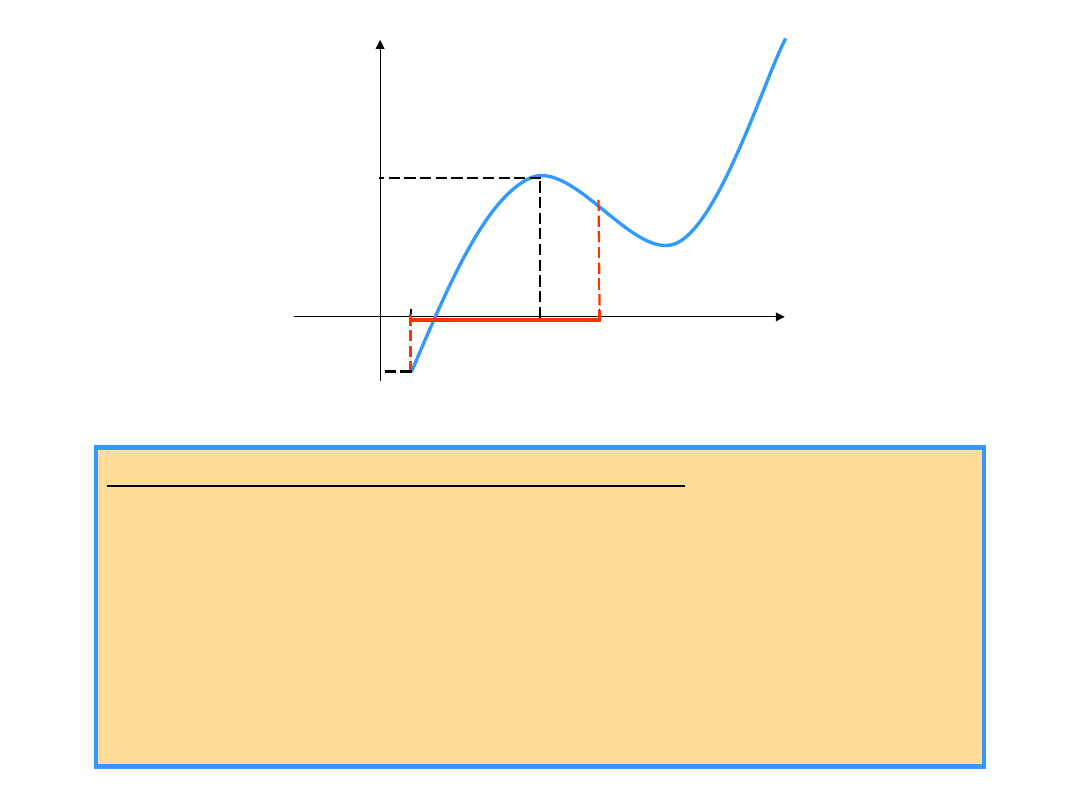
This theorem means, that the range of f ([a, b]) of a function f
continuous in an interval [a, b] contains the smallest element
f(c
1
) and the largest element f(c
2
).
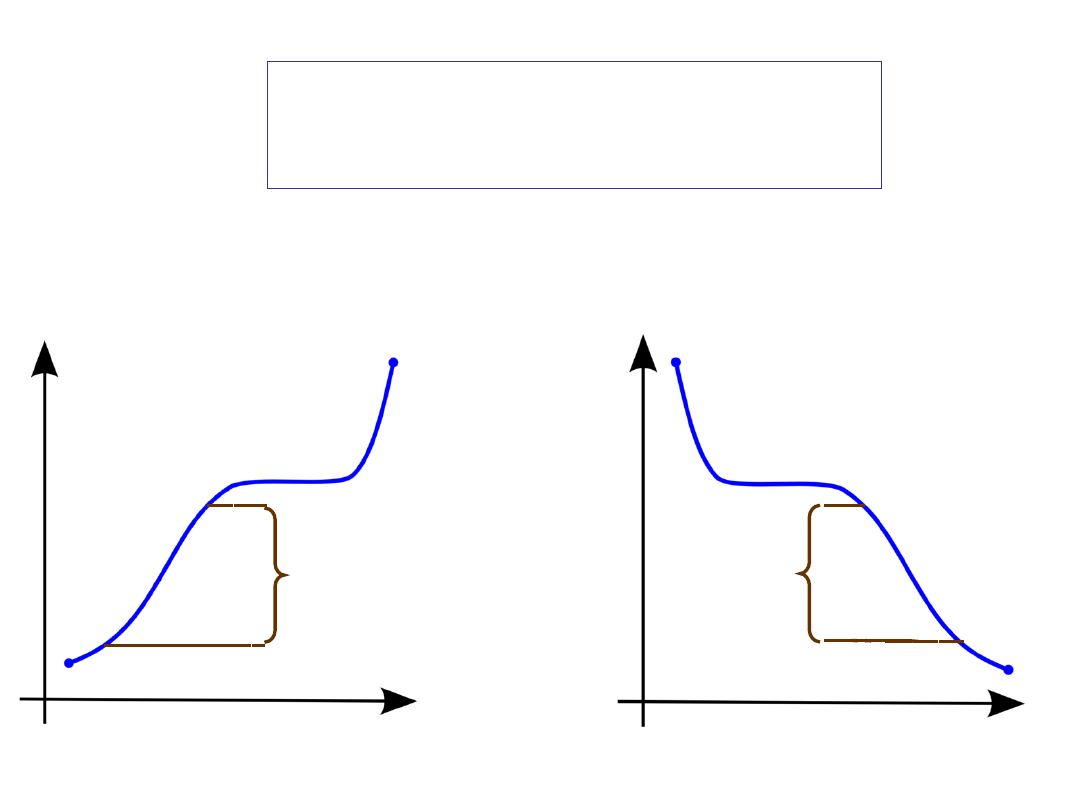
MONOTONE
FUNCTIONS
strictly increasing
strictly decreasing
i
n
c
r
e
a
s
i
n
g
increasing
decreasing

MONOTONE FUNCTIONS
We say that the function f is increasing if whenever t and x
belong to S and for t < x we have f(t) ≤ f(x).
The function f is strictly increasing if whenever t and x
belong to S and
t < x we have f(t) < f(x).
A function that is either increasing or decreasing is said to
be monotone, and a function that is either strictly increasing
or strictly decreasing is said to be strictly monotone.
We say that the function f is decreasing if whenever t and x
belong to S and for t < x we have f(t) < f(x).
The function f is strictly decreasing if whenever t and x
belong to S and
t < x we have f(t) > f(x).
Suppose that S is a set of real numbers and that f : S → R.
We see at once that a strictly monotone function is
always one-one. However, a one-one function does not
have to be strictly monotone.

EXTREMA
MINIMUM, MAXIMUM

A function has a global maximum at x
0
, if f(x
0
) ≥ f(x) for all x from the domain
A function has a global minimum at x
0
, if f(x
0
) < f(x) for all x from the domain

An extremum is a maximum or minimum.
An extremum may be local ( i.e. a relative extremum; an
extremum in a given region which is not the overall maximum
or minimum) or global (absolute).
Extrema: minimum,
maximum
A real-valued function f defined on the real line is said to have
a local maximum at the point x
0
,
if there exists some ε > 0, such that f(x
0
) ≥ f(x) when |x − x
0
| <
ε.
The value of the function at this point is called local maximum
of the function.
A real-valued function f defined on the real line is said to have
a local minimum at the point x
0
,
if there exists some ε > 0, such that f(x
0
) < f(x) when |x − x
0
| <
ε.
The value of the function at this point is called local minimum
of the function.
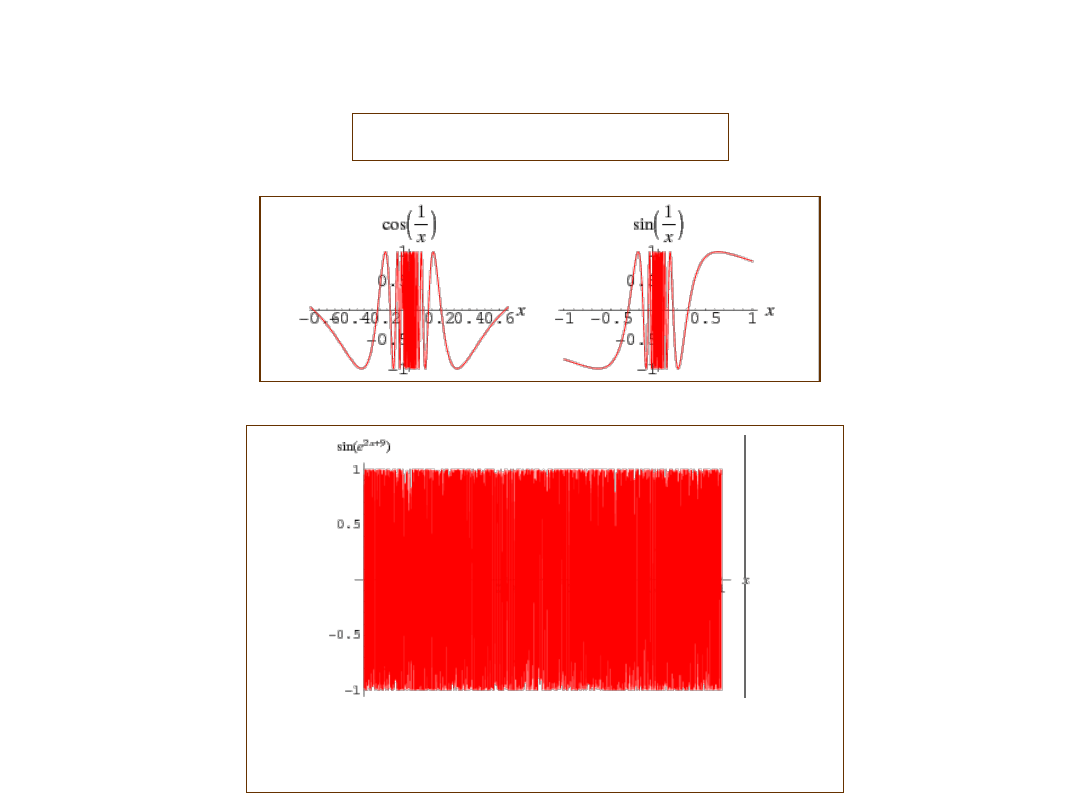
Functions with many extrema can be very dificult to graph.
Pathological Examples
This function f(x) = sin(e
2x+9)
has 16 480 extrema
in the closed interval [0,1]

PECULIAR FUNCTIONS


THE POPCORN FUNCTION
This function was originally defined by the mathematician Johannes Thomae
http://demonstrations.wolfram.com/TheModifiedDirichletFunction/

Theta, little-oh, big-Oh
Θ(.), o(.), O(.),
A theoretical measure of the execution of an algorithm, usually
the time or memory needed, given the problem size n, which is
usually the number of items.
RATE OF GROWTH
A big confusion in notations

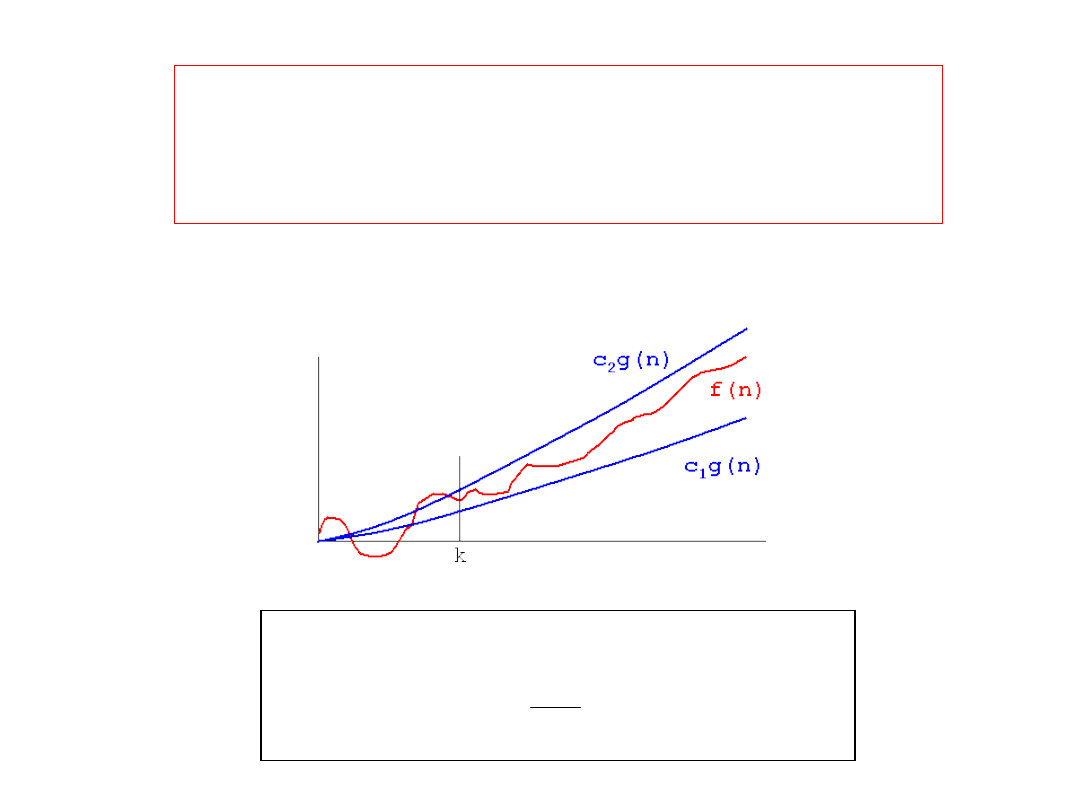
f(n) = Θ (g(n))
means there are positive constants c
1
, c
2
,
and k, such that
0 ≤ c
1
g(n) ≤ f(n) ≤ c
2
g(n)
for all n ≥ k.
The values of c
1
, c
2
, and k must be fixed for the function f and must
not depend on n.
read: „ f is Theta of g ".
)
,
0
(
,
const
)
n
(
g
)
n
(
f
lim
)
n
(
g
(
)
n
(
f
n
Often Θ is confused with O
The same rate of growth
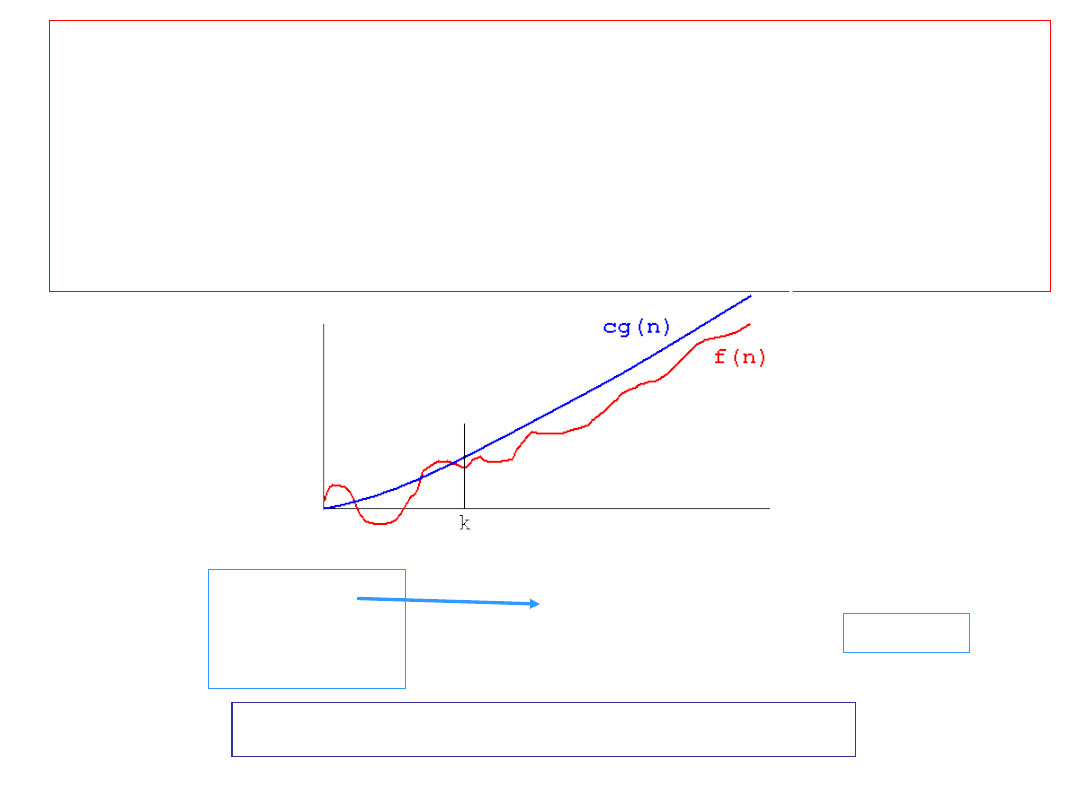
f(n) = O(g(n))
read: „ f is
big Oh of g ".
means there are positive constants c and k, such that
0 ≤ f(n) ≤ cg(n) for all n
≥ k.
The values of c and k must be fixed for the function f and must not
depend on n.
2n
2
= O(n
3
)
(c = 1, k =
2)
not really an equality, should be
)
n
(
O
n
2
3
2
Often big-Oh is treated like Theta
f(n) is at most the order of g(n)

f(n) = o(g(n))
means for all c > 0 there exists some k > 0 such that
0 ≤ f(n) < c g(n) for
all n ≥ k.
The value of k must not depend on n, but may depend on c.
g(n) grows much faster
than f(n).
,
0
)
n
(
g
)
n
(
f
lim
)
n
(
g
(
o
)
n
(
f
n
When the limits exist:
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
Wyszukiwarka
Podobne podstrony:
141 Future Perfect Continuous
CALC1 L 11 12 Differenial Equations
Symmetrical components method continued
PRESENT CONTINUOUS, Dokumenty zawodowe, Czasy gramatyczne
present i past simple i continuous
tezowanie continental?n
1 Continuity
present continuous Graded Grammar
PAST PERFECT CONTINUOUS, Dokumenty zawodowe, Czasy gramatyczne
present continuous verbs
present simple or present continuous
Present Simple vs Present Continuous ćwiczenia4
PPAP Manual Continental
Present Continuous Budowa
Future Continuous Użycie
present i past simple i continuous odpowiedzi
Past Continuous Forma
Uses of the Present Continuous
present continuous
więcej podobnych podstron