Momenty bezwładności

figur płaskich

Przekroje poprzeczne prętów, wałów i
belek (figury płaskie) charakteryzują się
następującymi parametrami:
• polem powierzchni przekroju [mm

2

, cm

2

,

m

2

],

• położeniem środka ciężkości przekroju,
[mm],
• momentami statycznymi [cm

3

, m

3

],

• momentami bezwładności [cm

4

, m

4

].

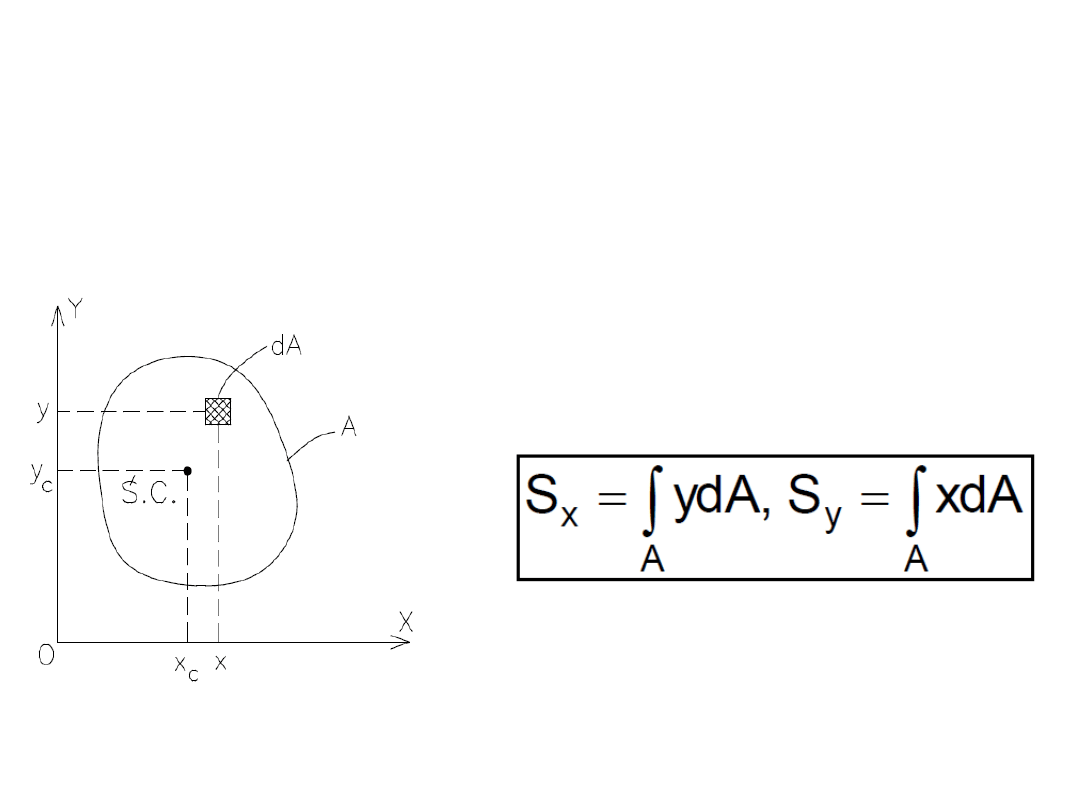
Moment statyczny

• Definicja momentu

statycznego w
układzie osi X i Y:

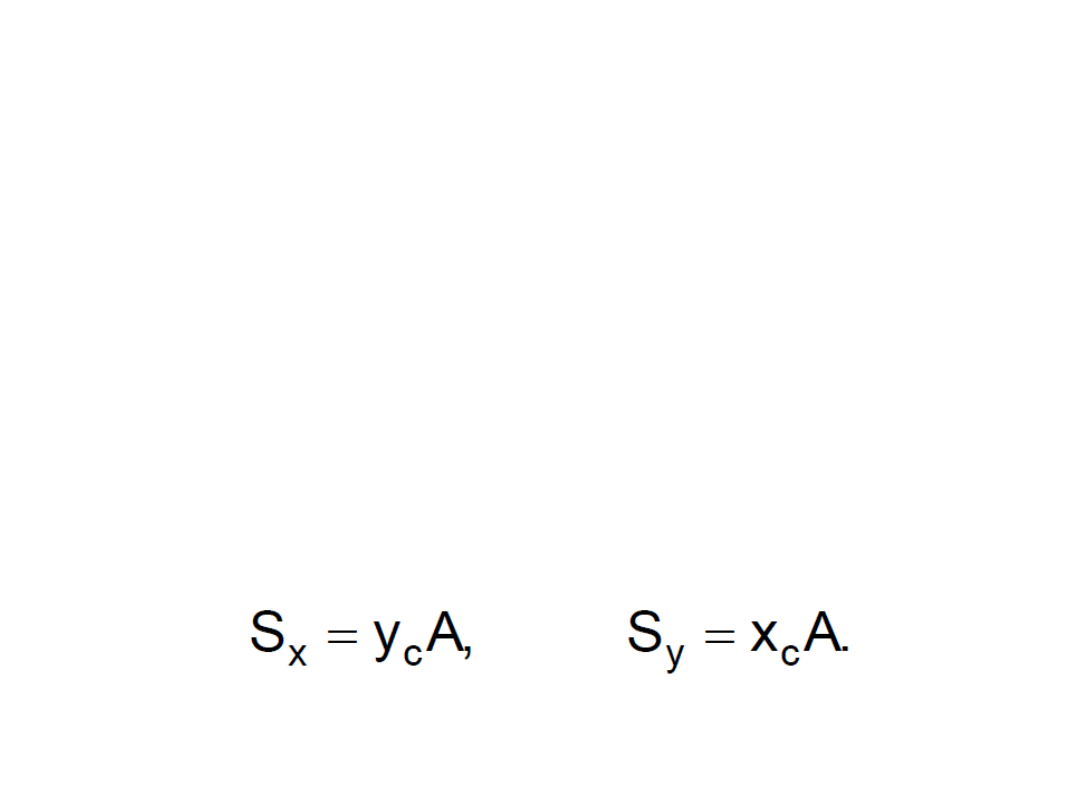
• W zależności od położenia przekroju

względem osi układu współrzędnych
momenty statyczne mogą przyjmować
wartości dodatnie i ujemne.

• Wykorzystując znane ze statyki pojęcie

środka sił, dla środka ciężkości można
napisać:

Współrzędne środka ciężkości

przekroju

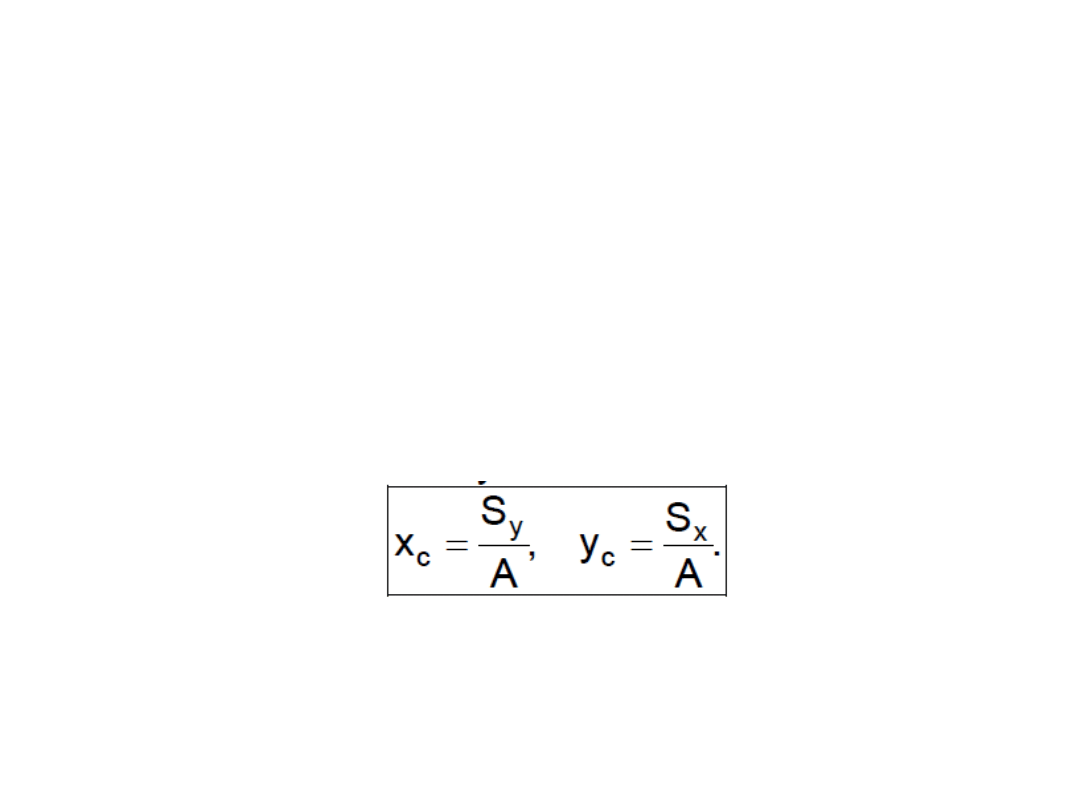
• Korzystając z tych zależności,

współrzędne środka ciężkości figury
płaskiej można obliczyć ze wzoru:

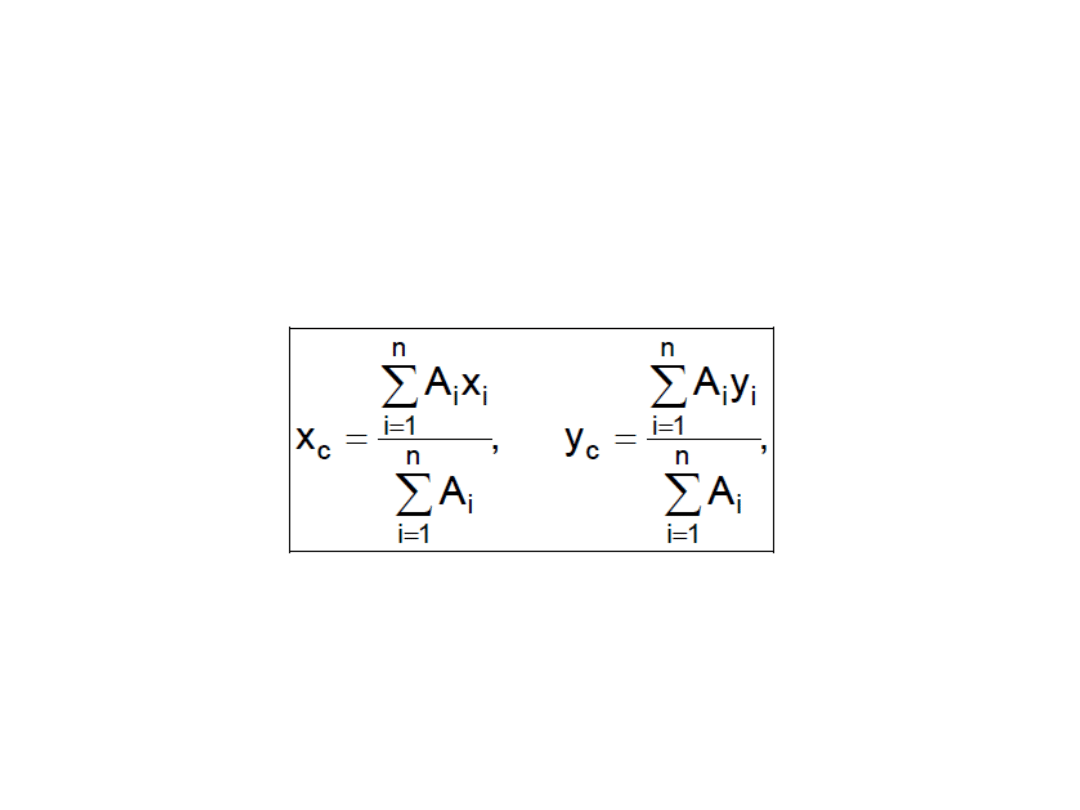
• Środek ciężkości przekrojów

złożonych podział przekroju na
figury proste.

Ai – pola powierzchni figur prostych,
xi, yi – współrzędne środków ciężkości
poszczególnych figur prostych.

PRZYKŁAD

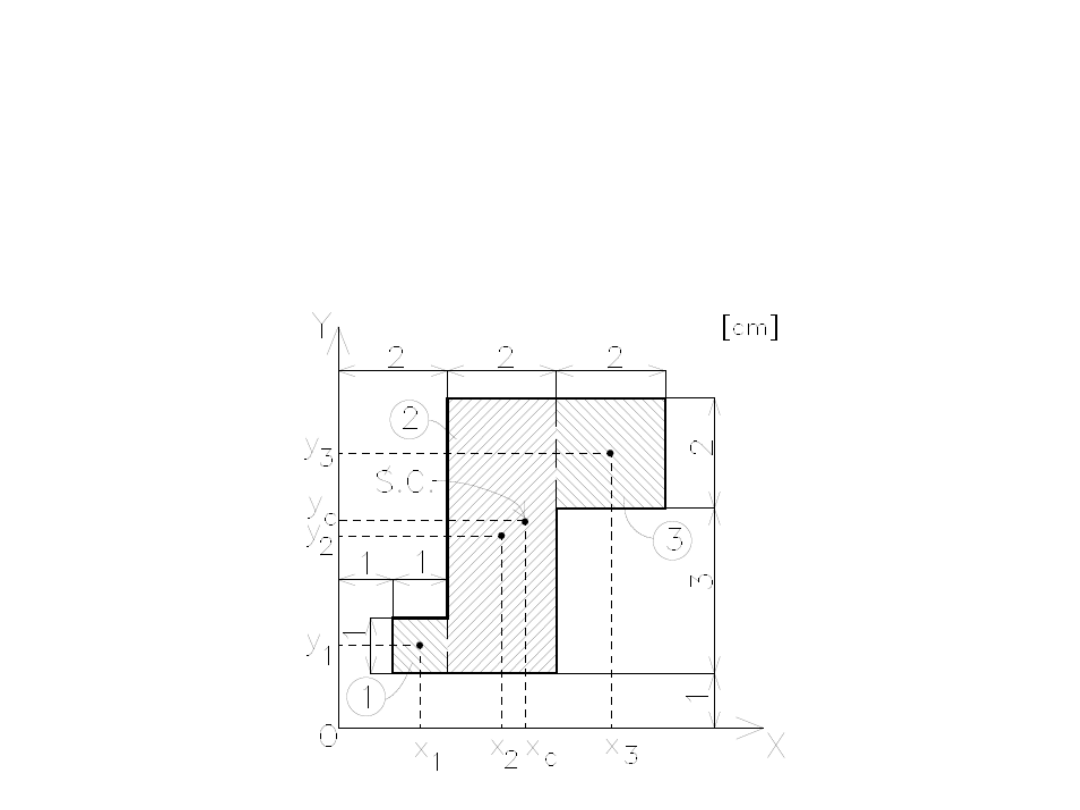
• Określić położenie środka ciężkości fi-

gury przedstawionej na rysunku.

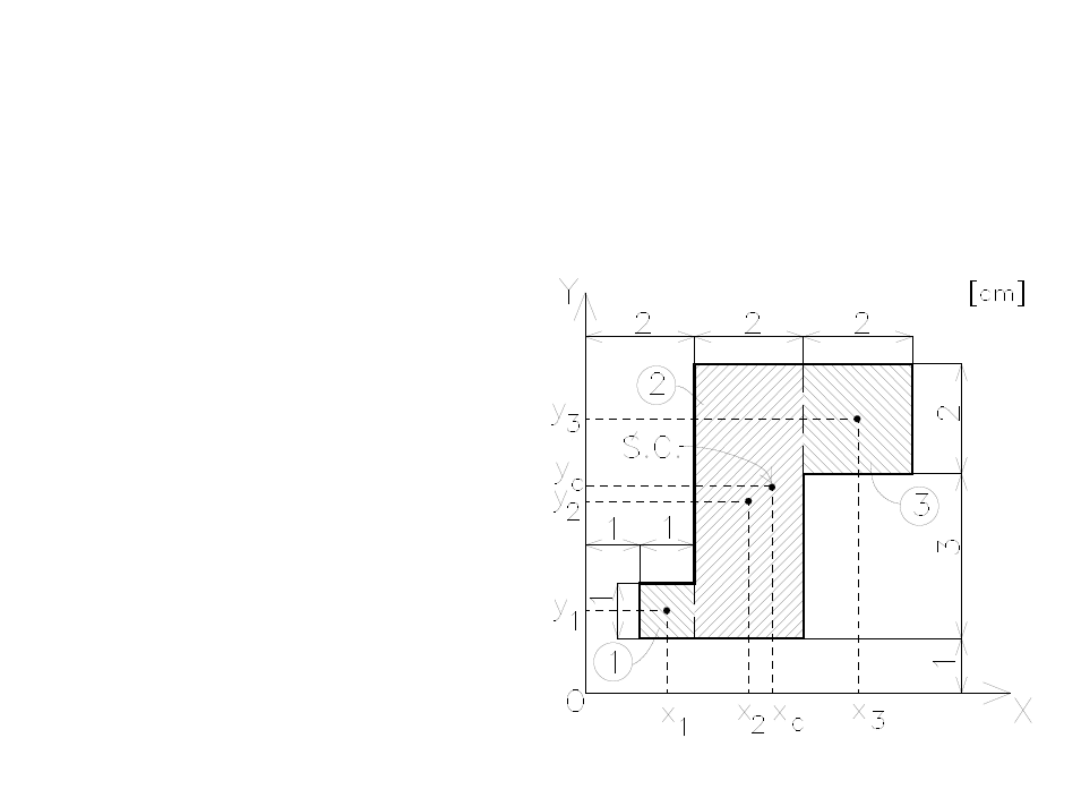
• Przekrój podzielono

na trzy prostokąty o
następujących
polach powierzchni:

• A1 = 1 x 1 = 1 cm

2

,

• A2 = 2 x 5 = 10

cm

2

,

• A3 = 2 x 2 = 4 cm

2

.

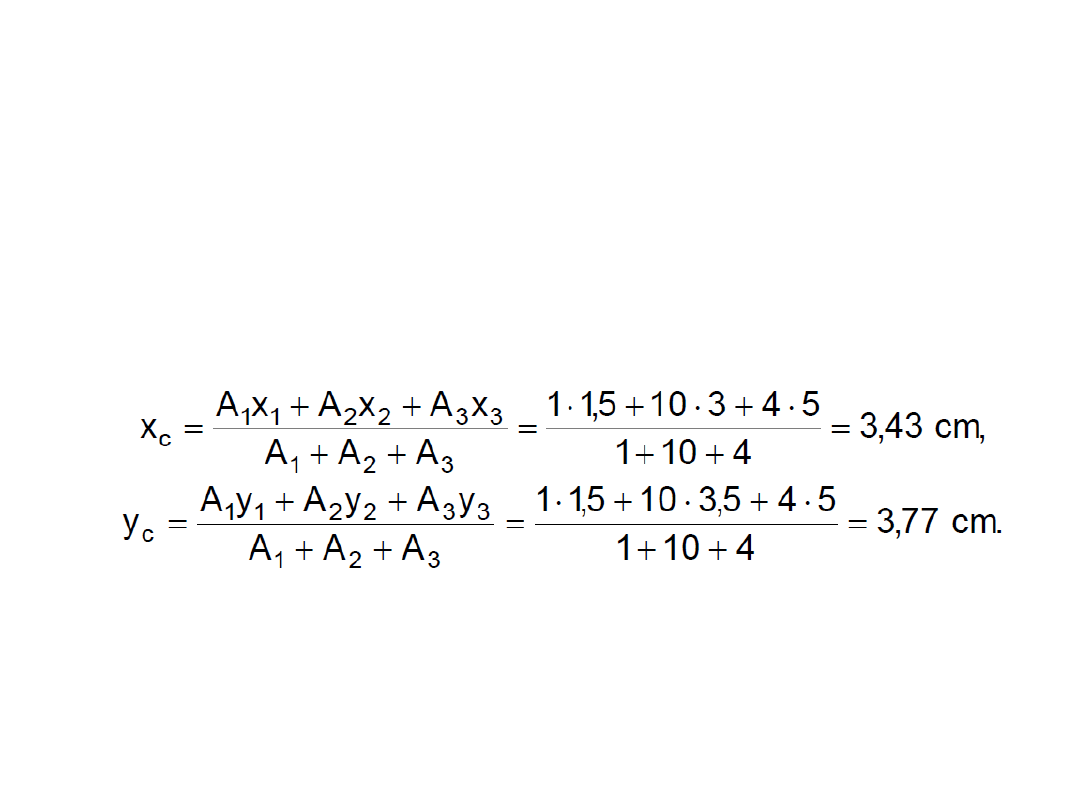
• Współrzędne środka ciężkości całej

figury wynoszą

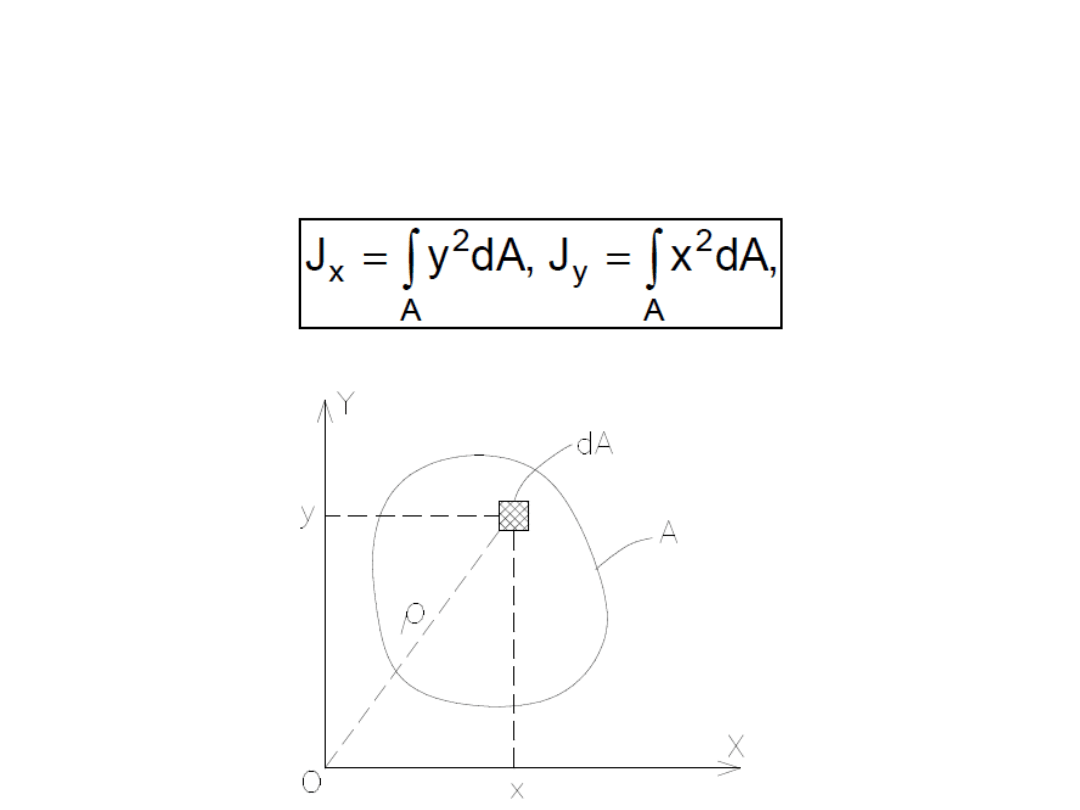
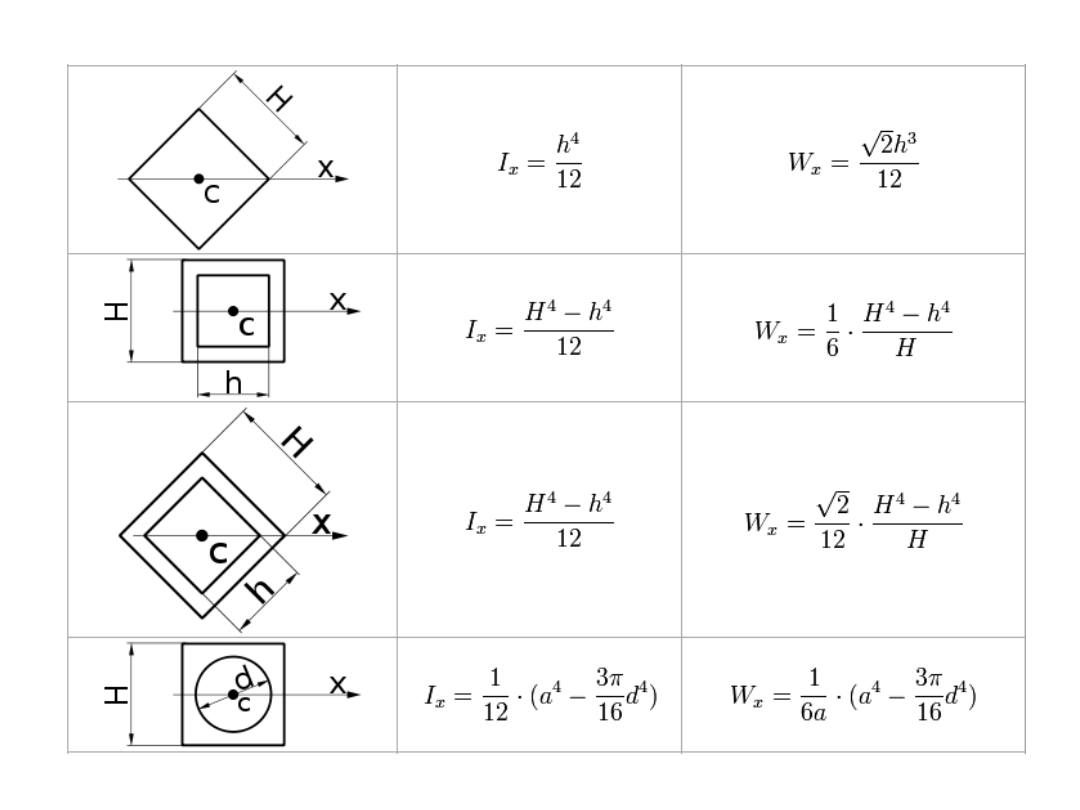
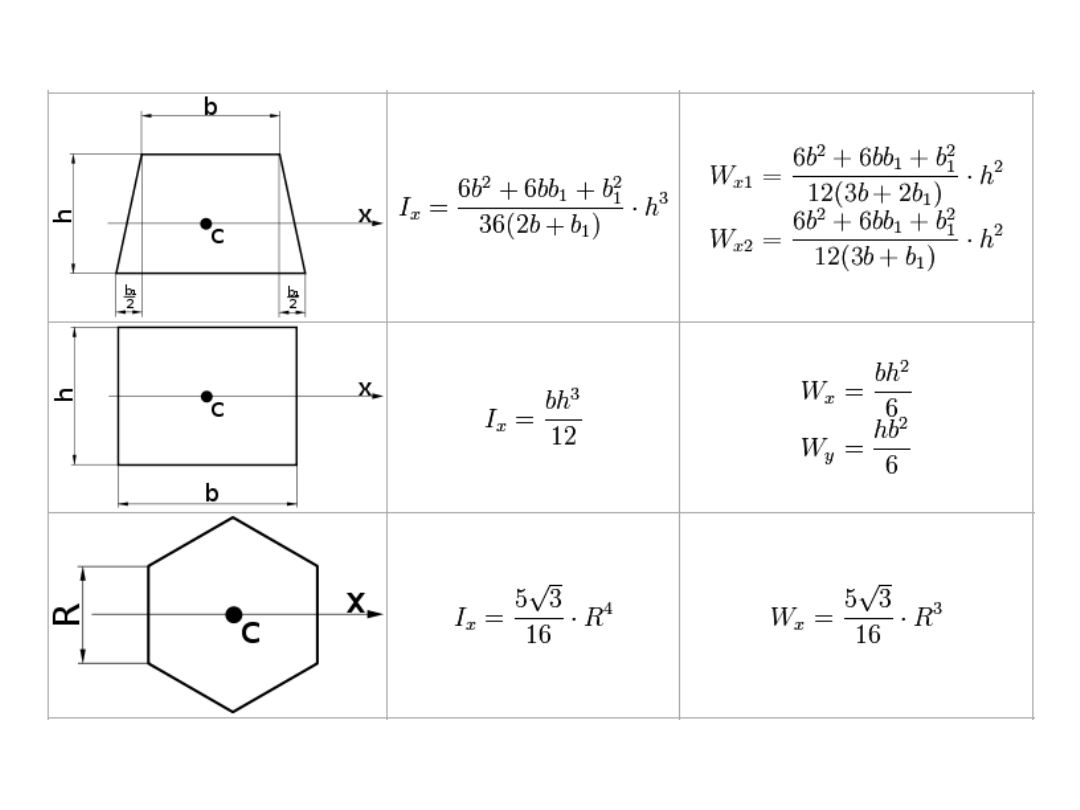
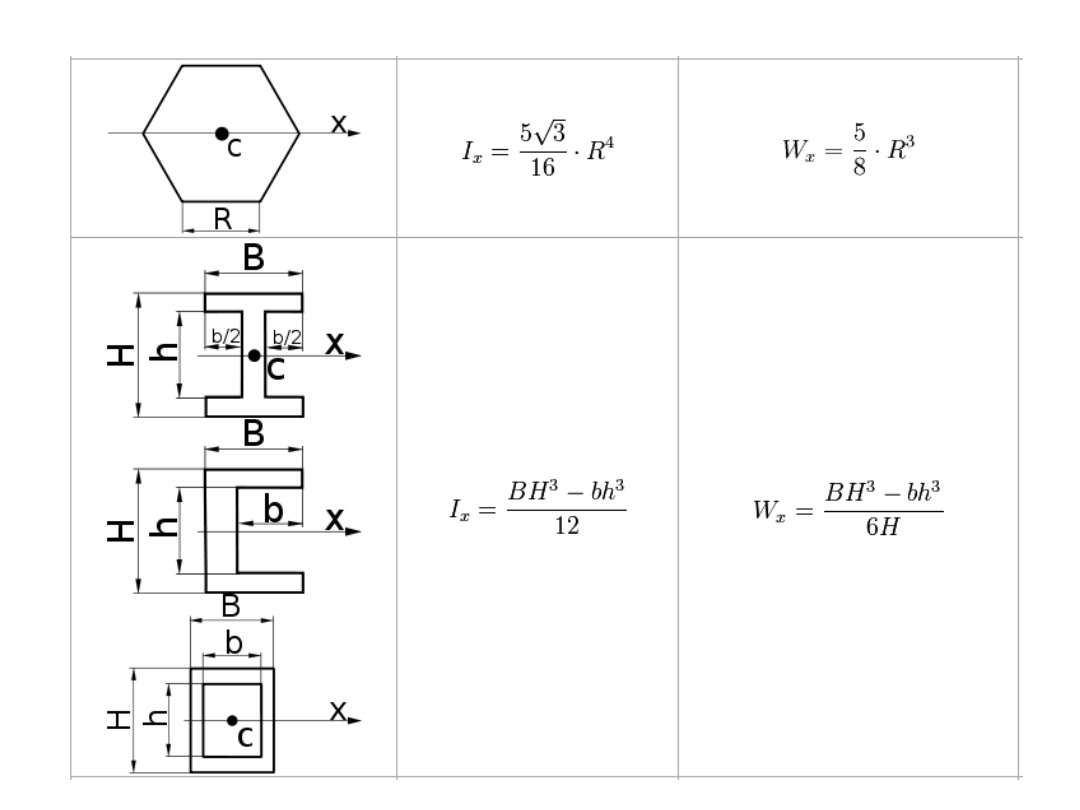
Momenty bezwładności

• osiowe momenty bezwładności

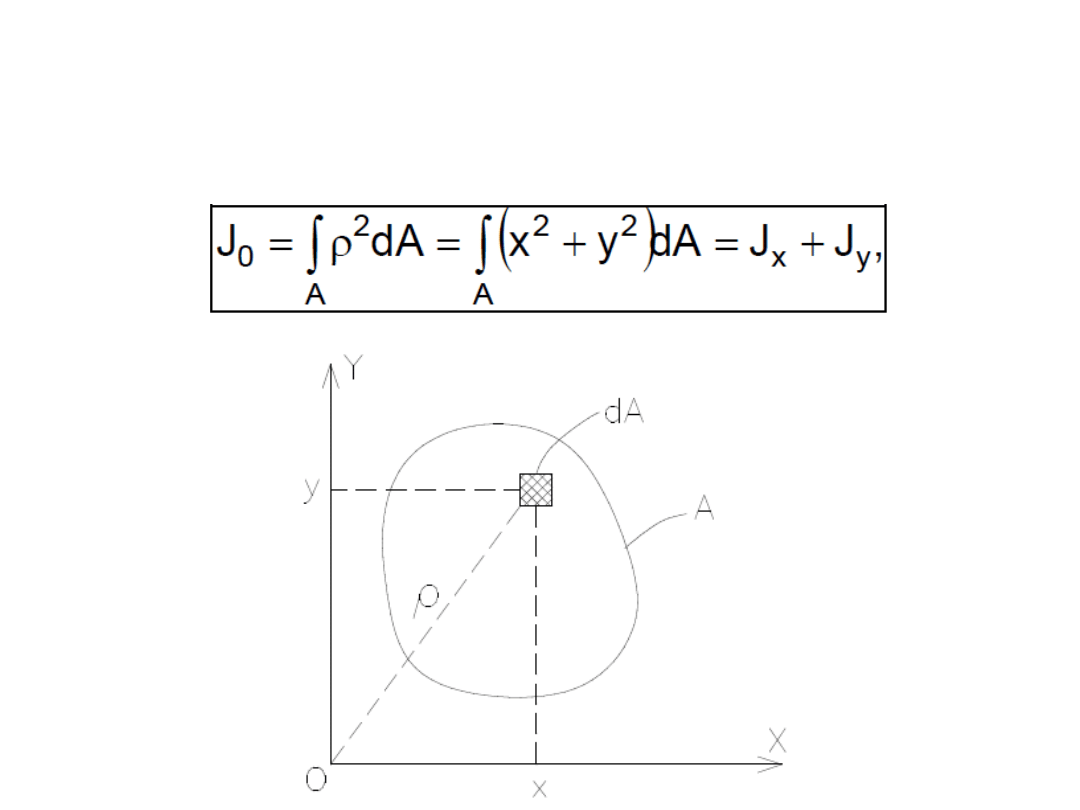
• biegunowy moment bezwładności

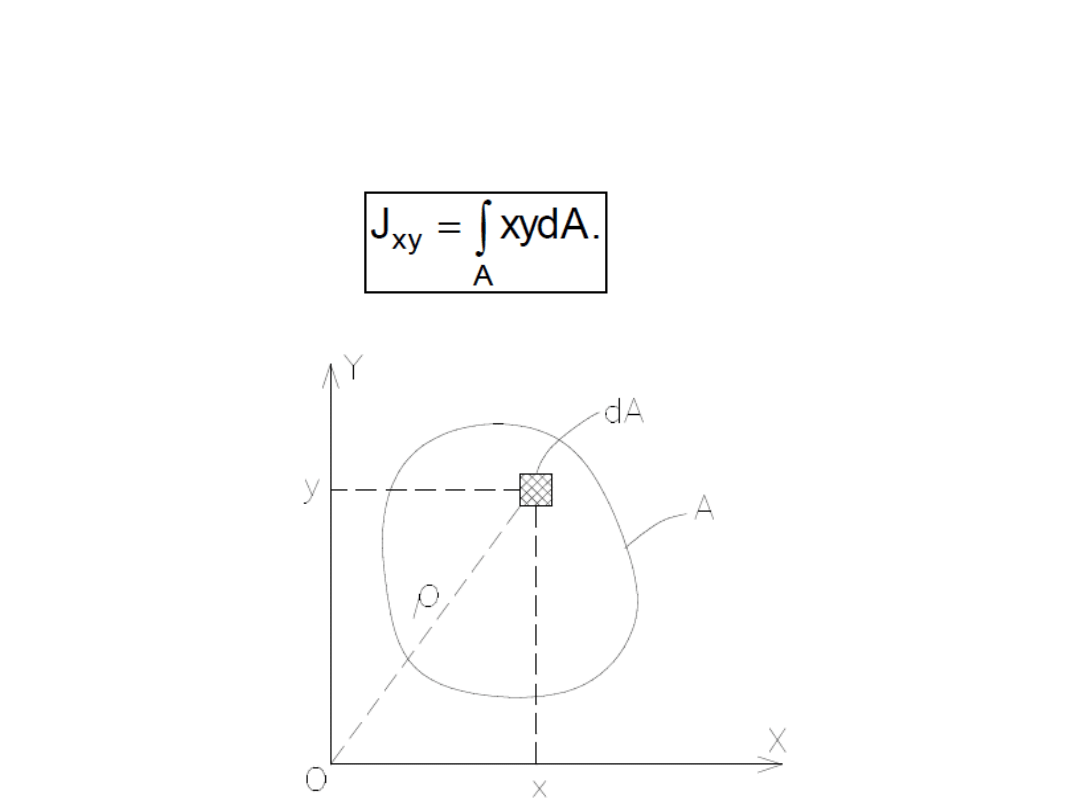
• moment dewiacyjny (zboczenia, odśrodkowy)

• Momenty osiowe oraz moment

biegunowy są

zawsze dodatnie

,

natomiast moment dewiacyjny
może być

dodatni lub ujemny

• Momenty bezwładności figur złożonych

są sumą momentów bezwładności
prostych figur składowych.

• Figura złożona może składać się z figur

„pełnych” oraz „pustych”.

• Przy sumowaniu momentów

bezwładności figury „puste” uważa się
za figury z ujemnymi polami
powierzchni.

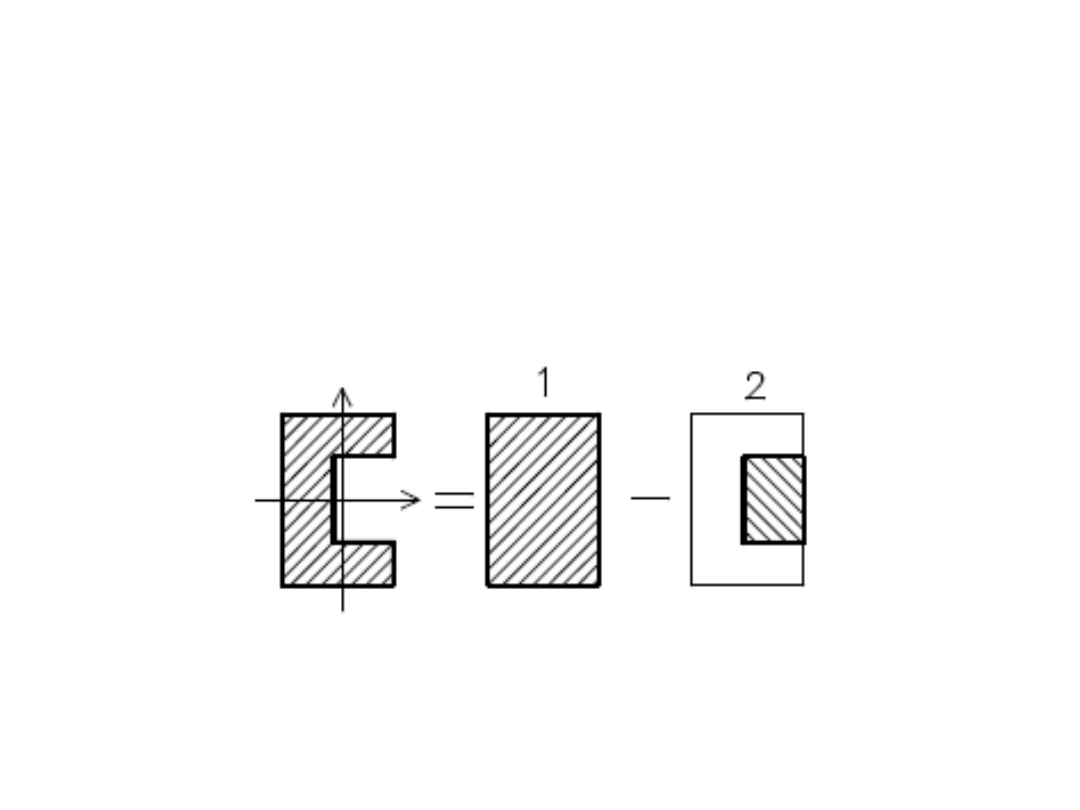
PRZYKŁAD

• Figury złożone przedstawione na

rysunku podzielić na figury proste.

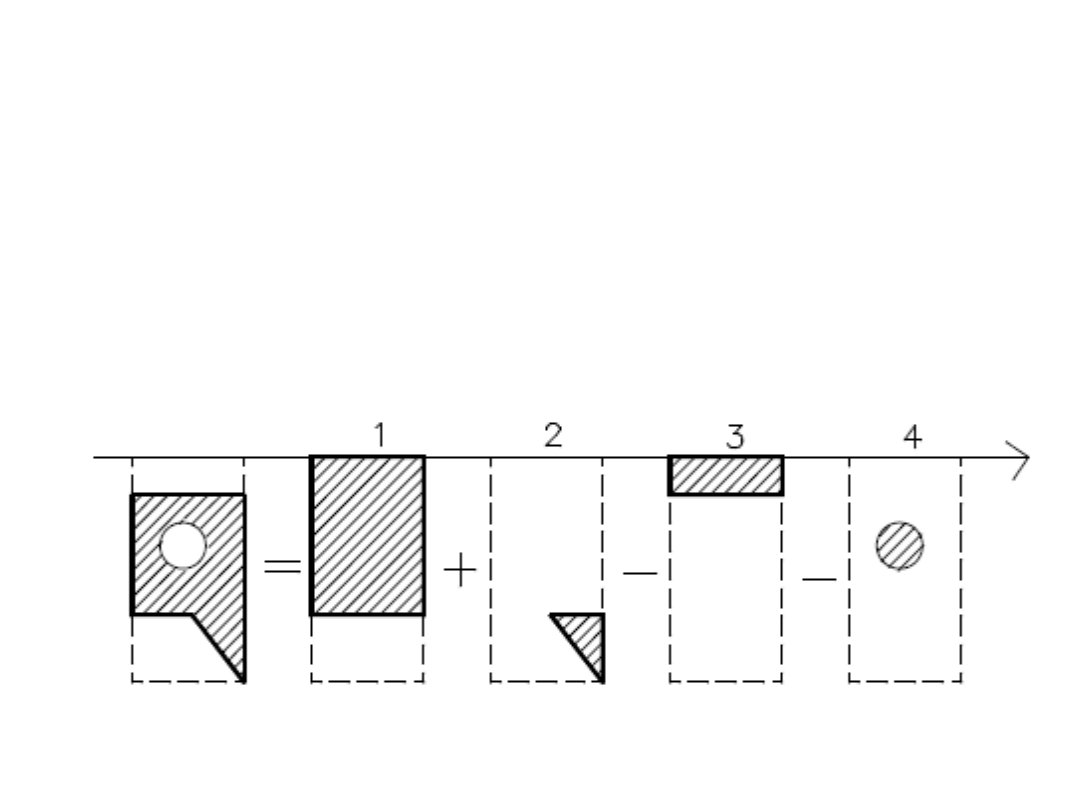
PRZYKŁAD

• Figury złożone przedstawione na

rysunku podzielić na figury proste.

Twierdzenie Steinera

• Twierdzenie Steinera umożliwia obliczanie

momentów bezwładności figur płaskich

względem osi równolegle przesuniętych

w stosunku do osi centralnych (osi

przechodzących przez środek

ciężkości przekroju).

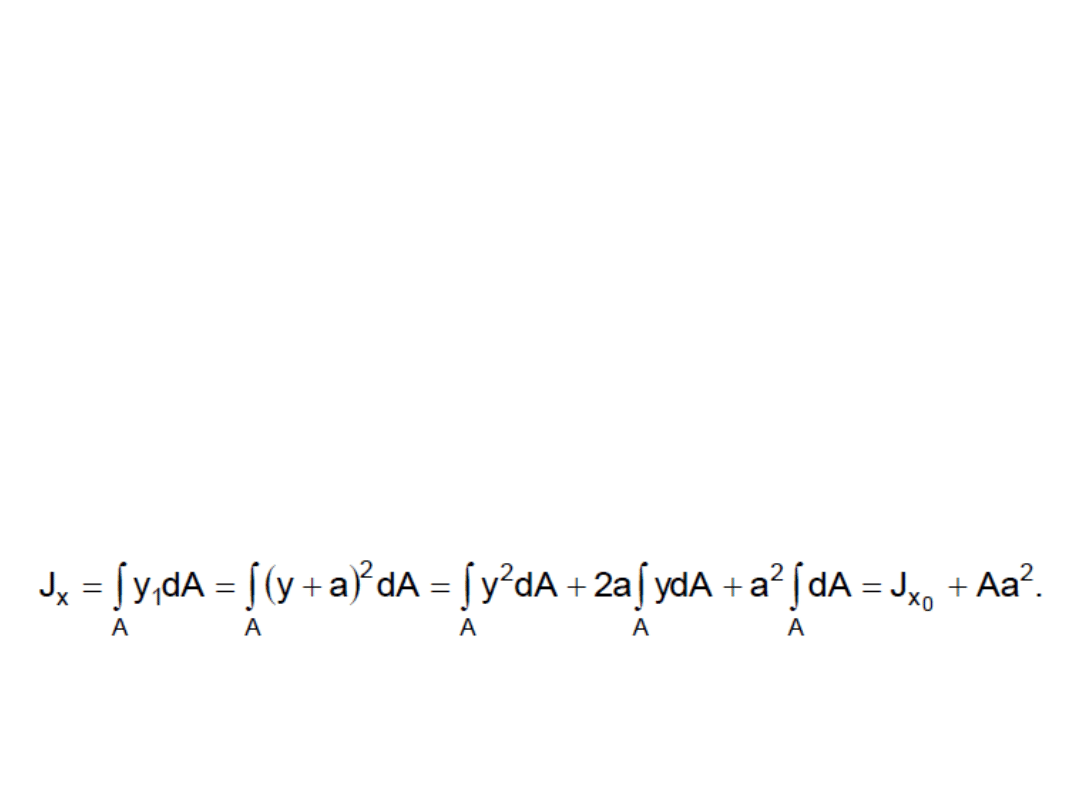
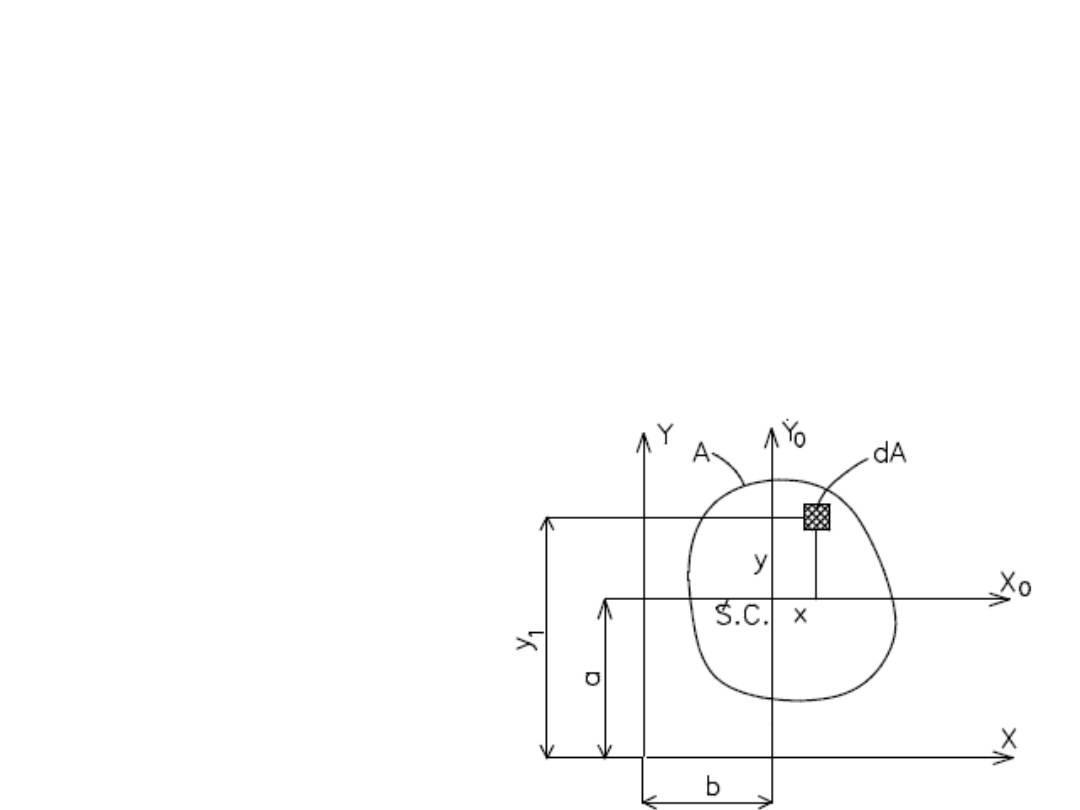
• Dla figury płaskiej o powierzchni A,

obliczyć momenty bezwładności
względem osi X–Y, równolegle
przesuniętych w stosunku do osi
centralnych (środkowych) X

0

–Y

0

o

odcinki a i b.

• Na podstawie definicji momentu

bezwładności moment osiowy
względem osi X dla y

1

= y + a

wyraża wzór:

• Osiowy moment bezwładności figury

płaskiej względem osi równoległej
odległej od środka ciężkości o określoną
wartość jest równy momentowi
względem osi równoległej
przechodzącej przez środek ciężkości
figury, powiększonemu o iloczyn
powierzchni figury i kwadratu odległości
między osiami.

• Moment dewiacyjny figury płaskiej

względem osi równolegle
przesuniętych jest równy momentowi
dewiacyjnemu względem osi
centralnych, powiększonemu o
iloczyn powierzchni i obu składowych
równoległego przesunięcia.

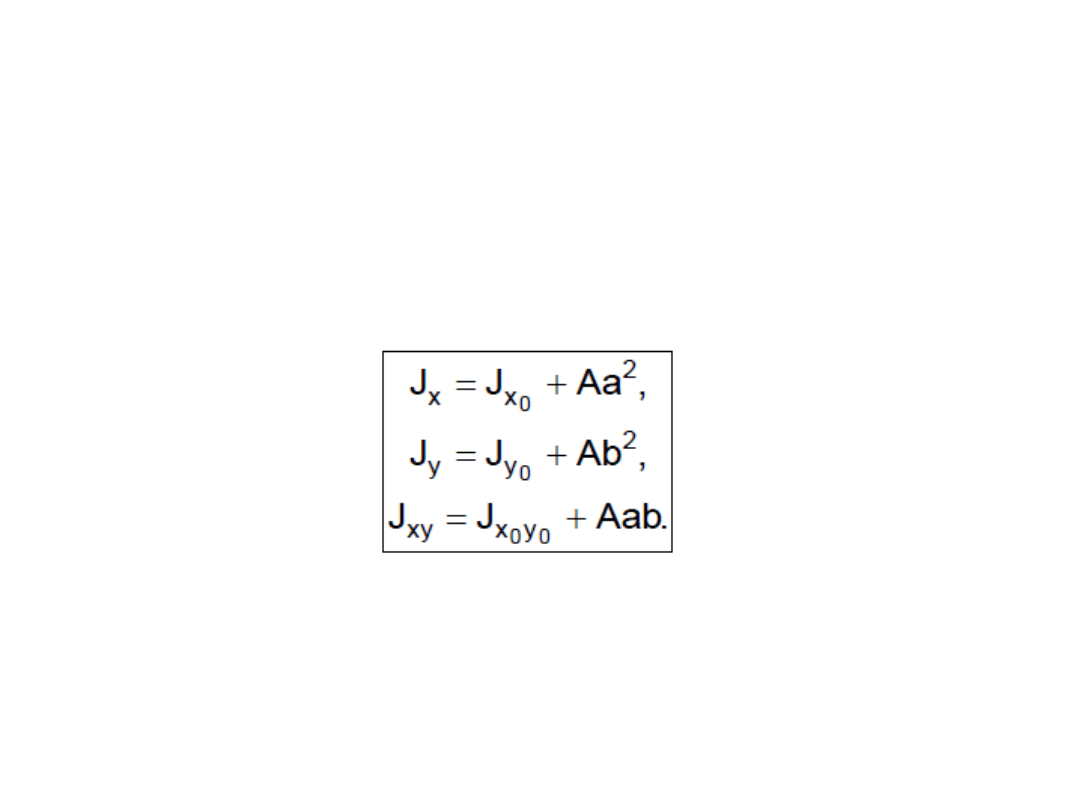
• Twierdzenie Steinera ma następująca

postać matematyczną: